Как найти диагональ куба объяснение

Куб или как его еще называют гексаэдр – это правильный многогранник, каждая из граней которого имеет форму квадрата. Куб – это частный случай призмы и параллелепипеда.

Разные дисциплины используют значение этого термина по отношению к различным свойствам геометрического прототипа. Например, в аналитике применяют аналитические многомерные кубы, которые позволяют наглядно сопоставить данные из разных таблиц.

Свойства куба

• В куб можно вписать тетраэдр двумя вариантами, причем вершины тетраэдра, а их четыре, будут совпадать с четырьмя вершинами куба. Все шесть ребер тетраэдра будут располагаться на всех шести гранях куба и будут равны диагонали грани квадрата.
• Четыре сечения куба это правильные шестиугольники, они проходят по центру куба перпендикулярно четырем диагоналям.
• В куб вписывается октаэдр, причем все шесть вершин октаэдра совместятся с центрами шести граней куба.
• Куб вписывается в октаэдр, причем все восемь вершин куба расположатся в центрах восьми граней октаэдра.
• В куб можно вписать икосаэдр, так, что шесть взаимно параллельных ребер икосаэдра расположатся на шести гранях куба, остальные двадцать четыре ребра внутри куба, все 12 вершин икосаэдра лягут по шести граням куба.

Формулы для куба

• Поверхность куба: A = 6*a2
• Объем куба: V = a3
• Диагональ куба: d = a*√3

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

• Вершины куба – это точки, являющиеся вершинами его граней.
  Всего их 8: A, B, C, D, A₁, B₁, C₁ и D₁.
• Ребра куба – это стороны его граней.
  Всего их 12: AB, BC, CD, AD, AA₁, BB₁, CC₁, DD₁, A₁B₁, B₁C₁, C₁D₁ и A₁D₁.
• Грани куба – это квадраты, из которого состоит фигура.
  Всего их 6: ABCD, A₁B₁C₁D₁, AA₁B₁B, BB₁C₁C, CC₁D₁D и AA₁D₁D.

Примечание: куб является частным случаем параллелепипеда или призмы.

Свойства куба

Свойство 1

Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:

• ABCD || A₁B₁C₁D₁
• AA₁B₁B || CC₁D₁D
• BB₁C₁C || AA₁D₁D

Свойство 2

Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

• AC₁ = BD₁ = A₁C = B₁D (диагонали куба).
• О – точка пересечения диагоналей:
  AO = OC₁ = BO = OD₁ = A₁O = OC = B₁O = OD.

Свойство 3

Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA₁B₁B является прямым.

Формулы для куба

Примем следующие обозначения, которые будут использоваться далее:

• a – ребро куба;
• d – диагональ куба или его грани.

Диагональ

Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.

Диагональ грани

Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

Периметр ребер

Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.

Объем

Объем куба равен длине его ребра, возведенной в куб.

Радиус описанного вокруг шара

Радиус шара, описанного около куба, равняется половине его диагонали.

Радиус вписанного шара

Радиус вписанного в куб шара равен половине длины его ребра.

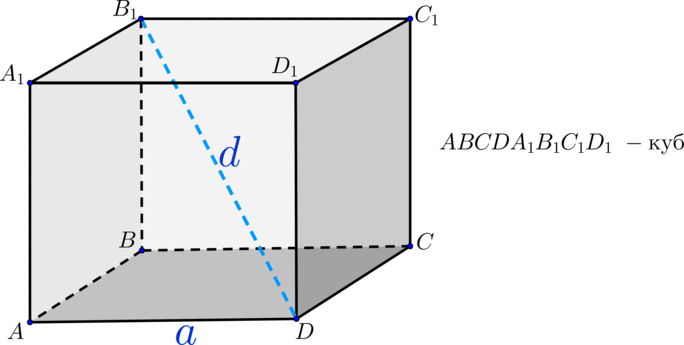
Факт 2.
(bullet) Если сфера вписана в куб (то есть касается всех его граней), то ее радиус равен (0,5a), где (a) – ребро куба.
(bullet) Если сфера описана около куба (то есть все вершины куба лежат на сфере), то ее радиус равен (0,5d), где (d) – диагональ куба.
(bullet) Центр сферы, вписанной в куб или описанной около куба, лежит в точке пересечения диагоналей куба.

A cube is defined as a 3D solid object which has six square faces and all sides equal to each other. It is one of the five platonic solids and is also known as a regular hexahedron. Six square faces, eight vertices, and twelve edges make up the cube. Its length, breadth and height all are same as it is a square with all sides of the same length. The common line between any two faces of a cube is called its edge. It acts as a boundary line between two faces.

Diagonal of a cube

A cube’s diagonal is the line segment connecting any two non-adjacent vertices of the cube. There are two types of cube diagonals, that is, face diagonal and body diagonal. A face diagonal joins two non-adjacent vertices via a single face while a body diagonal does the same by passing through the body of the cube. There are 12 face diagonals and 4 body diagonals possible inside a cube.

Face diagonal formula

Length of face diagonal of cube = √2a

where,

a is the side length of cube.

Body diagonal formula

Length of body diagonal of cube = √3a

where,

a is the side length of cube.

Derivation

Suppose we have a cube with side length a, face diagonal d and body diagonal D.

Now it is known that face diagonal is the hypotenuse of the right triangle it forms with two side lengths. 

So, using Pythagoras theorem we get,

d² = a² + a²

d² = 2a²

d = √2a   …….. (1)

Also, the face diagonal and one side length form a right triangle with body diagonal as hypotenuse.

Again using Pythagoras theorem we get,

D² = a² + d²

Using (1) we get,

D² = a² + (√2a)²

D² = a² + 2a²

D² = 3a²

D = √3a

This derives the formulas for face diagonals and body diagonals of a cube.

Sample Problems

Problem 1. Calculate the face diagonal of a cube of side length 2 m.

Solution:

We have,

a = 2

Using the formula we get,

d = √2a

= √2 (2)

= (1.414) (2)

= 2.83 m

Problem 2. Calculate the face diagonal of a cube of side length 5 m.

Solution:

We have,

a = 5

Using the formula we get,

d = √2a

= √2 (5)

= (1.414) (5)

= 7.07 m

Problem 3. Calculate the body diagonal of a cube of side length 3 m.

Solution:

We have,

a = 3

Using the formula we get,

D = √3a

= √3 (3)

= (1.732) (3)

= 5.196 m

Problem 4. Calculate the body diagonal of a cube of side length 7 m.

Solution:

We have,

a = 7

Using the formula we get,

D = √3a

= √3 (7)

= (1.732) (7)

= 12.12 m

Problem 5. Calculate the side length if the face diagonal of a cube is 6 m.

Solution:

We have,

d = 6

Using the formula we get,

d = √2a

=> a = d/√2

= 6/√2

= 4.24 m

Problem 6. Calculate the side length if the body diagonal of a cube is 13√3 m.

Solution:

We have,

D = 13√3

Using the formula we get,

D = √3a

=> a = D/√3

= 13√3/√3

= 13 m

Problem 7. Calculate the body diagonal of a cube if its face diagonal is 9√2 m.

Solution:

We have,

d = 9√2

Find the side length.

d = √2a

=> a = d/√2

= 9√2/√2

= 9 m

Now using the formula we get,

D = √3a

= √3 (9)

= 15.58 m

Last Updated :
15 May, 2022

Like Article

Save Article