Формула полезной мощности в физике
Формула полезной мощности
Определение и формула полезной мощности
Определение
Мощность – это физическая величина, которую использует как основную характеристику любого устройства, которое применяют
для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.
Отношение работы ($Delta A$) к промежутку времени за которое она выполнена ($Delta t$) называют средней мощностью ($leftlangle Prightrangle $) за это время:
[leftlangle Prightrangle =frac{Delta A}{Delta t}left(1right).]
Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $Delta tto 0$:
[P={mathop{lim }_{Delta tto 0} frac{Delta A}{Delta t} }=A'(t)left(2right).]
Приняв во внимание, что:
[Delta A=overline{F}cdot Delta overline{r }left(3right),]
где $Delta overline{r }$ – перемещение тела под действием силы $overline{F}$, в выражении (2) имеем:
[P={mathop{lim }_{Delta tto 0} left(frac{overline{F}cdot Delta overline{r }}{Delta t}right) }=overline{F}{mathop{lim }_{Delta tto 0} left(frac{Delta overline{r }}{Delta t}right)= }overline{F}cdot overline{v}left(4right),]
где $ overline{v}-$ мгновенная скорость.
Коэффициент полезного действия
При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($eta $), при этом:
[eta =frac{P_p}{P}left(5right),]
где $P_p$ – полезная мощность; $P$ – затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:
[P_p=eta P left(6right).]
Формула полезной мощности источника тока
Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:
[P=?I left(7right),]
где $?$ – ЭДС источника тока; $I$ – сила тока. При этом $P$ – полная мощность цепи.
Обозначим $U$ – напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:
[P=?I=UI+I^2r=P_p+P_0left(8right),]
где $P_p=UI=I^2R=frac{U^2}{R}(9)$ – полезная мощность; $P_0=I^2r$ – мощность потерь. При этом КПД источника определяют как:
[eta =frac{P_p}{P_p+P_0}left(9right).]
Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50% общей мощности.
При коротком замыкании (когда $Rto 0;;Uto 0$) или в режиме холостого хода $(Rto infty ;;Ito 0$) полезная мощность равна нулю.
Примеры задач с решением
Пример 1
Задание. Коэффициент полезного действия электрического двигателя равен $eta $ =42%. Какой будет его полезная мощность, если при напряжении $U=$110 В через двигатель идет ток силой $I=$10 А?
Решение. За основу решения задачи примем формулу:
[P_p=eta P left(1.1right).]
Полную мощность найдем, используя выражение:
[P=IUleft(1.2right).]
Подставляя правую часть выражения (1.2) в (1.1) находим, что:
[P_p=eta IU.]
Вычислим искомую мощность:
[P_p=eta IU=0,42cdot 110cdot 10=462 left(Втright).]
Ответ. $P_p=462$ Вт
Пример 2
Задание. Какова максимальная полезная мощность источника тока, если ток короткого замыкания его
равен $I_k$? При соединении с источником тока сопротивления $R$, по цепи (рис.1) идет ток силой $I$.
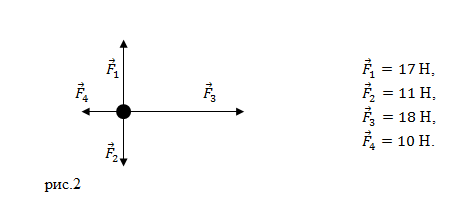
Решение. По закону Ома для цепи с источником тока мы имеем:
[I=frac{varepsilon}{R+r}left(2.1right),]
где $varepsilon$ – ЭДС источника тока; $r$ – его внутреннее сопротивление.
При коротком замыкании считаем, что сопротивление внешней нагрузки равно нулю ($R=0$), тогда сила тока короткого замыкания равна:
[I_k=frac{varepsilon}{r} left(2.2right).]
Максимальная полезная мощность в цепи рис.1 электрический ток даст, при условии:
[R=r left(2.3right).]
Тогда сила тока в цепи равна:
[I’=frac{varepsilon}{r+r}=frac{varepsilon}{2r}left(2.4right).]
Максимальную полезную мощность найдем, используя формулу:
[P_{p max}={I’}^2r={left(frac{varepsilon}{2r}right)}^2cdot r=frac{varepsilon^2}{4r}=frac{varepsilon^2}{4R}left(2.5right).]
Мы получили систему из трех уравнений с тремя неизвестными:
[left{ begin{array}{c}
I’=frac{varepsilon}{2r}, \
I_k=frac{varepsilon}{r}, \
P_{p max}={left(I’right)}^2r end{array}
left(2.6right).right.]
Используя первое и второе уравнения системы (2.6) найдем $I’$:
[frac{I’}{I_k}=frac{varepsilon}{2r}cdot frac{r}{varepsilon}=frac{1}{2}to I’=frac{1}{2}I_kleft(2.7right).]
Используем уравнения (2.1) и (2.2) выразим внутреннее сопротивление источника тока:
[varepsilon=Ileft(R+rright);; I_kr=varepsilon to Ileft(R+rright)=I_krto rleft(I_k+Iright)=IRto r=frac{IR}{I_k-I}left(2.8right).]
Подставим результаты из (2.7) и (2.8) в третью формулу системы (2.6), искомая мощность будет равна:
[P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}.]
Ответ. $P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}$
Читать дальше: формула равнодействующей всех сил.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Для школьников.
На рисунке изображена замкнутая электрическая цепь, состоящая из источника постоянного тока и переменной нагрузки во внешней части цепи.
Источником постоянного тока может быть электрическая машина, о которой говорится в статье “Искровой разряд“; батарея гальванических элементов, аккумулятор и др.
Роль источника тока заключается в создании (генерировании) электрической энергии: в разделении положительных и отрицательных зарядов; в создании и поддерживании разности потенциалов между конечными точками цепи, в которую включена нагрузка (электрическая лампочка, электроплитка. электродвигатель и т. д.).
При прохождении тока через нагрузку электрическая энергия превращается в другие виды энергии :тепловую (в электроплитке); в тепло и свет (в электрической лампе); в механическую энергию (в электродвигателе).
Превращение энергии из одного вида в другой всегда связано с работой.
При прохождении тока по проводнику совершается работа, её совершают электрические силы (или электрическое поле). Кратко эту работу называют работой тока.
Рассматривая участок цепи, по которому проходит ток, получим следующее выражение для работы тока:
Работа тока равна произведению напряжения между концами участка на протекающий ток и время его протекания.
В случае, если участок цепи однородный (не содержит источника тока), то
тогда получим ещё две формулы для работы тока:
Если ток проходит через неподвижный проводник, то единственным результатом работы тока является его нагревание. Тогда количество выделившейся теплоты
Это запись закона Джоуля – Ленца.
Если кроме нагревания ток совершает ещё механическую работу, например, приводя в действие электродвигатель (мотор), то работа
лишь частично переходит в тепло.
В этом случае работа тока больше количества выделившейся теплоты, но закон Джоуля – Ленца выполняется.
Работа, совершаемая током в единицу времени, называется мощностью тока:
Единицей мощности тока является 1 Вт:
1 Вт – мощность выделяемая током 1 А в проводнике, между концами которого поддерживается напряжение 1 В.
Основная формула мощности для участка цепи:
Мощность постоянного тока на любом участке цепи выражается произведением силы тока на напряжение между концами участка цепи.
Так как для однородного участка цепи
то мощность можно найти ещё по формулам:
Обычно говорят не о работе, а о потребляемой из сети некоторым прибором (электроплитка, лампочки и др.) или двигателем (мотором) мощности электрического тока. Говоря о мощности (например, электродвигателя), отмечают, что работа двигателя совершается за счёт тока.
На приборах часто отмечается потребляемая ими мощность – мощность, необходимая для нормальной работы этого прибора.
Согласно закону сохранения энергии, для замкнутой электрической цепи можно записать:
Здесь
есть полная или затраченная работа, совершаемая сторонними силами, существующими внутри источника, по переносу заряда по цепи.
В гальваническом элементе такими силами являются силы химической реакции.
– это полезная работа, совершаемая электрическим полем при прохождении тока через нагрузку;
это работа, совершаемая внутри источника, по преодолению его внутреннего сопротивления.
Так как работа, совершённая за единицу времени, есть мощность, то из уравнения (1) получим выражение для мощности:
Здесь
есть полная или затраченная мощность, это мощность развиваемая источником тока.
это мощность выделяемая внутри источника тока
это полезная мощность, создаваемая во внешней части цепи (на нагрузке).
Здесь U – напряжение на зажимах источника при замкнутой цепи (при разомкнутой цепи оно равно ЭДС источника).
Так как для однородного участка цепи напряжение равно произведению тока на сопротивление, то полезную мощность можно найти ещё по следующей формуле:
Ток в замкнутой цепи
тогда формулу для полезной мощности можно записать так:
Проанализируем зависимость полезной мощности от сопротивления нагрузки.
При коротком замыкании вся развиваемая источником мощность выделяется на его внутреннем сопротивлении в виде теплоты.
Таким образом, полезная мощность, развиваемая во внешней цепи, достигает максимального значения тогда, когда сопротивление нагрузки равно внутреннему сопротивлению источника.
На следующем рисунке показан график зависимости полезной мощности от сопротивления нагрузки.
Получена формула для нахождения максимальной полезной мощности
При этом ток в цепи в два раза меньше тока короткого замыкания:
Но чему при этом будет равно КПД источника?
Коэффициент полезного действия (КПД) источника показывает, какая часть затраченной (полной) работы источника пошла на пользу или КПД есть отношение полезной работы к затраченной:
Получается, что если добиваться максимальной мощности во внешней цепи, то получим КПД работы всего 50%, то есть половина затраченной мощности источника расходуется бесполезно – переходит в тепло, нагревая источник тока.
Выгоднее брать сопротивление нагрузки больше внутреннего сопротивления источника. Тогда ток в цепи уменьшится, а КПД источника увеличится.
Подумайте над решением следующих задач.
1. ЭДС аккумулятора 2 В, его внутреннее сопротивление 0,4 Ом, сопротивление внешней цепи 1 Ом. Найти разность потенциалов на зажимах аккумулятора и КПД его работы. Ответ: 1,43 В; 71 %.
2. Какую максимальную полезную мощность может выделить аккумулятор с ЭДС 10 В и внутренним сопротивлением 1 Ом? Каково при этом сопротивление внешней цепи? Ответ: 25 Вт; 1 Ом.
3. КПД источника тока, замкнутого на внешнее сопротивление R, равно 60%. Каков будет КПД источника, если внешнее сопротивление увеличить в 6 раз? Ответ: 90%.
Ответ: 7,7 Вт; 12 Вт; 40%; 25%.
Ответ: 2,7 10 4 кг.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Работа и мощность электрического тока. Лампы накаливания.
Следующая запись: Ещё раз о зарядке и разрядке конденсатора.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Рассмотрим
электрическую цепь, состоящую из
источника постоянного тока и внешнего
сопротивления R
(рис. 1). При протекании тока через
такую цепь источником ЭДС выполняется
работа и в цепи выделяется мощность.
П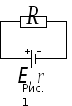 олезной
олезной
мощностью называют
мощность, которая выделяется на внешнем
сопротивлении. Из закона Джоуля-Ленца
(10*) полезная
мощность равняется
![]() ,
,
а из закона Ома для участка цепи![]() .
.
Тогда полезная мощность будет
|
|
(1) |
где
![]() – падение напряжения на внешнем
– падение напряжения на внешнем
сопротивлении. При протекании тока по
цепи также выделяется „бесполезная”
мощность – разогревается источник ЭДС.
По закону Джоуля-Ленца эта мощность
равняется![]() .
.
Полная мощность, которая выделяется во
всей цепи, равняется![]() .
.
Используя закон Ома для полной цепи![]() ,
,
можно найти полную мощность
|
|
(2) |
И так,
так,
полная мощность, которая выделяется в
цепи, равняется произведению силы тока
на ЭДС источника тока.
Пусть
в цепи можно менять внешнее сопротивление
![]() .
.
Проанализируем, как полезная и полная
мощности зависят от силы тока и внешнего
сопротивления.
Полезная
мощность
равняется разности между полной мощностью
и „бесполезной”:
|
|
(3) |
![]()

Рис. 2
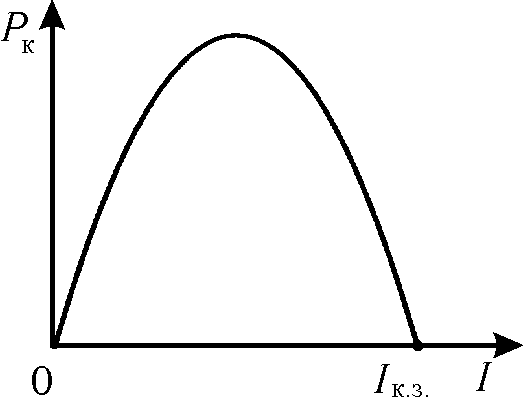
Из этого
выражения видно, что полезная мощность
является квадратичной функцией силы
тока I.
График этой функции будет представлять
собой параболу (рис. 2).
Из рис. 2
вытекает, что
![]() в двух случаях:
в двух случаях:
-
когда
цепь разомкнута (R = ∞),
то сила тока в цепи I = 0; -
когда
возникло короткое заключение, при этом
R = 0,
а сила тока в цепи будет максимальной
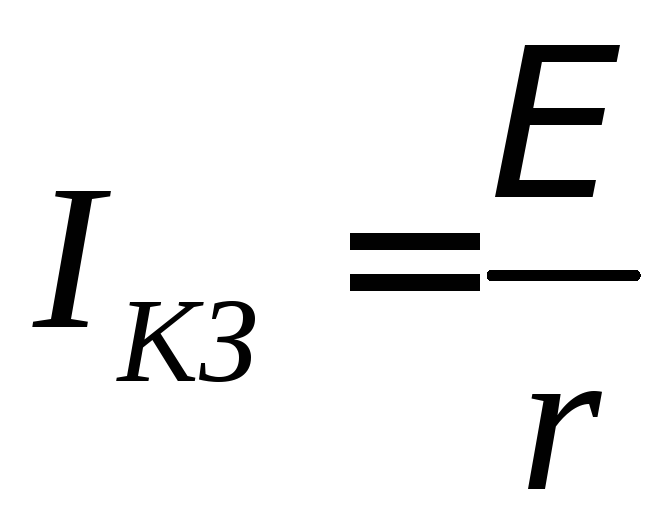 .
.
Меняя
величину внешнего сопротивления, можно
достичь некоторого значения силы тока
в цепи, при котором полезная мощность
будет максимальной. Найдем этот ток.
Для этого найдем первую производную
![]() и приравняем ее нулю. Из выражения (3)
и приравняем ее нулю. Из выражения (3)
имеем:
|
|
(4) |
Отсюда
вытекает
|
|
(5) |
а ток
![]() ,
,
при котором выделяется максимальная
полезная мощность, равняется![]() .
.
С другой стороны, на основании закона
Ома для полной цепи![]() ,
,
где![]() – сопротивление, при котором выделяется
– сопротивление, при котором выделяется
максимальная полезная мощность.
Приравнивая два последних выражения![]() ,
,
находим, что
|
|
(6) |
Таким
образом, полезная
мощность будет максимальной при условии
равенства внешнего и внутреннего
сопротивлений.
Зависимость
полезной мощности от внешнего сопротивления
можно найти из закона
Джоуля-Ленца
![]() и закона Ома для полной цепи
и закона Ома для полной цепи![]()
|
|
(7) |
График
зависимости
![]() показан на рис. 3 (криваяб).
показан на рис. 3 (криваяб).
Максимум функции
![]() можно найти, приравнивая
можно найти, приравнивая![]() нулю
нулю
|
|
(8) |
Из
(8) также вытекает ожидаемое равенство
![]() .
.
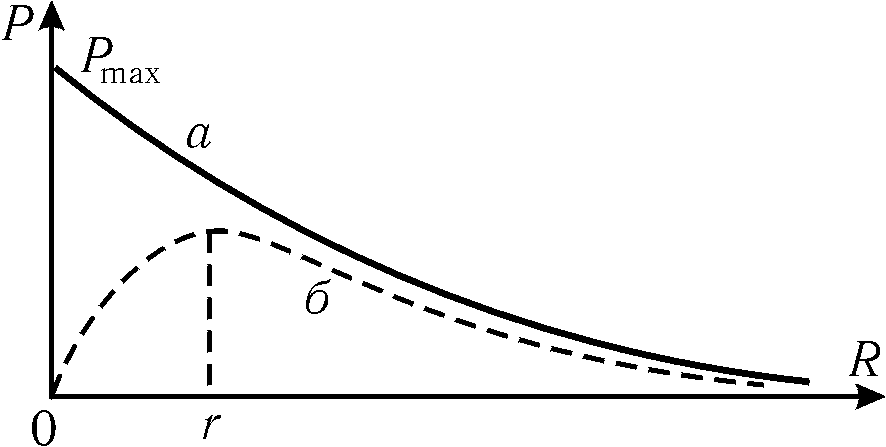

а
– полная мощность
б
– корисна потужність
Рис.
3
Рассмотрим
теперь, как полная мощность
зависит от внешнего сопротивления.
Используя выражение (2) и закон Ома для
полной цепи
![]() находим зависимость полной мощности
находим зависимость полной мощности
от внешнего сопротивления:
![]() .
.
(9)
График этой
зависимости показана на рис. 3 (кривая
а). При
изменении внешнего сопротивления от
нуля (короткое заключение) до бесконечности
(цепь разомкнута) полная мощность будет
убывать от максимального значения
![]() до нуля.
до нуля.
-
Зависимость
коэффициента полезного действия
источника электрического тока от силы
тока и внешнего сопротивления цепи
К оэффициент
оэффициент
полезного действия
(КПД) равняется отношению полезной
мощности (1) к полной мощности (2), которая
выделяется во всей цепи
|
|
(10) |
С начала
начала
найдем зависимость КПД
от силы тока. Если
разделить выражение (3) для полезной
мощности на выражение (1) для полной
мощности, получим
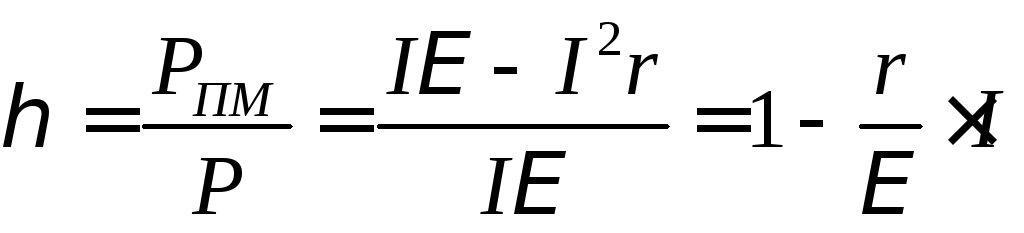
(11)
И так,
так,
КПД представляет собой линейную функцию
от силы тока (рис. 4). Когда I → 0
(цепь разомкнут), то
![]() .
.
При коротком заключении![]() ,
,
ток короткого заключения
|
|
(12) |
и
КПД будет
![]() .
.
Чтобы найти
зависимость КПД от
внешнего сопротивления,
подставим в (9) выражение для
![]() из закона Ома для участки цепи
из закона Ома для участки цепи![]() ,
,
а выражение для![]() – из закона Ома для полной цепи
– из закона Ома для полной цепи![]() .
.
Тогда
|
|
(13) |
Из соотношения (13)
вытекает:
-
при
R
® 0
(короткое заключение,
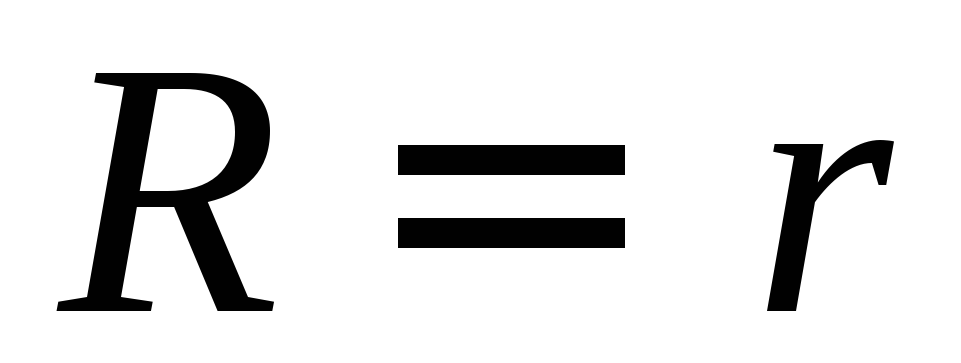 )
) ;
; -
при
R
® ¥
( цепь разомкнут,
 )
) ;
; -
при
R = r
(условие максимума полезной мощности)
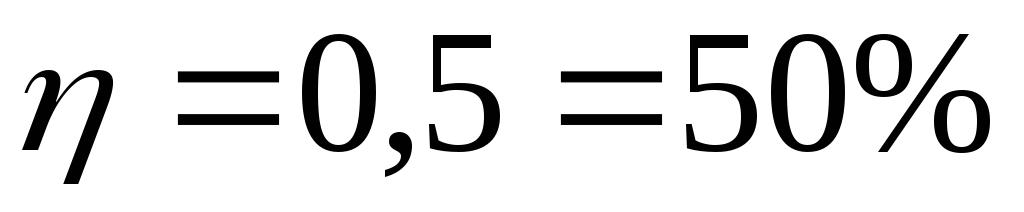 .
.
Приведенный
анализ показывает, что при увеличении
внешнего сопротивления КПД асимптотично
приближается к единице (рис. 5).
Соседние файлы в папке doc-формат
- #
- #
- #
- #
- #
- #
Что важно знать о полезной мощности двигателя в физике
Содержание:
- Определение и формула полезной мощности
- Взаимосвязь полезной мощности и КПД
- Достижение максимального КПД
- Примеры задач с решением
Определение и формула полезной мощности
Мощность является физической величиной, применяемой в качестве ключевого параметра какого-либо устройства, которое предназначено для совершения работы.
Полезной мощностью называют такую мощность, которую можно использовать, чтобы выполнить некую поставленную задачу.
Средняя мощность (leftlangle Prightrangle) представляет собой отношение работы (Delta A) к временному интервалу (Delta t), в течение которого данная работа была выполнена:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(leftlangle Prightrangle =frac{Delta A}{Delta t})
Мгновенную мощность чаще всего называют просто мощностью, данная величина обозначает предел отношения (leftlangle Prightrangle =frac{Delta A}{Delta t}left(1right) при Delta tto 0:)
(P={mathop{lim }_{Delta tto 0} frac{Delta A}{Delta t} }=A'(t))
Заметим, что:
(Delta A=overline{F}cdot Delta overline{r })
Здесь (Delta overline{r }) обозначает перемещение, совершаемое неким телом под воздействием силы (overline{F}). В таком случае, можно преобразовать выражение:
(P={mathop{lim }_{Delta tto 0} left(frac{overline{F}cdot Delta overline{r }}{Delta t}right) }=overline{F}{mathop{lim }_{Delta tto 0} left(frac{Delta overline{r }}{Delta t}right)= }overline{F}cdot overline{v})
Здесь ( overline{v}) является мгновенной скоростью.
Рассмотрим такое понятие, как полезная мощность электрического источника. Представим, что некая активная цепь включает в себя источник тока с сопротивлением r. Пусть нагрузка при этом равна сопротивлению R. В результате формула мощности такого источника примет вид:
P=EI
Здесь E представляет собой ЭДС источника тока, I обозначает силу тока. При этом P является полной мощностью цепи.
Введем обозначение U в качестве напряжения на внешнем участке цепи, и перепишем формулу мощности таким образом:
(P=EI=UI+I^2r=P_p+P_0)
Здесь (P_p=UI=I^2R=frac{U^2}{R}) определяется, как полезная мощность, (P_0=I^2r) является мощностью потерь.
Исходя из представленных формул, можно вывести определение для коэффициента полезного действия:
(eta =frac{P_p}{P_p+P_0}left(9right).)
Максимальная величина полезной мощности (или мощности на нагрузке) электрического тока достижима при равенстве внешнего сопротивления цепи внутреннему сопротивлению источника тока. В этом случае, полезная мощность составит 50 % от общей мощности. При возникновении короткого замыкания (то есть (Rto 0;;Uto 0)), либо при холостом ходу (то есть (Rto infty ;;Ito 0)), полезная мощность принимает нулевое значение.
Взаимосвязь полезной мощности и КПД
В процессе выполнения нужной (полезной) работы, в том числе механической, требуется выполнять большую работу. Это связано с существованием силы сопротивления в реальных условиях и частичной подверженности энергии диссипации, то есть рассеиванию.
Коэффициент полезного действия (eta) обозначает эффективность совершения работы:
(eta =frac{P_p}{P}left(5right))
Здесь (P_p) определяется, как полезная мощность, P является мощностью, которая была затрачена.
С помощью записанной формулы можно преобразовать уравнение для расчета мощности:
(P_p=eta P)
Справедливыми являются и такие соотношения:
(eta =frac{A_1}{W}cdot 100%)
(eta =frac{N_1}{N_2}cdot 100%)
Здесь (N_1) и (N_2) будут называться полезной и затраченной мощностью соответственно.
Достижение максимального КПД
Разные двигатели характеризуются определенным КПД. Запишем некоторые примеры:
- электрический двигатель до 98 %;
- двигатель внутреннего сгорания до 40 %;
- паровая турбина до 30 %.
Существует зависимость КПД от мощности. Так коэффициент полезного действия можно рассчитать, как отношение полезной мощности к полной мощности, выдаваемой источником. В любых условиях (eta leq 1. ) С целью увеличения коэффициента полезного действия таких агрегатов, как подъемные краны, насосные установки нагнетательного типа, моторы самолетов, асинхронные двигатели, требуется снизить силу трения механизмов или сопротивления воздуха. Задача решается с помощью: использования разнообразных смазочных материалов, подшипников повышенного класса (что позволяет заменить скольжение качением); изменения геометрических параметров крыла.
Максимальные показатели энергии или мощности на выходе источника питания достигаются за счет согласования сопротивления нагрузки Rн и внутреннего сопротивления R0. При равенстве данных характеристик КПД достигает 50 %, что является приемлемым значением в случае слаботочных цепей и радиотехники.
Подобное решение не реализуемо для электрических установок, в том числе нагревателей. С целью снизить бесполезное потребление больших мощностей подбирают такой эксплуатационный режим генераторов, выпрямителей, трансформаторов, электрических двигателей, при котором коэффициент полезного действия стремится к 95 % и более.
Добиться высокого КПД для теплового двигателя можно с помощью следующих решений:
- введение в цикл расширения дополнительного рабочего тела, обладающего другими физическими свойствами;
- максимально полно перед расширением использовать два вида энергии рабочего тела;
- выполнять генерацию дополнительного рабочего тела непосредственно при расширении газообразного.
Известно, что КПД в случае ДВС можно увеличить с помощью нагнетателя турбонаддува, многократного или распределенного впрыска, увеличения влажности воздуха, перевод топлива при впрыске в парообразное состояние. Однако подобные меры не позволяют существенно повысить значение коэффициента полезного действия.
Примеры задач с решением
Задача 1
Имеется электродвигатель, КПД которого равен 42 %. Если напряжение составляет 110 В, то двигатель пропускает через себя ток силой 10 А. Требуется определить полезную мощность силового агрегата.
Решение
Запишем формулу для нахождения мощности:
(P_p=eta P left(1.1right))
Рассчитаем, чему равна полная мощность:
(P=IUleft(1.2right))
Путем подстановки получим:
(P_p=eta IU)
Определим искомую мощность:
(P_p=eta IU=0,42cdot 110cdot 10=462 left(Втright))
Ответ: (P_p=462 Вт)
Задача 2
Существует некий источник электрического тока с показателем тока короткого замыкания, равным . При включении источника тока в цепь с сопротивлением R, как показано на рисунке, сила тока составляет I. Требуется рассчитать самое большое значение, которое может принимать полезная мощность рассматриваемого источника.
Решение
Вспомним закон Ома, знакомый с уроков по физике:
(I=frac{varepsilon}{R+r}left(2.1right))
Здесь (varepsilon) является ЭДС источника тока, r представляет собой внутреннее сопротивление источника.
Если возникает короткое замыкание, то сопротивление внешней нагрузки принимает нулевое значение. В таком случае, силу тока короткого замыкания можно определить по формуле:
(I_k=frac{varepsilon}{r} left(2.2right).)
Максимальное значение полезной мощности в цепи достигается, если соблюдается условие:
(R=r left(2.3right))
Определим силу тока:
(I’=frac{varepsilon}{r+r}=frac{varepsilon}{2r}left(2.4right))
Вычислим максимальное значение полезной мощности:
(P_{p max}={I’}^2r={left(frac{varepsilon}{2r}right)}^2cdot r=frac{varepsilon^2}{4r}=frac{varepsilon^2}{4R}left(2.5right).)
Получилась система с тремя уравнениями и тремя неизвестными:
(left{ begin{array}{c}
I’=frac{varepsilon}{2r}, \
I_k=frac{varepsilon}{r}, \
P_{p max}={left(I’right)}^2r end{array}.right.)
Вычислим I’:
(frac{I’}{I_k}=frac{varepsilon}{2r}cdot frac{r}{varepsilon}=frac{1}{2}to I’=frac{1}{2}I_k)
Далее составим выражение для внутреннего сопротивления источника тока:
(varepsilon=Ileft(R+rright);; I_kr=varepsilon to Ileft(R+rright)=I_krto rleft(I_k+Iright)=IRto r=frac{IR}{I_k-I})
Методом подстановки найдем искомую мощность:
(P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I})
Ответ: (P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}.)
Задача 3
Электропоезд благодаря моторам движется со скоростью 54 км/ч. При этом его полезная мощность составляет 720 кВт. Нужно найти силу тяги моторов.
Решение
Запишем формулу для определения мощности двигателей электропоезда:
(N=Fcdot v)
Тогда сила тяги моторов составит:
(F=frac{N}{v})
Выполним перевод единиц измерения в СИ:
(v=54 км/ч =15 м/с)
В результате:
(N=720 kBt=720000 Bt)
Выполним вычисления:
(F=frac{720000}{15}=48000 H=48 kH)
Ответ: сила тяги моторов равна 48 КН.
Задача 4
Масса машины составляет 2200 кг. Трогаясь с места, автомобиль осуществляет подъем в гору с углом наклона 0,018. Преодолев путь в 100 м, машина приобретает скорость 32,4 км/ч. Коэффициент трения равен 0,04. Требуется вычислить среднюю мощность, которую развивает двигатель автомобиля в процессе движения.
Решение
Формула средней мощности двигателя во время движения машины:
(leftlangle Nrightrangle =Fcdot leftlangle vrightrangle)
Автомобиль движется со средней скоростью:
(leftlangle vrightrangle =frac{v}{2})
Отметим на рисунке все силы, под действием которых находится автомобиль:
Перечислим все силы:
- сила тяжести (moverline{g};)
- сила реакции опоры (overline{N};)
- сила трения ({overline{F}}_{fr};)
- сила тяги двигателей (overline{F}.)
Уравнение второго закона Ньютона:
(moverline{g}+overline{N}+{overline{F}}_{fr}+overline{F}=moverline{a})
Если спроецировать записанное соотношение на координатные оси, получим:
({ begin{cases} F-F_{fr}-mgsinalpha =ma \ N-mgcosalpha =0 end{cases}})
Заметим, что:
(N=mgcosalpha)
(F_{fr}=mu N=mu mgcosalpha)
Преобразуем уравнение:
(F-mu mgcosalpha -mgsinalpha =ma)
Таким образом:
(F=mleft(mu gcosalpha +gsinalpha +aright))
Рассчитаем ускорение машины:
(a=frac{v^2}{2s})
Заметим, что:
(cosalpha =sqrt{1-{sin}^2alpha })
Выполним подстановку:
(F=mleft(mu gsqrt{1-{sin}^2alpha }+gsinalpha +frac{v^2}{2s}right))
Двигатель в процессе движения развивает среднюю мощность:
(leftlangle Nrightrangle =mleft(mu gsqrt{1-{sin}^2alpha }+gsinalpha +frac{v^2}{2s}right)cdot frac{v}{2})
Известно, что ускорение свободного падения равно (9,8 м/с ^{2}). Переведем единицы измерения в СИ:
(v=32,4 км/ч =9 м/с.)
Выполним вычисления:
(leftlangle Nrightrangle =2200cdot left(0,04cdot 9,8cdot sqrt{1-{0,018}^2}+9,8cdot 0,018+frac{9^2}{2cdot 100}right)cdot frac{9}{2}=9512,9 Bt=9,5 kBt)
Ответ: мотор машины имеет среднюю мощность 9,5 кВт.
Мощность (физика) — это… Что такое Мощность (физика)?
Мощность
— физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Эффективная мощность
Читайте также: Выпрямители напряжения: основные понятия
, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу. Различают полезную, полную и номинальную Э. м. двигателя. Полезной называют Э. м.
двигателя за вычетом затрат мощности на приведение в действие вспомогательных агрегатов или механизмов, необходимых для его работы, но имеющих отдельный привод (не от двигателя непосредственно). Полная Э. м. — мощность двигателя без вычета указанных затрат. Номинальная Э. м., или просто номинальная мощность, — Э. м.
, гарантированная заводом-изготовителем для определённых условий работы. В зависимости от типа и назначения двигателя устанавливаются Э. м.
, регламентируемые стандартами или техническими условиями (например, наибольшая мощность судового реверсивного двигателя при определённой частоте вращения коленчатого вала в случае заднего хода судна — так называемая мощность заднего хода, наибольшая мощность авиационного двигателя при минимальном удельном расходе топлива — так называемая крейсерская мощность и т. п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.[1]
Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.
Единицы измерения
В системе СИ единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.
Другой распространённой единицей измерения мощности является лошадиная сила.
Соотношения между единицами мощности Единицы Вт кВт МВт кгс·м/с эрг/с л. с.
| 1 ватт | 1 | 10-3 | 10-6 | 0,102 | 107 | 1,36·10-3 |
| 1 киловатт | 103 | 1 | 10-3 | 102 | 1010 | 1,36 |
| 1 мегаватт | 106 | 103 | 1 | 102·103 | 1013 | 1,36·103 |
| 1 килограмм-сила-метр в секунду | 9,81 | 9,81·10-3 | 9,81·10-6 | 1 | 9,81·107 | 1,33·10-2 |
| 1 эрг в секунду | 10-7 | 10-10 | 10-13 | 1,02·10-8 | 1 | 1,36·10-10 |
| 1 лошадиная сила[2] | 735,5 | 735,5·10-3 | 735,5·10-6 | 75 | 7,355·109 | 1 |
Виды мощности постоянного тока
Любая мощностная величина определяется работой, которая совершается за определенную единицу времени. Чаще всего ею становится секунда. Она означает величину, характеризующую, насколько быстро совершается работа. Касаемо электрической мощности это расход электроэнергии за одну секунду.

Мощностная характеристика тока соответствует отношению его работы ко времени
Работой тока называется процесс превращения электроэнергии в какую-либо другую энергию (механическую, тепловую или световую). Именно по мощности, которая обозначается буквой «P» или «W», и оценивается работоспособность электротока.
К сведению! Вообще у тока постоянного значения нет активной и реактивной P. Для этого вида сети характерна только мгновенная характеристика.
Мгновенная мощность
Если говорить о сетях переменного электротока, то рассматриваемая величина в них, как и электроток или напряжение, регулярно меняет свои значения. Это напрямую влияет на другие параметры. При константном течении зарядов все остается неизменным. Именно поэтому и возникает термин «мгновенная мощность».
Силы в сети регулярного тока остаются неизменными и равняются мгновенным их значениям, взятым в произвольный момент времени. Такую характеристику можно высчитать по мгновенным значениям. Для этого подходит формула мощности постоянного тока в цепи: P = I * U.

Рассматриваемая величина может быть найдена из произведения силы электротока и напряжения
Если сеть пассивна и в ней соблюдается закон Ома, то справедливо равенство. В случае подключения источника ЭДС нужна другая формула: P = I * E, где E — это электродвижущая сила.
Активная мощность
Активная мощность — это среднее за период значение мгновенной P. При активной P происходит конвертация мощности тока в энергию любого вида (механическую, световую или тепловую). Подобный перевод электротока нельзя выполнить в обратном направлении. Активный тип также измеряется в ваттах. 1 Ватт равен 1 вольту умноженному на 1 ампер.

Работа неразрывно связана с определением мощностных характеристик
К сведению! В бытовых и уж тем более промышленных масштабах единицу измерения ватт никогда не используют. Для этих целей задействуют показатели на порядок выше: мегаватты в киловатты.
Реактивная мощность
Реактивная мощностная характеристика определяет нагрузку, которая создается электрическими устройствами определенными колебаниями энергии электромагнитного поля в сетях синусоидального тока переменной частоты. Она равна произведению среднеквадратичных значений напряжения и силы тока, умноженных на синус угла, на который сдвигается фаза между ними. Реактивный параметр неразрывно связан с полной P и активным параметром.

Все основные величины могут быть найдены с использованием закона Ома
Если говорить про физический смыл реактивности, то он представляет собой некую энергию, которая перекачивается из источника к реактивным элементам приемника (конденсатор, обмотка генератора, катушка индуктивности и т. д.), а потом возвращается обратно в источник за время одного периода колебаний.
Полная мощность
Полная P электротока представляет собой значение, соответствующее произведению силы электротока и напряжения в цепи. Она неразрывно связана с активной и реактивной величинами и определяется следующим уравнением: , где Sos = полная мощность, а P и Q — ее активная и реактивная характеристики соответственно.

Общая мощность, которую можно представить в виде кружки пива
Если говорить проще, то активная P есть везде, где присутствует нагрузка активного плана. Например, в спиральных нагревателях, сопротивлении проводов и т. д. Реактивный параметр характерен для реактивной нагрузки, которая имеется в элементах индуктивности или емкости.
Определение и формула полезной мощности
Стоит рассмотреть понятие полезной мощности и формулу на примере электрической цепи. Та мощность, которую источник питания (ИП), в частности, тока, развивает в замкнутой цепи, будет полной мощностью.
Схема цепи
Цепь включает в себя: источник тока, имеющий ЭДС (E), внешнюю цепь с нагрузкой R и внутреннюю цепь ИП, сопротивление которого R0. Формула полной (общей) мощности равна:
Pобщ = E*I.
Здесь I – это значение тока, проходящего по цепи (А), а E – величина ЭДС (В).
Внимание! Падение напряжения на каждом из участков будет равно U и U0, соответственно.
Значит, формула примет вид:
Pобщ = E*I = (U + U0) *I = U*I + U0*I.
Видно, что значение произведения U*I равняется мощности, отдаваемой источником на нагрузке, и соответствует полезной мощности Pпол.
Величина, равная произведению U0*I, соответствует мощности, которая теряется внутри ИП на нагрев и преодоление внутреннего сопротивления R0. Это мощность потерь P0.
Подставляемые в формулу значения показывают, что сумма полезной и потерянной мощностей составляют общую мощность ИП:
Pобщ=Pпол+P0.
Важно! При работе любого аппарата (механического или электрического) полезной мощностью будет та, которая останется для совершения нужной работы после преодоления факторов, вызывающих потери (нагрев, трение, противодействующие силы).
Полная, полезная мощности и КПД цепи постоянного тока
Рассмотрим замкнутую неразветвленную цепь, состоящую из источника тока и резистора.
Применим закон сохранения энергии ко всей цепи:
Так как , а для замкнутой цепи точки 1 и 2 совпадают, мощность электрических сил в замкнутой цепи равна нулю. Это равносильно утверждению о потенциальности электрического поля постоянного тока, о которой уже упоминалось ранее.
Итак, в замкнутой цепи всё тепло выделяется за счет работы сторонних сил: , или , и мы снова приходим к закону Ома, теперь для замкнутой цепи: .
Полной мощностью цепи называют мощность сторонних сил, она же равна полной тепловой мощности:
Полезнойназывают тепловую мощность, выделяемую во внешней цепи (независимо от того, полезна она или вредна в данном конкретном случае):
Роль электрических сил в цепи. Во внешней цепи, на нагрузке R
, электрические силы совершают положительную работу, а при перемещении заряда внутри источника тока – такую же по величине отрицательную. Во внешней цепи теплота выделяется за счет работы электрического поля. Работу, отданную во внешней цепи, электрическое поле «возвращает» себе внутри источника тока. В итоге вся теплота в цепи «оплачена» работой сторонних сил: источник тока постепенно теряет запасенную в нем химическую (или какую-то другую) энергию. Электрическое же поле играет роль «курьера», доставляющего энергию во внешнюю цепь.
Зависимость полной, полезной мощностей и КПД от сопротивления нагрузки R.
Эти зависимости получаем из формул (1 – 2) и закона Ома для полной цепи:
Графики этих зависимостей вы видите на рисунке.
Полная мощность монотонно убывает с ростом , т.к. убывает сила тока в цепи. Максимальная полная мощность выделяется при , т.е. при коротком замыкании
Формула мощности тока. Фактическая и номинальная мощность. КПД электрического прибора :
Действие всех известных электрических приборов происходит за счет электрической энергии. В результате этого мы получаем свет, тепло, звук, механическое движение, то есть разные виды энергии. В этой статье мы рассмотрим и изучим такое физическое понятия, как мощность электрического тока.
Под мощностью тока так же, как и в механике, понимают работу, которая выполняется за единицу времени. Рассчитать мощность, зная работу, которую выполняет электрический ток за некоторый промежуток времени, поможет физическая формула.

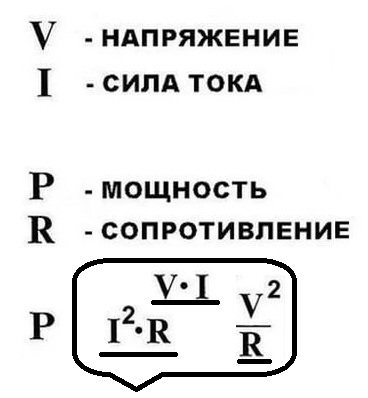
- Ток, напряжение, мощность в электростатике связаны равенством, которое можно вывести из формулы A = UIt. По ней определяют работу, которую выполняет электрический ток:
- P = A/t = UIt/t = UI Таким образом, формула мощности постоянного тока на любом участке цепи выражается как произведение силы тока на напряжение между концами участка.
Используя закон Ома, формула мощности тока P = UI записывается в таком виде:

P = UI = U2/R = I2/R Итак, мощность, выделяемая на проводниках, прямо пропорциональна силе тока, протекающей через проводник, и напряжению на его концах.
Как известно, идеальных машин и механизмов не существует (то есть таких, которые бы полностью превращали один вид энергии в другой или генерировали бы энергию).
Во время работы устройства обязательно часть затраченной энергии уходит на преодоление нежелательных сил сопротивления или просто «рассеивается» в окружающую среду.
Таким образом, только часть затраченной нами энергии уходит на выполнение полезной работы, для выполнения которой и было создано устройство.
Физическая величина, которая показывает, какая часть полезной работы в затраченной, называется коэффициентом полезного действия (далее КПД).
- Другими словами, КПД показывает, насколько эффективно используется затраченная работа при ее выполнении, например, электрическим прибором.
- КПД (обозначается греческой буквой η («эта»)) — физическая величина, которая характеризует эффективность электрического прибора и показывает, какая часть полезной работы в затраченной.
- КПД определяется (как и в механике) по формуле:
- η = AП/AЗ·100%
- Если известна мощность электрического тока, формулы для определения ККД будут выглядеть так:
- η = PП/PЗ·100%
- Прежде чем определять КПД некоторого устройства, необходимо определить, что является полезной работой (для чего создано устройство), и что является затраченной работой (работа выполняется или какая энергия затрачивается для выполнения полезной работы).
Формула полезной мощности источника тока
Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:
[P=?I left(7right),]
где $?$ – ЭДС источника тока; $I$ – сила тока. При этом $P$ – полная мощность цепи.
Обозначим $U$ – напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:
[P=?I=UI+I^2r=P_p+P_0left(8right),]
где $P_p=UI=I^2R=frac{U^2}{R}(9)$ – полезная мощность; $P_0=I^2r$ – мощность потерь. При этом КПД источника определяют как:
[eta =frac{P_p}{P_p+P_0}left(9right).]
Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50% общей мощности.
При коротком замыкании (когда $Rto 0;;Uto 0$) или в режиме холостого хода $(Rto infty ;;Ito 0$) полезная мощность равна нулю.
Взаимосвязь полезной мощности и КПД
Коэффициент полезного действия (КПД) – величина безразмерная, численно выражается в процентах. КПД обозначают буквой η.
Формула имеет вид:
η = А/Q,
где:
- А – полезная работа (энергия);
- Q – затраченная энергия.
По мере увеличения КПД в различных двигателях допустимо выстроить следующую линейку:
- электродвигатель – до 98%;
- ДВС – до 40%;
- паровая турбина – до 30%.
Что касается мощности, КПД равен отношению полезной мощности к полной мощности, которую выдает источник. В любом случае η ≤ 1.
Важно! КПД и Pпол не одно и то же. В разных рабочих процессах добиваются максимума или одного, или другого.
Получение максимальной энергии на выходе ИП
К сведению. Чтобы увеличить КПД подъёмных кранов, нагнетательных насосов или двигателей самолётов, нужно уменьшить силы трения механизмов или сопротивления воздуха. Этого достигают применением разнообразных смазок, установкой подшипников повышенного класса (заменив скольжение качением), изменением геометрии крыла и т.д.
Максимальная энергия или мощность на выходе ИП может быть достигнута при согласовании сопротивления нагрузки Rн и внутреннего сопротивления R0 ИП. Это значит, что Rн = R0. В этом случае КПД равен 50%. Это вполне приемлемо для малоточных цепей и радиотехнических устройств.
Однако этот вариант не подходит для электрических установок. Чтобы впустую не тратились большие мощности, режим эксплуатации генераторов, выпрямителей, трансформировав и электродвигателей таков, что к.п.д. приближается к 95% и выше.
Достижение максимального КПД
Формула КПД источника тока имеет вид:
η = Pн/Pобщ = R/Rн+r,
где:
- Pн – мощность нагрузки;
- Pобщ – общая мощность;
- R – полное сопротивление цепи;
- Rн – сопротивление нагрузки;
- r – внутреннее сопротивление ИТ.
Как видно из графика, изображённого на рис. выше, мощность Pн с уменьшением тока в цепи стремится к нулю. КПД, в свою очередь, достигнет максимального значения, когда цепь будет разомкнута, и ток равен нулю, при коротком замыкании в цепи станет равным нулю.
Если обратиться к элементарному тепловому двигателю, состоящему из поршня и цилиндра, то у него степень сжатия равна степени расширения. Повышение КПД такого мотора возможно в случае:
- изначально высоких параметров: давления и температуры рабочего тела перед началом расширения;
- приближения их значений к параметрам окружающей среды по окончании расширения.
Достижение ηmax доступно лишь при наиболее эффективном изменении давления рабочего компонента во вращательное движение вала.
К сведению. Термический коэффициент полезного действия повышается с повышением доли теплоты, подаваемой к рабочему телу, которая преобразуется в работу. Подаваемая теплота делится на два вида энергии: внутренняя в виде температуры и энергия давления.
Механическую работу, по сути, совершает только второй вид энергии. Это порождает целый ряд минусов тормозящих процесс повышения КПД:
- некоторая часть давления уходит на внешнюю среду;
- достижение максимального коэффициента полезного действия невозможно без увеличения процента использования энергии давления для преобразования в работу;
- нельзя поднять КПД тепловых двигателей, не изменяя S поверхности приложения давления, и без удаления этой поверхности от точки вращения;
- использование только газообразного рабочего тела не способствует повышению η тепловых двигателей.
Для достижения высокого коэффициента полезного действия теплового двигателя нужно определяться с рядом решений. Этому способствуют следующие модели устройства:
- ввести в цикл расширения ещё одно рабочее тело с другими физическими свойствами;
- наиболее полно перед расширением использовать оба вида энергии рабочего тела;
- осуществлять генерацию добавочного рабочего тела прямо при расширении газообразного.
Информация. Все доработки двигателей внутреннего сгорания в виде: нагнетателя турбонадува, организации многократного или распределённого впрыска, а также повышения влажности воздуха, доведения топлива при впрыске до состояния пара, не дали ощутимых результатов резкого повышения КПД.
Реактивный коэффициент
По-другому он называется коэффициентом мощности и является безразмерной величиной, вводимой для вычисления реактивной составляющей. Говоря научным языком, он показывает, насколько сдвигается фаза переменного тока, протекающего через нагрузку, от возникшего на ней напряжения. Численно он принимается равным косинусу сдвига. Математически это сдвиг интерпретируется как косинус угла между векторными значениями тока и напряжения.
Простыми же словами, коэффициент мощности, обозначаемый φ, указывает на ту часть расходуемой электроэнергии, которая преобразуется в полезную работу. Например, при cos φ = 0,9 девяносто процентов от полной энергии уйдёт на совершение полезного действия, а остальные десять будут считаться потерями. Поэтому если в паспорте на какой-либо прибор указано, что мощность изделия составляет 500 Вт, а cos φ = 0,5, то полный расход его энергии будет составлять 500/0,5 = 250 ВА.
То есть коэффициент φ находится из отношения потребляемой устройством энергии к значению полной мощности. Нередко в паспорте оборудования указывается и составляющая φ (характер нагрузки). Она может быть резистивно-ёмкостной или резистивно-индуктивной. При этом сам коэффициент соответственно является опережающим или отстающим.
Если же напряжение в цепи изменяется по синусоидальному закону, а ток по несинусоидальному, то нагрузка никакой реактивной составляющей иметь не будет, а коэффициент принимается равным главной волне (первой гармонике). Под несинусоидальными понимаются искажения электрического сигнала, связанные с гармониками, преобладающими над основной частотой.
В математике формулой для нахождения коэффициента мощности является выражение: cos φ= P/S. Поэтому чем больше его значение, тем меньше потребляет устройство энергию из сети. Существуют различные способы поднятия значения cos φ, даже до максимального значения, равного единице, называемые коррекцией. Наиболее эффективным является добавление в схему сложного электронного узла, размещаемого на входе устройства.
Определение и формула полезной мощности
Стоит рассмотреть понятие полезной мощности и формулу на примере электрической цепи. Та мощность, которую источник питания (ИП), в частности, тока, развивает в замкнутой цепи, будет полной мощностью.
Схема цепи
Цепь включает в себя: источник тока, имеющий ЭДС (E), внешнюю цепь с нагрузкой R и внутреннюю цепь ИП, сопротивление которого R0. Формула полной (общей) мощности равна:
Pобщ = E*I.
Здесь I – это значение тока, проходящего по цепи (А), а E – величина ЭДС (В).
Внимание! Падение напряжения на каждом из участков будет равно U и U0, соответственно.
Значит, формула примет вид:
Pобщ = E*I = (U + U0) *I = U*I + U0*I.
Видно, что значение произведения U*I равняется мощности, отдаваемой источником на нагрузке, и соответствует полезной мощности Pпол.
Величина, равная произведению U0*I, соответствует мощности, которая теряется внутри ИП на нагрев и преодоление внутреннего сопротивления R0. Это мощность потерь P0.
Подставляемые в формулу значения показывают, что сумма полезной и потерянной мощностей составляют общую мощность ИП:
Pобщ=Pпол+P0.
Важно! При работе любого аппарата (механического или электрического) полезной мощностью будет та, которая останется для совершения нужной работы после преодоления факторов, вызывающих потери (нагрев, трение, противодействующие силы).
Параметры источника питания
На практике часто приходится думать, какой должна быть мощность источника тока, сколько нужно ватт (вт) или киловатт (квт) для обеспечения бесперебойной работы устройства. Для понимания сути нужно иметь представления о таких понятиях, применяемых в физике, как:
- полная энергия цепи;
- ЭДС и напряжение;
- внутреннее сопротивление источника питания;
- потери внутри ИП;
- полезная мощность.
Независимо от того, какую энергию выдаёт источник (механическую, электрическую, тепловую), мощность его должна подбираться с небольшим запасом (5-10%).
При включении в цепь нагрузки, которая будет потреблять энергию от источника тока (ИТ), ток будет совершать работу. Энергия, выделяемая на всех включенных в цепь потребителях и элементах цепи (провода, электронные компоненты т.д.), носит название полной. Источник энергии может быть любой: генератор, аккумулятор, тепловой котёл. Цифра значения полной энергии будет складываться из энергии, затрачиваемой источником на потери, и количества, затрачиваемого на выполнение конкретной работы.
В чём разница между этими двумя понятиями?
ЭДС – электродвижущая сила, это напряжение, которое сторонние силы (химическая реакция, электромагнитная индукция) создают внутри источника тока (ИТ). ЭДС – это сила перемещения электрических зарядов в ИТ.
ЭДС определение
К сведению. Измерить значение E (ЭДС) представляется возможным только в режиме холостого хода (х.х.). Подключение любой нагрузки вызывает потерю напряжения внутри ИП.
Напряжение (U) – физическая величина, представляющая собой разность потенциалов ϕ1 и ϕ2 на выходе источника напряжения (ИН).
Определение понятия полной мощности применяют не только в отношении электрических цепей. Оно применимо и по отношению к электродвигателям, трансформаторам и прочим устройствам, способным потреблять, как активную, так и реактивную составляющую энергии.
Подобные потери происходят на внутреннем сопротивлении двухполюсника. У аккумулятора это сопротивление электролита, у генератора – обмоточное сопротивление, провода выводов которого выходят из корпуса.
Взять и просто измерить R0 тестером не получится, узнать его обязательно нужно для вычисления потерь Р0. Поэтому применяют косвенные методы.
Косвенный метод определения R0 заключается в следующем:
- в режиме х.х. замеряют E (В);
- при включенной нагрузке Rн (Ом) измеряют Uвых (В) и ток I (А);
- падение напряжения внутри источника считают по формуле:
U0=E-Uвых.
На последнем этапе находят R0=U0/I.
Схема для измерения R0
Зависимость мощности от силы тока, формула мощности, физический смысл

Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами. Отцом же науки об электричестве считается французский ученый Кулон – именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор. Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно – расстоянию между ними, возведенному в квадрат.
Выясним, что же представляет собой понятие электричество?
Если коротко, то это – направленное движение потока заряженных частиц. Тела, через которые они проходят, называются проводниками. Каждый проводник имеет определенное сопротивление электрическому току, которое раз
И, перед тем, как перейти к основным законам, несколько слов о заряженных частицах: они бывают, условно говоря, положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные – притягиваются.
А теперь, перейдем к главному
Основа-основ науки об электричестве – закон Ома.
Эксперимент, который провел этот немецкий физик, привел его к следующему убеждению: сила тока I, проходящего через металлический проводник, пропорциональна напряжению на его концах, или I = U/R
Здесь напряжением называется разность, образно говоря, «давлений», созданных двумя точками электрической цепи. Измеряют его в вольтах.
Электрический ток представляет собой число электронов, которые пропускает участок электрической цепи и измеряется в амперах. Сопротивлением считается свойство цепи помешать этому движению. В честь упомянутого физика, его измеряют в омах.
Иначе говоря, проводник, через который проходит ток в 1 ампер при напряжении в 1 вольт, обладает сопротивлением в 1 ом.
Вся остальная электротехника «пляшет» от этого.
О мощности электрического тока
В физике мощностью считают скорость выполнения работы. Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.
Так же и в случае с электрическим током: ее мощность представляет собой отношение работы, произведенной движущимися электрическими зарядами к промежутку времени, которое для этого понадобилось.
Проще говоря, для того, чтобы получить электрическую мощность в 1 ватт, когда источник тока имеет напряжение 1 вольт, необходимо пропустить через проводник ток в 1 ампер. Другими словами, мощность (P) можно посчитать, перемножив друг на друга электрическое напряжение и ток:
P = U*I.
Запомнив эту нехитрую формулу, на практике можно рассчитать мощность. Например, если известны значения тока и сопротивления, а о напряжении сведений нет, можем воспользоваться законом Ома, подставив в формулу вместо него I*R. Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление.
Этот закон точно так же придет на помощь, если известны величины напряжения и сопротивления. В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.
Закон Ома и мощность
Используя закон Ома, формула мощности тока P = UI записывается в таком виде:

P = UI = U2/R = I2/R Итак, мощность, выделяемая на проводниках, прямо пропорциональна силе тока, протекающей через проводник, и напряжению на его концах.
Коэффициент полезного действия электрического прибора
Как известно, идеальных машин и механизмов не существует (то есть таких, которые бы полностью превращали один вид энергии в другой или генерировали бы энергию).
Во время работы устройства обязательно часть затраченной энергии уходит на преодоление нежелательных сил сопротивления или просто «рассеивается» в окружающую среду.
Таким образом, только часть затраченной нами энергии уходит на выполнение полезной работы, для выполнения которой и было создано устройство.
Физическая величина, которая показывает, какая часть полезной работы в затраченной, называется коэффициентом полезного действия (далее КПД).
- Другими словами, КПД показывает, насколько эффективно используется затраченная работа при ее выполнении, например, электрическим прибором.
- КПД (обозначается греческой буквой η («эта»)) — физическая величина, которая характеризует эффективность электрического прибора и показывает, какая часть полезной работы в затраченной.
- КПД определяется (как и в механике) по формуле:
- η = AП/AЗ·100%
- Если известна мощность электрического тока, формулы для определения ККД будут выглядеть так:
- η = PП/PЗ·100%
- Прежде чем определять КПД некоторого устройства, необходимо определить, что является полезной работой (для чего создано устройство), и что является затраченной работой (работа выполняется или какая энергия затрачивается для выполнения полезной работы).
Активная, реактивная и полная (кажущаяся) мощности
Простое объяснение с формулами
Активная мощность (P)
Другими словами активную мощность можно назвать: фактическая, настоящая, полезная, реальная мощность. В цепи постоянного тока мощность, питающая нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, то есть
P = V I
потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.
Но при синусоидальных сигналах, то есть в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активная мощность), которая в действительности питает нагрузку, определяется как:
P = V I Cosθ
В цепи переменного тока, если она чисто активная (резистивная), формула для мощности та же самая, что и для постоянного тока: P = V I.
Формулы для активной мощности
P = V I – в цепях постоянного тока
P = V I cosθ – в однофазных цепях переменного тока
P = √3 VL IL cosθ – в трёхфазных цепях переменного тока
P = 3 VPh IPh cosθ
P = √ (S2 – Q2) или
P =√ (ВА2 – вар2) или
Активная мощность = √ (Полная мощность2 – Реактивная мощность2) или
кВт = √ (кВА2 – квар2)
Реактивная мощность (Q)
Также её мощно было бы назвать бесполезной или безваттной мощностью.
Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, известна как реактивная (Q).
Реактивной называется мощность, которая потребляется и затем возвращается нагрузкой из-за её реактивных свойств. Единицей измерения активной мощности является ватт, 1 Вт = 1 В х 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного поля или электрического поля в случае, соответственно, индуктивности или конденсатора.
Реактивная мощность определяется, как
Q = V I sinθ
и может быть положительной (+Ve) для индуктивной нагрузки и отрицательной (-Ve) для емкостной нагрузки.
Единицей измерения реактивной мощности является вольт-ампер реактивный (вар): 1 вар = 1 В х 1 А. Проще говоря, единица реактивной мощности определяет величину магнитного или электрического поля, произведённого 1 В х 1 А.
Формулы для реактивной мощности
Q = V I sinθ
Реактивная мощность = √ (Полная мощность2 – Активная мощность2)
вар =√ (ВА2 – P2)
квар = √ (кВА2 – кВт2)
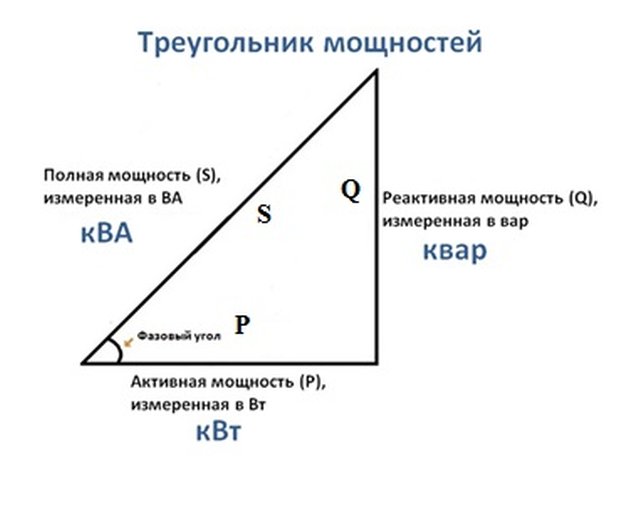
Полная мощность (S)
Полная мощность – это произведение напряжения и тока при игнорировании фазового угла между ними. Вся мощность в сети переменного тока (рассеиваемая и поглощаемая/возвращаемая) является полной.
Комбинация реактивной и активной мощностей называется полной мощностью. Произведение действующего значения напряжения на действующее значение тока в цепи переменного тока называется полной мощностью.
Она является произведением значений напряжения и тока без учёта фазового угла. Единицей измерения полной мощности (S) является ВА, 1 ВА = 1 В х 1 А. Если цепь чисто активная, полная мощность равна активной мощности, а в индуктивной или ёмкостной схеме (при наличии реактивного сопротивления) полная мощность больше активной мощности.
Формула для полной мощности
S = V I
Полная мощность = √ (Активная мощность2 + Реактивная мощность2)
kVA = √(kW2 + kVAR2)
Следует заметить, что:
- резистор потребляет активную мощность и отдаёт её в форме тепла и света.
- индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
- конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.
Все эти величины тригонометрически соотносятся друг с другом, как показано на рисунке:
Предыдущая
РазноеЭнергия конденсатора
Следующая
РазноеАвтоматические выключатели
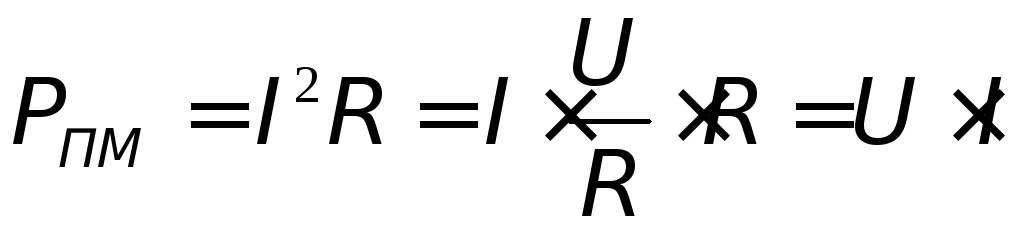 ,
,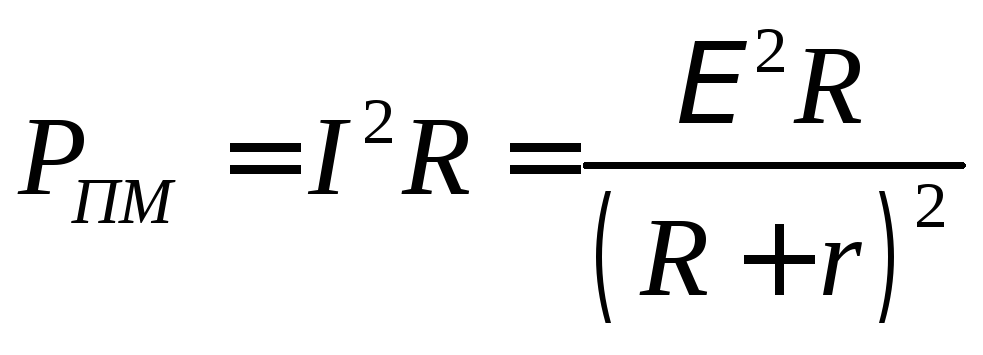 .
.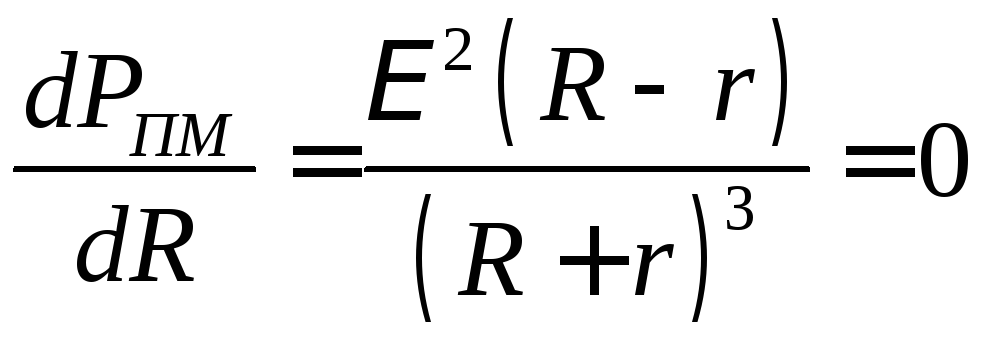 .
.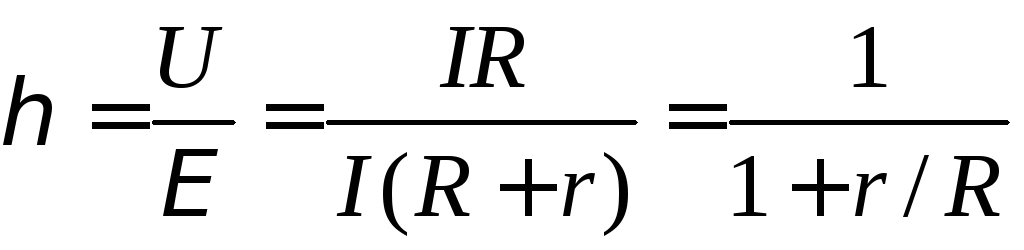 .
.