Определением реакций опор называют расчет величины и направления реактивных (т.е. ответных) сил и моментов, возникающих в опорах конструкций под действием системы заданных внешних нагрузок.
В рассмотренных ниже примерах, для наглядности, заданные внешние нагрузки показаны синим или зеленым цветом, а реакции опор — красным или оранжевым.
При решении задач, определяемые реакции опор могут обозначаться по разному:
- буквой R (от англ. Reaction). В этом случае, для уточнения точки приложения и направления силы могут добавляться соответствующие индексы (например, RAy — это реакция в точке A направленная вдоль оси Y);
- буквами V (Vertical) и H (Horizontal) обозначаются соответственно вертикальная и горизонтальная составляющие полной реакции (например, HB — это реакция в точке B направленная вдоль оси балки);
- Также возможно обозначение реакций по осям координат — YA, XB и т.д.
Сохранить или поделиться с друзьями
Рассмотрим решение всех типов задач по расчету величины и направления опорных реакций в заделках, шарнирных опорах и стержнях:
Примеры нахождения реакций опор
Примеры нахождения реакций опор для различных способов закрепления и нагружения бруса, балок, рам и других элементов конструкций.
Реакции опоры и стержня системы
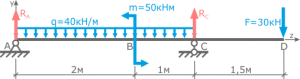
Невесомая балка удерживается в горизонтальном положении шарнирно-неподвижной опорой в т. A и вертикальным стержнем BC.
В точке D к балке приложена сосредоточенная сила F=30кН под углом 50°.
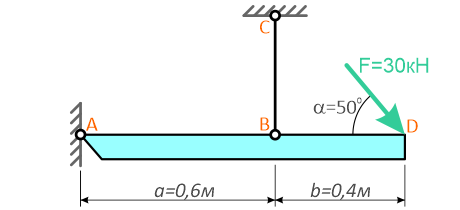
Требуется найти реакции, возникающие в опоре A и стержне BC.
Решение
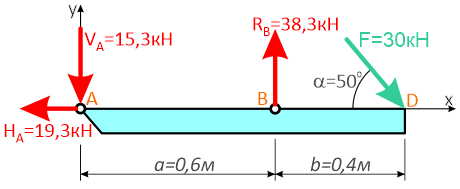
Для решения задачи, покажем систему координат x-y и зададим произвольное направление реакций.
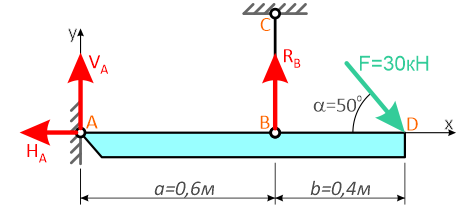
В точке A реакция в опоре раскладывается на две составляющие — вертикальную VA и горизонтальную HA.
Реакция в стержне (RB) всегда направлена вдоль самого стержня.
Для определения трех реакций требуется три уравнения равновесия.
Это будут два уравнения суммы моментов относительно точек в опорах и сумма проекций всех сил на ось x равные нулю.
Составим их:
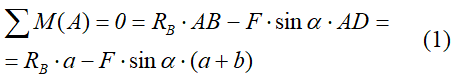
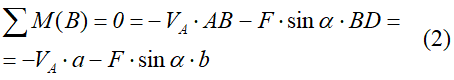
![]()
Из полученных уравнений выражаем и находим искомые реакции опор
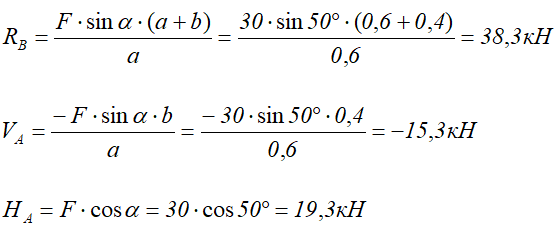
Вертикальная реакция в опоре A получилась отрицательной, это значит что она направлена в противоположную сторону.
Направляем ее вниз, изменив знак на «плюс».
Выполним проверку найденных реакций, проецируя все силы на ось y.
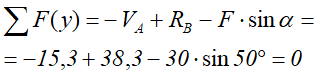
Равенство нулю суммы проекций всех сил и реакций показывает то, что реакции опор найдены верно.
Таким образом, заданная балка удерживается в равновесии под действием одной активной и трех реактивных сил.
Расчет реакций опор балки
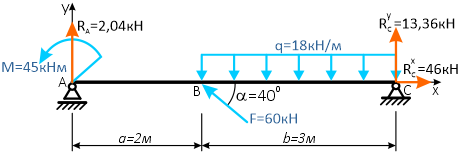
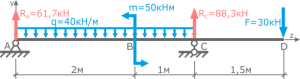
Простая балка на двух шарнирных опорах нагружена системой усилий, включающей силу F=60кН, приложенную под углом 40°, момент M=45кНм и равномерно распределенную нагрузку q=18кН/м.
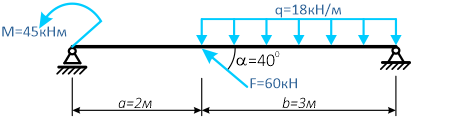
Требуется определить реакции в опорах A и C.
Решение
Вычерчиваем заданную схему в масштабе, показываем численные значения нагрузок, систему координат x-y и задаем произвольное направление реакций.
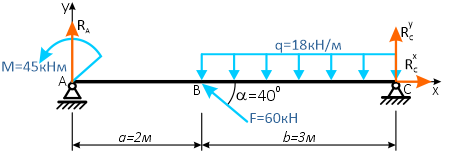
Здесь, в шарнирно-подвижной опоре будет только одна составляющая реакции.
Для упрощения решения, распределенную нагрузку можно заменить её равнодействующей, которая при равномерном распределении q будет приложена по её центру
![]()
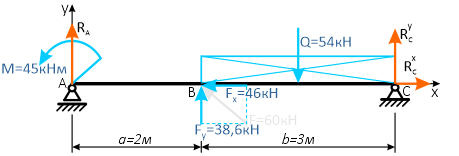
а силу F можно разложить на составляющие, спроецировав её на оси x и y.
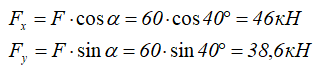
В следющих примерах эти действия выполнять не будем, проводя вычисления напрямую со значениями q и F.
Аналогично тому, как это делалось при решении предыдущей задачи, записываем уравнения равновесия балки: нулевые суммы моментов всех нагрузок и искомых реакций относительно опор
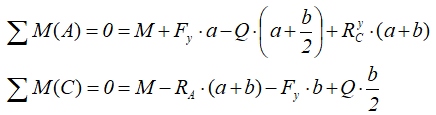
и проекций сил на ось балки
![]()
Откуда находим все три опорные реакции
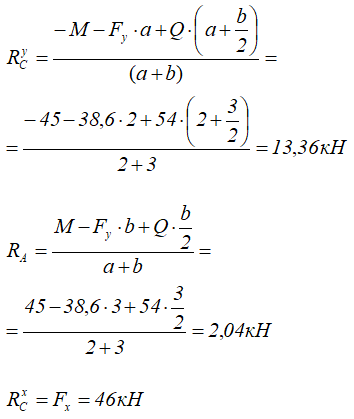
Все результаты положительны, следовательно, направление реакций было выбрано верно.
Проверяем найденные значения.
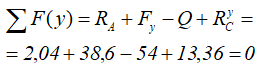
Величина реакций рассчитана правильно.
Подробное решение данного типа задач
Остальные задачи по определению опорных реакций с детальным разбором выполняемых действий:
При растяжении-сжатии стержней
Определение реакций в опорах стержней и стержневых систем при действии продольных сил.
- Расчет опорной реакции при растяжении-сжатии
- Расчет опорной реакции ступенчатого бруса
- Опорная реакция в заделке стержня с продольно распределенной нагрузкой
При кручении
Примеры расчета опорных моментов и реакций в подшипниках вала при кручении.
- Определение неизвестного крутящего момента вала
- Определение реакций подшипников пространственно нагруженного вала
- Расчет уравновешивающего момента вала
При изгибе балок и рам
Определение реакций в шарнирных опорах и заделках консольных балок и рам при действии систем внешних сил, моментов и распределенных нагрузок.
- Определение реакций в опорах двухопорной балки
- Расчет опорных реакций консольной балки
- Определение опорных реакций в жесткой заделке при изгибе
- Определение реакций опор балки, когда сила приложена под углом
- Проверка опорных реакций балки
- Расчет реакций в опорах рамы
- Определение опорных реакций балки (Видео)
Наш короткий видеоурок по расчету реакций опор балки:
Другие видео
Другие примеры определения реакций опор
Расчет реакций в опорах нестандартных систем.
- Определение реакции шарнира и опоры
- Реакции в шарнирах
- Реакции опор и шарнира
- Расчет веса противовеса и реакций в шарнирах
- Величина груза обеспечивающая равновесие и реакции в подшипниках
- Определение усилий в стержнях
- Натяжение троса и реакция опоры
- Реакции опор в точках системы
- Опорные реакции невесомой конструкции
- Опорные реакции в скользящей заделке
- Давление в шарнире и реакции в бискользящей заделке
- Реакции в скользящей заделке
- Расчет усилия в стержне
Типы опор и их реакции
В механике различают тела свободные: возможность перемещения, которых в любом направлении ничем не ограничена, и несвободные, когда перемещение данного тела ограничивают другие тела.
Сами тела ограничивающие свободу перемещения данного тела называют опорами (связями), а силы, с которыми опоры удерживают данное тело в равновесии, называют реакциями опор.
Направление реакций зависит от вида опор и схемы нагружения.
При решении задач очень важно правильно заменить опоры их реакциями, иначе записанные уравнения равновесия окажутся неверными.
И здесь важно помнить о том, что реакции могут появляться только по тем направлениям, в которых перемещение невозможно.
Рассмотрим определение реакций в основных типах опор:
Другие видео
Реакция гладкой поверхности
Пусть некоторое тело опирается на гладкую поверхность.
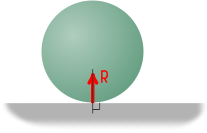
Здесь перемещение тела возможно только вдоль поверхности.
Движение перпендикулярно ей исключено.
Потому что перемещению в сторону поверхности препятствует сама поверхность, а при движении от нее нарушится сама связь.
Таким образом, гладкая поверхность препятствует перемещению тела только в направлении нормали, поэтому реакция гладкой поверхности всегда направлена по нормали к этой поверхности.
При взаимодействии криволинейных поверхностей аналогично, реакция направлена нормально к касательной в точке контакта тел.
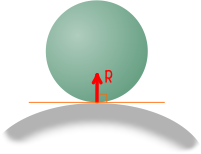
То же самое будет при контакте в двух точках.
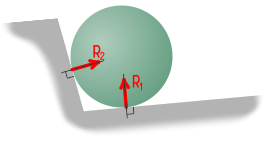
Реакция ребра
В случае, когда прямая балка опирается на ребро, реакции будут направлены перпендикулярно опираемой или опирающейся плоскости в точке их касания.
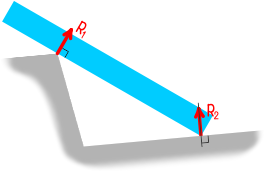
При повороте балки реакция всегда будет оставаться нормальной к соответствующей поверхности.
Гибкая связь
Для тела, подвешенного на нерастяжимой нити или тросе, связь не позволяет телу удаляться от точки подвеса в направлении самой нити.
Поэтому реакция гибкий связи будет направлена всегда только вдоль самой нити.
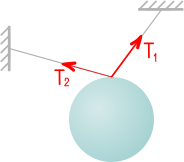
Реакции в стержнях
Как и в предыдущем пункте, в стержнях, которые с помощью шарниров соединяют какие-либо элементы с опорами, реакции направлены вдоль самих стержней.
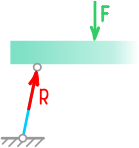
Но в отличие от нитей, здесь может быть одно из двух направлений: растягивающее стержень или сжимающее его.
Реакции в шарнирных опорах
На плоскости возможны только три направления перемещения:
Линейные — вдоль осей x и y, и вращение относительно оси Z.
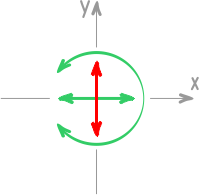
Поэтому в двумерных системах каждая опора может давать не более трех реакций.
Если свободное тело закрепить шарнирно-неподвижной опорой, которая допускает вращение, но исключает любые линейные перемещения, то в такой опоре могут возникать две реакции.
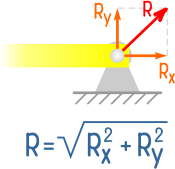
Они являются осевыми проекциями полной реакции опоры, которая может быть найдена как корень из суммы квадратов её составляющих.
Направление вектора полной реакции зависит от схемы нагружения элемента.
Встречаются разные способы изображения шарнирно-неподвижных опор в расчетных схемах.
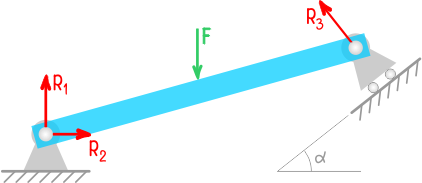
В шарнирно-подвижных опорах, помимо вращения возможно линейное перемещение вдоль поверхности, поэтому здесь будет только одна, нормальная к поверхности, составляющая реакции, которая по направлению и величине будет совпадать с полной.
У таких опор так же существуют дополнительные варианты схематичного изображения.
Пример направления реакций опор для балки на двух шарнирных опорах.
Реакции в заделках
Вид связи, при котором брус жестко закреплен в опоре называется глухой заделкой.
В этом случае исключены любые перемещения элемента.
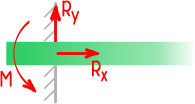
Поэтому в плоских заделках может возникать до трех реакций: горизонтальная и вертикальная составляющие полной реакции, а также момент.
Скользящая заделка допускает линейное перемещение вдоль одной из осей.
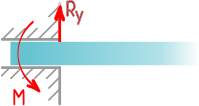
Следовательно, по этой оси реакции не будет.
В бискользящей заделке исключается только угловое перемещение элемента.
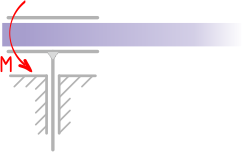
Здесь из реакций будет один момент.
Реакции опор в трехмерных системах
В пространстве возможно уже шесть направлений движения:
Поступательные вдоль каждой из осей и вращение относительно них.
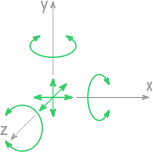
Поэтому в трехмерных системах опоры могут давать до шести реакций.
Шкив на валу, закрепленном подшипниками, может вращаться относительно продольной оси вала.
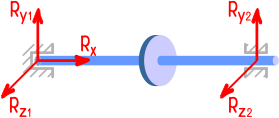
Любые другие перемещения невозможны.
В силу конструктивных особенностей подшипников моментов в них не возникает.
Здесь имеют место только реактивные силы.
В радиальном подшипнике (который справа) все реакции поперечны оси вала.
В радиально-упорном (который слева) добавляется еще и продольная.
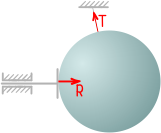
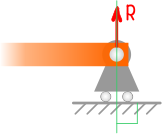
В трехмерном шарнире исключены любые линейные перемещения и возможны только повороты относительно трех осей, что дает до трех составляющих полной реакции R.
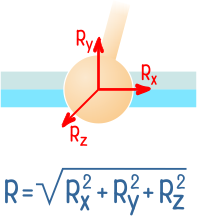
В жесткой заделке при общем случае нагружения может возникать до шести реакций: трёх сил и трех моментов.
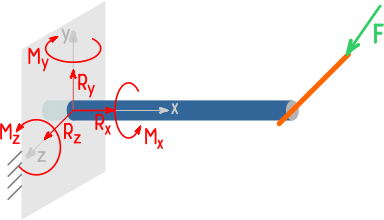
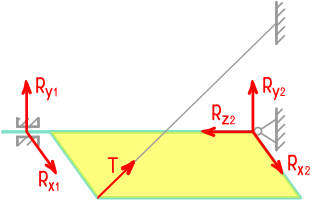
Пример замены опор их реакциями для трехмерной системы:
Порядок расчета опорных реакций
В рассмотренных выше примерах при определении реакций в опорах выполняется следующая последовательность действий:
- Вычерчивается (в масштабе) расчетная схема элемента с указанием всех размеров и приложенных внешних нагрузок;
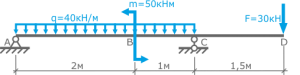
Расчетная схема балки - Выбирается система координат и обозначаются характерные сечения бруса;
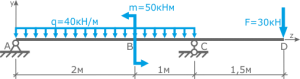
Система координат для балки - Определяется количество и возможное направление связей;
Направление опорных реакций балки - Записываются уравнения статики (по количеству неизвестных реакций);
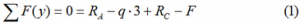
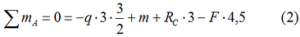
- Из уравнений равновесия находим величину и направление (по знаку) опорных реакций.
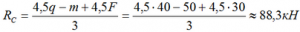
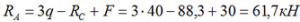
Опорные реакции балки
После расчетов выполняется проверка найденных значений.
Более подробно порядок расчета опорных реакций рассматривается в разделе «Статика» теоретической механики.
Другие примеры решения задач >
Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:



Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:

Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
![]()
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:

Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:


Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Содержание:
- Задача с решением 75-14.
- Задача с решением 76-14;
- Задача с решением 77-14.
- Задача с решением 79-14.
- Задача с решением 80-14*.
- Задача с решением 82-14.
- Определение реакций в общем случае
- Пример с решением 58.
- Пример с решением 59.
Как известно, любую плоскую систему сил можно привести к главному вектору  и главному моменту
и главному моменту 
Если же система сил уравновешена (тело, находящееся под действием такой системы сил, либо неподвижно, либо равномерно вращается около неподвижной оси, либо находится в равномерном и прямолинейном поступательном движении), то  и
и 
Эти равенства выражают два необходимых и достаточных условия равновесия любой системы сил.
Для произвольной плоской системы сил из этих двух условий непосредственно получаем три уравнения равновесия:

Первое и второе выражения — уравнения проекций — образуются из условия —  третье выражение – уравнение моментов – из условия
третье выражение – уравнение моментов – из условия 
Если на тело действует система параллельных сил, то уравнений равновесия получится только два: уравнение проекций на ось, параллельную силам, и уравнение моментов

При решении некоторых задач одно или оба уравнения проекций целесообразно заменить уравнениями моментов относительно каких-либо точек, т. е. систему уравнений равновесия можно представить в таком виде:

или

В первом случае линия, проходящая через точки  и
и  не перпендикулярна к оси
не перпендикулярна к оси  Во втором случае центры моментов
Во втором случае центры моментов 
 и
и  не лежат на одной прямой линии.
не лежат на одной прямой линии.
Для системы параллельных сил соответственно получаем два уравнения моментов:

В этом случае точки  и
и  не лежат на прямой, параллельной силам.
не лежат на прямой, параллельной силам.
В задачах, решаемых при помощи уравнений равновесия, обычно рассматриваются тела, находящиеся в состоянии покоя, тогда система сил, действующих на это тело, уравновешена.
Возможно вам будут полезны данные страницы:
Силы, действующие на тело, делятся на две группы. Одна группа сил называется нагрузками (активные силы), вторая группа сил называется реакциями связей (пассивные силы).
Нагрузки, как правило, бывают заданы. Они имеют числовое значение, точку приложения к телу и направление их действия.
В рассматриваемых ниже задачах используются лишь три разновидности нагрузок: сосредоточенные силы, равномерно распределенные силы* и пары сил (статические моменты)**.
Сосредоточенными называются силы, приложенные к точке тела. Если, например, на тело действуют нагрузки  или
или  как показано
как показано

на рис. 91, а, действия этих нагрузок можно считать приложенными соответственно к точкам  или
или  тела и на расчетных схемах изобразить так, как это выполнено на рис. 91, б.
тела и на расчетных схемах изобразить так, как это выполнено на рис. 91, б.
Равномерно распреде.генные нагрузки, например кирпичная кладка (рис. 92, а), или собственный вес однородного тела (бруса, балки) постоянного поперечного сечения по всей его длине задается при помощи двух параметров —интенсивности  и длины
и длины  па протяжении которой они действуют. На расчетных схемах эти нагрузки изображаются так, как показано на рис. 92, б.
па протяжении которой они действуют. На расчетных схемах эти нагрузки изображаются так, как показано на рис. 92, б.
- Пара сил (сосредоточенный момент), например, может быть образована двумя одинаковыми грузами
 действующими на тело так, как показано на рис. 93, а. Условное изображение пары сил, действующей на тело, показано на рис. 93, б.
действующими на тело так, как показано на рис. 93, а. Условное изображение пары сил, действующей на тело, показано на рис. 93, б.
Очень часто в каком-либо месте тела возникает совместное действие сосредоточенной силы и момента. Пусть, например, груз  подвешен на конце бруса, жестко заделанного другим концом
подвешен на конце бруса, жестко заделанного другим концом

в каком-либо теле (рис. 94, а). Если перенести действие силы в точку  тела (рис. 94, б), то получим в ней совместное действие сосредоточенной силы и момента.
тела (рис. 94, б), то получим в ней совместное действие сосредоточенной силы и момента.
Как правило, в задачах по статике реакции связей —искомые величины. Для каждой искомой реакции связи обычно необходимо
знать ее направление и числовое значение (модуль).
Направления реакций идеальных связей —связей без трения — определяют в зависимости от вида связи по следующим правилам.
1. При свободном опирании тела на связь реакция связи направлена от связи к телу перпендикулярно либо к поверхности тела ( рис. 95), либо к поверхности связи (
рис. 95), либо к поверхности связи ( рис. 95), либо к общей касательной обеих поверхностей (
рис. 95), либо к общей касательной обеих поверхностей ( рис. 95).
рис. 95).

Во всех этих случаях связь препятствует движению тела в одном направлении —перпендикулярном к опорной поверхности.
2. Если связями являются нити, цепи, тросы (гибкая связь), то они препятствуют движению тела только будучи натянутыми.
Поэтому реакции нитей, цепей, тросов всегда направлены вдоль их самих в сторону от тела к связи ( и
и  рис. 96).
рис. 96).
3. Если связь тела с какой-либо опорной поверхностью осуществляется при помощи подвижного шарнира (рис. 97), то его реакция направлена перпендикулярно к опорной поверхности. Таким

образом, подвижный шарнир (т. е. шарнир, ось которого может передвигаться вдоль опорной поверхности) представляет собой конструктивный вариант свободного опирания.
4. Если соединение тела со связью осуществляется при помощи неподвижного шарнира (рис. 98), то определить непосредственно направление реакции нельзя, за исключением тех частных случаев, которые описаны ниже.

Шарнирное соединение препятствует поступательному перемещению тела во всех направлениях в плоскости, перпендикулярной к оси шарнира. Направление реакции неподвижного шарнира может быть любым в зависимости от направления действия остальных сил. Потому сначала определяют две взаимно перпендикулярные составляющие  и
и  (или
(или  и
и  ) реакции шарнира, а затем, если нужно, по правилу параллелограмма или треугольника можно определить как модуль, так и направление полной реакции
) реакции шарнира, а затем, если нужно, по правилу параллелограмма или треугольника можно определить как модуль, так и направление полной реакции  (или
(или  ).
).
Направление реакции неподвижного шарнира непосредственно определяют в двух следующих случаях:
а) если, кроме реакции шарнира, все остальные силы (нагрузки и реакция другой связи) образуют систему параллельных сил, то реакция неподвижного шарнира также параллельна всем силам;
б) если, кроме реакции шарнира, на тело действуют еще только две непараллельные силы, то линия действия реакции неподвижного шарнира проходит через ось шарнира и точку пересечения двух других сил (задачи 47-9 и 48-9).
5. Движение тела может быть ограничено жесткой заделкой в какой-либо опоре (рис. 99). В этом случае даже одна жесткая заделка обеспечивает равновесие тела при любых нагрузках.
Так же как и неподвижный шарнир, жесткая заделка препятствует поступательному перемещению тела. Поэтому направление
ее реакции заранее определить нельзя и сначала определяют составляющие  и
и  Кроме того, жесткая заделка препятствует повороту тела в плоскости действия сил, поэтому, кроме силы реакции, на тело действует еще момент заделки
Кроме того, жесткая заделка препятствует повороту тела в плоскости действия сил, поэтому, кроме силы реакции, на тело действует еще момент заделки  уравновешивающий стремление нагрузок повернуть тело (вывернуть тело из заделки).
уравновешивающий стремление нагрузок повернуть тело (вывернуть тело из заделки).

Таким образом, если опорой тела является жесткая заделка, то со стороны последней на тело действуют реакция заделки, которую можно заменить двумя взаимно перпендикулярными составляющими, и момент заделки.
6. Иногда тело удерживается в равновесии при помощи жестких стержней, шарнирно соединенных с телом и с опорами (рис. 100). В отличие от гибкой связи (см. п. 2) такие стержни могут испытывать не только растяжение, но и сжатие.
Возможны и такие случаи, когда нельзя заранее установить, какие стержни растянуты, а какие сжаты. Поэтому при составлении уравнений равновесия исходят из того, что все стержни растянуты. Если же некоторые стержни окажутся в действительности сжатыми, tq в результате решения числовые значения реакций таких стержней получатся отрицательными.
Задача с решением 75-14.
На горизонтальную балку  левый конец которой имеет шарнирно-неподвижную опору, а правый — шарнирно-подвижную, в точках
левый конец которой имеет шарнирно-неподвижную опору, а правый — шарнирно-подвижную, в точках  и
и  поставлены два груза:
поставлены два груза:  и
и  (рис. 101, а). Определить реакции опор балки.
(рис. 101, а). Определить реакции опор балки.

Решение.
1. Рассмотрим равновесие балки  на которую в точках
на которую в точках  и
и  действуют две вертикальные нагрузки
действуют две вертикальные нагрузки  и
и  (рис. 101, б).
(рис. 101, б).
2. Освободив правый конец балки от связи и заменив ее действие реакцией  направленной перпендикулярно к опорной поверхности, увидим, что на балку действует система
направленной перпендикулярно к опорной поверхности, увидим, что на балку действует система
параллельных сил. Поэтому, если освободить и левый конец балки от шарнирно неподвижной опоры, то ее реакция будет также направлена вертикально (рис. 101, б).
3. Составим систему уравнений равновесия вида (5), приняв для одного уравнения за центр моментов точку  а для другого — точку
а для другого — точку 

4. Решая уравнения, из (1) находим 
из (2)
 5. Проверим правильность решения, составив уравнение проекций сил на вертикальную ось
5. Проверим правильность решения, составив уравнение проекций сил на вертикальную ось 

Подставляя в это уравнение числовые значения, получаем тождество
 или
или 
Значит задача решена правильно.
Реакции опор:
 и
и 
При решении задач рекомендуется не пренебрегать проверкой. От правильности определения реакций опор зависит правильность всего остального решения или расчета.
Задача с решением 76-14;
На консольную балку, имеющую в точке  шарнирно-непод-вижную, а в точке
шарнирно-непод-вижную, а в точке  шарнирно-под-вижную опору, действуют две сосредоточенные нагрузки:
шарнирно-под-вижную опору, действуют две сосредоточенные нагрузки:  и
и 
 как показано на рис. 102, а; угол
как показано на рис. 102, а; угол  Определить реакции опор балки.
Определить реакции опор балки.

Решение.
1. Рассматривая находящуюся в равновесии балку  видим, что в точке
видим, что в точке  на нее действует вертикально вниз нагрузка
на нее действует вертикально вниз нагрузка  а в точке
а в точке  под углом
под углом  к
к  действует другая нагрузка
действует другая нагрузка  (рис. 102, б).
(рис. 102, б).
2. Освобождаем балку от связей и заменим их действие реакциями. В месте шарнирно-подвижной опоры  возникает вертикальная реакция
возникает вертикальная реакция  Направление реакции шарнпрно-неподвиж-ной опоры в данном случае непосредственно определить нельзя, поэтому заменим эту реакцию се двумя составляющими
Направление реакции шарнпрно-неподвиж-ной опоры в данном случае непосредственно определить нельзя, поэтому заменим эту реакцию се двумя составляющими  и
и 
3. Для полученной системы из пяти сил, произвольно расположенных в плоскости, составим систему уравнений равновесия вида (3), расположив ось  вдоль балки, а за центры моментов приняв точки
вдоль балки, а за центры моментов приняв точки  и
и 


4. Решаем полученные уравнения. Из (1)

Так как

то из (2)

Замечая, что

из (3) получаем

Знак минус, получившийся в последнем случае, показывает, что  — вертикальная составляющая реакция неподвижного шарнира—направлена вниз, а не вверх, как предполагалось перед составлением уравнения (3).
— вертикальная составляющая реакция неподвижного шарнира—направлена вниз, а не вверх, как предполагалось перед составлением уравнения (3).
5. При необходимости реакцию  шарнира
шарнира  легко определить (рис. 102, в).
легко определить (рис. 102, в).
Модуль реакции шарнира  найдем из формулы
найдем из формулы

Направление реакции  установим, определив угол
установим, определив угол


откуда

6. Проверим правильность решения задачи. Так как при решении не использовано уравнение проекций на ось  то используем его для проверки:
то используем его для проверки:

Уравнение составлено по рис. 102, б.
После подстановки в это уравнение известных значений получим:

В данном случае, проверка решения при помощи уравнения проекций не дает возможности установить правильность определения полной реакции  шарнира
шарнира  Чтобы проверить и этот этап решения, составим уравнение моментов относительно точки
Чтобы проверить и этот этап решения, составим уравнение моментов относительно точки  воспользовавшись рис. 102, в, на котором изображена реакция так, как она направлена в действительности:
воспользовавшись рис. 102, в, на котором изображена реакция так, как она направлена в действительности:

Подставляем в это уравнение числовые значения, имея в виду, что


Расхождение в результатах, равное  получается из-за округлений при вычислениях.
получается из-за округлений при вычислениях.
В следующих задачах проверка решения не приводится и ее рекомендуется производить самостоятельно.
Задача с решением 77-14.
Горизонтальная балка имеет в точке  шарнирно-подвижную опору, плоскость которой наклонена к горизонту под углом
шарнирно-подвижную опору, плоскость которой наклонена к горизонту под углом  (рис. 103, а), а в точке
(рис. 103, а), а в точке  — шарнирно-неподвижную опору. Балка нагружена в точках
— шарнирно-неподвижную опору. Балка нагружена в точках  и
и  двумя сосредоточенными силами
двумя сосредоточенными силами  кн и
кн и  Определить реакции опор.
Определить реакции опор.

Решение.
1. Так же как и в задаче 75-14, балка нагружена двумя параллельными силами, но в отличие от этой задачи здесь реакция подвижного шарнира  направлена не параллельно вертикальным нагрузкам, а под углом
направлена не параллельно вертикальным нагрузкам, а под углом  к вертикали – перпендикулярно к опорной поверхности шарнира (рис. 103,6). Поэтому реакция неподвижного шарнира не будет направлена вертикально и, так же как в задаче 76-14, ее целесообразно заменить двумя составляющими
к вертикали – перпендикулярно к опорной поверхности шарнира (рис. 103,6). Поэтому реакция неподвижного шарнира не будет направлена вертикально и, так же как в задаче 76-14, ее целесообразно заменить двумя составляющими  и
и 
2. Расположив оси  и
и  как показано на рис. 103, б, составляем уравнения равновесия вида (I):
как показано на рис. 103, б, составляем уравнения равновесия вида (I):

3. Решаем полученные уравнения. Из уравнения (3) находим 

Из уравнения (2) находим 

Из уравнения (1) находим 

Таким образом, реакция шарнира 

а составляющие реакции шарнира 

и

4. Проверку решения производим при помощи уравнения моментов относительно точки  или
или 
Следующую задачу рекомендуется решить самостоятельно.
Задача с решением 79-14.
На консольную балку, имеющую в точке  шарнирно-неподвижную, а в точке
шарнирно-неподвижную, а в точке  шарнирно-подвижную опору, действуют две нагрузки (рис. 104, а): в точке
шарнирно-подвижную опору, действуют две нагрузки (рис. 104, а): в точке  — сосредоточенная нагрузка
— сосредоточенная нагрузка  а на участке
а на участке  — равномерно распределенная нагрузка интенсивностью
— равномерно распределенная нагрузка интенсивностью  Определить реакции опор.
Определить реакции опор.

Решение.
1. В этой задаче, кроме сосредоточенной силы  на участке
на участке  действует равномерно распределенная сила, интенсивность которой
действует равномерно распределенная сила, интенсивность которой  Полная величина этой нагрузки (ее равнодействующая) равна
Полная величина этой нагрузки (ее равнодействующая) равна  и приложена в точке
и приложена в точке  посредине участка
посредине участка  (рис. 104,6), т. е.
(рис. 104,6), т. е.

2. Так же как в задаче 75-14, реакция  подвижного шарнира направлена вертикально (перпендикулярно к опорной поверхности). Следовательно, и реакция
подвижного шарнира направлена вертикально (перпендикулярно к опорной поверхности). Следовательно, и реакция  неподвижного шарнира направлена вертикально. Таким образом, на балку действует система параллельных сил (см. рис. 104, б).
неподвижного шарнира направлена вертикально. Таким образом, на балку действует система параллельных сил (см. рис. 104, б).
3. Составим два уравнения моментов относительно точек  и
и 

Из уравнения (1)

Отрицательное значение реакции  означает, что она направлена вниз, а не вверх, как показано на рис. 104, б, потому что момент силы
означает, что она направлена вниз, а не вверх, как показано на рис. 104, б, потому что момент силы  относительно опоры
относительно опоры  больше, чем момент равномерно распределенной нагрузки.
больше, чем момент равномерно распределенной нагрузки.
Из уравнения (2) находим 

Таким образом, реакция шарнира  равна
равна  и направлена вертикально вниз; реакция шарнира
и направлена вертикально вниз; реакция шарнира  составляет
составляет  и направлена вертикально вверх.
и направлена вертикально вверх.
5. Для проверки решения можно использовать уравнение проекций на вертикальную ось.
Задача с решением 80-14*.
На двухконсольную балку с шарнирно-неподвижной опорой в точке  и с шарнирно-подвижной в точке
и с шарнирно-подвижной в точке  действуют, как показано на рис. 105,а, сосредоточенная сила
действуют, как показано на рис. 105,а, сосредоточенная сила  сосредоточенный момент (пара сил)
сосредоточенный момент (пара сил)  и равномерно распределенная нагрузка интенсивностью
и равномерно распределенная нагрузка интенсивностью  Определить реакции опор.
Определить реакции опор.

Решение.
1. В отличие от предыдущей задачи здесь, кроме сосредоточенной силы и равномерно распределенной-нагрузки, равнодействующая  которой приложена в точке
которой приложена в точке  посредине участка
посредине участка  на балку действует момент
на балку действует момент  направленный по часовой стрелке (рис. 105, б).
направленный по часовой стрелке (рис. 105, б).
2. После освобождения балки от связей и замены связей их реакциями  и
и  получаем уравновешенную систему, составленную из четырех параллельных сил и одной пары сил (момента).
получаем уравновешенную систему, составленную из четырех параллельных сил и одной пары сил (момента).
3. Составим два уравнения моментов относительно точек  и
и 

4. Решая эти уравнения, находим, что
 и
и 
Задача с решением 82-14.
Жестко заделанная у левого конца консольная балка  (рис. 107, а) нагружена равномерно распределенной нагрузкой интенсивностью
(рис. 107, а) нагружена равномерно распределенной нагрузкой интенсивностью 
 сосредоточенной силой
сосредоточенной силой  и моментом
и моментом 
 Определить реакции заделки.
Определить реакции заделки.


Решение.
1. На балку действуют три нагрузки: в точке  — вертикальная сосредоточенная сила
— вертикальная сосредоточенная сила  по всей длине балки — равномерно распределенная нагрузка, которую заменим сосредоточенной силой
по всей длине балки — равномерно распределенная нагрузка, которую заменим сосредоточенной силой  приложенной в точке
приложенной в точке 
 Правый конец балки нагружен моментом
Правый конец балки нагружен моментом  действующим против хода часовой стрелки (рис. 107, б).
действующим против хода часовой стрелки (рис. 107, б).
2. Равновесие балки обеспечивается жесткой заделкой у точки  Освободив балку от связи, заменим ее действие силой — реакцией связи
Освободив балку от связи, заменим ее действие силой — реакцией связи  и реактивным моментом
и реактивным моментом  Но так как реакцию
Но так как реакцию  заделки сразу определить нельзя (по тем же причинам, что и направление реакции неподвижного шарнира), заменим
заделки сразу определить нельзя (по тем же причинам, что и направление реакции неподвижного шарнира), заменим  ее составляющими
ее составляющими  и
и  совместив их с осями
совместив их с осями  и
и  (см. рис. 107, б).
(см. рис. 107, б).
3. Составим уравнения равновесия — уравнение проекции на оси  и
и  и уравнение моментов относительно точки
и уравнение моментов относительно точки 



4. Из уравнения (1)

а это означает, что горизонтальная составляющая реакции заделки  равна нулю, так как в данном случае нет усилий, смещающих балку
равна нулю, так как в данном случае нет усилий, смещающих балку  в горизонтальном направлении. Из уравнения (2)
в горизонтальном направлении. Из уравнения (2)

Выше найдено, что  ; значит реакция заделки
; значит реакция заделки  перпендикулярна к оси
перпендикулярна к оси  Следовательно,
Следовательно,

Из уравнения (3)

Таким образом,
 и
и 
5. Проверку правильности решения можно произвести при помощи уравнения моментов относительно точки  или
или  В любое из них входят обе найденные величины.
В любое из них входят обе найденные величины.
Следующую задачу рекомендуется решить самостоятельно.
Определение реакций в общем случае
Один из способов определения реакций связей был уже рассмотрен при изучении уравнений равновесия с множителями Лагранжа, когда связи задаются неявными уравнениями или неравенствами. В общем же случае связи, наложенные на систему материальных точек, всегда могут быть заменены соответствующими силами реакций, действие которых эквивалентно действию связей. После такой замены система может рассматриваться как свободная от связей, но подверженная действию как активных, так и пассивных сил. Принцип Бернулли для такой свободной системы дает необходимые и достаточные условия равновесия в виде уравнения

где  — проекции активных сил на неподвижные оси координат;
— проекции активных сил на неподвижные оси координат;  — проекции сил реакции на те же оси. Величины
— проекции сил реакции на те же оси. Величины  теперь полностью произвольны, так что равенство (а) будет выполняться для всех возможных перемещений лишь в том случае, когда обращаются в нуль все коэффициенты при
теперь полностью произвольны, так что равенство (а) будет выполняться для всех возможных перемещений лишь в том случае, когда обращаются в нуль все коэффициенты при  т. е.
т. е.

Последние уравнения и служат для определения реакций связи. Если по условиям задачи требуется определять не все, а лишь некоторые силы реакции, то система освобождается только от тех связей, реакции которых необходимо определить. Освобождая систему от связей, тем самым добавляем ей возможные перемещения, которые раньше не допускались связями и на которых будут работать реакции освобожденных связей.
Подсчитывая сумму работ активных сил и сил реакции связей на освобожденном перемещении, получим условия для определения реакций связи.
Пример с решением 58.
Исследовать условия равновесия твердого тела, у которого закреплены две точки  и
и  и на которое действуют активные силы
и на которое действуют активные силы  приложенные к точкам
приложенные к точкам  (рис. 138).
(рис. 138).
Решение. Выберем начало неподвижной системы координат в точке  а ось
а ось  направим по прямой
направим по прямой  Наложенные езязи допускают вращение твердого тела вокруг оси
Наложенные езязи допускают вращение твердого тела вокруг оси  Подсчитывая работу активных сил на этом возможном перемещении, получим
Подсчитывая работу активных сил на этом возможном перемещении, получим

где  — угол поворота твердого тела вокруг оси
— угол поворота твердого тела вокруг оси  Отсюда сразу же получаем условие равновесия твердого тела, которое сводится к равенству нулю суммы моментов всех активных сил, действующих на твердое тело, относительно оси
Отсюда сразу же получаем условие равновесия твердого тела, которое сводится к равенству нулю суммы моментов всех активных сил, действующих на твердое тело, относительно оси 

Для определения реакции в точке  освободим твердое тело от связи в этой точке, заменив действие последней действием неизвестной силы
освободим твердое тело от связи в этой точке, заменив действие последней действием неизвестной силы Освобожденное от связи тело может вращаться как вокруг оси
Освобожденное от связи тело может вращаться как вокруг оси  так и вокруг оси
так и вокруг оси  Сообщим твердому телу бесконечно малое возможное перемещение, повернув его вокруг оси
Сообщим твердому телу бесконечно малое возможное перемещение, повернув его вокруг оси  на угол
на угол  и подсчитаем работу всех сил на этом возможном перемещении. Возможные перемещения точек твердого тела определятся из матрицы
и подсчитаем работу всех сил на этом возможном перемещении. Возможные перемещения точек твердого тела определятся из матрицы

так что


Из принципа Бериулли для освобожденного твердого тела будем иметь

подставляя сюда значения вариаций координат, получим

или, после сокращения на 

где  — сумма моментов активных сил относительно оси
— сумма моментов активных сил относительно оси  a
a  — расстояние
— расстояние 
Точно таким же путем можно получить реакцию  рассматривая поворот твердого тела вокруг оси
рассматривая поворот твердого тела вокруг оси  Возможные перемещения в этом случае будут определяться из матрицы
Возможные перемещения в этом случае будут определяться из матрицы

так что

Подставляя найденные значения вариаций координат в общее уравнение статики, получим

или

Реакция  таким способом не может быть найдена, потому что любое возможное перемещение точки
таким способом не может быть найдена, потому что любое возможное перемещение точки  твердого тела ортогонально направлению силы
твердого тела ортогонально направлению силы  , и задача оказывается статически неопределимой.
, и задача оказывается статически неопределимой.
Пример с решением 59.
На гладкой горизонтальной плоскости лежат несколько одинаковых однородных цилиндрических труб. Чтобы трубы не раскатывались, они подпираются двумя брусьями  и
и  как показано на рис. 139. Определить реакции брусьев.
как показано на рис. 139. Определить реакции брусьев.
Решение. Для определенности рассмотрим пятнадцать труб, расположенных, как указано на чертеже. Чтобы избежать рассмотрения статически неопределимой задачи, предположим, что расстояние между брусками  и
и  больше суммы диаметров нижних труб. Положение системы определим четырьмя параметрами
больше суммы диаметров нижних труб. Положение системы определим четырьмя параметрами  и
и  (углы, которые образуют прямые, соединяющие центры труб нижнего и верхнего ряда с горизонталью), которые связаны соотношением
(углы, которые образуют прямые, соединяющие центры труб нижнего и верхнего ряда с горизонталью), которые связаны соотношением

где  — сколь угодно малое число. Углы
— сколь угодно малое число. Углы  и
и  подчиняются еще условиям
подчиняются еще условиям

Будем предполагать сначала, что последние условия выполняются лишь в виде неравенств. Определив вертикальные координаты центров труб

Запишем принцип Торричелли для системы с удерживающими связями:

или, после подстановки значений 

где величины  и
и  связаны соотношением
связаны соотношением

Определив из последнего уравнения 

и подставив это значение в равенство (с), получим уравнение для независимых параметров 


Приравнивая нулю коэффициенты при  и
и  приходим к следующим условиям равновесия системы:
приходим к следующим условиям равновесия системы:


которые можно переписать в виде

Принимая во внимание неравенства (b), получим условия равновесия

Величины и
и  должны удовлетворять уравнению (а), которое перепишется в виде
должны удовлетворять уравнению (а), которое перепишется в виде

При  отсюда находим предельное значение для
отсюда находим предельное значение для 

В самом деле,

При уменьшении  левая часть равенства (f) будет увеличиваться, а следовательно, будет возрастать и
левая часть равенства (f) будет увеличиваться, а следовательно, будет возрастать и  Таким образом, предполагая связи (Ь) в положении равновесия выполненными в виде неравенств, устанавливаем, что в положении равновесия должно быть
Таким образом, предполагая связи (Ь) в положении равновесия выполненными в виде неравенств, устанавливаем, что в положении равновесия должно быть

Лишь при выполнении этого неравенства нижине трубы в положении равновесия не будут касаться друг друга. Уменьшая  мы вынуждены будем отказаться от предположения, что все связи (Ь) в положении равновесия выполняются в виде неравенств. Из условий (е) следует, что первыми переходят в равенство связи
мы вынуждены будем отказаться от предположения, что все связи (Ь) в положении равновесия выполняются в виде неравенств. Из условий (е) следует, что первыми переходят в равенство связи
 и
и 
Рассмотрим теперь только такие состояния системы, для которых выполняются условия

Уравнение связи для возможных перемещений (d) приобретает вид

Общее уравнение статики для рассматриваемой системы перепишем в виде

Система линейных относительно  и
и  уравнений (d’) и (с7) обладает ненулевым решением, если обращается в нуль определитель
уравнений (d’) и (с7) обладает ненулевым решением, если обращается в нуль определитель
или

Отсюда следует, что в положении равновесия должно быть

Тогда из уравнения связи (а) находим

Как видно из последнего соотношения, при  получим
получим
 Для определения реакции в точке
Для определения реакции в точке  освободим систему от связи, убрав брус
освободим систему от связи, убрав брус  и заменив его действие силой реакции
и заменив его действие силой реакции  После такого освобождения системы параметры
После такого освобождения системы параметры  и
и  можно изменять независимо друг от друга. При этом должно выполняться условие
можно изменять независимо друг от друга. При этом должно выполняться условие  (при отличных от нуля
(при отличных от нуля  или
или  системе сообщается освобождающее перемещение, на котором будут совершать отличную от нуля работу силы реакции труб, находящихся при равнозесии в соприкосновении). Сообщим системе перемещение
системе сообщается освобождающее перемещение, на котором будут совершать отличную от нуля работу силы реакции труб, находящихся при равнозесии в соприкосновении). Сообщим системе перемещение

и подсчитаем работу всех сил, в том числе и работу силы  на возможном перемещении системы. Будем иметь
на возможном перемещении системы. Будем иметь

откуда следует

Если  то
то  и
и

Заметим, что на рассматриваемом перемещении опускаются вниз четыре трубы. У остальных труб вертикальные координаты не изменяются. Если обозначить через  вес опускающихся труб (в нашем случае
вес опускающихся труб (в нашем случае  ), то предельное значение силы реакции будет равно
), то предельное значение силы реакции будет равно

Задача. Расчет рамы. Для рамы построить эпюры продольных сил N, поперечных сил Q и изгибающих моментов М.

- Определим опорные реакции


Нанесем значения опорных реакций на расчетную схему.

2. Строим эпюру продольных сил N методом сечений. Имеем три характерных участка и три сечения на них.

Правило знаков продольных сил – продольная сила считается положительной, если сила растягивает стержень, и отрицательной, если сила сжимает стержень. Положительные значения откладываем влево от стойки и вверх от ригеля.

Строим эпюру продольных сил.

3. Строим эпюру поперечных сил Q методом сечений. Правило знаков – если сила относительно сечения направлена по часовой стрелке, то поперечная сила считается положительной и наоборот. Положительные значения откладываются влево от стоек и вверх от ригеля.

Строим эпюру поперечных сил

4. Строим эпюру изгибающих моментов М методом характерных точек. Расставляем точки: А – опора, В,С, — узлы рамы, D – свободный конец, К – середина равномерно распределенной нагрузки (точки экстремума при построении эп.Q не обнаружено). Эпюру М строим на сжатых волокнах (для машиностроительных специальностей), знак не ставим.

Строим эпюру моментов.

5. Вырезаем узлы С и В и проверяем их равновесие.

Узлы находятся в равновесии, значит эпюры построены верно.
Для балки с жесткой заделкой построить эпюры Q и М.

Расставляем сечения от свободного конца балки — в этом случае можно построить эпюры, не определяя опорных реакций. Рассматривать в каждом случае будем правую часть — справа от сечения. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 2 участка, 2 сечения.

Сечение 2-2 проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z2 вправо от сечения до начала участка. Определяем поперечные силы в сечениях. Правило знаков см. — здесь.

Строим эпюру Q.

Построим эпюру М методом характерных точек. Расставляем точки на балке — это точки начала и конца балки (D,A), сосредоточенного момента (B), а также отметим в качестве характерной точки середину равномерно распределенной нагрузки (K) — это дополнительная точка для построения параболической кривой.

Определяем изгибающие моменты в точках. Правило знаков см. — здесь.
![]()
Момент в т. В будем определять следующим образом. Сначала определим:
![]()
Теперь:
![]()
Точку К возьмем в середине участка с равномерно распределенной нагрузкой.

Строим эпюру M. Участок АВ – параболическая кривая (правило «зонтика»), участок ВD – прямая наклонная линия.

Для балки определить опорные реакции и построить эпюры изгибающих моментов (М) и поперечных сил (Q).

- Обозначаем опоры буквами А и В и направляем опорные реакции RА и RВ.

Составляем уравнения равновесия.

Проверка

Записываем значения RА и RВ на расчетную схему.
2. Построение эпюры поперечных сил методом сечений. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 4 участка, 4 сечения.

сеч. 1-1 ход слева.
Сечение проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z1 влево от сечения до начала участка. Длина участка 2 м. Правило знаков для Q — см. здесь.

Строим по найденным значением эпюру Q.
сеч. 2-2 ход справа.
Сечение вновь проходит по участку равномерно распределенной нагрузкой, отмечаем размер z2 вправо от сечения до начала участка. Длина участка 6 м.

Строим эпюру Q.
сеч. 3-3 ход справа.

сеч. 4-4 ход справа.

Строим эпюру Q.

3. Построение эпюры М методом характерных точек.
Характерная точка – точка, сколь-либо заметная на балке. Это точки А, В, С, D, а также точка К, в которой Q=0 и изгибающий момент имеет экстремум. Также в середине консоли поставим дополнительную точку Е, поскольку на этом участке под равномерно распределенной нагрузкой эпюра М описывается кривой линией, а она строится, как минимум, по 3 точкам.

Итак, точки расставлены, приступаем к определению в них значений изгибающих моментов. Правило знаков — см. здесь.
Участки NA, AD – параболическая кривая (правило «зонтика» у механических специальностей или «правило паруса» у строительных ), участки DС, СВ – прямые наклонные линии.

Момент в точке D следует определять как слева, так и справа от точки D. Сам момент в эти выражения не входит. В точке D получим два значения с разницей на величину m – скачок на его величину.

Теперь следует определить момент в точке К (Q=0). Однако сначала определим положение точки К, обозначив расстояние от нее до начала участка неизвестным х.

Т. К принадлежит второму характерному участку, его уравнение для поперечной силы (см. выше)

Но поперечная сила в т. К равна 0, а z2 равняется неизвестному х.
Получаем уравнение:

Теперь, зная х, определим момент в точке К с правой стороны.

Строим эпюру М. Построение выполним для механических специальностей, откладывая положительные значения вверх от нулевой линии и используя правило «зонтика».

Для заданной схемы консольной балки требуется построить эпюры поперечной силы Q и изгибающего момента M, выполнить проектировочный расчет, подобрав круглое сечение.
Материал — дерево, расчетное сопротивление материала R=10МПа, М=14кН·м,q=8кН/м
Строить эпюры в консольной балке с жесткой заделкой можно двумя способами — обычным, предварительно определив опорные реакции, и без определения опорных реакций, если рассматривать участки, идя от свободного конца балки и отбрасывая левую часть с заделкой. Построим эпюры обычным способом.
1. Определим опорные реакции.
Равномерно распределенную нагрузку q заменим условной силой Q= q·0,84=6,72 кН
В жесткой заделке три опорные реакции — вертикальная, горизонтальная и момент, в нашем случае горизонтальная реакция равна 0.
Найдем вертикальную реакцию опоры RA и опорный момент МA из уравнений равновесия.
2. Строим эпюру поперечных сил.
На первых двух участках справа поперечная сила отсутствует. В начале участка с равномерно распределенной нагрузкой (справа) Q=0, в заделеке — величине реакции RA. 3. Для построения эпюры изгибающих моментов M составим выражения для их определения на участках. Эпюру моментов построим на растянутых волокнах, т.е. вниз.
3. Для построения эпюры изгибающих моментов M составим выражения для их определения на участках. Эпюру моментов построим на растянутых волокнах, т.е. вниз. 
4.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Максимальный изгибающий момент с эпюры М=14 кН·м. Определим осевой момент сопротивления сечения

Таким образом, подбираем сечение с диаметром 25 см.
Требуется построить эпюры Q и M и подобрать стальную балку двутаврового поперечного сечения при расчетном сопротивлении R=160 МПа.

1.Определение реакций:
Сумма моментов относительно опор:
Опора А: 
Опора В:

Сумма проекций всех сил на ось У (проверка):
![]()
2.Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.
1) Первый участок:

2) Второй участок:

3) Третий участок:

3.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Подобрать стальную балку двутаврового поперечного сечения при R=160 МПа:
С эпюры берем максимальный момент:

По сортаменту подбираем двутавр № 20 с ![]()
Двутавр можно взять чуть меньше, при условии, что перенапряжение составляет меньше 5%:

Для заданной балки требуется построить эпюры Q и M, найти Mmax и сделать проектировочный расчет — подобрать деревянную балку круглого поперечного сечения. Расчетное сопротивление материала Ru=10 МПа.

1.Определение реакций:
Сумма проекций всех сил на ось z: ![]()
Сумма проекций всех сил на ось y: ![]()
Сумма моментов относительно точки А: 
После нахождения опорных реакций следует выполнить проверку, использовав уравнение равновесия (сумма моментов относительно любой выбранной точки должна быть равна нулю).
2. Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.
Q — поперечная сила, считается положительной, если стремится повернуть рассматриваемую часть балки по часовой стрелке.
M— изгибающий момент, считается положительным, если растягивает нижние волокна.
1)Первый участок:

2) Второй участок:

3) Третий участок:

Следует отметить ,что на втором и третьем участке для построения плавной кривой потребуются дополнительные точки, в которых следует посчитать значение изгибающего момента.
3.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Подберем деревянную балку круглого поперечного сечения при Ru=10 МПа
С эпюры берем максимальный момент и рассчитываем требуемый осевой момент сопротивления, после чего вычисляем необходимый диаметр балки.
Задача 1. Построить эпюры Q и M в балке с шарниром.

1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.
Если рассмотреть левую часть, то в уравнении ![]() будут присутствовать две неизвестные RА и МА. Значит, следует рассмотреть правую часть (из него найдем RВ).
будут присутствовать две неизвестные RА и МА. Значит, следует рассмотреть правую часть (из него найдем RВ).

Теперь ![]() из него найдем МА
из него найдем МА

Следующее уравнение ![]() из него найдем RА
из него найдем RА

2. Строим эпюру Q.
Участок первый — АС, смотрим левую часть
Участок второй — СВ, смотрим правую часть

3. Строим эпюру М

Определим момент в точке, где Q=0 (момент имеет экстремум), это момент в точке К, т.е. МК , для этого определим положение точки К.
![]() Это уравнение первого участка, на котором находится точка К
Это уравнение первого участка, на котором находится точка К
в точке К 
Строим эпюры. Задача решена.
Задача 2. Построить эпюры Q и M в балке с шарниром.

1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.
Если рассмотреть правую часть, то в уравнении ![]() будут присутствовать две неизвестные Rд и Rв. Значит, следует рассмотреть левую часть.
будут присутствовать две неизвестные Rд и Rв. Значит, следует рассмотреть левую часть.

Знак «-» говорит о том, что реакция RВ направлена в обратную сторону.
Проверка:
2. Построение эпюры Q.
Участок первый – ЕА, смотрим левую часть
Участок второй – АС, смотрим левую часть
Участок третий – СВ, смотрим левую часть
Участок четвертый – ВД, смотрим правую часть

3. Построение эпюры М

Т.к. точки экстремума на эп.Q не наблюдается, определяем изгибающий момент в середине участка ВД

Строим эпюры, задача решена.
Задача 1. Построить эпюры внутренних усилий для рамы ( рис.а).
Дано: F=30кН, q=40 кН/м, М=50кНм, а=1,8м, h=2м.

Решение.
Для рассматриваемой рамы опорные реакции можно не определять, поскольку будем рассматривать участки, идя от свободных концов рамы к заделке.
Вычислим значения внутренних усилий N, Q и М в характерных сечениях рамы. Правило знаков для поперечных сил Q и изгибающих моментов М такие же,как в балках. Эпюры моментов построим на сжатых волокнах. Для продольной N, силы правило знаков: растягивающая сила – положительна, сжимающая – отрицательна.
Участок ВС: ![]() (сжаты нижние волокна).
(сжаты нижние волокна).
![]() (сжаты нижние волокна).
(сжаты нижние волокна).
Участок DC:  (сжаты верхние волокна).
(сжаты верхние волокна).
Участок СК: ![]() (сжаты левые волокна)
(сжаты левые волокна)
![]() (сжаты левые волокна)
(сжаты левые волокна)
На рисунке – эпюры нормальных (продольных) сил — (б), , поперечных сил — (в) и изгибающих моментов — (г).
Проверка равновесия узла С:

Задача 2 Построить эпюры внутренних усилий для рамы (рис. а).
Дано: F=30кН, q=40 кН/м, М=50кНм, а=3м, h=2м.

Определим опорные реакции рамы:

Из этих уравнений найдем:

Поскольку значения реакции RK имеет знак минус, на рис. а изменяется направление данного вектора на противоположное, при этом записывается RK=83,33кН.
Определим значения внутренних усилий N, Q и М в характерных сечениях рамы:
Участок ВС:
(сжаты правые волокна).
Участок CD: 
(сжаты правые волокна);
![]()
(сжаты правые волокна).
Участок DE: 
(сжаты нижние волокна);

(сжаты нижние волокна).
Участок КС

(сжаты левые волокна).
Построим эпюры нормальных (продольных) сил (б), поперечных сил (в) и изгибающих моментов (г).
Рассмотрим равновесие узлов D и Е

Из рассмотрения узлов Dи Е видно, что они находятся в равновесии.
Задача 3. Для рамы с шарниром построить эпюры внутренних усилий.
Дано: F=30кН, q=40 кН/м, М=50кНм, а=2м, h=2м.

Решение. Определим опорные реакции. Следует отметить ,что в обеих шарнирно-неподвижных опорах по две реакции. В связи с этим следует использовать свойство шарнира С — момент в нем как от левых ,так и от правых сил равен нулю. Рассмотрим левую часть.
Уравнения равновесия для рассматриваемой рамы можно записать в виде:

Из решения данных уравнений следует:

На схеме рамы направление действия силы НВ изменяется на противоположное (НB=15кН).
Определим усилия в характерных сечениях рамы.
Участок BZ: 
(сжаты левые волокна).
Участок ZC:

(сжаты левые волокна);

Участок КD: ![]()
(сжаты левые волокна);

(сжаты левые волокна).
Участок DС:

(сжаты нижние волокна);

Определение экстремального значения изгибающего момента на участке CD :

(сжаты верхние волокна).
Строим эпюры внутренних усилий. Проверяем равновесие узлов рамы.
Узлы C и D находятся в равновесии.
Построение эпюр М и Q в балке с жесткой заделкой с определенными опорными реакциями. Построение методом характерных точек.

1. Построение эпюры поперечных сил. Для консольной балки (рис. а) характерные точки: А – точка приложения опорной реакции VA; С – точка приложения сосредоточенной силы; D, B– начало и конец распределенной нагрузки. Для консоли поперечная сила определяется аналогично двухопорной балке. Итак, при ходе слева:

Для проверки правильности определения поперечной силы в сечениях пройдите балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Помните, что правило знаков при этом изменятся. Результат должен получиться тот же. Строим эпюру поперечной силы (рис,б).
2. Построение эпюры моментов
Для консольной балки эпюра изгибающих моментов строится аналогично предыдущему построению.Характерные точки для этой балки (см. рис. а) следующие: А – опора; С — точка приложения сосредоточенного момента и силы F; D и В — начало и конец действия равномерно распределенной нагрузки. Поскольку эпюра Qx на участке действия распределенной нагрузки нулевую линию не пересекает, для построения эпюры моментов на данном участке (параболическая кривая) следует выбрать произвольно дополнительную точку для построения кривой, к примеру в середине участка.
Ход слева:

Ходом справа находим MB = 0.
По найденным значениям строим эпюру изгибающих моментов (см. рис. в).
Построение эпюр М и Q в балке на двух опорах с определенными опорными реакциями. Построение методом характерных точек.

1. Построение эпюры Qу. Из теоретического курса известно, что на участке балки с равномерно распределенной нагрузкой эпюра Qу ограничивается наклонной прямой, а на участке, на котором нет распределенной нагрузки, — прямой, параллельной оси, поэтому для построения эпюры поперечных сил достаточно определить значения Qу в начале и конце каждого участка. В сечении, соответствующем точке приложения сосредоточенной силы, поперечная сила должна быть вычислена чуть левее этой точки (на бесконечно близком расстоянии от нее) и чуть правее ее; поперечные силы в таких местах обозначаются соответственно ![]() .
.
Строим эпюру Qу методом характерных точек, ходом слева. Для большей наглядности отбрасываемую часть балки на первых порах рекомендуется закрывать листом бумаги. Характерными точками для двухопорной балки (рис. а) будут точки C и D – начало и конец распределенной нагрузки, а также A и B – точки приложения опорных реакций, E– точка приложения сосредоточенной силы. Проведем мысленно ось y перпендикулярно оси балки через точку С и не будем менять ее положение, пока не пройдем всю балку от C до E. Рассматривая левые отсеченные по характерным точкам части балки, проецируем на ось y действующие на данном участке силы с соответствующими знаками. В результате получаем:
Для проверки правильности определения поперечной силы в сечениях можно пройти балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Результат должен получиться тот же. Совпадение результатов может служить контролем построения эпюры Qу. Проводим нулевую линию под изображением балки и от нее в принятом масштабе откладываем найденные значения поперечных сил с учетом знаков в соответствующих точках. Получим эпюру Qу (рис. б).
Построив эпюру, обратите внимание на следующее: эпюра под распределенной нагрузкой изображается наклонной прямой, под ненагруженными участками — отрезками, параллельными нулевой линии, под сосредоточенной силой на эпюре образуется скачок, равный значению силы. Если наклонная линия под распределенной нагрузкой пересекает нулевую линию, отметьте эту точку, то это точка экстремума, и она является теперь для нас характерной, согласно дифференциальной зависимости между Qу и Мx, в этой точке момент имеет экстремум и его нужно будет определить при построении эпюры изгибающих моментов. В нашей задаче это точка К. Сосредоточенный момент на эпюре Qу себя никак не проявляет, так как сумма проекций сил, образующих пару, равна нулю.
2. Построение эпюры моментов.Строим эпюру изгибающих моментов, как и поперечных сил, методом характерных точек, ходом слева. Известно, что на участке балки с равномерно распределенной нагрузкой эпюра изгибающих моментов очерчивается кривой линией (квадратичной параболой), для построения которой надо иметь не менее трех точек и, следовательно, должны быть вычислены значения изгибающих моментов в начале участка, конце его и в одном промежуточном сечении. Такой промежуточной точкой лучше всего взять сечение, в котором эпюра Qу пересекает нулевую линию, т.е. где Qу= 0. На эпюре М в этом сечении должна находиться вершина параболы. Если же эпюра Qу не пересекает нулевую линию, то для построения эпюры М следует на данном участке взять дополнительную точку, к примеру, в середине участка (начала и конца действия распределенной нагрузки), помня, что выпуклостью парабола всегда обращена вниз, если нагрузка действует сверху вниз (для строительных специальностей). Существует правило «дождя», которое очень помогает при построении параболической части эпюры М. Для строителей это правило выглядит следующим образом: представьте, что распределенная нагрузка — это дождь, подставьте под него зонт в перевернутом виде, так чтобы дождь не стекал, а собирался в нем. Тогда выпуклость зонта будет обращена вниз. Точно так и будет выглядеть очертание эпюры моментов под распределенной нагрузкой. Для механиков существует так называемое правило «зонта». Распределенная нагрузка представляется дождем, а очертание эпюры должно напоминать очертания зонтика. В данном примере эпюра построена для строителей.
Если требуется более точное построение эпюры, то должны быть вычислены значения изгибающих моментов в нескольких промежуточных сечениях. Условимся для каждого такого участка изгибающий момент сначала определить в произвольном сечении, выражая его через расстояние х от какой-либо точки. Затем, давая расстоянию х ряд значений, получим значения изгибающих моментов в соответствующих сечениях участка. Для участков, на которых нет распределенной нагрузки, изгибающие моменты определяют в двух сечениях, соответствующих началу и концу участка, так как эпюра М на таких участках ограничивается прямой. Если к балке приложен внешний сосредоточенный момент, то обязательно надо вычислять изгибающий момент чуть левее места приложения сосредоточенного момента и чуть правее его.
Для двухопорной балки характерные точки следующие: C и D – начало и конец распределенной нагрузки; А – опора балки; В – вторая опора балки и точка приложения сосредоточенного момента; Е – правый конец балки; точка К, соответствующая сечению балки, в котором Qу = 0.
Ход слева. Правую часть до рассматриваемого сечения мысленно отбрасываем (возьмите лист бумаги и прикройте им отбрасываемую часть балки). Находим сумму моментов всех сил, действующих слева от сечения относительно рассматриваемой точки. Итак,

Прежде чем определить момент в сечении К, необходимо найти расстояние х=АК. Составим выражение для поперечной силы в данном сечении и приравняем его к нулю (ход слева):

Это расстояние можно найти также из подобия треугольников KLN и KIG на эпюре Qу (рис.б).
Определяем момент в точке К:

Пройдем оставшуюся часть балки ходом справа.

Как видим, момент в точке D при ходе слева и справа получился одинаковый – эпюра замкнулась. По найденным значениям строим эпюру. Положительные значения откладываем вниз от нулевой линии, а отрицательные – вверх (см. рис. в).
Решение многих
задач статики сводится к определению
реакций опор, с помощью которых
закрепляются балки и мостовые фермы.
В
технике обычно встречаются три типа
опорных закреплений (кроме рассмотренных
в § 2):
1. Подвижная
шарнирная опора (рис. 28,
опора А). Реакция
![]() такой опоры направлена по нормали к
такой опоры направлена по нормали к
поверхности на которую опираются катки
подвижной опоры.
2. Неподвижная
шарнирная опора (рис. 28,
опора В). Реакция
![]() такой опоры проходит через ось шарнира
такой опоры проходит через ось шарнира
и может иметь любое направление в
плоскости чертежа. При решении задач
будем реакцию![]() изображать ее составляющими
изображать ее составляющими![]() и
и![]() по направлениям координатных осей.
по направлениям координатных осей.
Модуль![]() определим по формуле
определим по формуле
![]() .
.
3. Жесткая
заделка (рис. 29, а).
Рассматривая заделанный конец балки и
стену как одно целое, жесткую заделку
изображают так, как показано на рис. 29, б.
В этом случае на балку в ее поперечном
сечении действует со стороны заделанного
конца система распределенных сил
(реакций). Считая эти силы приведенными
к центру А сечения, можно их заменить
одной силой
![]() и парой с неизвестным моментомmA
и парой с неизвестным моментомmA
(рис. 29, а).
Силу
![]() можно изобразить ее составляющими
можно изобразить ее составляющими![]() ,
,![]() (рис. 29, б).
(рис. 29, б).
Таким
образом, для нахождения реакции жесткой
заделки надо определить три неизвестные
величины XA,
YA,
mA.


Рис. 28
Рис. 29
Отметим также, что
в инженерных расчетах часто приходится
встречаться с нагрузками, распределенными
вдоль поверхности по тому или иному
закону. Рассмотрим некоторые примеры
распределенных сил.
Плоская система
распределенных сил характеризуется ее
интенсивностью q, т.е. значением силы,
приходящейся на единицу длины нагруженного
отрезка. Измеряется интенсивность в
ньютонах, деленных на метры (Н/м).
а) Силы,
равномерно распределенные вдоль отрезка
прямой (рис. 30, а).
Для такой системы интенсивность q имеет
постоянное значение. При расчетах эту
систему сил можно заменить равнодействующей
![]() .
.
По модулю
Q = aq
.
(33)
Приложена сила Q
в середине отрезка АВ.
б) Силы,
распределенные вдоль отрезка прямой
по линейному закону (рис. 30, б).
Для этих сил интенсивность q является
величиной переменной, растущей от нуля
до максимального значения qm.
Модуль равнодействующей
![]() в этом случае определяется по формуле
в этом случае определяется по формуле
Q = 0,5aqm
.
(34)
Приложена
сила
![]() на расстоянииа/3
на расстоянииа/3
от стороны ВС треугольника АВС.

Рис.
30
Задача 3.
Определить реакции неподвижной шарнирной
опоры А и подвижной опоры В балки
(рис. 31), на которую действуют активные
силы: одна известная сосредоточенная
сила F = 5 кН,
приложенная в точке С под углом 600,
и одна пара сил с моментом m = 8 кНм.
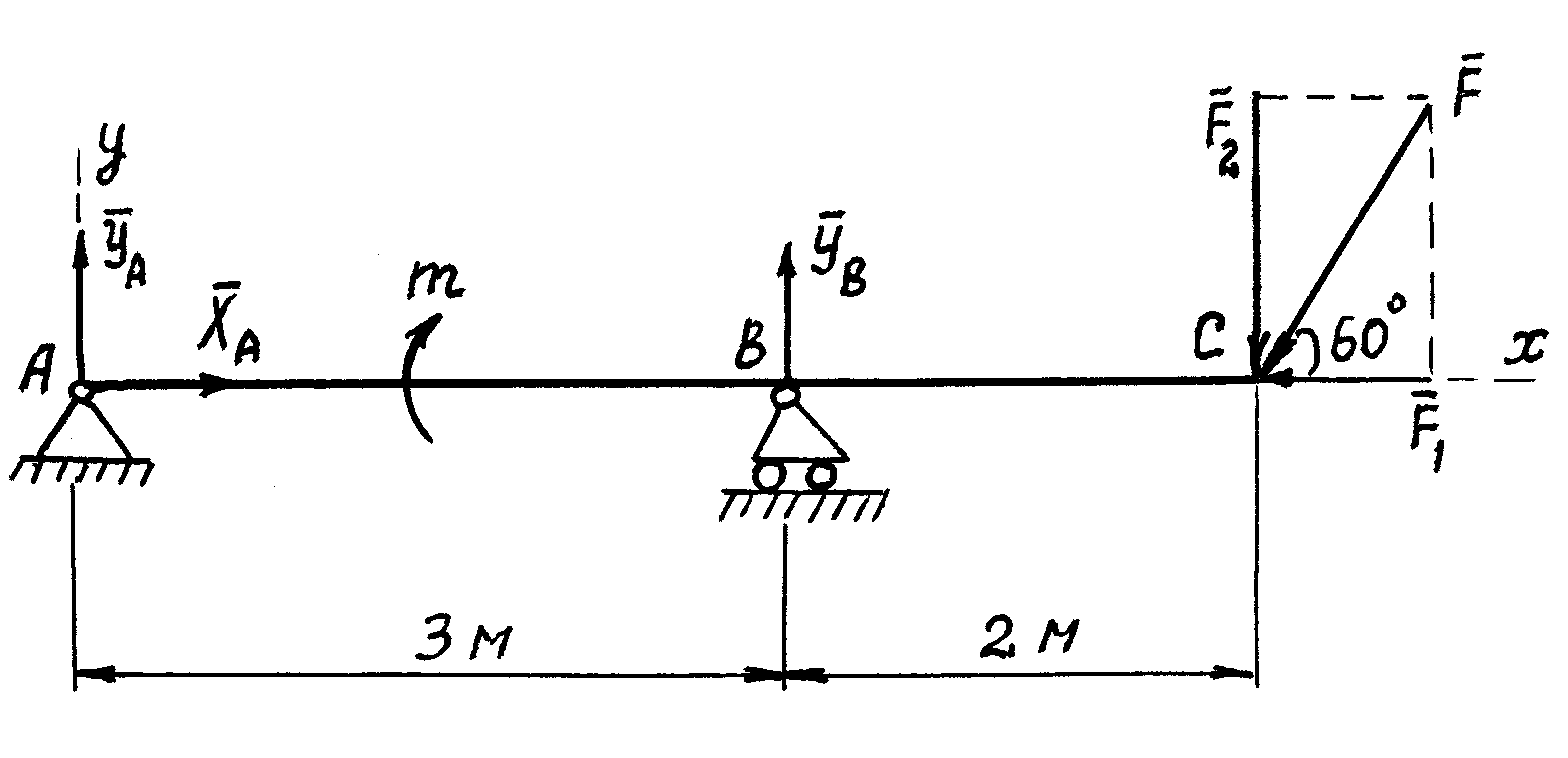
Рис.
31
Решение.
1) Выбираем
объект исследования, т.е. рассматриваем
равновесие балки АВС. 2) Изобразим
внешние силы, действующие на балку: силу
![]() ,
,
пару сил с моментомm
и реакции связей
![]() ,
,
![]() ,
,
![]()
(реакцию неподвижной шарнирной опоры
А изображаем двумя ее составляющими).
В результате имеем произвольную плоскую
систему сил. 3) Проведем координатные
оси x,
y
и составляем условия равновесия (28). Для
вычисления момента силы
![]() ,
,
иногда, удобно разложить ее на составляющие
![]()
и
![]() ,
,
модули которых равняются
F1 = F cos600 = 2,5 кН,
F2 = F cos300 = 4,33 кН.
Тогда получим:
![]() ,
,
![]() ,
,
![]() .
.
Решая эту систему
уравнений, найдем:
XA = F1 = 2,5 кН,
YB = (m + F2∙5)/3 = 9,88 кН,
YA = F2 – YB = – 5,55 кН.
Знак
минус реакции YA
показывает, что эта реакция направлена
вертикально вниз.
Для проверки
составим уравнение моментов относительно
нового центра, например, относительно
точки В:
![]() ,
,
5,55∙3 – 8 – 4,33∙2 = – 0,01 ≈ 0.
Задача 4.
Определить реакции заделки консольной
балки (рис. 32), на которую действуют
активные силы: сосредоточенная сила
F = 6 кН,
приложенная в точке С под углом 450,
равномерно распределенная нагрузка
интенсивностью q = 2 кН/м
и пара сил с моментом m = 3 кНм.
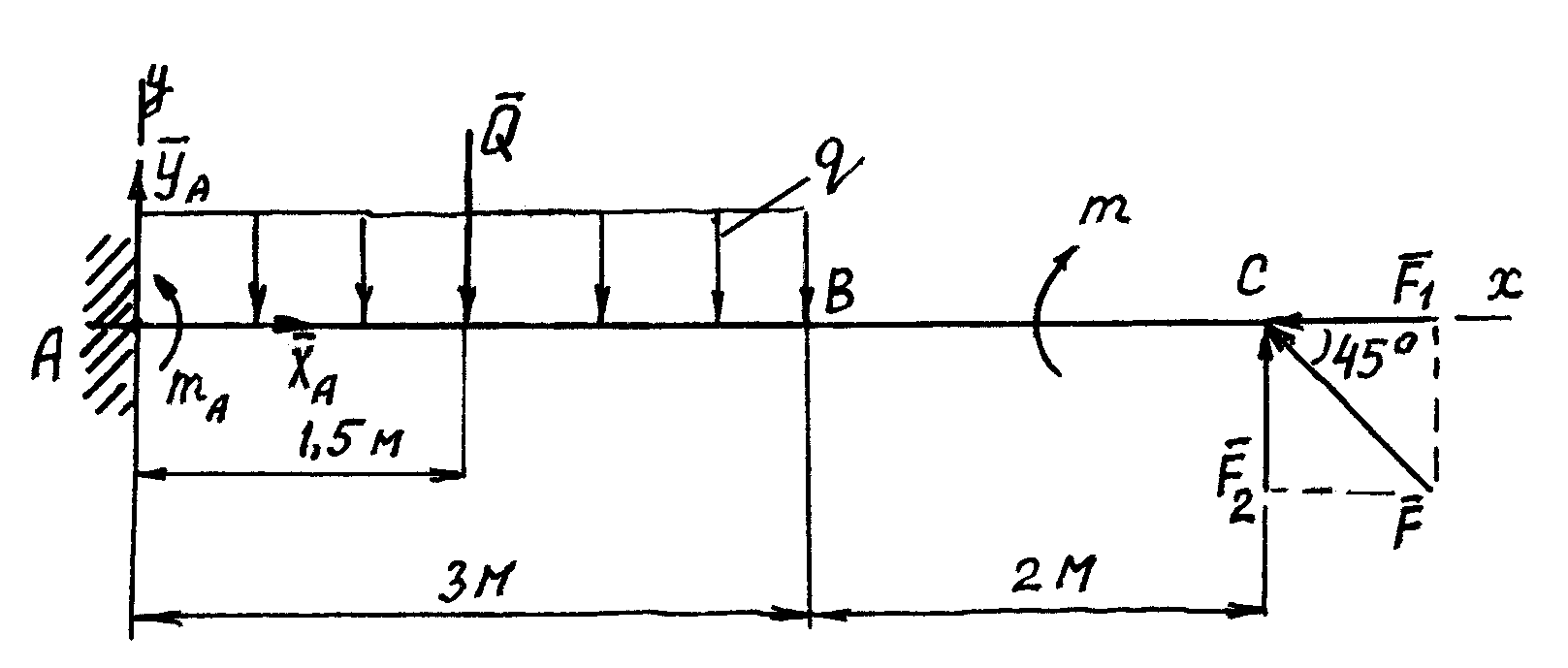
Рис. 32
Решение.
1) Выбираем
объект исследования, т.е. рассматриваем
равновесие балки АВС. 2) Изобразим
внешние силы, действующие на балку: силу
![]() ,
,
равномерно распределенную нагрузку
интенсивностьюq,
пару сил с моментом m
и реакции заделки, т.е. три неизвестные
величины XA,
YA,
mA
(реакцию жесткой заделки изображаем
двумя ее составляющими XA,
YA,
а пару – неизвестным моментом mA,
как на рис. 29). Силу
![]() разложим на две составляющие
разложим на две составляющие
![]()
и
![]() ,
,
модули которых равняются
F1 = F2 = F cos450 = 4,24 кН,
а распределенную нагрузку интенсивностью
q
заменим сосредоточенной силой
![]()
с модулем равным
Q = 3∙q = 6 кН.
Сила
![]()
приложена в середине отрезка АВ. В
результате имеем произвольную плоскую
систему сил. 3) Проведем координатные
оси x,
y
и составляем уравнения равновесия (2):
![]() ,
,
![]() ,
,
![]() .
.
Решая эти уравнения,
найдем:
XA = F1 = 4,24 кН,
YA = Q – F2 = 1,76 кН,
mA = Q∙1,5 + m – F2∙5 = – 9,2 кНм.
Для проверки
составим уравнение моментов относительно
точки С:
![]() ,
,
– 9,2 + 21 – 3 – 8,8 = 0.
Задача 5.
Определить реакции опор А, В, С и усилие
в промежуточном шарнире D
составной конструкции (рис. 33), на
которую действуют активные силы:
сосредоточенная сила F = 4 кН,
приложенная в точке Е под углом 450,
равномерно распределенная нагрузка
интенсивностью q = 2 кН/м
и пара сил с моментом m = 10 кНм.
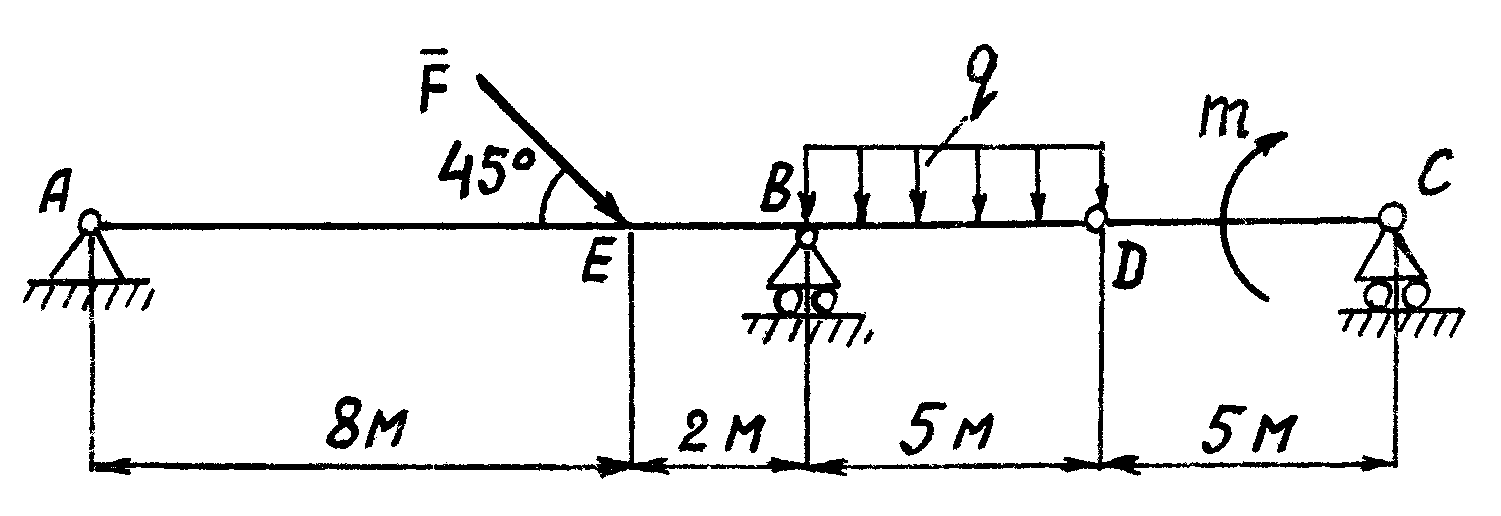
Рис. 33
Решение.
Один из способов решения задач об
определении реакции опор составной
конструкции состоит в том, что конструкцию
расчленяют на отдельные тела и составляют
условия равновесия каждого из тел в
отдельности. Воспользуемся этим способом
и разобьем конструкцию на две части:
левую AD
и правую DC.
В результате приходим к задаче о
равновесии двух тел. Силовые схемы
задачи показаны на рис. 7,8. Для упрощения
вычислений разложим силу
![]()
на составляющие
![]()
и
![]() ,
,
модули которых равны F1 = F2 = F cos450 = 2,83 кН,
а распределенную нагрузку интенсивностью
q
заменим сосредоточенной силой
![]() с модулем равнымQ = 10 кН.
с модулем равнымQ = 10 кН.
Сила
![]() приложена в середине отрезкаBD.
приложена в середине отрезкаBD.


Рис. 34
Рис. 35
Анализ
приведенных силовых схем показывает,
что они включают шесть неизвестных
величин: XA,
YA,
YB,
XD,
YD,
YC.
Так
как на рис. 34,35
имеются плоские системы уравновешенных
сил, то для них можно записать условия
равновесия (28) в виде шести линейных
алгебраических уравнений:
Левая часть
Правая
часть
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Поскольку
составленная система шести уравнений
зависит от шести неизвестных XA,
YA,
YB,
XD,
YD,
YC,
то она является замкнутой.
Решая систему,
найдем:
XA = – 2,83 кН,
YA = – 0,93 кН,
YB = 11,76 кН,
YC = 2 кН,
XD = 0,
YD = 2 кН.
Для
проверки составим уравнение моментов
относительно точки D:
![]()
= 2,83∙7 – (– 0,93)∙15 – 11,76∙5 + 10∙2,5 – 10 + 2∙5 = – 0,04 ≈ 0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
