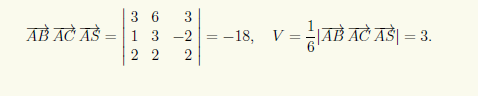Как найти площадь прямоугольника по векторам

Площадь по заданным координатам. Как найти (вычислить) площадь фигуры (треугольник, четырехугольник, трапеция, многоугольник и др.) по координатам? Какие есть формулы и методы, позволяющие находить площадь через координаты? бонус за лучший ответ (выдан): 5 кредитов Для вычисления площади простого многоугольника с любым количеством вершин, представленных в виде списка координат, при последовательном обходе которых, не образуются пересекающиеся линии, применяется формула Гаусса, иначе называемая “формулой землемера”, “формулой геодезиста”, “формулой шнурования”, “алгоритмом шнурования”, а так же “методом треугольников”. Суть метода заключается в построении треугольников, состоящих из сторон многоугольника и лучей проведённых из начала координат к вершинам многоугольника, и сложении площадей треугольников, включающих внутреннюю часть многоугольника с вычитанием площадей треугольников, расположенных снаружи. Площадь, вычисленная по приведенной формуле, будет иметь отрицательное значение при обходе фигуры по часовой стрелке и положительное при обходе против часовой стрелки. Фигура многоугольника может иметь произвольную геометрию. 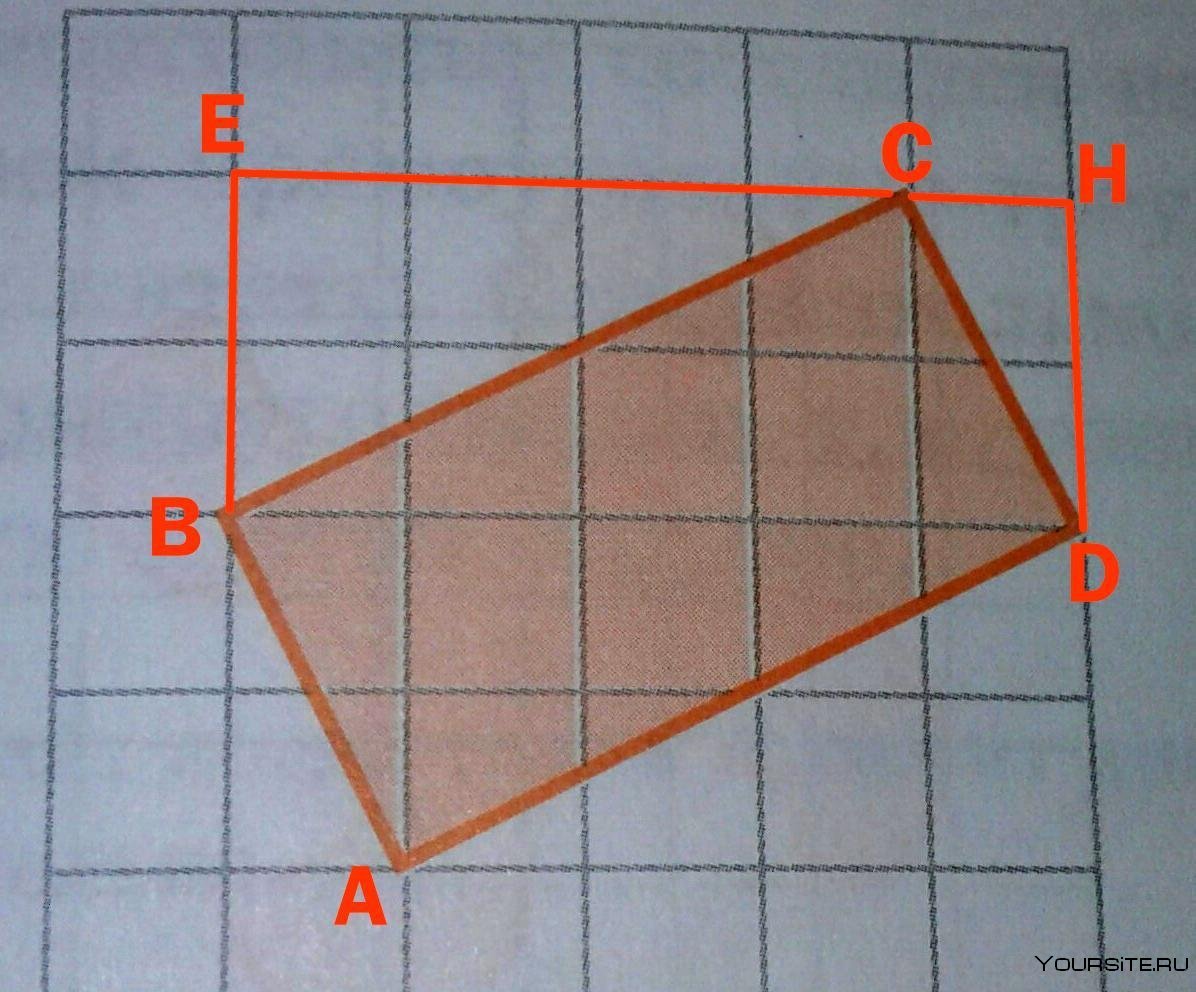Например: Список координат многоугольника представлен в виде массива: (x1, y1), (x2, y2), (x3, y3),…(xn, yn). Для многоугольника на первом рисунке он задан точками: (3,4), (5,11), (12,8), (9,5), (5,6). Его площадь будет равна: Существует также метод трапеций, основанный на сложении и вычитании площадей трапеций, образованных каждой из сторон многоугольника, её проекцией на ось абсциссы и перпендикулярами, опущенных из вершин на абсциссу. При обходе вершин по часовой стрелке учитывается величина координаты вершин. Если первая вершина меньше второй, то площадь трапеции прибавляется, если нет, то отнимается. Для многоугольника ABCDE на левом нижнем рисунке существует 5 трапеций : ABJH, CBJF, CDIF, EDIG и EAHG. Так как X1<X2, X3<X4 и X5<X1, то площади трапеций ABJH, CDIF и EAHG складываются, а X3>X4 и X4<X5, следовательно, площади трапеций CBJF и EDIG вычитаются: S = S(ABJH) – S(CBJF) + S(CDIF) – S(EDIG) + S(EAHG) Площади трапеций рассчитываются по формуле; Sтрапеции = 1/2 *((a+b))*h, где a, b – основания трапеции, h – высота трапеции. Значения a, b и h вычисляются по координатам. В декартовых координатах круг может быть представлен двумя точками: центр А и любая точка В, лежащая на окружности. Для расчета площади круга необходимо вычислить его радиус по формуле: автор вопроса выбрал этот ответ лучшим Ксарф­акс [156K] 5 лет назад  Площадь фигуры по координатам вершин Если известны координаты всех вершин, то площадь заданной геометрической фигуры (треугольника, прямоугольника, трапеции, ромба и т.д) можно найти по стандартным формулам. Но предварительно нужно найти длину сторон, диагоналей и т.п. (всё зависит от фигуры) с помощью формулы нахождения длины отрезка по заданным координатам. Эта формула выглядит следующим образом: Здесь: AB – отрезок, точка A имеет координаты (x1, y1), точка B имеет координаты (x2, y2). Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(2,3); B(6,7); C(5,0). Его площадь можно найти по формуле Герона: Здесь: S – площадь треугольника, a, b, c – стороны, p – полупериметр, который равен половине суммы сторон a, b и c. Найдём, чему равны стороны треугольника по формуле нахождения длины отрезка по координатам: AB = √(4² + 4²) = √32 ≈ 5,66. AC = √(3² + (-3)²) = √18 ≈ 4,24. BC = √((-1)² + (-7)²) = √50 ≈ 7,07. Полупериметр треугольника будет равен (5,66 + 4,24 + 7,07) / 2 ≈ 16,97 / 2 ≈ 8,49. Отсюда площадь треугольника ABC ≈ √(8,49 * 2,83 * 4,25 * 1,42) ≈ √145 ≈ 12,04. 2) Ромб ABCD имеет координаты A(1,2); B(3,4); C(5,2); D(3,0). Площадь можно найти через диагонали: Здесь: S – площадь ромба, d1 и d2 – диагонали. Таким образом, нам нужно найти диагонали AC и BD. AC = √(4² + 0) = √16 = 4. BD = √(0 + (-4)²) = √16 = 4. Отсюда площадь ромба ABCD = 0,5 * 4 * 4 = 8. 3) Трапеция ABCD имеет координаты A(1,1); B(3,4); C(5,4); D(6,1). Стандартная формула площади трапеции такая: Здесь: S – площадь трапеции, a и b – основания, h – высота. Высота трапеции (пусть это будет BE) – это перпендикуляр, который был опущен из вершины трапеции (из точки B) на её основание (в нашем случае это AD). Определим координаты её отрезка: координаты первой точки совпадают с точкой B, это (3,4). координаты 2 точки (точка E) будут (3,1) – так как абсцисса совпадает с абсциссой точки B, а ордината совпадает с ординатой точек A и D. Высота трапеции BE = √(0 + (-3)²) = √9 = 3. Теперь посчитаем длину оснований: BC = √(2² + 0) = √4 = 2. AD = √(5² + 0) = √25 = 5. Таким образом, площадь трапеции ABCD = 3 * 0,5 * (2 + 5) = 10,5. Степа­н-16 [34.5K] 5 лет назад  Первоначально нужно вычислить длины сторон. В этом здесь будет основная задача. Получив стороны, вычисляем площади по стандартным формулам. Самый простой случай – для прямоугольника, когда его стороны параллельны осям координат. Тогда одна сторона будет равна разнице абсцисс, вторая ординат. Треугольник. Допустим, основание параллельно оси абсцисс. Вычисляем его длину, как разницу абсцисс. Далее нужно найти высоту. Она будет равна разнице ординат третьей вершины и ординаты любой из вершин основания. Затем – площадь по формуле: половина произведения основания на высоту. И т.д. Если же стороны фигуры не параллельны осям, то находить длины сторон придется уже более сложными расчетами. Допустим, прямоугольник. Первую сторону будем искать, как если бы она была гипотенузой в составе прямоугольного треугольника. Каждая сторона будет равна квадратному корню из суммы квадратов абсцисс и ординат концов отрезков стороны. Так и для любой фигуры. Вначале определяем длины сторон как гипотенузу треугольника. После чего применяем стандартные формулы площадей. Элени­я [445K] 3 года назад  Рассчитать площадь какой угодно геометрической фигуры, зная координаты, не составляет сложности. Каждая из точек, соответствующая вершинам искомой фигуры, будь это треугольник, четырех- или многоугольник, имеет определенную координату, а значит у нее есть значение, через которое можно рассчитать площадь. Координаты, как найти на графике, чтобы узнать площадь фигуры? Проецируем на оси абсцисс и ординат прямые, проведя перпендикуляр из каждой точки. Полученные значения будут исходной величиной. Каждая из сторон фигуры – это разница двух точек на горизонтальную и вертикальную оси. Разница между значениями означает длину стороны фигуры. А зная все стороны и их значение, по формуле находим площадь. Пример 1. Ищем площадь треугольника. Мы видим два отрезка зеленого цвета AB и BC, которые образуют стороны равнобедренного треугольника, а основание есть отрезок на оси абсцисс AC. Даны значения: AC основание в промежутке от “-4” до “+4”, то есть длина основания равна восьми. Будет лучше, если посчитать площадь этого треугольника, как сумму из образовавших его двух треугольников, которые являются прямыми, ABO и BOC, совпадающие прямым углом с координатой “0” на графике. Известна длина каждй из сторон, образующих прямой угол (AO или OC) х = 4 – 0 = 4 и y = 2 – 0 = 2 (BO). Зная длину двух сторон, образующих прямой угол (AO и BO), находим длину основания (AB или BC). Тогда уже знаем все длины каждой из сторон обоих прямых треугольников. Остается только найти площадь по формуле: Зная площадь каждого из прямых треугольников, умножаем на два, получаем сумму заштрихованного треугольника на графике ABC. И еще математически можно записать решение следующим образом, исходя из того, что имеем изначально следующую систему неравенств: Пример 2. Пример 3. Есть парабола, ищем площадь фигуры, ограниченную кривой параболы. Чтобы посчитать, используем интеграл. Бекки Шарп [71.2K] 3 года назад  Рассмотрим простой случай, где буквально на пальцах можно посчитать площадь через обычную формулу, а затем применим к этой задаче формулу Гаусса. У нас есть трапеция, у которой известны координаты вершин. (3:2) (5:2) (9:6) (6:6). Мы знаем, что площадь трапеции равна сумме оснований, деленной на 2 и умноженной на высоту. S = (a+b)/2 х h Считаем площадь: S = (3+2):2х4 = 10. Ответ – 10. А теперь по теореме Гаусса. Не смотря на страшный вид, формула очень простая. В квадратных скобках мы перемножаем абсциссу первой точки с ординатой второй, прибавляем абсциссу второй, умноженную на ординату третьей и так идем по кругу фигуры. Далее вычитаем ординату первой умноженную на абсциссу второй и т.д. В квадратных скобках у нас может получиться отрицательное число. S= 0,5 х [3х6+6х6+9х2+5х2 – 2х6-6х9-6х5-2х3] = 10 Таким образом можно найти площадь любой сложной фигуры, зная ее координаты. dydyS­acha [10.8K] 5 лет назад  Можно взять милиметровку и нанести точки с заданными координатами, согласно осей абсцис и ординат. Соединить эти точки между собой и замерить длины образовавшихся сторон, а с помощью формулы по определению площади образовавшейся фигуры узнать её значение подставив данные в эту формулу. Алиса в Стран­е [363K] 3 года назад  Существует специальная формула, называемая формулой Гаусса, она и позволит нам определить искомую площадь по координатам. Вот как эта формула выглядит: Формула выглядит немного устрашающе, но давайте попробуем в ней разобраться. У нас есть многоугольник и есть его координаты, подсчитать n – количество сторон многоугольника несложно, а дальше просто нужно подставлять значения в эту формулу, нужно только быть внимательным и не перепутать какие координаты куда надо писать. Давайте теперь приведем пример нахождения такой площади через формулу Гаусса. Допустим, у нас есть вот такой пятиугольник: Координаты его пяти вершин, как мы видим: (3, 4), (5, 11), (12, 8), (9, 5), (5, 6). Теперь нам остается только очень внимательно подставить эти координаты в нашу формулу, n = 5, координаты известны, вот что у нас получится: Когда разбираешься в этой формуле, понимаешь, насколько она проста и даже легко запоминается, несмотря на то, что сначала кажется очень сложной. dusel­ldorf [4.3K] 5 лет назад  Для вычисления площади геометрической фигуры по координатам ее вершин, нужно воспользоваться формулой Гаусса, иногда ее называют формулой землемера или формулой геодезиста, так как она применяется геодезистами для определения площади земельного участка, например, при межевании: где А – площадь многоугольника с заданными координатам его вершин, n – количество сторон многоугольника, (xi, yi) – координаты вершин многоугольника, i = 1, 2,…, n — номер вершины многоугольника. Барха­тные лапки [382K] 3 года назад  Находим площадь вот такого несложного четырехугольника. Координаты его вершин нам известны. Применяем формулу Гаусса, которая выглядит так: S (площадь) = 0,5 [6х4 +9х7 + 10х6 + 7х3 – 3х9 – 4х10 – 7х7 – 6х6] = 8 (квадратных единиц) Как видим если применять при решении формулу Гаусса то решить такую задачку несложно. Не вижу здесь серьезных проблем. Мы, как я понял, имеем готовые точки координат, которые нужно проставить на координатной плоскости. Далее, соединяя эти точки, получаем фигуру, как в примере вопроса – квадрат, треугольник и т.п. Теперь вычисляем площадь любой из полученных фигур по формуле ей соответствующей. Знаете ответ?

Векторное произведение векторов

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение векторного произведения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.

Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.

Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.

Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.

Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.

Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.

В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.

И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.

Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!

Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:

• он является нулевым, если векторы →a и →b коллинеарны;
• он перпендикулярен и вектору →a и вектору →b;
• длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
• тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.

Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.

Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:

Векторное произведение векторов →a и →b обозначается как [→a • →b].

Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.

Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

• Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
• Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
• Если определитель равен нулю, то векторы компланарны (линейно зависимы).

Координаты векторного произведения

Рассмотрим векторное произведение векторов в координатах.

Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.

В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор

→i, →j, →k — координатные векторы.

Это определение показывает нам векторное произведение в координатной форме.

Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:

Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:

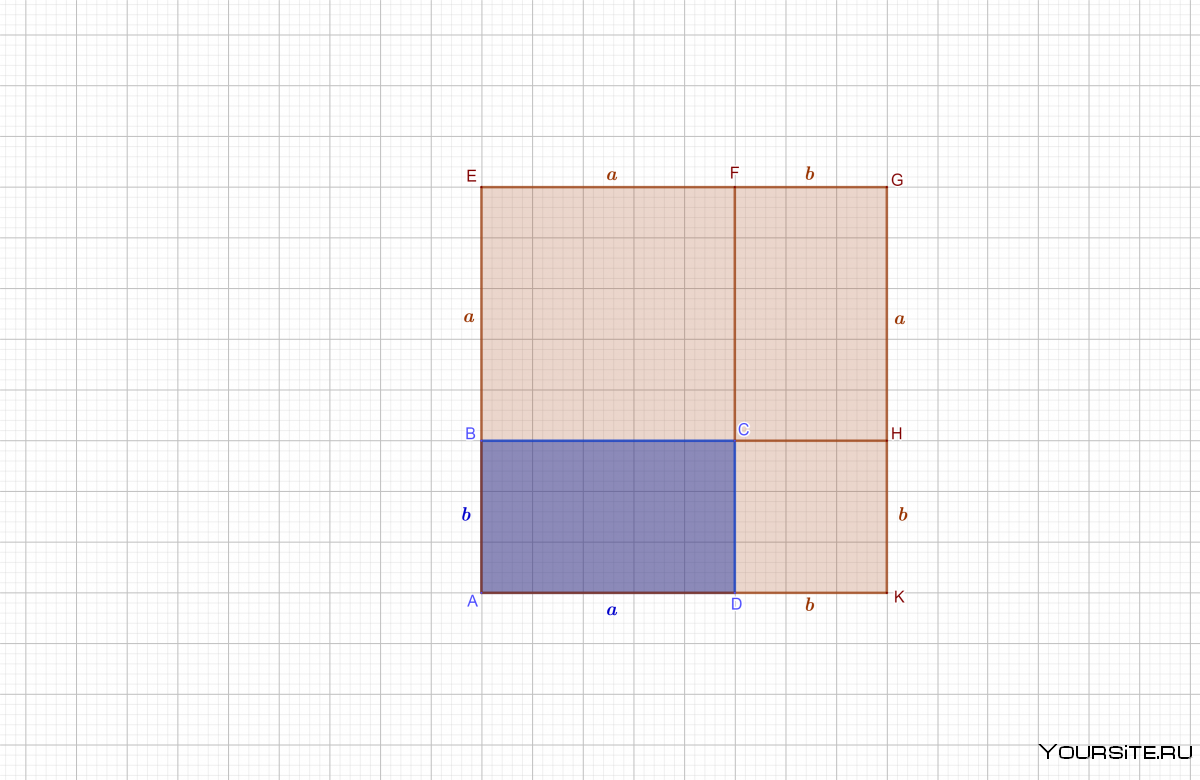
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.

Свойства векторного произведения

Векторное произведение в координатах представляется в виде определителя матрицы:

На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:

1. Антикоммутативность
2. Свойство дистрибутивности

Сочетательное свойство

, где λ произвольное действительное число.

Для большей ясности докажем свойство антикоммутативности векторного произведения.

Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому

что доказывает свойство антикоммутативности векторного произведения.

Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.

Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).

Примеры решения задач

Пример 1

а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:

Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.

б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:

Пример 2

Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.

По условию снова нужно найти длину векторного произведения. Используем нашу формулу:

Согласно ассоциативным законам, выносим константы за переделы векторного произведения.

Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.

Пример 3

Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.

Сначала найдём векторы:

Затем векторное произведение:

Вычислим его длину:

Подставим данные в формулы площадей параллелограмма и треугольника:

Геометрический смысл векторного произведения

По определению длина векторного произведения векторов равна

А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.

Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.

Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].

Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.

Ориентированные площади и объёмы

Ориентированная площадь параллелограмма

Ориентированной площадью параллелограмма , построенного на неколлинеарных векторах и , называется его площадь , взятая со знаком плюс, если ориентация пары векторов и правая , и со знаком минус, если ориентация — левая

Внешним (косым) произведением неколлинеарных векторов и на плоскости называется число, равное ориентированной площади параллелограмма, построенного на этих векторах. Если векторы и коллинеарны, то их внешнее произведение считается равным нулю. Внешнее произведение обозначается . Его свойства повторяют алгебраические свойства векторного произведения, т.е. для любых векторов на плоскости и любого числа справедливы равенства:

4) Если векторы и в правом ортонормированием базисе имеют координаты и соответственно, то внешнее произведение этих векторов находится по формуле

Если — координатные столбцы векторов в стандартном базисе на плоскости, то их внешнее произведение находится по формуле

Приведенные свойства внешнего произведения следуют из алгебраических свойств векторного произведения, если векторы на плоскости рассматривать как векторы в пространстве с нулевыми аппликатами.

Рассмотрим задачу разложения вектора по базису на плоскости. Отложим все векторы от произвольной точки . Сначала разберем случаи, когда векторы и коллинеарны: одинаково направлены (рис.1.49,а) или противоположно направлены (рис. 1.49,6). В этих случаях ордината вектора равна нулю, а абсцисса находится как отношение

так как пара в первом случае правая (рис.1.49,а), а во втором случае — левая (рис.1.49,б).

Пусть теперь векторы и не коллинеарны (рис.1.49,в). Построим проекции и на прямые, содержащие базисные векторы: . Из концов векторов и опустим перпендикуляры и соответственно на прямую, содержащую вектор . Учитывая, что векторы и противоположно направлены, а также подобие прямоугольных треугольников с гипотенузами и , находим абсциссу вектора :

так как пара — правая, а пара — левая. Аналогично находится ордината (векторы и одинаково направлены)

Таким образом, вектор имеет следующее разложение по базису на плоскости:

Рассмотрим применение формулы (1.19) для решения системы двух линейных уравнений с двумя неизвестными:

Эту систему можно записать в виде .Рассматривая полученные столбцы как координатные столбцы векторов в стандартном базисе на плоскости, получаем разложение .

Таким образом, нахождение решения системы уравнений свелось к задаче разложения вектора по векторам и . Предполагая, что коэффициенты при неизвестных не пропорциональны, т.е. (векторы и не коллинеарны), по формуле (1.19), полагая , получаем:

Ориентированный объем параллелепипеда

Ориентированным объемом параллелепипеда , построенного на некомпланарных векторах , называется его объем , взятый со знаком плюс, если ориентация тройки векторов правая и со знаком минус, если ориентация — левая .

Внешним (косым) произведением некомпланарных векторов называется число, равное ориентированному объему параллелепипеда, построенного на этих векторах. Если векторы компланарны, то их внешнее произведение считается равным нулю. Внешнее произведение обозначается .

Внешнее произведение трех векторов совпадает с их смешанным произведением (в силу первого геометрического свойства смешанного произведения), т.е. . В ортонормированием базисе

так как определитель транспонированной матрицы равен определителю исходной матрицы.

При помощи ориентированных объемов задача разложения вектора по базису в пространстве решается так же как и на плоскости с использованием ориентированных площадей. В результате получаем

Формула (1.21) соответствует правилу Крамера решения системы трех линейных уравнений с тремя неизвестными.

Пример 1.23. Заданы координатные столбцы

векторов в стандартном базисе. Разложить вектор по векторам .

Решение. По формуле (1.20) находим смешанные произведения

Коэффициенты разложения определяем по формуле (1.21):

Вычисление площадей и объемов векторы

В. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников

.Геометрическое определение вектора

.Алгебраические операции над направленными отрезками

..Сложение направленных отрезков

..Умножение направленных отрезков на число

..Параллельное проектирование вектора в пространстве

. Проекция точки на плоскость

. Проекция вектора на плоскость

..Ортогональная проекция вектора в пространстве

. Ортогональная проекция вектора на плоскость

. Ортогональная проекция вектора на прямую и направленную ось

..Векторы в трехмерном геометрическом пространстве

..Линейная зависимость векторов и размерность пространства

..Различные формы записи векторов

..Линейные операции над векторами в координатной форме

. Свойства скалярного умножения

. Скалярное умножение в декартовых координатах

..Некоторые примеры использования скалярного умножения

.Измерение площадей и объемов

..Площадь параллелограмма, построенного на векторах

..Задачи на применение определителей

..Определитель третьего порядка и его свойства

..Векторное умножение векторов базиса декартовой системы координат

.Ковариантные и контравариантные координаты вектора

..Индексная форма записи для выражений с определителями

..Свойства символов Веблена

..Операция векторного умножения в произвольных косоугольных координатах

.Линейный оператор и его матрица

.Доказательство теоремы об определителе

.Общие определения алгебраических операций с тензорами

.Примеры на применение тензоров в физике

..Задачи на тождественные преобразования

..Площадь параллелограмма, построенного на векторах

Задачи на измерение длин отрезков, расстояний между точками, площадей поверхностей и объемов тел относятся к важному классу проблем, которые принято называть метрическими. В предыдущем разделе мы познакомились с тем, как использовать векторную алгебру для вычисления длин отрезков и расстояний между точками. Теперь мы собираемся найти способы вычисления площадей и объемов. Векторная алгебра позволяет ставить и решать подобные задачи только для достаточно простых случаев. Для вычисления площадей произвольных поверхностей и объемов произвольных тел требуются методы анализа. Но методы анализа в свою очередь существенным образом опираются на те результаты, которые дает векторная алгебра.

Для решения поставленной задачи, мы избрали достаточно долгий и непростой путь, подсказанный Гильбертом Стренгом [19], связанный с многочисленными геометрическими преобразованиями и кропотливыми алгебраическими вычислениями. Мы избрали этот путь несмотря на то, что существуют другие подходы, которые быстрее приводят к цели потому, что он показался нам прямым и естественным. Прямой путь в науке не всегда оказывается самым простым. Люди искушенные знают об этом и предпочитают пути окольные, но если не попытаться пройти прямиком, то можно так и остаться в неведении относительно некоторых тонкостей теории.

На избранном нами пути естественным образом появляются такие понятия как ориентация пространства, определитель, векторное и смешанное произведения. Особенно наглядно, как под микроскопом, проявляется геометрический смысл определителя и его свойств. Традиционно понятие определителя вводится в теории систем линейных уравнений, но именно для решения таких систем определитель почти бесполезен. Геометрический же смысл определителя существенен для векторной и тензорной алгебры.

А теперь запасемся терпением и начнем с самых простых и понятных случаев.

1. Векторы ориентированы вдоль координатных осей декартовой системы координат.

Рис. 21

Пусть вектор направлен по оси x , а вектор вдоль оси y . На рис. 21 показаны четыре различных варианта расположения векторов по отношению к осям координат.

Векторы и в координатной форме:

;

.

Где a и b означают модуль соответствующего вектора, а – знак координаты вектора.

Поскольку векторы ортогональны, то параллелограммы, построенные на них, являются прямоугольниками. Их площади равны просто произведению их сторон. Выразим эти произведения через координаты векторов для всех четырех случаев.

1. ;

2. ;

3. ;

4. .

Все четыре формулы для вычисления площади одинаковы за исключением знака. Можно было бы просто закрыть на это глаза и записать, что во всех случаях. Однако более продуктивной оказывается другая возможность: придать знаку какой-то смысл. Посмотрим внимательно на рис. 21. В тех случаях, когда , поворот вектора к вектору осуществляется по часовой стрелке. В тех же случаях, когда мы вынуждены использовать в формуле знак минус, поворот вектора к вектору осуществляется против часовой стрелки. Это наблюдение позволяет связать знак в выражениях для площади с ориентацией плоскости.

Будем считать, что векторы и , взятые в указанном порядке задают ориентацию в плоскости, совпадающую с направлением поворота вектора к вектору по кратчайшему пути.

Площадь прямоугольника, построенного на векторах и , со знаком плюс или минус будем считать ориентированной площадью, при этом знак будем связывать с ориентацией, задаваемой векторами. Для ориентированной площади мы можем записать единую формулу для всех рассмотренных четырех случаев: . Знак “векторной” черты над буквой S вводится для того, чтобы отличить обычную площадь, которая всегда положительна, от ориентированной.

При этом, очевидно, что те же самые векторы, взятые в другом порядке, определяют противоположную ориентацию, поэтому, . Просто площадь будем по-прежнему обозначать буквой S и, следовательно, .

Теперь, когда казалось бы ценой расширения понятия площади, мы получили общее выражение, внимательный читатель скажет, что мы рассмотрели не все возможности. Действительно, кроме четырех вариантов расположения векторов, представленных на рис. 21, имеются еще четыре (рис. 22).

Рис. 22

Запишем снова векторы и в координатной форме:

;

.

Выразим площади через координаты векторов.

1. ;

2. ;

3. ;

4. .

Знаки в новых выражениях не поменялись, но, к сожалению, поменялась ориентация по отношению к предыдущим четырем случаям. Поэтому для ориентированной площади мы вынуждены записать: . Хотя надежда на гениальную простоту и не оправдалась, но, тем не менее, мы все-таки можем записать общее выражение для всех четырех случаев.

.

То есть, ориентированная площадь прямоугольника, построенного на векторах, как на сторонах, равна определителю, составленному из координат векторов, как из столбцов.

Мы полагаем, что с теорией определителей читатель знаком, поэтому, мы не останавливаемся подробно на этом понятии. Тем не менее, мы даем соответствующие определения, для того чтобы изменить акценты и показать, что к этому понятию можно прийти из чисто геометрических соображений.

Итак, , , , – различные формы обозначения для одного и того же понятия – определителя, составленного из координат векторов, как из столбцов. Равенство может быть принято за его определение для двухмерного случая.

Теперь мы можем считать, что для всех частных случаев расположения векторов относительно декартовой системы координат у нас есть общее выражение для ориентированной площади.

2. Вектор не параллелен оси x ; вектор является произвольным вектором.

Для того чтобы свести этот случай к уже известным, рассмотрим некоторые геометрические преобразования параллелограмма, построенного на векторах и (рис. 23).

Рис. 23

Преобразуем вектор в вектор и перейдем от параллелограмма ABCD к параллелограмму . – произвольное действительное число. Очевидно, что площади и ориентации обоих параллелограммов одинаковы. Следовательно, для ориентированных площадей можно записать: . Аналогично можно записать, что . Такие преобразования пар векторов будем называть линейными преобразованиями. Линейные преобразования векторов не изменяют ориентированной площади параллелограммов, построенных на них.

Пусть теперь нам даны два произвольных вектора и , про которые нам известно, что вектор не параллелен оси x (рис. 24).

Рис. 24

Преобразуем вектор в вектор таким образом, чтобы вектор оказался параллельным оси x . Это можно сделать, соответствующим образом подобрав коэффициент , так как вектор не параллелен оси x . При этом . Найдем координаты вектора .

Поскольку , , , то мы приходим к системе линейных уравнений:

, решая которую, получаем:

и .

Следовательно, .

Продолжим наши преобразования и перейдем от вектора к вектору , параллельному оси y (рис. 25).

Рис. 25

Найдем координаты вектора .

Поскольку , , , то мы приходим к системе линейных уравнений:

.

В данном случае можно не искать – и без того очевидно, что . Следовательно, .

По построению, ориентированная площадь параллелограмма, построенного на векторах и , равна ориентированной площади прямоугольника, построенного на векторах и . Но для прямоугольника мы результат уже знаем:

.

Следовательно, и для общего случая справедлива формула:

.

Осталось проверить еще одну возможность, а именно:

3. Вектор параллелен оси x , а вектор является вектором общего положения.

Если вектор параллелен оси x , то мы не можем с помощью преобразования получить вектор, параллельный этой оси. Используем другую возможность, показанную на рис. 26.

Рис. 26

Преобразуем вектор в вектор , параллельный оси y . И без вычислений ясно, что . Ориентированная площадь для векторов и равна:

.

Теперь можно считать, что формула:

справедлива для всех возможных случаев.

Осталось сделать еще одно замечание. Представим, что один из базисных векторов системы координат поменял направление на противоположное. В этом случае соответствующие координаты векторов и изменят свой знак, и, следовательно, изменится знак определителя. Но ведь ориентация, которую задают векторы и , при этом останется прежней! Все дело в том, что знак определителя в формуле для ориентированной площади говорит об относительной ориентации по отношению к той ориентации, которую задают в плоскости базисные векторы. Если векторы и задают такую же ориентацию, что и векторы i и j , то определитель положителен, а если противоположную, то отрицателен. Поскольку у нас нет никаких оснований для выделения одной из двух возможных ориентаций в плоскости, то и ориентированную площадь удобно рассматривать только по отношению к базисной ориентации.

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=orientirovannye-ploshchadi-i-obemy

http://rdt45m.narod.ru/tenzor_html/vector3_1_1.htm

[/spoiler]

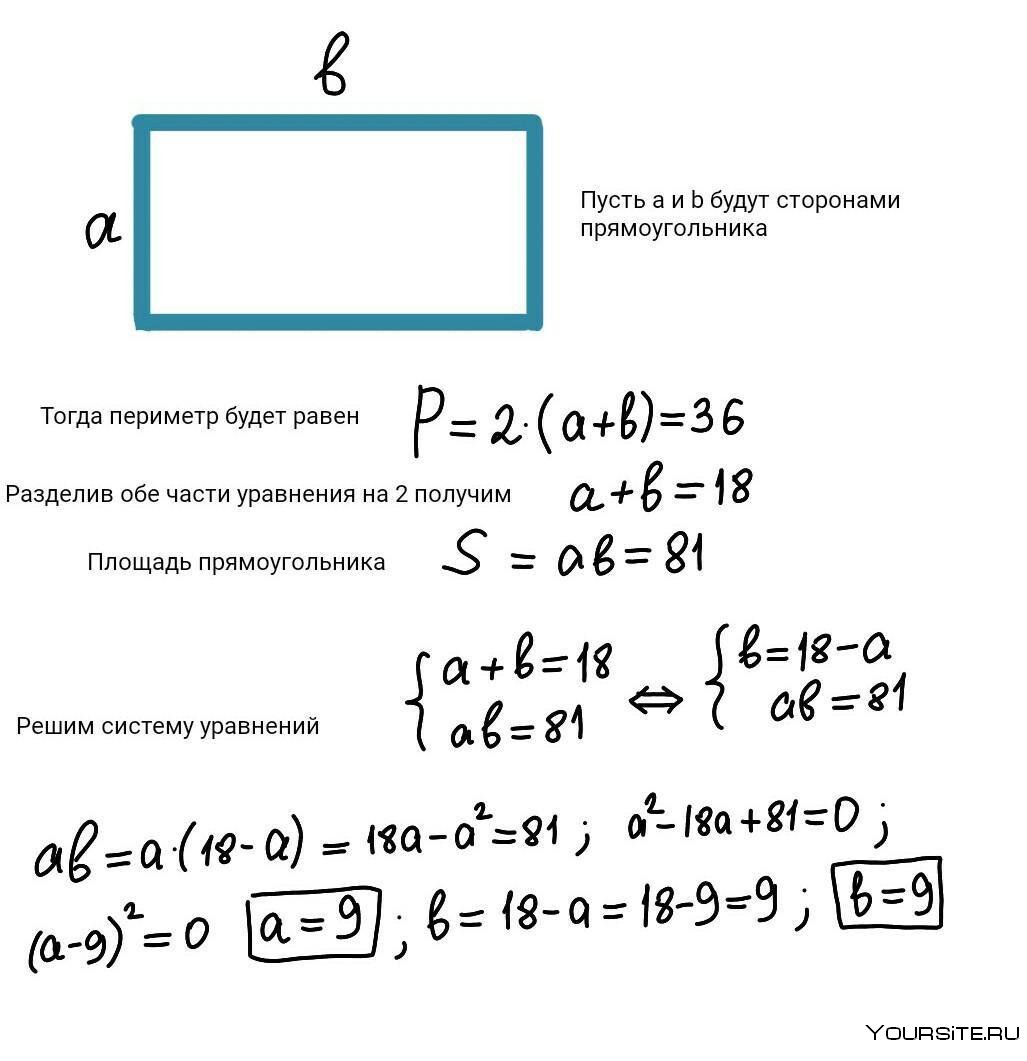
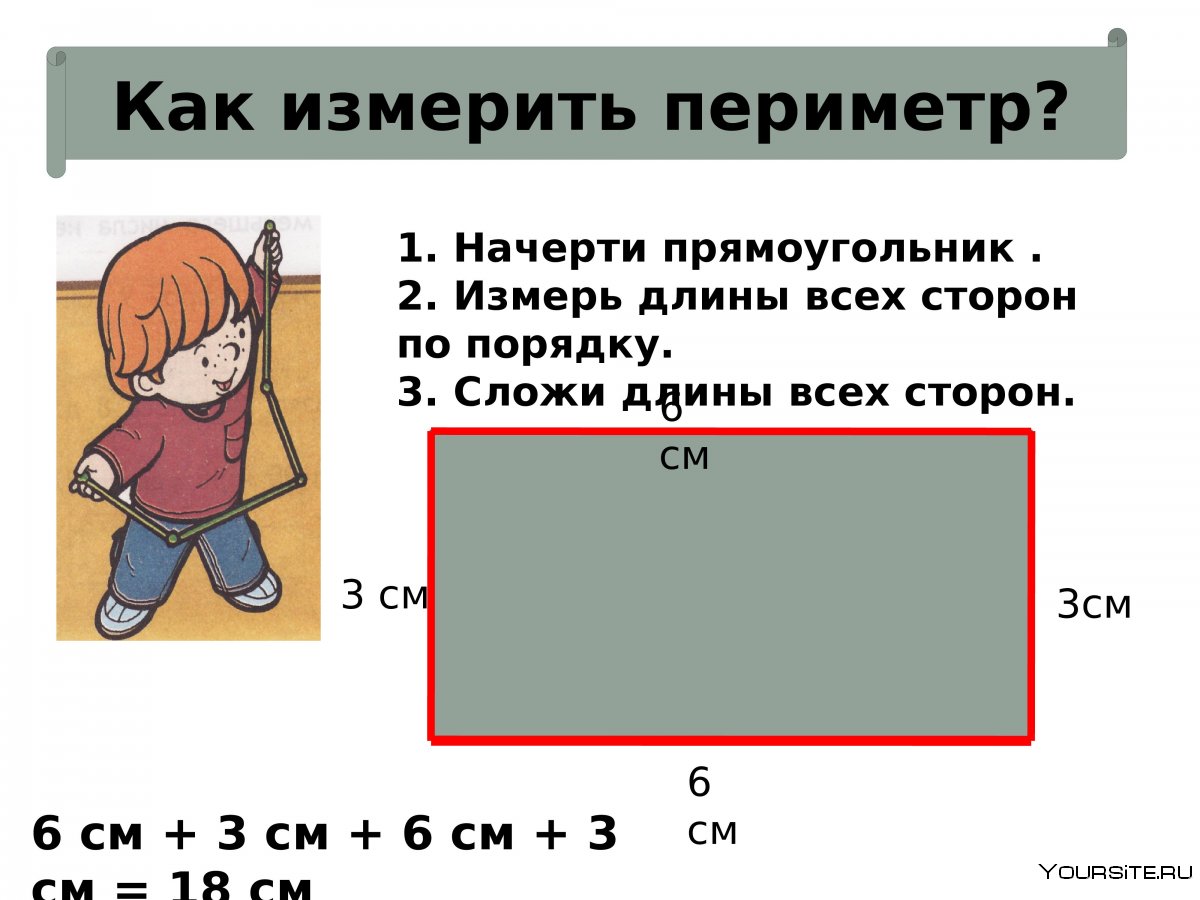
Теорема о площади прямоугольника с доказательством

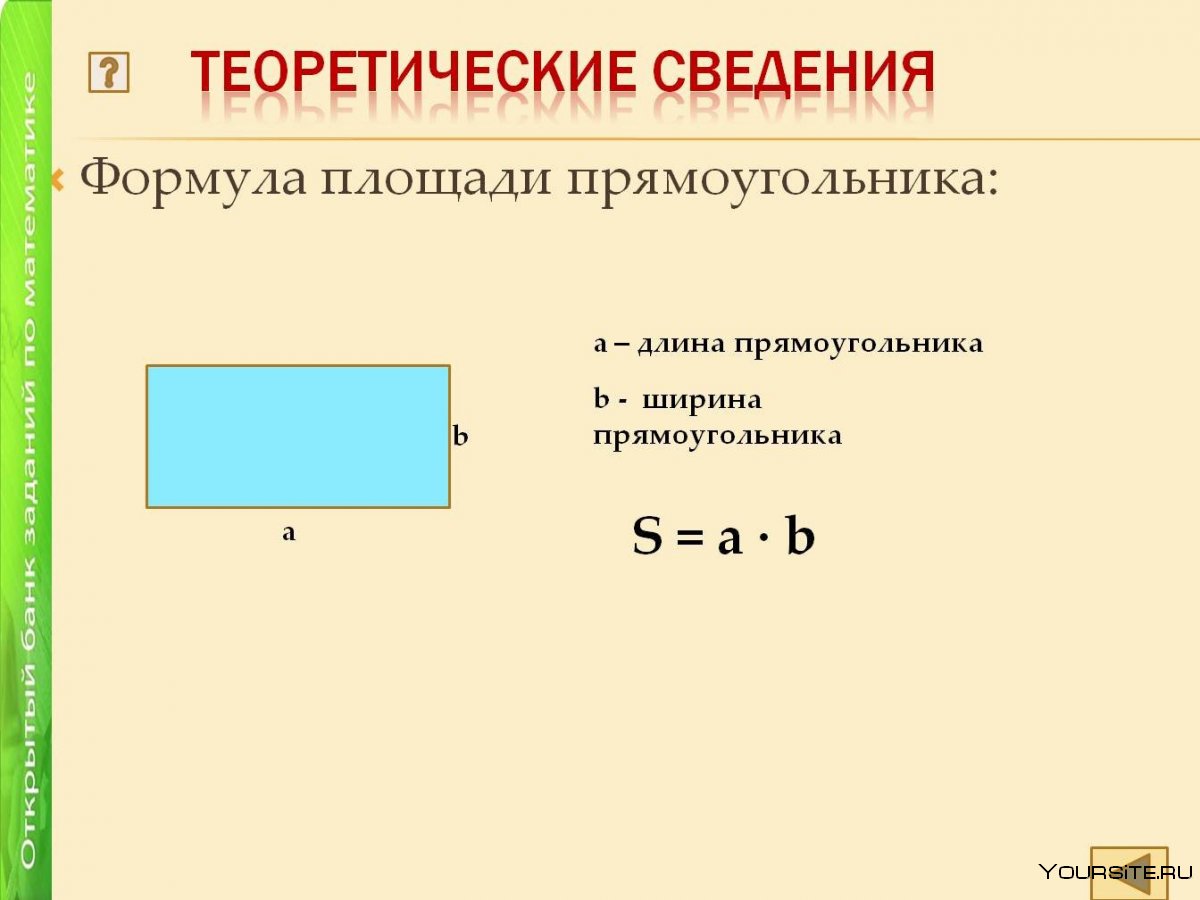
Площадь прямоугольника

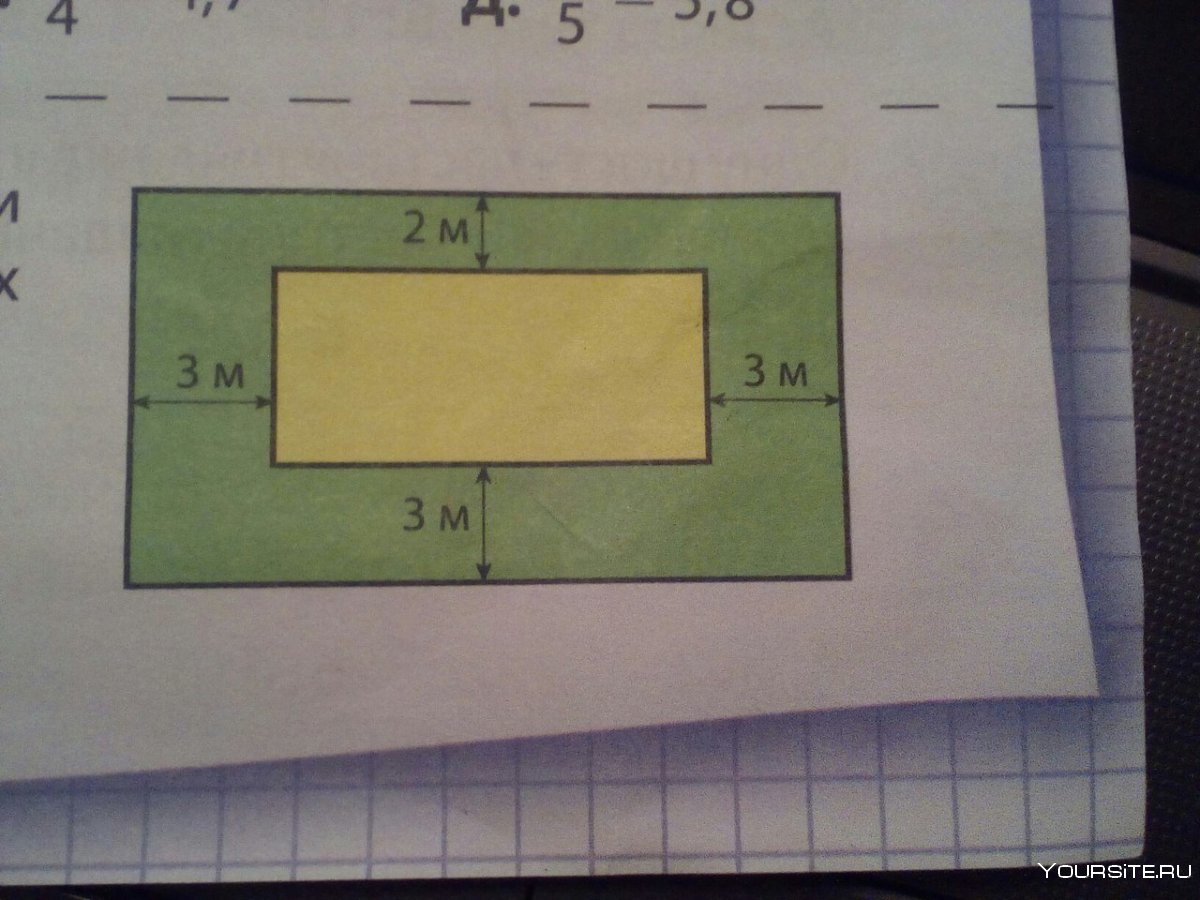
Периметр и площадка многоугольника

Что такое площадь прямоугольника 2 класс правило

Площадь прямоугольника

Чему равна s прямоугольника

Как доказать теорему о площади квадрата

Площадь прямоугольника по векторам

Площадь прямоугольника

Площадь прямоугольника в м2

Площадь прямоугольника с диагональю

Способы вычисления площади прямоугольника

Площадь прямоугольника

Длинная сторона прямоугольника

Площадь прямоугольника разными способами

Невидимые вершины прямоугольника

Прямоугольник в фотографии

Периметр прямоугольника равен

Формула нахождения площади прямоугольника

Два прямоугольника

Квадрат фото размер

Площадь прямоугольника

Прямоугольник фото

Площадь и периметр квадрата

Площадь прямоугольного треугольника теорема

Начертить квадрат

Площадь наклонного прямоугольника

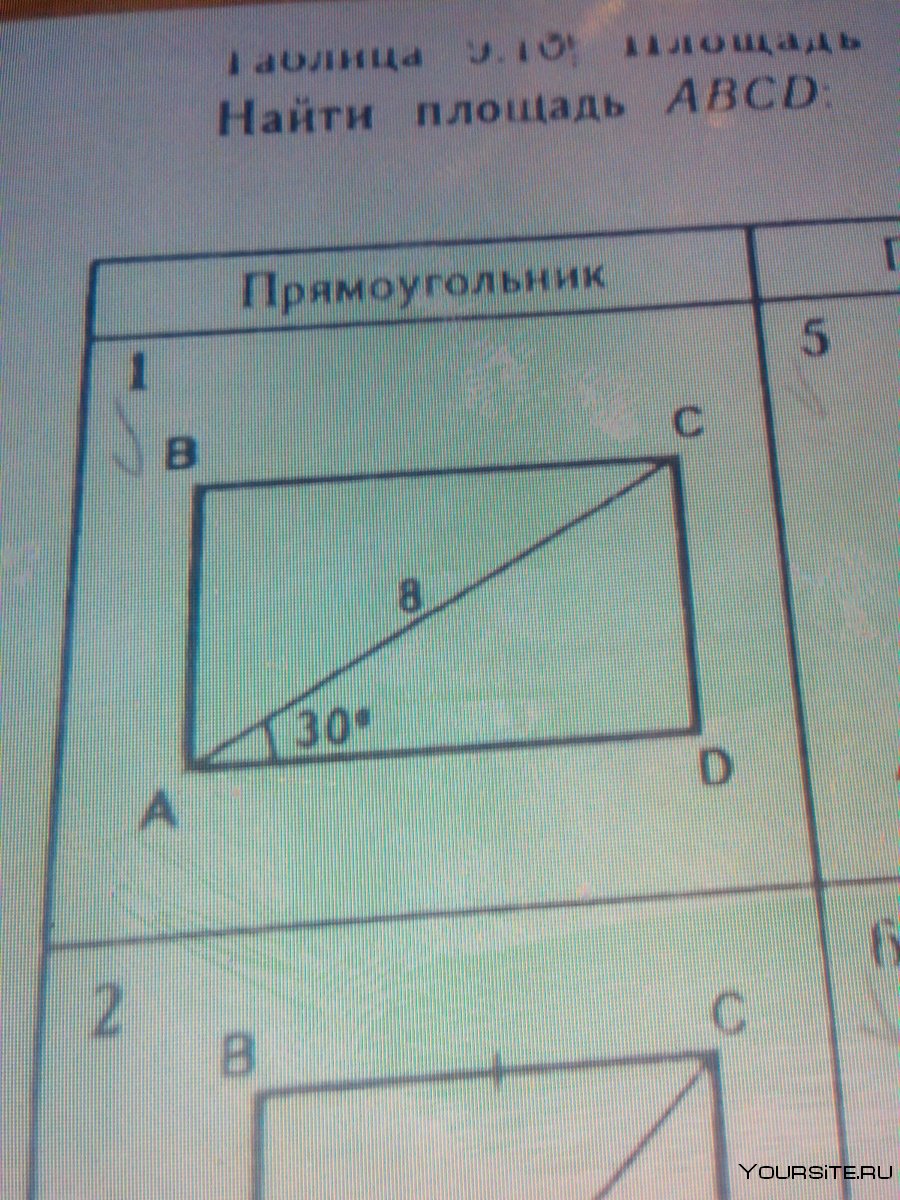
Свойство биссектрисы соседних углов параллелограмма

Найди периметр данной фигуры

Периметр прямоугольника квадрата треугольника формулы 2 класс

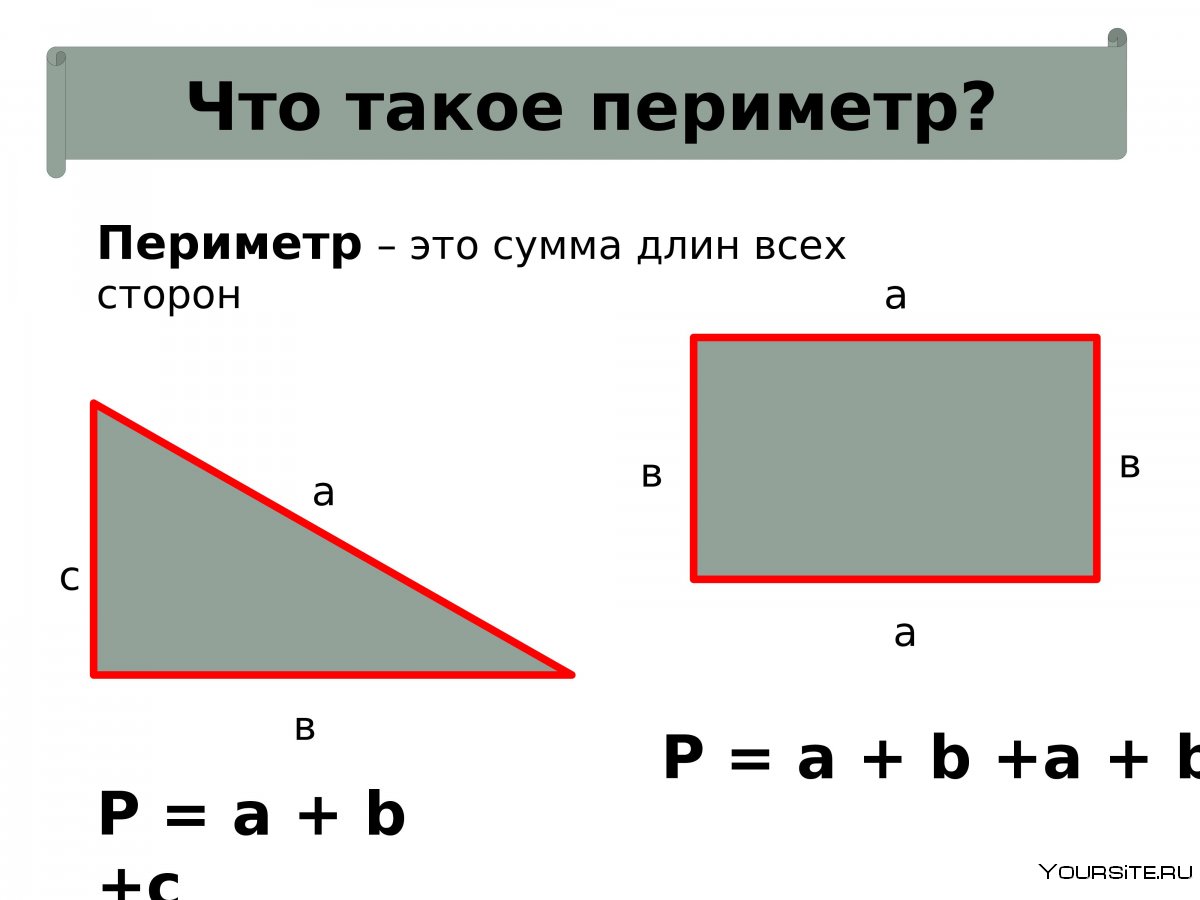
Формула вычисления площади прямоугольника

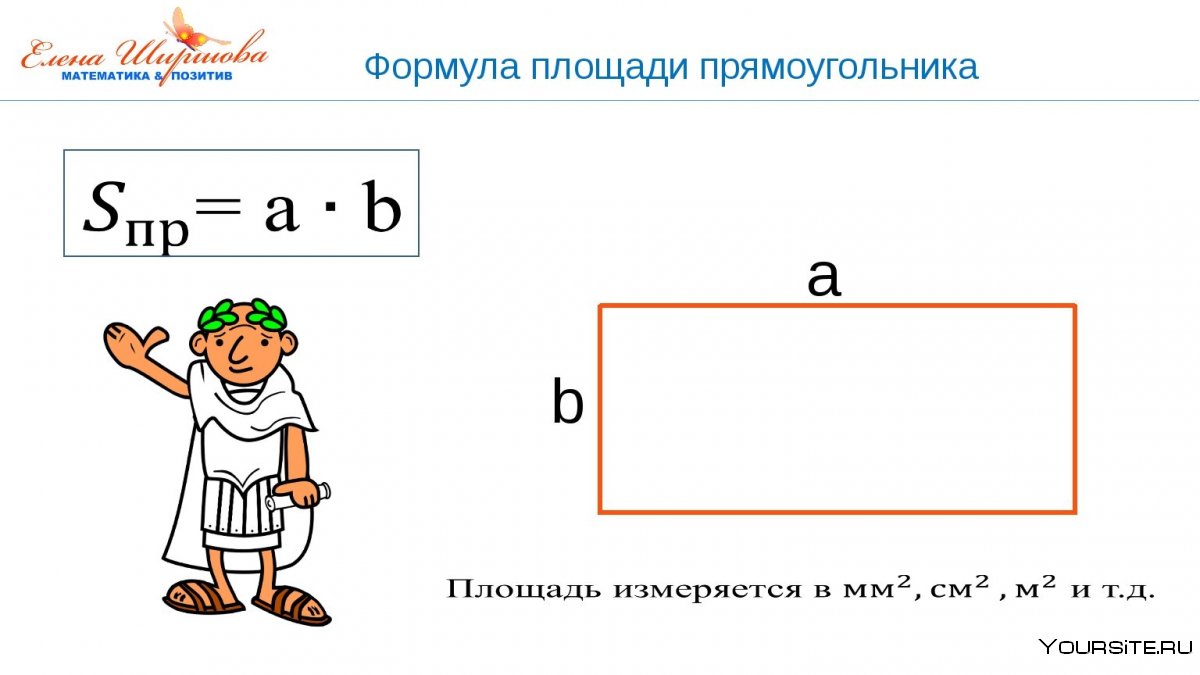
Стороны прямоугольника

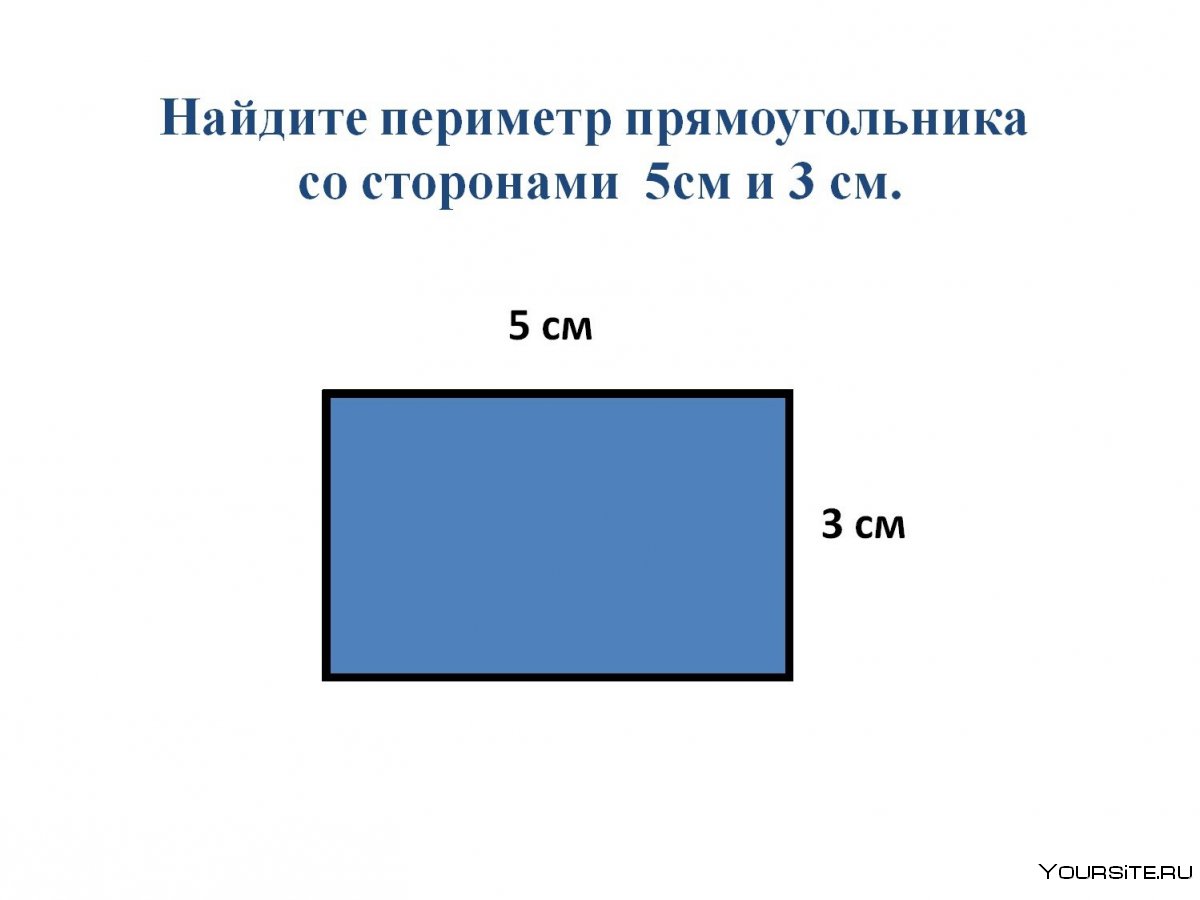
Площадь 5 класс

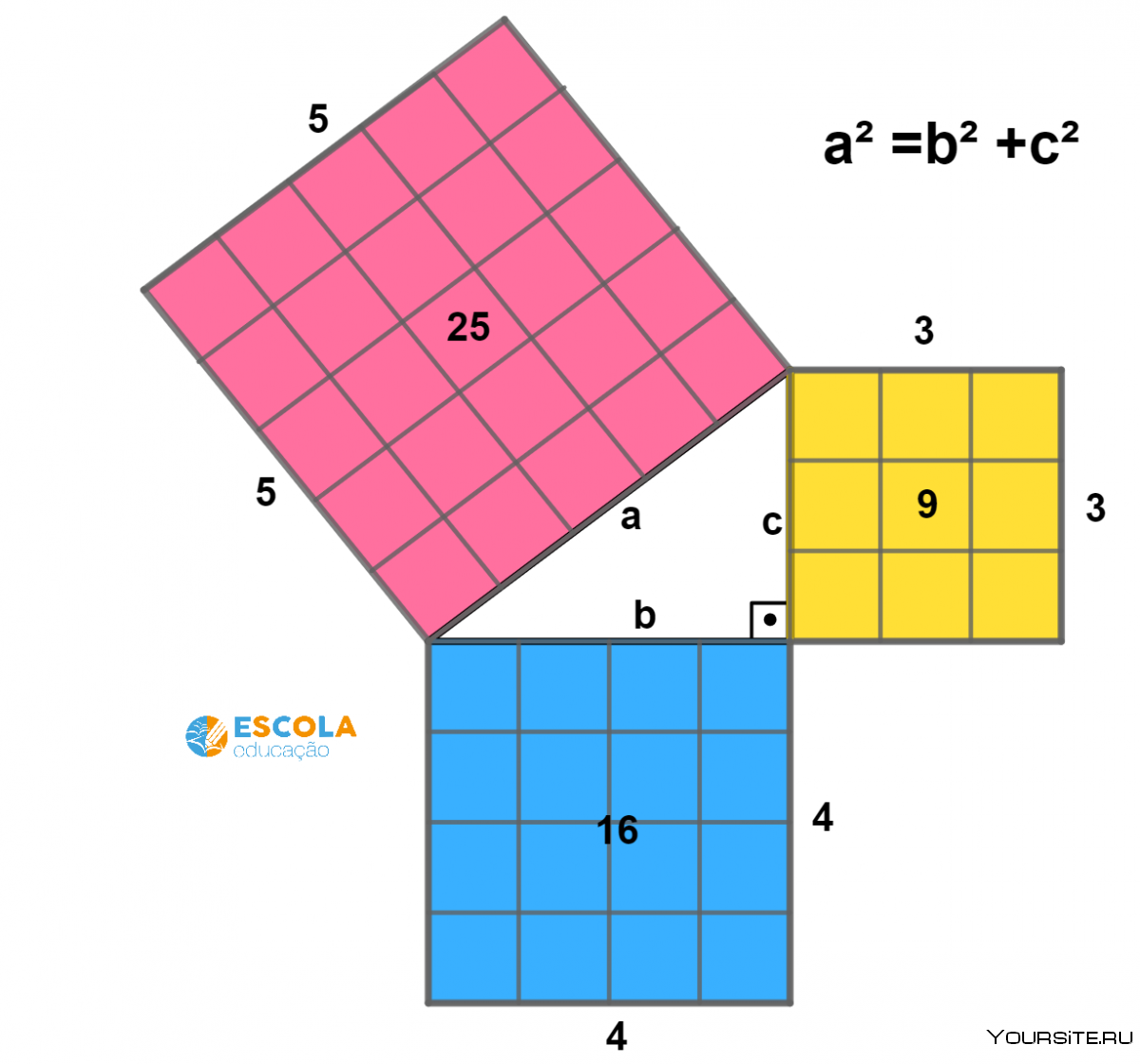
Теорема Пифагора таблица 12

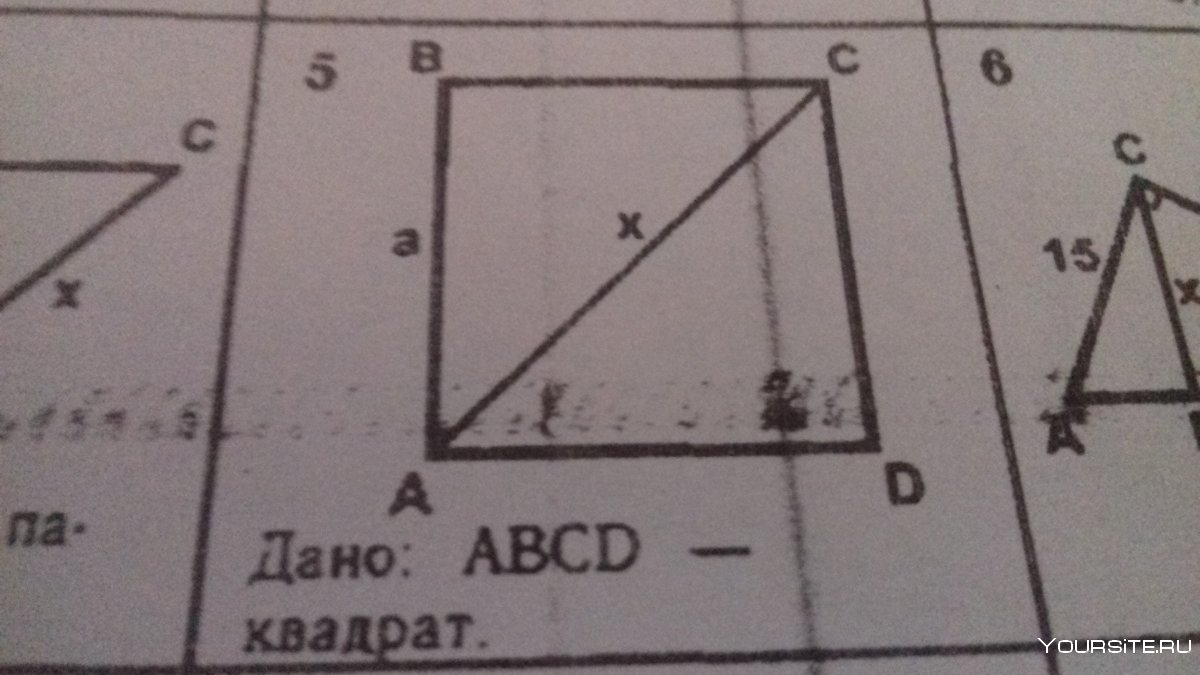
Площадь прямоугольника ABCD AE=2,5 корень из 3

Площадь прямоугольника с синусом

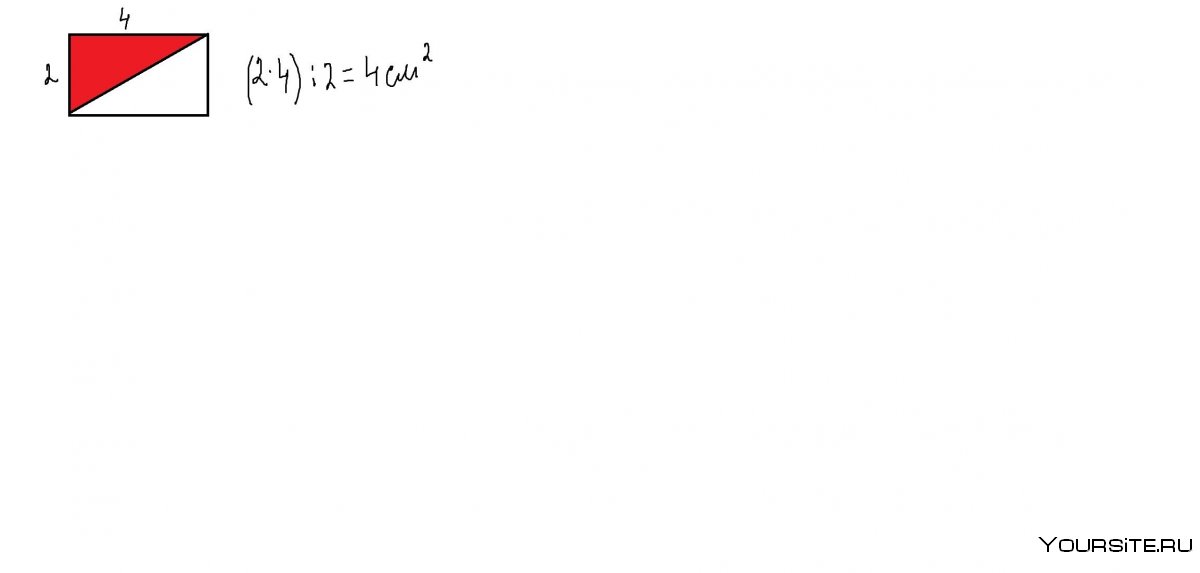
Док-во площади треугольника

Найдите площадь прямоугольника изображенного на рисунке

Теорема Пифагора формула квадрата

Эволюция образования прямоугольник

Теорема Пифагора сериал

Учебник по геометрии 7-9 класс Атанасян теоремы

Прямая проведенная в плоскости через основание наклонной

Как вычислить периметр прямоугольника 4

Теорема Пифагора с углом 30 градусов

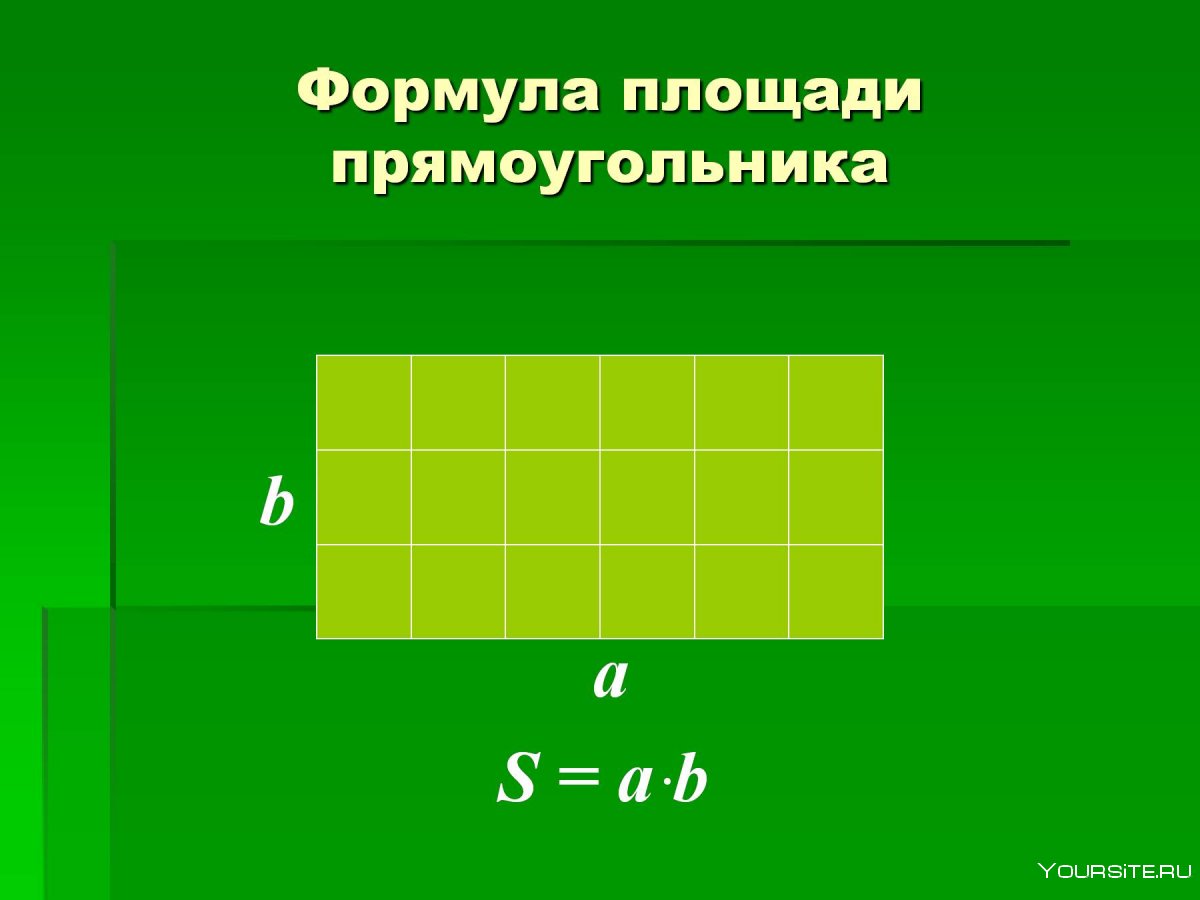
Площадь прямоугольника

Обратная теорема Пифагора 8 класс

Доказательство первого свойства параллелограмма

Точка пересечения тупого прямоугольника

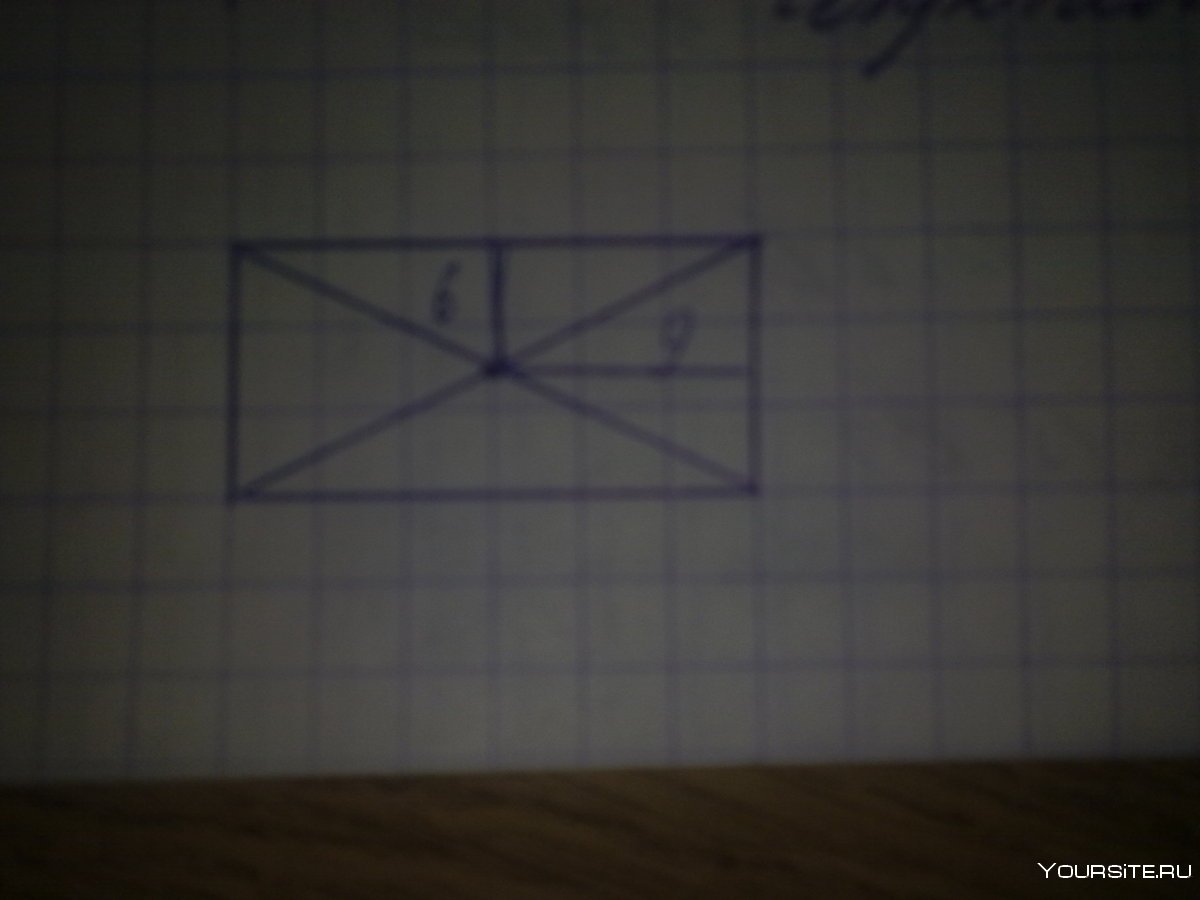
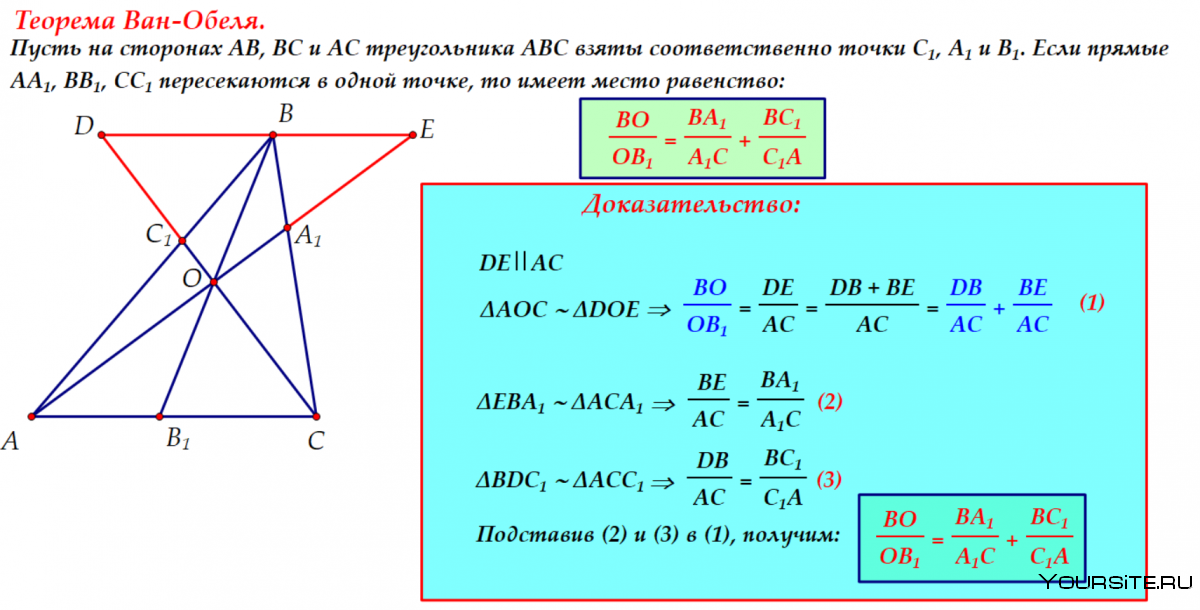
Ван Обеля Менелая

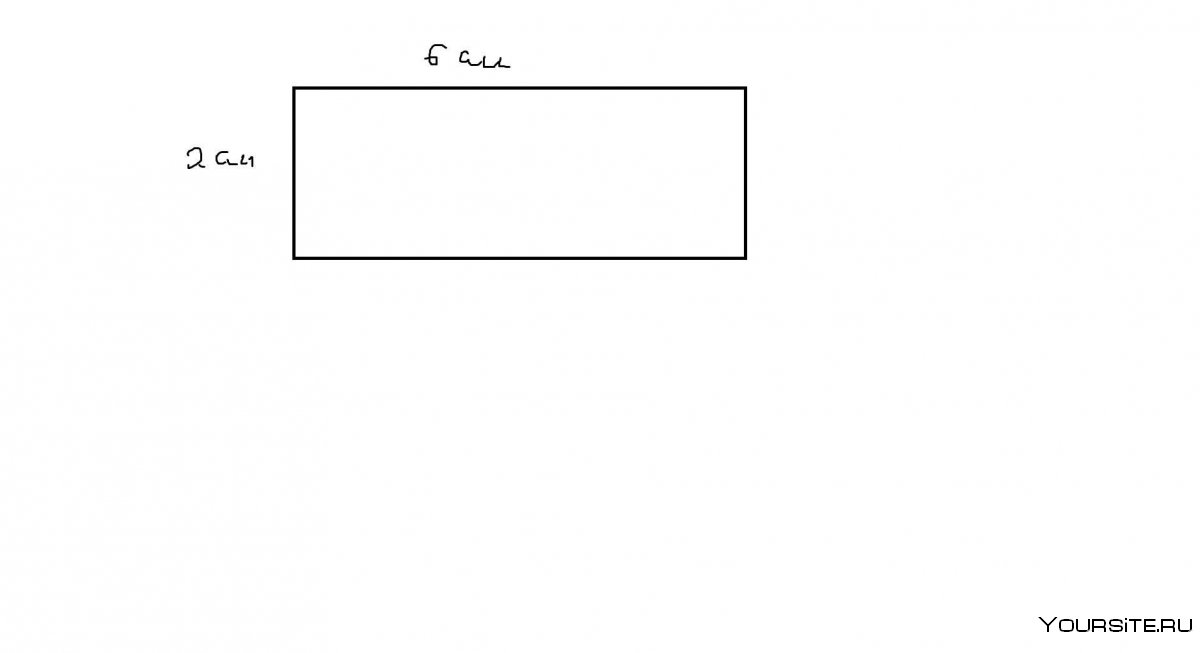
Прямоугольник а=11см в=12см s-?

Геометрия 8 класс Атанасян площадь многоугольника

Как находится диагональ квадрата

Прямоугольник разбит на три прямоугольника

Доказательство теоремы о площади треугольника через синус

Прямоугольник 30 см квадратных

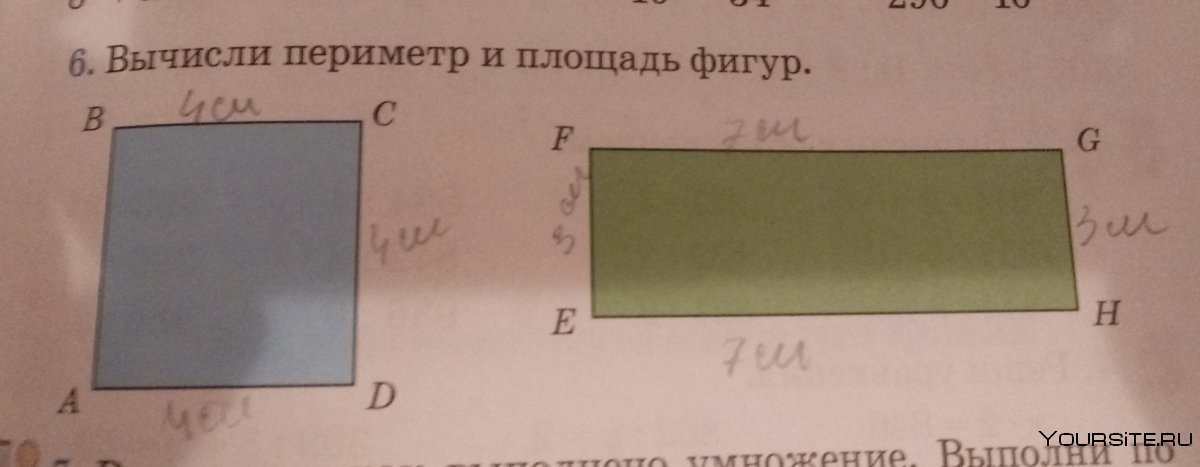
Вычисли периметр каждого прямоугольника

Периметр закрашенной фигуры

Площадь прямоугольника ab

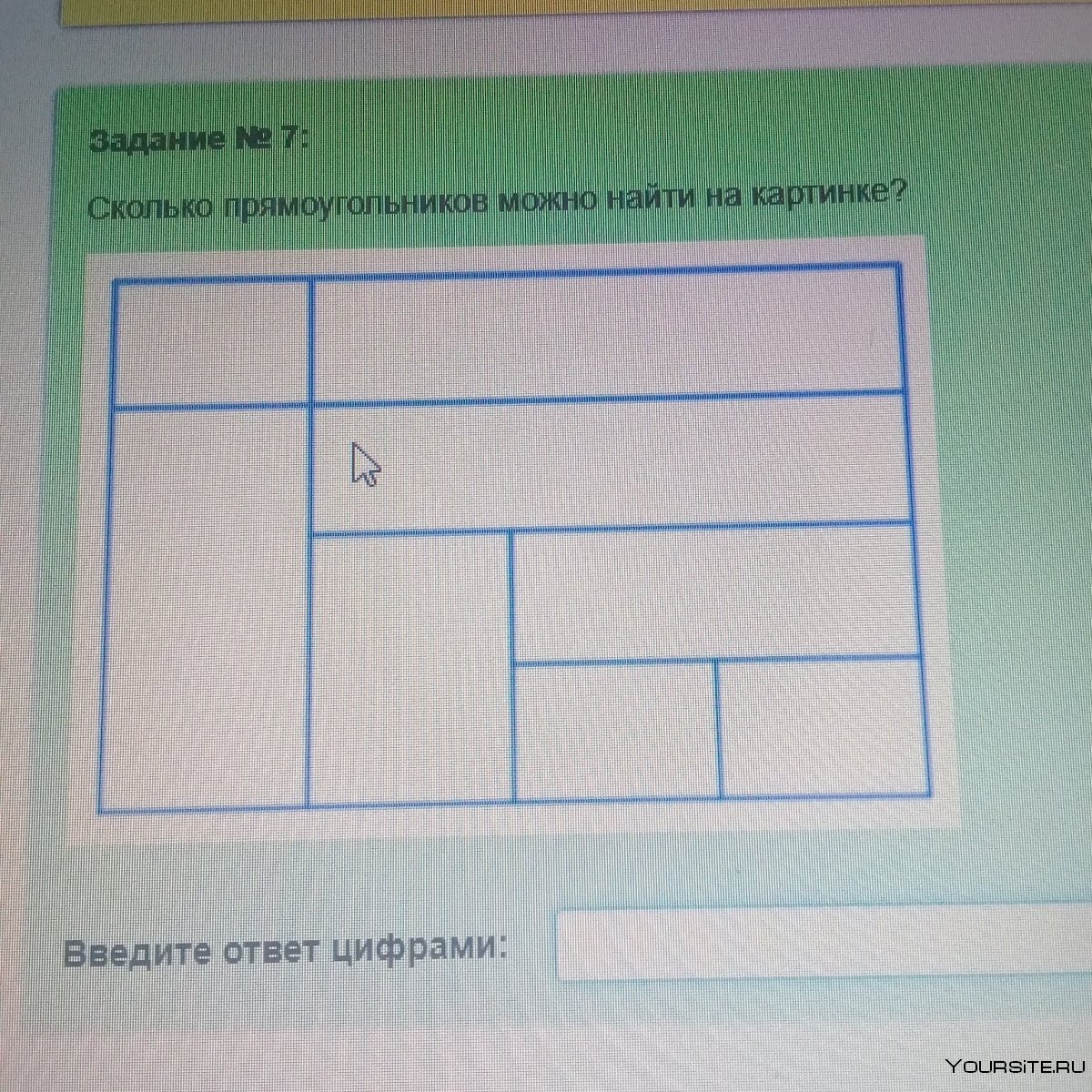
Сколькопрямоугольн Ков

Измерь стороны и Найди периметр

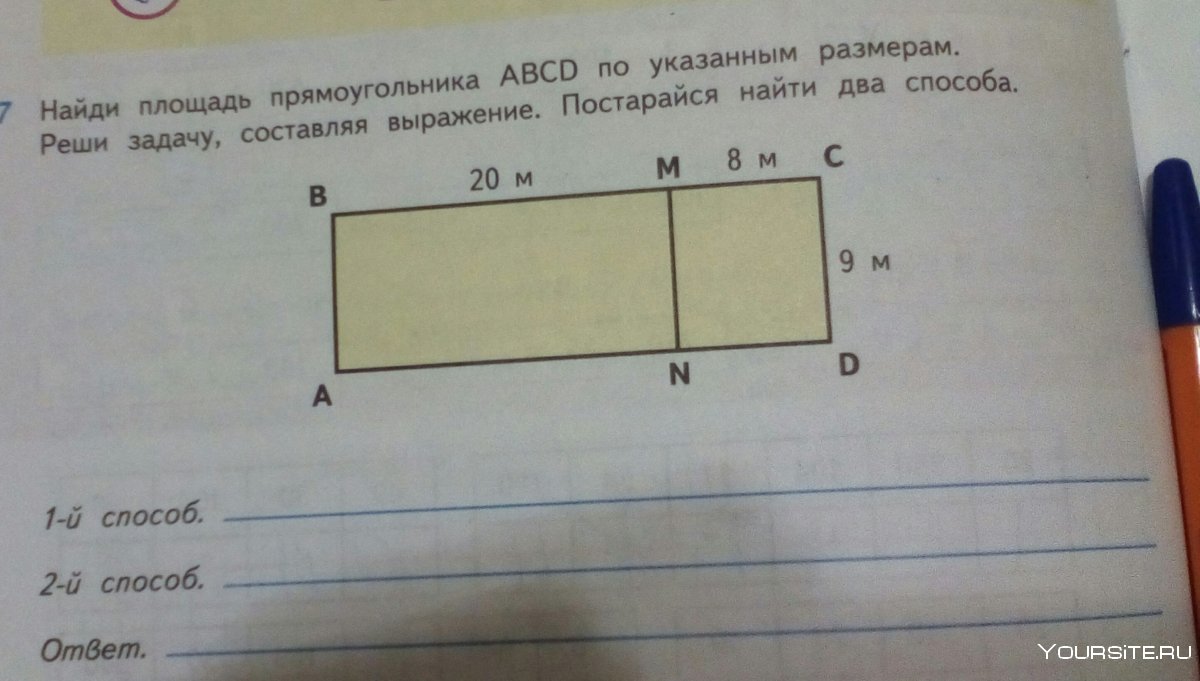
Площадь прямоугольника двумя способами

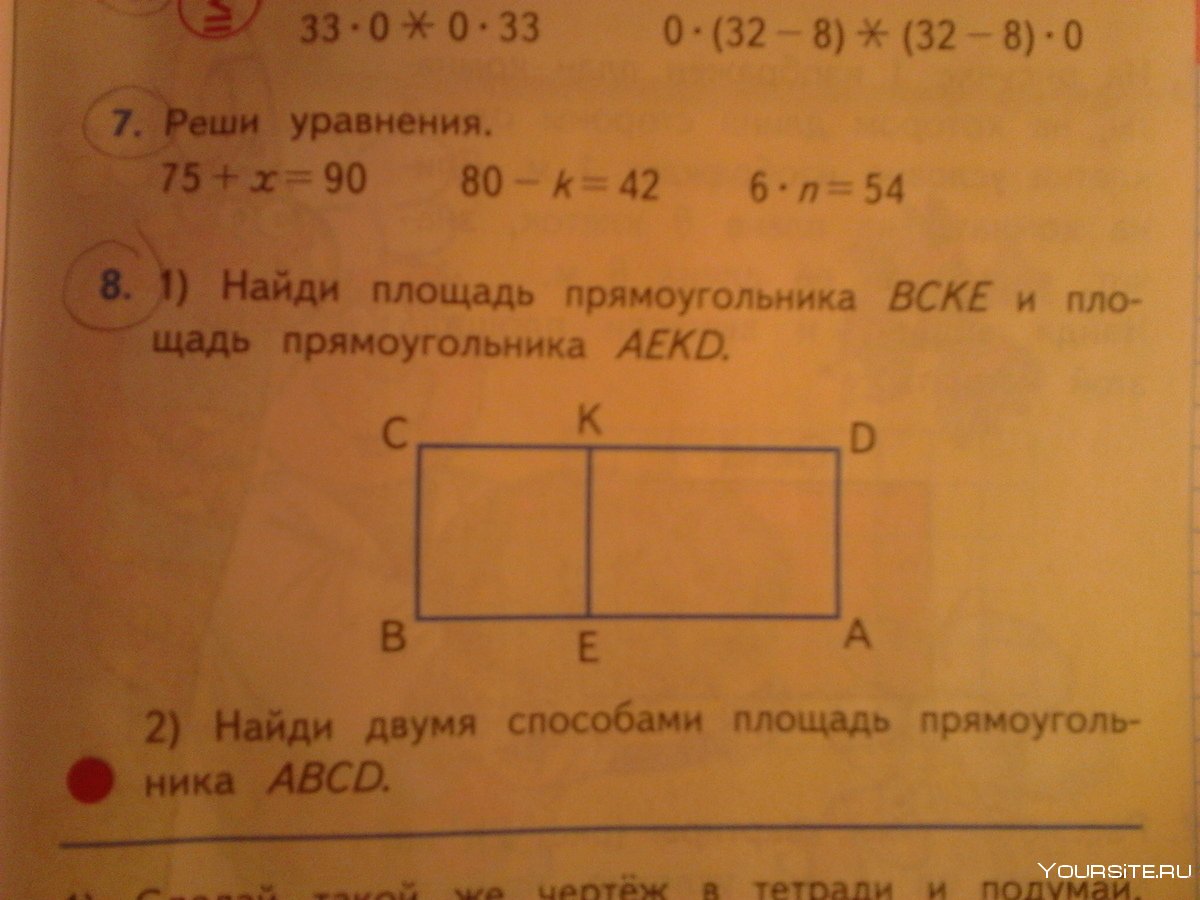
Прямоугольник сторона корень из 3

Площадь и периметр прямоугольника

Площадь прямоугольника через диагональ и угол

Найдите площадь прямоугольник одна сторона 10 другая 12

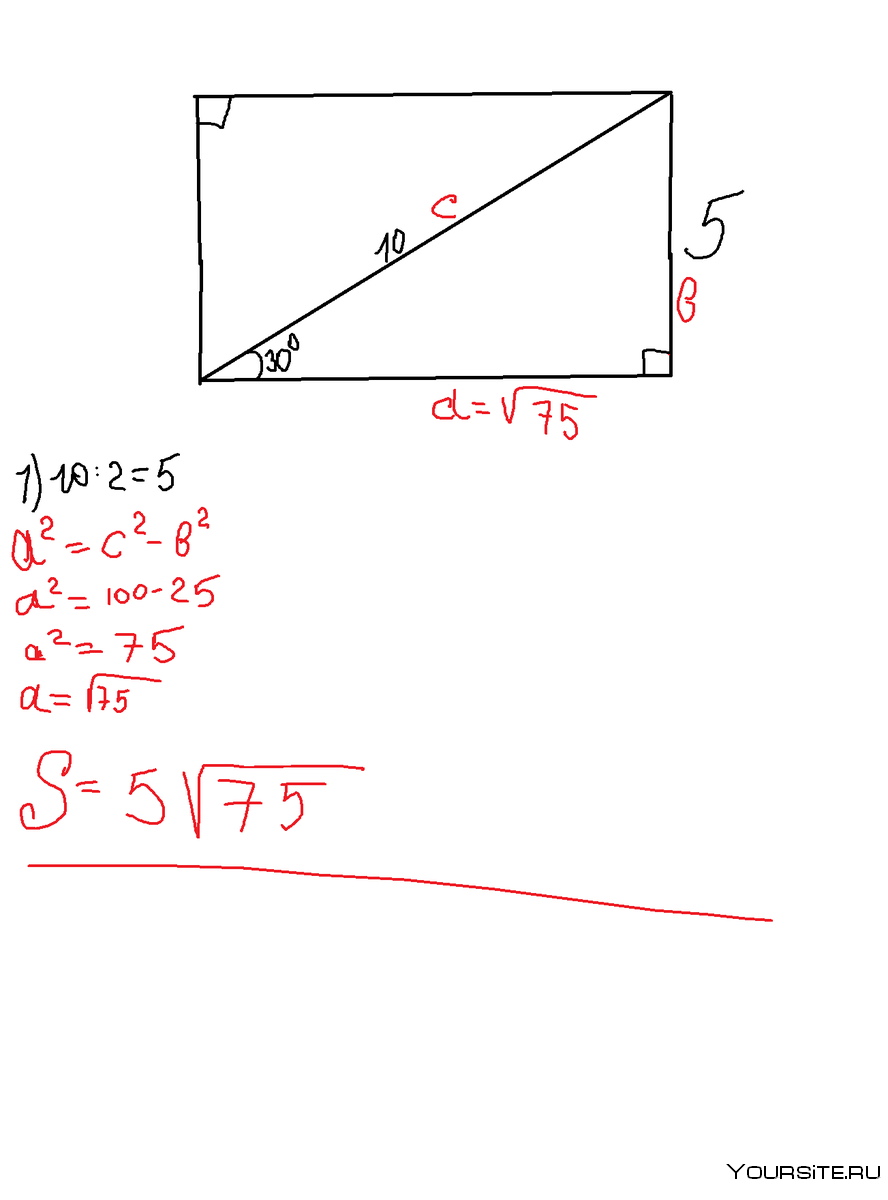
Формула нахождения площади

Объясните почему верно равенство

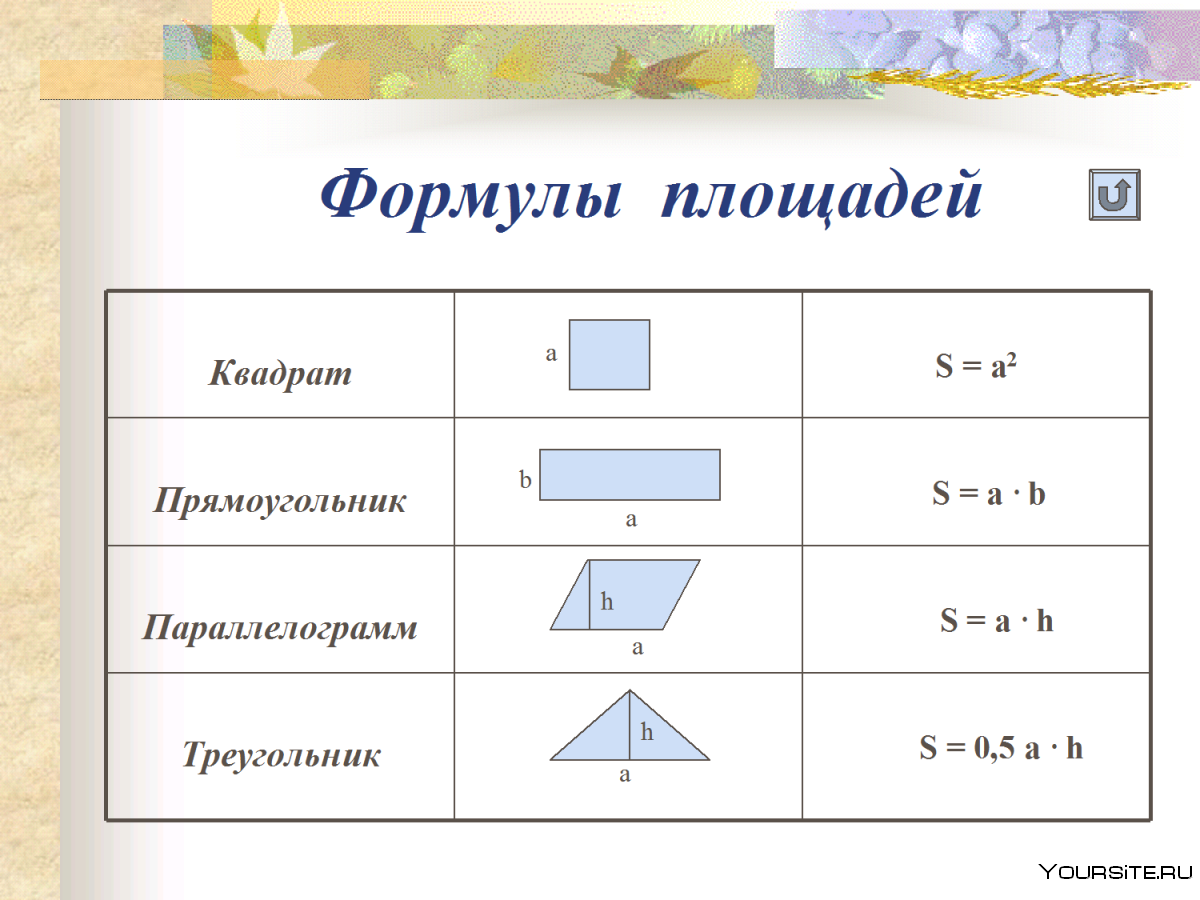
СМПЛОЩАДЬ прямоугольника АСЕF равна

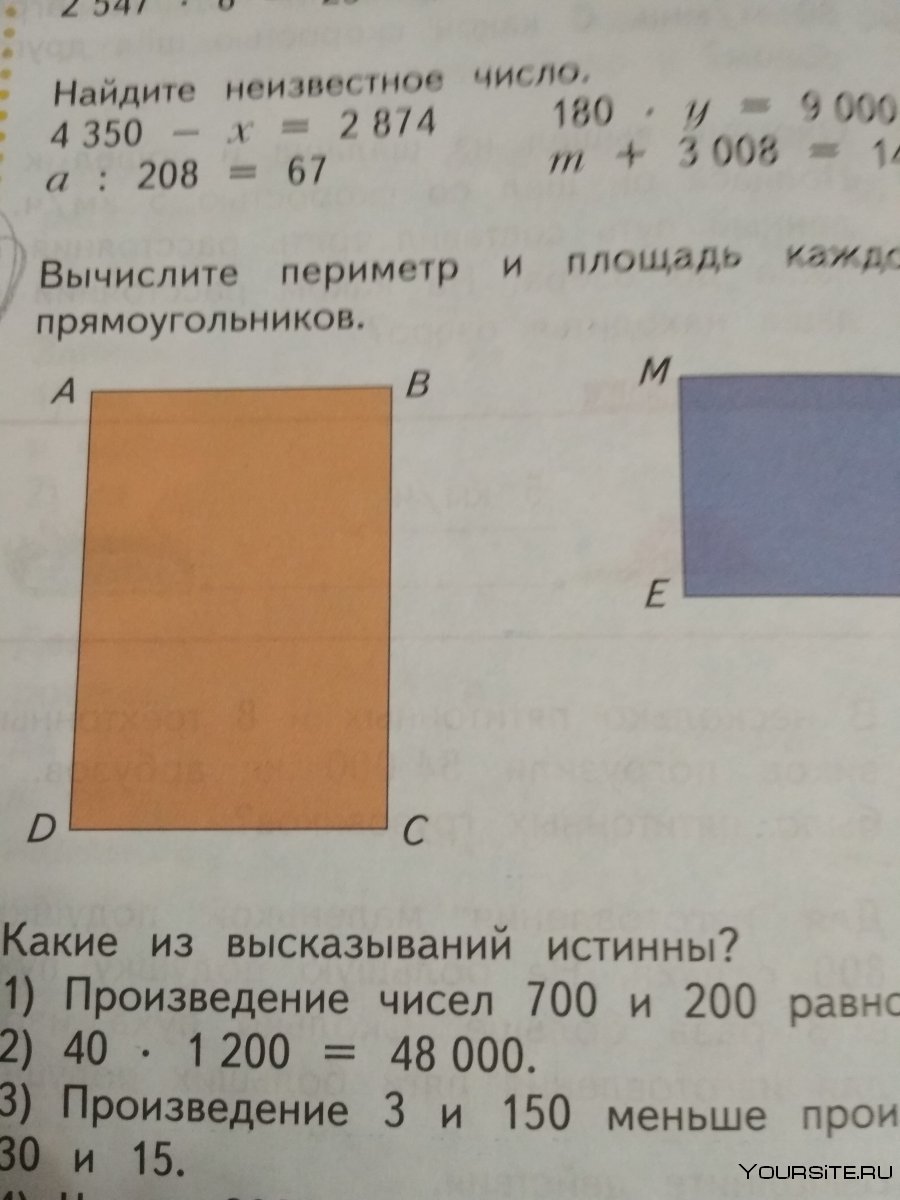
Вычислите площадь и периметр каждого прямоугольника

Прямоугольник 2 х 5

Вычисление площадей многоугольников и объемов многогранников, заданных координатами своих вершин в прямоугольной системе координат, основывается на использовании скалярного, векторного и смешанного произведений векторов.

Если параллелограмм задан в пространстве координатами своих вершин, то для вычисления его площади нужно найти координаты двух векторов, соответствующих смежным сторонам параллелограмма, а затем модуль их векторного произведения. Аналогично вычисляется площадь треугольника, равная половине модуля векторного произведения векторов, на которых он построен как на смежных сторонах.

Пример 4.2. Пусть три вершины треугольника заданы своими координатами: A(4;4;4), B(1; 2; 3), C(3; —1;2).

Для определения площади ΔABC с помощью (4.10) найдем координаты векторов AB и AC: AB = {1 — 4; 2 — 4; 3 — 4} = { — 3; —2; —1}, —1 = {3 — 4; —1 — 4; 2 — 4} = { — 1; —5; —2}.

Затем по (3.2) вычислим их векторное произведение:

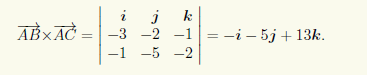
Модуль этого векторного произведения равен |AB×AC| = √((—1)² + (—5)² + 13²) = √195, и следовательно, S ΔABC = |AB×AC|/2 = √195/2 #

Для вычисления объема параллелепипеда, заданного координатами своих вершин, нужно найти координаты трех векторов, соответствующих смежным ребрам, а затем вычислить модуль смешанного произведения этих векторов. Через смешанное произведение вычисляется и объем произвольной треугольной пирамиды SABC (см. пример 3.2), поскольку он равен 1/6 объема параллелепипеда, построенного на ребрах AB, AC и AS. Таким образом, объем этой пирамиды равен VSABC = |ABACAS|/6.

Пример 4.3. Найдем объем V пирамиды SABC, заданной координатами своих вершин: A(2; —1;1), B(5; 5; 4), C(3; 2; —1), S(4;1;3).

Используя (4.10), вычисляем координаты векторов, направленных по ребрам пирамиды: AB = {5 — 2; 5 — (—1);4 — 1} = {3; 6; 3}, AC = {3 — 2; 2 — (—1); —1 — 1} = {1;3; —2},= AS {4 — 2;1 — (—1); 3 — 1} = {2;2;2}, и определяем объем с помощью смешанного произведения найденных векторов: