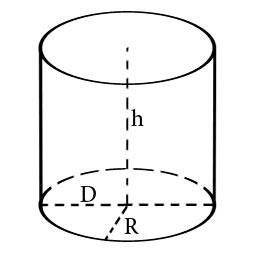
Как рассчитать объем цилиндра
На данной странице калькулятор поможет рассчитать объем цилиндра онлайн. Для расчета задайте высоту, радиус или площадь основания. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
По высоте и радиусу
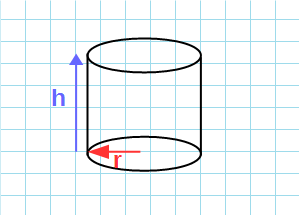
Формула объема цилиндра через высоту и радиус:
V=π·r²·h
π – константа равная (3.14); r – радиус основания; h – высота цилиндра.
Через площадь основания и высоту
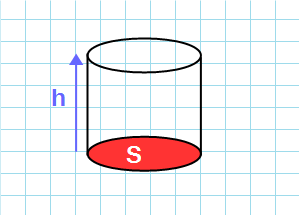
Формула объема цилиндра через высоту и площадь основания:
V=S·h
S – площадь основания цилиндра; h – высота цилиндра.
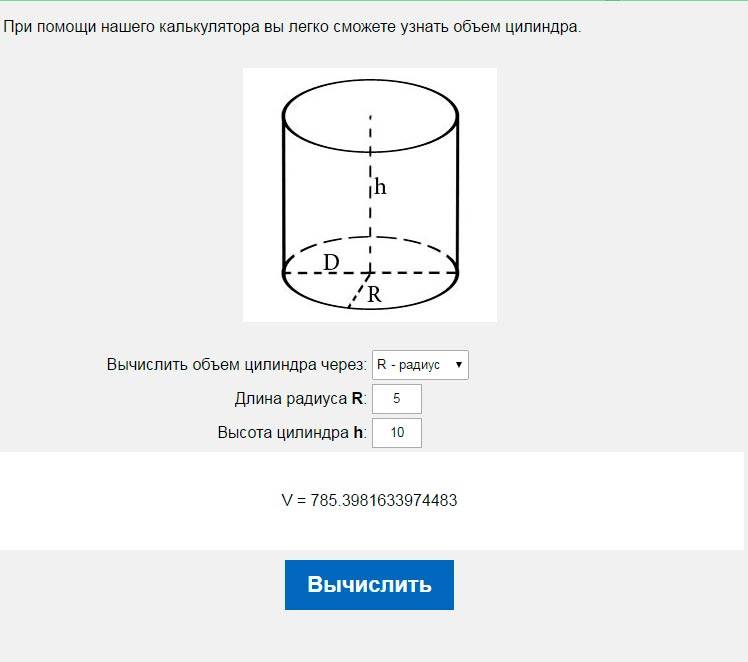
При помощи нашего калькулятора вы легко сможете узнать объем цилиндра. Так же если вам необходимо узнать объем бочки, круглой цистерны, круглого бака и т.д., то это калькулятор то, что Вам нужно.
|
|
|
| Вычислить объем цилиндра через: | |
| Длина радиуса R: | |
| Высота цилиндра h: |
Для того что бы вычислить объем цилиндра необходимо знать его высоту и радиус или диаметр. Если нам известны указанные величины, для нас не составит труда вычислить объем.
Объем цилиндра рассчитывается по следующим формулам:
- Если нам известен радиус:
V=πR2h
- Если нам известен диаметр:
V=πD2/4h
Где V – объем, R – радиус, D – диаметр, h – высота, π – число Пи которое всегда примерно равно 3,14.
Расчет объема цилиндра |
 |
Многие сложные детали (конструкции) можно представить совокупностью различных элементов, объем которых можно вычислить, воспользовавшись набором online-калькуляторов с данной страницы.
Представлены программы для расчета объемов фигур, базисом которых является квадрат или прямоугольник, а также имеющих в основании окружность: цилиндра, конуса и шаровых элементов.
В конструкторской работе при различных расчетах возникает потребность использования значений объема элементарных фигур: параллелепипеда, куба, призмы и пр. В частности это может иметь место при расчете заполнения вагонов и платформ упакованной в транспортную тару готовой продукцией. Такой расчет требует учета многих факторов, в том числе боковой ветровой нагрузки, смещения центра тяжести и пр.
Если неправильно рассчитать объем тары подлежащего отгрузке упакованного товара, можно не вместить в вагон заявленное количество изделий. В результате предприятие потерпит убытки. Онлайн калькуляторы нашего сайта позволят избежать проблемных ситуаций. Расчеты объемов различных фигур выполняются с большой точностью.

{V= pi R^2 h}
Цилиндр представляет собой простое геометрическое тело, получаемое при вращении прямоугольника вокруг одной из его сторон.
Другое определение: цилиндр – это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Рассчитать объем цилиндра можно по нескольким формулам. Для расчета необходимо знать высоту цилиндра и один из параметров – радиус основания, диаметр основания или площадь основания.
Содержание:
- калькулятор объема цилиндра
- формула объема цилиндра через высоту и радиус
- формула объема цилиндра через высоту и площадь основания
- формула объема цилиндра через высоту и диаметр
- примеры задач
Формула объема цилиндра через высоту и радиус
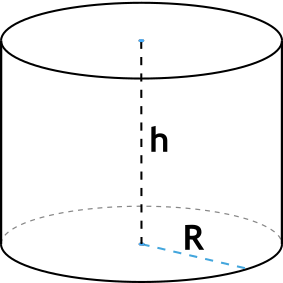
{V= pi R^2 h}
R – радиус основания цилиндра
h – высота цилиндра
Если внимательно посмотреть на эту формулу, то можно заметить, что {pi R^2} – это формула площади круга, а в нашем случае – площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
Формула объема цилиндра через высоту и площадь основания
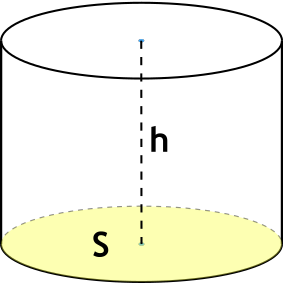
{V= S h}
S – площадь основания цилиндра
h – высота цилиндра
Так как диаметр окружности равен двум радиусам, мы легко можем преобразовать формулу объема цилиндра через радиус и высоту в формулу через диаметр и высоту. Для этого выразим радиус через диаметр и получим необходимую формулу:
D = 2R to R = dfrac{D}{2}
V = pi R^2 h = pi {Big( dfrac{D}{2} Big) }^2 h = pi dfrac{D^2}{4} h
Формула объема цилиндра через высоту и диаметр
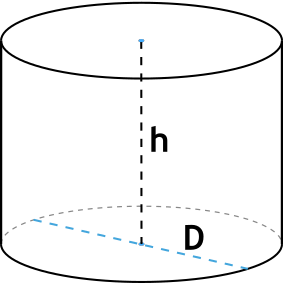
{V= pi {dfrac{D^2}{4}} h}
D – диаметр основания цилиндра
h – высота цилиндра
Примеры задач на нахождение объема цилиндра
Задача 1
Найти объём цилиндра с высотой 3см и диаметром основания 6см.
Решение
Так как в условии задачи нам дан диаметр основания цилиндра, мы будем использовать формулу объема через диаметр. Подставим в нее известные высоту и диаметр, чтобы получить объем цилиндра.
V = pi dfrac{D^2}{4} h = pi dfrac{6^2}{4} 3 = pi dfrac{36}{4} 3 = pi cdot 9 cdot 3 = 27 pi : см^3 approx 84.823 : см^3
Ответ: 27 pi : см^3 approx 84.823 : см^3
Ответ легко проверить с помощью калькулятора .
Задача 2
Найдите объем цилиндра с радиусом основания 5см и высотой 16см.
Решение
Для решения этой задачи воспользуемся формулой объема через радиус.
V = pi R^2 h = pi cdot 5^2 cdot 16 = pi cdot 25 cdot 16 = pi cdot 25 cdot 16 = 400 pi : см^3 approx 1 256.63706 : см^3
Ответ: 400 pi : см^3 approx 1 256.63706 : см^3
Проверить ответ поможет калькулятор .