Как найти угол по картинке

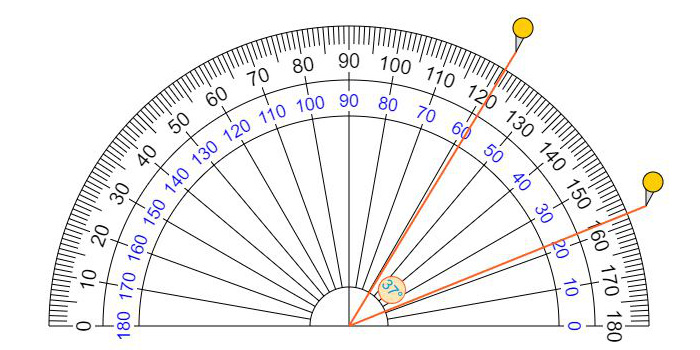
Это прозрачный онлайн транспортир,
вы можете легко измерить угол любого объекта вокруг вас,
и это поможет вам измерить углы на картинке,
сделать снимок и загрузить его,
затем перетащите середину транспортира в вершину угла,
наш виртуальный транспортир очень точен, он может увеличивать и уменьшать масштаб, вращать и перемещать положение.

Как пользоваться этим онлайн транспортиром?

• Вы можете измерить угол любого фактического объекта прямо на экране.
• Если вы хотите переместить транспортир, перетащите его середину
• Если вы хотите, чтобы размер транспортира был меньше или больше, вы можете изменить радиус транспортира
• Вы можете вращать транспортир так же, как традиционный транспортир
• Щелкните край за пределами транспортира, чтобы добавить на него канцелярскую кнопку.
• Размещение двух канцелярских кнопок покажет градусы этого угла
• Двойной щелчок по канцелярской кнопке удалит ее, перетащите ее, чтобы переместить ее положение.
• Эти действия также можно выполнить с помощью кнопок внутри панели управления.
• Выберите изображение в качестве фона, фон можно увеличивать и уменьшать, а наш транспортир может измерять прямо на изображении.
• Вы можете перетащить изображение на фон.
• Нажмите Ctrl+V, чтобы вставить изображение на фон
• Вы можете скачать свой дизайн и поделиться им с другими, это бесплатно
• Браузер на мобильном телефоне не поддерживает операцию перетаскивания, просто используйте кнопки
• Если вам нужно больше рабочего пространства, попробуйте полноэкранный режим (F11).

История нашего транспортира

Каждый раз, когда я хочу измерить угол, я всегда не могу найти транспортир.
После того, как я попробовал виртуальные транспортиры других людей в Интернете, я не чувствовал себя очень удовлетворенным,
поэтому я решил сам создать более практичный онлайн-транспортир.
Эта идея была у меня в голове, я думал об этом целый год,
а потом я потратил некоторое время, чтобы сделать это, когда я был свободен.

Такая удобная и полезная вещь,
Я должен поделиться этим со всеми вами,
так что нам всем сегодня повезло, вот удобный и полезный онлайн-транспортир.
Теперь мы можем измерить угол всего вокруг нас в любое время и в любом месте, используя наш ноутбук, компьютер, планшет или смартфон.

Если вы хотите измерить что-то маленькое,
просто поместите его на экран и измерьте непосредственно;
Если вы хотите измерить что-то большее,
Вы можете сделать снимок и загрузить его,
затем переместите центр транспортира, чтобы измерить его угол.

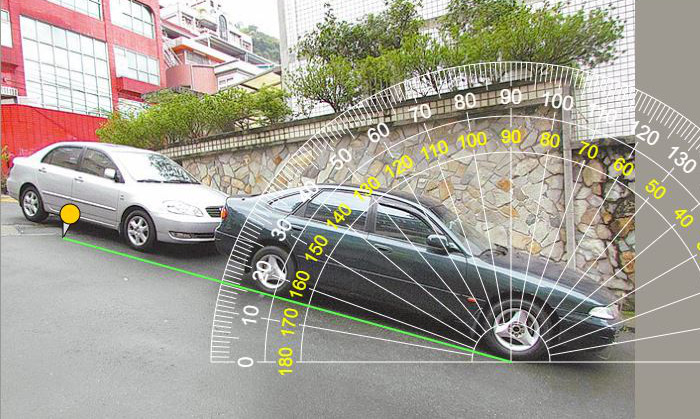
Используйте камеру или изображение для измерения угла

Вы можете сфотографировать любой объект, который вы хотели бы измерить,
например, автомобиль, дорога, дом, лестница или гора,
транспортир прозрачный,
после того как вы загрузили изображение, оно будет отображаться в фоновом режиме.
затем вы можете убрать транспортир или добавить кнопки, чтобы определить градусы углов,
загрузить файл только принять файл изображения в форматах JPG, JPEG, GIF, PNG

На панели управления
если цвет фона близок к транспортиру,
и это не легко отличить,
Вы можете изменить цвет транспортира, чтобы видеть это ясно.
Также вы можете переместить его,
уменьшить или увеличить размер транспортира,
в соответствии с вашими потребностями.

Углы и градусы

• Углы измеряются в градусах. Символом градусов является маленький кружок °
• Полный круг составляет 360 ° (360 градусов)
• Полукруг или прямой угол 180 °
• Четверть круга или прямой угол составляет 90 °

Что вы думаете об этом транспортире?

Посетите эту страницу на вашем смартфоне

Изменить текстовое описание на этой странице

Мы всегда стремимся обеспечить лучший интерфейс и пользовательский опыт,
любые предложения по улучшению приветствуются.
Текст этой веб-страницы автоматически генерируется Google Translate,
это может быть неправильно, если вы хотите предоставить лучшее текстовое описание, пожалуйста, нажмите эту кнопку. ›››

Пожалуйста, будьте вежливы и не используйте это злонамеренно.

В предыдущей статье была приведена задача, в которой нужно было найти угол по рисунку. Других данных не приведено.

Задача 18. ОГЭ 2021. (№14)

14) Найти угол АВС по данным чертежа.

• На данном чертеже для нахождения угла нужно найти с помощью дополнительных построений такие параметры заданного угла, которые помогут найти его значение.
• Таким дополнительным построением будет построение центрального угла, опирающего на ту же дугу АС, что и заданный угол АВС.
• Приведём чертёж.

• В приведённом угле <ОАС из точки С проведён на радиус ОА перпендикуляр СД.
• Тангенс угла tg (<OAC) = СД/ОД = 4/4 = 1.
• Откуда угол <ОАС = 45°.
• Так как вписанный на дугу АС угол <АВС = 1/2 (<АОС) = 45°/2 = 22,5°.

А далее очень интересная задача по нахождению угла на клеточной бумаге, но более усложнённая.

Какие будут предложения по решению такой задачи?

Приветствую любые адекватные комментарии к статье. А вот эта задача вызывает на первый взгляд затруднения.

Подписывайтесь на канал Тесты_математика.

Спасибо за прочтение статьи.

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Доказательства теорем об углах, связанных с окружностью

Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 8.

Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 9.

Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

Доказательство . Рассмотрим рисунок 10.

Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 11.

Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 12.

Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство

Углы в окружности, центральный и вписанный. Свойства и способы нахождения

Планиметрия – это раздел геометрии, изучающий свойства плоских фигур. К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?

Что такое центральный угол?

Для того чтобы понять, что такое центральный угол, нужно дать определение окружности. Окружность – это совокупность всех точек, равноудаленных от данной точки (центра окружности).

Очень важно отличать ее от круга. Нужно запомнить, что окружность – это замкнутая линия, а круг – это часть плоскости, ограниченная ею. В окружность может быть вписан многоугольник или угол.

Центральный угол – это такой угол, вершина которого совпадает с центром окружности, а стороны пересекают окружность в двух точках. Дуга, которую угол ограничивает точками пересечения, называется дугой, на которую опирается данный угол.

Рассмотрим пример №1.

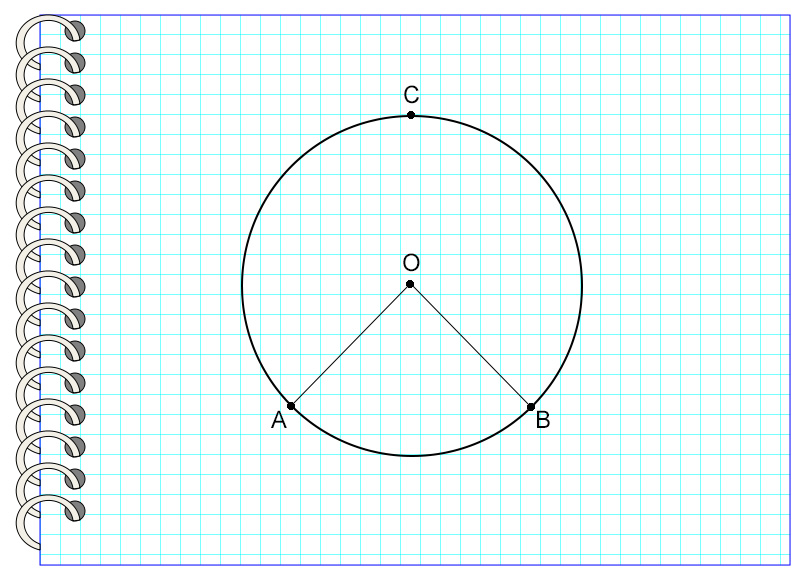
На картинке угол AOB – центральный, потому что вершина угла и центр окружности – это одна точка О. Он опирается на дугу AB, не содержащую точку С.

Чем вписанный угол отличается от центрального?

Однако кроме центральных существуют также вписанные углы. В чем же их различие? Так же как и центральный, вписанный в окружность угол опирается на определенную дугу. Но его вершина не совпадает с центром окружности, а лежит на ней.

Приведем следующий пример.

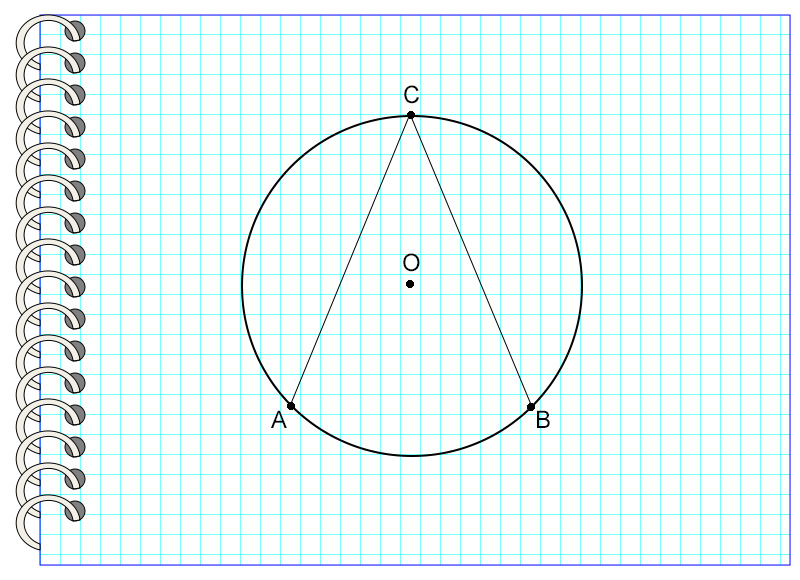
Угол ACB называется углом, вписанным в окружность с центром в точке О. Точка С принадлежит окружности, то есть лежит на ней. Угол опирается на дугу АВ.

Чему равен центральный угол

Для того чтобы успешно справляться с задачами по геометрии, недостаточно уметь различать вписанный и центральный углы. Как правило, для их решения нужно точно знать, как найти центральный угол в окружности, и уметь вычислить его значение в градусах.

Итак, центральный угол равен градусной мере дуги, на которую он опирается.

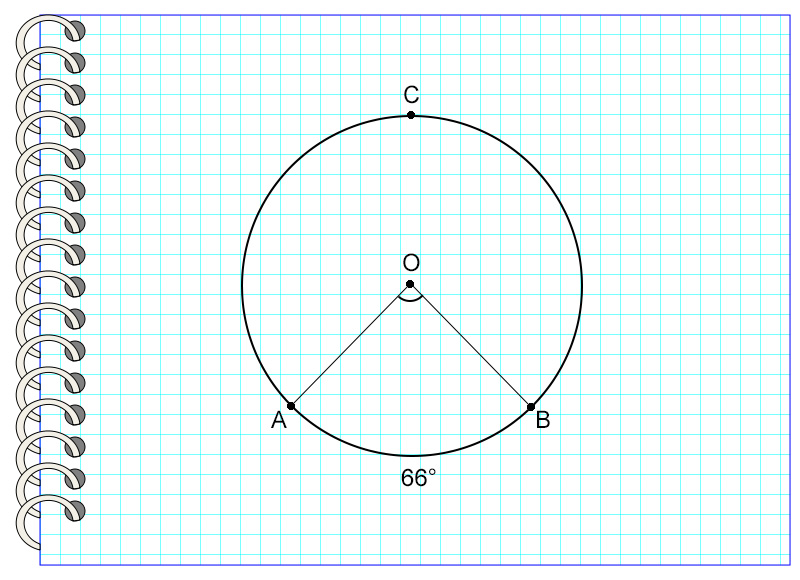
На картинке угол АОВ опирается на дугу АВ, равную 66°. Значит, угол АОВ также равен 66°.

Таким образом, центральные углы, опирающиеся на равные дуги, равны.

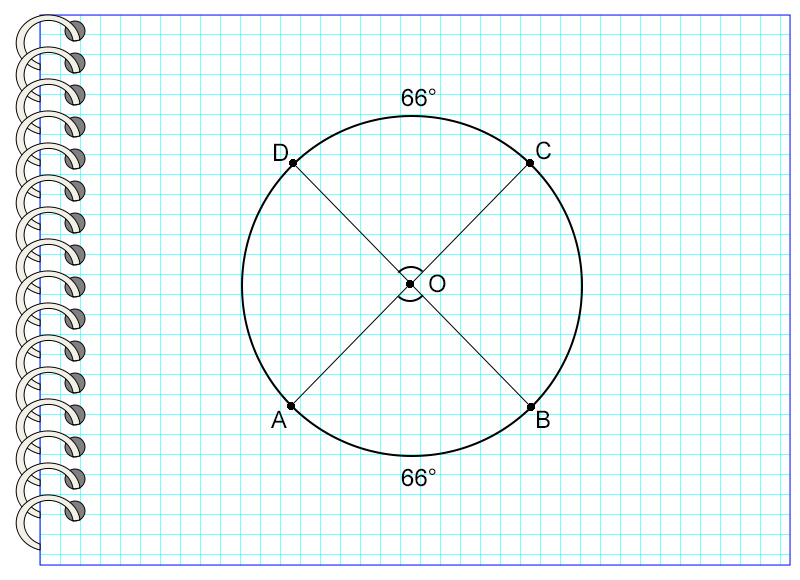
На рисунке дуга DC равна дуге AB. Значит, угол АОВ равен углу DOC.

Как найти вписанный угол

Может показаться, что угол, вписанный в окружность, равен центральному углу, который опирается на ту же дугу. Однако это грубая ошибка. На самом деле, даже просто посмотрев на чертеж и сравнив эти углы между собой, можно увидеть, что их градусные меры будут иметь разные значения. Так чему же равен вписанный в окружность угол?

Градусная мера вписанного угла равна одной второй от дуги, на которую он опирается, или половине центрального угла, если они опираются на одну дугу.

Рассмотрим пример. Угол АСВ опирается на дугу, равную 66°.

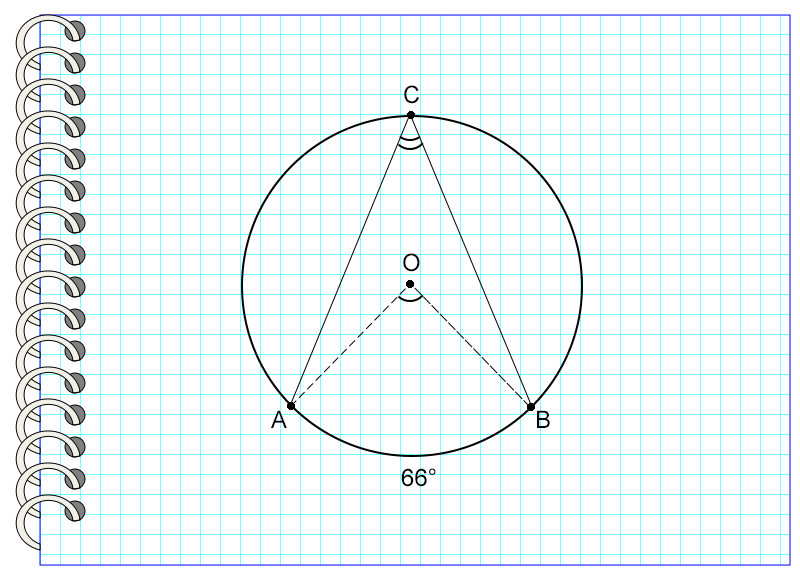
Значит, угол АСВ = 66° : 2 = 33°

Рассмотрим некоторые следствия из этой теоремы.

• Вписанные углы, если они опираются на одну и ту же дугу, хорду или равные дуги, равны.
• Если вписанные углы опираются на одну хорду, но их вершины лежат по разные стороны от нее, сумма градусных мер таких углов составляет 180°, так как в этом случае оба угла опираются на дуги, градусная мера которых в сумме составляет 360° (вся окружность), 360° : 2 = 180°
• Если вписанный угол опирается на диаметр данной окружности, его градусная мера равна 90°, так как диаметр стягивает дугу равную 180°, 180° : 2 = 90°
• Если центральный и вписанный углы в окружности опираются на одну дугу или хорду, то вписанный угол равен половине центрального.

Где могут встретиться задачи на эту тему? Их виды и способы решения

Так как окружность и ее свойства – это один из важнейших разделов геометрии, планиметрии в частности, то вписанный и центральный углы в окружности – это тема, которая широко и подробно изучается в школьном курсе. Задачи, посвященные их свойствам, встречаются в основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Как правило, для решения этих задач следует найти углы на окружности в градусах.

Углы, опирающиеся на одну дугу

Этот тип задач является, пожалуй, одним из самых легких, так как для его решения нужно знать всего два простых свойства: если оба угла являются вписанными и опираются на одну хорду, они равны, если один из них – центральный, то соответствующий вписанный угол равен его половине. Однако при их решении нужно быть крайне внимательным: иногда бывает сложно заметить это свойство, и ученики при решении таких простейших задач заходят в тупик. Рассмотрим пример.

Дана окружность с центром в точке О. Угол АОВ равен 54°. Найти градусную меру угла АСВ.

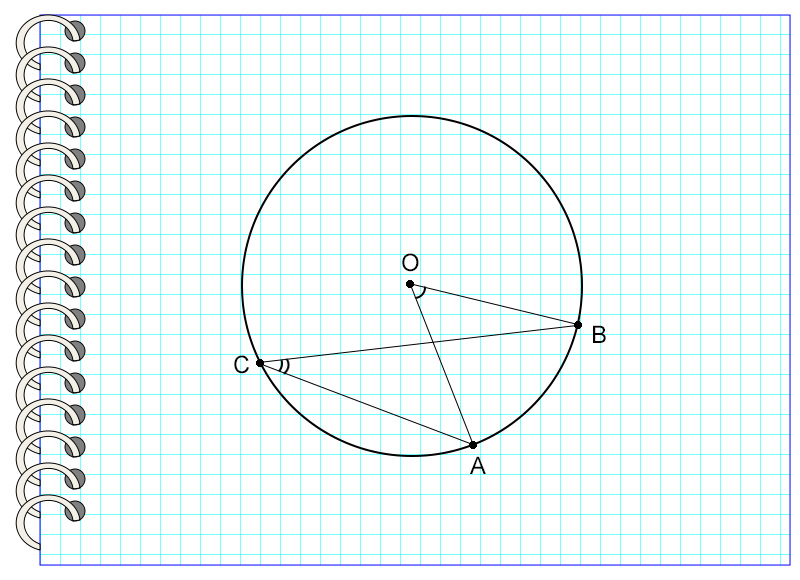
Эта задача решается в одно действие. Единственное, что нужно для того, чтобы найти ответ на нее быстро – заметить, что дуга, на которую опираются оба угла – общая. Увидев это, можно применять уже знакомое свойство. Угол АСВ равен половине угла АОВ. Значит,

1) АОВ = 54° : 2 = 27°.

Углы, опирающиеся на разные дуги одной окружности

Иногда в условиях задачи напрямую не прописана величина дуги, на которую опирается искомый угол. Для того чтобы ее вычислить, нужно проанализировать величину данных углов и сопоставить их с известными свойствами окружности.

В окружности с центром в точке О угол АОС равен 120°, а угол АОВ – 30°. Найдите угол ВАС.

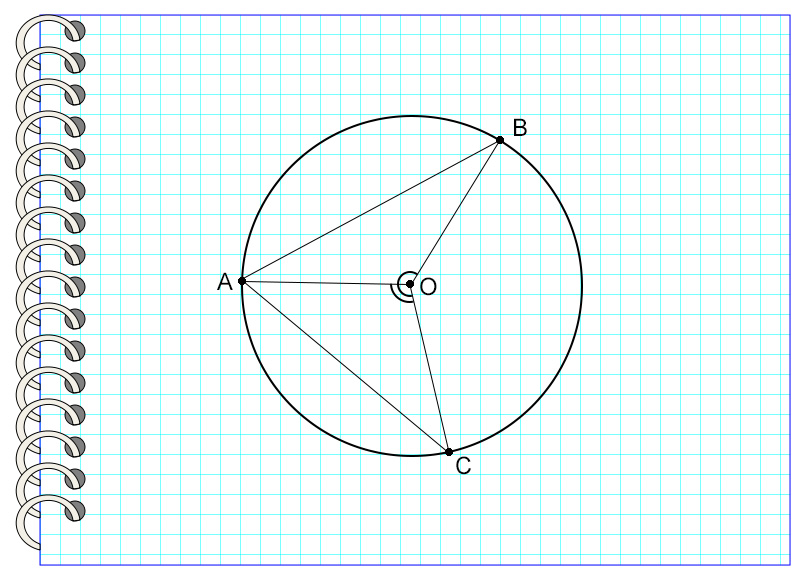
Для начала стоит сказать, что возможно решение этой задачи с помощью свойств равнобедренных треугольников, однако для этого потребуется выполнить большее количество математических действий. Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.

Итак, угол АОС опирается на дугу АС и является центральным, значит, дуга АС равна углу АОС.

Точно так же угол АОВ опирается на дугу АВ.

Зная это и градусную меру всей окружности (360°), можно с легкостью найти величину дуги ВС.

ВС = 360° – АС – АВ

ВС = 360° – 120° – 30° = 210°

Вершина угла САВ, точка А, лежит на окружности. Значит, угол САВ является вписанным и равен половине дуги СВ.

Угол САВ = 210° : 2 = 110°

Задачи, основанные на соотношении дуг

Некоторые задачи вообще не содержат данных о величинах углов, поэтому их нужно искать, исходя только из известных теорем и свойств окружности.

Найдите угол, вписанный в окружность, который опирается на хорду, равную радиусу данной окружности.

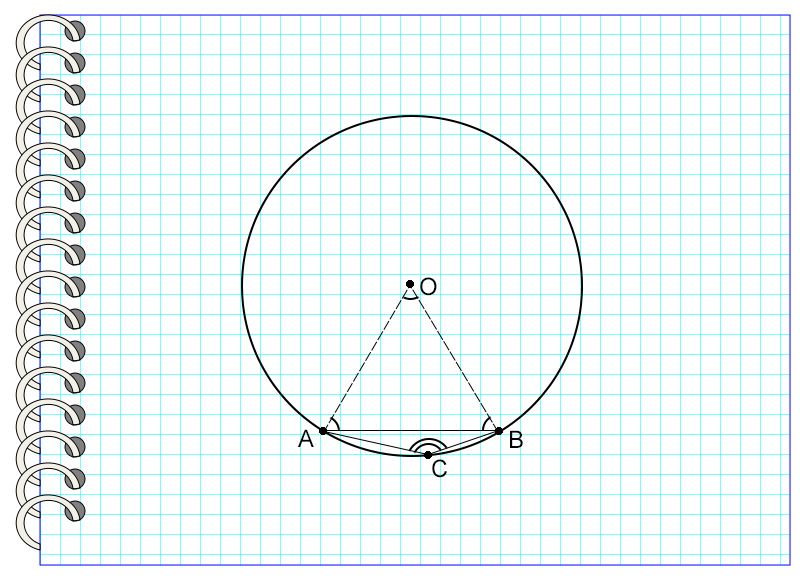
Если мысленно провести линии, соединяющие концы отрезка с центром окружности, то получится треугольник. Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.

АВ = 360° – 60° = 300°

Угол АВС = 300° : 2 = 150°

В окружности с центром в точке О дуги соотносятся как 3:7. Найдите меньший вписанный угол.

Для решения обозначим одну часть за Х, тогда одна дуга равна 3Х, а вторая соответственно 7Х. Зная, что градусная мера окружности равна 360°, составим уравнение.

По условию, нужно найти меньший угол. Очевидно, что если величина угла прямо пропорциональна дуге, на которую он опирается, то искомый (меньший) угол соответствует дуге, равной 3Х.

Значит, меньший угол равен (36° * 3) : 2 = 108° : 2 = 54°

В окружности с центром в точке О угол АОВ равен 60°, а длина меньшей дуги – 50. Вычислите длину большей дуги.

Для того чтобы вычислить длину большей дуги, нужно составить пропорцию – как меньшая дуга относится к большей. Для этого вычислим величину обеих дуг в градусах. Меньшая дуга равна углу, который на нее опирается. Ее градусная мера составит 60°. Большая дуга равна разности градусной меры окружности (она равна 360° вне зависимости от остальных данных) и меньшей дуги.

Большая дуга равна 360° – 60° = 300°.

Так как 300° : 60° = 5, то большая дуга в 5 раз больше меньшей.

Большая дуга = 50 * 5 = 250

Итак, конечно, существуют и другие подходы к решению подобных задач, но все они так или иначе основаны на свойствах центральных и вписанных углов, треугольников и окружности. Для того чтобы успешно их решать, необходимо внимательно изучать чертеж и сопоставлять его с данными задачи, а также уметь применять свои теоретические знания на практике.

Центральные и вписанные углы

О чем эта статья:

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

[spoiler title=”источники:”]

http://fb.ru/article/445770/uglyi-v-okrujnosti-tsentralnyiy-i-vpisannyiy-svoystva-i-sposobyi-nahojdeniya

http://skysmart.ru/articles/mathematic/centralnye-i-vpisannye-ugly

[/spoiler]

№8. Найдите тангенс угла AOB, изображенного на рисунке.

Решение:

Опустим перпендикуляр AH на сторону OB.

Рассмотрим прямоугольный △ A O H :

Тангенс угла – отношение противолежащего катета к прилежащему.

tg ∠ A O H = A H O H = 4 2 = 2

Ответ: 2

№9. Найдите тангенс угла A треугольника ABCб изображённого на рисунке.

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ B A C = B C A C = 2 5 = 0,4

Ответ: 0,4

№10. На рисунке изображена трапеция ABCD. Используя рисунок, найдите sin ∠ B A H .

Решение:

Рассмотрим прямоугольный △ A B H :

Синус угла – отношение противолежащего катета к гипотенузе.

sin ∠ A = B H A B

Найдем AB по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 3 2 + 4 2

A B 2 = 9 + 16 = 25

A B = ± 25 = [ − 5 не подходит 5 подходит

A B = 5

sin ∠ A = B H A B = 4 5 = 0,8

Ответ: 0,8

№11. На рисунке изображен ромб ABCD. Используя рисунок, найдите tg ∠ O B C .

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ O B C = O C B O = 3 4 = 0,75

Ответ: 0,75

№12. На рисунке изображена трапеция ABCD. Используя рисунок, найдите cos ∠ H B A .

Решение:

Рассмотрим прямоугольный △ A B H :

Косинус угла – отношение прилежащего катета к гипотенузе.

cos ∠ A B H = B H A B

Найдем A B по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 6 2 + 8 2

A B 2 = 36 + 64 = 100

A B = ± 100 = [ − 10 не подходит 10 подходит

A B = 10

cos ∠ A B H = B H A B = 8 10 = 0,8

Ответ: 0,8

№13. Найдите тангенс угла, изображенного на рисунке.

Решение:

tg β = tg ( 180 ° − α ) = − tg α

Рассмотрим прямоугольный △ B C H .

Тангенс угла – отношение противолежащего катета к прилежащему.

tg α = C H B H = 3 1

tg β = − tg α = − 3

Ответ: -3

№14. Найдите тангенс угла AOB.

Решение:

Опустим высоту BH на сторону OA.

Рассмотрим прямоугольный △ O B H :

tg ∠ O = B H O H

Найдем B H и O H по теореме Пифагора:

B H 2 = 2 2 + 8 2 = = 4 + 64 = 68

B H = ± 68   = ± 4 ⋅ 17 = ± 4 ⋅ 17 = ± 2 17 = [ − 2 17 не подходит 2 17 подходит

B H   =   2 17

O H 2 = 1 2 + 4 2 = 1 + 16 = 17

O H = ± 17 = [ − 17 не подходит 17 подходит

O H   =   17

tg ∠ O = B H O H = 2 17 17 = 2

Ответ: 2

Не каждый из школьников может похвастаться хорошими знаниями в области алгебры и геометрии. Но при этом становиться круглым троечником по предмету не хочется. Как ни старайся понять эти формулы и теоремы, ничего не выходит. В этих случаях есть выход. Можно получать неплохие оценки, если знать как решать задачи геометрии по фотографии. Для этого в интернете есть специальные сервисы, о которых мы не только расскажем, но и объясним как пользоваться.

Перейти к онлайн-сервису Mathway

Photomath — решает задачи по фото

Приложение под названием Photomath широко распространено среди учащихся школ и институтов. Установить его можно на смартфон на ОС Android и IOS, и всегда воспользоваться, когда это необходимо. Весь функционал полностью бесплатный, а благодаря простому и понятному интерфейсу во время работы с программой не возникнет сложностей. С помощью Photomath можно решить огромное количество задач и уравнений, вписывать их вручную, редактировать, а также узнавать ответы с помощью фото. Что понадобится для решения задач?

1. В первую очередь установите приложение из Play Маркет или App Store на свой телефон и запустите.
   
2. Выберите язык интерфейса. По умолчанию будет предложен Русский, но если необходим другой, нажмите на кнопку «Прочее».
   
3. Прочитайте инструкцию, которую предложит программа, либо нажмите кнопку «Пропустить», если считаете, что самостоятельно разберётесь со всеми возможностями.
   
4. Установите свой возраст. Приложение не ограничено по возрастной категории.
   
5. Теперь отметьте кем вы являетесь. На выбор есть – родитель, ученик или учитель.
   
6. После приложение запросит доступ к камере вашего устройства, нажмите «Разрешить». Это действий необходимо для того, чтобы решать уравнения с помощью фото.
   
7. После найдите задачу, на которую нужно получить ответ, наведите на нее камеру прямо в приложении, и нажмите на кнопку красного круга снизу, чтобы сделать снимок.

Через несколько секунд программа предоставит вам готовый результат, а ответ вы сможете вписать себе.

Геометрия — отличный решебник с формулами

Геометрия, или второе название, Pocket Edition – это ещё одно приложение для мобильных устройств, которое обязательно вам поможет. Это не просто справочник или решебник, это целое образовательное приложение, которое сможет помочь с решением геометрии всего школьного курса.

Главная особенность программы – ваш экран смартфона, словно тетрадный лист, на котором вам предстоит нарисовать поставленную задачу.

Pocket Edition обладает простым интерфейсом. Снизу на панели вы увидите несколько кнопок:

• Инструменты рисования;
• Инструменты выделения;
• Инструменты связи;
• Запуск решения или создание новой задачи.

Уже после того, как вы выберите нужный вам раздел, высветился ещё несколько дополнительных функций. Именно с их помощью пользователь и должен наглядно изобразить поставленную перед ним задачу по геометрии.

Ученики и студенты знают, что в геометрии важен не просто результат. Каждую теорему нужно доказать и объяснить. Разработчики учли все эти моменты и создали идеальное приложение. Оно в логической последовательности даёт ответы и показывает полученные выводы.

Каждый шаг сопровождается иллюстрациями, доводами и обоснованиями. Также, приложение подскажет как подойти к противоречию, если определенную теорему нельзя доказать.

Геометрия доступна в App Store и в Play Маркете. Скачать можно бесплатно, также как в бесплатном доступе вы сможете лишь попробовать для решения одну задачу. В целом, этого достаточно, чтобы ознакомиться с функционалом. Если вы планируете постоянно пользоваться данной программой, придется платить деньги. Pocket Edition станет настоящей палочкой-выручалочкой на экзамене.

Рекомендуем прочитать: как узнать название цветка по фото

Mathway — приложения для решения задач по фото

Mathway – ещё одно умное приложение для смартфонов. Если вы предпочитаете использовать настольный компьютер или ноутбук, то можно воспользоваться веб-версией сайта, правда за символическую оплату.

На телефон же скачать приложение можно бесплатно из App Store и Play Market. Разработчики – опытные программисты, а само приложение способно решить задачи разной сложности, как по фотографии, так и если введёте уравнения вручную.

Чтобы воспользоваться возможностями, нужно:

1. Скачать и установить приложение на свой смартфон, запустить.
   
2. Предоставить доступ к камере, нажав на кнопку «Разрешить».
3. Сфотографировать поставленную задачу;
4. Получить результат и записать все действия к себе.

Mathway не просто даёт готовый ответ, а прописывает каждое действие последовательно. В итоге получается развернутое решение.

В приложении доступно решение задач по начальной математике, алгебре, тригонометрии, конечной математики, математический анализ, построение графиков, химия, статистика и начало анализа.

Видео

Заключение

Пользуйтесь данными сервисами, если нужна помощь с домашним заданием или на контрольной работе. Но не увлекайтесь, ведь знания – сила, а учиться можно всю жизнь