Как найти площадь поверхности образованной вращением кривой – Сайт, где вы сможете решить свои вопросы

Площадь поверхности P, что образована вращением гладкой кривой AB вокруг оси Ox где y(x) – непрерывная гладкая функция равняется
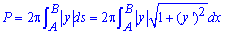, где ds – дифференциал дуги.

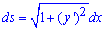
Основные формулы теории расчета площади поверхности Вы имеете, теперь перейдем к примерам, что Вас ожидают на практике и экзаменах.
Задание подобрано из учебной программы для студентов мех-мату Львовского национального университета имени Ивана Франко.
Другие Вузы имеют подобную программу учебы, задания похожие, а в ряде случаев те же.
Номера в примерах отвечает номеру из сборника Б. П. Демидовича. Для изучения основных моментов формулы интегрирования для вычисления площади поверхности вращения будут повторяться из примера в пример.
Часть заданий проиллюстрируем графиками кривых.

Пример 2486 Найти площадь поверхности вращения кривой 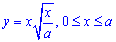вокруг оси Ox.
Решение: Найдем дифференциал дуги:
для этого вычисляем производную функции и, возведя к квадрату, подставляем в формулу

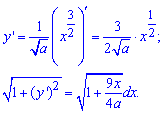
Запишем пределы интегрирования (известно за условием):

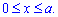
Интегрированием находим площадь поверхности вращения:

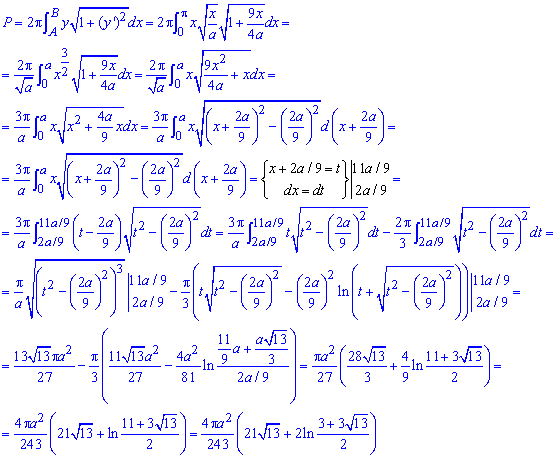
Как видите больше всего трудностей возникает при нахождении интеграла.
Здесь пришлось выделить полные квадраты под корнем, а дальше перейти к новой переменной под интегралом.
Не забывайте, что это приводит к изменению пределов интегрирования. Также здесь и в следующих примерах будем искать лишь интеграл, то что площадь измеряется в единицах квадратных Вы должны знать еще из школы.

Пример 2487 Найти площадь поверхности вращения кривой 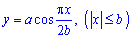вокруг оси Ox.
Решение: Вычисляем дифференциал дуги кривой:

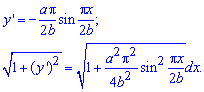
За условием предела интегрирования: xє[-b;b].
За формулой находим площадь поверхности вращения:

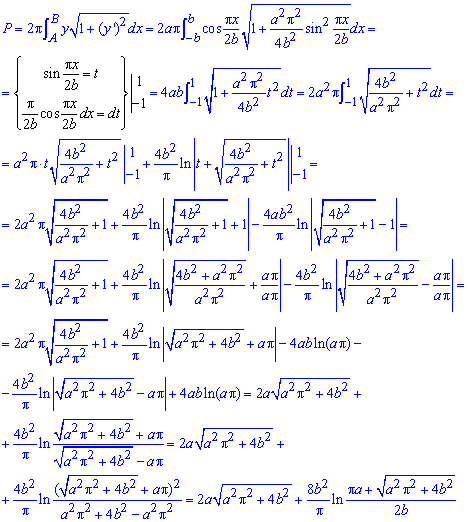
Здесь также под интегралом переходим к новой переменной, дальше после возведения к табличным интегралам подставляем пределы и упрощаем логарифмы.

Пример 2492 Найти площадь поверхности вращения астроиды 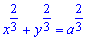вокруг оси Ox. (Смотри 2429)
Решение: Записываем уравнение астроиды в параметрическом виде:

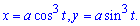
Находим дифференциал дуги параметрически заданной кривой по формуле:

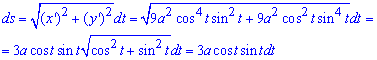
Заметьте, что для параметрически заданной кривой формула несколько иная.
Запишем пределы интегрирования: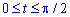
и при интегрировании результат умножим на 2 (в силу симметрия).
Вычислим площадь поверхности вращения:

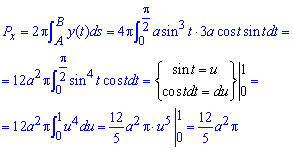
Замена переменных упрощает интегрирование.

Пример 2495 Найти площадь поверхности вращения кривой, заданной параметрически x=a(t-sin (t)), y=a(1-cos(t)), t[0;2pi]
а) вокруг оси Ox;
б) вокруг оси Oy;
в) вокруг прямой y=2a.
Решение: Найдем дифференциал дуги параметрически заданной кривой:

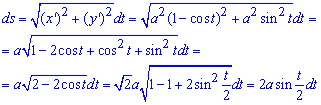
При упрощении использовали известные тригонометрические зависимости.
Пределы интегрирования:

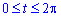
Найдем площадь поверхности вращения вокруг осей:
а)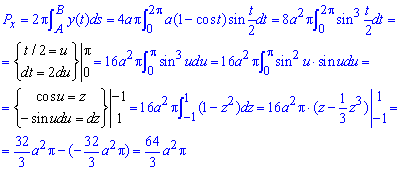
б)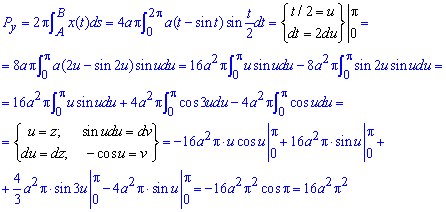
в) площадь поверхности вращения вокруг прямой y=2a

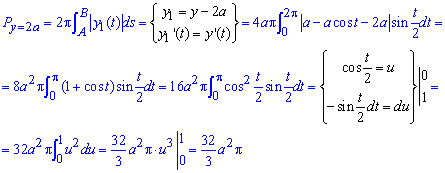
Здесь использовали симметрию относительно прямой x₁=a*Pi, поэтому результат умножили на 2.

Пример 2497 Найти площадь поверхности вращения кардиоиды 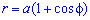вокруг полярной оси.
графики кардиоиды
Решение: Для кривой заданной в полярных координатах дифференциал дуги находим по формуле:

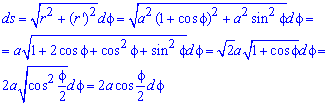
Пределы интегрирования: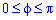

Вычислим площадь поверхности вращения кардиоиды:
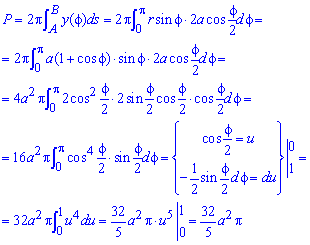
площадь поверхности вращения вокруг оси
Здесь также использовали замену переменных под интегралом.

Использованная литература:
1. Практикум из математического анализа. Часть 2. Заболоцький М. В., Фединяк С. И., Филевич П. В. – Львов: Издательский центр ЛНУ имени Ивана Франко, 2006. – 68 с.
2. Демидович Б. П. Сборник задач и упражнений по математическому анализу. Учебное пособие для студентов физических и механико-математических специальностей ВУЗов.-9-е изд.-М.: Наука, главная редакция физико-математической литературы, 1977. – 528 с.
3. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, том ІІ : – М.: Наука, главная редакция физико-математической литературы, 1966. – 800 с.
4. Справочное пособие по математическому анализу, часть И -К. : “Высшая школа”, 1978. – 696 с.

Источник

Занятие 20

2.6. Вычисление
площадей поверхностей вращения

Площадь поверхности, образованной
вращением гладкой кривой АВ вокруг
оси
,
равна

где

– дифференциал дуги.

№2489. Найти площадь поверхности,
образованной вращением кривой

а) вокруг оси
;

б) вокруг оси
.

Прежде всего, надо вычислить

– дифференциал дуги.

В случаи вращения вокруг оси

работает формула

По ней и вычисляем

=

=
=

=

=
=
.

В случаи вращения вокруг оси

роль радиуса круга вращения играет
,
поэтому работает формула

Вычисляем площадь поверхности.

=

=

=

=
=

=
=
.

№2496. Найти площадь поверхности,
образованной вращением кривой

вокруг прямой
.

Как и в ранее рассмотренной задаче,
прежде всего, надо вычислить

– дифференциал дуги.

=

=
=
.

Кроме того, надо вычислить расстояние
от точки плоскости

до прямой
,
которое и будет радиусом круга. Не
трудно догадаться, что

=
.

Симметричность кривой позволяет
вычислить площадь поверхности как
удвоенную площадь половины поверхности.

=

=
=

=
=

–
–
.

Получены два интеграла, являющиеся
дифференциальными биномами относительно

и

соответственно. В ответе получится
.

№2497. Найти площадь поверхности,
образованной вращением кривой

вокруг полярной оси.

Вычисляем дифференциал длины дуги.

=

=
=

=

=
.

Радиусом вращения вокруг полярной оси
является расстояние до неё, или

Осталось составить интеграл и вычислить
площадь поверхности вращения.

=

=

(тригонометрические преобразования
приводят к результату)

=

=

=
=

=

Аналогично решаются №№ 2490, 2495(б),
2498(в).

Домашнее задание №№ 2493, 2495(в), 2498(б).

Соседние файлы в папке практикаинтегралы

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 ноября 2021 года; проверки требует 1 правка.

Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой). Например, если прямая пересекает ось вращения, то при её вращении получится коническая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — гиперболоид. Одна и та же поверхность может быть получена вращением самых разнообразных кривых.

Поверхность, полученная вращением кривой x=2+cos z вокруг оси z

Является объектом изучения в математическом анализе, аналитической, дифференциальной и начертательной геометрии.

Примеры[править | править код]

Круговая цилиндрическая поверхность (получается вращением прямой вокруг параллельной ей прямой).
Конус (получается вращением прямой вокруг другой прямой, пересекающей первую).
Сфера (получается вращением окружности вокруг оси, лежащей в той же плоскости и проходящей через её центр).
Тор (получается вращением окружности вокруг не пересекающей её оси, лежащей в той же плоскости).
Эллипсоид вращения ― эллипсоид, длины двух полуосей которого совпадают (получается вращением эллипса вокруг одной из его осей).
Параболоид вращения ― эллиптический параболоид, полученный вращением параболы вокруг своей оси.
Катеноид (получается вращением цепной линии).

Площадь[править | править код]

Площадь поверхности вращения, образованной вращением плоской кривой конечной длины вокруг оси, лежащей в плоскости кривой, но не пересекающей кривую, равна произведению длины кривой на длину окружности с радиусом, равным расстоянию от оси до центра масс кривой. Это утверждение называется второй теоремой Паппа — Гульдина, или теоремой Паппа о центроиде.

Например, для тора с радиусами ${displaystyle r,R}$ , площадь поверхности равна

$S=(2pi r)cdot (2pi R)=4pi ^{2}rR$ .

Площадь поверхности вращения, образованной вращением кривой $y=f(x), aleq xleq b$ вокруг оси $0x$ можно вычислить по формуле

$S=2pi int limits _{a}^{b}f(x){sqrt {1+left(f'(x)right)^{2}}}dx$

Площадь поверхности вращения, образованной вращением кривой $x=x(t), y=y(t), alpha leq tleq beta$ вокруг оси $0x$ можно вычислить по формуле

$S=2pi int limits _{alpha }^{beta }y(t){sqrt {left(x'(t)right)^{2}+left(y'(t)right)^{2}}}dt$

Для случая, когда кривая задана в полярной системе координат $r=rho (varphi ), alpha leq varphi leq beta$ действительна формула

$S=2pi int limits _{alpha }^{beta }rho (varphi )|sin varphi |{sqrt {left(rho (varphi )right)^{2}+left(rho '(varphi )right)^{2}}}dvarphi$

Объём[править | править код]

Объём, ограниченный поверхностью вращения, образованной вращением плоской замкнутой несамопересекающейся кривой вокруг оси, лежащей в плоскости кривой, но не пересекающей кривую, равен произведению площади плоской фигуры, ограниченной кривой, на длину окружности с радиусом, равным расстоянию от оси до центра тяжести плоской фигуры.

Объём поверхности вращения, образованной вращением кривой $y=f(x), aleq xleq b$ вокруг оси $0x$ можно вычислить по формуле

$V=pi int limits _{a}^{b}f^{2}(x)dx$

Вариации и обобщения[править | править код]

Искривлённое произведение

Примечания[править | править код]

Источник

Площадь поверхности вращения тела

Пусть даны прямая и кривая Gamma , лежащая в одной плоскости с и расположенная по одну сторону от этой прямой. При вращении кривой Gamma вокруг оси получается поверхность lambda , площадь которой мы и хотим сначала определить, а потом вычислить (см. 46).

Начнем со случая, когда Gamma — отрезок, один конец которого отстоит от на , а другой — на (рис. 58). Тогда, как доказывается в школьном курсе геометрии, площадь поверхности вращения (боковой поверхности усеченного конуса) выражается формулой P(lambda)=pi(r+R)ell . В этом случае при r leqslant R имеем:

Прямая и кривая, лежащая в одной плоскости с прямой

2picdot rcdot ell leqslant P(lambda) leqslant 2picdot Rcdot ell,.

(1)

Таким образом, боковая поверхность конуса заключена между произведением длины образующей на длину наименьшей окружности и произведением длины образующей на длину наибольшей окружности.

То же самое неравенство будет иметь место и при вращении любой ломаной линии, расположенной по одну сторону от оси вращения:

2picdot rcdot ell leqslant P(lambda) leqslant 2picdot Rcdot ell,.

(2)

где и — наименьшее и наибольшее расстояния точек ломаной от оси , и ell — длина ломаной.

Для доказательства достаточно применить неравенство (1) к каждому звену ломаной, сложить полученные результаты и учесть что Sigmaell_k=ell и для любого звена имеем r leqslant r_k и R_k leqslant R (здесь r_k и R_k — наименьшее и наибольшее расстояния точек k-ro звена от оси вращения).

Естественно потребовать, чтобы неравенства (2) выполнялись для любой спрямляемой кривой. Кроме того, потребуем, чтобы площадь поверхности вращения обладала свойством аддитивности: при разбиении дуги Gamma на части $gamma_0, gamma_1, ldots, gamma_{n-1}$ должно выполняться равенство

$P(lambda)= sum_{k=0}^{n-1} P(omega_k),$

(3)

где lambda — поверхность, полученная при вращении всей дуги Gamma , а omega_k — при вращении части gamma_k .

Если применить к каждой части omega_k неравенства (2), то получим, что

2picdot r_kcdot ell_k leqslant P(omega_k) leqslant 2picdot R_kcdot ell_k,,

где ell_k=ell(gamma_k) — длина дуги gamma_k , а r_k и R_k — наименьшее и наибольшее расстояния точек этой дуги gamma_k от оси вращения. Складывая эти неравенства и учитывая требование аддитивности, получаем, что

$2pi sum_{k=0}^{n-1} r_kell_k leqslant P(lambda) leqslant 2pi sum_{k=0}^{n-1} R_kell_k,.$

(4)

Иными словами, площадь поверхности вращения должна разделять множества

$Biggl{~2pi sum_{k=0}^{n-1} r_kell_k~Biggr},qquad Biggl{~2pi sum_{k=0}^{n-1} R_kell_k~Biggr}.$

Именно это требование мы и примем за определение площади поверхности вращения.

Если Gamma — плоская спрямляемая кривая, лежащая по одну сторону от оси , то площадью поверхности lambda , получаемой при вращении этой кривой вокруг оси , называется число P(lambda) , разделяющее множества

$Biggl{~2pi sum_{k=0}^{n-1} r_kell_k~Biggr},qquad Biggl{~2pi sum_{k=0}^{n-1} R_kell_k~Biggr},$

соответствующие всевозможным разбиениям дуги Gamma . Здесь r_k,,R_k и ell_k имеют указанный выше смысл.

Докажем сейчас, что это число существует и единственно, а затем выведем для него выражение в виде интеграла. Выберем на плоскости систему координат, такую, что ось абсцисс совпадает с осью вращения. Зададим параметризацию кривой Gamma , выбрав в качестве параметра длину ell дуги , соединяющей в заданном направлении фиксированную точку кривой Gamma с произвольной точкой этой кривой (рис. 59). Тогда r_k и R_k будут наименьшими и наибольшими значениями ординаты для точек части gamma_k .

Произвольная точка на кривой

Поэтому суммы, стоящие в неравенствах (4) слева и справа, являются не чем иным, как суммами Дарбу для интеграла $2piintlimits_{0}^{L} y(ell),dell$ , где через обозначена длина всей кривой Gamma . Поскольку функция y(ell) непрерывна в силу непрерывности кривой Gamma , то существование и единственность числа, разделяющего эти суммы Дарбу, вытекают из теоремы существования интеграла от непрерывной функции. При этом мы доказали, что площадь поверхности вращения, т. е. число P(lambda) , разделяющее эти суммы, равняется интегралу:

$P(lambda)= 2piintlimits_{0}^{L} y(ell),dell,.$

(5)

Из формулы (5) получаются различные частные случаи в зависимости от того, как задана кривая Gamma . Если она задана параметрически:

$begin{cases}x=varphi(t),\ y=psi(t),end{cases} t_0 leqslant t leqslant T$ , то $dell= sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2},dt$ ,

и формула (5) принимает вид:

$P(lambda)= 2pi intlimits_{t_0}^{T} psi(t) sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2},dt$

(6)

(когда ell меняется от до , переменная { t} меняется от ${ t_0}$ до ).

В частности, если кривая Gamma задана явным уравнением y=f(x),~ a leqslant x leqslant b , то

$P(lambda)= 2pi intlimits_{a}^{b} f(x) sqrt{1+bigl(f'(x)bigr)^2},dx= 2pi intlimits_{a}^{b}ysqrt{1+(y')^2},dx,.$

(7)

Если кривая Gamma задана в полярных координатах уравнением rho=f(varphi) , где alpha leqslant varphi leqslant beta , а функция имеет непрерывную производную f'(varphi) на [alpha;beta] , то, учитывая, что y= rhosinvarphi= f(varphi)sinvarphi , a $dell= sqrt{rho_{varphi}^{prime2}+ rho^2},dvarphi$ , получим:

$P=2pi intlimits_{alpha}^{beta} rhosinvarphi sqrt{rho_{varphi}^{prime2}+ rho^2},dvarphi,.$

(8)

Пример 1. Найдем площадь поверхности шара радиуса .

Решение. Поместим начало координат в центр шара. Будем рассматривать поверхность шара как поверхность, полученную в результате вращения полуокружности x^2+y^2=R^2 вокруг оси . Тогда площадь поверхности шара найдется по формуле

$P=2pi intlimits_{-R}^{R} ysqrt{1+(y')^2},dx,.$

Так как $y=sqrt{R^2-x^2}$ — функция четная, то

$P=4pi intlimits_{0}^{R} ysqrt{1+(y')^2},dx,.$

Найдя $y'= frac{-x}{sqrt{R^2-x^2}}$ и вычислив сумму $1+(y')^2= 1+frac{x^2}{R^2-x^2}= frac{R^2}{R^2-x^2}$ , получим:

$P= 4pi intlimits_{0}^{R}! sqrt{R^2-x^2}cdot frac{R,dx}{sqrt{R^2-x^2}}= 4pi Rintlimits_{0}^{R}dx= Bigl.{4pi Rx}Bigr|_{0}^{R}= 4pi nR^2.$

Пример 2. Вычислить площадь поверхности, образованной вращением одной арки циклоиды вокруг Ox:

$begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}),end{cases} 0 leqslant t leqslant 2pi,.$

Решение. Найдем $x'_t=a(1-cos{t}),~ y'_t=asin{t}$ . Тогда

$(x'_t)^2+(y'_t)^2= 2a^2(1-cos{t})= 4a^2sin^2frac{t}{2},.$

Искомая площадь поверхности вращения равна

$begin{aligned}P&= 2pi intlimits_{0}^{2pi} a(1-cos{t})2asin frac{t}{2},dt= 8pi a^2 intlimits_{0}^{2pi}sin^3 frac{t}{3},dt= 8pi a^2 intlimits_{0}^{2pi}! left(1-cos^2 frac{t}{2} right)! sin frac{t}{2},dt=\ &= left.{8pi a^2! left(-2cos frac{t}{2}+ frac{2}{3}cos^3 frac{t}{2}right)}right|_{0}^{2pi}= frac{64}{3},pi a^2.end{aligned}$

Пример 3. Найдем площадь поверхности, образованной вращением лемнискаты rho^2=a^2cos2varphi вокруг полярной оси.

Решение. Имеем: $rho= asqrt{cos2varphi}~ Rightarrow~ rho'_{varphi}= frac{-asin2varphi}{sqrt{cos2varphi}}$ . Поэтому

$rho^{2}+rho_{varphi}^{prime2}= a^2cos2varphi+ frac{a^{2} sin^{2}2varphi}{cos2varphi}= a^2! left(cos2varphi+ frac{sin^{2}2varphi}{cos2varphi}right)= frac{a^{2}}{cos2varphi},.$

Пользуясь формулой (8) для вычисления площади поверхности в полярных координатах, найдем сначала половину искомой площади поверхности:

$frac{1}{2}P= 2pi intlimits_{0}^{pi/4} asqrt{cos2varphi}, frac{sinvarphicdot a}{sqrt{cos2varphi}}, dvarphi= 2pi a^2 intlimits_{0}^{pi/4} sinvarphi,dvarphi= 2pi a^2cdot frac{2-sqrt{2}}{2}= pi a^2bigl(2-sqrt{2}bigr).$

Вся площадь данной поверхности будет равна $P=2bigl(2-sqrt{2}bigr)pi a^2$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Примеры[править | править код]

Площадь[править | править код]

Объём[править | править код]

Вариации и обобщения[править | править код]

Примечания[править | править код]

Площадь поверхности вращения тела

Вам также может понравиться

Как найти активное сопротивление индуктивной катушки

Как составить методические указания к выполнению практической работы

Anonymous как их найти

Добавить комментарий Отменить ответ