Как найти площадь поверхности сферического сегмента – Сайт, где вы сможете решить свои вопросы

У этого термина существуют и другие значения, см. сегмент.

Пример сферического сегмента (окрашен синим цветом). Вторая половина сферы также представляет собой сферический сегмент

Сфери́ческий сегме́нт — поверхность, часть сферы, отсекаемая от неё некоторой плоскостью. Плоскость отсекает два сегмента: меньший сегмент называется также сферическим кругом^[1].
Если секущая плоскость проходит через центр сферы, то высота обоих сегментов равна радиусу сферы, и каждый из таких сферических сегментов называют полусферой.

Шарово́й сегме́нт — геометрическое тело, часть шара, отсекаемая от него некоторой плоскостью. Поверхностью шарового сегмента является объединение сферического сегмента и круга (основания шарового сегмента), границы которых совпадают.

Объём и площадь поверхности[править | править код]

Если радиус основания сегмента равен $a$ , высота сегмента равна $h$ , тогда объём шарового сегмента равен ^[2]

${displaystyle V={frac {pi h}{6}}(3a^{2}+h^{2}),}$

площадь поверхности сегмента равна

${displaystyle A=2pi rh}$

или

${displaystyle A=2pi r^{2}(1-cos theta ).}$

Параметры $a$ , $h$ и $r$ связаны соотношениями

${displaystyle r^{2}=(r-h)^{2}+a^{2}=r^{2}+h^{2}-2rh+a^{2},}$

${displaystyle r={frac {a^{2}+h^{2}}{2h}}.}$

Подстановка последнего выражения в первую формулу для вычисления площади приводит к равенству

${displaystyle A=2pi {frac {(a^{2}+h^{2})}{2h}}h=pi (a^{2}+h^{2}).}$

Заметим, что в верхней части сферы (синий сегмент на рисунке) ${displaystyle h=r-{sqrt {r^{2}-a^{2}}},}$ в нижней части сферы ${displaystyle h=r+{sqrt {r^{2}-a^{2}}},}$ следовательно, для обоих сегментов справедливо выражение ${displaystyle a={sqrt {h(2r-h)}}}$ и можно привести другое выражение для объёма:

${displaystyle V={frac {pi h^{2}}{3}}(3r-h).}$

Формула для определения объёма также может быть получена при интегрировании поверхности вращения:

${displaystyle V=int _{x}^{r}pi left(r^{2}-x^{2}right)dx=pi left({frac {2}{3}}r^{3}-r^{2}x+{frac {1}{3}}x^{3}right)={frac {pi }{3}}r^{3}(cos theta +2)(cos theta -1)^{2}.}$

Применение[править | править код]

Объём объединения и пересечения двух пересекающихся сфер[править | править код]

Объём объединения двух сфер радиусов r₁ и r₂ равен
^[3]

${displaystyle V=V^{(1)}-V^{(2)}}$ ,

где

${displaystyle V^{(1)}={frac {4pi }{3}}r_{1}^{3}+{frac {4pi }{3}}r_{2}^{3}}$

является суммой объёмов двух сфер по отдельности, а

${displaystyle V^{(2)}={frac {pi h_{1}^{2}}{3}}(3r_{1}-h_{1})+{frac {pi h_{2}^{2}}{3}}(3r_{2}-h_{2})}$

является суммой объёмов двух сферических сегментов, образующих пересечение данных сфер. Пусть d < r₁ + r₂ — расстояние между центрами сфер, тогда исключение величин h₁ и h₂ приводит к выражению ^[4]^[5]

${displaystyle V^{(2)}={frac {pi }{12d}}(r_{1}+r_{2}-d)^{2}left(d^{2}+2d(r_{1}+r_{2})-3(r_{1}-r_{2})^{2}right).}$

Площадь поверхности, ограниченной кругами разных широт[править | править код]

Площадь поверхности, ограниченной кругами разных широт, является разностью площадей поверхности двух соответствующих сферических сегментов. Для сферы радиуса r и широт φ₁ и φ₂ данная площадь равна ^[6]

${displaystyle A=2pi r^{2}|sin varphi _{1}-sin varphi _{2}|.}$

Площадь квадратного участка поверхности шара[править | править код]

Участок, вырезанный на сфере радиуса r четырьмя дугами больших кругов, имеющими одинаковую угловую длину θ и попарно перпендикулярными (сферический квадрат, аналог квадрата на плоскости), имеет площадь

${displaystyle A=8r^{2}(1-cos theta /2).}$

Если угол θ мал (по сравнению с 1 радианом), то справедливо приближённое равенство, основывающееся на приближении ${displaystyle cos xto 1-x^{2}/2}$ при ${displaystyle xto 0:}$

${displaystyle Aapprox 8r^{2}{frac {theta ^{2}}{8}}=r^{2}theta ^{2}.}$

Например, площадь квадратного участка поверхности Земли (R_⊕ = 6378 км) со сторонами, равными 1 градусу, составляет

${displaystyle A(1^{circ })=8cdot R_{oplus }^{2}(1-cos 0{,}5^{circ })approx R_{oplus }^{2}cdot left({frac {pi }{180}}right)^{2}approx 12,391,{text{км}}^{2}.}$

1 квадратная секунда поверхности Земли имеет площадь в 3600² раз меньше: A(1′′) ≈ 12 391 км² / (60 · 60)² ≈ 956 м².

Обобщения[править | править код]

Сечения других тел[править | править код]

Сфероидальный сегмент получается при отсечении части сфероида таким образом, что она обладает круговой симметрией (обладает осью вращения). Аналогичным образом определяют эллипсоидальный сегмент.

Сегмент гиперсферы[править | править код]

Объём $n$ -мерного сегмента гиперсферы высотой $h$ и радиуса $r$ в $n$ -мерном евклидовом пространстве определяется по формуле ^[7]

${displaystyle V={frac {pi ^{frac {n-1}{2}},r^{n}}{,Gamma left({frac {n+1}{2}}right)}}int limits _{0}^{arccos left({frac {r-h}{r}}right)}sin ^{n}t,mathrm {d} t,}$

где $Gamma$ (гамма-функция) задаётся выражением ${displaystyle Gamma (z)=int _{0}^{infty }t^{z-1}mathrm {e} ^{-t},mathrm {d} t.}$

Выражение для объёма $V$ можно переписать в терминах объёма единичного $n$ -мерного шара ${displaystyle C_{n}={pi ^{n/2}/Gamma left[1+{frac {n}{2}}right]}}$ и гипергеометрической функции ${displaystyle {}_{2}F_{1}}$ или регуляризованной неполной бета-функции ${displaystyle I_{x}(a,b)}$ как

${displaystyle V=C_{n},r^{n}left({frac {1}{2}},-,{frac {r-h}{r}},{frac {Gamma [1+{frac {n}{2}}]}{{sqrt {pi }},Gamma [{frac {n+1}{2}}]}}{,,}_{2}F_{1}left({tfrac {1}{2}},{tfrac {1-n}{2}};{tfrac {3}{2}};left({tfrac {r-h}{r}}right)^{2}right)right)={frac {1}{2}}C_{n},r^{n}I_{(2rh-h^{2})/r^{2}}left({frac {n+1}{2}},{frac {1}{2}}right).}$

Формула для площади поверхности $A$ может быть записана в терминах площади поверхности единичного $n$ -мерного шара ${displaystyle A_{n}={2pi ^{n/2}/Gamma left[{frac {n}{2}}right]}}$ как

${displaystyle A={frac {1}{2}}A_{n},r^{n-1}I_{(2rh-h^{2})/r^{2}}left({frac {n-1}{2}},{frac {1}{2}}right),}$

где ${displaystyle 0leq hleq r.}$

Также справедливы следующие формулы^[8]:
${displaystyle A=A_{n}p_{n-2}(q),quad V=V_{n}p_{n}(q),}$ где
${displaystyle q=1-h/r(0leq qleq 1),quad p_{n}(q)={frac {1-G_{n}(q)/G_{n}(1)}{2}},}$

${displaystyle G_{n}(q)=int limits _{0}^{q}(1-t^{2})^{(n-1)/2}dt.}$

При ${displaystyle n=2k+1:}$

${displaystyle G_{n}(q)=sum _{i=0}^{k}(-1)^{i}{binom {k}{i}}{frac {q^{2i+1}}{2i+1}}.}$

Было показано^[9], что при ${displaystyle nto infty }$ и ${displaystyle q{sqrt {n}}={text{const }}}$ ${displaystyle p_{n}(q)to 1-F({q{sqrt {n}}}),}$ где ${displaystyle F()}$ — стандартное нормальное распределение.

Литература[править | править код]

А. И. Маркушевич, А. Я. Хинчин, П. С. Александров. Основные понятия сферической геометрии // Энциклопедия элементарной математики. Книга 4 – Геометрия. — Москва: ГИФМЛ, 1963.

Примечания[править | править код]

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.

Определение сегмента шара
Формулы для нахождения площади сегмента шара
- Площадь основания
- Площадь сферической поверхности
- Площадь полной поверхности
Пример задачи

Определение сегмента шара

Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.

Сегмент шара

R – радиус шара;
r – радиус основания сегмента;
h – высота сегмента; это длина перпендикуляра от центра его основания (точка O₂) до точки на поверхности шара.

Связь между радиусом основания сегмента, его высотой и радиусом шара:

Формулы для нахождения площади сегмента шара

Площадь основания

Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):

S_осн. = πr²

Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть: r = d/2.

Площадь сферической поверхности

Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.

S_{сфер. пов.} = 2πRh

Площадь полной поверхности

Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.

S_полн. = S_осн. + S_{сфер. пов.} = π (2Rh + r²)

Пример задачи

Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см.

Решение

Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.

S_осн. = 3,14 ⋅ (4,7 см)² = 69,3626 см²

S_{сфер. пов.} = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см = 90,432 см²

S_полн. = S_осн. + S_{сфер. пов.} = 69,3626 см² + 90,432 см² = 159,7946 см²

Источник

Площадь поверхности шарового сегмента

{S_{бок} = 2pi Rh} newline
{S_{осн} = pi h(2R-h)} newline
{S_{полн} = S_{бок}+S_{осн}}

С помощью приведенных на странице онлайн калькулятора и формулы вы можете рассчитать площадь поверхности шарового сегмента, которая состоит из площади боковой поверхности и площади основания. Введите радиус шара и высоту шарового слоя и получите результат.

Шарово́й сегмент — часть шара, отсеченная от него плоскостью.

Содержание:

калькулятор площади поверхности шарового сегмента
формула площади боковой поверхности шарового сегмента
формула площади основания шарового сегмента
формула площади полной поверхности шарового сегмента

Шаровой сегмент

Формула площади боковой поверхности шарового сегмента

Площадь боковой поверхности шарового сегмента

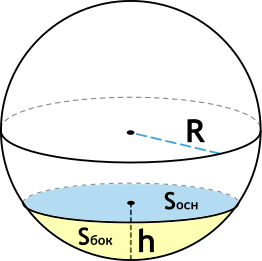
{S_{бок} = 2pi Rh}

R – радиус шара

h – высота шарового сегмента

Формула площади основания шарового сегмента

Площадь основания шарового сегмента

{S_{осн} = pi h(2R-h)}

R – радиус шара

h – высота шарового сегмента

Формула полной поверхности шарового сегмента

Площадь основания шарового сегмента

{S_{осн} = S_{бок} + S_{осн}}

S_бок – площадь боковой поверхности шарового сегмента

S_осн – площадь основания шарового сегмента

Источник

Главная Учёба Площадь поверхности сферического сегмента

Площадь поверхности сферического сегмента

Сферический сегмент — часть сферы, что отсекается от сферы плоскостью.

Вам нужно указать радиус сферы (R), высоту (h) сферического сегмента.

Формула площади поверхности сферического сегмента: S = 2*π*R*h
Два умножается на число PI, на радиус и высоту.

Площадь поверхности сферического сегмента

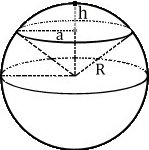
Объем шарового сегмента

Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!

Нет комментариев.

Оставить комментарий

Заполните все поля.

Источник

Площадь поверхности шарового сегмента

Площадь поверхности шарового сегмента
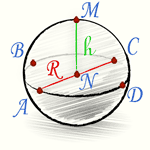
Часть шара, [шар, сфера] осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом. Основанием шарового сегмента называется круг ABCD. Высотой шарового сегмента называется отрезок NM, т.е. длина перпендикуляра, восстановленного из центра N основания до пересечения с поверхностью шара. Точка M называется вершиной шарового сегмента.

Площадь поверхности шарового сегмента равняется произведению его высоты на окружность большого круга шара.

[ S = 2 pi R h ]

(R – радиус большого круга шара, h=NM – высота шарового сегмента)

Формулы шара, сферы

Вычислить, найти площадь поверхности шарового сегмента по формуле (1)

Площадь поверхности шарового сегмента	стр. 318

Источник

Объём и площадь поверхности[править | править код]

Применение[править | править код]

Объём объединения и пересечения двух пересекающихся сфер[править | править код]

Площадь поверхности, ограниченной кругами разных широт[править | править код]

Площадь квадратного участка поверхности шара[править | править код]

Обобщения[править | править код]

Сечения других тел[править | править код]

Сегмент гиперсферы[править | править код]

Литература[править | править код]

Примечания[править | править код]

Определение сегмента шара

Формулы для нахождения площади сегмента шара

Площадь основания

Площадь сферической поверхности

Площадь полной поверхности

Пример задачи

Содержание:

Формула площади боковой поверхности шарового сегмента

Формула площади основания шарового сегмента

Формула полной поверхности шарового сегмента

Площадь поверхности сферического сегмента

Оставить комментарий

Площадь поверхности шарового сегмента

Формулы шара, сферы

Вычислить, найти площадь поверхности шарового сегмента по формуле (1)

Площадь поверхности шарового сегмента

Вам также может понравиться

Как найти папку модс для майнкрафт

Как найти 4000 за день

Как исправить звук в google chrome

Добавить комментарий Отменить ответ