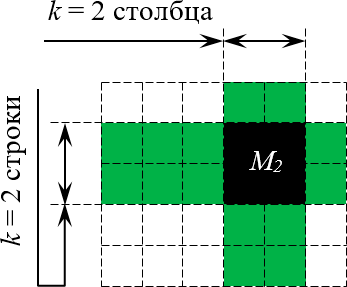
Определи́тель (детермина́нт) в линейной алгебре — скалярная величина, которая характеризует ориентированное «растяжение» или «сжатие» многомерного евклидова пространства после преобразования матрицей; имеет смысл только для квадратных матриц. Стандартные обозначения определителя матрицы 



Определитель квадратной матрицы 










История[править | править код]
Теория определителей возникла в связи с задачей решения систем линейных уравнений.
К понятию определителя близко подошли авторы древнекитайского учебника «Математика в девяти книгах»[2].
В Европе определители матриц 2 × 2 встречаются у Кардано в XVI веке.
Для старших размерностей определение детерминанта дано Лейбницем в 1693 году.
Первая публикация принадлежит Крамеру. Теория определителей создана Вандермондом, Лапласом, Коши и Якоби. Термин «определитель» в современном его значении ввёл О. Коши (1815), хотя ранее (1801) «детерминантом» К. Гаусс назвал дискриминант квадратичной формы.
Японский математик Сэки Такакадзу ввёл определители независимо в 1683 году[3].
Определения[править | править код]
Через перестановки[править | править код]
Для квадратной матрицы 


,
где суммирование проводится по всем перестановкам 



Таким образом, в определитель входит 
Эквивалентная формула:
,
где коэффициент 
- 0, если не все индексы
различны,
- 1, если все индексы
различны и подстановка
чётна,
- −1, если все индексы
различны и подстановка
нечётна.
Аксиоматическое построение (определение на основе свойств)[править | править код]
Понятие определителя может быть введено на основе его свойств. А именно, определителем вещественной матрицы называется функция 
— кососимметрическая функция строк (столбцов) матрицы
.
— полилинейная функция строк (столбцов) матрицы
.
, где
— единичная
-матрица.
Значение определителя матрицы[править | править код]
Для матрицы первого порядка значение детерминанта равно единственному элементу этой матрицы:
Матрицы 2 x 2[править | править код]

Схема расчета определителя матрицы 2×2.

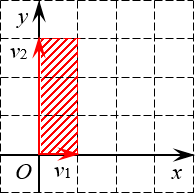
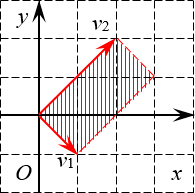
Площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма.
Для матрицы 
Эта матрица A может быть рассмотрена как матрица линейного отображения, преобразующего единичный квадрат в параллелограмм с вершинами (0, 0), (a, b), (a + c, b + d), и (c, d).
Абсолютное значение определителя 
Значение определителя со знаком (ориентированная площадь параллелограмма) помимо коэффициента масштабирования также показывает, выполняет ли преобразование A отражение.
Матрицы 3 x 3[править | править код]
Определитель матрицы 
Для более удобного вычисления определителя третьего порядка можно воспользоваться правилом Саррюса или правилом треугольника.
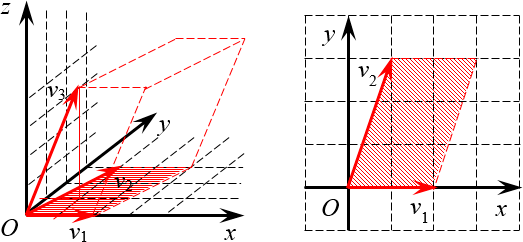
Определитель матрицы, составленной из векторов 

Матрицы N × N[править | править код]
В общем случае, для матриц более высоких порядков (выше 2-го порядка) 
-
, где
— дополнительный минор к элементу
. Эта формула называется разложением по строке.
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):
Также справедливо и аналогичное разложение по любой строке (столбцу):
Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым 
Альтернативные методы вычисления[править | править код]
- Метод конденсации Доджсона, основанный на рекурсивной формуле:
.
Основные свойства определителей[править | править код]
Следующие свойства отражают основные результаты теории определителей, применение которых выходит далеко за пределы этой теории:
(Определитель единичной матрицы равен 1);
(Определитель является однородной функцией степени
на пространстве матриц размера
);
(Определитель матрицы не меняется при её транспонировании);
(Определитель произведения матриц равен произведению их определителей,
и
— квадратные матрицы одного и того же порядка);
, причём матрица
обратима тогда и только тогда, когда обратим её определитель
;
- Существует ненулевое решение уравнения
тогда и только тогда, когда
(или же
должен быть нетривиальным делителем нуля в случае, если
— не целостное кольцо).
Определитель как функция строк (столбцов) матрицы[править | править код]
При изучении теории определителей полезно иметь в виду, что в основе этой теории лежит техника манипулирования со строками и столбцами матриц, разработанная К.Ф. Гауссом (преобразования Гаусса). Суть этих преобразований сводится к линейным операциям над строками (столбцами) и их перестановке. Эти преобразования достаточно простым образом отражаются на определителе, и при их изучении удобно “расчленить” исходную матрицу на строки (или столбцы) и считать определитель функцией, определённой над наборами строк (столбцов). Далее буквами 

- 1. Определитель — полилинейная функция строк (столбцов) матрицы. Полилинейность означает линейность функции по каждому аргументу при фиксированных значениях остальных аргументов:
- 2. Определитель — кососимметрическая функция строк (столбцов) матрицы, то есть при перестановке двух строк (столбцов) матрицы её определитель умножается на −1:
- 3. Если две строки (столбца) матрицы совпадают, то её определитель равен нулю:
Замечание. Свойства 1-3 являются основными свойствами определителя как функции строк (столбцов), они легко доказываются непосредственно из определения. Свойство 2 (кососимметричность) является логическим следствием свойств 1 и 3. Свойство 3 является логическим следствием свойства 2, если в кольце 
- 4. Общий множитель элементов какой-либо строки (столбца) определителя можно вынести за знак определителя (следствие свойства 1).
- 5. Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю (следствие свойства 4).
- 6. Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю (следствие свойств 1 и 3).
- 7. При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится (следствие свойств 1 и 6).
Фактом, имеющим фундаментальное значение, является универсальность определителя как полилинейной кососимметрической функции полного ранга, аргументами которой являются элементы конечномерного векторного пространства 


- Теорема. Пусть
— свободный
-модуль ранга
(
-мерное векторное пространство над
, если
— поле). Пусть
—
-значная функция на
, обладающая свойствами 1-3. Тогда при выборе базиса
пространства
существует константа
такая, что при всех значениях
справедливо равенство:
,
где 


Одним из важнейших следствий универсальности определителя является следующая теорема о мультипликативности определителя.
- Теорема. Пусть
— матрица размера
. Тогда
для любой матрицы
размера
.
Доказательство
Рассмотрим на пространстве столбцов 



■
Определитель и ориентированный объём[править | править код]
Пусть 



Функция ориентированного объёма 

Функция 














Применяя теорему об универсальности определителя как кососимметрической полилинейной функции, получаем, что при выборе ортонормированного базиса 

,
где 

Таким образом, определитель матрицы коэффициентов векторов относительно ортонормированного базиса имеет смысл ориентированного объёма параллелепипеда, построенного на этих векторах.
Всё вышесказанное без существенных изменений переносится на пространство 
Разложение определителя по строке/столбцу и обращение матриц[править | править код]
Формулы разложения определителя по строке/столбцу позволяют сводить вычисление определителей к рекурсивной процедуре, использующей вычисление определителей меньших порядков. Для вывода этих формул сгруппируем и просуммируем в формуле для определителя матрицы 


,
где 



Так как произвольный элемент 



.
Величина 

Учитывая, что каждый член разложения определителя с ненулевым коэффициентом содержит ровно один элемент из i-ой строки, можно разложить определитель по членам этой строки:
— Формула разложения определителя по i-ой строке
Аналогично, учитывая, что каждый член разложения определителя с ненулевым коэффициентом содержит ровно один элемент из j-го столбца, можно разложить определитель по членам этого столбца:
— Формула разложения определителя по j-ому столбцу
Если элементы k-й строки матрицы 
— Формула “фальшивого” разложения определителя по i-ой строке (
).
Аналогично для столбцов:
— Формула “фальшивого” разложения определителя по j-ому столбцу (
)
Полученные формулы полезно записать в матричном виде. Введём матрицу алгебраических дополнений к элементам матрицы 

Тогда, согласно с полученными формулами,
.
Следствие 1 (Критерий обратимости матриц). Квадратная матрица 



Следствие 2. Если произведение матриц равно нулю 


Решение систем линейных алгебраических уравнений с помощью определителей[править | править код]
Формула Крамера позволяет выразить решение системы линейных алгебраических уравнений в виде отношения определителей, в знаменателе которого стоит определитель системы, а в числителе — определитель матрицы системы, в которой столбец коэффициентов при соответствующей переменной заменён на столбец из правых частей уравнений.
Формула Крамера. Пусть задана система линейных алгебраических уравнений в матричном виде: 





Из этой формулы следует, в частности, что если 
Одной из важнейших теорем в теории определителей является следующая теорема о решениях однородной системы линейных уравнений.
Теорема. Пусть 


Доказательство
Необходимость условия содержится в следствии 2 предыдущего раздела. Докажем необходимость.
Если матрица 

Пусть 


Введём вектора 

Поскольку матрица 



Введём две матрицы:
и
.
У матрицы 








Из соотношения 



Тогда 

Данная теорема используется, в частности, для нахождения собственных значений и собственных векторов матриц.
Критерий полноты и линейной независимости системы векторов[править | править код]
Тесно связанными с понятием определителя является понятие линейной зависимости и полноты систем векторов в векторном пространстве.
Пусть 








Теорема (Критерий полноты и линейной независимости системы векторов).
- (1) Система векторов
линейно зависима тогда и только тогда, когда
.
- (2) Система векторов
полна, тогда и только тогда, когда матрица
не вырождена (
).
Доказательство
(1) Доказательство основано на том, что вектор 


Если 




Обратно, если 



(2) Если матрица 





Обратно, пусть матрица 







■
Следствие. В векторном пространстве 

- (1) всякая система, состоящая менее, чем из
векторов, не полна;
- (2) всякая система, состоящая более, чем из
векторов, линейно зависима;
- (3) всякий базис пространства
содержит ровно
векторов.
Таким образом, размерность векторного пространства 
Некоторые специальные свойства определителей[править | править код]
- Определитель матрицы равен произведению её собственных значений.
- Если квадратная матрица выражает линейное преобразование, то её определитель не меняется при замене базиса линейного пространства.
Алгоритмическая реализация[править | править код]
- Прямые методы вычисления определителя могут быть основаны непосредственно на его определении, как суммы по перестановкам, или на разложении Лапласа по определителям меньшего порядка. Однако такие методы очень неэффективны, так как требуют О(n!) операций для вычисления определителя
-го порядка. В то же время они универсальны, применимы в тех случаях, когда элементы матрицы не являются числами (функции, многочлены, дифференциальные формы чётной степени и т. д.), и не требуют выполнения операций деления.
- Можно вычислить определитель и выполнив меньшее количество операций умножения; точнее, можно для матрицы
обойтись лишь количеством слагаемых, равным количеству разбиений числа
вместо
, например 5 вместо 6 для
[6]:
.
- Один из наиболее быстрых численных методов вычисления определителя заключается в простой модификации метода Гаусса. Следуя методу Гаусса, произвольную матрицу
можно привести к ступенчатому виду (Верхнетреугольная матрица), используя лишь две следующие операции над матрицей — перестановку двух строк и добавление к одной из строк матрицы другой строки, умноженной на произвольное число. Из свойств определителя следует, что вторая операция не изменяет определителя матрицы, а первая лишь меняет его знак на противоположный. Определитель матрицы, приведённой к ступенчатому виду, равен произведению элементов на её диагонали, так как она является треугольной, поэтому определитель исходной матрицы равен:
- где
— число перестановок строк, выполненных алгоритмом, а
— ступенчатая форма матрицы
, полученная в результате работы алгоритма. Сложность этого метода, как и метода Гаусса, составляет
, для его реализации необходимо использование операции деления.
- Определитель можно вычислить, зная LU-разложение матрицы. Если
, где
и
— треугольные матрицы, то
. Определитель треугольной матрицы равен просто произведению её диагональных элементов.
- Если доступен алгоритм, выполняющий умножение двух матриц порядка
за время
, где
, для некоторого
, то определитель матрицы порядка
может быть вычислен за время
.[7] В частности это означает, что, используя для умножения матриц алгоритм Копперсмита — Винограда, определитель можно вычислить за время
.
Специальные виды определителей[править | править код]
- Определитель Вронского (Вронскиан)
- Определитель Вандермонда
- Определитель Грама
- Определитель Якоби (Якобиан)
См. также[править | править код]
- Циркулянт
- Перманент
- Пфаффиан
- Результант
Примечания[править | править код]
- ↑ Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — 13-е изд., исправленное. — М.: Наука, 1986.
- ↑ Э. И. Березкина. Математика древнего Китая. — М.: Наука, 1980.
- ↑ H. W. Eves. An Introduction to the History of Mathematics. — Saunders College Publishing, 1990.
- ↑ Скорняков Л. А. Элементы алгебры. — М.: Наука, 1986. — С. 16-23. — Тираж 21 000 экз.
- ↑ Определитель матрицы и геометрический смысл определителя матрицы (рус.). Математика для всех.
- ↑ Houston, Robin; Goucher, Adam P. & Johnston, Nathaniel (2023), A New Formula for the Determinant and Bounds on Its Tensor and Waring Ranks, arΧiv:2301.06586 [math.CO].
- ↑ J. R. Bunch and J.E. Hopcroft. Triangular factorization and inversion by fast matrix multiplication, Mathematics of Computation, 28 (1974) 231—236.
Литература[править | править код]
- В. А. Ильин, Э. Г. Позняк Линейная алгебра, М.: Наука — Физматлит, 1999.
- Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2000.
- Кострикин А. И. Введение в алгебру. Часть 1. Основы алгебры: Учебник для вузов. М.: Физматлит, 2004.
- Боревич З. И. Определители и матрицы. – М.: Наука, 1988.
- Виды матриц.
- Матрица A размера m×n — это прямоугольная таблица чисел, расположенных в m строках и n столбцах

где aij (i =1, …, m; j =1, …, n) — это элементы матрицы A. Первый индекс i — это номер строки, второй индекс j — это номер столбца, на пересечении которых расположен элемент aij.
Сокращённое обозначение матрицы A=(aij)m×n. - Порядок матрицы — это число ее строк или столбцов.
- Главная диагональ квадратной матрицы — это диагональ, идущая из левого верхнего в правый нижний угол.
- Прямоугольная матрица — это матрица, у которой число строк не равно числу столбцов.
- Квадратная матрица — это матрица у которой число строк равно числу столбцов:
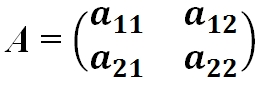
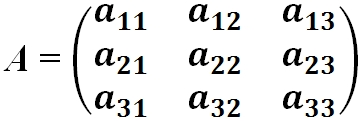
- Матрица-столбец — это матрица, у которой всего один столбец:
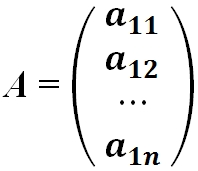
- Матрица-строка — это матрица, у которой всего одна строка:
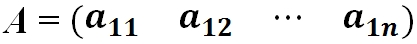
- Диагональная матрица — это квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю.
- Единичная матрица — это диагональная матрица, у которой все диагональные элементы равны единице:
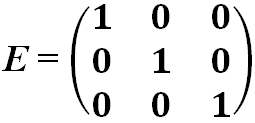
- Матрица квадратная диагональная:
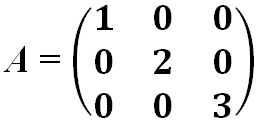
- Треугольная матрица — это квадратная матрица, у которой все элементы, расположенные по одну сторону главной диагонали, равны нулю.
- Матрица верхняя треугольная:
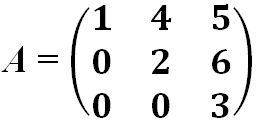
- Матрица нижняя треугольная:
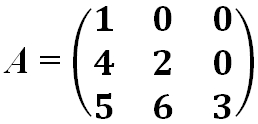
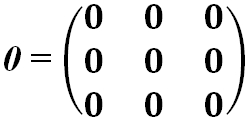
- Нулевая матрица — это матрица, все элементы которой равны 0:
- Операции над матрицами.
- Равенство матриц.
Две матрицы A (aij), B (bij) совпадают |A=B|, если совпадают их размеры и соответствующие элементы равны,
то есть при всех i, j aij=bij. - Сложение матриц.
Суммой двух матриц A=(aij)m×n и B=(bij) m×n одинаковых размеров называется матрица C=(cij)m×n=A+B тех же размеров, элементы которой определяются равенствами cij=aij+bij. Пример 1. - Умножение матрицы на число.
Произведением матрицы A=(aij)m×n на число λ ∈ R называется матрица B=(bij)m×n=λA, элементы которой определяются равенствами bij=λaij. Пример 2. - Умножение матриц.
Произведением матрицы A=(aij)m×k на матрицу B=(bij)k×n называется матрица C=(cij)m×n=A· B размера m×n, элементы которой cij определяются равенством
cij=ai1b1j+ai2b2j+ … aikbkj.
Таким образом, элемент матрицы C=A·B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Пример 3. - Транспонированные матрицы.
Транспонированием матрицы А называется замена строк этой матрицы ее столбцами с сохранением их номеров.
Полученная матрица обозначается через A’ или AT. Пример 4.
Квадратная матрица называется симметричной, если A=A’, то есть для элементов выполнены равенства aij=aji. - Обратная матрица.
Квадратная матрица n–го порядка называется вырожденной, если определитель этой матрицы равен нулю, |A| = 0, и невырожденной, если |A| ≠ 0.
Матрица А-1 называется обратной матрицей для некоторой квадратной матрицы А, если выполняется соотношение:

Если матрица А-1 не вырождена, то существует, и притом единственная, обратная матрица А-1, равная , где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
, где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
1)
2)
3)
4)
- Алгоритм нахождения А-1 заключается в следующих пунктах:
1) Находим det A, проверяем det A ≠ 0.
2) Находим Mij — все миноры матрицы A.
3) Определяем
4) Строим матрицу алгебраических дополнений и транспонируем:
и транспонируем: 
5) Делим каждый элемент матрицы на det A: Пример 5.
Пример 5. - Элементарные преобразования строк (столбцов) матрицы:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число α ≠ 0;
3) прибавление к элементам строки (столбца) матрицы элементов другой строки (столбца), умноженных на некоторое число. - Решение матричных уравнений.
Матричное уравнение — это уравнение, содержащее неизвестную матрицу X и известные матрицы A, B, …, .
Простейшие типы матричных уравнений:
1) . Матрица A – квадратная и невырожденная,
. Матрица A – квадратная и невырожденная,
|A| ≠ 0, следовательно, существует обратная матрица A-1.
Умножим уравнение на A-1 слева:
2) . Матрица A – квадратная, |A| ≠ 0.
. Матрица A – квадратная, |A| ≠ 0.
Умножим уравнение на A-1 справа: .
.
3) . Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
. Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
Умножим уравнение на A-1 слева:
Умножим уравнение на B-1 справа: .
. - Ранг матрицы.
Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров.
Mk этой матрицы:
Матрицы называются эквивалентными, что обозначается
A ∼ B, если .
.
Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований. - Метод окаймляющих миноров.
Пусть в матрице A элемент aij ≠ 0, тогда M1 ≠ 0 и r(A) ≥ 1. Окаймляем этот элемент элементами соседнего столбца и соседней строки (например, (j+1)–го столбца и (i+1)–й строки), получаем минор 2-го порядка: .
.
Если M2, то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка.
Если все миноры второго порядка равны нулю, то r(A) = 1; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то r(A) ≥ 1.
Выбираем отличный от нуля минор 2-го порядка M2 и окаймляем его элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие: Mr ≠ 0, но все Mr+1 = 0. Пример 6. - Метод элементарных преобразований.
Элементарные преобразования матрицы не меняют ее ранга.
К элементарным преобразованиям матрицы относятся следующие: транспонирование; перестановка строк (столбцов); умножение строки (столбца) на число α ≠ 0; прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число; отбрасывание нулевой строки (столбца) матрицы.
Для определения ранга матрицы A методом элементарных преобразований следует:
1) Переставить строки и столбцы так, чтобы в верхнем левом углу матрицы был ненулевой элемент.
2) Все элементы первого столбца, кроме a11, обратить в ноль с помощью элементарных преобразований строк:
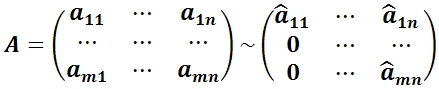
3) Переставить строки со 2–й по m и столбцы со 2–го по n так, чтобы a22 ≠ 0. Повторить операцию (2) со вторым столбцом: во втором столбце все элементы, кроме a12 и a22, обратить в ноль.
Окончательно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:
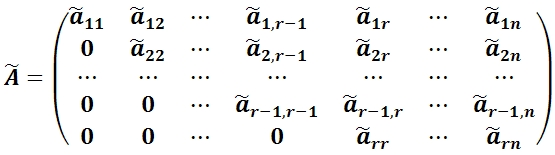
Тогда ранг матрицы A равен: rang A = rang Ã.
- Свойства определителей.
- Определитель квадратной матрицы А не меняется при транспонировании: |AT|=|A|.
- При перестановке местами любых двух строк (столбцов) определитель |A| меняет знак:

- Определитель, содержащий две одинаковые строки (столбца), равен нулю.
- Умножение всех элементов некоторой строки (столбца) определителя |A| на число k равносильно умножению определителя на это число:

- Если все элементы некоторой строки (столбца) определителя |A| равны нулю, то и сам определитель равен нулю (вытекает из предыдущего свойства при (k = 0):

- Если все элементы двух строк (столбцов) определителя |A| пропорциональны, то определитель равен нулю.
- Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей:


- Если к элементам какой-нибудь строки (столбца) определителя |A| прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится:

- Определитель |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения:

- Определитель произведения матриц А и В равен произведению их определителей:
 .
.
- Определители n–го порядка.
- Минор Мij или Δij элемента аij ( иначе – дополнительный минор элемента аij) определителя n-го порядка — это определитель (n–1) порядка, полученный из исходного вычеркиванием i–й строки и j–го столбца, на пересечении которых стоит элемент aij.
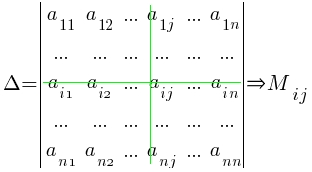
- Алгебраическое дополнение Аij элемента аij — это его минор со знаком (-1)i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент aij, Аij=(-1)i+jMij или Аij=(-1)i+jΔij. Пример 8.
Для определителей n-го порядка имеют место все перечисленные выше свойства определителей. - Правило выбора знака перед минором в алгебраическом дополнении:

- Определитель n-го порядка |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения.
- Метод сведения к треугольному виду.
Используя свойства (1–9), определитель преобразуют к виду, когда элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. Преобразованный таким образом определитель равен произведению элементов, лежащих на главной диагонали.
Формулы, уравнения, теоремы, примеры решения задач
Содержание:
Определение: Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов:
В дальнейшем будем писать матрицу в сокращенном виде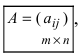
Определение: Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой 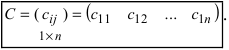
Определение: Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом 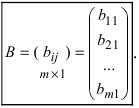
Пример:
Следующие таблицы являются матрицами
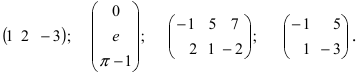
Определение: Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.
Всякой квадратной матрице соответствует определитель, составленный из тех же матричных элементов, который в теории матриц называется детерминантом матрицы 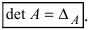
Определение: Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы – на соответствующие строки.
Замечание: Согласно свойству 1. для определителей (см. Лекцию № 1) для квадратных матриц детерминант исходной матрицы равен детерминанту транспонированной матрицы.
Определение: Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной

Определение: Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали, называется диагональной 
Определение: Единичной матрицей называется диагональная матрица, у которой на главной диагонали все элементы равны единице, а остальные элементы равны нулю: 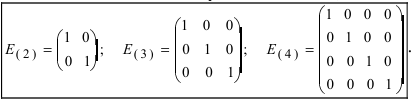
Действия над матрицами
1. Суммой (разностью) двух матриц 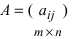 и
и 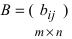 одинаковой структуры называется матрица той же размерности
одинаковой структуры называется матрица той же размерности 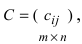 элементы которой вычисляются по формуле:
элементы которой вычисляются по формуле: 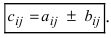
Пример:
Найти сумму (разность) матриц 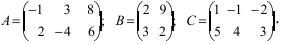
Решение:
Из приведенных матриц складывать (вычитать) можно только матрицы А и С, которые имеют одинаковую структуру. Найдем сумму:
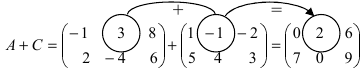
и разность этих матриц:
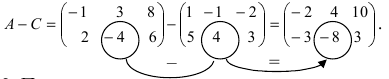
2. При умножении вещественного числа k на матрицу 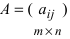 все элементы матрицы умножаются на это число.
все элементы матрицы умножаются на это число.
Пример:
Умножить (-2) на матрицу 
Решение:
Результат умножения имеет вид 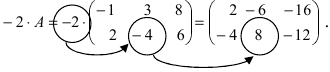
3. Произведением матриц 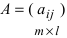 и
и 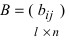 называется матрица
называется матрица 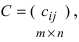 элементы которой вычисляются по формуле:
элементы которой вычисляются по формуле: 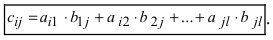
Замечание: Перемножать можно лишь те матрицы, для которых количество столбцов первой перемножаемой матрицы совпадает с количеством строк второй перемножаемой матрицы. Матрица, получаемая в результате перемножения, имеет количество строк равное количеству строк первой матрицы и количество столбцов равное количеству столбцов второй матрицы.
Пример:
Найти (возможные) произведения матриц
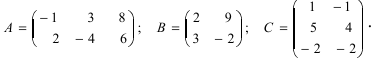
Решение:
Матрица А имеет структуру 2×3, матрица В – 2×2, матрица С – 3×2. Согласно определению можно найти произведения 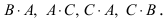 Не существуют произведения
Не существуют произведения 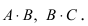 Вычислим произведение
Вычислим произведение 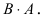 Прежде всего, определим структуру результирующей матрицы: имеем размерности
Прежде всего, определим структуру результирующей матрицы: имеем размерности 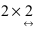 и
и 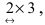 убирая подчеркнутые цифры, получим структуру результирующей матрицы 2×3. Вычислим ее элементы. Для того чтобы найти элементы возможных произведений, надо просуммировать произведения элементов строки первой матрицы на соответствующие элементы столбца второй матрицы:
убирая подчеркнутые цифры, получим структуру результирующей матрицы 2×3. Вычислим ее элементы. Для того чтобы найти элементы возможных произведений, надо просуммировать произведения элементов строки первой матрицы на соответствующие элементы столбца второй матрицы:
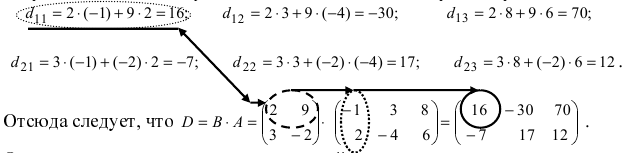
Остальные возможные произведения найти самостоятельно.
Замечание: Из приведенного примера видно, что в общем случае произведение матриц некоммутативно (неперестановочно), т. е.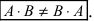
Определение: Обратной матрицей к исходной квадратной матрице 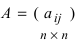 называется матрица
называется матрица 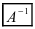 той же структуры, произведение которой с матрицей А коммутативно и равно единичной матрице, то есть
той же структуры, произведение которой с матрицей А коммутативно и равно единичной матрице, то есть 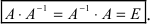
Рассмотрим схему построения обратной матрицы 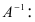
Замечание: Обращаем внимание на то, что матрица алгебраических дополнений записана в транспонированном виде.
Пример:
Найти обратную матрицу к матрице 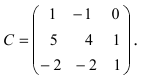
Решение:
Вычислим детерминант данной матрицы 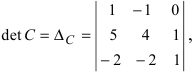 раскроем этот определитель по элементам первой строки:
раскроем этот определитель по элементам первой строки:
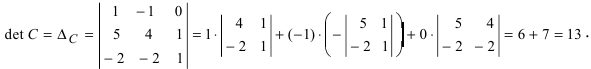
Вычислим алгебраические дополнения всех элементов определителя: 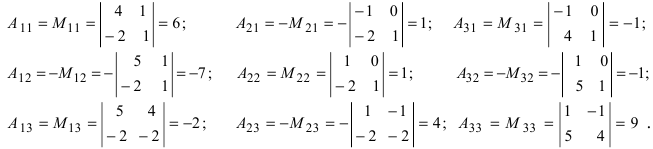 Запишем обратную матрицу
Запишем обратную матрицу 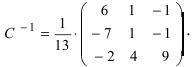
Проверим правильность нахождения обратной матрицы, для чего воспользуемся ее определением. Умножим найденную матрицу на исходную матрицу, вычислим элементы результирующей матрицы
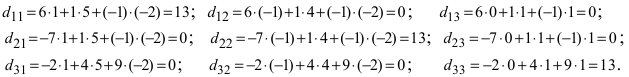
Таким образом, 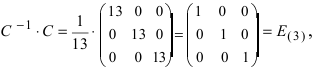 т.е. найдена верно.
т.е. найдена верно.
Основные сведения о матрицах
Понятие матрицы и основанный на нем раздел математики — матричная алгебра — имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное — компактной матричной форме.
Матрицей размера 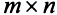 называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: 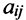 , где
, где 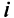 — номер строки,
— номер строки, 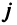 — номер столбца.
— номер столбца.
Например, матрица
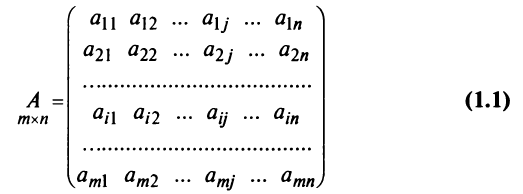
или, в сокращенной записи, 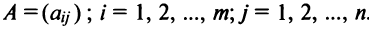
Например, 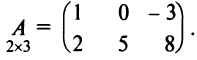 Наряду с круглыми скобками используются и другие обозначения матрицы:
Наряду с круглыми скобками используются и другие обозначения матрицы: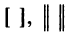
Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. 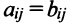 для любых
для любых 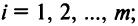
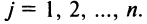
С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.) 
может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям: 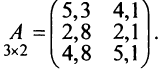
В этой записи, например, матричный элемент 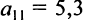 показывает, сколько электроэнергии потребляет промышленность, а элемент
показывает, сколько электроэнергии потребляет промышленность, а элемент 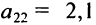 — сколько трудовых ресурсов потребляет сельское хозяйство.
— сколько трудовых ресурсов потребляет сельское хозяйство.
Виды матриц
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца — матрицей (вектором)-столбцом: 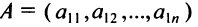 — матрица-строка;
— матрица-строка;
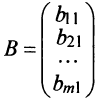 — матрица-столбец.
— матрица-столбец.
Матрица называется квадратной  -го порядка, если число ее строк равно числу столбцов и равно
-го порядка, если число ее строк равно числу столбцов и равно 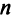 .
.
Например, 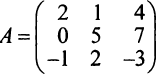 — квадратная матрица третьего порядка.
— квадратная матрица третьего порядка.
Элементы матрицы 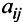 , у которых номер столбца равен номеру строки
, у которых номер столбца равен номеру строки 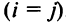 , называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы
, называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы 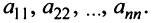
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,
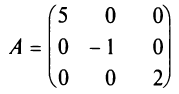 —диагональная матрица третьего порядка.
—диагональная матрица третьего порядка.
Если у диагональной матрицы  -го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей
-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей  -го порядка, она обозначается буквой Е.
-го порядка, она обозначается буквой Е.
Например,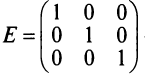 — единичная матрица третьего порядка.
— единичная матрица третьего порядка.
Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю:

Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые – специфические.
Умножение матрицы на число
Произведением матрицы А на число 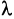 называется матрица
называется матрица 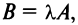 элементы которой
элементы которой 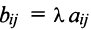 для
для 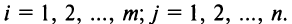
Например, если 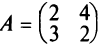 , то
, то 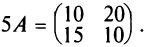
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например, 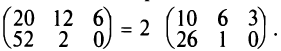
В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е. 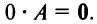
Сложение матриц
Суммой двух матриц А и В одинакового размера  называется матрица
называется матрица 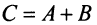 , элементы которой
, элементы которой 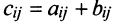 для
для 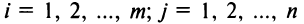 (т.е. матрицы складываются поэлементно).
(т.е. матрицы складываются поэлементно).
Например,
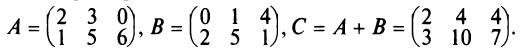 В частном случае A + 0 = A.
В частном случае A + 0 = A.
Вычитание матриц
Разность двух матриц одинакового размера определяется через предыдущие операции: 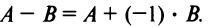
Умножение матриц
Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй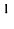 . Тогда произведением матриц
. Тогда произведением матриц 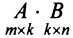 называется такая матрица
называется такая матрица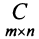 , каждый элемент которой
, каждый элемент которой 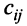 равен сумме произведений элементов
равен сумме произведений элементов  -й строки матрицы А на соответствующие элементы
-й строки матрицы А на соответствующие элементы 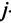 -го столбца матрицы В:
-го столбца матрицы В:
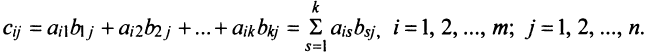
Пример №1
Вычислить произведение матриц 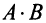 , где
, где
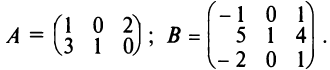
Решение:
1. Найдем размер матрицы-произведения (если умножение матриц возможно): 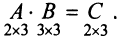
2. Вычислим элементы матрицы-произведения С, умножая элементы каждой строки матрицы А на соответствующие элементы столбцов матрицы В следующим образом:
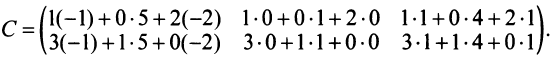
Получаем 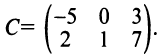 ►
►
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из определений этих операций):
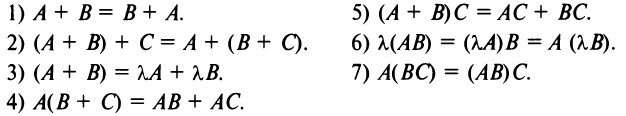
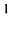 этом случае матрица А называется согласованной с матрицей В.
этом случае матрица А называется согласованной с матрицей В.
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
а)Если произведение матриц 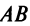 существует, то после перестановки сомножителей местами произведения матриц
существует, то после перестановки сомножителей местами произведения матриц 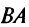 может и не существовать. Действительно, в примере 1.1 получили произведение матриц
может и не существовать. Действительно, в примере 1.1 получили произведение матриц 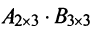 , а произведения
, а произведения 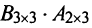 не существует, так как число столбцов первой матрицы не совпадает с числом строк второй матрицы.
не существует, так как число столбцов первой матрицы не совпадает с числом строк второй матрицы.
б)Если даже произведения  и
и  существуют, то они могут быть матрицами разных размеров.
существуют, то они могут быть матрицами разных размеров.
Пример №2
Найти произведения матриц  и
и  :
:
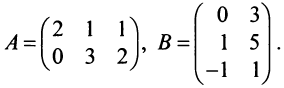
Решение:
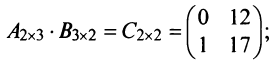
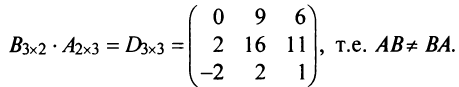 ► в) В случае, когда оба произведения
► в) В случае, когда оба произведения  и
и  существуют и оба — матрицы одинакового размера (это возможно только при умножении квадратных матриц А и В одного порядка), коммутативный (переместительный) закон умножения, вообще говоря, не выполняется, т.е.
существуют и оба — матрицы одинакового размера (это возможно только при умножении квадратных матриц А и В одного порядка), коммутативный (переместительный) закон умножения, вообще говоря, не выполняется, т.е.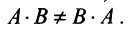
Пример №3
Найти произведения матриц  и
и  , где
, где 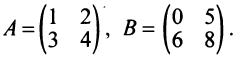
Решение:
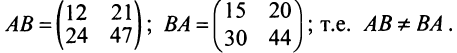 В частном случае коммутативным законом обладает произведение любой квадратной матрицы А
В частном случае коммутативным законом обладает произведение любой квадратной матрицы А 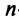 -гo порядка на единичную матрицу Е того же порядка, причем это произведение равно А:
-гo порядка на единичную матрицу Е того же порядка, причем это произведение равно А:
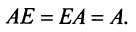
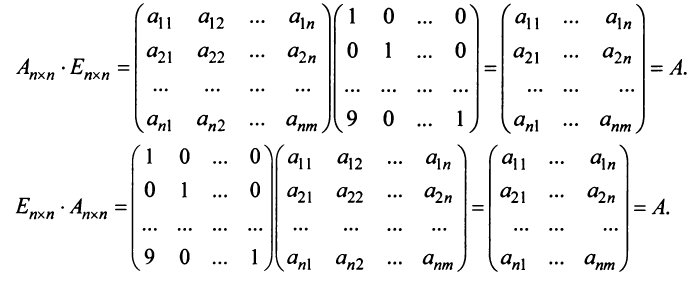
Таким образом, единичная матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.
г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что 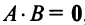 , не следует, что
, не следует, что 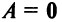 или,
или,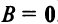 . Например,
. Например, 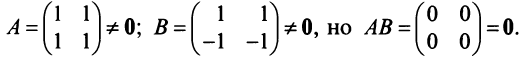
Возведение в степень
Целой положительной степенью 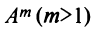 квадратной матрицы
квадратной матрицы 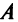 называется произведение
называется произведение 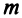 матриц, равных
матриц, равных  , т.е.
, т.е.
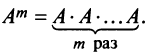
Заметим, что операция возведения в степень определяется только для квадратных матриц.
По определению полагают 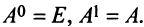 Нетрудно показать, что
Нетрудно показать, что 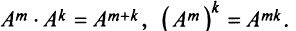
Пример №4
Найти 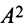 , где
, где 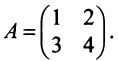
Решение:
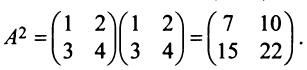
Обращаем внимание на то, что из равенства 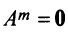 еще не следует, что матрица
еще не следует, что матрица 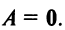 ►
►
Транспонирование матрицы
Транспонирование матрицы — переход от матрицы  к матрице
к матрице  , в которой строки и столбцы поменялись местами с сохранением порядка. Матрица
, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица  называется транспонированной относительно матрицы
называется транспонированной относительно матрицы  :
: 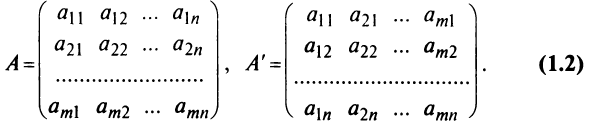 Из определения следует, что если матрица
Из определения следует, что если матрица  имеет размер
имеет размер 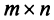 , то транспонированная матрица
, то транспонированная матрица  имеет размер
имеет размер 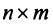 .
.
Например, 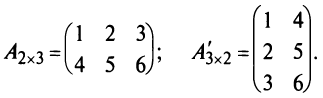
В литературе встречаются и другие обозначения транспонированной матрицы, например, 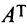 .
.
Свойства операции транспонирования:

Рекомендуем читателю доказать их самостоятельно. Рассмотренные выше операции над матрицами позволяют упростить решения некоторых экономических задач.
Пример №5
Предприятие выпускает продукцию трех видов: 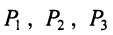 и использует сырье двух типов:
и использует сырье двух типов: 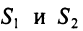 . Нормы расхода сырья характеризуются матрицей
. Нормы расхода сырья характеризуются матрицей 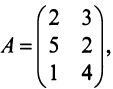
где каждый элемент 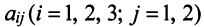 показывает, сколько единиц сырья
показывает, сколько единиц сырья
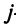 -го типа расходуется на производство единицы продукции
-го типа расходуется на производство единицы продукции 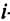 -го вида. План выпуска продукции задан матрицей-строкой
-го вида. План выпуска продукции задан матрицей-строкой 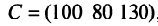 , стоимость единицы каждого типа сырья (ден. ед.) — матрицей-столбцом
, стоимость единицы каждого типа сырья (ден. ед.) — матрицей-столбцом 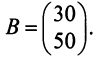
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Решение:
Затраты 1-го сырья составляют 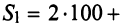
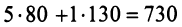 ед. и 2-го —
ед. и 2-го — 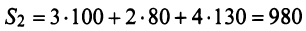 ед., поэтому матрица-строка затрат сырья
ед., поэтому матрица-строка затрат сырья 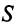 может быть записана как произведение
может быть записана как произведение 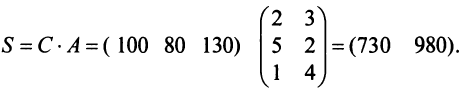
Тогда общая стоимость сырья 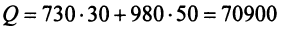 ден. ед. может быть записана в матричном виде
ден. ед. может быть записана в матричном виде 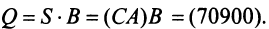 Общую стоимость сырья можно вычислить и в другом порядке: вначале вычислим матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу
Общую стоимость сырья можно вычислить и в другом порядке: вначале вычислим матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу
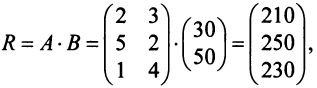 а затем общую стоимость сырья
а затем общую стоимость сырья
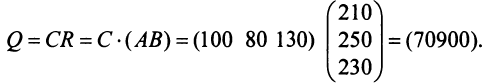

На данном примере мы убедились в выполнении свойства 7 (см. с. 13) — ассоциативного закона произведения матриц: 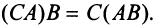
Определители квадратных матриц
Необходимость введения определителя — числа, характеризующего квадратную матрицу 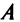 , — тесно связана с решением систем линейных уравнений (см. гл. 2). Определитель матрицы
, — тесно связана с решением систем линейных уравнений (см. гл. 2). Определитель матрицы 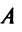 обозначается
обозначается 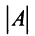 или
или 
Определителем матрицы первого порядка 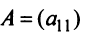 , или определителем первого порядка, называется элемент
, или определителем первого порядка, называется элемент 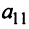 :
:
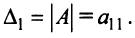 Например, пусть
Например, пусть 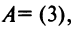 тогда
тогда 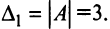
Определителем матрицы второго порядка 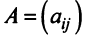 , или определителем второго порядка, называется число, которое вычисляется по формуле:
, или определителем второго порядка, называется число, которое вычисляется по формуле:
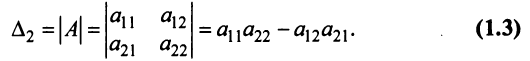
Произведения а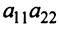 и
и 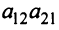 называются членами определителя второго порядка. Например, пусть
называются членами определителя второго порядка. Например, пусть 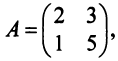 тогда
тогда
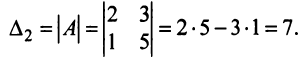
Пусть дана квадратная матрица третьего порядка:  Определителем матрицы третьего порядка
Определителем матрицы третьего порядка 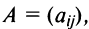 , или определителем третьего порядка, называется число, которое вычисляется по формуле:
, или определителем третьего порядка, называется число, которое вычисляется по формуле:
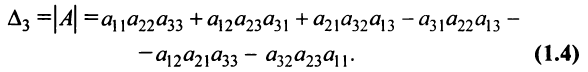
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу (1.4), легко запомнить, пользуясь схемой (рис. 1.1), которая называется правилом треугольников или правилом Сарруса.

Пример №6
Вычислить определитель третьего порядка
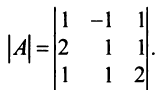
Решение:
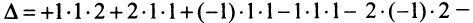
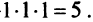 ►
►
Для того чтобы ввести понятие определителя более высокого порядка, потребуются некоторые дополнительные понятия. Рассмотрим квадратную матрицу 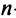 -гo порядка:
-гo порядка: 
Из общего числа 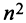 элементов этой матрицы выберем набор, содержащий
элементов этой матрицы выберем набор, содержащий 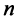 элементов, таким образом, чтобы в него входило по одному элементу из каждой строки и каждого столбца. Например, набор элементов
элементов, таким образом, чтобы в него входило по одному элементу из каждой строки и каждого столбца. Например, набор элементов 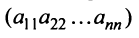 или
или 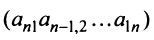 соответственно главной и побочной диагоналей матрицы.
соответственно главной и побочной диагоналей матрицы.
Любой такой набор можно упорядочить, записав сначала элемент из 1-й строки, затем из 2-й и т.д., т.е.

Номера столбцов 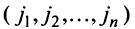 образуют при этом перестановку
образуют при этом перестановку 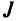 из
из 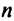 чисел:
чисел:  Всего существует
Всего существует 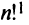 различных перестановок из
различных перестановок из 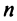 натуральных чисел.
натуральных чисел.
Введем понятие беспорядка, или инверсии, в перестановке 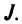 Это наличие пары чисел, в которой большее число предшествует меньшему. Например, в перестановке из трех чисел
Это наличие пары чисел, в которой большее число предшествует меньшему. Например, в перестановке из трех чисел 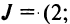
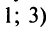 имеется одна инверсия (2; 1), а в перестановке
имеется одна инверсия (2; 1), а в перестановке 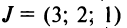 — три: (3; 2), (3; 1), (2; 1). Обозначим через
— три: (3; 2), (3; 1), (2; 1). Обозначим через 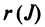 количество инверсий в перестановке
количество инверсий в перестановке 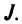
Возвращаясь к наборам (1.5) из элементов матрицы 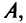 мы можем каждому такому набору поставить в соответствие произведение его элементов:
мы можем каждому такому набору поставить в соответствие произведение его элементов:

и число 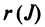 , равное количеству инверсий в перестановке
, равное количеству инверсий в перестановке 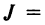
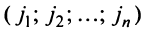 из номеров соответствующих столбцов.
из номеров соответствующих столбцов.
Определение. Определителем квадратной матрицы 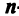 -го порядка, или определителем
-го порядка, или определителем 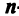 -го порядка, называется число, равное алгебраической сумме
-го порядка, называется число, равное алгебраической сумме 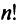 членов, каждый из которых является произведением
членов, каждый из которых является произведением 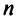 элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как
элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как 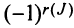 , где
, где 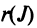 — число инверсий в перестановке
— число инверсий в перестановке 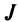 из номеров столбцов элементов матрицы, ест при этом номера строк записаны в порядке возрастания:
из номеров столбцов элементов матрицы, ест при этом номера строк записаны в порядке возрастания:
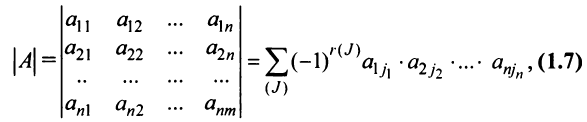 где сумма берется по всем перестановкам
где сумма берется по всем перестановкам 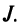 Проверим, например, что при
Проверим, например, что при 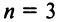 мы получаем введенный ранее определитель третьего порядка (1.4):
мы получаем введенный ранее определитель третьего порядка (1.4):
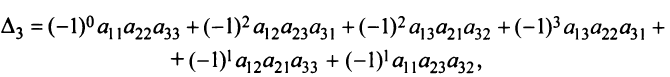
то же число, что и по формуле (1.4).
Заметим, что с ростом  резко увеличивается число членов определителя
резко увеличивается число членов определителя 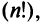 поэтому даже для
поэтому даже для 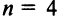 использование формулы (1.7) весьма трудоемко (получим 24 слагаемых!).
использование формулы (1.7) весьма трудоемко (получим 24 слагаемых!).
На практике при вычислении определителей высоких порядков используют другие формулы. Для их рассмотрения необходимо ввести новые понятия.
Пусть дана квадратная матрица 
 -го порядка.
-го порядка.
Минором 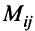 элемента
элемента 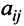 матрицы
матрицы  -го порядка называется
-го порядка называется
определитель матрицы  -го порядка, полученной из матрицы
-го порядка, полученной из матрицы  вычеркиванием
вычеркиванием 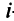 -й строки и
-й строки и 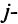 го столбца.
го столбца.
Например, минором элемента 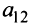 матрицы
матрицы  третьего порядка будет:
третьего порядка будет: 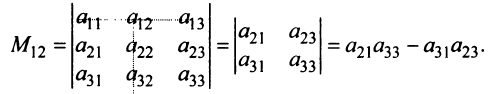 Каждая матрица
Каждая матрица  -го порядка имеет
-го порядка имеет 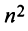 миноров
миноров 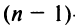 -го порядка.
-го порядка.
Алгебраическим дополнением 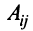 элемента
элемента 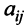 матрицы
матрицы  -го порядка называется его минор, взятый со знаком
-го порядка называется его минор, взятый со знаком 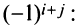

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца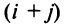 — четное число, и отличается от минора знаком, когда
— четное число, и отличается от минора знаком, когда 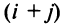 — нечетное число.
— нечетное число.
Например, 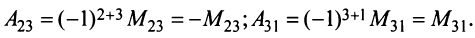
Пример №7
Найти алгебраические дополнения всех элементов матрицы (из примера 1.6):
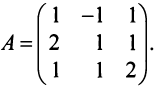
Решение:
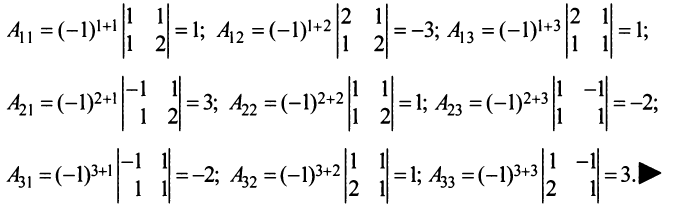 Важное значение для вычисления определителей имеет следующая теорема.
Важное значение для вычисления определителей имеет следующая теорема.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
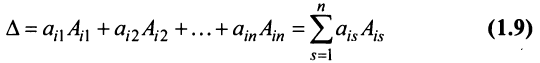
(разложение по элементам  -й строки;
-й строки; 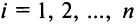 );
);
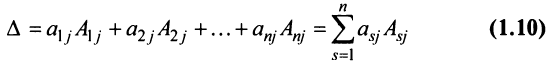
(разложение по элементам  -го столбца;
-го столбца; 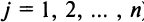 ).
).
 Убедимся в справедливости теоремы Лапласа на примере определителя матрицы третьего порядка. Разложим его вначале по элементам первой строки:
Убедимся в справедливости теоремы Лапласа на примере определителя матрицы третьего порядка. Разложим его вначале по элементам первой строки: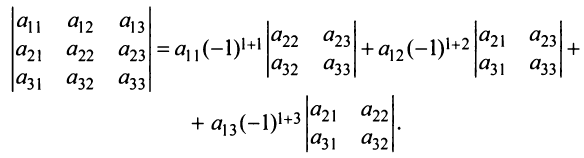
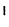 Точнее данная теорема является частным случаем теоремы Лапласа.
Точнее данная теорема является частным случаем теоремы Лапласа.
После преобразований (представляем их сделать читателю) нетрудно убедиться в том, что полученное выражение совпадает с определением (1.4). Аналогичный результат получаем разложением определителя матрицы по любой строке или столбцу.
Пример №8
Вычислить определитель треугольной матрицы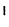 :
:

Решение:
Раскладывая по первому столбцу, получаем:
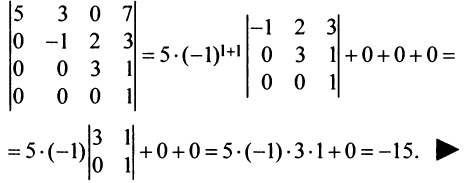
На частном примере мы убедились в том, что определитель треугольной (и, очевидно, диагональной) матрицы равен произведению элементов главной диагонали.
Значение теоремы Лапласа состоит в том, что позволяет свести вычисление определителей 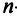 -го порядка к вычислению более простых определителей
-го порядка к вычислению более простых определителей 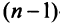 -го порядка.
-го порядка.
Свойства определителей
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число 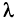 , то ее определитель умножится на это число
, то ее определитель умножится на это число  .
.
Пусть определитель исходной матрицы равен  . Для определенности первую строку матрицы умножим на
. Для определенности первую строку матрицы умножим на  , получим новый определитель
, получим новый определитель 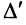 , который разложим по элементам первой строки:
, который разложим по элементам первой строки:
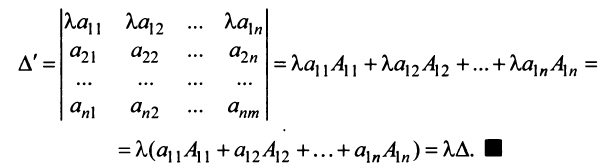
Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех ее элементов. Например, 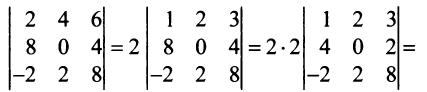
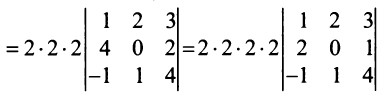 , но
, но 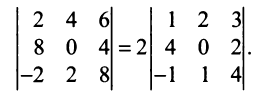
3. При транспонировании матрицы ее определитель не изменяется: 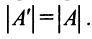
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
□ Предположим вначале, что переставлены две соседние строки матрицы: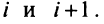 Разложим определитель исходной матрицы
Разложим определитель исходной матрицы  по элементам
по элементам  -й строки, а определитель новой матрицы (с переставленными строками)
-й строки, а определитель новой матрицы (с переставленными строками) 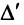 — по элементам
— по элементам 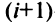 -й строки. Разложения будут отличаться только знаком, так как в формуле (1.9) для
-й строки. Разложения будут отличаться только знаком, так как в формуле (1.9) для 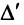 каждое алгебраическое дополнение будет иметь противоположный знак (множители
каждое алгебраическое дополнение будет иметь противоположный знак (множители 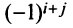 сменятся на множители
сменятся на множители 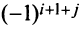 , поэтому
, поэтому 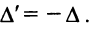
Если переставить не соседние строки, а, скажем,  -ю и
-ю и 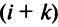 -ю, то такую перестановку можно представить как последовательное смещение
-ю, то такую перестановку можно представить как последовательное смещение  -й строки на
-й строки на 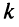 строк вниз (при этом каждый раз знак определителя меняется),
строк вниз (при этом каждый раз знак определителя меняется), 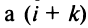 -й строки на
-й строки на 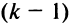 вверх, что тоже сопровождается
вверх, что тоже сопровождается 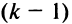 изменением знака, т.е. знак поменяется нечетное число
изменением знака, т.е. знак поменяется нечетное число 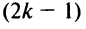 раз:
раз: 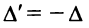 .
.
Доказательство для столбцов аналогично.
 Квадратная матрица называется треугольной, если все ее элементы, расположенные ниже (или выше) главной диагонали, равны нулю.
Квадратная матрица называется треугольной, если все ее элементы, расположенные ниже (или выше) главной диагонали, равны нулю.
5. Если квадратная матрица содержит две одинаковые строки {столбца), то ее определитель равен 0.
□Действительно, переставим эти строки (столбцы). С одной стороны, определитель не изменится, но, с другой стороны, по свойству 4 поменяет знак, т.е.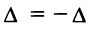 , откуда
, откуда 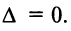
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
□ Пусть для определенности пропорциональны первая и вторая строки. Тогда, вынося коэффициент пропорциональности  , получаем по свойству
, получаем по свойству 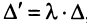 , где
, где  имеет две одинаковые строки и по свойству 5 равен 0.
имеет две одинаковые строки и по свойству 5 равен 0.
7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
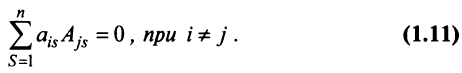
Рассмотрим квадратную матрицу  и вспомогательную матрицу
и вспомогательную матрицу 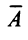 , полученную из матрицы
, полученную из матрицы  заменой
заменой  -й строки на
-й строки на  -ю:
-ю:
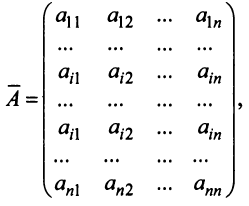
т.е. матрица 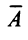 имеет две одинаковые строки, поэтому согласно свойству 5 ее определитель равен 0. Вычисляя его разложением по элементам
имеет две одинаковые строки, поэтому согласно свойству 5 ее определитель равен 0. Вычисляя его разложением по элементам  -й строки, получаем:
-й строки, получаем:
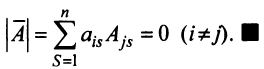
Замечание. Объединяя результат теоремы Лапласа и свойство 7, получаем:
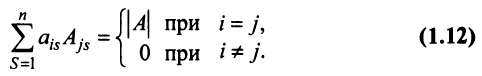 8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
Пусть для определенности к элементам  -Й строки матрицы прибавим элементы
-Й строки матрицы прибавим элементы  -й строки, умноженные на
-й строки, умноженные на 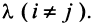 Тогда первая строка матрицы имеет вид:
Тогда первая строка матрицы имеет вид: 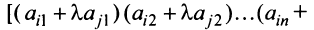
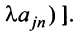 Определитель полученной матрицы вычислим разложением по элементам
Определитель полученной матрицы вычислим разложением по элементам  -й строки:
-й строки:
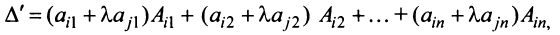
где 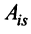 — алгебраические дополнения элементов
— алгебраические дополнения элементов  -й строки исходной матрицы
-й строки исходной матрицы 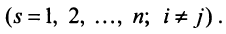 Раскроем скобки и получим после преобразования:
Раскроем скобки и получим после преобразования:
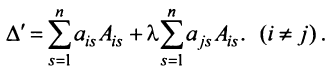
Используя формулу (1.12), получаем, что первая сумма равна определителю исходной матрицы, а вторая — 0, т.е.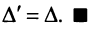
9. Сумма произведений произвольных чисел 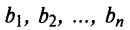 на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа
на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа 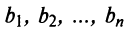 .
.
Свойство вытекает непосредственно из теоремы Лапласа.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: 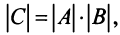 где
где 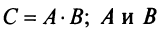 —матрицы
—матрицы 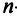 -го порядка.
-го порядка.
Замечание. Из свойства 10 следует, что даже если 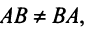 то
то 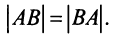
Перечисленные свойства определителей позволяют существенно упростить их вычисление, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств 1—9, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу).
Пример №9
Вычислить определитель четвертого порядка:
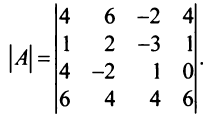
Решение:
Преобразуем матрицу так, чтобы в 3-й строке все элементы, кроме одного, обращались в 0. Для этого умножим, например, элементы 3-го столбца на (-4) и на 2 и прибавим их соответственно к элементам 1-го и 2-го столбцов. Раскладывая полученный определитель по элементам третьей строки, найдем  Полученный определитель третьего порядка можно вычислить по правилу треугольников или с помощью теоремы Лапласа, однако можно продолжить упрощение матрицы. «Обнулим» в матрице третьего порядка элементы 2-й строки (кроме одного). Для этого элементы 3-го столбца матрицы, предварительно умножив на (—13) и на 4, сложим с элементами 1-го и 2-го столбцов соответственно:
Полученный определитель третьего порядка можно вычислить по правилу треугольников или с помощью теоремы Лапласа, однако можно продолжить упрощение матрицы. «Обнулим» в матрице третьего порядка элементы 2-й строки (кроме одного). Для этого элементы 3-го столбца матрицы, предварительно умножив на (—13) и на 4, сложим с элементами 1-го и 2-го столбцов соответственно: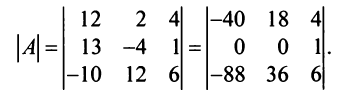
Раскладывая по элементам множители, получаем: 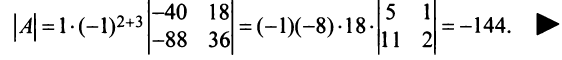
Обратная матрица
Для каждого числа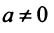 существует обратное число
существует обратное число 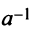 такое, что произведение
такое, что произведение 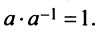 Для квадратных матриц тоже вводится аналогичное понятие.
Для квадратных матриц тоже вводится аналогичное понятие.
Определение. Матрица 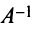 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице  , если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.
Однако не каждая квадратная матрица имеет обратную. Если 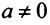 является необходимым и достаточным условием существования числа
является необходимым и достаточным условием существования числа 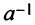 то для существования матрицы
то для существования матрицы  таким условием является требование
таким условием является требование 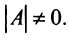
Если определитель матрицы отличен от нуля 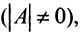 то такая квадратная матрица называется невырожденной, или неособенной; в противном случае (при
то такая квадратная матрица называется невырожденной, или неособенной; в противном случае (при 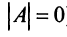 )— вырожденной, или особенной.
)— вырожденной, или особенной.
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица  существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.
существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.
Необходимость. Пусть матрица  имеет обратную
имеет обратную  , т.е
, т.е 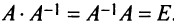 . По свойству 10 определителей имеем
. По свойству 10 определителей имеем
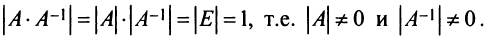
Достаточность. Пусть 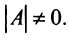 Рассмотрим квадратную матрицу
Рассмотрим квадратную матрицу 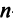 -го порядка,
-го порядка, 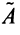 называемую присоединенной*, элементы которой являются алгебраическими дополнениями элементов матрицы
называемую присоединенной*, элементы которой являются алгебраическими дополнениями элементов матрицы  , транспонированной к
, транспонированной к 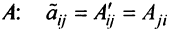
 Тогда элементы произведения матриц
Тогда элементы произведения матриц 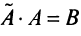 определяются по правилу умножения матриц:
определяются по правилу умножения матриц: 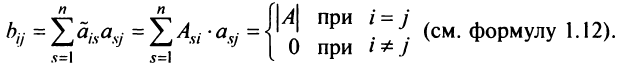 Поэтому матрица
Поэтому матрица 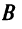 является диагональной, элементы ее главной диагонали равны определителю исходной матрицы:
является диагональной, элементы ее главной диагонали равны определителю исходной матрицы:
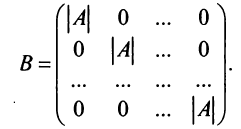
Аналогично доказывается, что произведение  на
на 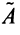 равно той же матрице
равно той же матрице 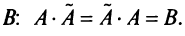 Отсюда следует, что если в качестве обратной матрицы взять матрицу.
Отсюда следует, что если в качестве обратной матрицы взять матрицу.
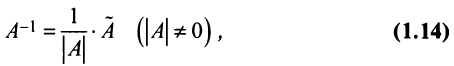
то произведения 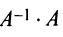 и
и 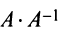 равны единичной матрице
равны единичной матрице 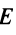
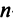 -го порядка:
-го порядка: 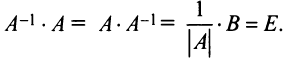
Докажем единственность обратной матрицы. Предположим, что существуют еще матрицы 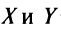 такие, что
такие, что 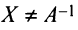 и
и 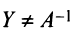 , где матрица
, где матрица  получена по формуле (1.14), и выполняются равенства:
получена по формуле (1.14), и выполняются равенства: 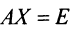 и
и 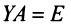 . Тогда, умножая на
. Тогда, умножая на слева первое из них, получаем:
слева первое из них, получаем: 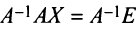 , откуда
, откуда 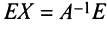 , т.е.
, т.е. 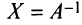 . Аналогично, умножая второе равенство на
. Аналогично, умножая второе равенство на  справа, получаем
справа, получаем 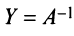 . Единственность доказана.
. Единственность доказана. 
Алгоритм вычисления обратной матрицы:
Пример №10
Найти матрицу, обратную к данной:
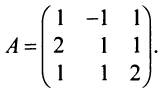
Решение:
1°. Определитель матрицы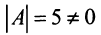 (см. пример 1.6), т.е. матрица
(см. пример 1.6), т.е. матрица  — невырожденная и обратная матрица
— невырожденная и обратная матрица  существует.
существует.
2°. Находим матрицу  , транспонированную к
, транспонированную к  :
:
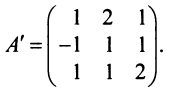
3°. Находим алгебраические дополнения элементов матрицы  и составляем из них присоединенную матрицу
и составляем из них присоединенную матрицу 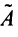 , учитывая, что
, учитывая, что 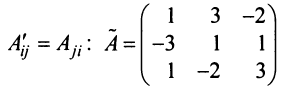
4° . Вычисляем обратную матрицу 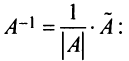
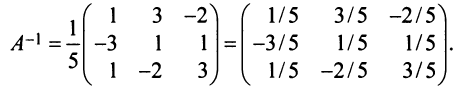 5°. Проверяем правильность вычисления обратной матрицы по формулам:
5°. Проверяем правильность вычисления обратной матрицы по формулам:
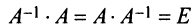 (рекомендуем в этом убедиться самому читателю). ►
(рекомендуем в этом убедиться самому читателю). ►
Для невырожденных матриц выполняются следующие свойства:
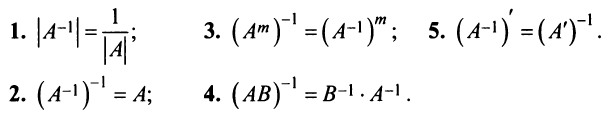
Ранг матрицы
Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.
В матрице  размера
размера 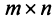 вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы
вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы 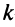 -то порядка, где
-то порядка, где 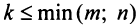 . Определители таких подматриц называются минорами
. Определители таких подматриц называются минорами 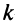 -го порядка матрицы
-го порядка матрицы  .
.
Например, из матрицы 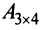 можно получить подматрицы первого, второго и третьего порядков.
можно получить подматрицы первого, второго и третьего порядков.
Определение. Рангом матрицы  называется наивысший порядок отличных от нуля миноров этой матрицы.
называется наивысший порядок отличных от нуля миноров этой матрицы.
Ранг матрицы  обозначается
обозначается 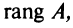 или
или 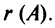
Из определения следует: а) ранг матрицы 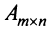 не превосходит меньшего из ее размеров, т.е.
не превосходит меньшего из ее размеров, т.е. 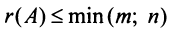 ;
;
б) 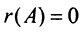 тогда и только тогда, когда все элементы матрицы равны нулю, т.е.
тогда и только тогда, когда все элементы матрицы равны нулю, т.е. 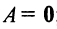 ;
;
в) для квадратной матрицы 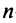 -го порядка
-го порядка 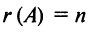 тогда и только тогда, когда матрица
тогда и только тогда, когда матрица  — невырожденная.
— невырожденная.
Пример №11
Вычислить ранг матрицы
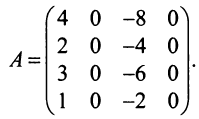
Решение:
Матрица  имеет четвертый порядок, поэтому
имеет четвертый порядок, поэтому 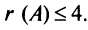 Однако
Однако 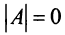 так как матрица
так как матрица  содержит нулевой столбец, поэтому
содержит нулевой столбец, поэтому 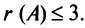 Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют нулевые определители, значит
Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют нулевые определители, значит 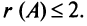 Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвертый), либо имеют пропорциональные столбцы (первый и третий), поэтому тоже имеют нулевые определители; таким образом
Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвертый), либо имеют пропорциональные столбцы (первый и третий), поэтому тоже имеют нулевые определители; таким образом 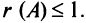 Поскольку матрица
Поскольку матрица  содержит ненулевые элементы, т.е. невырожденные подматрицы первого порядка, то
содержит ненулевые элементы, т.е. невырожденные подматрицы первого порядка, то 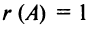 . ►
. ►
Пример №12
Вычислить ранг матрицы

Решение:
Для матрицы 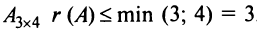 .
.
Проверим, равен ли ранг 3-м, для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего 4, они получаются при вычеркивании одного из столбцов матрицы):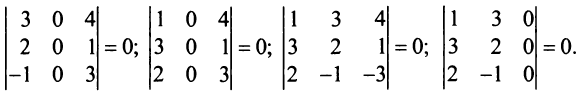
Поскольку все миноры третьего порядка нулевые,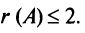 Так как существует ненулевой минор второго порядка, например,
Так как существует ненулевой минор второго порядка, например,
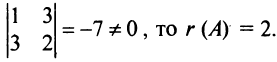 ►
►
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются преобразования, сохраняющие ранг матрицы.
Назовем элементарными преобразованиями матрицы следующие:
- Отбрасывание нулевой строки (столбца).
- Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
- Изменение порядка строк (столбцов) матрицы.
- Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
- Транспонирование матрицы.
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
 При изучении свойств определителей было показано, что при преобразованиях квадратных матриц их определители либо сохраняются, либо умножаются на число, не равное нулю. В результате сохраняется наивысший порядок отличных от нуля миноров исходной матрицы, т.е. ее ранг не изменяется.
При изучении свойств определителей было показано, что при преобразованиях квадратных матриц их определители либо сохраняются, либо умножаются на число, не равное нулю. В результате сохраняется наивысший порядок отличных от нуля миноров исходной матрицы, т.е. ее ранг не изменяется. 
С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.
Матрица  называется ступенчатой, если она имеет вид:
называется ступенчатой, если она имеет вид: 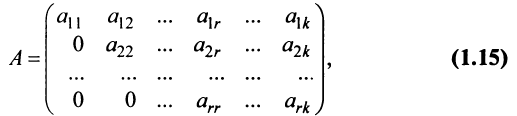 где
где 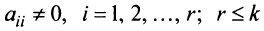 .
.
Замечание. Условие 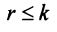 всегда может быть достигнуто транспонированием матрицы.
всегда может быть достигнуто транспонированием матрицы.
Очевидно, что ранг ступенчатой матрицы равен  , так как имеется минор
, так как имеется минор 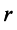 -го порядка, не равный нулю:
-го порядка, не равный нулю:
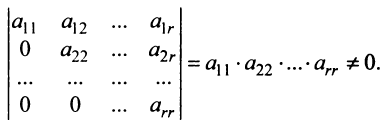
Покажем на примере алгоритм вычисления ранга матрицы с помощью элементарных преобразований.
Пример №13
Найти ранг матрицы
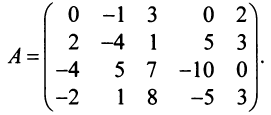
Решение:
1°. Если 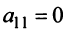 , то при перестановке строк или столбцов добиваемся того, что
, то при перестановке строк или столбцов добиваемся того, что 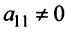 . В данном примере поменяем местами, например, 1-ю и 2-ю строки матрицы (см. ниже).
. В данном примере поменяем местами, например, 1-ю и 2-ю строки матрицы (см. ниже).
2°. Если 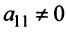 , то умножая элементы 2-й, 3-й и 4-й строк на подходящие числа (именно на
, то умножая элементы 2-й, 3-й и 4-й строк на подходящие числа (именно на 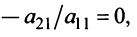
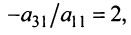
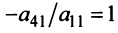 ) и прибавляя полученные числа соответственно к элементам 2-й1, 3-й и 4-й строк, добьемся того, чтобы все элементы 1-го столбца (кроме
) и прибавляя полученные числа соответственно к элементам 2-й1, 3-й и 4-й строк, добьемся того, чтобы все элементы 1-го столбца (кроме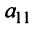 ) равнялись нулю:
) равнялись нулю:
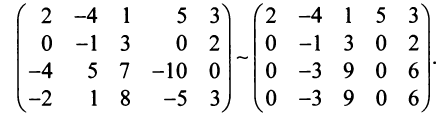 3°. Если в полученной матрице
3°. Если в полученной матрице 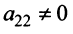 (у нас
(у нас 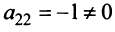 ), то умножая элементы 3-й и 4-й строк на подходящие числа (а именно, на
), то умножая элементы 3-й и 4-й строк на подходящие числа (а именно, на 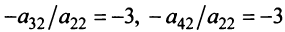 ), добьемся того, чтобы все элементы 2-го столбца (кроме
), добьемся того, чтобы все элементы 2-го столбца (кроме 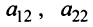 ) равнялись нулю. Если в процессе преобразований получаются строки (или столбцы), целиком состоящие из нулей (как в данном примере), то отбрасываем эти строки (или столбцы):
) равнялись нулю. Если в процессе преобразований получаются строки (или столбцы), целиком состоящие из нулей (как в данном примере), то отбрасываем эти строки (или столбцы):
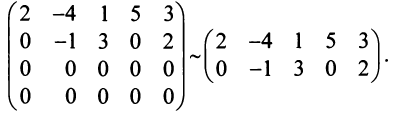
Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка, не равные нулю, например,
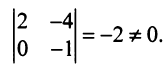 Поэтому ранг полученной ступенчатой, а следовательно, и данной матрицы равен 2. ►
Поэтому ранг полученной ступенчатой, а следовательно, и данной матрицы равен 2. ►
Для рангов матриц справедливы следующие соотношения:

5)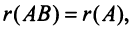 если
если  — квадратная матрица и
— квадратная матрица и 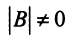
6) 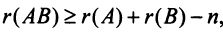 где
где 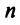 – число столбцов матрицы
– число столбцов матрицы  или строк матрицы
или строк матрицы  .
.
Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов.
 матрице
матрице  обозначим ее строки следующим образом:
обозначим ее строки следующим образом:
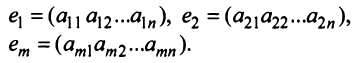
Две строки матрицы называются равными, если равны их соответствующие элементы: 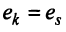 , если
, если 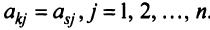
Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:
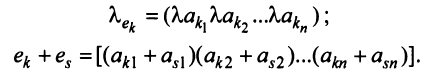
Строка е называется линейной комбинацией строк 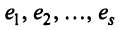 матрицы, если она равна сумме произведений этих строк на произвольные действительные числа:
матрицы, если она равна сумме произведений этих строк на произвольные действительные числа: 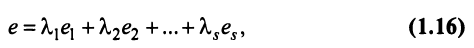
где 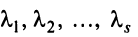 — любые числа.
— любые числа.
Строки матрицы 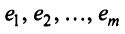 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 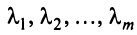 .т, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
.т, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
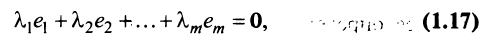
где 0 = (0 0…0).
Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных.
 Действительно, пусть для определенности в формуле (1.17)
Действительно, пусть для определенности в формуле (1.17) 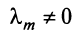 , тогда
, тогда 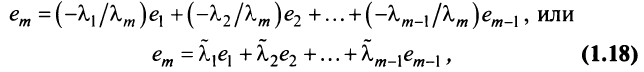
где 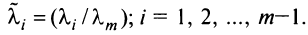
Таким образом, строка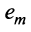 является линейной комбинацией остальных строк.
является линейной комбинацией остальных строк. 
Если линейная комбинация строк (1.17) равна нулю тогда и только тогда, когда все коэффициенты 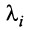 равны нулю, т.е.
равны нулю, т.е. 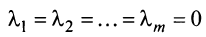 , то строки
, то строки 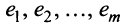 называются линейно независимыми.
называются линейно независимыми.
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки {столбцы).
 Пусть матрица
Пусть матрица  размера
размера 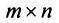 имеет
имеет 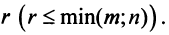
Это означает, что существует отличный от нуля минор  -го порядка. Всякий ненулевой минор
-го порядка. Всякий ненулевой минор  -го порядка будем называть базисным минором. Пусть для определенности это минор
-го порядка будем называть базисным минором. Пусть для определенности это минор

Тогда строки матрицы  линейно независимы. Действительно, предположим противное, т.е. одна из этих строк, например
линейно независимы. Действительно, предположим противное, т.е. одна из этих строк, например 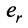 , является линейной комбинацией остальных:
, является линейной комбинацией остальных:
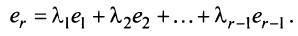
Вычтем из элементов  -й строки элементы 1-й строки, умноженные на
-й строки элементы 1-й строки, умноженные на 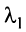 , элементы 2-й строки, умноженные на
, элементы 2-й строки, умноженные на 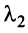 , и т.д., наконец, элементы
, и т.д., наконец, элементы 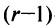 -й строки, умноженные на
-й строки, умноженные на 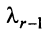 . На основании свойства 8 (см. § 1.4) при таких преобразованиях матрицы ее определитель
. На основании свойства 8 (см. § 1.4) при таких преобразованиях матрицы ее определитель  не изменится, но так как теперь г-я строка будет состоять из одних нулей, то
не изменится, но так как теперь г-я строка будет состоять из одних нулей, то 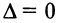 — противоречие, и наше предположение о том, что строки
— противоречие, и наше предположение о том, что строки  матрицы линейно зависимы, неверно.
матрицы линейно зависимы, неверно.
Строки  назовем базисными.
назовем базисными.
Покажем, что любые 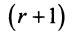 строк матрицы линейно зависимы, т.е. любая строка выражается через базисные.
строк матрицы линейно зависимы, т.е. любая строка выражается через базисные.
Рассмотрим минор 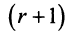 -го порядка, который получается
-го порядка, который получается
при дополнении рассматриваемого минора элементами еще одной строки 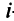 и столбца
и столбца 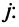

Этот минор равен нулю, так как ранг матрицы равен  , поэтому любой минор более высокого порядка равен нулю.
, поэтому любой минор более высокого порядка равен нулю.
Раскладывая его по элементам последнего (добавленного) столбца, получаем 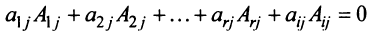 , где последнее алгебраическое дополнение
, где последнее алгебраическое дополнение 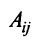 совпадает с базисным минором
совпадает с базисным минором  и поэтому отлично от нуля, т.е.
и поэтому отлично от нуля, т.е. 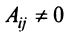 .
.
Разделив последнее равенство на 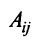 , можем выразить элемент
, можем выразить элемент 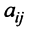 как линейную комбинацию:
как линейную комбинацию:

где 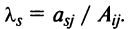
Фиксируем значение 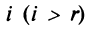 и получаем, что для любого
и получаем, что для любого 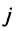
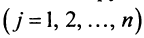 элементы
элементы 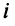 -й строки
-й строки 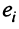 линейно выражаются через элементы строк
линейно выражаются через элементы строк  т.е.
т.е. 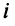 -я строка есть линейная комбинация базисных:
-я строка есть линейная комбинация базисных:
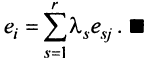
Теорема о ранге матрицы играет принципиальную роль в матричном анализе, в частности при исследовании систем линейных уравнений.
Матрицы в линейной алгебре
Прямоугольная таблица:
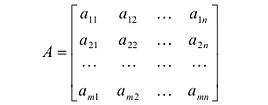 (9.1)
(9.1)
состоящая из m строк и n столбцов, называется матрицей размера m х n или (n,m)-матрицей.
Матрицу (9.1) будем обозначать А или 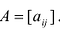 . Числа
. Числа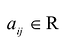 называются элементами матрицы, индекс i обозначает номер строки, а индекс j – номер столбца, на пересечении которых расположен элемент.
называются элементами матрицы, индекс i обозначает номер строки, а индекс j – номер столбца, на пересечении которых расположен элемент.
Если m = n, то матрица (9.1) называется квадратной матрицей порядка n.
В квадратной матрице n-го порядка диагональ, состоящая из элементов 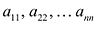 называется главной диагональю, состоящая из элементов а,п,
называется главной диагональю, состоящая из элементов а,п, 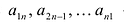 – побочной диагональю.
– побочной диагональю.
Квадратная матрица: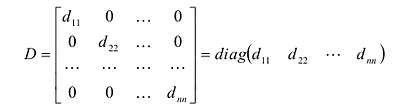
называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е. 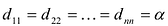 , то такая матрица называется скалярной. Скалярная матрица, у которой
, то такая матрица называется скалярной. Скалярная матрица, у которой 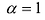 называется единичной и обозначается буквой Е. Например, единичная матрица третьего порядка:
называется единичной и обозначается буквой Е. Например, единичная матрица третьего порядка:
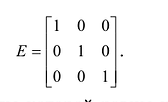
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.
Матрицы А и В называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
Операции над матрицами
Суммой двух матриц 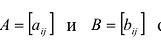 одинакового размера называется матрица
одинакового размера называется матрица 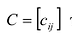 того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е.
того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е. 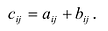
Сложение матриц обладает следующими свойствами:
- Коммутативность, т.е. А + В = В + А.
- Ассоциативность, т.е. (А + B)+ С = А + (В + С).
- Для любых двух матриц А и В одинакового размера существует единственная матрица X такая, что А + X = В. Матрица X обозначается X = В-А и называется разностью матриц В и А. Урав-=нение А + Х = 0 имеет решение Х = 0-А, получающаяся при этом матрица называется противоположной А и обозначается – А.
Произведением матрицы 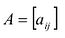 на число
на число 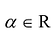 называется матрица, все элементы которой равны соответствующим элементам матрицы А, умноженным на число
называется матрица, все элементы которой равны соответствующим элементам матрицы А, умноженным на число 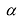 .
.
Умножение матрицы на действительное число обладает следующими свойствами:
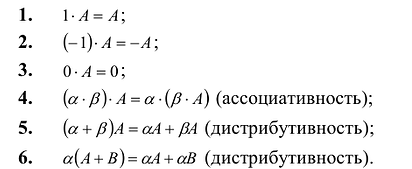
Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. В этом случае произведением матрицы 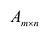 на матрицу
на матрицу 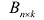 называется матрица
называется матрица
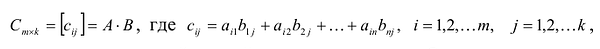
т.е. элемент, стоящий в n -той строке и j-том столбце матрицы произведения равен сумме произведений элементов n’-той строки матрицы А на соответствующие элементы j -го столбца матрицы В.
Свойства умножения:
- Если матрица А согласована с матрицей В, а матрица В согласована с матрицей С, то А • В• С = (А
 В)- С = А
В)- С = А  (В
(В  С) – ассоциативность умножения;
С) – ассоциативность умножения; - (А + ВС = АС + ВС, А-(В + С)= АВ + АС – свойство дистрибутивности;
- Умножение матриц не коммутативно, т.е., как правило,
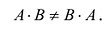
Транспонированием матрицы А называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е. i-я строка матрицы А становится i -тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице А обозначается 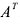 .
.
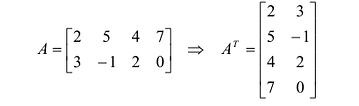
Свойства транспонирования: 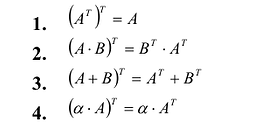
Определитель матрицы
Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.
Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 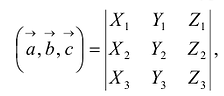 , или в свернутой форме
, или в свернутой форме 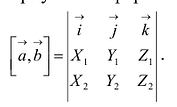
Предыдущая формула получается разложением определителя по первой строке.
Возьмем теперь квадратную матрицу n -го порядка
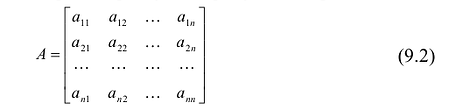
Для записи определителя n-го порядка матрицы А будем применять обозначения 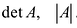 . При n = 1 матрица A состоит из одного элемента и ее определитель равен этому элементу. При n = 2 получаем определитель
. При n = 1 матрица A состоит из одного элемента и ее определитель равен этому элементу. При n = 2 получаем определитель 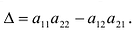
Минором 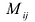 элемента
элемента  матрицы A называют определитель матрицы (n-1)-го порядка, получаемого из матрицы Л вычеркиванием i-той строки и j-го столбца.
матрицы A называют определитель матрицы (n-1)-го порядка, получаемого из матрицы Л вычеркиванием i-той строки и j-го столбца.
Пример №14
Найти минор 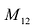 матрицы:
матрицы:
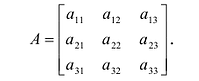
По определению, минор 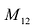 элемента
элемента 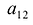 есть определитель матрицы, получаемой из матрицы А вычеркиванием первой строки и второго столбца. Следовательно,
есть определитель матрицы, получаемой из матрицы А вычеркиванием первой строки и второго столбца. Следовательно, 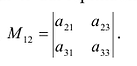
Алгебраическим дополнением элемента  матрицы А называется минор
матрицы А называется минор 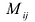 взятый со знаком
взятый со знаком 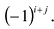 Алгебраическое дополнение элемента
Алгебраическое дополнение элемента  обозначается
обозначается 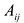 следовательно,
следовательно, 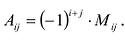
Пример №15
Найти алгебраическое дополнение элемента 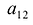 , матрицы А из примера 7.
, матрицы А из примера 7.
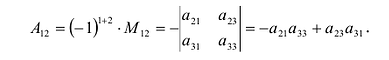
Определителем квадратной матрицы А n-го порядка 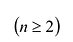 называется число:
называется число:
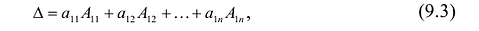
где аи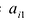 – элементы первой строки матрицы (9.2), а
– элементы первой строки матрицы (9.2), а 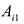 их алгебраические дополнения
их алгебраические дополнения 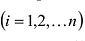 .
.
Запись по формуле (9.3) называется разложением определителя но первой строке.
Рассмотрим свойства определителей.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:
Определителем квадратной матрицы А n-го порядка 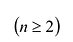 называется число:
называется число:
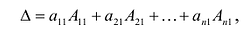 (9.4)
(9.4)
где 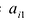 – элементы первого столбца матрицы (9.2), а
– элементы первого столбца матрицы (9.2), а 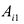 их алгебраические дополнения
их алгебраические дополнения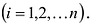 .
.
Свойство 2. Если поменять местами две строки или два столбца матрицы А, то ее определитель изменит знак на противоположный.
Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:
Определитель квадратной матрицы n-го порядка (будем в дальнейшем говорить определитель n-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
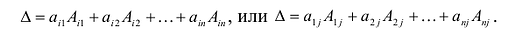
Свойство 3. Определитель, y которого две строки или два столбца одинаковы, равен нулю.
Действительно, поменяем в определителе  две одинаковые сроки местами. Тогда, по свойству 2 получим определитель
две одинаковые сроки местами. Тогда, по свойству 2 получим определитель 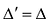 , но с другой стороны, определитель не изменится, т.е.
, но с другой стороны, определитель не изменится, т.е.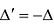 . Отсюда
. Отсюда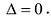 .
.
Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя  умножить на число
умножить на число 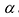 , то определитель умножится на
, то определитель умножится на 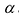 .
.
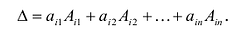
Умножим элементы i-той строки на 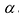 . Тогда получим определитель:
. Тогда получим определитель:
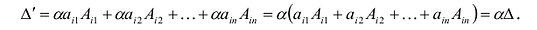
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пронорциональныу равен нулю.
Пусть i-я строка пропорциональна j-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Свойство 6. Если каждый элемент строки (столбца) определителя  есть сумма двух слагаемых, то определитель
есть сумма двух слагаемых, то определитель  равен сумме двух определителей: у одного из них i-той строкой (столбцом) служат первые слагаемые, а у другого – вторые.
равен сумме двух определителей: у одного из них i-той строкой (столбцом) служат первые слагаемые, а у другого – вторые.
Разложив определитель  по i -той строке получим:
по i -той строке получим:
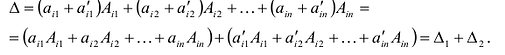
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Прибавив к элементам i-той строки определителя  соответствующие элементы j-ой строки, умноженные на число
соответствующие элементы j-ой строки, умноженные на число 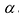 , получим определитель
, получим определитель 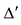 Определитель
Определитель  равен сумме двух определителей: первый есть
равен сумме двух определителей: первый есть , а второй равен нулю, так как у него i-тая и j-тая строки пропорциональны.
, а второй равен нулю, так как у него i-тая и j-тая строки пропорциональны.
Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.:

Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Рассмотрим вспомогательный определитель  , который получается из данного определителя
, который получается из данного определителя  заменой j-той строки i-той строкой. Определитель
заменой j-той строки i-той строкой. Определитель  равен нулю, так как у него две одинаковые строки. Разложив его по j-той строке получим:
равен нулю, так как у него две одинаковые строки. Разложив его по j-той строке получим:
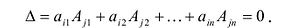
Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.
Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.
Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т.е. 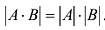 .
.
Ранг матрицы
Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы А обозначают rankA или rА.
Если все миноры порядка к данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
Если все миноры первого порядка (элементы матрицы А) равны нулю, то rankA = 0. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то rankA = 1. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка к, окаймляющие ненулевой минор (A-l)-ro порядка равны нулю, либо таких миноров нет. Тогда rankA = к -1.
Пример №16
Вычислить ранг матрицы 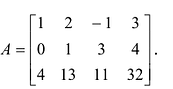
Минор первого порядка (элемент 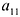 ) отличен от нуля. Окаймляющий его минор
) отличен от нуля. Окаймляющий его минор 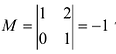 тоже не равен нулю.
тоже не равен нулю.
Далее рассмотрим миноры, окаймляющие минор М :
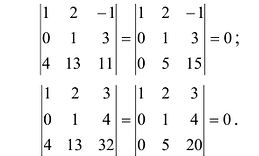
Все эти миноры равны нулю, значит rankA = 2. Приведенный алгоритм нахождения ранга матрицы не всегда удобен, поскольку связан с вычислением большого числа определителей. Наиболее удобно пользоваться при вычислении ранга матрицы элементарными преобразованиями, при помощи которых матрица приводится к столь простому виду, что очевидно, чему равен ее ранг.
Элементарными преобразованиями матрицы называют следующие преобразования:
- > умножение какой-нибудь строки (столбца) матрица на число, отличное от нуля;
- > прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число.
Полужордановым преобразованием строк матрицы:

с разрешающим элементом 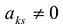 называется следующая совокупность преобразований со строками матрицы:
называется следующая совокупность преобразований со строками матрицы:
- > k первой строке прибавить k-ю, умноженную на число
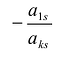 и т.д.;
и т.д.;
> k последней строке прибавить k — го, умноженную на число 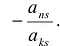 После выполнения этих преобразований получается матрица:
После выполнения этих преобразований получается матрица:
Полужордановым преобразованием столбцов матрицы с разрешающим элементом 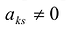 называется следующая совокупность преобразований со столбцами матрицы:
называется следующая совокупность преобразований со столбцами матрицы:
- > к первому столбцу прибавить k-й, умноженный на число
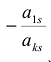 и т.д.;
и т.д.; - > к последнему столбцу прибавить k -й, умноженный на число
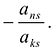
После выполнения этих преобразований получается матрица:
Полужорданово преобразование строк или столбцов квадратной матрицы не изменяет ее определителя. Элементарные преобразования матрицы не изменяют ее ранга. Покажем на пример, как вычислить ранг матрицы, пользуясь элементарными преобразованиями.
Пример №17
Вычислить ранг матрицы 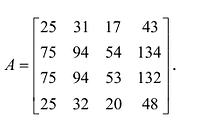
Применим к матрице А элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.

Вычитая далее вторую строку из третьей и последней, имеем:

Последняя матрица содержит отличный от нуля минор 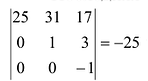 третьего порядка, определитель же самой матрицы А равен нулю. Следовательно,
третьего порядка, определитель же самой матрицы А равен нулю. Следовательно, 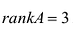
Отметим два важных свойства ранга матрицы:
- Ранг матрицы не меняется при ее транспонировании;
- Если ранг матрицы равен г, то любые ее г + 1 строк (столбцов) линейно зависимы.
Обратная матрица
Пусть А – квадратная матрица порядка n. Матрица В называется обратной матрицей к матрице А, если выполняются равенства А-В = В■ А = Е, где Е – единичная матрица порядка n.
Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.
Пусть 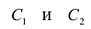 – матрицы, обратные к матрице А. Тогда
– матрицы, обратные к матрице А. Тогда 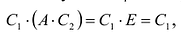 с другой стороны,
с другой стороны, 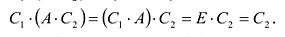
Откуда 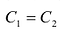 . Обратную матрицу к матрице А обозначают
. Обратную матрицу к матрице А обозначают  .
.
Теорема 2. Матрица А имеет обратную матрицу тогда и только тогда, когда  .
.
Пусть А имеет обратную матрицу. Тогда 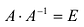 и, применяя теорему об умножении определителей, получаем
и, применяя теорему об умножении определителей, получаем 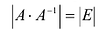 или
или 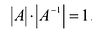
Следовательно,  .
.
Пусть  . Укажем явное выражение матрицы
. Укажем явное выражение матрицы  через элементы матрицы А, а именно: если
через элементы матрицы А, а именно: если 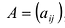 , то:
, то:
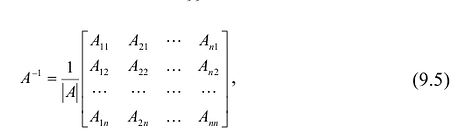
здесь 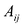 – алгебраическое дополнение к элементу
– алгебраическое дополнение к элементу 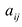 . Матрица (9.5) получается из матрицы А следующим образом. Сначала вместо каждого элемента
. Матрица (9.5) получается из матрицы А следующим образом. Сначала вместо каждого элемента 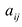 пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную
пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную 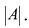
Непосредственное умножение А на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) – матрица, обратная к А.
Пример №18
Найти обратную матрицу к матрице

Так как 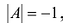 , то
, то  существует. Вычислим алгебраические дополнения элементов матрицы А:
существует. Вычислим алгебраические дополнения элементов матрицы А: 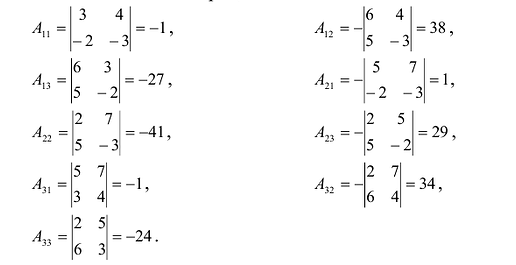
Матрицу  находим в два приема, согласно формуле (9.5). Сначала запишем матрицу В, состоящую из алгебраических дополнений элементов
находим в два приема, согласно формуле (9.5). Сначала запишем матрицу В, состоящую из алгебраических дополнений элементов 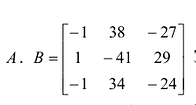 Затем матрица В транспонируется и умножается на число обратное
Затем матрица В транспонируется и умножается на число обратное 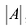 , в данном случае – на (-1). Окончательно получаем:
, в данном случае – на (-1). Окончательно получаем:
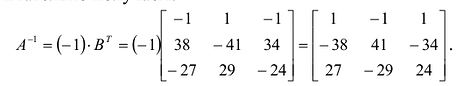
Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если А и В – невырожденные матрицы одинакового порядка, то: 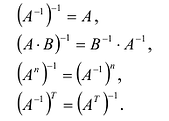
Матрицы и определители
Определение и типы матриц
Определение 3.1.1. Прямоугольная таблица 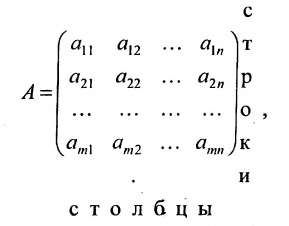 (3.1.1) состоящая из m строк и n столбцов, называется матрицей размером
(3.1.1) состоящая из m строк и n столбцов, называется матрицей размером 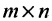 .
.
Числа 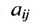 называются элементами матрицы. Каждый элемент матрицы имеет два индекса, первый индекс i обозначает номер строки, второй индекс j – номер столбца.
называются элементами матрицы. Каждый элемент матрицы имеет два индекса, первый индекс i обозначает номер строки, второй индекс j – номер столбца.
Матрицы удобно обозначать в виде 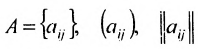 , при
, при 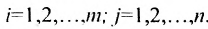 . Фигурные (круглые) скобки, двойные прямые вертикальные линии показывают, что
. Фигурные (круглые) скобки, двойные прямые вертикальные линии показывают, что 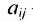 – типовой элемент матрицы А, в котором индексы i и j последовательно принимают все значения от 1 до указанных конечных величин.
– типовой элемент матрицы А, в котором индексы i и j последовательно принимают все значения от 1 до указанных конечных величин.
Превратим в матрице (3.1.1) строки в столбцы, а столбцы в строки, получим матрицу  которая называется транспонированной по отношению к А. Если размер А
которая называется транспонированной по отношению к А. Если размер А 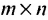 , то
, то 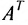 размерности
размерности 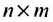 . Повторное транспонирование приводит к исходной матрице:
. Повторное транспонирование приводит к исходной матрице: 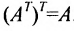 .
.
Пример №19
Рассмотрим матрицу

элементы которой характеризуют зависимость средних розничных цен на автомобили от срока их службы в 1998, 1999 и 2000 гг. Строки матрицы соответствуют продолжительности эксплуатации автомобиля, а столбцы – годам. Содержательное значение каждого элемента матрицы определяется его местом в данном массиве чисел. Например, число 3100 во второй строке и втором столбце, элемент с/22> представляет среднюю розничную цену автомобиля прослужившего два года в 1999 г. Следовательно, числа, записанные в строку, характеризуют цены автомобилей, прослуживших один и гот же срок службы в разные годы 1998-2000 гг., а числа в столбце – цены автомобилей различного срока службы в данном году.
В той мере, в какой это связано с характеристикой цен па автомобили, такой выбор строк матрицы полностью произволен, и мы могли бы сразу же поменять местами строки и столбцы без какой-либо потери информации, получив строки для отдельных лет и столбцы для сроков службы, т.е. получили бы транспонированную матрицу по отношению к матрице Р:

Хотя элементы матрицы 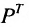 те же, что и матрицы Р, обе матрицы не одинаковые. Взаимосвязь этих матриц проявляется в том, что строки матрицы Р являются столбцами матрицы
те же, что и матрицы Р, обе матрицы не одинаковые. Взаимосвязь этих матриц проявляется в том, что строки матрицы Р являются столбцами матрицы 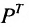 .
.
Если, элементы 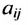 матрицы А неотрицательные (положительные) действительные числа
матрицы А неотрицательные (положительные) действительные числа 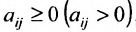 , то матрица А называется неотрицательной (положительной) и записывается
, то матрица А называется неотрицательной (положительной) и записывается 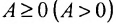 .
.
Матрица Р в примере 3.1.1 является положительной матрицей, так как её элементы положительные действительные числа.
Матрица, состоящая из одной строки 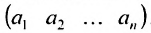 , называется матрицей-строкой. Матрица, состоящая из одного столбца
, называется матрицей-строкой. Матрица, состоящая из одного столбца
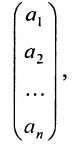
называется матрицей-столбцом. Транспонированием переводят матрицу-строку в матрицу-столбец, и наоборот.
Если m=n, то матрица называется квадратной, при этом число строк (столбцов) называется порядком квадратной матрицы.
Рассмотрим некоторые виды квадратных матриц.
Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной. Она обозначается символом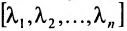 :
: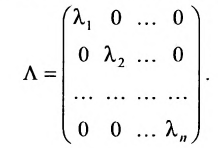
Если в диагональной матрице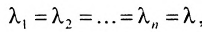 то она называется скалярной. Скалярная матрица, у которой диагональные элементы равны 1, называется единичной:
то она называется скалярной. Скалярная матрица, у которой диагональные элементы равны 1, называется единичной:
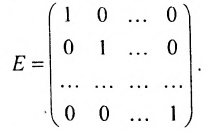 Квадратная матрица, у которой все элементы, стоящие ниже главной диагонали, равны нулю, называется верхнетреугольной (“матрица А). Аналогично, если в квадратной матрице нулю равны все элементы, стоящие выше главной диагонали, то она называется нижнетреугольной (матрица В).
Квадратная матрица, у которой все элементы, стоящие ниже главной диагонали, равны нулю, называется верхнетреугольной (“матрица А). Аналогично, если в квадратной матрице нулю равны все элементы, стоящие выше главной диагонали, то она называется нижнетреугольной (матрица В).
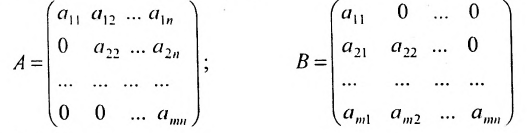
Например, 
Матрица A – верхнеугольная, а В – нижнетреугольная. Квадратная матрица называется ленточной, если все её элементы, не стоящие на главной диагонали и в соседних с ней косых строках, равны нулю. Например,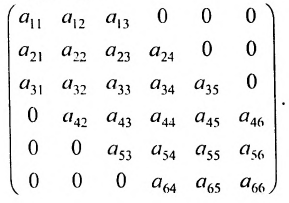
В ленточной матрице не равные нулю элементы заполняют «ленту», осью которой служит главная диагональ. Ленточная матрица называется модулированной, если в каждой косой строке стоят одинаковые элементы: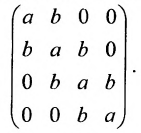
Квадратная матрица называется симметрической, если её элементы, расположенные симметрично относительно главной диагонали, одинаковы: 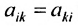 ; если же
; если же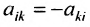 , то матрица А называется кососимметрической. Симметрическая матрица совпадает с транспонированной матрицей, т.е.
, то матрица А называется кососимметрической. Симметрическая матрица совпадает с транспонированной матрицей, т.е. 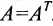 .
.
Например, матрица, характеризующая влияние факторов на инвестиции и запасы, является симметрической матрицей вида:

Элемент 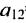 =0,29, характеризующий зависимость использования мощностей и изменения объёмов запасов, совпадает с элементом
=0,29, характеризующий зависимость использования мощностей и изменения объёмов запасов, совпадает с элементом 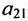 =0,29, характеризующим зависимость между изменением объёмов запасов и использованием мощностей; элемент
=0,29, характеризующим зависимость между изменением объёмов запасов и использованием мощностей; элемент 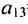 =0,15, характеризующий зависимость между изменением общей величины хозяйственных запасов и суммой совокупного оборота с поправкой на сезонность, совпадает с элементом
=0,15, характеризующий зависимость между изменением общей величины хозяйственных запасов и суммой совокупного оборота с поправкой на сезонность, совпадает с элементом 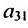 =0,15, характеризующим зависимость между суммой совокупного оборота с поправкой на сезонность и изменением общей величины хозяйственных запасов; элемент
=0,15, характеризующим зависимость между суммой совокупного оборота с поправкой на сезонность и изменением общей величины хозяйственных запасов; элемент 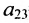 =0,71, характеризующий зависимость между степенью использования производственных мощностей и суммой совокупного оборота с поправкой на сезонность, совпадает с элементом
=0,71, характеризующий зависимость между степенью использования производственных мощностей и суммой совокупного оборота с поправкой на сезонность, совпадает с элементом 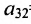 =0,71, характеризующим зависимость между суммой совокупного оборота с поправкой на сезонность и степенью использования производственных мощностей.
=0,71, характеризующим зависимость между суммой совокупного оборота с поправкой на сезонность и степенью использования производственных мощностей.
Очевидно, что транспонированная симметричная матрица равна самой матрице.
Квадратная матрица, у которой на главной диагонали стоит одно и го же число 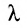 и все элементы одного ряда выше диагонали равны единице, а все другие элементы равны нулю, называется клеткой Жордана:
и все элементы одного ряда выше диагонали равны единице, а все другие элементы равны нулю, называется клеткой Жордана:

Матрица, у которой на главной диагонали стоят любые клетки Жордана, а все элементы вне этих клеток равны нулю, называется Жордаповой матрицей. Например, матрица является Жордановой.

Она содержит четыре клетки Жордана: две клетки второго порядка с числом 3 на диагонали, одну клетку третьего порядка с числом нуль на диагонали и одну клетку первого порядка с числом нуль на диагонали.
Из приведенных примеров следует, что понятие матрицы широко используется в экономике. Кроме того, можно подчеркнуть, что планирование производства должно основываться на надлежащим образом упорядоченной системе информации, записанной в виде матрицы, с помощью которой просто и сжато описываются зависимости, имеющие место в материальном производстве. Так, например, планирование на предприятии основывают, пользуясь нормами как системой информации. Если на предприятии производится четыре продукта 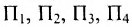 и для их производства используются материалы
и для их производства используются материалы 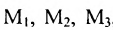 , то система норм материальных затрат, которая представляет собой основу плана снабжения, может быть представлена в виде таблицы (матрицы):
, то система норм материальных затрат, которая представляет собой основу плана снабжения, может быть представлена в виде таблицы (матрицы):

где 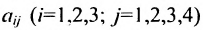 есть норма расхода
есть норма расхода 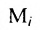 i-го материала на производство единицы
i-го материала на производство единицы 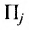 j-го продукта. Так норма расхода материала
j-го продукта. Так норма расхода материала 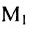 на производство единицы продукта
на производство единицы продукта 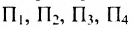 соответственно равна
соответственно равна 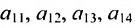 и т.д.
и т.д.
Можно привести следующий пример использования матриц: два предприятия передают свою продукцию на три оптовых склада, причём расходы на перевозку единицы продукции с предприятия 1 на отдельные склады соответственно равняются 2,3,4; а с предприятия 2 они составляют 1,5,2. Тогда матрица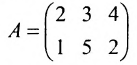
есть матрица удельных транспортных расходов.
Следует отметить использование матриц в межотраслевом балансе производства (матрица технологических коэффициентов производства), в определении совокупных затрат труда (матрица коэффициентов материальных затрат) и т.д.
Пример №20
Продавец мороженого решает вопрос о том, сколько пакетов мороженого ему следует закупить. К покупке пакетов мороженого он может прибегнуть один раз. Каждый пакет стоит 10 ден.ед. и может быть продан за 12 ден.ед. Пакеты мороженого, оставшиеся не распроданными, никакой стоимости не представляют. Известно, что количество пакетов мороженого, которое он сможет продать, колеблется от 1 до 5. Составим матрицу денежных сумм, выручаемых в зависимости от его решения и от результатов продажи. По строкам расположим результаты того или иного решения продавца мороженого, а по столбцам – возможный исход продаж.
Решение:
Предположим, что продавец мороженого закупает один пакет. Тогда он его продаст и получает прибыль в 2 ден.ед.
Следовательно, первая строка матрицы будет иметь вид: 2 2 2 2 2. Сели он закупит 2 пакета, то продав один, он потеряет 8 ден.ед.; продав 2 пакета, он получит прибыль 4 ден.ед. Следовательно, вторая строка примет вид: -8 4 4 4 4. Рассуждая аналогичным образом, получаем матрицу:
Арифметические операции над матрицами
Матрицы А и В считаются равными, если они одинаковой размерности и всс элементы 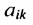 матрицы А совпадают с соответствующими элементами
матрицы А совпадают с соответствующими элементами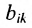 матрицы В, т.е. выполняются
матрицы В, т.е. выполняются 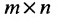 скалярные равенства
скалярные равенства 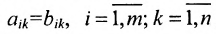 , которые равносильны равенству А=В.
, которые равносильны равенству А=В.
Определение 3.2.1. Суммой матриц А а В размерности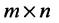 называется матрица S=A+B той же размерности, элементы которой Sik равны суммам соответствующих элементов матриц А и В:
называется матрица S=A+B той же размерности, элементы которой Sik равны суммам соответствующих элементов матриц А и В: 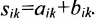
Из определения следует, что складывают матрицы с одинаковыми размерами, при этом сумма будет матрицей с теми же размерами.
Например,
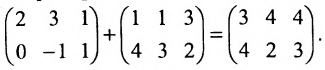
Определение 3.2.2. Произведением матрицы А на скаляр 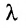 называется матрица
называется матрица 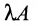 той же размерности, что и А, элементы которой получены из элементов матрицы А умножением на
той же размерности, что и А, элементы которой получены из элементов матрицы А умножением на 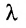 . Например,
. Например,
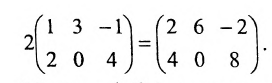
Матрица (-1)A записывается -А и называется матрицей, противоположной матрице А. Если все элементы матрицы равны нулю, го она называется нуль-матрицей и обозначается 0.
Введенные операции сложения матриц и умножения матрицы на скаляр 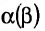 обладают свойствами:
обладают свойствами:
- А + В = В + А – (перемсстительный) коммутативный закон.
- (А + В) + С = А + (B + C);
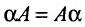 .
.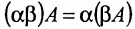 .
.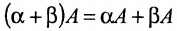 .
.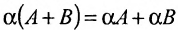 .
.
Определение 3.2.3. Разностью матриц одинаковой размерности называется матрица той же размерности: 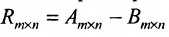 , её элементы равны разностям соответствующих элементов матриц А и В:
, её элементы равны разностям соответствующих элементов матриц А и В: 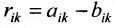 .
.
Например,
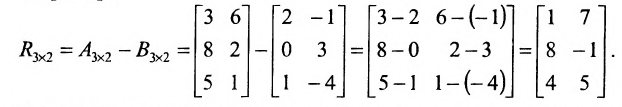
Как и при операции сложения, можно вычитать друг из друга только те матрицы, которые имеют одинаковую размерность.
Прежде чем вводить произведение матриц, рассмотрим произведение векторов. И для пояснения общего метода воспользуемся числовыми примерами.
Предположим, что объем различных продаж за месяц некоторого товара некоторой компании «а» составил 58, 26, 12, 25 единиц за первую, вторую, третью и четвертую недели соответственно, и что цена этого товара по неделям соответственно равна 3, 5, 10, 4 ден.ед. Следовательно, общий доход за месяц от продажи товара равен 58-3 + 26-5+ 12-10 + 25-4 = 524ден.ед. Представим данные
о продажах при помощи матрицы-строки:
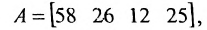
а соответствующие цены с помощью матрицы-столбца:
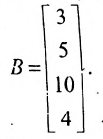
Тогда общий доход от продажи товара, равный 524 ден.ед., представляет собой сумму произведений элементов матрицы-строки A (количество проданного товара по неделям) на соответствующие элементы матрицы-столбца В (цены по неделям на товар): 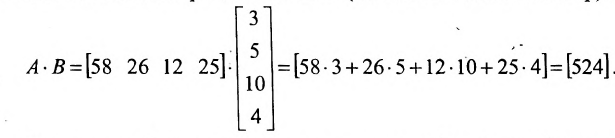
Приведенный пример помогает уяснить общую методику вычисления произведения матрицы-строки на матрицу-столбец: для этого каждый элемент матрицы-строки А нужно умножить на соответствующий элемент матрицы-столбца В и сложить полученные произведения.
Предположим теперь, что компания «а» имеет отделения в трёх различных регионах. Данные о количестве проданного товара по регионам запишем в виде матрицы С:

Цена по неделям за месяц была такой же. Доход от розничной продажи в первом регионе был вычислен; аналогичные расчёты могут быть произведены и по двум другим регионам:
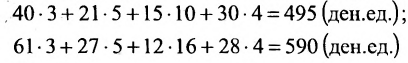
Представим итоговые данные по выручке в виде матрицы-столбца:
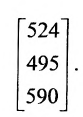
Взглянув на вычисления, можно убедиться в том, что элементы этой матрицы-столбца получаются так же, как и описанное ранее произведение матрицы-строки А на матрицу-столбец В, причем в качестве матрицы-строки А в каждом случае взята последующая строка матрицы С. Полученный результат представляет произведение СВ:
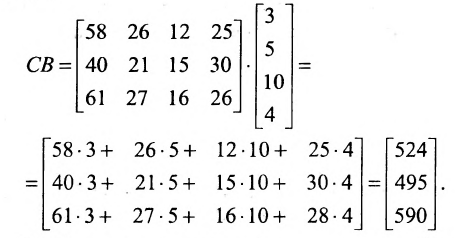
В общем случае произведение матрицы С на матрицу-столбец В, это вектор-столбец,i-Й элемент которого представляет сумму произведений каждого из элементов i-й строки матрицы С на соответствующие элементы вектора-столбца В.
Из этого примера следует, что произведение 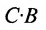 существует только в том случае, когда число элементов в строках матрицы С (т.е. число столбцов) равно числу элементов, составляющих вектор-столбец В (т.е. числу строк). При соблюдении этого равенства, произведение
существует только в том случае, когда число элементов в строках матрицы С (т.е. число столбцов) равно числу элементов, составляющих вектор-столбец В (т.е. числу строк). При соблюдении этого равенства, произведение 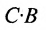 образует вектор-столбец, содержащий столько элементов, сколько строк насчитывается в матрице С. Следовательно, если в матрице С содержится т строк и q столбцов и порядок матрицы-столбца В равен q, тогда произведение
образует вектор-столбец, содержащий столько элементов, сколько строк насчитывается в матрице С. Следовательно, если в матрице С содержится т строк и q столбцов и порядок матрицы-столбца В равен q, тогда произведение 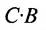 представляет собой матрицу-столбец порядка т, причем i-й элемент этого вектора равен
представляет собой матрицу-столбец порядка т, причем i-й элемент этого вектора равен
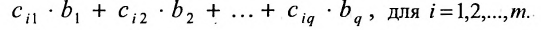
Аналогичным образом определяется произведение матрицы-строки 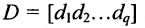 на матрицу Р. Оно существует в том случае,
на матрицу Р. Оно существует в том случае,
если число элементов матрицы-строки D равно числу элементов в столбцах матрицы Р (т.е. равно числу строк этой матрицы). В этом случае произведении 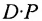 образует матрицу-строку, содержащую столько же элементов, сколько столбцов насчитывается в матрице Р. При этом произведение
образует матрицу-строку, содержащую столько же элементов, сколько столбцов насчитывается в матрице Р. При этом произведение 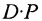 равно
равно 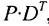 , произведение
, произведение 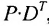 может к не существовать, несмотря на то что, существует произведение
может к не существовать, несмотря на то что, существует произведение 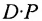 , и наоборот.
, и наоборот.
Пример №21
Пусть матрица

характеризует переход подписчика от одной газеты к другой в зависимости от продолжительности подписки. В этой матрице перехода данные сгруппированы по строкам и столбцам в соответствии с продолжительностью подписки: до одного года, от одного года до двух лет, более двух лет и, наконец, аннулирование подписки. Элементы первой строки характеризуют состояние подписчиков газет с продолжительностью подписки до одного года; второй строки – с продолжительностью подписки от одного года до двух лет; третья строка – с продолжительностью подписки более двух лет; элементы четвертой строки характеризуют аннулирование подписки. Элементы первого столбца характеризуют возможность остаться в категории подписчиков до одного года; элементы второго столбца – возможность продолжить подписку от одного до двух лет, если подписчик имеет продолжительность подписки до одного года; элементы третьего столбца- возможность продолжить подписку более двух лет: элементы четвертого столбца – возможность аннулировать подписку.
Предположим, что известно распределение 5000 подписчиков по продолжительности подписки на газеты: 3000 имеют продолжительность подписки до одного года (категория 1), 800 – имеют продолжительность подписки от одного до двух лет (категория 2), 1200 подписчиков имеют, продолжительность подписки более двух лет (категория 3). Представим эти данные в виде матрицы-строки Q =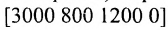 .
.
Для того чтобы определить возможное количество подписчиков в каждой из этих категорий через год, умножим матрицу-строку Q на матрицу Р:

Матрица-строка, полученная в результате умножения, показывает, что из I категории через год возможно 2100 подписчиков будут принадлежать к категории II, 1720- к категории III, и 1180 возможно аннулируют подписку.
Учитывая введенные операции, умножение двух матриц А и В можно представить как многократное умножение матрицы А на матрицы-столбцы, рассматривая вторую матрицу В как набор мат-риц-столбцов. При этом произведение матриц А и В может иметь смысл только в том случае, когда j-й столбец матрицы В (а, следовательно, и все ее столбцы) насчитывают тоже число элементов, что и i-я строка матрицы А (а, следовательно, и все ее строки). Поскольку количество элементов в столбце матрицы равно числу строк в ней (а количество элементов в строке равно количеству столбцов) это означает, что в матрице В должно быть столько же строк, сколько столбцов содержит матрица А.
Таким образом, произведение матрицы 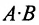 определено, когда число столбцов в А равно числу строк в В. Тогда произведение
определено, когда число столбцов в А равно числу строк в В. Тогда произведение 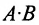 содержит то же количество строк, что и матрица А, и то же количество столбцов, что и матрица В.
содержит то же количество строк, что и матрица А, и то же количество столбцов, что и матрица В.
Если число столбцов в А равно числу строк в В, то матрицы называются согласованными для умножения А на В. При этом если А размерности т * п, а В размерность 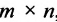 , то произведение
, то произведение 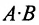 является матрицей размерности
является матрицей размерности 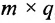 , т. е.:
, т. е.:
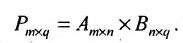
Определение 3.2.4. Произведением матрицы А размерности 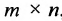 на матрицу В размерности
на матрицу В размерности 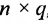 называется матрица Р размерности
называется матрица Р размерности 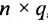 , элементы которой
, элементы которой 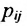 определяется формулами:
определяется формулами:
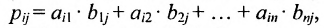
, при 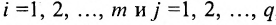 , т.е.
, т.е. 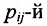 элемент равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-ого столбца матрицы В.
элемент равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-ого столбца матрицы В.
- Заказать решение задач по высшей математике
Пример №22
Пусть 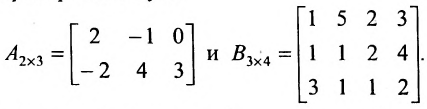 Матрица А содержит три столбца, а В содержит три строки. Следовательно, матрицы А и В согласованные для умножения. Тогда
Матрица А содержит три столбца, а В содержит три строки. Следовательно, матрицы А и В согласованные для умножения. Тогда 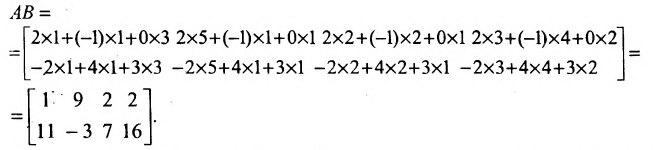
Произведение матриц, вообще говоря, не коммутативно, т.е. А В не всегда равно 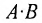 . Например,
. Например, 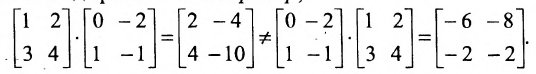
Из приведенного примера следует, что, перемножая матрицы А и В, можно получить два произведения 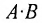 к
к 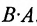 . Если размеры матрицы A равны
. Если размеры матрицы A равны 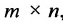 , то оба произведения существуют только в том случае, когда размеры матрицы В равны
, то оба произведения существуют только в том случае, когда размеры матрицы В равны 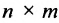 . Тогда произведение
. Тогда произведение 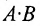 образует квадратную матрицу порядка m, а произведение
образует квадратную матрицу порядка m, а произведение 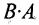 – квадратную матрицу n. Поэтому размеры АВ могут быть равны ВА в том случае, когда m = n, т.е. когда обе матрицы квадратные и имеют один и тот же порядок равный m. При этом указанные произведения матриц могут не иметь ни одного одинакового элемента, полученного в результате суммирования произведений соотвстствующих элементов исходных матриц. Поэтому, если даже существуют оба произведения АВ и ВА и оба они имеют одинаковый порядок, вообще говоря, они не обязательно должны быть равны между собой, что и показывает приведенный выше пример.
– квадратную матрицу n. Поэтому размеры АВ могут быть равны ВА в том случае, когда m = n, т.е. когда обе матрицы квадратные и имеют один и тот же порядок равный m. При этом указанные произведения матриц могут не иметь ни одного одинакового элемента, полученного в результате суммирования произведений соотвстствующих элементов исходных матриц. Поэтому, если даже существуют оба произведения АВ и ВА и оба они имеют одинаковый порядок, вообще говоря, они не обязательно должны быть равны между собой, что и показывает приведенный выше пример.
Из сказанного не следует, что АВ и ВА всегда должны различаться между собой, в отдельных случаях они могут быть равны. Например, 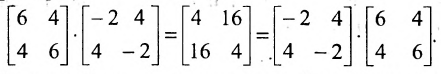
В двух случаях, имеющих особо важное значение, произведение матриц обладает свойством коммутативности:
1) в случае умножения на нулевую матрицу: если 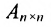 представляет собой квадратную матрицу п-ого порядка, а
представляет собой квадратную матрицу п-ого порядка, а 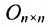 – аналогичную матрицу, все элементы которой составляют нули, тогда
– аналогичную матрицу, все элементы которой составляют нули, тогда
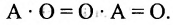
Нулевая матрица выполняет роль нуля в матричной алгебре;
2) в случае умножения на единичную матрицу: если 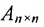 представляет собой квадратную матрицу n-ого порядка, а
представляет собой квадратную матрицу n-ого порядка, а 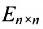 – аналогичную единичную матрицу, то
– аналогичную единичную матрицу, то
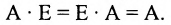
Единичная матрица того же порядка служит единицей в матричной алгебре. Например, 
Отметим, что произведение матрицы на скалярную величину так же коммутативно: 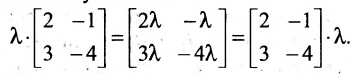
Матрицу А можно умножить саму на себя тогда и только тогда, когда она квадратная. Если n – натуральное число, больше единицы, то 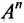 есть произведение n матриц равных А. Для действий со степенями матриц справедливы следующие правила:
есть произведение n матриц равных А. Для действий со степенями матриц справедливы следующие правила: 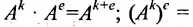
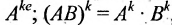 ,если АВ = ВА.
,если АВ = ВА.
Значением многочлена
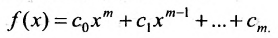
с числовыми коэффициентами 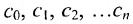 от матрицы А или значением многочлена
от матрицы А или значением многочлена 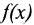 при х = А называется матрица
при х = А называется матрица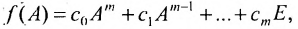
где Е- единичная матрица.
Многочленной матрицей называется прямоугольная (в частности квадратная) матрица А, элементы которой являются многочленами от одной переменной х с числовыми коэффициентами. Матричным многочленом называется выражение вида
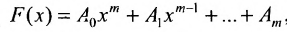
где х- переменное и 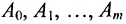 – квадратные матрицы с числовыми элементами одного и того же порядка n. Число n называется порядком многочлена F(x). Если
– квадратные матрицы с числовыми элементами одного и того же порядка n. Число n называется порядком многочлена F(x). Если 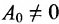 , то число m называется степенью матричного многочлена F{x). Если матрица
, то число m называется степенью матричного многочлена F{x). Если матрица 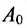 не вырождена, т.е.
не вырождена, т.е. 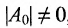 , то матричный многочлен F(x) называется регулярным.
, то матричный многочлен F(x) называется регулярным.
Два матричных многочлена одинакового порядка можно складывать, вычитать и умножать аналогично обычным многочленам с числовыми коэффициентами, с той разницей, что умножение числовых матриц, а потому и матричных многочленов не обязательно коммутативно.
Операцию умножения для матриц можно ввести иначе. Пусть задана матрица размерности 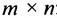 :
: 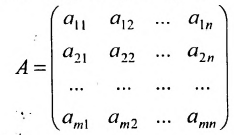
Обозначим столбцы матрицы А следующим образом: 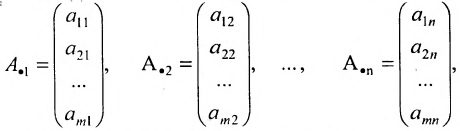
их называют векторами-столбцами; а строки:
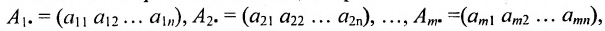
которые называют векторами-строками.
Пример №23
Пусть число трёх типов игрушек, которые нужно изготовить, равно соответственно 20, 30, 40. Определим число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа на них.
Решение:
Составим матрицу А, в которой по строкам укажем число деталей одного вида, необходимых для производства трёх типов игрушек, а по столбцам – число деталей трех видов, необходимых для производства одной игрушки трёх типов:
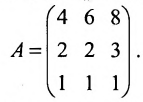
Число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа определим умножением матрицы А на матрицу-столбец, характеризующую число игрушек:

Зная количество деталей, необходимых для производства одной игрушки, можно определить потребность в сырье для производства одной игрушки, если известны нормы расхода сырья для производства одной детали, которые приведены в таблице 3.2.2.

Эти потребности в сырье определяются умножением матриц
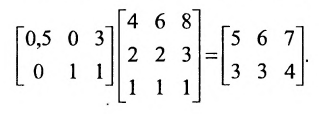
Умножив результат произведения матриц на количество игрушек, определим потребности в сырье для выполнения заказа
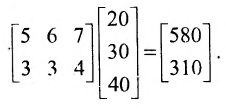
Приведенный пример иллюстрирует простоту решения задачи при помощи умножения матриц.
Пример №24
Предположим, что затраты рабочего времени в часах на каждом рабочем месте и на каждое изделие заданы в таблице 3.2.3. Количество изделий (в штуках) в каждом заказе задано в таблице 3.2.4. Часовая заработная плата (в рублях) на каждом рабочем месте задана в таблице 3.2.5
Решение:
Рассчитаем заработную плату, приходящуюся при производстве различных изделий на каждый заказ. 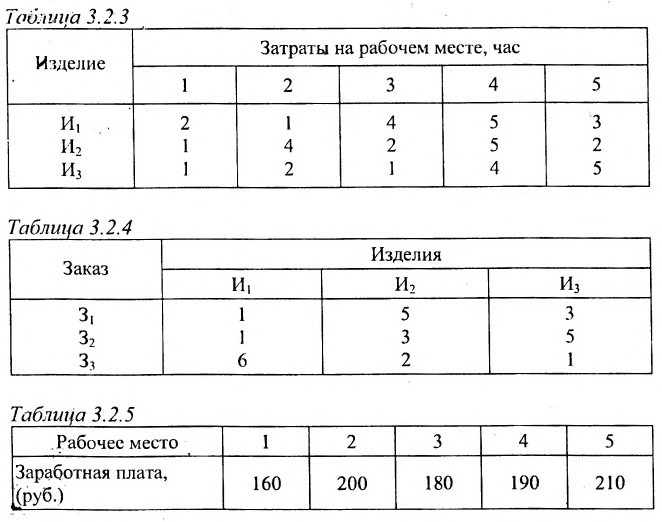
Решение. Введем в рассмотрение следующие матрицы:
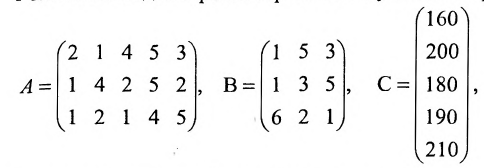 где А – матрица затрат, В – матрица спроса, С – матрица почасовой зарплаты.
где А – матрица затрат, В – матрица спроса, С – матрица почасовой зарплаты.
Так как матрица С задает зависимость между величиной заработной платы и затратами рабочего времени на каждом рабочем месте, а матрица А – между затратами времени на каждом рабочем месте и выпуском изделий, то произведение АС задает линейную зависимость между выпуском одного изделия и величиной заработной платы. Поскольку матрица В определяет количество изделий в каждом заказе, то произведение В(АС) определяет выполнение каждого заказа. Поэтому, вычислив произведение В (АС):
 находим заработную плату, приходящуюся на заказ
находим заработную плату, приходящуюся на заказ 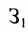 равную 23920 руб., на заказ
равную 23920 руб., на заказ 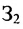 – 23640 руб. и на заказ
– 23640 руб. и на заказ  – 24850 руб.
– 24850 руб.
Блочные матрицы и действия над ними
Для упрощения действий над матрицами больших размеров выполняют переход к матрицам меньших размеров путём разбиения их на клетки горизонтальными и вертикальными прямыми, пересекающими всю матрицу.
Например, проведём в матрице А две горизонтальные и две вертикальные прямые: 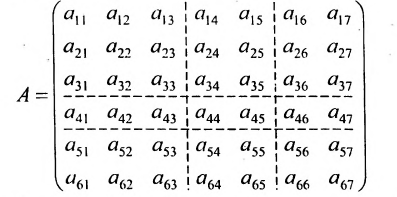
Получим 9 клеток, каждая из которых будет некоторой матрицей. Введём для них обозначения:
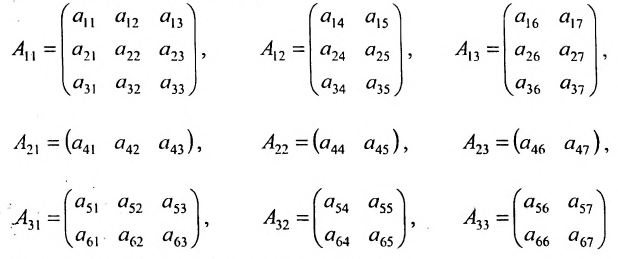
Тогда матрицу А можно записать в виде:
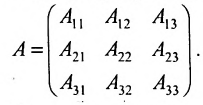
Полученную матрицу называют блочной, или клеточной. Любую матрицу множеством способов можно представить в блочной форме. Особый интерес представляют блочные матрицы, имеющие квадратные диагональные клетки. Например, 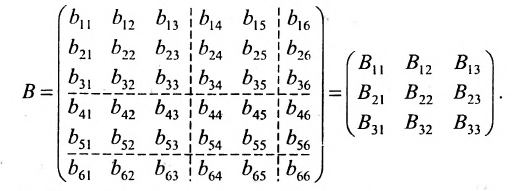
В матрице В клетки 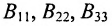 – квадратные матрицы третьего, второго и первого порядка соответственно.
– квадратные матрицы третьего, второго и первого порядка соответственно.
Если у блочных матриц число диагональных клеток одинаково, причём соответственные диагональные клетки имеют один и тот же порядок, то такие матрицы называются конформными.
Блочная матрица, у которой все клетки, кроме стоящих на главной диагонали, являются нуль-матрицами, называется квазидиагональной. Примером квазидиагональной матрицы является матрица
вида: 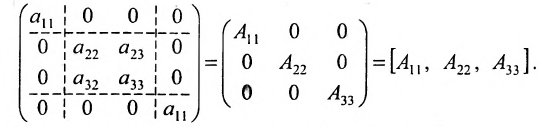 Квазидиагональная матрица обозначается
Квазидиагональная матрица обозначается 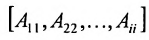 , где
, где
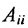 – её диагональные квадратные клетки.
– её диагональные квадратные клетки.
Если к квадратной матрице а добавить снизу матрицу-строку, справа – матрицу-столбец и в правом нижнем углу добавить элемент, то полученная блочная матрица называется окаймлённой.
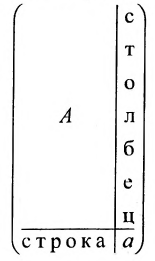
Арифметические операции над блочными матрицами выражаются через операции над клетками матриц. Такое выражение возможно для конформных матриц.
1) Сложение блочных матриц производится аналогично правилу сложения обычных матриц: 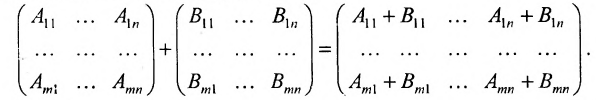 Подчеркнем, что можно складывать только конформные матрицы. В противном случае равенство не имеет смысла.
Подчеркнем, что можно складывать только конформные матрицы. В противном случае равенство не имеет смысла.
2) При умножении блочной матрицы на скаляр все клетки блочной матрицы умножаются на этот скаляр: 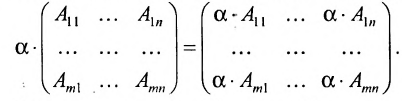
3) Произведение конформных блочных матриц формально совпадает с правилом умножения обычных матриц:
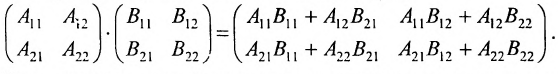
При умножении матриц соответственные диагональные клетки умножаемых матриц должны иметь одинаковый порядок. В противном случае блочные матрицы не будут конформными и их умножать нельзя.
Произведением конформных квазидиагональных матриц является квазидиагональная матрица с той же структурой, причём каждая диагональная клетка произведения является произведением соответствующих диагональных клеток сомножителей:
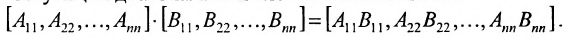
При транспонировании квазидиагональной матрицы получаем квазидиагональную матрицу, диагональные клетки которой являются транспонированными матрицами:
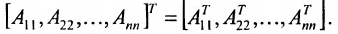
Матрица А, которую одновременной перестановкой строк и столбцов можно привести к блочному виду
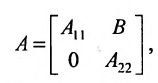
где 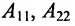 – квадратные блоки, включающие ненулевые элементы; О – блок, состоящий только из нулей; В – блок, элементы которого могут принимать любые значения, называется разложимой матрицей.
– квадратные блоки, включающие ненулевые элементы; О – блок, состоящий только из нулей; В – блок, элементы которого могут принимать любые значения, называется разложимой матрицей.
Матрица неразложима если для неё не существует таких одновременных перестановок строк и столбцов, которые приводили бы сё к разложимой форме.
Оператор суммирования и его свойства
В экономических исследованиях часто употребляются переменные, определенные на дискретных множествах 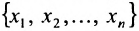
или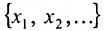 и рассматриваются их суммы. Символом операции
и рассматриваются их суммы. Символом операции
суммирования служит заглавная греческая буква 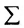 (сигма). Тогда,
(сигма). Тогда,
например, сумму 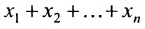 можно записать в видех
можно записать в видех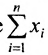 . Числа сточщие под знаком
. Числа сточщие под знаком 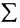 и над ним, называются пределами суммирования и указывают наибольшие и наименьшие значения индекса суммирования, между которыми расположены его промежуточные значения.
и над ним, называются пределами суммирования и указывают наибольшие и наименьшие значения индекса суммирования, между которыми расположены его промежуточные значения.
Для оператора суммирования справедливы следующие тождества:
- 1.
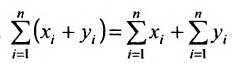
- 2.
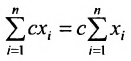
- 3.
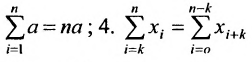 ;
; - 5.
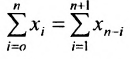
Существует также способ записи операции умножения с помощью прописной греческой буквы «пи» – П : Так, например, произ-ведение пяти множителей можно сокращенно записать:
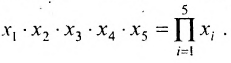
Перестановки
Рассмотрим n целых чисел (элементов) 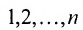 . Их можно располагать в различном порядке. Всевозможные расположения этих чисел называются перестановками. Перестановка
. Их можно располагать в различном порядке. Всевозможные расположения этих чисел называются перестановками. Перестановка 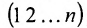 , в которой числа идут в порядке возрастания, называется натуральной. Например, из трех чисел можно составить 6 перестановок: (123), (132), (213), (231), (312), (321). Справедливо следующее утверждение: «Из n чисел можно составить n! перестановок». Символ n! читается юн факториал» и обозначает произведение последовательных натуральных чисел: 0!=1; 1!=1;
, в которой числа идут в порядке возрастания, называется натуральной. Например, из трех чисел можно составить 6 перестановок: (123), (132), (213), (231), (312), (321). Справедливо следующее утверждение: «Из n чисел можно составить n! перестановок». Символ n! читается юн факториал» и обозначает произведение последовательных натуральных чисел: 0!=1; 1!=1; 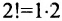 ;
; 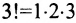 ; …
; … 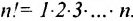 .
.
Назовем беспорядком (или инверсией) в перестановке тот факт, что большее число стоит перед меньшим. Если перестановка имеет четное число инверсий, то она называется четной, в противном случае – нечетной. Обмен местами двух элементов в перестановке называется транспозицией. Например:
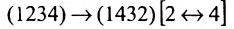
Транспозиция переводит одну перестановку в другую и меняет четность перестановки.
Определение определителя
Рассмотрим квадратную матрицу размерности п и составим из ее элементов таблицу вида

или более компактно: 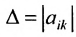 . Каждый элемент
. Каждый элемент 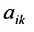 имеет два индекса, первый из которых указывает, какой строке принадлежит элемент, а второй – какому столбцу.
имеет два индекса, первый из которых указывает, какой строке принадлежит элемент, а второй – какому столбцу.
Этой таблице соотнесем число, называемое определителем, вычисляемое по правилу, сформулированному в следующем определении.
Определение 3.6.1. Определителем n-го порядка называется алгебраическая сумма n! членов, каждый из которых представляет собой произведение n элементов 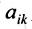 , взятых по одному из каждой
, взятых по одному из каждой
строки и каждого столбца; при этом член определителя берется со знаком «+», если вторые индексы его элементов образуют чётную перестановку, и со знаком «—», если эта перестановка нечетная, а первые индексы образуют натуральную перестановку.
Определитель n-то порядка обозначается в виде таблицы (3.6.1), где горизонтали – строки, а вертикали – столбцы.
Введем величину:
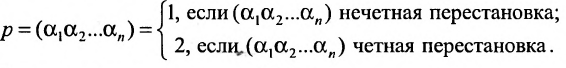
Тогда в силу определения 3.6.1 определитель n-то порядка запишется в виде:
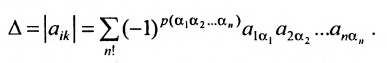
Суммирование распространяется на все перестановки 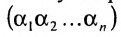 из n чисел 1,2,…,n, что условно обозначили символом n!
из n чисел 1,2,…,n, что условно обозначили символом n!
В частности, определителем второго порядка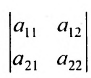 называется алгебраическая сумма двух слагаемых
называется алгебраическая сумма двух слагаемых 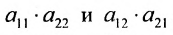 , каждое из которых равно произведению двух элементов. Согласно определению 3.6.1, первое слагаемое имеет знак «+», а второе – знак «-». Следовательно, для нахождения определителя второго порядка, нужно из произведения элементов, стоящих на главной диагонали вычесть произведение элементов стоящих на побочной диагонали:
, каждое из которых равно произведению двух элементов. Согласно определению 3.6.1, первое слагаемое имеет знак «+», а второе – знак «-». Следовательно, для нахождения определителя второго порядка, нужно из произведения элементов, стоящих на главной диагонали вычесть произведение элементов стоящих на побочной диагонали:
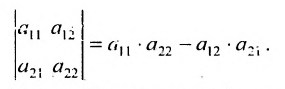
Таким образом, каждой квадратной матрице А можно поставить в соответствие некоторое число, называемое определителем матрицы и обозначаемое 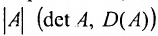 .
.
Свойства определителя n-го порядка
Свойствами, сформулированными ниже, обладают определители любого порядка, в частности второго и третьего порядков.
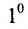 . Величина определителя при его транспонировании (т. е. при замене его строк соответствующими столбцами) не меняется.
. Величина определителя при его транспонировании (т. е. при замене его строк соответствующими столбцами) не меняется.
Доказательство. Рассмотрим определитель 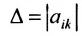 . Протранспонируем его; получим определитель
. Протранспонируем его; получим определитель 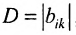 , т. е. элементы строки и i-го столбца определителя
, т. е. элементы строки и i-го столбца определителя 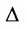 совпадают с элементами из i-й строки и k-го столбца определителя D. Тогда по определению
совпадают с элементами из i-й строки и k-го столбца определителя D. Тогда по определению
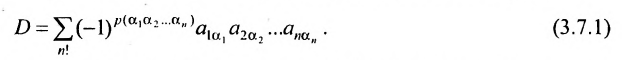
В каждом слагаемом формулы (4.1) переставим сомножители таким образом, чтобы их первые индексы составили натуральную перестановку; вторые индексы образуют произвольную перестановку:
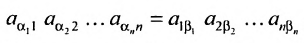
Перестановки 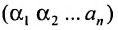 и
и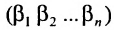 разные, но обладают одинаковой четностью, так как одним и тем же числом транспозиций перестановка
разные, но обладают одинаковой четностью, так как одним и тем же числом транспозиций перестановка 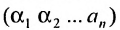 переводится в натуральную, а перестановку
переводится в натуральную, а перестановку 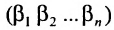 получаем из натуральной. Поэтому
получаем из натуральной. Поэтому 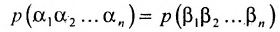 , и равенство (3.7.1) принимает вид:
, и равенство (3.7.1) принимает вид:
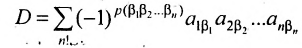
Так как 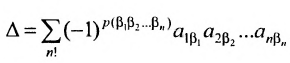 то
то 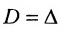 чтo и требовалось доказать.
чтo и требовалось доказать.
Из свойства 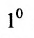 вытекает, что строки и столбцы определителя равноправны. Поэтому любое свойство доказанное для строк, справедливо и для столбцов.
вытекает, что строки и столбцы определителя равноправны. Поэтому любое свойство доказанное для строк, справедливо и для столбцов.
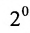 . Если в определителе поменять местами две строки (столбца), то у него изменится только знак, а абсолютная величина останется прежней.
. Если в определителе поменять местами две строки (столбца), то у него изменится только знак, а абсолютная величина останется прежней.
Доказательство. Рассмотрим определитель 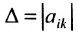 , в котором переставим l-ую и m-ую строки. При этом считаем, что
, в котором переставим l-ую и m-ую строки. При этом считаем, что 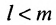 . Получим определитель
. Получим определитель 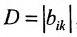 , элементы которого связаны с элементами определителя
, элементы которого связаны с элементами определителя  соотношениями
соотношениями
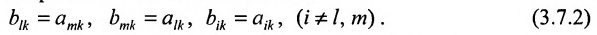
В силу равенств (3.7.2) преобразуем определитель
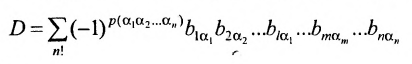
к виду
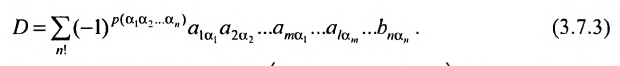
Выполним в перестановке 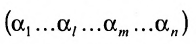 одну транспозицию
одну транспозицию 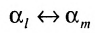 , в результате четность перестановки изменится на противоположную:
, в результате четность перестановки изменится на противоположную:
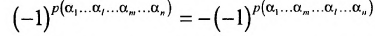
Затем поменяем местами сомножители 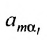 и
и 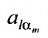 в произведении
в произведении 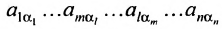 . Произведение при этом не изменится, а равенство (3.7.3) примет вид
. Произведение при этом не изменится, а равенство (3.7.3) примет вид
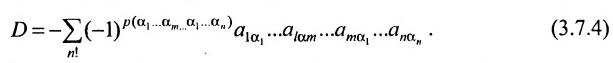
В равенстве (3.7.4) первые индексы элементов образуют натуральную перестановку 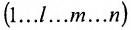 , т. к.
, т. к. 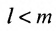 , а перестановка из
, а перестановка из
вторых индексов такая же, как и в выражении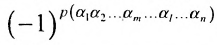 . Поэтому сумма правой части формулы (3.7.4) равна определителю
. Поэтому сумма правой части формулы (3.7.4) равна определителю 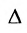 , т. е.
, т. е. 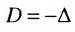 . что и требовалось доказать.
. что и требовалось доказать.
 . Определитель с двумя одинаковыми строками (столбцами) равен нулю.
. Определитель с двумя одинаковыми строками (столбцами) равен нулю.
Доказательство. Так как по условию две строки одинаковы, то их перестановка не меняет величины  определителя. С другой стороны, по свойству
определителя. С другой стороны, по свойству  в результате перестановки знак определителя изменится, т. с.
в результате перестановки знак определителя изменится, т. с. 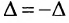 . Следовательно,
. Следовательно, 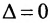 .
.
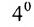 . Если все элементы строки (столбца) содержат общий множитель, то его можно вынести за знак определителя.
. Если все элементы строки (столбца) содержат общий множитель, то его можно вынести за знак определителя.
Доказательство. Пусть в определителе 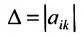 l-тая строка содержит общий множитель, тогда по определению его можно записать в виде:
l-тая строка содержит общий множитель, тогда по определению его можно записать в виде:
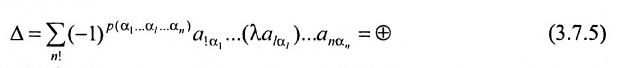
Из (3.7.5) следует, что каждое слагаемое содержит множителем число 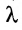 , его можно вынести за знак суммы, т. с. преобразовать
, его можно вынести за знак суммы, т. с. преобразовать
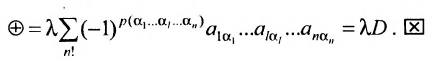
Из свойства  вытекает:
вытекает:
Следствие 3.7.1. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
Действительно, по свойству 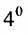 общий множитель у одной из строк, пропорциональной другой, можно вынести за знак определителя. Получим определитель с двумя одинаковыми строками, а в силу свойства
общий множитель у одной из строк, пропорциональной другой, можно вынести за знак определителя. Получим определитель с двумя одинаковыми строками, а в силу свойства 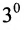 он равен нулю.
он равен нулю.
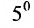 . Если все элементы строки (столбца) являются суммами из одинакового числа слагаемых, то определитель равен сумме определителей, у которых элементами этой строки (столбца) служат отдельные слагаемые.
. Если все элементы строки (столбца) являются суммами из одинакового числа слагаемых, то определитель равен сумме определителей, у которых элементами этой строки (столбца) служат отдельные слагаемые.
Доказательство. Пусть все элементы 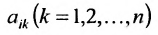 i-той строки определителя
i-той строки определителя  являются суммами из одинакового числа слагаемых:
являются суммами из одинакового числа слагаемых: 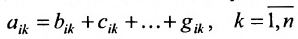 . Тогда определитель имеет вид:
. Тогда определитель имеет вид:
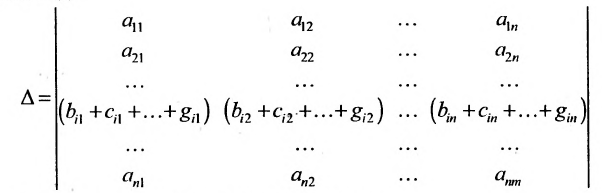
В силу определения его можно записать:
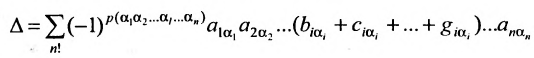
но так как 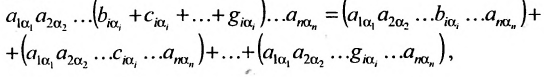
то
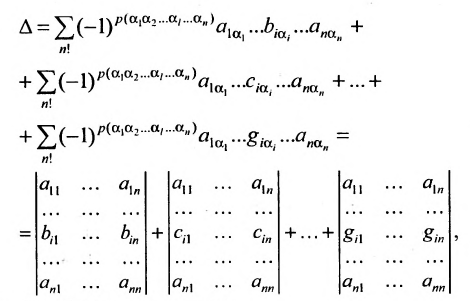
что и требовалось доказать.
Следствие 3.7.2. Величина определителя не изменится, если /с элементам любой его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умножив их предварительно на один и тот же множитель.
Действительно, если мы рассмотрим определитель
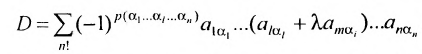 полученный из
полученный из 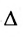 прибавляем к элементам l строки соответствующие элементы m строки, то в силу свойства
прибавляем к элементам l строки соответствующие элементы m строки, то в силу свойства 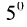 его можно представить в виде суммы двух определителей, т. е.
его можно представить в виде суммы двух определителей, т. е.

так как второе слагаемое равно 0 как определитель с двумя пропорциональными строками.
Миноры и алгебраические дополнения
Определение 3.8.1. Если в определителе n-го порядка вычеркнем i-ую строку и k-ый столбец, на пересечении которых находится элемент 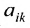 , то полученный определитель (n-1)-го порядка называется минором исходного определителя
, то полученный определитель (n-1)-го порядка называется минором исходного определителя  , соответствующего элементу
, соответствующего элементу 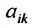 , и обозначается
, и обозначается 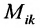 . Например, если
. Например, если
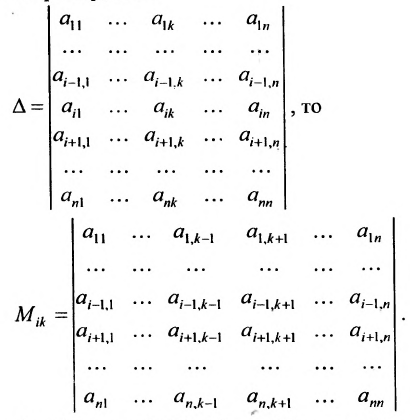
Определение 3.8.1. Минор 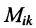 с определенным знаком, зависящим от четности суммы i+k номеров строки и столбца, на пересечении которых находится элемент
с определенным знаком, зависящим от четности суммы i+k номеров строки и столбца, на пересечении которых находится элемент 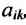 называется алгебраическим дополнением элемента
называется алгебраическим дополнением элемента 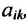 в определителе
в определителе  и обозначается
и обозначается
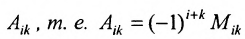 .
.
С помощью алгебраических дополнений определитель порядка п может быть выражен через определители порядка n-1. Этот факт справедлив для определителей имеющих специальную структуру, т. е. имеют место
Лемма 3.8.1. Если в определителе порядка n все элементы последней строки (столбца), кроме элемента, стоящего в правом нижнем углу, равны нулю, то определитель равен произведению этого элемента на соответствующий ему минор.
Лемма 3.8.2. Если в определителе порядка n все элементы какой-либо строки (столбца), кроме одного, равны нулю, то определитель равен произведению этого элемента на его алгебраическое дополнение.
Из сформулированных лемм вытекают следующие теоремы:
Теорема 3.8.1. (теорема разложения). Определитель порядка п равен сумме парных произведений элементов любой строки (столбца) на их алгебраические дополнения: 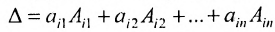 .
.
Доказательство. Так как строки и столбцы равносильны, то достаточно проверить справедливость равенства: 
Представим каждый элемент i-й строки определителя в виде суммы n слагаемых, из которых n-1 слагаемое равно нулю
в виде суммы n слагаемых, из которых n-1 слагаемое равно нулю
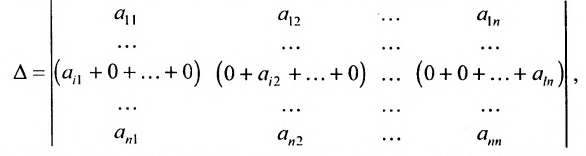
тогда его можно представить в виде суммы определителей (по свойству 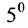 ):
):

Определитель 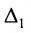 по лемме 2 равен произведению элемента
по лемме 2 равен произведению элемента 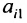 на его алгебраическое дополнение в этом определителе. Но так как определитель
на его алгебраическое дополнение в этом определителе. Но так как определитель 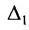 отличается от
отличается от  лишь элементами i-й строки, го это алгебраическое дополнение совпадает с алгебраическим дополнением
лишь элементами i-й строки, го это алгебраическое дополнение совпадает с алгебраическим дополнением 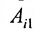 элемента
элемента 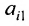 , определителя
, определителя 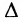 , так как эта строка и столбец будут вычеркнуты, а все остальные элементы определителя
, так как эта строка и столбец будут вычеркнуты, а все остальные элементы определителя 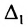 , и
, и 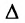 совпадают.
совпадают.
Следовательно,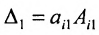 .
.
Аналогично 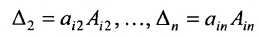 и поэтому (т. к.
и поэтому (т. к. 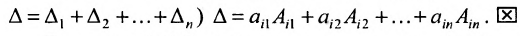
Теорема 3.8.2. (теорема аннулирования). Сумма парных произведений элементов любой строки (столбца) определителя на алгебраические дополнения параллельной строки (столбца) равна нулю:
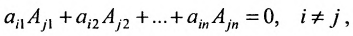 , где i, j – строки определителя
, где i, j – строки определителя 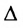 .
.
Вычисление определителей
Укажем некоторые способы вычисления определителей.
1) По теореме 3.8.1 определитель любого порядка п выражается через n определителей (n-1)-го порядка. Применяя эту теорему несколько раз, можно преобразовать исходный определитель к некоторому числу определителей третьего порядка, вычисление которых не представляет труда. Однако для упрощения вычислений целесообразно предварительно преобразовать определитель так, чтобы в одном из его рядов все элементы, кроме одного, обратились в нуль. Тогда данный определитель сведется к определителю более низкого порядка, и т. д.
2) Пользуясь свойствами определителя, приводят его к треугольному виду, когда все элементы, стоящие по одну сторону от главной диагонали, равны нулю. Полученный определитель треугольного вида равен произведению элементов главной диагонали, т. е. 
Если удобнее получить нули по одну сторону от побочной диагонали, то 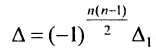 где
где 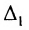 приведен уже к треугольному виду.
приведен уже к треугольному виду.
3) Если определитель  порядка n после разложения по строке или столбцу и после преобразования, выражается через определители того же вида, но более низких порядков, то полученное равенство называется рекуррентным. Вычисляют столько определителей данного вида начальных порядков, сколько их входит в правую часть рекуррентного соотношения. Далее вычисляют определители высших порядков, используя рекуррентные соотношения, до тех пор, пока не удастся заметить общую закономерность для получаемых выражений. Для общего случая доказывают индукцией по п эту закономерность.
порядка n после разложения по строке или столбцу и после преобразования, выражается через определители того же вида, но более низких порядков, то полученное равенство называется рекуррентным. Вычисляют столько определителей данного вида начальных порядков, сколько их входит в правую часть рекуррентного соотношения. Далее вычисляют определители высших порядков, используя рекуррентные соотношения, до тех пор, пока не удастся заметить общую закономерность для получаемых выражений. Для общего случая доказывают индукцией по п эту закономерность.
Определитель квазидиагональной матрицы равен произведению определителей её диагональных клеток:
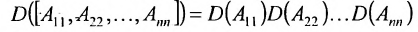 .
.
Определитель второго порядка, согласно определению 3.6.1 равен произведению диагональных элементов минус произведение элементов побочной диагонали. Например,
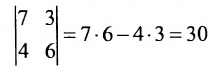 .
.
Определитель третьего порядка по определению 3.6.1. равен алгебраической сумме шести слагаемых. Построение этой суммы можно выполнить по правилу Саррюса. Со знаком “+” и рассматривая произведение элементов определителя, обозначенных на схеме точками
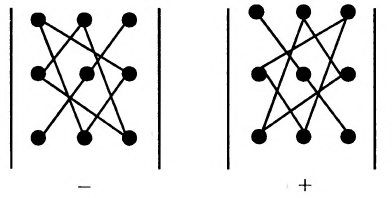
Hстример,
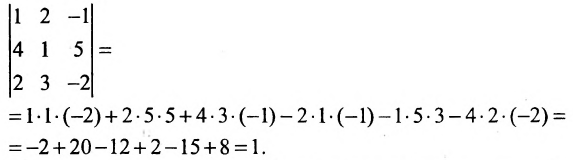
Определители выше третьего порядков вычисляются либо сведением к треугольному виду, либо используя теорему разложения или используя рекуррентную формулу. Например,

(последовательно умножим первую строку на 2; 4; 3 и вычтем получающиеся при этом строки из второй, третьей и четвертой строк)
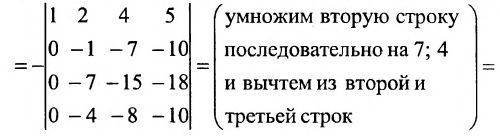

(умножим третью строку на 20/34 и вычтем из четвертой строки; сомножитель четвертой строки 1/34 вынесем за знак определителя; в результате получим определитель верхнетреуголыюго вида, который равен произведению элементов, стоящих на главной диагонали) .
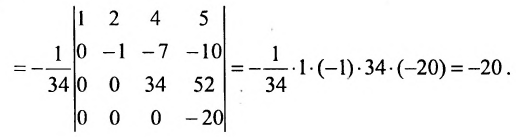
Матрицы и операции над матрицами
Матрицей размера  называется прямоугольная таблица чисел
называется прямоугольная таблица чисел 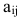
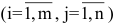 вида
вида 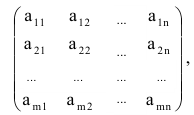 состоящая из m строк и n столбцов. Числа
состоящая из m строк и n столбцов. Числа 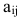 называются элементами матрицы, где i – индекс строки, j – индекс столбца. Обозначение:
называются элементами матрицы, где i – индекс строки, j – индекс столбца. Обозначение: 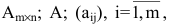
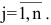
Например, элемент 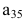 (читается «а три пять») в таблице будет расположен в третьей строке и пятом столбце.
(читается «а три пять») в таблице будет расположен в третьей строке и пятом столбце.
Суммой двух матриц одинакового размера 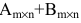 называется матрица
называется матрица 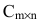 того же порядка, каждый элемент которой равен сумме соответствующих элементов матриц
того же порядка, каждый элемент которой равен сумме соответствующих элементов матриц 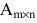 и
и 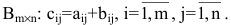
Например,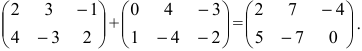
Произведением матрицы 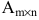 на действительное число
на действительное число 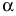 . называется такая матрица
. называется такая матрица 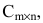 что
что 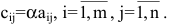
Например,
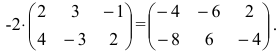 Если количество столбцов первой матрицы (множимой) равно количеству строк второй матрица (множителя), то матрицы называются согласованными.
Если количество столбцов первой матрицы (множимой) равно количеству строк второй матрица (множителя), то матрицы называются согласованными.
Внимание! Умножаются только согласованные матрицы.
Произведением матрицы А размера 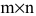 (n столбцов) на матрицу В размера
(n столбцов) на матрицу В размера 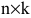 (n строк) называется матрица С размера
(n строк) называется матрица С размера 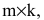 каждый элемент которой
каждый элемент которой 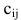 равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-ro столбца матрицы В, т.е.
равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-ro столбца матрицы В, т.е. 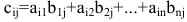 («i-ю строку первой матрицы умножаем на j-й столбец второй матрицы»). Число строк матрицы произведения С равно числу строк матрицы А, а число столбцов матрицы С равно числу столбцов матрицы В.
(«i-ю строку первой матрицы умножаем на j-й столбец второй матрицы»). Число строк матрицы произведения С равно числу строк матрицы А, а число столбцов матрицы С равно числу столбцов матрицы В.
Пример:
Даны матрицы
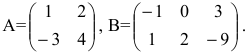
Найти то из произведений АВ, В А, которое существует.
Решение:
Найдем произведение матриц АВ. Оно существует, т.к. количество столбцов матрицы А равно количеству строк матрицы В и равно двум.
Например, элемент произведения матриц с индексом 12 равен по определению сумме произведений элементов 1-й строки матрицы А на соответствующие элементы 2-го столбца матрицы В:
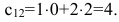
Тогда 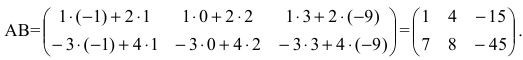
Рассмотрим произведение матриц ВА. Число столбцов матрицы В (n=3) не совпадает с числом строк матрицы А (m=2). Произведение матриц ВА не существует.
Вывод. В общем случае произведение матриц не коммутативно, т.е. не всегда АВ=ВА.
Если АВ=ВА, то матрицы А и В называются перестановочными.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначение: 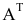 или
или 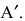
Например, 
- Линейный оператор – свойства и определение
- Многочлен – виды, определение с примерами
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
- Прямая – понятие, виды и её свойства
- Плоскость – определение, виды и правила
- Кривые второго порядка
- Евклидово пространство
Определитель матрицы и его свойства
8 февраля 2018
В этом уроке мы детально рассмотрим несколько ключевые вопросов и определений, благодаря чему вы раз и навсегда разберётесь и с матрицами, и с определителями, и со всеми их свойствами.
Определители — центральное понятие в алгебре матриц. Подобно формулам сокращённого умножения, они будут преследовать вас на протяжении всего курса высшей математики. Поэтому читаем, смотрим и разбираемся досконально.:)
И начнём мы с самого сокровенного — а что такое матрица? И как правильно с ней работать.
Правильная расстановка индексов в матрице
Матрица — это просто таблица, заполненная числами. Нео тут ни при чём.
Одна из ключевых характеристик матрицы — это её размерность, т.е. количество строк и столбцов, из которых она состоит. Обычно говорят, что некая матрица $A$ имеет размер $left[ mtimes n right]$, если в ней имеется $m$ строк и $n$ столбцов. Записывают это так:
[A=left[ mtimes n right]]
Или вот так:
[A=left( {{a}_{ij}} right),quad 1le ile m;quad 1le jle n.]
Бывают и другие обозначения — тут всё зависит от предпочтений лектора/ семинариста/ автора учебника. Но в любом случае со всеми этими $left[ mtimes n right]$ и ${{a}_{ij}}$ возникает одна и та же проблема:
Какой индекс за что отвечает? Сначала идёт номер строки, затем — столбца? Или наоборот?
При чтении лекций и учебников ответ будет казаться очевидным. Но когда на экзамене перед вами — только листик с задачей, можно переволноваться и внезапно запутаться.
Поэтому давайте разберёмся с этим вопросом раз и навсегда. Для начала вспомним обычную систему координат из школьного курса математики:
Помните её? У неё есть начало координат (точка $O=left( 0;0 right)$) оси $x$и $y$, а каждая точка на плоскости однозначно определяется по координатам: $A=left( 1;2 right)$, $B=left( 3;1 right)$ и т.д.
А теперь давайте возьмём эту конструкцию и поставим её рядом с матрицей так, чтобы начало координат находилось в левом верхнем углу. Почему именно там? Да потому что открывая книгу, мы начинаем читать именно с левого верхнего угла страницы — запомнить это легче лёгкого.
Но куда направить оси? Мы направим их так, чтобы вся наша виртуальная «страница» была охвачена этими осями. Правда, для этого придётся повернуть нашу систему координат. Единственно возможный вариант такого расположения:
Теперь всякая клетка матрицы имеет однозначные координаты $x$ и $y$. Например запись ${{a}_{24}}$ означает, что мы обращаемся к элементу с координатами $x=2$ и $y=4$. Размеры матрицы тоже однозначно задаются парой чисел:
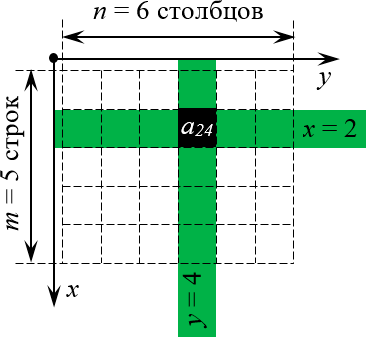
Просто всмотритесь в эту картинку внимательно. Поиграйтесь с координатами (особенно когда будете работать с настоящими матрицами и определителями) — и очень скоро поймёте, что даже в самых сложных теоремах и определениях вы прекрасно понимаете, о чём идёт речь.
Разобрались? Что ж, переходим к первому шагу просветления — геометрическому определению определителя.:)
Геометрическое определение
Прежде всего хотел бы отметить, что определитель существует только для квадратных матриц вида $left[ ntimes n right]$. Определитель — это число, которое cчитается по определённым правилам и является одной из характеристик этой матрицы (есть другие характеристики: ранг, собственные вектора, но об этом в других уроках).
Ну и что это за характеристика? Что он означает? Всё просто:
Определитель квадратной матрицы $A=left[ ntimes n right]$ — это объём $n$-мерного параллелепипеда, который образуется, если рассмотреть строки матрицы в качестве векторов, образующих рёбра этого параллелепипеда.
Например, определитель матрицы размера 2×2 — это просто площадь параллелограмма, а для матрицы 3×3 это уже объём 3-мерного параллелепипеда — того самого, который так бесит всех старшеклассников на уроках стереометрии.
На первый взгляд это определение может показаться совершенно неадекватным. Но давайте не будем спешить с выводами — глянем на примеры. На самом деле всё элементарно, Ватсон:
Задача. Найдите определители матриц:
[left| begin{matrix} 1 & 0 \ 0 & 3 \end{matrix} right|quad left| begin{matrix} 1 & -1 \ 2 & 2 \end{matrix} right|quad left| begin{matrix}2 & 0 & 0 \ 1 & 3 & 0 \ 1 & 1 & 4 \end{matrix} right|]
Решение. Первые два определителя имеют размер 2×2. Значит, это просто площади параллелограммов. Начертим их и посчитаем площадь.
Первый параллелограмм построен на векторах ${{v}_{1}}=left( 1;0 right)$ и ${{v}_{2}}=left( 0;3 right)$:
Определитель 2×2 — это площадь параллелограмма Очевидно, это не просто параллелограмм, а вполне себе прямоугольник. Его площадь равна
[S=1cdot 3=3]
Второй параллелограмм построен на векторах ${{v}_{1}}=left( 1;-1 right)$ и ${{v}_{2}}=left( 2;2 right)$. Ну и что с того? Это тоже прямоугольник:
Ещё один определитель 2×2 Стороны этого прямоугольника (по сути — длины векторов) легко считаются по теореме Пифагора:
[begin{align} & left| {{v}_{1}} right|=sqrt{{{1}^{2}}+{{left( -1 right)}^{2}}}=sqrt{2}; \ & left| {{v}_{2}} right|=sqrt{{{2}^{2}}+{{2}^{2}}}=sqrt{8}=2sqrt{2}; \ & S=left| {{v}_{1}} right|cdot left| {{v}_{2}} right|=sqrt{2}cdot 2sqrt{2}=4. \end{align}]
Осталось разобраться с последним определителем — там уже матрица 3×3. Придётся вспоминать стереометрию:
Определитель 3×3 — это объём параллелепипеда Выглядит мозговыносяще, но по факту достаточно вспомнить формулу объёма параллелепипеда:
[V=Scdot h]
где $S$ — площадь основания (в нашем случае это площадь параллелограмма на плоскости $OXY$), $h$ — высота, проведённая к этому основанию (по сути, $z$-координата вектора ${{v}_{3}}$).
Площадь параллелограмма (мы начертили его отдельно) тоже считается легко:
[begin{align} & S=2cdot 3=6; \ & V=Scdot h=6cdot 4=24. \end{align}]
Вот и всё! Записываем ответы.
Ответ: 3; 4; 24.
Небольшое замечание по поводу системы обозначений. Кому-то наверняка не понравится, что я игнорирую «стрелочки» над векторами. Якобы так можно спутать вектор с точкой или ещё с чем.
Но давайте серьёзно: мы с вами уже взрослые мальчики и девочки, поэтому из контекста прекрасно понимаем, когда речь идёт о векторе, а когда — о точке. Стрелки лишь засоряют повествование, и без того под завязку напичканное математическими формулами.
И ещё. В принципе, ничто не мешает рассмотреть и определитель матрицы 1×1 — такая матрица представляет собой просто одну клетку, а число, записанное в этой клетке, и будет определителем. Но тут есть важное замечание:
В отличие от классического объёма, определитель даст нам так называемый «ориентированный объём», т.е. объём с учётом последовательности рассмотрения векторов-строк.
И если вы хотите получить объём в классическом смысле этого слова, придётся взять модуль определителя, но сейчас не стоит париться об этом — всё равно через несколько секунд мы научимся считать любой определитель с любыми знаками, размерами и т.д.:)
Алгебраическое определение
При всей красоте и наглядности геометрического подхода у него есть серьёзный недостаток: он ничего не говорит нам о том, как этот самый определитель считать.
Поэтому сейчас мы разберём альтернативное определение — алгебраическое. Для этого нам потребуется краткая теоретическая подготовка, зато на выходе мы получим инструмент, позволяющий считать в матрицах что и как угодно.
Правда, там появится новая проблема… но обо всём по порядку.
Перестановки и инверсии
Давайте выпишем в строчку числа от 1 до $n$. Получится что-то типа этого:
[1;2;3;4;5;…;n-1;n]
Теперь (чисто по приколу) поменяем парочку чисел местами. Можно поменять соседние:
[1;3;2;4;5;…;n-1;n]
А можно — не особо соседние:
[n;2;3;4;5;…;n-1;1]
И знаете, что? А ничего! В алгебре эта хрень называется перестановкой. И у неё есть куча свойств.
Определение. Перестановка длины $n$ — строка из $n$ различных чисел, записанных в любой последовательности. Обычно рассматриваются первые $n$ натуральных чисел (т.е. как раз числа 1, 2, …, $n$), а затем их перемешивают для получения нужной перестановки.
Обозначаются перестановки так же, как и векторы — просто буквой и последовательным перечислением своих элементов в скобках. Например: $p=left( 1;3;2 right)$ или $p=left( 2;5;1;4;3 right)$. Буква может быть любой, но пусть будет $p$.:)
Далее для простоты изложения будем работать с перестановками длины 5 — они уже достаточно серьёзны для наблюдения всяких подозрительных эффектов, но ещё не настолько суровы для неокрепшего мозга, как перестановки длины 6 и более. Вот примеры таких перестановок:
[begin{align} & {{p}_{1}}=left( 1;2;3;4;5 right) \ & {{p}_{2}}=left( 1;3;2;5;4 right) \ & {{p}_{3}}=left( 5;4;3;2;1 right) \end{align}]
Естественно, перестановку длины $n$ можно рассматривать как функцию, которая определена на множестве $left{ 1;2;…;n right}$ и биективно отображает это множество на себя же. Возвращаясь к только что записанным перестановкам ${{p}_{1}}$, ${{p}_{2}}$ и ${{p}_{3}}$, мы вполне законно можем написать:
[{{p}_{1}}left( 1 right)=1;{{p}_{2}}left( 3 right)=2;{{p}_{3}}left( 2 right)=4;]
Количество различных перестановок длины $n$ всегда ограничено и равно $n!$ — это легко доказуемый факт из комбинаторики. Например, если мы захотим выписать все перестановки длины 5, то мы весьма заколебёмся, поскольку таких перестановок будет
[n!=5!=1cdot 2cdot 3cdot 4cdot 5=120]
Одной из ключевых характеристик всякой перестановки является количество инверсий в ней.
Определение. Инверсия в перестановке $p=left( {{a}_{1}};{{a}_{2}};…;{{a}_{n}} right)$ — всякая пара $left( {{a}_{i}};{{a}_{j}} right)$ такая, что $i lt j$, но ${{a}_{i}} gt {{a}_{j}}$. Проще говоря, инверсия — это когда большее число стоит левее меньшего (не обязательно соседнего).
Мы будем обозначать через $Nleft( p right)$ количество инверсий в перестановке $p$, но будьте готовы встретиться и с другими обозначениями в разных учебниках и у разных авторов — единых стандартов тут нет. Тема инверсий весьма обширна, и ей будет посвящён отдельный урок. Сейчас же наша задача — просто научиться считать их в реальных задачах.
Например, посчитаем количество инверсий в перестановке $p=left( 1;4;5;3;2 right)$:
[left( 4;3 right);left( 4;2 right);left( 5;3 right);left( 5;2 right);left( 3;2 right).]
Таким образом, $Nleft( p right)=5$. Как видите, ничего страшного в этом нет. Сразу скажу: дальше нас будет интересовать не столько само число $Nleft( p right)$, сколько его чётность/ нечётность. И тут мы плавно переходим к ключевому термину сегодняшнего урока.
Что такое определитель
Пусть дана квадратная матрица $A=left[ ntimes n right]$. Тогда:
Определение. Определитель матрицы $A=left[ ntimes n right]$ — это алгебраическая сумма $n!$ слагаемых, составленных следующим образом. Каждое слагаемое — это произведение $n$ элементов матрицы, взятых по одному из каждой строки и каждого столбца, умноженное на (−1) в степени количество инверсий:
[left| A right|=sumlimits_{n!}{{{left( -1 right)}^{Nleft( p right)}}cdot {{a}_{1;pleft( 1 right)}}cdot {{a}_{2;pleft( 2 right)}}cdot …cdot {{a}_{n;pleft( n right)}}}]
Принципиальным моментом при выборе множителей для каждого слагаемого в определителе является тот факт, что никакие два множителя не стоят в одной строчке или в одном столбце.
Благодаря этому можно без ограничения общности считать, что индексы $i$ множителей ${{a}_{i;j}}$ «пробегают» значения 1, …, $n$, а индексы $j$ являются некоторой перестановкой от первых:
[j=pleft( i right),quad i=1,2,…,n]
А когда есть перестановка $p$, мы легко посчитаем инверсии $Nleft( p right)$ — и очередное слагаемое определителя готово.
Естественно, никто не запрещает поменять местами множители в каком-либо слагаемом (или во всех сразу — чего мелочиться-то?), и тогда первые индексы тоже будут представлять собой некоторую перестановку. Но в итоге ничего не поменяется: суммарное количество инверсий в индексах $i$ и $j$ сохраняет чётность при подобных извращениях, что вполне соответствует старому-доброму правилу:
От перестановки множителей произведение чисел не меняется.
Вот только не надо приплетать это правило к умножению матриц — в отличие от умножения чисел, оно не коммутативно. Но это я отвлёкся.:)
Матрица 2×2
Вообще-то можно рассмотреть и матрицу 1×1 — это будет одна клетка, и её определитель, как нетрудно догадаться, равен числу, записанному в этой клетке. Ничего интересного.
Поэтому давайте рассмотрим квадратную матрицу размером 2×2:
[left[ begin{matrix} {{a}_{11}} & {{a}_{12}} \ {{a}_{21}} & {{a}_{22}} \end{matrix} right]]
Поскольку количество строк в ней $n=2$, то определитель будет содержать $n!=2!=1cdot 2=2$ слагаемых. Выпишем их:
[begin{align} & {{left( -1 right)}^{Nleft( 1;2 right)}}cdot {{a}_{11}}cdot {{a}_{22}}={{left( -1 right)}^{0}}cdot {{a}_{11}}cdot {{a}_{22}}={{a}_{11}}{{a}_{22}}; \ & {{left( -1 right)}^{Nleft( 2;1 right)}}cdot {{a}_{12}}cdot {{a}_{21}}={{left( -1 right)}^{1}}cdot {{a}_{12}}cdot {{a}_{21}}={{a}_{12}}{{a}_{21}}. \end{align}]
Очевидно, что в перестановке $left( 1;2 right)$, состоящей из двух элементов, нет инверсий, поэтому $Nleft( 1;2 right)=0$. А вот в перестановке $left( 2;1 right)$ одна инверсия имеется (собственно, 2 < 1), поэтому $Nleft( 2;1 right)=1.$
Итого универсальная формула вычисления определителя для матрицы 2×2 выглядит так:
[left| begin{matrix} {{a}_{11}} & {{a}_{12}} \ {{a}_{21}} & {{a}_{22}} \end{matrix} right|={{a}_{11}}{{a}_{22}}-{{a}_{12}}{{a}_{21}}]
Графически это можно представить как произведение элементов, стоящих на главной диагонали, минус произведение элементов на побочной:
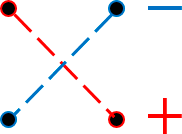
Рассмотрим пару примеров:
Задача. Вычислите определитель:
[left| begin{matrix} 5 & 6 \ 8 & 9 \end{matrix} right|;quad left| begin{matrix} 7 & 12 \ 14 & 1 \end{matrix} right|.]
Решение. Всё считается в одну строчку. Первая матрица:
[5cdot 9-8cdot 6=45-48=-3]
И вторая:
[7cdot 1-14cdot 12=7-168=-161]
Ответ: −3; −161.
Впрочем, это было слишком просто. Давайте рассмотрим матрицы 3×3 — там уже интересно.
Матрица 3×3
Теперь рассмотрим квадратную матрицу размера 3×3:
[left[ begin{matrix} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} \ {{a}_{21}} & {{a}_{22}} & {{a}_{23}} \ {{a}_{31}} & {{a}_{32}} & {{a}_{33}} \end{matrix} right]]
При вычислении её определителя мы получим $3!=1cdot 2cdot 3=6$ слагаемых — ещё не слишком много для паники, но уже достаточно, чтобы начать искать какие-то закономерности. Для начала выпишем все перестановки из трёх элементов и посчитаем инверсии в каждой из них:
[begin{align} & {{p}_{1}}=left( 1;2;3 right)Rightarrow Nleft( {{p}_{1}} right)=Nleft( 1;2;3 right)=0; \ & {{p}_{2}}=left( 1;3;2 right)Rightarrow Nleft( {{p}_{2}} right)=Nleft( 1;3;2 right)=1; \ & {{p}_{3}}=left( 2;1;3 right)Rightarrow Nleft( {{p}_{3}} right)=Nleft( 2;1;3 right)=1; \ & {{p}_{4}}=left( 2;3;1 right)Rightarrow Nleft( {{p}_{4}} right)=Nleft( 2;3;1 right)=2; \ & {{p}_{5}}=left( 3;1;2 right)Rightarrow Nleft( {{p}_{5}} right)=Nleft( 3;1;2 right)=2; \ & {{p}_{6}}=left( 3;2;1 right)Rightarrow Nleft( {{p}_{6}} right)=Nleft( 3;2;1 right)=3. \end{align}]
Как и предполагалось, всего выписано 6 перестановок ${{p}_{1}}$, … ${{p}_{6}}$ (естественно, можно было бы выписать их в другой последовательности — суть от этого не изменится), а количество инверсий в них меняется от 0 до 3.
В общем, у нас будет три слагаемых с «плюсом» (там, где $Nleft( p right)$ — чётное) и ещё три с «минусом». А в целом определитель будет считаться по формуле:
[left| begin{matrix} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} \ {{a}_{21}} & {{a}_{22}} & {{a}_{23}} \ {{a}_{31}} & {{a}_{32}} & {{a}_{33}} \end{matrix} right|=begin{matrix} {{a}_{11}}{{a}_{22}}{{a}_{33}}+{{a}_{12}}{{a}_{23}}{{a}_{31}}+{{a}_{13}}{{a}_{21}}{{a}_{32}}- \ -{{a}_{13}}{{a}_{22}}{{a}_{31}}-{{a}_{12}}{{a}_{21}}{{a}_{33}}-{{a}_{11}}{{a}_{23}}{{a}_{32}} \end{matrix}]
Вот только не надо сейчас садиться и яростно зубрить все эти индексы! Вместо непонятных цифр лучше запомните следующее мнемоническое правило:
Правило треугольника. Для нахождения определителя матрицы 3×3 нужно сложить три произведения элементов, стоящих на главной диагонали и в вершинах равнобедренных треугольников со стороной, параллельной этой диагонали, а затем вычесть такие же три произведения, но на побочной диагонали. Схематически это выглядит так:
Определитель матрицы 3×3: правило треугольников
Именно эти треугольники (или пентаграммы — кому как больше нравится) любят рисовать во всяких учебниках и методичках по алгебре. Впрочем, не будем о грустном. Давайте лучше посчитаем один такой определитель — для разминки перед настоящей жестью.:)
Задача. Вычислите определитель:
[left| begin{matrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 1 \end{matrix} right|]
Решение. Работаем по правилу треугольников. Сначала посчитаем три слагаемых, составленных из элементов на главной диагонали и параллельно ей:
[begin{align} & 1cdot 5cdot 1+2cdot 6cdot 7+3cdot 4cdot 8= \ & =5+84+96=185 \end{align}]
Теперь разбираемся с побочной диагональю:
[begin{align} & 3cdot 5cdot 7+2cdot 4cdot 1+1cdot 6cdot 8= \ & =105+8+48=161 \end{align}]
Осталось лишь вычесть из первого числа второе — и мы получим ответ:
[185-161=24]
Вот и всё!
Ответ: 24.
Тем не менее, определители матриц 3×3 — это ещё не вершина мастерства. Самое интересное ждёт нас дальше.:)
Общая схема вычисления определителей
Как мы знаем, с ростом размерности матрицы $n$ количество слагаемых в определителе составляет $n!$ и быстро растёт. Всё-таки факториал — это вам не хрен собачий довольно быстро растущая функция.
Уже для матриц 4×4 считать определители напролом (т.е. через перестановки) становится как-то не оч. Про 5×5 и более вообще молчу. Поэтому к делу подключаются некоторые свойства определителя, но для их понимания нужна небольшая теоретическая подготовка.
Готовы? Поехали!
Что такое минор матрицы
Пусть дана произвольная матрица $A=left[ mtimes n right]$. Заметьте: не обязательно квадратная. В отличие от определителей, миноры — это такие няшки, которые существуют не только в суровых квадратных матрицах. Выберем в этой матрице несколько (например, $k$) строк и столбцов, причём $1le kle m$ и $1le kle n$. Тогда:
Определение. Минор порядка $k$ — определитель квадратной матрицы, возникающей на пересечении выбранных $k$ столбцов и строк. Также минором мы будем называть и саму эту новую матрицу.
Обозначается такой минор ${{M}_{k}}$. Естественно, у одной матрицы может быть целая куча миноров порядка $k$. Вот пример минора порядка 2 для матрицы $left[ 5times 6 right]$:
Выбор $k = 2$ столбцов и строк для формирования минора
Совершенно необязательно, чтобы выбранные строки и столбцы стояли рядом, как в рассмотренном примере. Главное, чтобы количество выбранных строк и столбцов было одинаковым (это и есть число $k$).
Есть и другое определение. Возможно, кому-то оно больше придётся по душе:
Определение. Пусть дана прямоугольная матрица $A=left[ mtimes n right]$. Если после вычеркивания в ней одного или нескольких столбцов и одной или нескольких строк образуется квадратная матрица размера $left[ ktimes k right]$, то её определитель — это и есть минор ${{M}_{k}}$. Саму матрицу мы тоже иногда будем называть минором — это будет ясно из контекста.
Как говорил мой кот, иногда лучше один раз навернуться с 11-го этажа есть корм, чем мяукать, сидя на балконе.
Пример. Пусть дана матрица
[A=left[ begin{matrix} begin{matrix} 1 \ 2 \ 3 \end{matrix} & begin{matrix} 7 \ 4 \ 0 \end{matrix} & begin{matrix} 9 \ 5 \ 6 \end{matrix} & begin{matrix} 0 \ 3 \ 1 \end{matrix} \end{matrix} right]]
Выбирая строку 1 и столбец 2, получаем минор первого порядка:
[{{M}_{1}}=left| 7 right|=7]
Выбирая строки 2, 3 и столбцы 3, 4, получаем минор второго порядка:
[{{M}_{2}}=left| begin{matrix} 5 & 3 \ 6 & 1 \end{matrix} right|=5-18=-13]
А если выбрать все три строки, а также столбцы 1, 2, 4, будет минор третьего порядка:
[{{M}_{3}}=left| begin{matrix} 1 & 7 & 0 \ 2 & 4 & 3 \ 3 & 0 & 1 \end{matrix} right|]
Считать этот определитель мне уже в лом. Но он равен 53.:)
Читателю не составит труда найти и другие миноры порядков 1, 2 или 3. Поэтому идём дальше.
Алгебраические дополнения
«Ну ok, и что дают нам эти миньоны миноры?» — наверняка спросите вы. Сами по себе — ничего. Но в квадратных матрицах у каждого минора появляется «компаньон» — дополнительный минор, а также алгебраическое дополнение. И вместе эти два ушлёпка позволят нам щёлкать определители как орешки.
Определение. Пусть дана квадратная матрица $A=left[ ntimes n right]$, в которой выбран минор ${{M}_{k}}$. Тогда дополнительный минор для минора ${{M}_{k}}$ — это кусок исходной матрицы $A$, который останется при вычёркивании всех строк и столбцов, задействованных при составлении минора ${{M}_{k}}$:
Дополнительный минор к минору ${{M}_{2}}$ Уточним один момент: дополнительный минор — это не просто «кусок матрицы», а определитель этого куска.
Обозначаются дополнительные миноры с помощью «звёздочки»: $M_{k}^{*}$:
[M_{k}^{*}=left| Anabla {{M}_{k}} right|]
где операция $Anabla {{M}_{k}}$ буквально означает «вычеркнуть из $A$ строки и столбцы, входящие в ${{M}_{k}}$». Эта операция не является общепринятой в математике — я её сам только что придумал для красоты повествования.:)
Дополнительные миноры редко используются сами по себе. Они являются частью более сложной конструкции — алгебраического дополнения.
Определение. Алгебраическое дополнение минора ${{M}_{k}}$ — это дополнительный минор $M_{k}^{*}$, умноженный на величину ${{left( -1 right)}^{S}}$, где $S$ — сумма номеров всех строк и столбцов, задействованных в исходном миноре ${{M}_{k}}$.
Как правило, алгебраическое дополнение минора ${{M}_{k}}$ обозначается через ${{A}_{k}}$. Поэтому:
[{{A}_{k}}={{left( -1 right)}^{S}}cdot M_{k}^{*}]
Сложно? На первый взгляд — да. Но это не точно. Потому что на самом деле всё легко. Рассмотрим пример:
Пример. Дана матрица 4×4:
[A=left[ begin{matrix} 1 & 2 & 3 & 4 \ 5 & 6 & 7 & 8 \ 9 & 10 & 11 & 12 \ 13 & 14 & 15 & 16 \end{matrix} right]]
Выберем минор второго порядка
[{{M}_{2}}=left| begin{matrix} 3 & 4 \ 15 & 16 \end{matrix} right|]
Капитан Очевидность как бы намекает нам, что при составлении этого минора были задействованы строки 1 и 4, а также столбцы 3 и 4. Вычёркиваем их — получим дополнительный минор:
[M_{2}^{*}=left| begin{matrix} 5 & 6 \ 9 & 10 \end{matrix} right|=50-54=-4]
Осталось найти число $S$ и получить алгебраическое дополнение. Поскольку мы знаем номера задействованных строк (1 и 4) и столбцов (3 и 4), всё просто:
[begin{align} & S=1+4+3+4=12; \ & {{A}_{2}}={{left( -1 right)}^{S}}cdot M_{2}^{*}={{left( -1 right)}^{12}}cdot left( -4 right)=-4end{align}]
Ответ: ${{A}_{2}}=-4$
Вот и всё! По сути, всё различие между дополнительным минором и алгебраическим дополнением — только в минусе спереди, да и то не всегда.
Наша задача сейчас — научиться быстро считать алгебраические дополнения, потому что они являются составной частью «Теоремы, Которую Нельзя Называть». Но мы всё же назовём. Встречайте:
Теорема Лапласа
И вот мы пришли к тому, зачем, собственно, все эти миноры и алгебраические дополнения были нужны.
Теорема Лапласа о разложении определителя. Пусть в матрице размера $left[ ntimes n right]$ выбрано $k$ строк (столбцов), причём $1le kle n-1$. Тогда определитель этой матрицы равен сумме всех произведений миноров порядка $k$, содержащихся в выбранных строках (столбцах), на их алгебраические дополнения:
[left| A right|=sum{{{M}_{k}}cdot {{A}_{k}}}]
Причём таких слагаемых будет ровно $C_{n}^{k}$.
Ладно, ладно: про $C_{n}^{k}$ — это я уже понтуюсь, в оригинальной теореме Лапласа ничего такого не было. Но комбинаторику никто не отменял, и буквально беглый взгляд на условие позволит вам самостоятельно убедиться, что слагаемых будет именно столько.:)
Мы не будем её доказывать, хоть это и не представляет особой трудности — все выкладки сводятся к старым-добрым перестановкам и чётности/ нечётности инверсий. Тем не менее, доказательство будет представлено в отдельном параграфе, а сегодня у нас сугубо практический урок.
Поэтому переходим к частному случаю этой теоремы, когда миноры представляют собой отдельные клетки матрицы.
Разложение определителя по строке и столбцу
То, о чём сейчас пойдёт речь — как раз и есть основной инструмент работы с определителями, ради которого затевались вся эта дичь с перестановками, минорами и алгебраическими дополнениями.
Читайте и наслаждайтесь:
Следствие из Теоремы Лапласа (разложение определителя по строке/столбцу). Пусть в матрице размера $left[ ntimes n right]$ выбрана одна строка. Минорами в этой строке будут $n$ отдельных клеток:
[{{M}_{1}}={{a}_{ij}},quad j=1,…,n]
Дополнительные миноры тоже легко считаются: просто берём исходную матрицу и вычёркиваем строку и столбец, содержащие ${{a}_{ij}}$. Назовём такие миноры $M_{ij}^{*}$.
Для алгебраического дополнения ещё нужно число $S$, но в случае с минором порядка 1 это просто сумма «координат» клетки ${{a}_{ij}}$:
[S=i+j]
И тогда исходный определитель можно расписать через ${{a}_{ij}}$ и $M_{ij}^{*}$ согласно теореме Лапласа:
[left| A right|=sumlimits_{j=1}^{n}{{{a}_{ij}}cdot {{left( -1 right)}^{i+j}}cdot {{M}_{ij}}}]
Это и есть формула разложения определителя по строке. Но то же верно и для столбцов.
Из этого следствия можно сразу сформулировать несколько выводов:
- Эта схема одинаково хорошо работает как для строк, так и для столбцов. На самом деле чаще всего разложение будет идти именно по столбцам, нежели по строкам.
- Количество слагаемых в разложении всегда ровно $n$. Это существенно меньше $C_{n}^{k}$ и уж тем более $n!$.
- Вместо одного определителя $left[ ntimes n right]$ придётся считать несколько определителей размера на единицу меньше: $left[ left( n-1 right)times left( n-1 right) right]$.
Последний факт особенно важен. Например, вместо зверского определителя 4×4 теперь достаточно будет посчитать несколько определителей 3×3 — с ними мы уж как-нибудь справимся.:)
Что ж, попробуем посчитать одну такую задачку?
Задача. Найдите определитель:
[left| begin{matrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 9 \end{matrix} right|]
Решение. Разложим этот определитель по первой строке:
[begin{align} left| A right|=1cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} 5 & 6 \ 8 & 9 \end{matrix} right|+ & \ 2cdot {{left( -1 right)}^{1+2}}cdot left| begin{matrix} 4 & 6 \ 7 & 9 \end{matrix} right|+ & \ 3cdot {{left( -1 right)}^{1+3}}cdot left| begin{matrix} 4 & 5 \ 7 & 8 \end{matrix} right|= & \end{align}]
[begin{align} & =1cdot left( 45-48 right)-2cdot left( 36-42 right)+3cdot left( 32-35 right)= \ & =1cdot left( -3 right)-2cdot left( -6 right)+3cdot left( -3 right)=0. \end{align}]
Ответ: 0.
Задача. Найдите определитель:
[left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|]
Решение. Для разнообразия давайте в этот раз работать со столбцами. Например, в последнем столбце присутствуют сразу два нуля — очевидно, это значительно сократит вычисления. Сейчас увидите почему.
Итак, раскладываем определитель по четвёртому столбцу:
[begin{align} left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|=0cdot {{left( -1 right)}^{1+4}}cdot left| begin{matrix} 1 & 0 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|+ & \ +1cdot {{left( -1 right)}^{2+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|+ & \ +1cdot {{left( -1 right)}^{3+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 1 \end{matrix} right|+ & \ +0cdot {{left( -1 right)}^{4+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right| & \end{align}]
И тут — о, чудо! — два слагаемых сразу улетают коту под хвост, поскольку в них есть множитель «0». Остаётся ещё два определителя 3×3, с которыми мы легко разберёмся:
[begin{align} & left| begin{matrix} 0 & 1 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|=0+0+1-1-1-0=-1; \ & left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 1 \end{matrix} right|=0+1+1-0-0-1=1. \end{align}]
Возвращаемся к исходнику и находим ответ:
[left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|=1cdot left( -1 right)+left( -1 right)cdot 1=-2]
Ну вот и всё. И никаких 4! = 24 слагаемых считать не пришлось.:)
Ответ: −2
Основные свойства определителя
В последней задаче мы видели, как наличие нулей в строках (столбцах) матрицы резко упрощает разложение определителя и вообще все вычисления. Возникает естественный вопрос: а нельзя ли сделать так, чтобы эти нули появились даже в той матрице, где их изначально не было?
Ответ однозначен: можно. И здесь нам на помощь приходят свойства определителя:
- Если поменять две строчки (столбца) местами, определитель поменяет знак;
- Если одну строку (столбец) умножить на число $k$, то весь определитель тоже умножится на число $k$;
- Если взять одну строку и прибавить (вычесть) её сколько угодно раз из другой, определитель не изменится;
- Если две строки определителя одинаковы, либо пропорциональны, либо одна из строк заполнена нулями, то весь определитель равен нулю;
- Все указанные выше свойства верны и для столбцов.
- При транспонировании матрицы определитель не меняется;
- Определитель произведения матриц равен произведению определителей.
Особую ценность представляет третье свойство: мы можем вычитать из одной строки (столбца) другую до тех пор, пока в нужных местах не появятся нули.
Чаще всего расчёты сводится к тому, чтобы «обнулить» весь столбец везде, кроме одного элемента, а затем разложить определитель по этому столбцу, получив матрицу размером на 1 меньше.
Давайте посмотрим, как это работает на практике:
Задача. Найдите определитель:
[left| begin{matrix} 1 & 2 & 3 & 4 \ 4 & 1 & 2 & 3 \ 3 & 4 & 1 & 2 \ 2 & 3 & 4 & 1 \end{matrix} right|]
Решение. Нулей тут как бы вообще не наблюдается, поэтому можно «долбить» по любой строке или столбцу — объём вычислений будет примерно одинаковым. Давайте не будем мелочиться и «обнулим» первый столбец: в нём уже есть клетка с единицей, поэтому просто возьмём первую строчку и вычтем её 4 раза из второй, 3 раза из третьей и 2 раза из последней.
В результате мы получим новую матрицу, но её определитель будет тем же:
[begin{matrix} left| begin{matrix} 1 & 2 & 3 & 4 \ 4 & 1 & 2 & 3 \ 3 & 4 & 1 & 2 \ 2 & 3 & 4 & 1 \end{matrix} right|begin{matrix} downarrow \ -4 \ -3 \ -2 \end{matrix}= \ =left| begin{matrix} 1 & 2 & 3 & 4 \ 4-4cdot 1 & 1-4cdot 2 & 2-4cdot 3 & 3-4cdot 4 \ 3-3cdot 1 & 4-3cdot 2 & 1-3cdot 3 & 2-3cdot 4 \ 2-2cdot 1 & 3-2cdot 2 & 4-2cdot 3 & 1-2cdot 4 \end{matrix} right|= \ =left| begin{matrix} 1 & 2 & 3 & 4 \ 0 & -7 & -10 & -13 \ 0 & -2 & -8 & -10 \ 0 & -1 & -2 & -7 \end{matrix} right| \end{matrix}]
Теперь с невозмутимостью Пятачка раскладываем этот определитель по первому столбцу:
[begin{matrix} 1cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} -7 & -10 & -13 \ -2 & -8 & -10 \ -1 & -2 & -7 \end{matrix} right|+0cdot {{left( -1 right)}^{2+1}}cdot left| … right|+ \ +0cdot {{left( -1 right)}^{3+1}}cdot left| … right|+0cdot {{left( -1 right)}^{4+1}}cdot left| … right| \end{matrix}]
Понятно, что «выживет» только первое слагаемое — в остальных я даже определители не выписывал, поскольку они всё равно умножаются на ноль. Коэффициент перед определителем равен единице, т.е. его можно не записывать.
Зато можно вынести «минусы» из всех трёх строк определителя. По сути, мы трижды вынесли множитель (−1):
[left| begin{matrix} -7 & -10 & -13 \ -2 & -8 & -10 \ -1 & -2 & -7 \end{matrix} right|=cdot left| begin{matrix} 7 & 10 & 13 \ 2 & 8 & 10 \ 1 & 2 & 7 \end{matrix} right|]
Получили мелкий определитель 3×3, который уже можно посчитать по правилу треугольников. Но мы попробуем разложить и его по первому столбцу — благо в последней строчке гордо стоит единица:
[begin{align} & left( -1 right)cdot left| begin{matrix} 7 & 10 & 13 \ 2 & 8 & 10 \ 1 & 2 & 7 \end{matrix} right|begin{matrix} -7 \ -2 \ uparrow \end{matrix}=left( -1 right)cdot left| begin{matrix} 0 & -4 & -36 \ 0 & 4 & -4 \ 1 & 2 & 7 \end{matrix} right|= \ & =cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right|=left( -1 right)cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right| \end{align}]
Можно, конечно, ещё поприкалываться и разложить матрицу 2×2 по строке (столбцу), но мы же с вами адекватны, поэтому просто посчитаем ответ:
[left( -1 right)cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right|=left( -1 right)cdot left( 16+144 right)=-160]
Вот так и разбиваются мечты. Всего-то −160 в ответе.:)
Ответ: −160.
Парочка замечаний перед тем, как мы перейдём к последней задаче:
- Исходная матрица была симметрична относительно побочной диагонали. Все миноры в разложении тоже симметричны относительно той же побочной диагонали.
- Строго говоря, мы могли вообще ничего не раскладывать, а просто привести матрицу к верхнетреугольному виду, когда под главной диагональю стоят сплошные нули. Тогда (в точном соответствии с геометрической интерпретацией, кстати) определитель равен произведению ${{a}_{ii}}$ — чисел на главной диагонали.
Идём дальше. Последняя задача в сегодняшнем уроке.
Задача. Найдите определитель:
[left| begin{matrix} 1 & 1 & 1 & 1 \ 2 & 4 & 8 & 16 \ 3 & 9 & 27 & 81 \ 5 & 25 & 125 & 625 \end{matrix} right|]
Решение. Ну, тут первая строка прямо-таки напрашивается на «обнуление». Берём первый столбец и вычитаем ровно один раз из всех остальных:
[begin{align} & left| begin{matrix} 1 & 1 & 1 & 1 \ 2 & 4 & 8 & 16 \ 3 & 9 & 27 & 81 \ 5 & 25 & 125 & 625 \end{matrix} right|= \ & =left| begin{matrix} 1 & 1-1 & 1-1 & 1-1 \ 2 & 4-2 & 8-2 & 16-2 \ 3 & 9-3 & 27-3 & 81-3 \ 5 & 25-5 & 125-5 & 625-5 \end{matrix} right|= \ & =left| begin{matrix} 1 & 0 & 0 & 0 \ 2 & 2 & 6 & 14 \ 3 & 6 & 24 & 78 \ 5 & 20 & 120 & 620 \end{matrix} right| \end{align}]
Раскладываем по первой строке, а затем выносим общие множители из оставшихся строк:
[cdot left| begin{matrix} 2 & 6 & 14 \ 6 & 24 & 78 \ 20 & 120 & 620 \end{matrix} right|=cdot left| begin{matrix} 1 & 3 & 7 \ 1 & 4 & 13 \ 1 & 6 & 31 \end{matrix} right|]
Снова наблюдаем «красивые» числа, но уже в первом столбце — раскладываем определитель по нему:
[begin{align} & 240cdot left| begin{matrix} 1 & 3 & 7 \ 1 & 4 & 13 \ 1 & 6 & 31 \end{matrix} right|begin{matrix} downarrow \ -1 \ -1 \end{matrix}=240cdot left| begin{matrix} 1 & 3 & 7 \ 0 & 1 & 6 \ 0 & 3 & 24 \end{matrix} right|= \ & =240cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} 1 & 6 \ 3 & 24 \end{matrix} right|= \ & =240cdot 1cdot left( 24-18 right)=1440 \end{align}]
Порядок. Задача решена.
Ответ: 1440
Всё. Хорош читать этот бред.:)
Смотрите также:
- Обратная матрица

- Умножение матриц

- Геометрическая вероятность

- Решение задач B12: №448—455

- Задачи на проценты: формула, упрощающая вычисления

- Задача B4 про три дороги — стандартная задача на движение

Часто в ВУЗе попадаются задачи по высшей математики, в которых необходимо вычислить определитель матрицы. К слову, определитель может быть только в квадратных матрицах. Ниже рассмотрим основные определения, какими свойствами обладает определитель и как его правильно вычислить.. Также на примерах покажем подробное решение.
Что такое определитель матрицы: вычисление определителя при помощи определения
Определитель матрицы
второго порядка – это число
.
Определитель матрицы обозначается – (сокращенно от латинского названия детерминант), или
.
Если:, тогда получается
Напомним ещё несколько вспомогательных определений:
Упорядоченный набор чисел, который состоит из элементов называется перестановкой порядка
.
Для множества, которое содержит элементов есть факториал (n), который всегда обозначается восклицательным знаком:
. Перестановки отличаются друг от друга всего лишь порядком следования. Чтобы вам было понятнее, приведём пример:
Рассмотрим множество из трёх элементов {3, 6, 7}. Всего перестановок 6, так как .:
;
;
;
;
;
Инверсия в перестановке порядка – это упорядоченный набор чисел (его ещё называют биекцией), где из них два числа образуют некий беспорядок. Это когда большее из чисел в данной перестановке расположено левее меньшего числа.
Выше мы рассматривали пример с инверсией перестановки, где были числа . Так вот, возьмём вторую строку, где судя по данным числам получается, что
, а
, так как второй элемент
больше третьего элемента
. Возьмём для сравнения шестую строку, где расположены числа:
. Здесь есть три пары:
, а
, так как
;
, так как
;
,
–
.
Саму инверсию мы изучать не будем, а вот перестановки нам очень пригодятся в дальнейшем рассмотрении темы.
Определитель матрицы x
– число:
, где
– перестановка чисел от 1 до бесконечного числа
, а
– число инверсий в перестановке. Таким образом, в определитель входит
слагаемых, которые называются “членами определителя”.
Можно вычислять определитель матрицы второго порядка, третьего и даже четвёртого. Также стоит упомянуть:
определитель матрицы – это число, которое равняется
Чтобы понять данную формулу, опишем её более подробно. Определитель квадратной матрицы x
– это сумма, которая содержит
слагаемых, а каждое слагаемое является собой произведением определённого количества
элементов матрицы. При этом, в каждом произведении есть элемент из каждой строки и каждого столбца матрицы.
Перед определённым слагаемым может появится в том случае, если элементы матрицы в произведении идут по порядку (по номеру строку), а количество инверсий
в перестановке
множество номеров столбцов нечётно.
Выше упоминалось о том, что определитель матрицы обозначается
или
, то есть, определитель часто называют детерминантом.
Итак, вернёмся к формуле:
Из формулы видно, что определитель матрицы первого порядка – это элемент этой же матрицы .
Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Вычисление определителя матрицы второго порядка
Чаще всего на практике определитель матрицы решается методами второго, третьего и реже, четвёртого порядка. Рассмотрим, как вычисляется определитель матрицы второго порядка:
В матрице второго порядка , отсюда следует, что факториал
. Прежде чем применить формулу
необходимо определить, какие данные у нас получаются:
1. ;
2. перестановки множеств: и
;
3. количество инверсий в перестановке :
и
, так как
;
4. соответствующие произведения :
и
.
Получается:
Исходя из вышесказанного мы получаем формулу для вычисления определителя квадратной матрицы второго порядка, то есть x
:
Рассмотрим на конкретном примере, как вычислять определитель квадратной матрицы второго порядка:
Задача
Вычислить определитель матрицы x
:
Решение
Итак, у нас получается ,
,
,
.
Для решения необходимо воспользоваться ранее рассмотренной формулой:
Подставляем числа с примера и находим:
Ответ
Определитель матрицы второго порядка = .
Вычисление определителя матрицы третьего порядка: пример и решение по формуле
Определитель матрицы третьего порядка – это число, полученное из девяти заданных чисел, расположенных в виде квадратной таблицы,
Определитель третьего порядка находится почти так же, как и определитель второго порядка. Разница лишь в формуле. Поэтому, если хорошо ориентироваться в формуле, тогда и проблем с решением не будет.
Рассмотрим квадратную матрицу третьего порядка *
:
Исходя из данной матрицы, понимаем, что , соответственно, факториал
=
, а это значит, что всего перестановок получается
Чтобы применить правильно формулу , необходимо найти данные:
Итак, всего перестановок множества :
.
, количество инверсий в перестановке
, а соответствующие произведения =
;
.
, количество инверсий в перестановке
, соответствующие произведения =
;
.
, инверсий в перестановке
, соответствующие произведение =
;
.
; инверсий в перестановке
, соответствующие произведение =
.
; инверсий в перестановке
, соответствующие произведение =
.
; инверсий в перестановке
, соответствующие произведение =
.
Теперь у нас получается:
Таким образом у нас получена формула для вычисления определителя матрицы порядка x
:
.
Нахождение матрицы третьего порядка по правилу треугольника (правило Саррюса)
Как говорилось выше, элементы определителя 3-го порядка расположены в трёх строках и трёх столбцах. Если ввести обозначение общего элемента , тогда первый элемент обозначает номер строки, а второй элемент из индексов – номер столбца. Есть главная (элементы
) и побочная (элементы
) диагонали определителя. Слагаемые в правой части называются членами определителя).
Видно, что каждый член определителя находится в схеме только по одному элементу в каждой строке и каждого столбца.
Вычислять определитель можно при помощи правила прямоугольника, который изображён в виде схемы. Красным цветом выделены члены определителя из элементов главной диагонали, а также члены из элементов, которые находятся в вершине треугольников, что имеют по одной стороне, параллельны главной диагонали (лева схема), беруться со знаком .
Члены с синими стрелками из элементов побочной диагонали, а также из элементов, которые находятся в вершинах треугольников, что имеют стороны, параллельные побочной диагонали (правая схема) берутся со знаком .
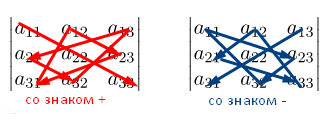
На следующем примере научимся, как вычислять определитель квадратной матрицы третьего порядка.
Задача
Вычислить определитель матрицы третьего порядка:
Решение
В этом примере:
,
,
,
,
,
,
,
,
.
Вычисляем определитель, применяя формулу или схему, которые рассматривались выше:
Ответ
Определитель матрицы третьего порядка =
Рекомендуем запомнить формулы для нахождения определителя матрицы второго и третьего порядка, так как они часто применяются на зачётах и экзаменах.
Основные свойства определителей матрицы третьего порядка
На основании предыдущих определений и формул рассмотрим основные свойства определителя матрицы.
1. Размер определителя не изменится при замене соответствующих строк, столбцов (такая замена называется транспонированием).
На примере убедимся, что определитель матрицы равен определителю транспонированной матрицы:
Вспомним формулу для вычисления определителя:
Транспонируем матрицу:
Вычисляем определитель транспонированной матрицы:
Мы убедились, что определитель транспортированной матрицы равен исходной матрице, что говорит о правильном решении.
2. Знак определителя изменится на противоположный, если в нём поменять местами любые два его столбца или две строки.
Рассмотрим на примере:
Даны две матрицы третьего порядка ( x
):
Нужно показать, что определители данных матриц противоположные.
Решение
В матрице и в матрице
поменялись строки (третья с первой, и с первой на третью). Согласно второму свойству определители двух матриц должны отличаться знаком. То есть, одна матрица с положительным знаком, а вторая – с отрицательным. давайте проверим данное свойство, применив формулу для вычисления определителя.
Свойство верно, так как .
3. Определитель равняется нулю, если в нём есть одинаковые соответствующие элементы в двух строках (столбцах). Пусть у определителя одинаковые элементы первого и второго столбцов:
Поменяв местами одинаковые столбцы, мы, согласно свойству 2 получим новый определитель: =
. С другой стороны, новый определитель совпадает с изначальным, поскольку одинаковые ответы элементы, то есть
=
. Из этих равенств у нас получается:
=
.
4. Определитель равняется нулю, если все элементы одной строки (столбца) нули. Это утверждение выплывает из того, что у каждого члена определителя по формуле (1) есть по одному, и только по одному элементу с каждой строки (столбца), у которого одни нули.
Рассмотрим на примере:
Покажем, что определитель матрицы равен нулю:
В нашей матрицы есть два одинаковых столбца (второй и третий), поэтому, исходя из данного свойства, определитель должен равняться нулю. Проверим:
И действительно, определитель матрицы с двумя одинаковыми столбцами равняется нулю.
5. Общий множитель элементов первой строки (столбца) можно вынести за знак определителя:
.
6. Если элементы одной строки или одного столбца определителя пропорциональны соответствующим элементам второй строки (столбца), тогда такой определитель равняется нулю.
Действительно, за свойством 5 коэффициент пропорциональности можно вынести за знак определителя, и тогда воспользоваться свойством 3.
7. Если каждый из элементов строк (столбцов) определителя является суммой двух слагаемых, то этот определитель можно подать в виде суммы соответствующих определителей:
.
Для проверки достаточно записать в развёрнутом виде по (1) определитель, что в левой части равенства, тогда отдельно сгруппировать члены, в которых содержатся элементы и
.Каждая из полученных групп слагаемых будет соответственно первым и вторым определителем с правой части равенства.
8. Значения определения не изменятся, если к элементу одной строки или одного столбца прибавить соответствующие элементы второй строки (столбца), умноженные на одно и то же число:
.
Это равенство получается исходя из свойств 6 и 7.
9. Определитель матрицы ,
,
равняется сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения.
Здесь по подразумевается алгебраическое дополнение элемента матрицы
. При помощи данного свойства можно вычислять не только матрицы третьего порядка, но и матрицы более высших порядков (
x
или
x
).Другими словами – это рекуррентная формула, которая нужна для того, чтобы вычислить определитель матрицы любого порядка. Запомните её, так как она часто применяется на практике.
Стоит сказать, что при помощи девятого свойства можно вычислять определители матриц не только четвёртого порядка, но и более высших порядков. Однако, при этом нужно совершать очень много вычислительных операций и быть внимательным, так как малейшая ошибка в знаках приведёт к неверному решению. Матрицы высших порядков удобнее всего решать методом Гаусса, и об этом поговорим позже.
10. Определитель произведения матриц одного порядка равен произведению их определителей.
Рассмотрим на примере:
Задача
Убедитесь, что определитель двух матриц и
равен произведению их определителей. Даны две матрицы:
Решение
Сначала находим произведение определителей двух матриц и
.
x
=
,
Теперь выполним умножение обеих матриц и таким образом, вычислим определитель:
Ответ
Мы убедились, что
Вычисление определителя матрицы при помощи метода Гаусса
Вспомним, как метод Гаусса помогает находить определитель матрицы: благодаря элементарным преобразованием в матрице все элементы (кроме ) нужно привести к нулю. Однако, такой метод подходит только к тем матрицам, в которых определитель отличен от нуля. Об этом поговорим позже, а сейчас объясним, для чего проделывается такая процедура.
Нулевые элементы необходимы для того, чтобы самым простым способом разложить определитель, исходя из элементов первого столбца. После такого преобразования, исходя из девятого свойства и , получается:
.
Здесь – это минор первого порядка, который получился из матрицы
путём вычёркивания элементов первой строки и первого столбца. Такая процедура проделывается до тех пор, пока все элементы первого столбца не превратятся в нулевые элементы.
Конечно же, сразу же назревает вопрос: “А как же получается нулевые элементы?” Рассмотрим алгоритм решения:
Если первый элемент в первой строке и в первом столбце прибавить к соответствующим элементом
– ой строки, где
. (Метод Гаусса не нужен только в том случае, если все элементы в первом столбцы нулевые). После данного преобразования “новый” элемент матрицы
. Определитель “новой” матрицы равен определителю исходной матрицы.
Если , тогда к каждому элементу второй строки прибавляем элемент первой строки, которые заранее умноженные на
, а к элементам третьей строки прибавляем определённые элементы первой строки, которые умножаются на
. И дальше вычисляем по такой же схеме. Метод Гаусса рассмотрен более подробно в отдельно теме. В итоге получится преобразованная матрица, где все элементы первого столбца окажутся нулевыми. Определитель полученной матрицы будет равен определителю изначальной матрицы.
Напомним, что величина определителя – ого порядка равна сумме произведений элементов какой-либо строки или столбца на соответствующее алгебраическое дополнение.
Рассмотрим записанный сначала формально определитель четвёртого порядка:
Вычёркивая в
– тую строку и
– тый столбец, на пересечении которого помещается элемент
, получим определитель третьего порядка, который называется минором элемента
и обозначается
. Тогда
– алгебраическое дополнение элемента
. Определитель 4-го порядка можно обозначить, как размещение по элементам, например, первого столбца:
Пусть введено понятие определителя – ого порядка, тогда определитель
– ого порядка:
Можно изобразить, как размещение по элементам первого столбца:
,
где – алгебраические дополнения, а
– миноры элементов первого столбца. Последние и есть определители
– го порядка.
Чтобы было более понятно, разберём матрицу четвёртого порядка, где нужно найти определитель:
Разберём на примере:
Задача
Нужно вычислить определитель матрицы высшего порядка x
:
Решение
Сначала вспомним тему про определители третьего порядка и превратим в нули элементы 1-го столбца, которые принадлежат 2, 3, 4 строкам. Для этого прибавим соответствующие элементы 1 и 2 строк. На месте элементов получим
,
,
,
.
Чтобы получить в 3 строке 1-го столбца, умножим на
элементы 1-ой строки и прибавим к соответствующим элементам третьей строки:
Умножим элементы 1-ой строки на и добавим к соответствующим элементам 4-ой строки. Получается:
Изначальный определитель впоследствии преобразований получается:
Дальше раскладываем последний определитель за элементами 1-го столбца. Поскольку , а остальные элементы 1-го столбца нули, тогда получим один определитель 3-го порядка.
Ответ
Определитель матрицы четвёртого порядка = .
Вычисление определителя матрицы при помощи теоремы Лапласа
Теорема Лапласа – это глубокое разложение определителя по элементам. При помощи данной теоремы можно решать матрицы не только третьего порядка, но и более высших порядков.
Напомним – минор – это определитель матрицы, который составлен методом вычёркивания – той строки и
– того столбца. А алгебраическое дополнение – соответствующий минор, который берётся со знаком минус
. Знаки же зависят от места элемента
в определителе и определяются по схеме:
Приведём пример решения алгебраических дополнений по схеме:
Задача
Найти алгебраические дополнения элементов определителя:
Решение
Понятия алгебраического дополнения даёт возможность ещё одного способа определения определителя, который утверждается теоремой Лапласа (про распределение определителя):
Определитель равняется сумме произведения элементов строк (столбца) на их алгебраические дополнения. Например,
. – это равенство проверяется непосредственно
Заметно, как последнее выражение совпадает с выражением из правила треугольника (правила Саррюса). Давайте по теореме Лапласа разберём несколько примеров:
Задача
Вычислить определитель матрицы, разложив его за элементами третьего порядка:
Решение
Ответ
.
Заключение
Итак, определитель квадратной матрицы – это число, полученное при помощи заданных чисел, расположенных в виде квадратной таблицы,которое вычисляется по рассмотренным выше формулам. Мы рассмотрели три основных способа вычисления определителя:
- через сумму двух произведений сочетаний элементов квадратной матрицы;
- по правилу разложения определителя по элементам строк (столбцов) квадратной матрицы;
- по методу Гаусса, когда матрицу нужно привести к треугольному виду.
Также были рассмотрены формулы для решения матрицы второго, третьего и высших порядков.
Мы разобрали 10 свойств определителя матриц, благодаря которым можно быстрее и легче найти определитель матрицы.
Удобно решать матрицу третьего порядка методом Гаусса, где нужно выполнить элементарные преобразования матрицы и привести её к ступенчатому виду. Определитель матрицы равняется произведению элементов, которые стоят на главной диагонали.
Полезная литература
![]() Белоусов И. В. Матрицы и определители, учеб. Пособие по линейной по алгебре/ – Кишинёв – 2006 – 91 с.
Белоусов И. В. Матрицы и определители, учеб. Пособие по линейной по алгебре/ – Кишинёв – 2006 – 91 с.
![]() Магазинников Л. И.- Практикум по линейной алгебре и аналитической геометрии: учеб. пособие для вузов/Магазинников Л. И., Магазинникова А. Л. – Томск – 2007 – 150 с.
Магазинников Л. И.- Практикум по линейной алгебре и аналитической геометрии: учеб. пособие для вузов/Магазинников Л. И., Магазинникова А. Л. – Томск – 2007 – 150 с.