Как рассчитать динамику показателей
Анализ динамики показателей начинается с того, как именно они изменяются (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за изменением рядов динамики во времени, рассчитываются показатели: абсолютное изменение, относительное изменение, темп изменения.
Инструкция
Учтите, что все данные показатели могут быть базисными, когда уровень одного периода сравнивается с уровнем начального периода, и цепными, когда сравнивается уровень двух соседних периодов.
Базисное абсолютное изменение (абсолютный прирост) вы можете рассчитать как разность конкретного и первого уровней ряда: У(б) = У(i ) – У(1). Оно показывает, насколько уровень конкретного периода больше или меньше базисного уровня. Цепное абсолютное изменение – это разность между конкретным и предыдущим уровнем ряда: У (ц) = У(i) – У(i-1). Оно показывает, на сколько единиц уровень конкретного периода больше или меньше предыдущего. Помните, что между базисным и цепным абсолютным изменением существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению.
При анализе динамики показателей вы можете рассчитать базисное относительное изменение (базисный темп роста). Он представляет собой отношение конкретного показателя к первому из ряда динамики: I(б) = У(i)/Y(1). Цепное относительное изменение – это соотношение конкретного и предыдущего уровня ряда: I(ц) = У(i)/Y(i-1). Относительное изменение показывает, во сколько раз уровень данного ряда больше уровня предыдущего ряда или какую часть его часть составляет. Относительное изменение может выражаться в процентах, путем умножения соотношения на 100 %. Между цепными и базисными относительными изменениями существует взаимосвязь: произведение цепных относительных изменений равно последнему базисному.
Кроме того, при анализе динамики показателей вы можете рассчитать темп изменения (темп прироста) уровней. Это относительный показатель, который показывает, на сколько процентов данный показатель больше или меньше другого, принимаемого за базу сравнения. Он определяется путем вычитания из относительного базисного или цепного изменения 100%: Т(i) = I(i) – 100%.
Источники:
- как найти абсолютное изменение
- Абсолютные и относительные статистические показатели
- Расчет абсолютных показателей
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
1 Статистический анализ динамики
Для выявления тенденции и закономерностей развития социально-экономических явлений и процессов в статистике строятся ряды динамики (иногда их называют временными рядами).
Ряды динамики – это ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке
Значения показателя, составляющие ряд динамики, называются уровнями ряда.
Каждый ряд динамики характеризуется двумя параметрами: значениями времени (i) и соответствующими им значениями уровней ряда (y).
В зависимости от значений времени различают моментные и интервальные ряды динамики. При этом моментные ряды динамики характеризуют значения уровней ряда по состоянию на конкретную дату (число, месяц, год). Интервальные ряды динамики характеризуют значения уровней ряда за определенный период времени (например, за месяц, квартал, год и т.д.).
Статистический анализ динамики осуществляется с помощью абсолютных, относительных и средних показателей динамики.
Расчет показателей динамики может осуществляться цепным и базисным методами. При цепном методе базой сравнения каждый раз выступает уровень предыдущего периода yi-1. При базисном методе за базу сравнения принимается постоянный уровень y0.
Абсолютные и относительные показатели динамики:
1) абсолютный прирост:
цепной метод:
базисный метод:
Показывает, на сколько сравниваемый уровень отличается от уровня, принятого за базу.
2) темп роста:
цепной метод:
базисный метод:
Показывает, сколько процентов составляет сравниваемый уровень по отношению к базисному. Если рассчитан в коэффициентах, то показывает, во сколько раз сравниваемый уровень отличается от базисного.
3) темп прироста.
Если темп роста представлен в процентах, то
.
Если темп роста представлен в коэффициентах, то
Темп прироста показывает, на какую долю единиц или на сколько процентов сравниваемый уровень больше или меньше базисного.
Средние показатели динамики:
1) средний уровень ряда динамики.
Если ряд динамики интервальный с равными промежутками времени, то
Если ряд динамики моментный с равными промежутками времени, то
.
Если ряд динамики моментный с неравными промежутками времени, то
где ti – продолжительность периода между двумя моментами времени в днях.
2) средний абсолютный прирост.
Из цепных абсолютных приростов:
где m – количество уровней ряда динамики, за исключением базисного.
Из базисных абсолютных приростов:
где n – количество уровней ряда динамики, включая базисный.
Средний абсолютный прирост показывает, на сколько в среднем в течение рассматриваемого периода времени изменялся (увеличивался или уменьшался) тот или иной показатель.
3) средний темп роста.
Из цепных темпов роста:
где m – количество уровней ряда динамики, за исключением базисного.
Из базисных темпов роста:
где n – количество уровней ряда динамики, включая базисный.
Если в процентах, то показывает, сколько процентов составлял темп роста в среднем в течение рассматриваемого периода времени.
Если в коэффициентах, то показывает, во сколько раз в среднем в течение рассматриваемого периода времени изменялся тот или иной показатель.
4) средний темп прироста.
Если средний темп роста выражен в процентах, то
.
Если средний темп роста выражен в коэффициентах, то
.
Показывает, на какую долю единиц или на сколько процентов в среднем в течение рассматриваемого периода времени изменялся тот или иной показатель.
Прогнозирование уровня развития социально-экономических
явлений и процессов
Анализ динамики социально-экономических явлений, выявление и характеристика основной тенденции развития дают основание для прогнозирования – определения будущих размеров уровня социально-экономического явления.
Процесс прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, т.е. прогноз основан на экстраполяции.
Можно выделить следующие элементарные методы экстраполяции:
1) на основе среднего абсолютного прироста,
2) на основе среднего темпа роста,
3) на основе аналитического выравнивания ряда, которое предполагает применение метода наименьших квадратов и представление развития явлений во времени в виде уравнения тренда.
Прогнозирование по среднему абсолютному приросту может быть выполнено в случае равномерного изменения уровней (под равномерностью понимается стабильность абсолютных приростов). В этом случае, чтобы получить прогноз на «i» шагов вперед (i – период упреждения), достаточно воспользоваться следующей формулой:
где – конечный уровень ряда динамики; – прогнозная оценка значения (n+1) уровня ряда; – значение среднего абсолютного прироста, рассчитанное для ряда динамики.
Прогнозирование по среднему темпу роста можно осуществлять в случае, если общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения прогнозного значения на «i» шагов вперед необходимо использовать следующую формулу:
где – средний коэффициент роста, рассчитанный для ряда динамики.
Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени: y = f(t).
Правильно построенная модель должна соответствовать характеру изменения тенденции исследуемого явления. Выбранная функция позволяет получить выровненные или теоретические значения уровней ряда динамики.
Для отображения основной тенденции развития явлений во времени применяются различные функции: полиномы разной степени, экспоненты, логистические кривые и другие виды.
Полиномы имеют следующий вид:
полином первой степени: ,
полином второй степени: ,
полином третьей степени: ,
полином n-ой степени: .
Здесь a0; a1; a2;…an – параметры полиномов; t – условное обозначение времени.
Оценка параметров в моделях находится методом наименьших квадратов. Суть его состоит в определении таких параметров (коэффициентов), при которых сумма квадратов отклонений расчетных значений уровней от фактических значений была бы минимальной. Таким образом, эти оценки находятся в результате минимизации выражения:
где – фактическое значение уровня ряда динамики, – расчетное значение, n – длина ряда динамики.
В результате минимизации данного выражения получается система нормальных уравнений:
где n – число членов в ряду динамики, t = 1, 2, …, n.
Система, состоящая из «р» уравнений, содержит в качестве известных величин Σy, Σyt, …, Σytp, т.е. суммы наблюдаемых значений уровней динамического ряда, умноженные на показатели времени в степени 1, 2, …, р, и неизвестных величин aj. Решение этой системы относительно a0, a1, …, ap и дает искомые значения параметров.
Системы для расчета параметров полиномов невысоких степеней намного проще. Обозначим последовательные параметры полиномов как а0, а1, а2. Тогда система нормальных уравнений для оценивания параметров прямой примет вид:
Решение приведенных выше систем уравнений можно упростить. Упрощение расчетов заключается в переносе начала координат в середину ряда динамики. В этом случае упрощаются сами нормальные уравнения, а также уменьшаются абсолютные значения величин, участвующих в расчете. Если до переноса начала координат t было равно 1, 2, 3, …, n, то после переноса:
– для нечетного числа уровней ряда t = …; -3; -2; -1; 0; 1; 2; 3; …
– для четного числа уровней ряда t = …; -3; -2; -1; 1; 2; 3; …
Следовательно, Σt и все Σtp , у которых «р» − нечетное число, равны 0. Таким образом, все члены уравнений, содержащие Σt с такими степенями, могут быть исключены.
Система нормальных уравнений для прямой теперь упрощается следующим образом:
При анализе рядов динамики иногда приходится прибегать к определению некоторых неизвестных уровней внутри данного ряда динамики, то есть к интерполяции. Как и экстраполяция, интерполяция может производиться на основе среднего абсолютного прироста, среднего темпа роста, а также с помощью аналитического выравнивания. При интерполяции предполагается, что ни выявленная тенденция, ни ее характер не претерпели существенных изменений в том промежутке времени, уровень (уровни) которого нам неизвестны.
Построение линии тренда с помощью программы Excel
1. Выделить диапазон ячеек, содержащих исходный ряд динамики.
2. Выполнить команду «Вставка – график».
3. Щелкнуть правой кнопкой мыши, выполнить команду «Выбрать данные».
4. В поле «Элементы легенды (ряды)» выделить Ряд 1. Нажать кнопку «Изменить». В поле «Имя ряда» задать новое имя: «Исходный ряд динамики». Так как исходный ряд динамики был выделен в начале, то диапазон значений ряда будет указан автоматически. Нажать O’k.
5. В поле «Подписи горизонтальной оси (категории)» нажать кнопку «Изменить». В открывшемся окне в поле «Диапазон подписей оси» задать диапазон ячеек таблицы, в котором указаны годы. Нажать O’k.
6. Еще раз нажать O’k.
7. На построенном графике выделить линию исходного ряда динамики. Щелкнуть правой кнопкой мыши. Выбрать команду «Добавить линию тренда». В открывшемся окне «Параметры линии тренда» указать:
а) линейная;
б) в поле «Название аппроксимирующей (сглаженной) кривой» выбрать «другое» и указать «Линия тренда»;
в) прогноз вперед на … (указать количество периодов) периодов;
г) отметить флажки: показывать уравнение на диаграмме; поместить на диаграмму величину достоверности аппроксимации (R^2). Закрыть окно «Параметры линии тренда».
Примечание. В данном случае в качестве условных дат t программа принимает следующие значения: t = 1, 2, 3, ….
8. Для того чтобы задать названия осей, нужно выделить диаграмму и перейти на вкладку «Макет». Затем выполнить команду «Подписи/Название осей/Название основной горизонтальной оси/Название под осью». На диаграмме появится поле, в котором задать имя горизонтальной оси «Годы».
Затем выполнить команду «Подписи/Название осей/Название основной вертикальной оси/Повернутое название». На диаграмме появится поле, в котором задать имя вертикальной оси «Число предприятий и организаций, единиц».
Рядами
динамики
называются статистические данные,
отображающие развитие изучаемого
явления во времени. В каждом ряду динамики
имеются два основных элемента: показатель
времени t; соответствующие им уровни
развития изучаемого явления у. В качестве
показаний времени в рядах динамики
выступают либо определенные даты
(моменты) времени, либо отдельные периоды
(годы, кварталы, месяцы, сутки).
Уровни рядов
динамики отображают количественную
оценку (меру) развития во времени
изучаемого явления. Они могут выражаться
абсолютными, относительными или средними
величинами.
В зависимости от
характера изучаемого явления уровни
рядов динамики могут относиться или к
определенным датам (моментам) времени,
или к отдельным периодам. В соответствии
с этим, ряды динамики подразделяются
на моментные и интервальные.
Моментные
ряды динамики
отображают состояние изучаемых явлений
на определенные даты (моменты) времени.
Особенностью
моментного ряда динамики является
то, что в его уровни могут входить одни
и те же единицы изучаемой совокупности.
Особенностью
интервального ряда динамики является
то, что каждый его уровень складывается
из данных за более короткие интервалы
времени.
Ряды
динамики могут быть полными и неполными.
Полный
ряд – ряд
динамики, в котором одноименные моменты
времени или периоды времени строго
следуют один за другим в календарном
порядке или равноотстоят друг от друга.
Неполный
ряд динамики
– ряд, в котором уровни зафиксированы в
неравноотстоящие моменты или периоды
времени.
В зависимости от
способов выражения уровней различают
ряды динамики, заданные:
а) рядом абсолютных
величин;
б) рядом относительных
величин;
в) рядом средних
величин.
Несопоставимость уровней рядов динамики
Уровни рядов
динамики должны быть сопоставимы между
собой. Для несопоставимых величин нельзя
вести расчеты показателей рядов динамики.
Несопоставимость
может быть:
-
по
территории, -
по
кругу охватываемых объектов, -
из-за
разных единиц измерения, -
из-за
изменения уровня явления на различные
даты, -
из-за
различного понимания единицы объекта, -
по
структуре.
Смыкание рядов
динамики
В
большинстве случаев уровни ряда
приводятся к сопоставимому уровню путем
пересчета. Например может использоваться
метод смыкания.
Суть
метода заключается в том, что уровень
базового года принимается за 100 %, а затем
производим соответствующий пересчет.
Получаем ряд относительных величин.
Определение
среднего уровня ряда динамики.
В
качестве обобщенной характеристики
уровней ряда динамики служит средний
уровень ряда динамики
![]() .
.
В зависимости от типа ряда динамики
используются различные расчетные
формулы.
Интервальный ряд
абсолютных величин с равными периодами
(интервалами времени):
![]()
Моментный ряд с
равными интервалами между датами:
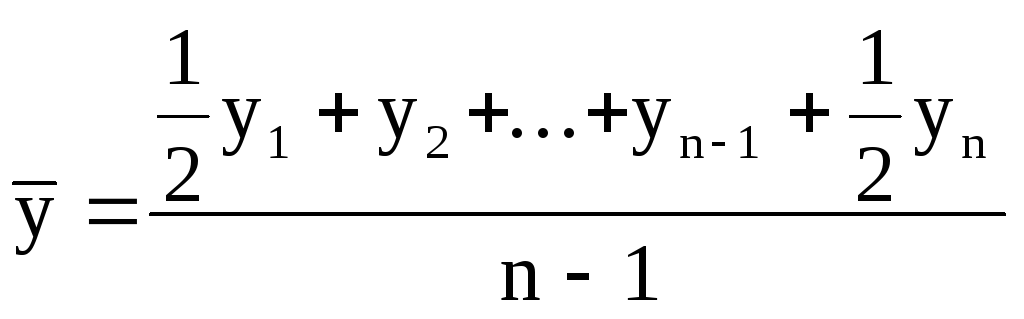
Моментный ряд с
неравными интервалами между датами:
![]()
где
![]() – уровни ряда, сохраняющиеся без
– уровни ряда, сохраняющиеся без
изменения на протяжении интервала
времени![]() .
.
Показатели
изменения уровней ряда динамики.
Одним из важнейших
направлений анализа рядов динамики
является изучение особенностей развития
явления за отдельные периоды времени.
С этой целью для
динамических рядов рассчитывают ряд
показателей:
К – темпы роста;
![]() –
–
абсолютные приросты;
![]() –
–
темпы прироста.
Темп
роста –
относительный показатель, получающийся
в результате деления двух уровней
одного ряда друг на друга. Темпы роста
могут рассчитываться как цепные, когда
каждый уровень ряда сопоставляется с
предшествующим ему уровнем:
![]() ,
,
либо как базисные, когда все уровни
ряда сопоставляются с одним и тем же
уровнем![]() ,
,
выбранным за базу сравнения:![]() . Темпы роста могут быть представлены
. Темпы роста могут быть представлены
в виде коэффициентов либо в виде
процентов.
Абсолютный
прирост –
разность между двумя уровнями ряда
динамики, имеет ту же размерность, что
и уровни самого ряда динамики. Абсолютные
приросты могут быть цепными и базисными,
в зависимости от способа выбора базы
для сравнения:
цепной
абсолютный прирост –
![]() ;
;
базисный
абсолютный прирост –
![]() .
.
Для относительной
оценки абсолютных приростов рассчитываются
показатели темпов прироста.
Темп
прироста –
относительный показатель, показывающий
на сколько процентов один уровень ряда
динамики больше (или меньше) другого,
принимаемого за базу для сравнения.
Базисные
темпы прироста:
![]()
![]() .
.
Цепные
темпы прироста:
![]() .
.
![]() и
и
![]() –
–
абсолютный базисный или цепной прирост;
![]() –
–
уровень ряда динамики, выбранный за
базу для определения базисных абсолютных
приростов;
![]() –
–
уровень ряда динамики, выбранный за
базу для определения i-го цепного
абсолютного прироста.
Существует связь
между темпами роста и прироста:
![]() К
К
= К – 1 или
![]() К
К
= К – 100 % (если темпы роста определены в
процентах).
Если
разделить абсолютный прирост (цепной)
на темп прироста (цепной) за соответствующий
период, получим показатель, называемый
– абсолютное
значение одного процента
прироста:
![]() .
.
Определение
среднего абсолютного прироста, средних
темпов роста и прироста.
По показателям
изменения уровней ряда динамики
(абсолютные приросты, темпы роста и
прироста), полученным в результате
анализа исходного ряда, могут быть
рассчитаны обобщающие показатели в
виде средних величин – средний абсолютный
прирост, средний темп роста, средний
темп прироста.
Средний абсолютный
прирост может быть получен по одной из
формул:
![]() или
или
![]() ,
,
где n – число уровней
ряда динамики;
![]() –
–
первый уровень ряда динамики;
![]() –
–
последний уровень ряда динамики;
![]() –
–
цепные абсолютные приросты.
Средний темп роста
можно определить, пользуясь формулами:
![]()
![]()
![]()
где n – число
рассчитанных цепных или базисных темпов
роста;
![]() –
–
уровень ряда, принятый за базу для
сравнения;
![]() –
–
последний уровень ряда;
![]() –
–
цепные темпы роста (в коэффициентах);
![]() –
–
первый базисный темп роста;
![]() –
–
последний базисный темп роста.
Между
темпами прироста
![]() и темпами роста К существует соотношение
и темпами роста К существует соотношение![]() =
=
К – 1, аналогичное соотношение верно и
для средних величин.
Определение в
рядах динамики общей тенденции развития.
Определение уровней
ряда динамики на протяжении длительного
периода времени обусловлено действием
ряда факторов, которые неоднородны по
силе и направлению воздействия,
оказываемого на изучаемое явление.
Рассматривая
динамические ряды, пытаются разделить
эти факторы на постоянно действующие
и оказывающие определяющее воздействие
на уровни ряда, формирующие основную
тенденцию развития, и случайные
факторы, приводящие к кратковременным
изменениям уровней ряда динамики.
Наиболее важна при анализе ряда
динамики его основная тенденция развития,
но часто по одному лишь внешнему виду
ряда динамики ее установить невозможно,
поэтому используют специальные методы
обработки, позволяющие показать основную
тенденцию ряда. Методы обработки
используются как простые, так и достаточно
сложные. Простейший способ обработки
ряда динамики, применяемый с целью
установления закономерностей развития
– метод
укрупнения интервалов.
Суть метода в том,
чтобы от интервалов, или периодов
времени, для которых определены исходные
уровни ряда динамики, перейти к более
продолжительным периодам времени и
посмотреть, как уровни ряда изменяются
в этом случае.
Исходные уровни
ряда динамики подвержены сезонным
изменениям; для определения общей
тенденции развития переходят, например,
от ежемесячных уровней к годовым уровням:
Эти цифры, полученные
в результате перехода к годовым уровням
ряда динамики, показывают общую тенденцию
роста реализации молочной продукции.
Другой
способ определения тенденции в ряду
динамики —
метод
скользящих средних.
Суть метода заключается в том, что
фактические уровни ряда заменяются
средними уровнями, вычисленными по
определённому правилу, например:
![]() —исходные
—исходные
или фактические уровни ряда динамики
заменяются средними уровнями:
![]()
![]()
![]()
…
…
…
![]()
В
результате получается сглаженный ряд,
состоящий из скользящих пятизвенных
средних уровней
![]() .
.
Между расположением уровней![]() и
и![]() устанавливается соответствие:
устанавливается соответствие:
![]()
— —
![]() — —,
— —,
сглаженный
ряд короче исходного на число уровней
![]() ,
,
где k – число уровней, выбранных для
определения средних уровней ряда.
Сглаживание методом
скользящих средних можно производить
по четырём, пяти или другому числу
уровней ряда, используя соответствующие
формулы для усреднения исходных уровней.
Полученные при
этом средние уровни называются
четырёхзвенными скользящими средними,
пятизвенными скользящими средними и
т.д.
При
сглаживании ряда динамики по чётному
числу уровней выполняется дополнительная
операция, называемая центрированием,
поскольку, при вычислении скользящего
среднего, например по четырём уровням,
![]() относится к временной точке между
относится к временной точке между
моментами времени, когда были зафиксированы
фактические уровни![]() и
и![]() .
.
Схема вычислений и расположений уровней
сглаженного ряда становится сложнее:
![]() …
…
— исходные уровни;
— —
![]() …
…
— сглаженные уровни;
— —
![]() …
…
— центрированные сглаженные уровни;
![]()
![]() .
.
Метод скользящих
средних не позволяет получить численные
оценки для выражения основной тенденции
в ряду динамики, давая лишь наглядное
графическое представление.
Наиболее
совершенным способом определения
тенденции развития в ряду динамики
является метод
аналитического выравнивания.
При этом методе исходные уровни ряда
динамики
![]() заменяются теоретическими или расчетными
заменяются теоретическими или расчетными![]() ,
,
которые представляют из себя некоторую
достаточно простую математическую
функцию времени, выражающую общую
тенденцию развития ряда динамики. Чаще
всего в качестве такой функции выбирают
прямую, параболу, экспоненту и др.
Например,
![]() ,
,
где
![]() – коэффициенты, определяемые в методе
– коэффициенты, определяемые в методе
аналитического выравнивания;
![]() –
–
моменты времени, для которых были
получены исходные и соответствующие
теоретические уровни ряда динамики,
образующие прямую, определяемую
коэффициентами
![]() .
.
Расчет
коэффициентов
![]() ведется на основе метода наименьших
ведется на основе метода наименьших
квадратов:
![]()
![]()
Если
вместо
![]() подставить
подставить![]() (или соответствующее выражение для
(или соответствующее выражение для
других математических функций), получим:
![]()
Это
функция двух переменных
![]() (все
(все![]() и
и![]() известны), которая при определенных
известны), которая при определенных![]() достигает минимума. Из этого выражения
достигает минимума. Из этого выражения
на основе знаний, полученных в курсе
высшей математики об экстремуме функций
n переменных, получают значения
коэффициентов![]() .
.
Для прямой:
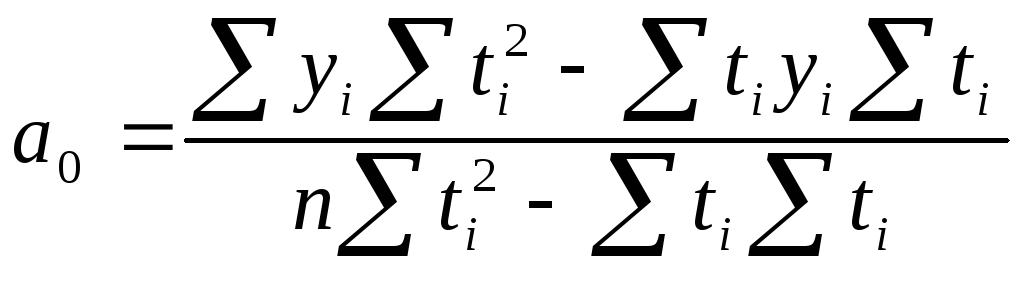
![]()
где
n — число моментов времени, для которых
были получены исходные уровни ряда
![]() .
.
Если
вместо абсолютного времени
![]() выбрать
выбрать
условное время таким образом, чтобы![]() ,
,
то записанные выражения для определения![]() упрощаются:
упрощаются:
![]()
![]()
Определение
в рядах внутригодовой динамики.
Многие процессы
хозяйственной деятельности, торговли,
сельского хозяйства и других сфер
человеческой деятельности подвержены
сезонным изменениям, например, продажа
мороженого, потребление электроэнергии,
производство молока, сахара, продажа
сельхозпродукции и др.
Для анализа рядов
динамики, подверженных сезонным
изменениям, используются специальные
методы, позволяющие установить и описать
особенности изменения уровней ряда.
Прежде, чем использовать методы изучения
сезонности, необходимо подготовить
данные, приведённые в сопоставимый вид,
за несколько лет наблюдения по месяцам
или кварталам. Изменения сезонных
колебаний производится с помощью
индексов сезонности. В зависимости от
существующих в ряду динамики тенденций
используются различные правила построения
индексов.
1. Ряд динамики не
имеет общей тенденции развития, либо
она не велика.
Индекс
сезонности:
![]() ,
,
где
![]() — средний уровень ряда, полученный в
— средний уровень ряда, полученный в
результате осреднения уровней ряда за
одноимённые периоды времени (например,
средний уровень января за все годы
наблюдения);
![]() —общий
—общий
средний уровень ряда за всё время
наблюдения.
Вывод о наличии
или отсутствия в ряду динамики ярко
выраженной тенденции может производиться,
например, при помощи метода укрупнения
интервалов.
Прогнозирование
(экстраполяция)
– это определение будущих размеров
экономического явления.
Интерполяция
– это
определение недостающих показателей
уровней ряда.
Наиболее
простым методом прогнозирования является
расчет средних характеристик роста
(средний абсолютный прирост, средний
темп роста и т.д.) и перенесение их на
будущие даты. Прогнозирование на основе
аналитического выравнивания является
наиболее распространенным методом.
Анализ
взаимосвязанных рядов динамики
Под
взаимосвязанными
понимаются
такие ряды динамики, в которых уровни
одного ряда в какой-то степени определяют
уровни другого. Например, ряд, отражающий
внесение удобрений на 1 га, связан с
временным рядом урожайности, ряд уровней
средней выработки — с рядом динамики
средней заработной платы, ряд среднегодового
поголовья молочного стада — с годовыми
уровнями надоев молока и т. д.
В простейших
случаях для характеристики взаимосвязи
двух и более рядов их приводят к общему
основанию, для чего берут в качестве
базисных уровни за один и тот же период
и исчисляют коэффициенты опережения
по темпам роста или прироста.
Коэффициенты
опережения по темпам роста —
это отношение темпов роста (цепных или
базисных) одного ряда к соответствующим
по времени темпам роста (также цепным
или базисным) другого ряда. Аналогично
находятся и коэффициенты опережения
по темпам прироста.
Анализ взаимосвязанных
рядов представляет наибольшую сложность
при изучении временных последовательностей.
Нередко совпадение общих тенденций
развития бывает вызвано не взаимной
связью, а прочими неучитываемыми
факторами. Поэтому в сопоставляемых
рядах предварительно следует избавиться
от влияния существующих в них тенденций,
а после этого провести анализ взаимосвязи
по отклонениям от тренда. Исследование
включает проверку рядов динамики
(отклонений) на автокорреляцию и
установление взаимосвязи между
признаками.
Под
автокорреляцией
понимается
зависимость последующих уровней ряда
от предыдущих. Проверка на наличие
автокорреляции осуществляется по
критерию Дарбина — Уотсона:
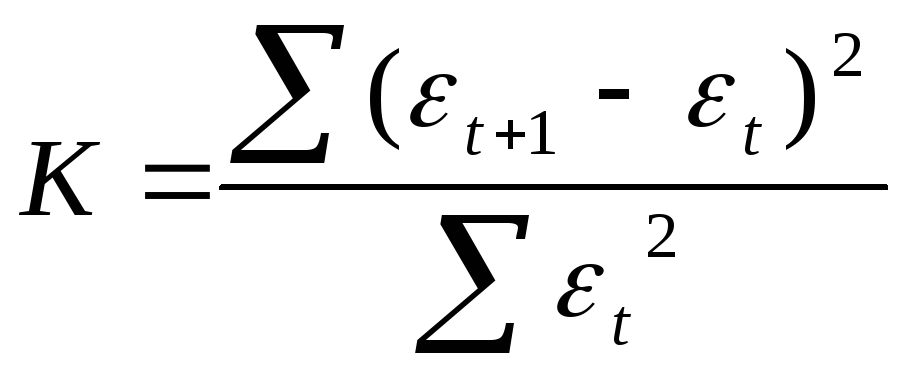 ,
,
где
εt
— отклонение фактического уровня ряда
в точке t
от теоретического
(выравненного) значения.
При
К = 0
имеется полная положительная
автокорреляция, при К
= 2 автокорреляция
отсутствует, при К
= 4 — полная
отрицательная
автокорреляция.
Чтобы получить выраженные в числах изменения социальной и экономической среды, в статистике применяются разные методы. Среди них выделяется упорядочивание данных с использованием временной последовательности. Ряд динамики – это статистические значения в хронологическом порядке.
Ряд динамики может состоять из:
- значений, связанных с определенным моментом, – датой, днем, и др.;
- данных, связанных с периодом времени. Уровень ряда динамики это и есть полученный показатель.
Виды рядов динамики
Объединение радов происходит по:
- Времени. Это моментные и интервальные ряды.
- Форме представления. К ним относятся абсолютные, относительные и средние величины.
- Интервалам времени. Подразделяются на равномерные и неравномерные ряды.
- Числу смысловых статистических величин. Это изолированные и комплексные ряды.
Чтобы без ошибок построить динамические ряды, необходимо сопоставлять уровни рядов разных периодов. Для этого у них должны быть однородные величины. Также ряды предполагают охват явления с одинаковой полнотой.
Не допускать погрешностей в анализе динамики помогает смыкание рядов динамики. Суть понятия в проведении подготовительной работы до основных расчетов. Во время подготовки ряды объединяются в один. Уровни этих рядов рассчитаны по разным методологиям. Смыкание также включает преобразования, при которых абсолютные уровни рядов приводятся к общему основанию. Это действие помогает избежать несопоставимости уровней.
Анализ показателей в рядах динамики
Ряд динамики характеризует изменения данных внутри этого ряда. Статистические данные необходимо сравнивать также между рядами. По формулам можно определить основные показатели.
Разность уровней ряда динамики называется абсолютным приростом. Показатель демонстрирует, на сколько изменился каждый последующий уровень.
∆УЦ=Уi-Уi-1,
где Уi – уровень У1-УЦ,
Уi-1 – уровень предыдущего периода.
Отношение уровней ряда динамики называется темпом (коэффициентом) роста. По нему видно, во сколько раз изменились последовательные значения.
τp=УiУi-1,
где У1 – начальный уровень ряда.
Темп прироста. Показывает процентное отличие между последовательными уровнями.
Тпр=Тр-1
Если сравнивать между собой числа без всякой системы, не получится грамотно проанализировать ситуацию и выстроить новую стратегию. Например, продвижение продукта на основе маркетинговой стратегии. Использование формул поможет высчитать, какую прибыль принесло компании конкретное решение за анализируемый период.
Анализ показателей за длительный промежуток
Если есть задача оценить изменения, которые касаются длинного временного отрезка, эффективно применить средние показатели. В статистике для их определения используются следующие понятия.
Средний уровень ряда динамики. Применим для интервальных равноотстоящих рядов
→y=∑yn,
где n – число уровней ряда.
Если ряды неравноотстоящие, средний уровень интервального ряда динамики определяется как
→y=∑yt∑t,
где t – длина интервалов времени между уровнями.
Использование перечисленных методов позволяет применять полученные значения в экономике. Определять эффективность финансовых вложений, прогнозировать результаты. В управление предприятиями и бухгалтерию также можно внедрить данные методы для планирования и распределения бюджета.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Что такое ряд динамики в статистике, и какие они бывают, мы рассмотрели в первой части этой темы. Теперь поговорим об анализе рядов динамики. Как уже отмечалось, ряды динамики характеризуют развитие явление во времени, а это развитие подлежит изучению. Ведь статистику интересует, как это явление развивается, какие есть тенденции (тренды) в развитии явления. Или наоборот тенденций нет.

Именно для целей изучения динамики или скорости изменений во временных периодах и используются показатели анализа рядов динамики.
Но прежде чем мы перейдем к самим показателям и формулам их расчета необходимо уточнить важнейший момент.
Анализ рядов динамики
Дело в том что сам анализ может проводиться двумя способами, в зависимости от того как и с чем мы будем проводить сравнение уровней ряда. Если мы хотим сравнить с каким-то одним данным это один способ, а если с непосредственно предшествующим, то это уже другой способ расчета.
Как правило, расчет проводится сразу и тем и другим способом, если мы говорим о полноценном исследовании.
- Расчет показателей анализа рядов динамики С ПОСТОЯННОЙ БАЗОЙ СРАВНЕНИЯ (БАЗИСНЫЕ показатели) – каждый уровень рядя сравнивается с одним и тем же уровнем выбранным за базу сравнения.
Например: база сравнение 2005 год, а уровни, начиная с 2006 по 2009, тогда получаем следующую последовательность расчетов уровень 2006 года с уровнем 2005 года, 2007 – с 2005, 2008 – с 2005 и 2009 – с 2005.
- Расчет показателей анализа рядов динамики С ПЕРЕМЕННОЙ БАЗОЙ СРАВНЕНИЯ (ЦЕПНЫЕ показатели) – в данном случае каждый уровень ряда сравнивается с тем который стоит перед ним, получается такое цепное сравнение или цепь расчетов взаимно перетекающих друг в друга, поэтому и второе название способа ЦЕПНЫЕ показатели анализа рядов динамики.
Например: имеем уровни начиная с 2005 по 2009 годы, тогда получаем следующую последовательность расчетов уровень 2006 года с уровнем 2005 года, 2007 – с 2006, 2008 – с 2007 и 2009 – с 2008.
Вот такие нехитрые расчеты. А теперь можем перейти к самим показателям анализа. Следует сказать, что эти показатели условно можно разделить на две группы:
— простые показатели анализа рядов динамики рассчитываются по каждому уровню ряда;
— обобщающие или средние показатели анализа рядов динамики они рассчитываются для всего ряда в целом, собственно как и любые средние величины.
А вот самих показателей всего пять.

- Абсолютный прирост – рассчитывается путем вычитания из текущего уровня базисного или предшествующего уровня, то есть простое математическое вычитание. В отличие от всех других показателей абсолютный прирост имеет те же единицы измерения, что и исходный уровень ряда. Может получиться отрицательным.
- Коэффициент роста – рассчитывается делением текущего уровня на базисный или предшествующий уровень. Показывает во сколько раз данный уровень больше или меньше базисного. Поскольку это относительная величина, то наименование у коэффициента роста нет.
- Темп роста – рассчитывается умножением коэффициента роста на 100%. Показывает, сколько процентов данный уровень составляет по отношению к базисному. Выражается в процентах.
- Темп прироста – рассчитывается вычитанием из темпа роста 100%. Показывает на сколько процентов данный уровень больше или меньше базисного. Выражается в процентах. Может получиться отрицательным.
- Абсолютное значение одного процента прироста – рассчитывается из имеющихся уже абсолютного прироста и темпа прироста путем деления первого на второй. Получаем как раз размер 1 % прироста, но в абсолютно выражении. Следует сказать, что данный показатель носит больше статистический характер и в широкой практике используется нечасто.
Формулы для анализа рядов динамики
Ниже в сводной таблице представим все формулы простых показателей анализа рядов динамики с постоянной и переменной базой сравнения.

Обобщающие показатели анализа рядов динамики имеют практически похожие названия, и выполняют роль средневзвешенных показателей, для упрощения анализа. Их также пять:
- Средний абсолютный прирост.
- Средний коэффициент роста – рассчитывается по формуле средней геометрической.
- Средний темп роста.
- Средний темп прироста.
- Среднее значение одного процента прироста.
Формулы для расчета вышеуказанных показателей сведем в общую таблицу. Также для полноты картины приведем и формулы расчета средних уровней, которые были разобраны в первой части.
 Задание. Для закрепления прочитанного материала попытайтесь решить вот такую задачу. По представленным данным проведи все возможные расчеты.
Задание. Для закрепления прочитанного материала попытайтесь решить вот такую задачу. По представленным данным проведи все возможные расчеты.
| Год | Выпуск продукции, млн. руб. |
| 2010 | 219,7 |
| 2011 | 221,4 |
| 2012 | 234,2 |
| 2013 | 254,1 |
| 2014 | 241,8 |
| Итого | 1171,2 |
А для простоты можно воспользоваться вот такой таблицей для занесения итоговых расчетов.
| Год | y | Δ | К | Тр | Тпр | α | |||||
| Б | Ц | Б | Ц | Б | Ц | Б | Ц | Б | Ц | ||
| 2010 | 219,7 | — | — | — | — | — | — | — | — | — | — |
| 2011 | 221,4 | ||||||||||
| 2012 | 234,2 | ||||||||||
| 2013 | 254,1 | ||||||||||
| 2014 | 241,8 |
Если вам что-то не понятно, вы всегда можете спросить в комментариях или написать в нашу группу вконтакте! А также вы можете выслать туда решение, чтобы мы проверили его!
