Как осуществить поиск функции по известным значениям?
Положим, имеется набор известных чисел:
a1, b1, с1, R1
a2, b2, c2, R2
…
an, bn, cn, Rn
Rn = F(an, bn, cn).
Задача в том, чтобы по известным наборам {an, bn, cn, Rn} найти вид F.
Подскажите, в каком направлении копать, подзабыл с института математику…
-
Вопрос заданболее трёх лет назад
-
3142 просмотра
Вас интересует Feature Selection. en.wikipedia.org/wiki/Feature_selection . Куда дальше копать, сейчас подсказать не могу. Если интересует просто уменьшение размерности, а не какая фича важнее, то можно использовать PCA. Самые популярные алгоритмы реализованы в библиотеках Machinle learning типа WEKA.
Пригласить эксперта
По известному набору точек можно лишь предположить вид функции, например набор (-1, 0), (0, 0), (1, 0) может принадлежать как прямой y=0, так и синусоиде y=sin(πx) или полиному y=x3-x. Обычно вид функции выбирается из физической модели процесса, для которого получены данные.
На самом деле, в наборах {a1, a2 … an} не 3, а где-то 50 значений, т.е F – функция от кучи переменных. Наборы (a1, a2 .. an, Rn) можно вычислить сколь угодно раз (вычисляет программа по неизвестной мне формуле).
На самом деле задача скорее в следующем. При изменении некоторых переменных, значение F изменяется слабо или не изменяется вообще (таких переменных много). Нужно найти переменные не влияющие/сильно влияющие на значение F. Т.е есть 2 массива:
{a1, a2 .. an, F()=R1}, {b1, b2 .. bn, F()=R2}
и нужо найти корреляцию между ними.
Если заранее неизвестен хотя бы общий вид функции, то, по моему, проще дизассемблировать программу и разобраться в вычислениях, чем пытаться определить взаимозависимости между 50 параметрами. Например, для такой функции двух переменных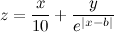
зависимость от y сильно проявляется только в малой области значений x в районе x=b. А ведь функция может быть и кусочно-непрерывной, например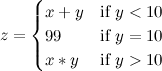
Про Feature Selection есть какая нибудь литература на русском?
В конце en.wikipedia.org/wiki/Feature_selection есть список с софтом. Может кто знает примеры/мануалы (желательно также на русском) практического применения?
-
Показать ещё
Загружается…
17 мая 2023, в 21:51
800 руб./за проект
17 мая 2023, в 21:34
500 руб./в час
17 мая 2023, в 21:27
2000 руб./за проект
Минуточку внимания
Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».
После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание.
Функция задана формулой «y = 2x − 1»
- Вычислить «y» при «x = 15»
- Найти значение «x», при котором
значение «y» равно «−19».
Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.
Запись решения выглядит следующим образом.
y(15) = 2 · 15 − 1 = 30 − 1 = 29
Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.
То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .
−19 = 2x − 1
Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.
Запомните!
![]()
Не забывайте про правило переноса в уравнениях.
При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.
−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.
−2x = 18 | · (−1)
2x = −18
Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .
2x = −18 | (: 2)
x = −9
Как проверить верно ли равенство для функции
Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».
Верно ли равенство
«f(−2) = −18»?
Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.
Важно!

Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.
Не забывайте использовать
правило знаков.
Неправильно
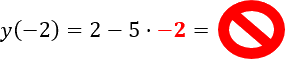
Правильно
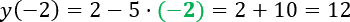
С помощью расчетов мы получили
«f(−2) = 12».
Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию «y = x2 −5x + 6»
Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).
Для этой задачи нет необходимости, строить график заданной функции.
Запомните!
![]()
Чтобы определить, принадлежит ли точка функции,
достаточно подставить её координаты в функцию (координату по оси
«Ox» вместо
«x» и координату по оси «Oy»
вместо «y»).
Если получится верное равенство, значит, точка принадлежит функции.
Вернемся к нашему заданию. Подставим в функцию «y = x2 − 5x + 6»
координаты точки (1; 2).
Вместо «x» подставим «1».
Вместо «y» подставим «2».
2 = 12 − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)
У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.
Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x2 − 5x + 6»?
Вместо «x» подставим «0».
Вместо «y» подставим «1».
1 = 02 − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)
В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x2 − 5x + 6»
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.
Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.
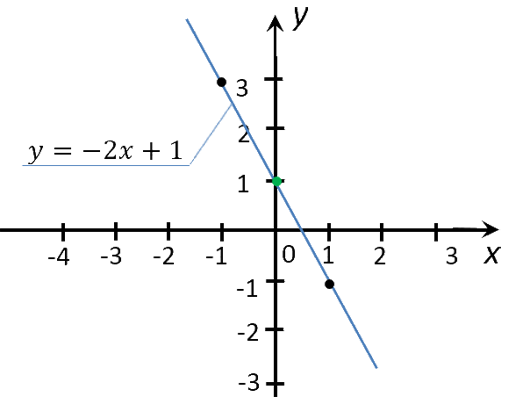
Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.
Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».
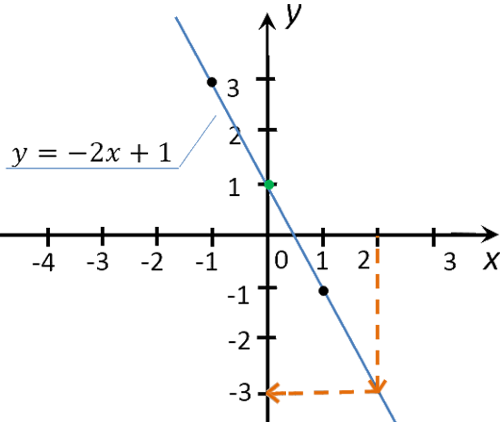
Полученное значение «−3» на оси «Oy» и будет искомым значением «y».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».
Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.
y(2) = −2 · 2 + 1 = −4 + 1 = −3
При расчетах мы также получили y = −3.
Значит, мы правильно получили координаты с графика функции.
Важно!

Все полученные координаты точки с графика функции обязательно проверяйте
подстановкой значений «x» в функцию.
При подстановке числового значения «x» в функцию в результате должно получиться
то же значение «y», которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
11 ноября 2018 в 15:46
Веточка Сакуры

Профиль
Благодарили: 0
Сообщений: 1

Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Функция y=f(x) является нечётной и при x ⩽0 задаётся формулой y= – x² — 8x.Найдите значение фун. в т. минимума (y min).
0
Спасибо
Ответить
12 ноября 2018 в 3:25
Ответ для Веточка Сакуры
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
ymin = y(4) = -16.
0
Спасибо
Ответить
17 сентября 2018 в 13:28
Alesger Mammedov

Профиль
Благодарили: 0
Сообщений: 1

Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Добрый день помогите пожалуйста с задачкой
f(x2-3x)=3x2+5x-4
f(3)=?
0
Спасибо
Ответить
17 сентября 2018 в 23:01
Ответ для Alesger Mammedov
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
f(3) = 26 ± 7√21
0
Спасибо
Ответить
13 ноября 2016 в 6:43
Роман Безбородов

Профиль
Благодарили: 0
Сообщений: 1

Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
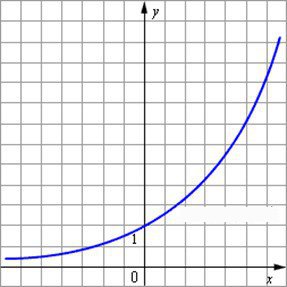 определите вид графика
определите вид графика
0
Спасибо
Ответить
14 ноября 2016 в 17:30
Ответ для Роман Безбородов
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
y = ax; a > 1.
0
Спасибо
Ответить
7 сентября 2016 в 22:08
Иван Баранов

Профиль
Благодарили: 0
Сообщений: 3

Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
у=Х2+2Х-3 найдите значение функции, если значение аргумента равно -2
у=3х-5 при каком значении аргумента значение функции раво 10
0
Спасибо
Ответить
8 сентября 2016 в 15:26
Ответ для Иван Баранов
Юлия Анарметова

Профиль
Благодарили: 0
Сообщений: 11

Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
аргумент это х значит у=(-2)2+2 · (-2)-3=4-4-3=-3
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5
0
Спасибо
Ответить
Как найти значение функции по значению аргумента
Как найти значение функции по значению аргумента? Это можно сделать с помощью формулы, задающей функцию.
Если функция задана формулой y=f(x), чтобы найти значение функции по данному значению аргумента, надо в формулу функции вместо каждого икса подставить это значение и вычислить значение y.
Пример.
1) Линейная функция задана формулой y=10x-7.
Найти значение функции, соответствующее значению аргумента, равному 3; -2,5; 1,4; 0.
Решение:
При x=3
при x=-2,5
при x=1,4
при x=0
2) Функция задана формулой
Найти значение функции при x, равном 10; -2; 1; 0.
Решение:
При x=10
при x=-2
при x=1
при x=0
Значение функции по данному значению аргумента можно найти также по графику. Как это сделать, мы рассмотрим в следующий раз.
www.algebraclass.ru
Как найти значение аргумента по значению функции
Как найти значение аргумента по значению функции? Это можно сделать с помощью формулы функции.
Если формула задана формулой вида y=f(x), чтобы найти значение аргумента по значению функции, надо в формулу вместо y подставить заданное значение функции и решить получившееся уравнение относительно икса.
Примеры.
1) Линейная функция задана формулой y=5x-8. Найти значение аргумента, при котором значение функции равно 7; -38;0.
Решение:
При y=7
Поменяем местами левую и правую часть, чтобы запись выглядела в привычном виде (знаки при этом менять не надо):
Это — линейное уравнение. Неизвестное — в одну сторону, известные — в другую (при переносе слагаемых из одной части в другую знаки меняются на противоположные):
Обе части уравнения делим на число, стоящее перед иксом:
Итак, при y=7 x=3.
При y= -38
При y= -38 x= -6.
При y=o
При y=0 x=1,6.
2) При каком значении аргумента значение функции
равно 0; 3?
Решение:
При y=0
Решаем квадратное уравнение.
При y=0 x=3 и x=0,5.
При y=3
Это — неполное квадратное уравнение. Общий множитель x выносим за скобки
и решаем уравнение типа «произведение равно нулю»:
При y=3 x=0 и x=3,5.
Значение аргумента по заданному значению функции можно также найти с помощью графика. О том, как это сделать, мы будем говорить в следующий раз.
www.algebraclass.ru
Как по значению аргумента найти соответствующее значение функции. ?
Как по значению аргумента найти соответствующее значение функции?
Аргумент — х, значение функции — y.
Нам известно некоторое значение аргумента, например, х = 2. Чтобы найти соответствующее ему значение функции нужно в формулу у = 6х + 12 вместо х подставить его значение, в нашем примере это число 2. Получаем:
у = 6*2 + 12 = 12 + 12 = 24
Итак, значению аргумента х = 2 соответствует значение функции у = 24.
Правило: чтобы по значению аргумента найти значение функции надо в формулу данной функции вместо х подставить его числовое значение.
б) Как найти значение аргумента, которому соответствует указанное значение функции?
Нам задано значение функции — y, например y = 6.
Чтобы найти значение аргумента, которому соответствует указанное значение функции нужно в формулу у = 6х + 12 вместо y подставить его значение, в нашем примере это число 6. Получаем уравнение:
6 = 6х + 12
6х = -6
х = -1
Итак, значению функции y = 6 соответствует значение аргумента х = -1.
Правило: чтобы по значению функции найти значение аргумента надо в формулу данной функции вместо y подставить его числовое значение.
подставляй найденный аргумент в условие и останется только одна переменная
Функцыя задана формулой y=5x-1.Найти значение функции, если значение аргумента равно -1.
а по графику как?
Большой ответ*
Надо подставить Х в формулу и решить
(получается уравнение)
touch.otvet.mail.ru
Вычислить значение функции — Мегаобучалка
Если у>0 ,вычислить и напечатать
Если у<0 ,напечатать ,y<0
Если у=0 ,вычислить и напечатать с=
Дано: b, c.
Если b=c, вычислить значения функций
и
где х изменяется на интервале от 0 до 5 с шагом 0,2.
Вывести на печать y,z,x.
Если b>c, вычислить .
Если b<c, вычисления закончить.
Если d 0, вывести на печать значения b,c.
Если d<0, вычисления закончить.
8. ВАРИАНТ
1.Вычислить
2. Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.
с заданной точностью e = 10-4
Дано: a, b, x
Если a>b,вычислить и напечатать значение функции
Если ,вычислить z=
Если z=0,напечатать “z=0”
Если z>0,вычислить и напечатать
Если z<0,вычисления закончить.
Дано: y, c, a.
Вычислить .
Если ,вычислить .
Если ,вычислить и ввести на печать только положительные значения функции , где x изменяется на интервале от –1 до 3 с шагом 0,1.
Если , вычисления закончить.
Если ,вывести на печать “d<0”.
9. ВАРИАНТ
1.Вычислить
2.Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.
при x=0.2 с заданной точностью e = 10-8
Дано: z, x
Вычислить
Если , вычислить
Если , вычислить
Если вычислить и напечатать
значение функции
Если , вычисления закончить.
4. Дано: а, b.
Вычислить
Если Вычислить
Если , напечатать значения a,b.
Если р>0, вычислить и напечатать
Если р<0, вычислить закончить.
Если P=0,вычислить функцию ,
где x изменяется на интервале от 1 до 5 с шагом 0,25;
Напечатать значения c,x,y.
10. ВАРИАНТ
1.Вычислить
2
. Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.
при x=0.7 с заданной точностью e = 10-3
(отсчёт начинается с нулевого члена)
Дано:a, b.
Если , вычислить
Если вычислить
Если вычисления закончить.
Если ,вычислить и напечатать
Если ,напечатать “Y ”
Если , вычислить и напечатать
Дано:b,а
Если ,вычислить
Если , вычислить значение функции ,
где x изменяется на интервале от –5 до 7 с шагом 1.
Вывести на печать только y>0.
Если с>11,5 , вычислить и напечатать .
Если ,вычислить и напечатать .
11. ВАРИАНТ
1.Вычислить
2. Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.
с заданной точностью e = 10-3
Дано: x ,y.
Вычислить
Если ,вычислить
Если t=0,напечатать x ,y
Если b>0, вычислить и напечатать
Если b<0, вычисления закончить
Еслиb=0, вычислить a=
Если a 0, вычислить и напечатать
Если a<0, вычислить закончить
Дано: а, b.
Если , вычислить
Если , напечатать значения a,b.
Если , вычисления закончить.
Если , вычислить значения функции ,
где х изменяется на интервале от –1 до 2 с шагом 0,1.
12. ВАРИАНТ
1.Вычислить
2. Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.
с заданной точностью e = 10-4
Дано:a,b,c
Если a+b c, вычислить r= ,
Если a+b=c, вычисления закончить
Если r<0, вычислить z=
Если r=0, напечатать “r=0”
Если r>0, вычислить y=
Если z ,вычислить и напечатать ,
Если z<15, вычислить и напечатать
Дано: a, b.
Вычислить
Если , вычислить значение функции
где x изменяется на интервале от 0.5 до 1.5 с шагом 0.1
Вывести на печать c, y, x.
Если Z<0, вычислить
Если вычисления закончить.
Если , напечатать “f>0”.
Если , напечатать значение .
13. ВАРИАНТ
1.Вычислить
2. Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.
при x=5 с заданной точностью e = 10-4
3. Дано: a, x, t, b, c, k=1, 2, 3,…..
Если , для функции ,
Определить и напечатать k, при котором z становится меньше a
Если b , вычислить y=
Если y< 0, напечатать ”y< 0”.
Если y³0, вычислить и напечатать
Дано: x, b, c.
Вычислить .
Если a>0,вычислить значения функции, ,
где x изменяется на интервале от -2 до 2 с шагом 0,2. Вывести на печать только y<0.
Если a<0,вычисления закончить.
Если a=0,вычислить и напечатать .
14. ВАРИАНТ
1.Вычислить
2. Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.
с заданной точностью e = 10-3
Дано: x , y , c .
Если x = 0 . Напечатать “ x = 0 “ .
Если x > 0 . Вычислить
Если x < 0 . Вычисления закончить.
Если a > 0 . Вычислить
Если a 0 . Напечатать x , y , c .
Дано: a, P
Если а<P, вычислить и напечатать
Если а< P, вычислить и напечатать b=0.6
Если а=P, вычислить
Y=
где x изменяется на интервале от -3 до 3 с шагом 0,4
Вывести на печать значения x,y
15. ВАРИАНТ
1.Вычислить
2. Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.
с заданной точностью e = 10-3
Дано:a,b,x
Если a>b,вычислить и напечатать значение функции
Если a<=b,вычислить z=
Если z=0,напечатать “z=0”
Если z>0,вычислить и напечатать
Если z<0,вычисления закончить.
Дано: b,а
Если b<a ,вычислить
Если , вычислить значение функции
, где x изменяется на интервале от –5 до 6 с шагом 1.
Вывести на печать только y>0.Если с>12,5 , вычислить и напечатать .
Если с 12,5 ,вычислить и напечатать .
16. ВАРИАНТ
1.Вычислить
2. Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.
с заданной точностью e = 10-4
Дано:y,c
Вычислить
Если x=0, напечатать”x=0”
Если x>0, вычислить
Если x<0,вычисления закончить
Если a>=12,5 ,вычислить и напечатать
Если a<12,5 ,вычислить и напечатать b=
Дано: с
Вычислить .
Если а=0, напечатать с
Если a>0, вычислить и напечатать значения функции
, где x изменяется на интервале от –1 до 5 с шагом 0,5,
y изменяется на интервале от 2 до 2 с шагом .
Если a<0, вычислить .
Если P , вычислить .
Если <5,8, вычисления закончить.
17. ВАРИАНТ
1.Вычислить
2.Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.
с заданной точностью e = 10-2
megaobuchalka.ru
Многое в поставленной вами задачи зависит от того Какие значения может
принимать Х изменяясь в своей области определения . Кроме того важно
сразу отметить что если вы ищете аналитическую закономерность (виде
некоторой формулы) то её может и не быть.
Если множество значений Х дискретно то можно использовать
любой из стандартных методов интерполяции : линейную, дробно-
линейную, многочлен Тейлора , Чебышева, Ньютана , Лагранжа и т.д
Приведу пример нахождения интерполяционного многочлена Тейлора
по следующим данным : при Х1=0 Y1=1 ,при X2=1 Y2=2 , при X3=2 Y3=1;
многочлен ищем ввиде: P(x)=A0+A1*X+A2*X^2 , где коэффициенты A0,A1,A2-
подлежат определению, подставляя последовательно вместо X значения Х1,Х2,Х3
а вместо P(x) значения Y1,Y2,Y3- соответственно получим следующию систему уравнений:
P(X1)=A0+A1*0+A2*0*0=A0=1 итак A0=1;
P(X2)=1+A1*1+A2*1*1=2
P(X3)=1+A1*2+A2*2*2=1+2*A1+4*A2=1 находим A1 и A2 из последних двух строк
Получим A1=-1 ,A2=2 итак искомый многочлен представляется P(x)=1 – X +2*X^2
Данный многочлен даёт представление о ВОЗМОЖНОЙ аналитической зависимости
между X и Y. Естественно этот результат не единственен.
Вообще же рекомендую прочитать книжку: Л.И. Турчак П.В. Плотников «Основы численных методов»
Ваша задача называется :- задачей Интерполяции.
Как найти значение функции по значению аргумента
Как найти значение функции по значению аргумента? Это можно сделать с помощью формулы, задающей функцию.
Если функция задана формулой y=f(x), чтобы найти значение функции по данному значению аргумента, надо в формулу функции вместо каждого икса подставить это значение и вычислить значение y.
Пример.
1) Линейная функция задана формулой y=10x-7.
Найти значение функции, соответствующее значению аргумента, равному 3; -2,5; 1,4; 0.
Решение:
При x=3
![]()
при x=-2,5
![]()
при x=1,4
![]()
при x=0
![]()
2) Функция задана формулой
![]()
Найти значение функции при x, равном 10; -2; 1; 0.
Решение:
При x=10
![]()
![]()
при x=-2
![]()
![]()
при x=1
![]()
при x=0
![]()
![]()
Значение функции по данному значению аргумента можно найти также по графику. Как это сделать, мы рассмотрим в следующий раз.
