Одним из распространённых форм деформации является сдвиг отдельных слоёв изделия в вертикальной или горизонтальной плоскости. Такое смещение называется – деформация сдвига. Изменение положения может вызывать постепенное или резкое изменение первоначальной формы конструкции или отдельной детали.
Виды деформации характеризуют порядок произведенного смещения и определяют порядок расчёта основных характеристик. В технической механике и сопромате рассматривают два вида деформации со сдвигом: плавное (смятие) и резкое (разрыв или срез).

Определение и общие сведения о деформации сдвига
Основным признаком, характеризующим деформацию сдвига, является сохранение постоянства объёма. Не зависимо от того, в каком направлении действуют силовые факторы этот параметр остаётся неизменным. Примеры проявления деформации сдвига можно обнаружить при проведении различного рода работ. К таким случаям относятся:
- при распиловке бруса;
- отрезание или рубка металла;
- в результате нарушения целостности крепления металлических или деревянных деталей, соединённых метизами;
- балки в местах крепления опор;
- места скрепления мостовых пролётов;
- крепёж на перемычках соединения железнодорожных рельс;
- разрезания листа бумаги ножницами.
При определённых условиях наблюдается чистый сдвиг. Он определяется как сдвиг, при котором на все четыре грани (например, прямоугольной детали) оказывают воздействие только напряжения, направленные по касательной к поверхности. В этом случае произойдёт плавный сдвиг всех слоёв детали от верхних к нижним слоям. Тогда внешняя сила изменяет форму детали, а объём сохраняется.
Для оценки величины сдвига и надёжности конструкции используют следующие параметры:
- величина, направление и точка приложения воздействующей силы;
- модуль сдвига;
- угол изменения внешних граней изделия;
- тангенциальное напряжение;
- модуль кручения (зависит от физико-механических характеристик материала);
Расчёт и практическое измерение этих параметров необходимы для оценки устойчивости и целостности конструкции. Формула, позволяющая вычислить допустимые изменения, учитывает все воздействия на конкретные слои детали и всю конструкции в целом.
Основными итоговыми параметрами считаются абсолютный и относительный сдвиг. Абсолютным он называется при равенстве углу возникшего отклонения от первоначального положения грани. Относительный равен частному от деления величины отклонения к расстоянию между гранями, расположенными на противоположных сторонах. Во время упругой деформации сдвига одни элементы подвергаются сжатию, другие расширению.
В случае воздействия деформации величина угла считается пропорциональной внешней силе. Увеличение степени воздействия может превратить деформацию сдвига в срез. Это приведёт к разрушению не только элементов крепления (болтов, шпилек, заклёпок), но и всей детали.
Для наглядности изменения формы детали при деформации сдвига динамика процесса обозначается с помощью величины угла смещения и векторов возникающих напряжений. Действующая сила направлена в сторону смещения слоёв рассматриваемой детали.

В современных условиях угол сдвига измеряется различными техническими приборами. Основным прибором для измерения параметров смещения является тензомер. Эти приборы работают на различных физических принципах:
- оптические (в том числе лазерные);
- акустические;
- рентгеновские; электрические;
- пневматические.
В этих приборах относительная деформация сдвига обрабатывается на современных вычислительных средствах с применением соответствующего программного обеспечения. Каждый метод обладает своими достоинствами и недостатками. Их применение зависит от поставленной задачи, технической и финансовой возможности.
Закон Гука
Основным соотношением, объединяющим физические параметры для описания протекающих процессов, является закона Гука для деформации сдвига. Этот закон позволят решить задачу нахождения угла отклонения грани объекта от исходного положения.
Небольшие напряжения вызывают углы отклонения, которые имеют небольшие величины. На итоговое значение влияют следующие параметры:
- сила упругости (её вектор направлен вдоль поверхности);
- модуль упругости второго рода;
- площадь поверхности.
Различные материалы обладают своим значением модуля упругости. Он является величиной постоянной и определяет способность материала оказывать сопротивление возникающему сдвигу.
Вычисляют касательное напряжение на гранях с помощью закона Гука. Он справедлив для малых углов и представляет произведение модуля сдвига на величину угла. Согласно теории упругости он позволяет установить связь с модулем Юнга и коэффициентом Пуассона.

Графически действие закона Гука представлено прямой линией. В качестве уравнения этой линии может использоваться уравнение прямой с угловым коэффициентом подробно описанном в аналитической геометрии. Она проходит начало координат, выбранной системы отсчёта.
Напряжение при сдвиге
Воздействие внешней силы на грань приводит к возникновению в изделии изменения формы. Все напряжения делятся на две категории: нормальные и касательные. Нормальными считаются внутренние напряжения, возникающие в различных слоях изделия, подверженного деформации.
Напряжения и деформации при сдвиге описываются с применением аналитических выражений и графических изображений. Общее состояние описывается пространственным (трёхкоординатным) напряжением. Если в конкретном случае можно выявить сечения, в которых оба вида напряжений равны нулю, можно перейти к более простым моделям описания этого процесса. Ими являются двухкоординатное (плоское) напряжённое состояние или линейное. Две последних модели являются частными случаями трёхкоординатного напряжённого состояния.

Касательные напряжения являются мерой скольжения одного поперечного слоя относительно другого. В изменениях на поверхности каждого слоя возникают только касательные напряжения. Для оценки полной картины деформации используют следующие теоретические положения:
- закон парности касательных напряжений;
- вычисление экстремальных нормальных напряжений;
- определение всех тангенциальных напряжений.
Оценка их всех при деформации смещения позволят оценить прочность конструкции.
Расчёты на прочность при сдвиге
Оценка прочностных характеристик изделий производится для определения наступления трёх моментов деформации:
- Смещение отдельных слоёв (появления угла деформации).
- Смятие элементов крепления.
- Сдвиг.
- Разрыв.
Расчёт на прочность необходим для определения условий наступления каждого из видов. На практике для более наглядной оценки характеристик прочности и стойкости к деформации решают существующие аналитические выражения и изображают эпюры отражающие направления воздействия различных видов напряжений.
Получение численных характеристик возможно благодаря применению разработанных методов решения систем дифференциальных уравнений. Уточнение аналитических выражений производится на основе принятых гипотез.
Расчёт допустимых напряжений производится на основании первой, третьей и четвёртой гипотезы прочности. Каждая из гипотез принимается для различных материалов, обладающих своими физико-механическими характеристиками.
Прочность находиться на каждом из этапов разработки конкретной детали. Сначала вычисляют величины допустимых напряжений и угол отклонения на предварительном (проверочном) этапе. Это позволяет определить их уровни, величины и направление приложенных сил. После этого приступают к проектированию. На этом этапе производится выбор материала детали и крепёжных элементов с учётом необходимой прочности каждого элемента конструкции. На конечном этапе ещё раз проверяют допустимые нормы нагрузки и способность готовой детали выдерживать допустимую и дополнительную нагрузку, то есть определяют запас прочности.
Наиболее показательными являются расчёты для чистого сдвига. В этом случае при расчёте рассматривают следующие аспекты решения задачи:
- Статический (составляется уравнение равновесия). В этом случае используется предположение о равномерности распределения касательных напряжений. Однако в некоторых случаях они распределяются не равномерно, что усложняет решение поставленной задачи. Он позволяет установить связь возникших напряжений с действующими внешними силами. Это производиться благодаря получению семейства решений дифференциальных уравнений равновесия для всего объёма детали.
- Геометрический (деформационный). Позволяет отобразить связь между отдельными небольшими участками исследуемой детали.
- Математический. Позволяет выбрать метод решения составленной системы уравнений. Провести математическое моделирование протекающих процессов.
- Физический. Устанавливает связь между физическими процессами при деформации с учётом физических свойств материала и возникшими напряжениями (механическими свойствами).
На математическом и физическом этапе рассмотрения поставленной задачи применяются следующие основные расчетные выражения и допущения:
- закон Гука для деформации смещения;
- гипотезы прочности (с учётом физических и механических свойств выбранного материала);
- выбор системы эквивалентных напряжений;
- упрощения при изображении эпюр, отображающих направления действующих сил и возникших напряжений;
- принятие основных положений для случая чистого сдвига.
Наиболее важный практический интерес представляют два случая – смятие и разрыв.
В первом случае происходит пластическая деформация детали, когда интенсивность возникших напряжений превышает предел текучести выбранного материала. Размеры такой деформации зависят от характера и интенсивности действия внешних сил, показателей прочности материала, изменения температурного режима. При интенсивности воздействия, превышающем прочность материала, происходит разрыв. Оба эти процесса приводят к нарушению механических соединений деталей (например, метизов, заклёпок, втулок).

Разработанные методы расчёта прочности позволяют проектировать и изготавливать детали с заданием, превышающим этот предел. Это позволяет существенно повысить надёжность и долговечность всей конструкции. В настоящее время разработан стройный математический аппарат создания моделей допустимой деформации. Его реализуют с применением созданных программных средств, которые позволяют получить числовые характеристики прочности и построить графические изображения эпюр в формате 3D графики.
В этой статье объясняется, как рассчитать деформацию сдвига. Деформация сдвига – это отношение изменения размеров из-за силы сдвига к исходным размерам заготовки.
Изменение размеров происходит в виде углового смещения. Сила сдвига действует параллельно плоскости поперечного сечения. Самолет смещается на некоторую величину, которая является линейным смещением. Угол, образованный этим смещением, дает угловое смещение.
Что такое сдвиг штамм?
Как обсуждалось в предыдущем разделе, деформация сдвига – это отношение изменения размеров из-за силы сдвига к исходным размерам заготовки. Он говорит нам о деформации в виде процентного значения.
Заготовка деформируется в плоскости, параллельной поперечному сечению заготовки. Создается впечатление, что слой заготовки движется.
Математически деформацию сдвига можно представить как
где,
гамма – деформация сдвига
L – исходная длина заготовки.

Изображение кредита: Боб Клеминтайм, Деформация одноосного сдвига, CC BY-SA 4.0
Что такое инженерное напряжение?
Техническая деформация – это безразмерное число, которое представляет собой отношение деформации заготовки к ее исходному размеру. Оно прямо пропорционально величине удлинения по длине.
Формула, приведенная в разделе выше, представляет собой инженерное напряжение. Когда тип деформации не упоминается, подразумевается, что имеется в виду инженерная деформация.
Что такое настоящий штамм?
Истинная деформация – это натуральное бревно от конечной длины заготовки к исходной длине заготовки. Он показывает мгновенную деформацию, развиваемую в заготовке.
Деформация, возникающая в заготовке в определенный момент, называется истинной деформацией. Это дает лучшее представление о том, что материал будет вести себя при нагрузке.
Математически истинную деформацию можно представить как
∈ = ln x (A0/A1)
где,
эта представляет собой истинный штамм
Как рассчитать деформацию сдвига?
Деформация сдвига – это отношение длины деформации заготовки к исходной длине заготовки.
Следующие шаги выполняются для рассчитать сдвиг штамм-
- Измерьте исходную длину заготовки.
- Приложите к материалу напряжение сдвига.
- Измерьте угол деформации.
- tan угла деформации дает деформацию сдвига.
Как рассчитать скорость деформации сдвига?
Скорость деформации можно определить как скорость изменения деформации во времени. Следовательно, это функция времени. Это первая разность деформации сдвига по времени.
Скорость деформации сдвига может быть рассчитывается по формуле приведен ниже-
γ = dγ/dt
где точка на гамме представляет скорость деформации сдвига
Скручивающее напряжение
Цилиндрический стержень испытывает на своей поверхности напряжение сдвига при скручивании. Напряжение скручивания – это напряжение, которое стремится повернуть плоскость цилиндрического стержня на некоторый угол.
Напряжение скручивания может быть задано соотношением, приведенным ниже. Формула скручивания может использоваться для определения угла скручивания, напряжения сдвига, крутящего момента деформации сдвига и т. Д., Если предоставлены соответствующие данные.
Как рассчитать деформацию сдвига при кручении?
Формула, описанная в предыдущем разделе, может использоваться для определения деформации сдвига, когда заготовка подвергается скручивающему напряжению.
Формула деформации сдвига обсуждается в разделах выше.
Из формулы на кручение деформация сдвига получается:
γ = Rθ/L
где,
тета – угол скручивания
L – длина заготовки
Как рассчитать деформацию сдвига по напряжению сдвига?
Модуль жесткости при сдвиге – это отношение напряжения сдвига к деформации сдвига. Чтобы найти деформацию сдвига из напряжения сдвига, мы делим напряжение сдвига на модуль сдвига. Мы получили,
где,
G – модуль жесткости
Как найти угол деформации сдвига?
Угол деформации сдвига – это угол, на который деформируется заготовка.
Угол деформации сдвига можно определить с помощью простой тригонометрии. Угол деформации сдвига – это тангенс угла между смещением X и исходной длиной L. Соседняя сторона образованного треугольника действует как исходная длина заготовки, а смещение действует как противоположная сторона в треугольнике.
Угол сдвига можно найти, используя приведенное ниже соотношение.
где,
Phi – угол деформации сдвига
Как найти среднюю деформацию сдвига?
Концепция деформации сдвига вступает в игру, когда заготовка испытывает деформацию с разных сторон.
Давайте рассмотрим деформацию сдвига, возникающую на двух концах, составляющую угол деформации сдвига альфа и бета соответственно.
Средняя деформация сдвига станет-
γ = α + β
Как найти угловую деформацию сдвига?
Деформация углового сдвига обсуждается в разделе выше. Деформация сдвига, которая описывает изменение угла между двумя линиями, которые изначально были перпендикулярны, называется угловой деформацией сдвига.
Математически это можно представить как
γ = тангенсаль
где,
альфа – угловая деформация сдвига
Напряжение сдвига в прямоугольной балке
Прямоугольная балка – это балка, поперечное сечение которой прямоугольное или квадратное. Величина напряжения сдвига, испытываемого в разных точках поперечного сечения, различна.
Это происходит потому, что расстояние от точки до приложения силы варьируется для разных точек. Столь разная сила, действующая на разные точки, приводит к переменному напряжению сдвига.
Напряжение сдвига максимально в центре тяжести и минимально на концах поперечного сечения. Напряжение сдвига параболически распределяется по прямоугольному поперечному сечению.
Что такое напряжение изгиба?
Как следует из названия, это напряжение вызывает изгиб заготовки при приложении нагрузки.
Напряжение изгиба – это напряжение, которое обычно действует на заготовку и вызывает изгиб вдоль продольной оси заготовки.
Что такое формула напряжения изгиба?
Аналогично торсионной формуле. Также существует формула изгиба, которая позволяет легко найти напряжение изгиба. формула напряжения изгиба приведено ниже
σb = Мy/I
Что такое полярный момент инерции?
Полярный момент инерции или второй момент инерции – это величина, используемая для объяснения сопротивления деформации, вызванной напряжением кручения.
Математически это можно представить как
где,
J – полярный момент инерции
Что такое модуль сечения?
Модуль сечения используется при проектировании изгибных элементов конструкции или балок. Его можно определить как отношение момента инерции поперечного сечения пучка относительно нейтральной оси к расстоянию крайнего волокна от центра.
Математически это можно представить как:
Z = I/гМакс
где,
Я момент инерции
Z – сечение модуля
Деформации сдвига
Р ассмотрим
ассмотрим
прямоугольный брусок, закрепленный
неподвижно нижней гранью. Под действием
касательной (тангенциальной) силы
F,
приложенной к верхней грани, брусок
получает деформацию, называемуюсдвигом.
Величина, равная тангенсу угла сдвига
![]() ,
,
называетсяотносительным сдвигом.
При упругих деформациях уголбывает очень мал, поэтому относительный
сдвиг определяется формулой:![]() .
.
Деформация сдвига приводит к возникновению
в каждой точке бруска тангенциального
напряжения,
которое определяется как модуль силы,
действующей на единицу площади
поверхности:
![]()
Закон Гука для сдвиговых деформаций
имеет вид:
![]() ,
,
где Gзависит только
от свойств материала и называетсямодулем сдвига. Для
большинства однородных изотропных тел![]() .
.
Модуль Юнга и модуль сдвига измеряются
в Паскалях.
Деформации кручения
Р ассмотрим
ассмотрим
стержень в виде прямого кругового
цилиндра радиусаr,
верхнее основание которого закреплено,
а в некотором произвольном сечении,
расположенном на расстоянииLот закрепленного, приложена пара
касательных силF,
момент которых по величине равен![]() и направлен вдоль оси цилиндра.
и направлен вдоль оси цилиндра.
Под действием вращающего момента все
сечения цилиндра поворачиваются на
угол тем больший,
чем дальше эти сечения расположены от
закрепленного основания. При
упругих деформациях угол кручения
пропорционален вращающему моменту:
![]()
Деформации кручения являются частным
случаем сдвиговых деформаций, поскольку
любое нижнее сечение испытывает сдвиг
относительно верхнего. Поэтому модуль
кручения можно выразить через модуль
сдвига. Детальный расчет приводит к
следующему выражению:
![]()
Силы трения
Т рение,
рение,
возникающее при относительном перемещении
сухих поверхностей твердого тела,
называетсясухим трением. Различают
три вида сухого
трения: трение покоя, скольжения и
качения..
Если на тело действует сила , но тело
сохраняет состояние покоя (неподвижно
относительно поверхности, на которой
оно находится), то это означает, что на
тело одновременно действует сила, равная
по величине и противоположная по
направлению, – сила трения покоя.
При увеличении силы , если тело сохраняет
состояние покоя, то увеличивается и
сила трения покоя. Сила трения покоя
всегда равна по величине и противоположна
по направлению внешней действующей
силе.
Сила трения скольжениявозникает
при скольжении данного тела по поверхности
другого тела. Чаще всего силу трения
скольжения принимают равной максимальной
силе трения покоя:
![]() ,
,
где - коэффициент
трения скольжения, зависящий от природы
и состояния соприкасающихся поверхностей
(в частности, от их шероховатости),N– сила нормального давления, прижимающая
трущиеся поверхности друг к другу.
Сила трения качениямала по сравнению
силой трения скольжения.
При движении твердого тела в жидкости
или газена него действует сила,
препятствующая движению. При малых
скоростяхсила сопротивленияпропорциональна первой степени скорости
тела:
![]() ,
,
при больших скоростях – приблизительно
пропорциональна квадрату скорости:
![]() .
.
Коэффициенты сопротивления k1иk2, а также
область скоростей, в которой осуществляется
переход от линейного закона к квадратичному,
в сильной степени зависят от формы и
размеров тела, направления его движения,
состояния поверхности тела и от свойств
окружающей среды.
Краткие сведения о законах, описывающих
разные виды взаимодействий, приведены
в таблице 4.
Информация о силах Таблица 4
|
Происхождение |
Законы |
|
Гравитационное притяжение материальных |
Закон всемирного тяготения
(G– |
|
Действие |
Сила тяжести
|
|
Действие |
Закон Гука
(x– смещение от положения равновесия) |
|
Взаимодействие |
Сила |
|
Сила |
|
|
сила |
|
|
Сопротивление |
Сила вязкого трения при малых скоростях |
|
Сила вязкого трения при больших скоростях |
|
|
Выталкивающая |
Закон Архимеда (m– масса вытесненной жидкости или газа) |
|
Действие |
(E |
|
Действие |
Сила Лоренца (B– вектор магнитной индукции) |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
20.11.2018320.51 Кб13T2.doc
- #
- #
- #
- #
- #
- #
- #
- #
Лекция 6. СДВИГ (СРЕЗ)
Понятие чистого сдвига. Элементы конструкций, работающих в условиях
чистого сдвига. Деформации, напряжения. Площадки чистого сдвига. Закон
Гука при сдвиге. Условие прочности при сдвиге (срезе).
Сдвиг (срез) – вид деформации, при котором одна часть стержня
смещается относительно другой (скользит). Сдвиг, как вид нагружения,
встречается редко и имеет место в заклепочных и сварных соединениях.
Деформация сдвига происходит в случае, если к стержню приложены две
равные по модулю противоположно направленные силы P , перпендикулярные
к его продольной оси. Расстояние между этими силами должно быть малым,
чтобы можно было пренебречь моментом, создаваемым силами.
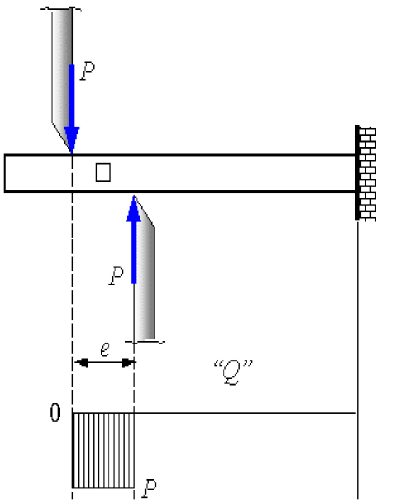
Рис. 16. Расчетная схема при сдвиге
Используя метод сечений (разрезая стержень между силами P), можно
установить, что в поперечном сечении стержня возникает только одно
внутреннее усилие – поперечная сила Q.
Такой вид нагружения, при котором в поперечных сечениях стержня действует только поперечная сила, называют чистым сдвигом.
Мера скольжения одного поперечного сечения относительно другого – касательные напряжения τ.
Принято, что касательные напряжения распределены по всей площади
поперечного сечения равномерно. Если в поперечном сечении стержня
площадью A возникает внутренняя поперечная сила Q = P, то касательные
напряжения в любой точке этого сечения будут равны: T = Q/A = P/A.
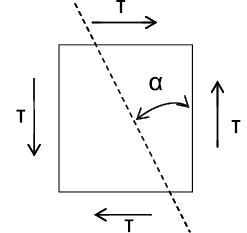
Рис. 17. Чистый сдвиг
При чистом сдвиге возникает плоское напряженное состояние, тогда
напряжения, действующие на площадке составляющей угол α с вертикальной
исходной площадкой равны:
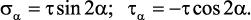
Касательные напряжения τ, приведенные на рис. 17, по абсолютной
величине больше касательных напряжений по любым другим площадкам. Таким
образом, они являются экстремальными, а площадки, по которым они
действуют – площадками сдвига. Так как по этим площадкам не действуют
нормальные напряжения, то их называют площадками чистого сдвига и они
образуют с главными площадками углы, равные 45°.
При чистом сдвиге нормальные напряжения на любых двух взаимно
перпендикулярных площадках равны друг другу по модулю и противоположны
по направлению.
Касательные напряженияτ измеряются в таких же единицах, что
и нормальные напряжения: мегапаскалях, килоньютонах на квадратные
сантиметры, килограммах силы на квадратный сантиметр (МПа, кН/см2,
кгс/см2) и т.п.
В результате сдвига одно поперечное сечение стержня смещается
относительно другого на величину δ, называемую абсолютным сдвигом.
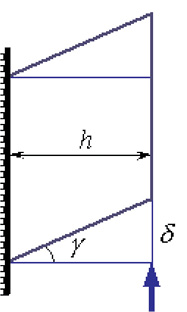
Рис. 18. Углы сдвига
Малый угол γ, на который изменится первоначально прямой угол, –
относительный сдвиг, выражается в радианах. Угол сдвига γ пропорционален
касательным напряжениям. Математическая зависимость между углом сдвига
и касательным напряжением называется законом Гука при сдвиге:
τ = γG.
Зависимость между модулем сдвига и модулем Юнга:
G = E/[2(1 + μ)].
Значение коэффициента Пуассона μ находится в пределах 0 ≤ μ ≤ 0,5.
Условие прочности при сдвиге имеет вид:
τ = Q/A ≤ [τ]. (7)
У этого термина существуют и другие значения, см. Сдвиг.

Сдвиг — в сопротивлении материалов — вид продольной деформации бруса, возникающий в том случае, если сила прикладывается касательно его поверхности (при этом нижняя часть бруска закреплена неподвижно) — одна боковая грань смещается параллельно противоположной грани.
Относительная деформация сдвига определяется по формуле:
,
где Δx — абсолютный сдвиг параллельных слоёв тела относительно друг друга; l — расстояние между слоями (для малых углов 
См. также[править | править код]
- Относительная деформация
