Как найти расстояние по диагонали по клеткам
Найдите расстояние между противоположными углами гаража (длину диагонали) в метрах.
На плане изображено домохозяйство по адресу с. Иволгино, 5-й Заречный пер, д. 3 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится сарай, а справа — гараж. Площадь, занятая гаражом, равна 48 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и сарая, на участке имеется теплица, расположенная на территории огорода (огород отмечен на плане цифрой 5). Перед гаражом имеется площадка, вымощенная тротуарной плиткой размером 0,2 м × 0,1 м и отмеченная на плане цифрой 6.
Тип 1 № 369666 
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | гараж | теплица | жилой дом | сарай |
|---|---|---|---|---|
| Цифры |
При входе на участок слева от ворот находится сарай, а справа — гараж. Значит, сарай отмечен цифрой 3, а гараж — цифрой 2. Жилой дом находится в глубине территории, поэтому жилой дом отмечен цифрой 4. Помимо гаража, жилого дома и сарая, на участке имеется теплица, расположенная на территории огорода (огород отмечен на плане цифрой 5). Следовательно, теплица отмечена цифрой 1.
Задание №19 ОГЭ по математике
В 19 задании необходимо найти какую-либо часть фигуры, нарисованной на клетчатой бумаге. Именно клетчатая бумага 1×1 является особенностью данного задания. Задание не сложное, необходимо внимательно посчитать количество клеток и при необходимости выполнить действие. Опять же нам понадобятся элементарные знания геометрии для успешного решения данного задания. Ниже я разобрал типичные задания. Давайте на них посмотрим.
Разбор типовых вариантов задания №19 ОГЭ по математике
Первый вариант задания
На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.
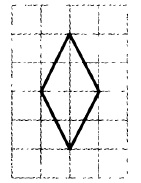
Решение:
Внимательно смотрим на рисунок и видим, что длина одной диагонали ромба равна 2, а второй 4.
Так как нас спрашивают длину большей диагонали, то в ответе нужно указать 4.
Второй вариант задания
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии.
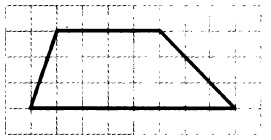
Решение:
Мы знаем, что средняя линия равна полусумме оснований. Нижнее основание данной трапеции равно 8 клеткам, а верхнее — 4 клеткам. Полусумма оснований:
Третий вариант задания
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
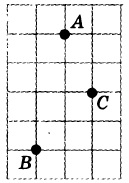
Решение:
Проведем необходимые отрезки:
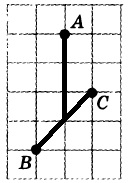
Из рисунка можно вычислить длину — это 3.
Демонстрационный вариант ОГЭ 2019
Найдите тангенс острого угла, изображённого на рисунке.
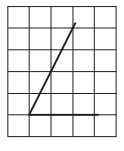
Решение:
Детализируем рисунок. Проведем вертикальную линию, которая отсекает от сторон угла 2 клетки по горизонтали . В результате получен прямоугольный ∆АВС:
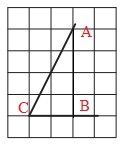
Чтобы получить ответ на вопрос задачи, требуется найти tg∠C.
Согласно определению тангенса, из треугольника ∆АВС можем записать:
По рисунку подсчитываем длины отрезков АВ и ВС (по кол-ву клеток):
Четвертый вариант задания
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
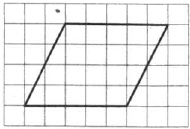
Решение:
Площадь параллелограмма вычисляется так:
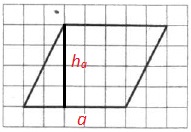
Теперь определим их длины по рисунку:
Вычисляем искомую площадь:
Пятый вариант задания
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.
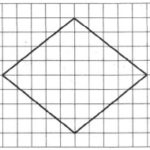
Решение:
Площадь ромба будем искать через его диагонали:
Линии диагоналей обозначим на рисунке красным:
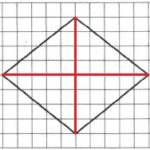
Обозначим меньшую диагональ через d1, большую – через d2 (можно наоборот). Определим их длины из рисунка:
Найдите расстояние между противоположными углами (диагональ) участка в метрах.

Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Решение.
Найдём расстояние между противоположными углами участка по теореме Пифагора:


СДАМ ГИА: РЕШУ ОГЭ
Образовательный портал для подготовки к экзаменам
Математика
сайты — меню — вход — новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
НАШИ БОТЫ
На сайте что-то не так? Отключите адблок
Новости
30 марта
Подготовься к ЕГЭ или ОГЭ за 1,5 месяца на курсе Флеш
21 марта
Новый сервис: рисование
9 февраля
Об ошибках в математике: проверьте браузер
31 января
Внедрили тёмную тему!
17 января
Разместили утвержденное расписание ОГЭ 2022
9 октября
Как восстановить доступ к Решу ЕГЭ, если у вас Windows XP
ЧУЖОЕ НЕ БРАТЬ!
Зайчиков и Поваляев стащили наши тесты
Задания
Версия для печати и копирования в MS Word
Задание 18 № 348446
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Спрятать решение
Решение.
По рисунку видно, что длина большей диагонали равна 10.
Ответ: 10.
Аналоги к заданию № 348446: 348586 349027 349478 350071 352059 352113 352152 352709 352791 353130 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2022
Характеристика задания
Задание 12 ОГЭ по математике представляет собой задачу по планиметрии на вычисление по готовому чертежу, изображённому на клетчатой бумаге. В таких задачах данные представлены в виде чертежа на бумаге в клетку, причём размеры клеток одинаковы и заданы условием. Это задачи на вычисление углов, расстояний, площадей, связанные со всеми изучаемыми в школьном курсе фигурами. Клетки в таких задачах по су- ти выполняют роль линейки: посчитав «по клеточкам» необходимые длины и используя известные геометрические факты и свойства, можно довольно быстро получить ответ на вопрос задачи. К этим задачам вплотную примыкают задания на вычисление элементов плоских фигур по готовому чертежу, на котором указаны координаты некоторых точек фигуры (например, вершин треугольника или четырёх- угольника), позволяющие после выполнения несложных вычислений ответить на вопрос задачи. При этом, как правило, не требуется применения дополнительных формул метода координат
Фигуры на квадратной решетке
В 12 задании необходимо найти какую-либо часть фигуры, нарисованной на клетчатой бумаге. Именно клетчатая бумага 1×1 является особенностью данного задания. Задание не сложное, необходимо внимательно посчитать количество клеток и при необходимости выполнить действие. Опять же нам понадобятся элементарные знания геометрии для успешного решения данного задания. Ниже я разобрал типичные задания. Давайте на них посмотрим.
На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.
Внимательно смотрим на рисунок и видим, что длина одной диагонали ромба равна 2, а второй 4.
Так как нас спрашивают длину большей диагонали, то в ответе нужно указать 4.
Ответ: 4.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии
Мы знаем, что средняя линия равна полусумме оснований. Нижнее основание данной трапеции равно 8 клеткам, а верхнее — 4 клеткам. Полусумма оснований:
( 8 + 4 ) / 2 = 6
Ответ: 6
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Проведем необходимые отрезки:
Из рисунка можно вычислить длину — это 3.
Ответ: 3.
Четвертый вариант задания (демонстрационный вариант 2017)
Найдите тангенс угла AOB треугольника, изображённого на рисунке.
Для успешного решения все что нам нужно — это определение тангенса: отношение противолежащего катета к прилежащему.
В нашем случае, это означает:
AB / AO
Длины возьмем, посчитав число клеток:
AB = 4
AO = 2
AB / AO = 4 / 2 = 2
Ответ: 2
Найдите площадь территории, которая не занята постройками и полями. Ответ дайте в квадратных метрах.
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м2 гравием, требуется 0,2 м3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Жилой дом | Репа | Капуста | Кукуруза |
|---|---|---|---|---|
| Цифры |
2
Гравий продаётся в больших мешках по 2 м3. Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между полями?
3
Найдите расстояние между противоположными углами (диагональ) участка в метрах.
4
Владимир планирует купить трактор для обслуживания полей. Он рассматривает два варианта: трактор с бензиновым двигателем и трактор с дизельным двигателем. Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице.
| Цена трактора |
Средний расход топлива |
Стоимость топлива руб. за л |
|
|---|---|---|---|
| Дизельный двигатель | 990 000 | 5,5 л/ч | 47 |
| Бензиновый двигатель | 900 000 | 7 л/ч | 53 |
Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?
Спрятать решение
Решение.
Площадь всего участка равна
м2.
Площадь гаража равна
м2.
Площадь жилого дома равна
м2.
Площадь полей, засеянных капустой, морковью и репой, равна
м2.
Площадь полей, засеянных кукурузой и картофелем, равна
м2.
Таким образом, площадь территории, которая не занята постройками или полями, равна
м2.
Ответ: 248.
Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.
Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Перечислим свойства квадрата:
- Все углы квадрата — прямые, все стороны квадрата — равны.
- Диагонали квадрата равны и пересекаются под прямым углом.
- Диагонали квадрата делят его углы пополам.

Площадь квадрата, очевидно, равна квадрату его стороны: .
Диагональ квадрата равна произведению его стороны на , то есть
.
Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.
1. Найдите сторону квадрата, диагональ которого равна .
Мы знаем, что . Тогда
.
2. Найдите радиус окружности, описанной около квадрата со стороной, равной .

Очевидно, радиус окружности равен половине диагонали квадрата.
Ответ: .
3. Найдите сторону квадрата, описанного около окружности радиуса .

Диаметр окружности равен стороне квадрата.
Ответ: .
4. Найдите радиус окружности, вписанной в квадрат , считая стороны квадратных клеток равными
.

Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.
Ответ: .
5. Найдите радиус окружности, вписанной в четырехугольник
. В ответе укажите
.

Считаем стороны клеток равными единице. Четырехугольник — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.
Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, . Она равна
. Тогда радиус вписанной окружности равен
. В ответ запишем
.
Ответ: .
|
Найдите расстояние между противоположными углами детской комнаты в метрах. Ответ запишите в виде
Задача, кажущаяся лёгкой на первый взгляд оказывается весьма сложной. Ведь нам нужно не что иное, как числовой параметр “d”
Ясно одно, что данные для множества задач, в которых присутствуют паркет, газ электричество, коридор и разнообразные комнаты. Но нас интересует только детская комната.
Самое интересное в этой задаче это игра с числами. Фактически мы ищем не гипотенузу одного из треугольников, а диагональ квадрата со стороной равной 2². Для этого существует аксиома, что диагональ квадрата со стороной равной 2² равна дроби в числителе которой сумма двух сторон, она равна 8, а в знаменателе корень квадратный основания стороны (которое равно 2) Я понимаю, что объяснение весьма путанное, но так и есть на самом деле. Поэтому решение выглядит вот так: (4 + 4) : √2 = 8 : √2; для красоты рисунок:
Но, а каков ответ? Он равен 5.65685424949 ~ 5.7 автор вопроса выбрал этот ответ лучшим Конгламерантус 2 года назад Итак, дано что сторона каждой клеточки на плане равна 1 метру. Справа от санузла и находится детская комната. Она отмечена на плане цифрой 4. Её площадь определяем просто путем умножения: 4×4=16м2 Как видно из плана, комната квадратная, и каждая сторона, это 4 клетки, то есть 4 метра. Для вычисления расстояния между противоположными углами детской комнаты, будем применять Теорему Пифагора. Это расстояние, являясь отрезком, разбивает квадрат комнаты на два равнобедренных треугольника, являясь при этом гипотенузой. Ответ на задачу запишем в требуемой форме: l=√4²+4²=√32=√16*2=√16*√2=4√2=4*√(4/2)=8/√2
noble-lion 2 года назад В условиях задания сказано, что каждая клетка плана квартиры – есть квадрат со сторонами 1 метр на 1 метр, то есть – один квадратный метр. Теперь, относительно детской комнаты. Она расположена в четвёртом квадрате (№ 4), со сторонами (4 x 4), что по площади составляет – 16 кв. метров. А далее, речь идёт о расстоянии между противоположными точками квадрата. Условно проведём линию и у нас получится “гипотенуза”, объединяющая два одинаковых по площади треугольника. Чтобы легче воспринимать, я нарисую этот треугольник. Обозначим длину нашей гипотенузы – L и согласно теоремы Пифагора: L = √16 + 16; Длина равна √32 или √16 x 2 или 4 x √2 или 4 x √4/2 что равнозначно = 8/√2
Пашенька 12 месяцев назад Перед нами – план квартиры. Для начала разберемся в расположении помещений.
В данной задаче нас интересует только детская комната, на плане она обозначена цифрой 4. Также из условия нас интересуют размеры клеточки, сторона – 1 метр. Подсчитываем и получаем, что параметры комнаты – 4х4.
Полученное расстояние – 4√2, однако условие требует ответ в другой форме.
Ответ: 4.
Росинка Роса 2 года назад Условие задачи, на мой взгляд, перегружено информацией. Скорее всего составители сделали это с намерением увести рассуждение решающего немного в сторону. Но мы не поддадимся, и оставим без внимания факт, что в квартире проведено электричество и газ, нам не нужно знать и количество комнат и их назначение. Для решения задачи нам нужно только знание размеров комнаты. Они вычисляются с помощью указанного масштаба: одна клетка на чертеже – квадрат со стороной 1м. Подсчитываем размеры – это будет 4 метра в ширину и 4 метра в длину. Квадрат. Соединив противоположные углы условной линией, мы разделим комнату как бы на два прямоугольных треугольника. Искомое расстояние – это расстояние гипотенузы треугольника. Она вычисляется по теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов) Сумма квадратов катетов будет следующая (4²+4²=32) Теперь остается извлечь квадратный корень из 32 и мы получим искомое расстояние = 8/√2 Если вычислить, то получится 5.65 м.
Дормидонт Павлов 3 года назад Детская – это комната №4. Её площадь 4*4=16 м2 Сторона комнаты – 4 м По теореме пифагора найдём расстояние между противоположными углами (l), которое фактически является гипотенузой прямоугольного равнобедренного треугольника. Следовательно: l=√4²+4²=√32=√16*2=√16*√2=4√2=4*√(4/2)=8/√2
габбас более года назад Сначала нужно определить по схеме детскую комнату. Читаем условие: “При входе в квартиру расположен коридор, отмеченный цифрой 2. Слева от него расположен балкон. Перед входом в квартиру располагается совмещённый санузел, а справа от него — детская комната.“. Далее определяем размеры комнаты в метрах. Так как по условию сторона клетки равна 1 метру, то длина и ширина детской комнаты соответственно равны 4 метрам. Теперь найдём расстояние между противоположными углами этой комнаты по теореме Пифагора:4^2+4^2 = 32, V32=4*V2 (4 корень из 2). Запишем ответ в требуемой форме: 4*V2/V2 =4. Ответ: 4. Знаете ответ? |
Версия для печати и копирования в MS Word
1
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
2
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до прямой BC. Ответ выразите в сантиметрах.
3
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.
4
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
5
На клетчатой бумаге с размером клетки 1х1 отмечены три точки: A, B и
Найдите расстояние от точки A до середины отрезка BC.
6
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
7
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
8
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
9
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
10
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
11
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
12
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
13
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
14
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
15
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
16
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
17
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

Бакирова Лариса Дамировна , МБОУ СОШ №11, Серовский ГО

Подготовка к ОГЭ. Задание №18 «Фигуры на квадратной решётке»

Задание 18 ОГЭ по математике представляет собой задачу по планиметрии на вычисление по готовому чертежу, изображённому на клетчатой бумаге. Данные в таких задачах даются в виде чертежа на бумаге в клетку, причём размеры клеток одинаковы и заданы условием. Это задачи на вычисление углов, расстояний, площадей, связанные со всеми изучаемыми в школьном курсе фигурами. Клетки в таких задачах по сути выполняют роль линейки: посчитав «по клеточкам» необходимые длины и используя известные геометрические факты и свойства, можно довольно быстро получить ответ на вопрос задачи. К этим задачам вплотную примыкают задания на вычисление элементов плоских фигур по готовому чертежу, на котором указаны координаты некоторых точек фигуры (например, вершин треугольника или четырёхугольника), позволяющие после выполнения несложных вычислений ответить на вопрос задачи. При этом, как правило, не требуется применения дополнительных формул метода координат.

Основные типы задач
- Определение тангенса угла;
- Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника);
- Определение расстояния от точки до прямой (отрезка);
- Определение длины средней линии треугольника и трапеции;
- Определение длины большего катета, большей диагонали;
- Определение площади сложных или составных фигур;
- Определение градусной меры вписанного угла.

- При решении задач с использованием клетчатой бумаги важно помнить, что «клеточки» должны помогать! А значит, нужно подумать как они могут помочь.
- По «клеточкам» легко построить прямоугольный треугольник. Следовательно, могут помочь все теоретические факты связанные с прямоугольным треугольником.

Расстояние от точки до прямой
Средняя линия треугольника
Средняя линия трапеции
Диагонали ромба

Определение расстояния от точки до прямой (отрезка)
Что нужно вспомнить:
- Расстояние от точки до прямой равно перпендикуляру, опущенному из этой точки на прямую.
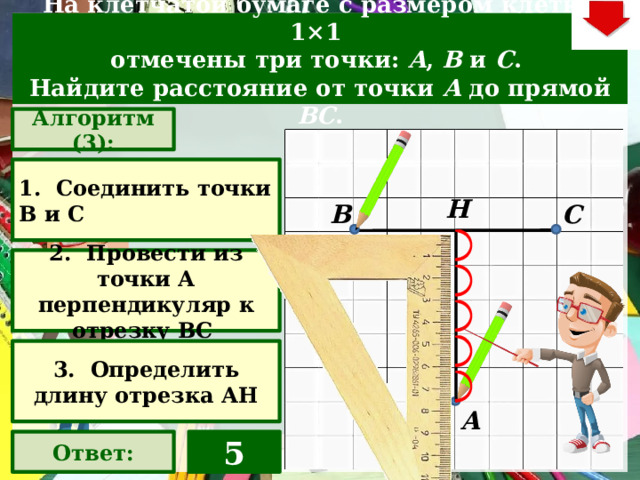
На клетчатой бумаге с размером клетки 1×1
отмечены три точки: A , B и C .
Найдите расстояние от точки A до прямой BC .
Алгоритм (3):
1. Соединить точки В и С
Н
В
С
2. Провести из точки А перпендикуляр к отрезку ВС
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм – последовательно три раза
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Определить длину отрезка АН
А
5
Ответ:
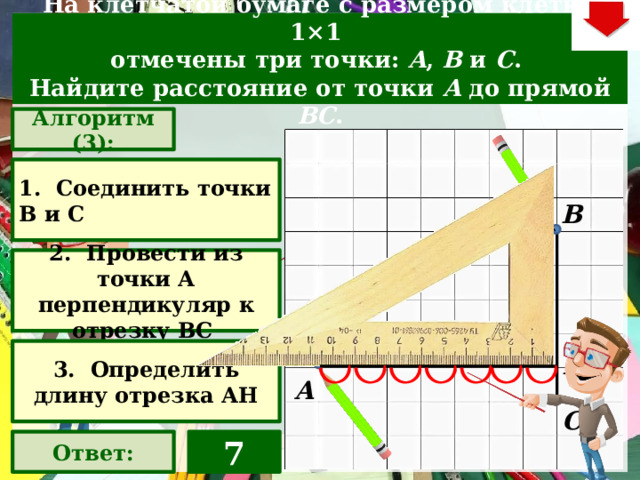
На клетчатой бумаге с размером клетки 1×1
отмечены три точки: A , B и C .
Найдите расстояние от точки A до прямой BC .
Алгоритм (3):
1. Соединить точки В и С
В
2. Провести из точки А перпендикуляр к отрезку ВС
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм – последовательно три раза
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Определить длину отрезка АН
Н
А
С
Ответ:
7

На клетчатой бумаге с размером клетки 1×1
отмечены три точки: A , B и C .
Найдите расстояние от точки A до прямой BC .
Ответ:
6
Проверка (3):
Н
С
В
1. Соединить точки В и С
2. Провести из точки А перпендикуляр к отрезку ВС
Задача. Решают учащиеся самостоятельно. После озвучивания и визуализации ответа (кнопка «Ответ»), необходимо визуализировать решение задачи (для всего класса) – нажимаем на прямоугольник «Проверка» – последовательно три раза.
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
6
3. Определить длину отрезка АН
А
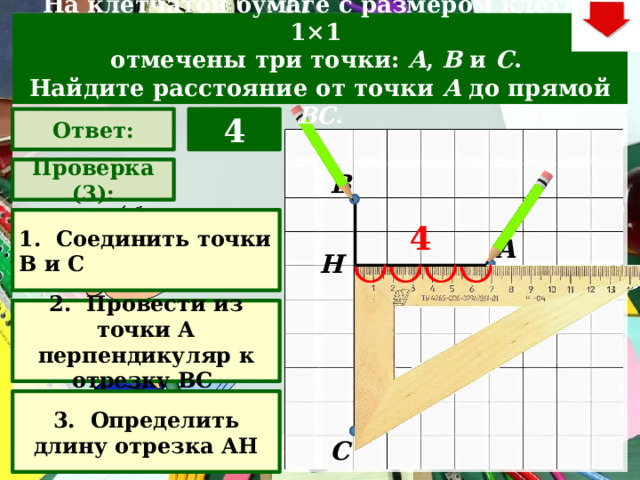
На клетчатой бумаге с размером клетки 1×1
отмечены три точки: A , B и C .
Найдите расстояние от точки A до прямой BC .
4
Ответ:
Проверка (3):
В
1. Соединить точки В и С
4
А
Н
2. Провести из точки А перпендикуляр к отрезку ВС
Задача. Решают учащиеся самостоятельно. После озвучивания и визуализации ответа (кнопка «Ответ»), необходимо визуализировать решение задачи (для всего класса) – нажимаем на прямоугольник «Проверка» – последовательно три раза.
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Определить длину отрезка АН
С

Определение длины средней линии треугольника и трапеции
Что нужно вспомнить:
- Средняя линия треугольника параллельна третьей стороне и равна её половине;
- Средняя линия трапеции равна полусумме оснований.

На клетчатой бумаге с размером клетки 1×1
изображён треугольник ABC .
Найдите длину его средней линии, параллельной АC .
Теория
В
Средняя линия тр-ка, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.
4
Алгоритм
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Теория!
- «Алгоритм» – визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
8
Определить длину отрезка АС и разделить пополам
С
А
4
Ответ:
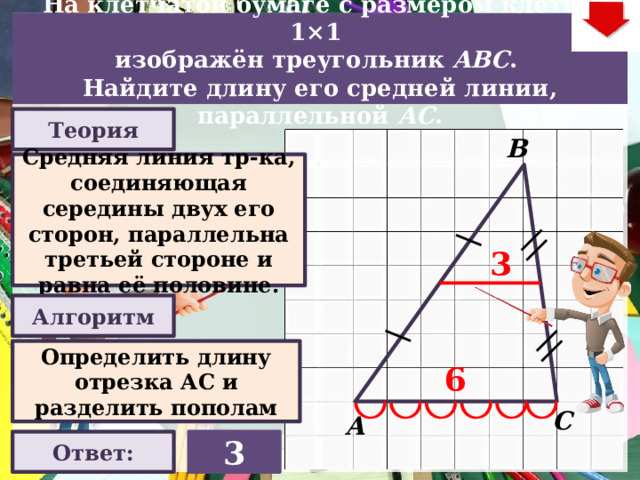
На клетчатой бумаге с размером клетки 1×1
изображён треугольник ABC .
Найдите длину его средней линии, параллельной АC .
Теория
В
Средняя линия тр-ка, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.
3
Алгоритм
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Теория!
- «Алгоритм» – визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
Определить длину отрезка АС и разделить пополам
6
С
А
3
Ответ:
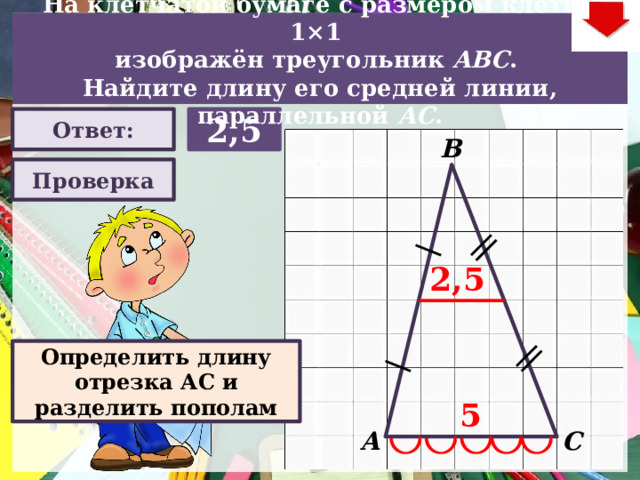
На клетчатой бумаге с размером клетки 1×1
изображён треугольник ABC .
Найдите длину его средней линии, параллельной АC .
2,5
Ответ:
В
Проверка
2,5
Задача. Решают учащиеся самостоятельно. После озвучивания и визуализации ответа (кнопка «Ответ»), необходимо визуализировать решение задачи (для всего класса) – нажимаем на прямоугольник «Проверка)
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
Определить длину отрезка АС и разделить пополам
5
А
С
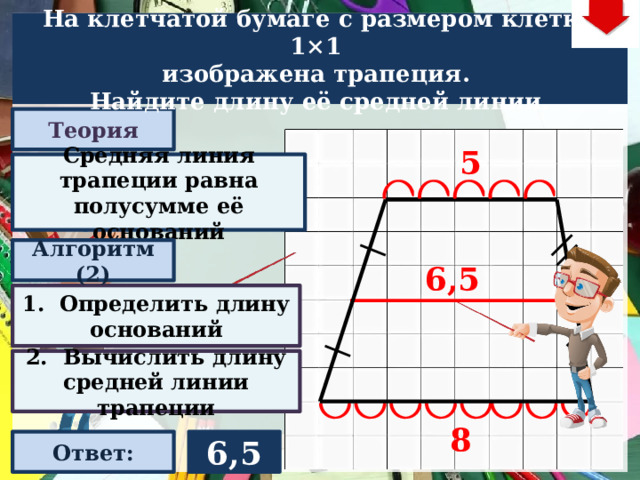
На клетчатой бумаге с размером клетки 1×1
изображена трапеция.
Найдите длину её средней линии.
Теория
5
Средняя линия трапеции равна полусумме её оснований
Алгоритм (2)
6,5
1. Определить длину оснований
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Теория!
- «Алгоритм» – последовательно 3 раза – визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
2. Вычислить длину средней линии трапеции
8
Ответ:
6,5
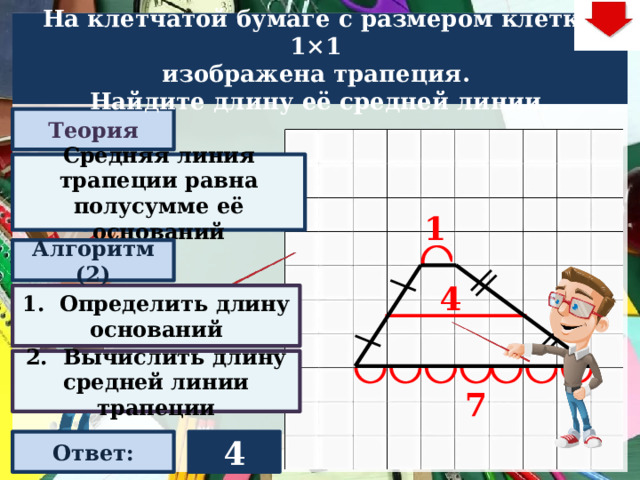
На клетчатой бумаге с размером клетки 1×1
изображена трапеция.
Найдите длину её средней линии.
Теория
Средняя линия трапеции равна полусумме её оснований
1
Алгоритм (2)
4
1. Определить длину оснований
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Теория!
- «Алгоритм» – последовательно 3 раза – визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
2. Вычислить длину средней линии трапеции
7
Ответ:
4
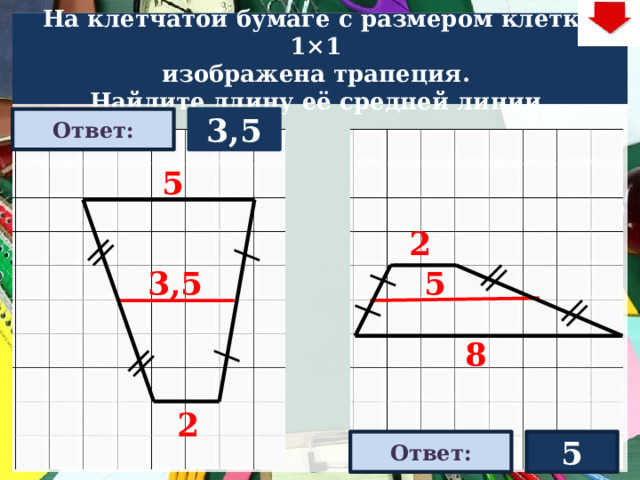
На клетчатой бумаге с размером клетки 1×1
изображена трапеция.
Найдите длину её средней линии.
3,5
Ответ:
5
2
3,5
5
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
8
2
Ответ:
5

Определение длины большего катета, большей диагонали
Что нужно вспомнить:
- Стороны прямоугольного треугольника: катеты – образуют прямой угол:
гипотенуза – лежит напротив прямого угла.
- Диагональ – отрезок соединяющий две не соседние вершины.
 4 1. Определить длину диагоналей ромба Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи. Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи. Алгоритм работы с триггерами 1. «Алгоритм» – последовательно 2 раза – визуализация исполнения решения настроена автоматически. «Ответ» В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ вернуться на слайд выбора следующей задачи 2. Сравнить длины диагоналей Ответ: 8 ” width=”640″
4 1. Определить длину диагоналей ромба Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи. Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи. Алгоритм работы с триггерами 1. «Алгоритм» – последовательно 2 раза – визуализация исполнения решения настроена автоматически. «Ответ» В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ вернуться на слайд выбора следующей задачи 2. Сравнить длины диагоналей Ответ: 8 ” width=”640″
На клетчатой бумаге с размером клетки 1×1
изображён ромб.
Найдите длину его большей стороны.
Алгоритм (2)
8 4
1. Определить длину диагоналей ромба
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
1. «Алгоритм» – последовательно 2 раза – визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
2. Сравнить длины диагоналей
Ответ:
8
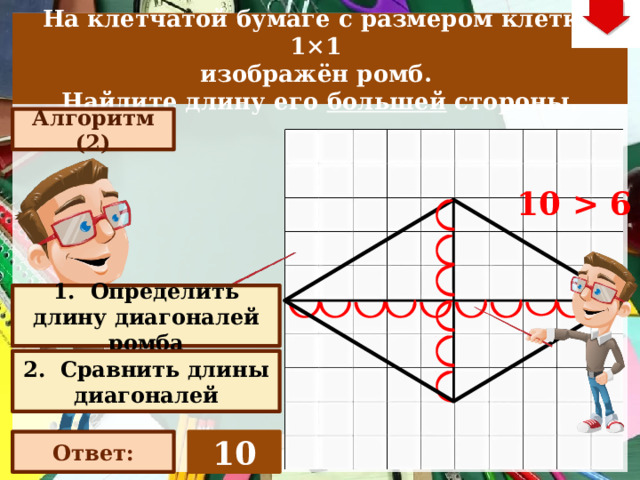 6 1. Определить длину диагоналей ромба Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи. Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи. Алгоритм работы с триггерами 1. «Алгоритм» – последовательно 2 раза – визуализация исполнения решения настроена автоматически. «Ответ» В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ вернуться на слайд выбора следующей задачи 2. Сравнить длины диагоналей 10 Ответ: ” width=”640″
6 1. Определить длину диагоналей ромба Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи. Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи. Алгоритм работы с триггерами 1. «Алгоритм» – последовательно 2 раза – визуализация исполнения решения настроена автоматически. «Ответ» В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ вернуться на слайд выбора следующей задачи 2. Сравнить длины диагоналей 10 Ответ: ” width=”640″
На клетчатой бумаге с размером клетки 1×1
изображён ромб.
Найдите длину его большей стороны.
Алгоритм (2)
10 6
1. Определить длину диагоналей ромба
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
1. «Алгоритм» – последовательно 2 раза – визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
2. Сравнить длины диагоналей
10
Ответ:
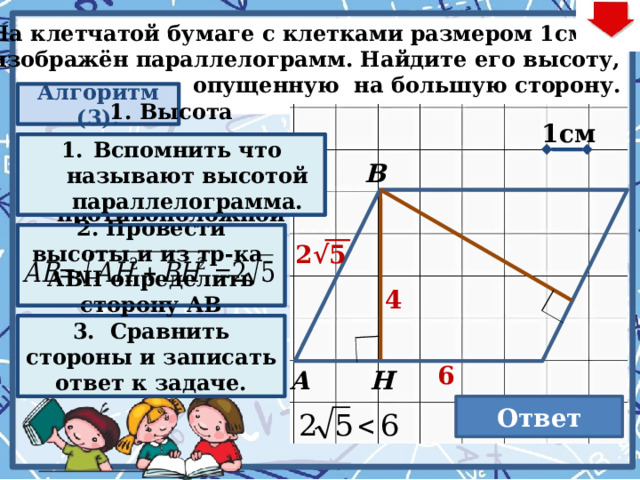
На клетчатой бумаге с клетками размером 1см×1см
изображён параллелограмм. Найдите его высоту,
опущенную на большую сторону.
Алгоритм (3):
1cм
1. Высота параллелограмма – перпендикуляр из вершины к противоположной стороне.
- Вспомнить что называют высотой параллелограмма.
В
2. Провести высоты и из тр-ка АВН определить
сторону АВ
2√5
4
.
Последовательность действий на слайде:
- Нажимаем кнопку «Алгоритм»
- Нажимаем на появившийся прямоугольник (анимированныя сорбонка)
- Нажимаем кнопку «Алгоритм»
- Нажимаем на второй появившийся прямоугольник (анимированныя сорбонка)
- Нажимаем кнопку «Алгоритм»
- Нажимаем на третий появившийся прямоугольник (анимированныя сорбонка) – 3 раза для визуализации ответов и решений
- Нажимаем кнопку «Ответ». При этом не забываем выполнить условие задачи.
3. Сравнить стороны и записать ответ к задаче.
6
Н
А
Ответ
4
22
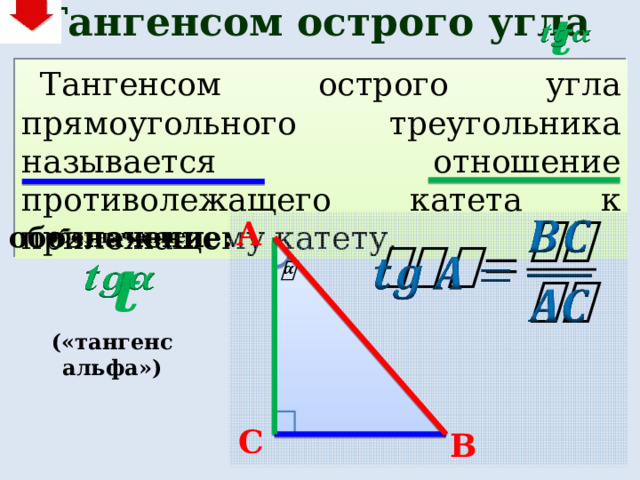
Тангенсом острого угла
t
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
A
обозначение:
t
(«тангенс альфа»)
C
B
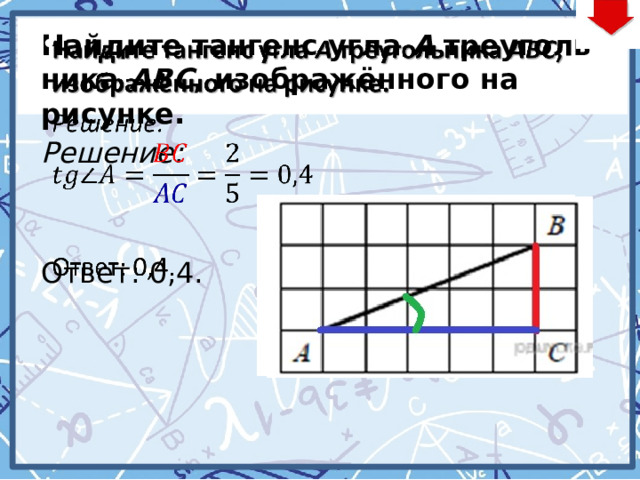
Найдите тангенс угла А треугольника ABC , изображённого на рисунке.
Решение:
Ответ: 0,4.
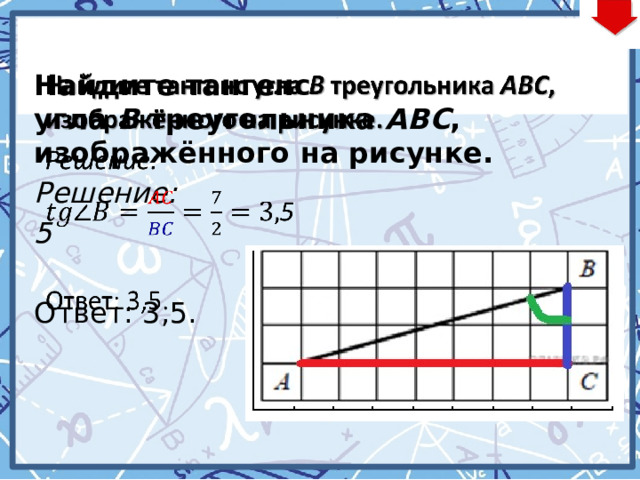
Найдите тангенс угла B треугольника ABC , изображённого на рисунке.
Решение:
5
Ответ: 3,5.
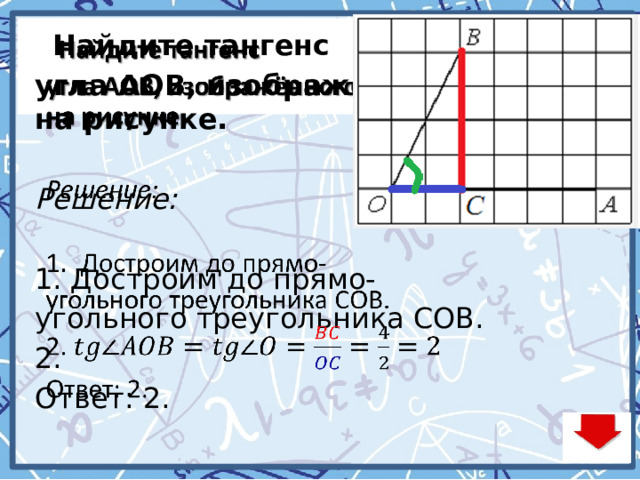
Найдите тангенс
угла AOB, изображённого на рисунке.
Решение:
- Достроим до прямо-
угольного треугольника СОВ.
2.
Ответ: 2.
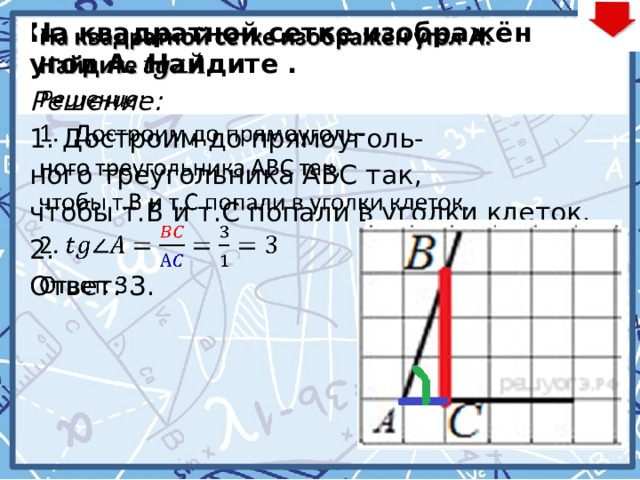
На квадратной сетке изображён угол А. Найдите .
Решение:
- Достроим до прямоуголь-
ного треугольника АВС так,
чтобы т.В и т.С попали в уголки клеток.
2.
Ответ: 3.

Площадь треугольника
Площадь параллелограмма
Площадь трапеции
Площадь фигуры

Определение площади фигуры
Нужно вспомнить формулы площадей фигур:
- параллелограмм треугольник – ромб – трапеция –
- параллелограмм
- треугольник –
- ромб –
- трапеция –
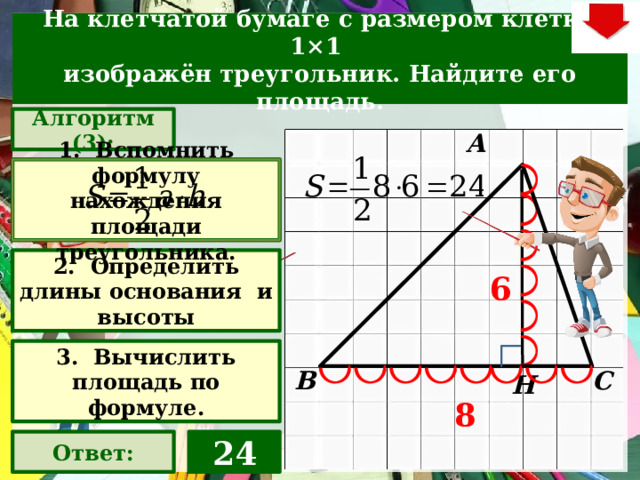
На клетчатой бумаге с размером клетки 1×1
изображён треугольник. Найдите его площадь.
Алгоритм (3):
А
1. Вспомнить формулу нахождения площади треугольника.
2. Определить длины основания и высоты
6
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм» – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади треугольника. При появлении второй и третьей подсказки нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Вычислить площадь по формуле.
В
С
Н
8
24
Ответ:
22
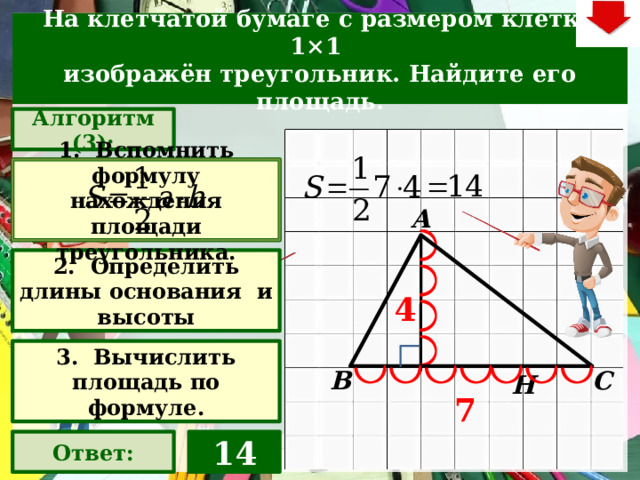
На клетчатой бумаге с размером клетки 1×1
изображён треугольник. Найдите его площадь.
Алгоритм (3):
1. Вспомнить формулу нахождения площади треугольника.
А
2. Определить длины основания и высоты
4
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм@ – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади треугольника. При появлении второй и третьей подсказки нажииать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Вычислить площадь по формуле.
В
С
Н
7
14
Ответ:
22
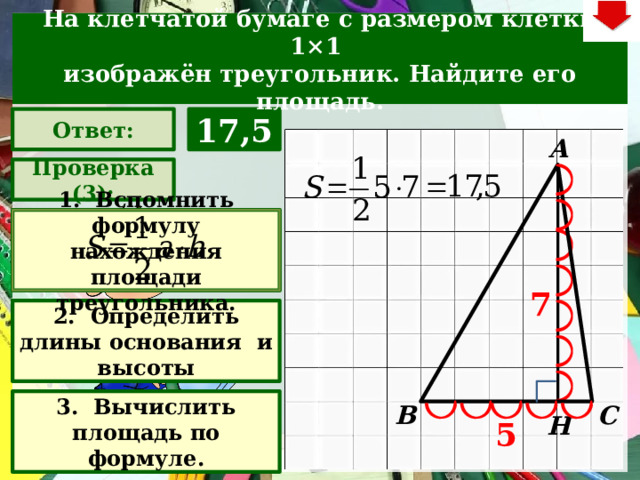
На клетчатой бумаге с размером клетки 1×1
изображён треугольник. Найдите его площадь.
Ответ:
17,5
А
Проверка (3):
1. Вспомнить формулу нахождения площади треугольника.
7
2. Определить длины основания и высоты
Задача. Решают учащиеся самостоятельно. После озвучивания и визуализации ответа (кнопка «Ответ»), необходимо визуализировать решение задачи (для всего класса) – нажимаем на прямоугольник «Проверка» – последовательно три раза. После появления первого прямоугольника– нажмите на него – появится формула нахождения площади треугольника. При появлении второго и третьего прямоугольников нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ вернуться на слайд выбора следующей задачи
3. Вычислить площадь по формуле.
С
В
Н
5
22
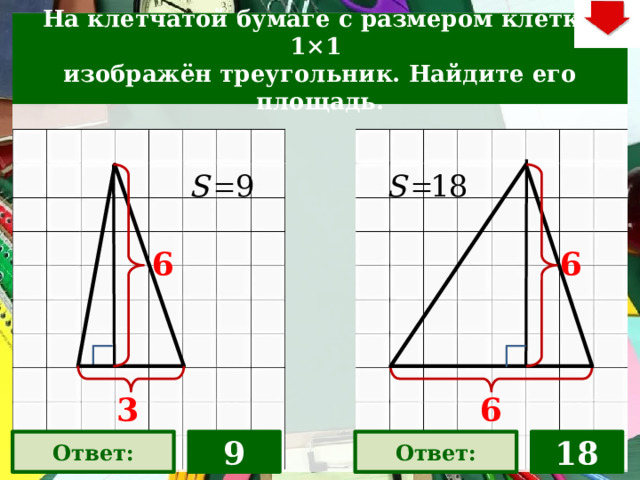
На клетчатой бумаге с размером клетки 1×1
изображён треугольник. Найдите его площадь.
6
6
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3
6
9
Ответ:
Ответ:
18
22
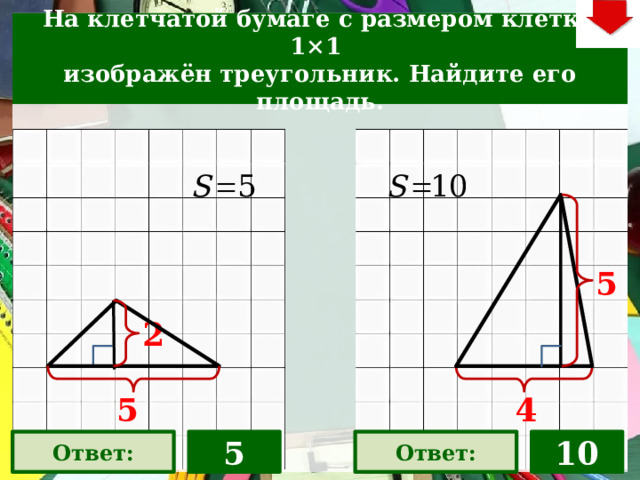
На клетчатой бумаге с размером клетки 1×1
изображён треугольник. Найдите его площадь.
5
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
С данного слайда возможет только возврат к слайду выбора следующей задачи (правый верхний угол слайда – кнопка «6»).
2
5
4
Ответ:
5
Ответ:
10
22
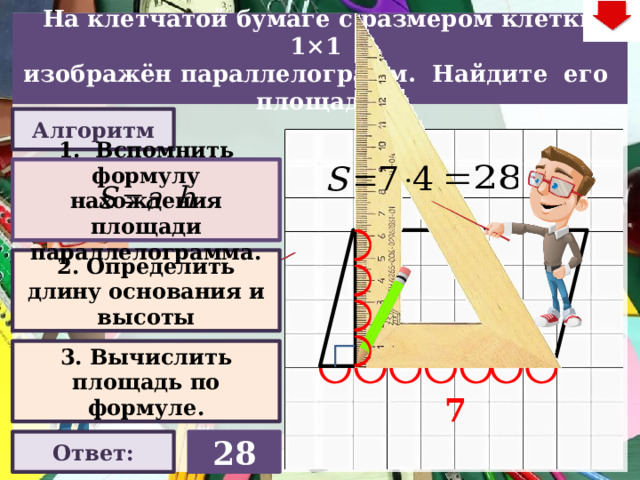
На клетчатой бумаге с размером клетки 1×1
изображён параллелограмм. Найдите его площадь.
Алгоритм
1. Вспомнить формулу нахождения площади параллелограмма.
2. Определить длину основания и высоты
4
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм» – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади параллелограмма. При появлении второй и третьей подсказки нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Вычислить площадь по формуле.
7
Ответ:
28
22
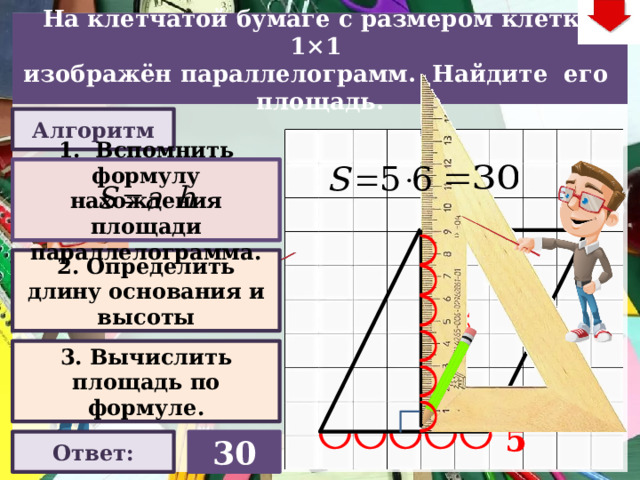
На клетчатой бумаге с размером клетки 1×1
изображён параллелограмм. Найдите его площадь.
Алгоритм
1. Вспомнить формулу нахождения площади параллелограмма.
2. Определить длину основания и высоты
6
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм» – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади параллелограмма. При появлении второй и третьей подсказки нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Вычислить площадь по формуле.
5
Ответ:
30
22
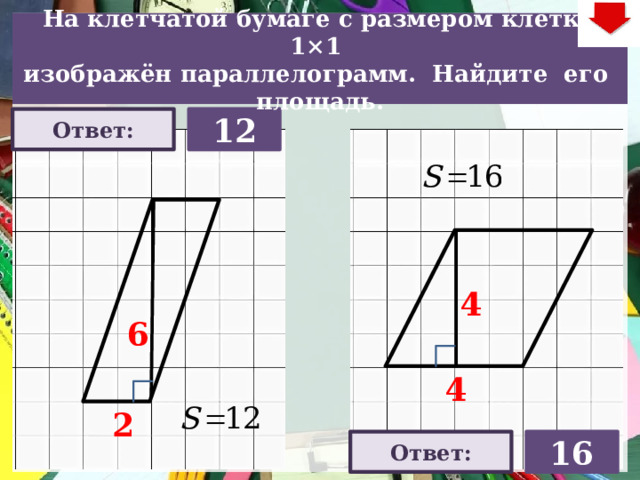
На клетчатой бумаге с размером клетки 1×1
изображён параллелограмм. Найдите его площадь.
Ответ:
12
4
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
6
4
2
16
Ответ:
22
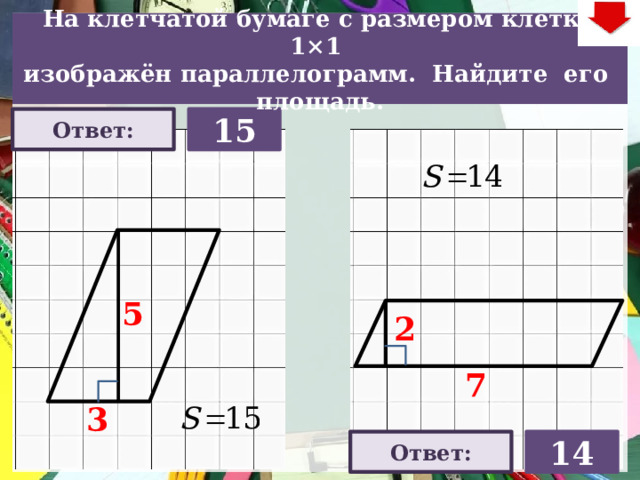
На клетчатой бумаге с размером клетки 1×1
изображён параллелограмм. Найдите его площадь.
Ответ:
15
5
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
С данного слайда возможен только возврат к слайду выбора следующей задачи (правый верхний угол слайда – кнопка «6»).
2
7
3
14
Ответ:
22
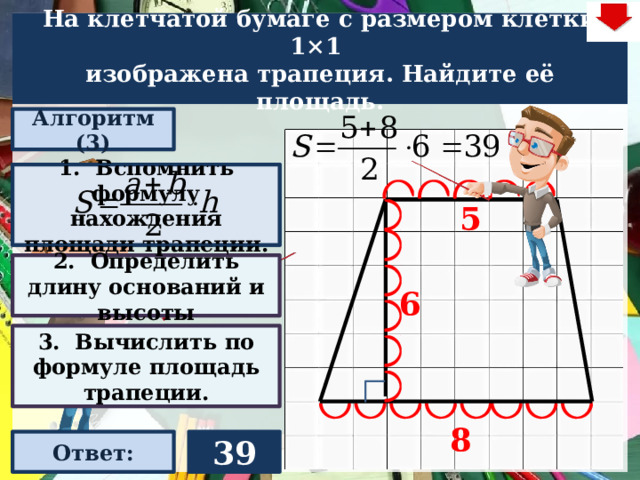
На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите её площадь.
Алгоритм (3)
1. Вспомнить формулу нахождения площади трапеции.
5
2. Определить длину оснований и высоты
6
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм» – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади трапеции. При появлении второй и третьей подсказки нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Вычислить по формуле площадь трапеции.
8
Ответ:
39
22
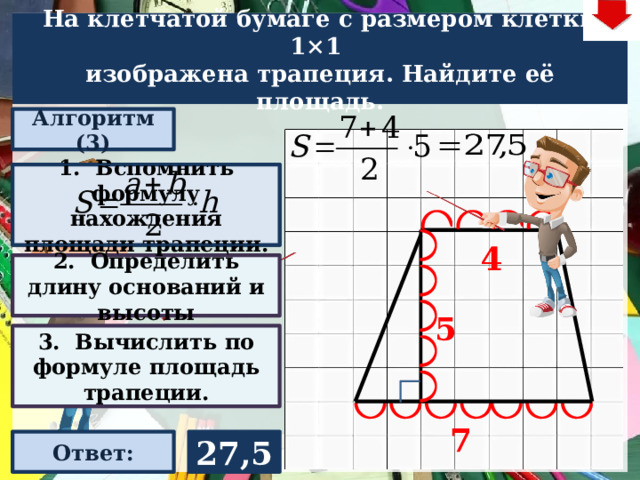
На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите её площадь.
Алгоритм (3)
1. Вспомнить формулу нахождения площади трапеции.
4
2. Определить длину оснований и высоты
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм» – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади трапеции. При появлении второй и третьей подсказки нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
5
3. Вычислить по формуле площадь трапеции.
7
27,5
Ответ:
22
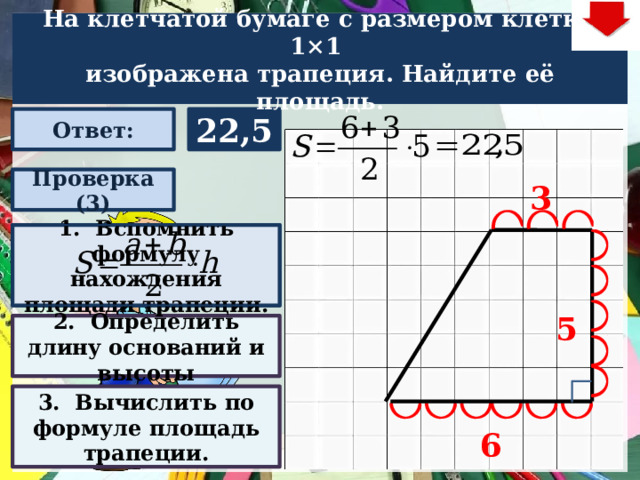
На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите её площадь.
22,5
Ответ:
Проверка (3)
3
1. Вспомнить формулу нахождения площади трапеции.
Задача. Решают учащиеся самостоятельно. После озвучивания и визуализации ответа (кнопка «Ответ»), необходимо визуализировать решение задачи (для всего класса) – нажимаем на прямоугольник «Проверка» – последовательно три раза. После появления первого прямоугольника– нажмите на него – появится формула нахождения площади трапеции. При появлении второго и третьего прямоугольников нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ вернуться на слайд выбора следующей задачи
5
2. Определить длину оснований и высоты
3. Вычислить по формуле площадь трапеции.
6
22
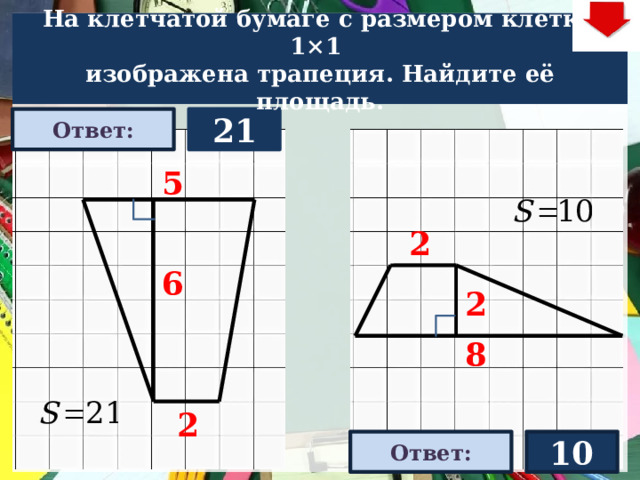
На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите её площадь.
21
Ответ:
5
2
6
2
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
8
2
Ответ:
10
22
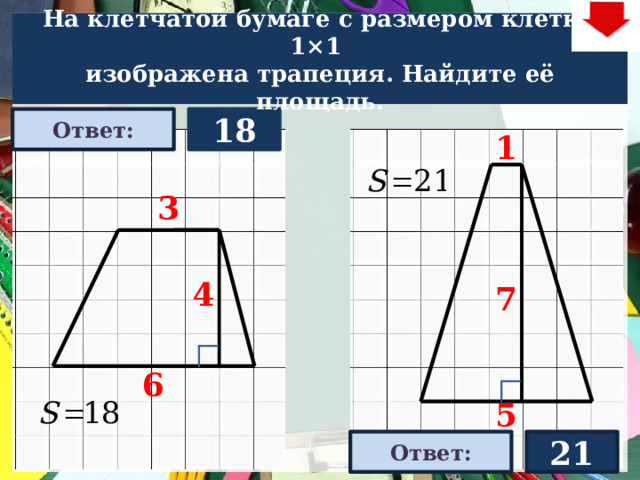
На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите её площадь.
18
Ответ:
1
3
4
7
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
С данного слайда возможен только возврат к слайду выбора следующей задачи (правый верхний угол слайда – кнопка «6»).
6
5
21
Ответ:
22

На клетчатой бумаге с размером клетки 1×1
изображена фигура. Найдите её площадь.
Алгоритм
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
1. «Алгоритм» – визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
Сосчитать количество клеточек из которых состоит фигура
19
Ответ:
22

На клетчатой бумаге с размером клетки 1×1
изображена фигура. Найдите её площадь.
Алгоритм
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
1. «Алгоритм» – визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
Сосчитать количество клеточек из которых состоит фигура
20
Ответ:
22
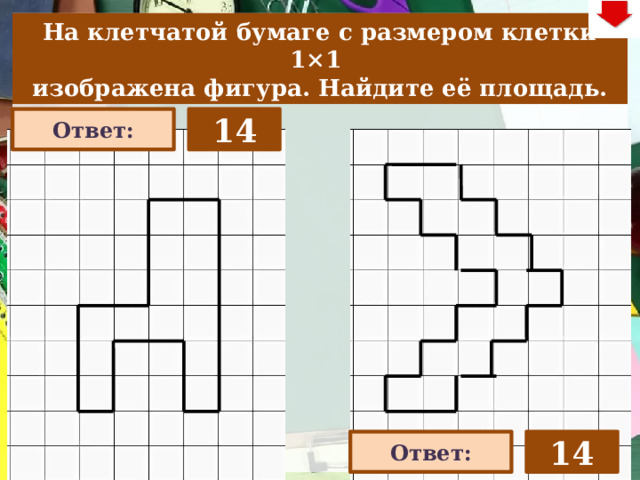
На клетчатой бумаге с размером клетки 1×1
изображена фигура. Найдите её площадь.
14
Ответ:
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
Ответ:
14
22
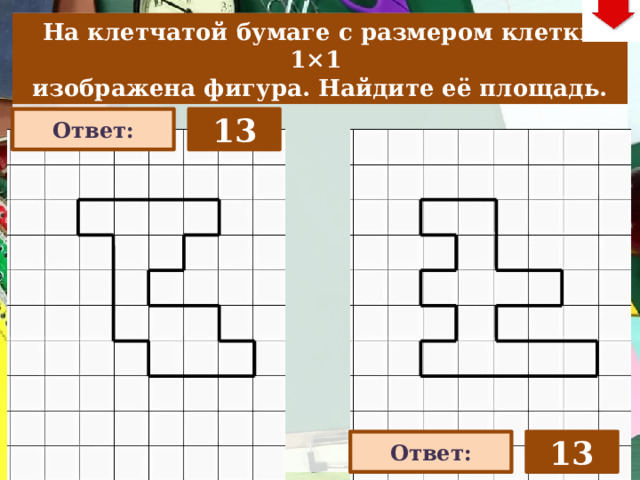
На клетчатой бумаге с размером клетки 1×1
изображена фигура. Найдите её площадь.
13
Ответ:
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
С данного слайда возможет только возврат к слайду выбора следующей задачи (правый верхний угол слайда – кнопка «6»).
13
Ответ:
22
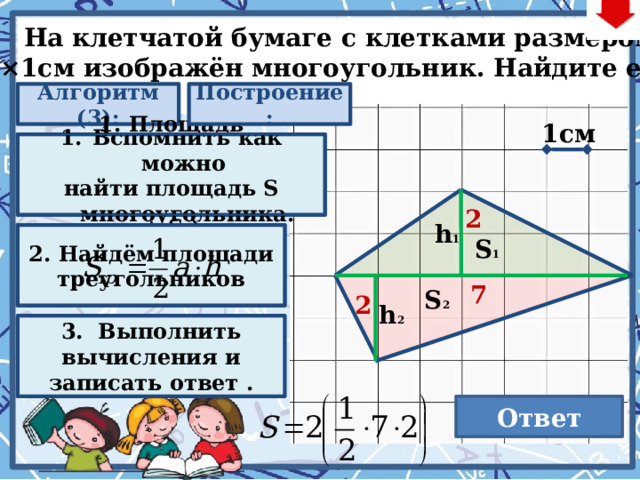
На клетчатой бумаге с клетками размером
1см×1см изображён многоугольник. Найдите его S.
Алгоритм (3):
Построение:
1cм
- Вспомнить как можно
1. Площадь многоугольника равна сумме площадей фигур из которых состоит (S 1 + S 2 )
найти площадь S многоугольника.
2
h 1
2. Найдём площади треугольников
S 1
7
S 2
2
h 2
.
Последовательность действий на слайде:
- Нажимаем кнопку «Алгоритм»
- Нажимаем на появившийся прямоугольник (анимированныя сорбонка)
- Нажимаем кнопку «Построение»
- Нажимаем кнопку «Алгоритм»
- Нажимаем на второй появившийся прямоугольник (анимированныя сорбонка)
- Нажимаем кнопку «Алгоритм»
- Нажимаем на третий появившийся прямоугольник (анимированныя сорбонка) – 3 раза для визуализации ответов и решений
- Нажимаем кнопку «Ответ». При этом не забываем выполнить условие задачи.
3. Выполнить вычисления и записать ответ .
Ответ
14
22
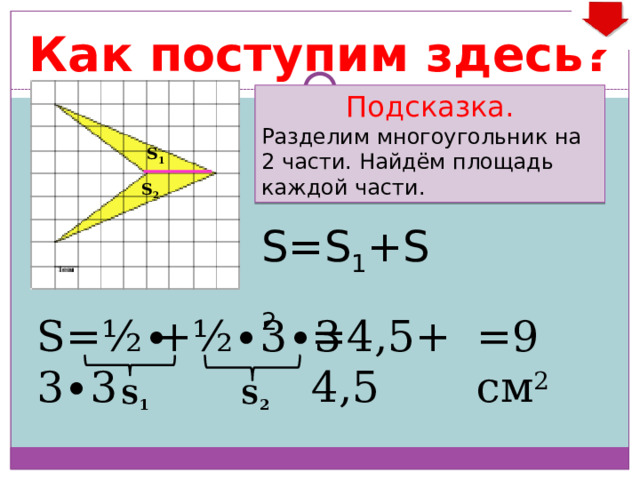
Как поступим здесь?
Подсказка.
Разделим многоугольник на 2 части. Найдём площадь каждой части.
S 1
S 2
S=S 1 +S 2
=4,5+4,5
S=½ ∙ 3 ∙ 3
=9 см 2
+½ ∙ 3 ∙ 3
S 1
S 2
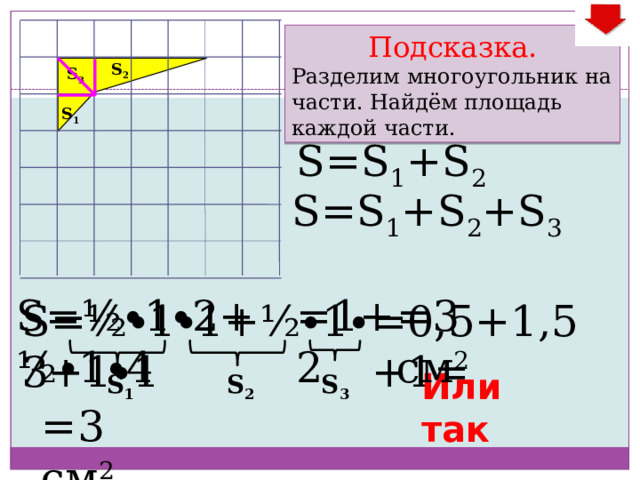
Подсказка.
Разделим многоугольник на части. Найдём площадь каждой части.
S 2
S 3
S 1
S=S 1 +S 2
S=S 1 +S 2 +S 3
S=½ ∙ 1 ∙ 2+½ ∙ 1 ∙ 4
=1+2
=3 см 2
=0,5+1,5+1=
S=½ ∙ 1 ∙ 1+½ ∙ 1 ∙ 3+1 ∙ 1
Или так
S 1
S 2
S 3
=3 см 2
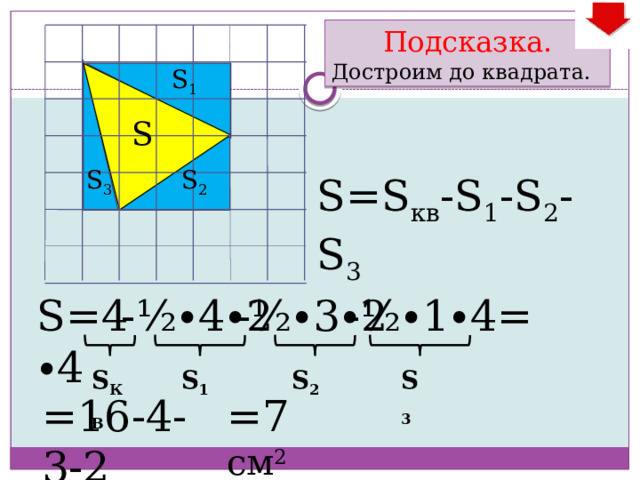
Подсказка.
Достроим до квадрата.
S 1
S
S 3
S 2
S=S кв -S 1 -S 2 -S 3
S= 4∙4
-½∙4∙2
-½∙3∙2
-½∙1∙4=
S КВ
S 1
S 3
S 2
=7 см 2
=16-4-3-2
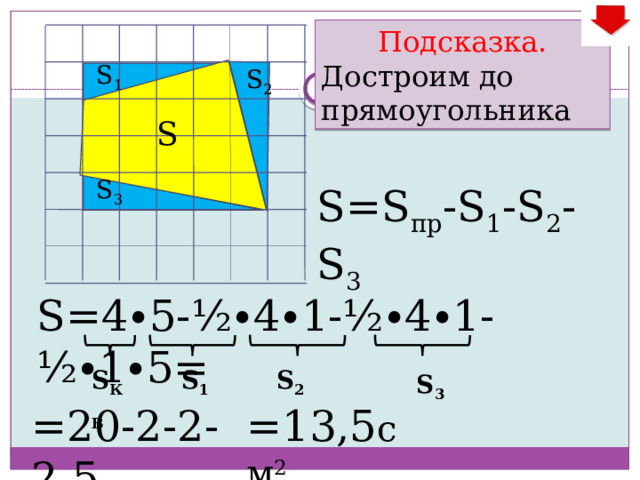
Подсказка.
Достроим до прямоугольника
S 1
S 2
S
S 3
S=S пр -S 1 -S 2 -S 3
S=4∙5-½∙4∙1-½∙4∙1- ½∙1∙5=
S КВ
S 2
S 1
S 3
=13,5 см 2
=20-2-2-2,5

А всегда ли Удобно
Таким способом находить площади фигур?
S 1
S 5
S 2
S 4
S
S=S кв -S 1 -S 2 -S 3 -S 4
S 3
S=5 ∙ 5-½ ∙ 3∙1-½ ∙ 5∙1- ½∙2∙5 – ½∙1∙2-1∙1=
S 2
S 5
S 1
S 4
S 3
S КВ
=13,5см 2
=25-1,5-2,5-5-1-1

Формула Пика
Позволит вам с необычайной легкостью находить площадь любого многоугольника на клетчатой бумаге с целочисленными вершинами.
Формула Пика очень удобна когда сложно догадаться, как разбить фигуру на удобные многоугольники или достроить до прямоугольника, квадрата …

Формула Пика
Определение: Точка координатной плоскости называется целочисленной, если обе её координаты целые числа.
Площадь многоугольника с целочисленными вершинами равна
где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
Г
– 1
B
+
2
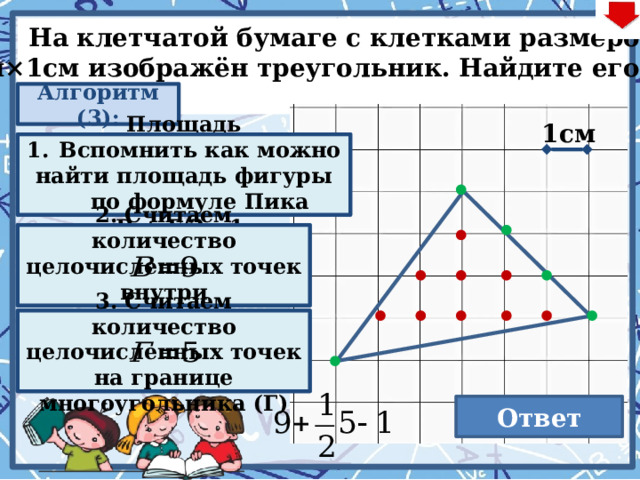
На клетчатой бумаге с клетками размером
1см×1см изображён треугольник. Найдите его S.
Алгоритм (3):
1cм
Площадь многоугоугольника с целочисленными вершинами равна сумме В + Г/2 – 1
- Вспомнить как можно
найти площадь фигуры по формуле Пика
2. Считаем количество целочисленных точек внутри многоугольника (В)
.
Последовательность действий на слайде:
- Нажимаем кнопку «Алгоритм»
- Нажимаем на появившийся прямоугольник (анимированная сорбонка) – 3 раза (можно два – в зависимости от целей демонстрации)
- Нажимаем кнопку «Алгоритм»
- Нажимаем на второй появившийся прямоугольник (анимированныя сорбонка) – количество определяете в зависимости от целей демонстрации
- Нажимаем кнопку «Алгоритм»
- Нажимаем на третий появившийся прямоугольник (анимированныя сорбонка) – для визуализации решений
- Нажимаем кнопку «Ответ». При этом не забываем выполнить условие задачи.
3. Считаем количество целочисленных точек на границе многоугольника (Г)
Ответ
10,5
55
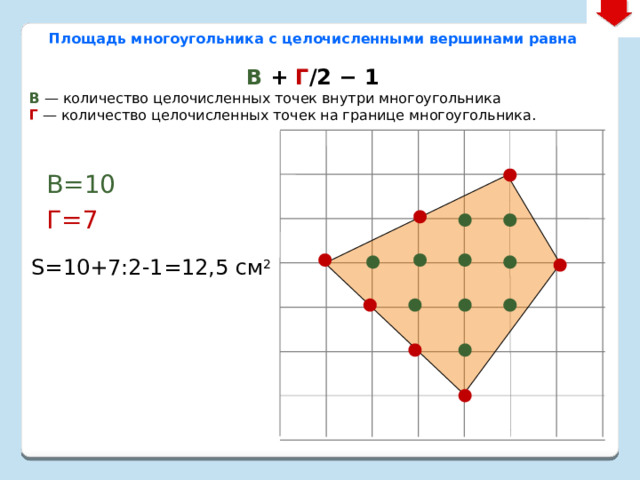
Площадь многоугольника с целочисленными вершинами равна
В + Г /2 − 1
В — количество целочисленных точек внутри многоугольника Г — количество целочисленных точек на границе многоугольника.
В=10
Г=7
S=10+7:2-1=12,5 см 2
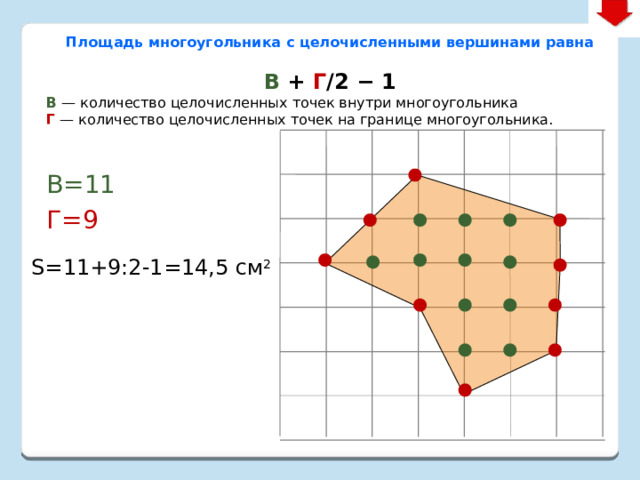
Площадь многоугольника с целочисленными вершинами равна
В + Г /2 − 1
В — количество целочисленных точек внутри многоугольника Г — количество целочисленных точек на границе многоугольника.
В=11
Г=9
S=11+9:2-1=14,5 см 2

На клетчатой бумаге нарисовано два круга.
Площадь внутреннего круга равна 27. Найдите S
закрашенной фигуры. (π =3)
Алгоритм (3):
S = S б – S м
- Вспомнить как можно
найти площадь S закрашенной фигуры.
4
2. Определим по рис. центр бóльшего круга и найдём его площадь .
Действия на слайде – по аналогии с предыдущими…
3. Выполнить вычисления и записать ответ .
21
Ответ
55

Определение градусной меры вписанного угла
Что нужно вспомнить:
- Вписанный угол – угол, вершина которого лежит на окружности, а стороны её пересекают.
- Центральный угол – угол, вершина которого совпадает с центром окружности, а стороны её пересекают.
Вписанный угол равен половине дуги, на которую опирается.

Определение градусной меры вписанного угла
Задача 1:
Найдите угол ABC . Ответ дайте
в градусах.
Решение:
Проведём вспомогательное
построение. Заметим, что
дуга AC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°.
Угол ABC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги AC : 90°/2 = 45°.
Ответ: 45.

Определение градусной меры вписанного угла
Задача 2:
Найдите угол ABC . Ответ дайте
в градусах.
Решение:
Угол ABC – опирается на большую дугу АC.
Проведём вспомогательное построение. Заметим, что дуга А C составляет всей окружности, следовательно, она равна
Угол AВC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине большой дуги АC : 270°/2 = 135°.
Ответ: 135.

Определение градусной меры вписанного угла
Задача 3:
Найдите угол ABC . Ответ дайте
в градусах.
Решение:
Проведём вспомогательное построение. Угол АОС – центральный и равен .
Угол АВС опирается на ту же дугу, что и угол АОС, но является вписанным, поутому равен половине угла АОС , т.е. .
Ответ: 22,5.

Всё возможно! Только смело На ОГЭ иди! Вперед ! Будь спокоен и без нервов! Голова не подведет!!!
Если учил уроки и…
ответственно готовился к экзамену!
Удачи!








