Данная статья представляет собой структурированную и подробную информацию, которая может пригодиться во время разбора упражнений и задач. Мы рассмотрим тему числовых рядов.
Данная статья начинается с основных определений и понятий. Далее мы стандартные варианты и изучим основные формулы. Для того, чтобы закрепить материал, в статье приведены основные примеры и задачи.
Базовые тезисы
Для начала представим систему: a1, a2…, an,… , где ak∈R, k=1,2….
Для примера, возьмем такие числа, как: 6,3,-32,34,38,-316,… .
Числовой ряд – это сумма членов ∑akk=1∞=a1+a2+…+an+… .
Чтобы лучше понять определение, рассмотрим данный случай, в котором q = -0.5: 8-4+2-1+12-14+…=∑k=1∞(-16)·-12k .
ak является общим или k–ым членом ряда.
Он выглядит примерно таким образом -16·-12k .
Частичная сумма ряда выглядит примерно таким образом Sn=a1+a2+…+an , в которой n –любое число. Sn является n-ой суммой ряда.
Например, ∑k=1∞(-16)·-12k есть S4=8-4+2-1=5 .
S1,S2,…,Sn,… образуют бесконечную последовательность числового ряда.
Для ряда n –ая сумму находится по формуле Sn=a1·(1-qn)1-q=8·1–12n1–12=163·1–12n . Используем следующую последовательность частичных сумм: 8,4,6,5,…,163·1–12n,… .
Ряд ∑k=1∞ak является сходящимся тогда, когда последовательность обладает конечным пределом S=lim Snn→+∞ . Если предела нет или последовательность бесконечна, то ряд ∑k=1∞ak называется расходящимся.
Суммой сходящегося ряда ∑k=1∞ak является предел последовательности ∑k=1∞ak=lim Snn→+∞=S .
В данном примере lim Snn→+∞=lim 163т→+∞·1-12n=163·lim n→+∞1–12n=163 , ряд ∑k=1∞(-16)·-12k сходится. Сумма равна 163: ∑k=1∞(-16)·-12k=163 .
В качестве примера расходящегося ряда можно привести сумму геометрической прогрессии со знаменателем большем, чем единица: 1+2+4+8+…+2n-1+…=∑k=1∞2k-1.
n-ая частичная сумма определяется выражением Sn=a1·(1-qn)1-q=1·(1-2n)1-2=2n-1, а предел частичных сумм бесконечен: limn→+∞Sn=limn→+∞(2n-1)=+∞.
Еще одим примером расходящегося числового ряда является сумма вида∑k=1∞5=5+5+…. В этом случае n-ая частичная сумма может быть вычислена как Sn=5n. Предел частичных сумм бесконечен limn→+∞Sn=limn→+∞5n=+∞.
Сумма подобного вида как ∑k=1∞=1+12+13+…+1n+… – это гармонический числовой ряд.
Сумма ∑k=1∞1ks=1+12s+13s+…+1ns+… , где s –действительное число, является обобщенно гармоническим числовым рядом.
Определения, рассмотренные выше, помогут вам для решения большинства примеров и задач.
Для того, чтобы дополнить определения, необходимо доказать определенные уравнения.
- ∑k=1∞1k – расходящийся.
Действуем методом от обратного. Если он сходится, то предел конечен. Можно записать уравнение как limn→+∞Sn=S и limn→+∞S2n=S . После определенных действий мы получаем равенство limn→+∞(S2n-Sn)=0 .
Напротив,
S2n-Sn=1+12+13+…+1n+1n+1+1n+2+…+12n–1+12+13+…+1n=1n+1+1n+2+…+12n
Справедливы следующие неравенства 1n+1>12n, 1n+1>12n,…, 12n-1>12n . Получаем, что S2n-Sn=1n+1+1n+2+…+12n>12n+12n+…+12n=n2n=12 . Выражение S2n-Sn>12 указывает на то, что limn→+∞(S2n-Sn)=0 не достигается. Ряд расходящийся.
- b1+b1q+b1q2+…+b1qn+…=∑k=1∞b1qk-1
Необходимо подтвердить, что сумма последовательности чисел сходится при q<1 , и расходится при q≥1 .
Согласно приведенным выше определениям, сумма n членов определяется согласно формуле Sn=b1·(qn-1)q-1 .
Если q<1 верно
limn→+∞Sn=limn→+∞b1·qn-1q-1=b1·limn→+∞qnq-1-limn→+∞1q-1==b1·0-1q-1=b1q-1
Мы доказали, что числовой ряд сходится.
При q = 1 b1+b1+b1+…∑k=1∞b1 . Суммы можно отыскать с использованием формулы Sn=b1·n , предел бесконечен limn→+∞Sn=limn→+∞b1·n=∞. В представленном варианте ряд расходится.
Если q = -1, то ряд выглядит как b1-b1+b1-…=∑k=1∞b1(-1)k+1 . Частичные суммы выглядят как Sn=b1 для нечетных n, и Sn=0 для четных n. Рассмотрев данный случай, мы удостоверимся, что предела нет и ряд является расходящимся.
При q>1 справедливо limn→+∞Sn=limn→+∞b1·(qn-1)q-1=b1·limn→+∞qnq-1-limn→+∞1q-1==b1·∞-1q-1=∞
Мы доказали, что числовой ряд расходится.
- Ряд ∑k=1∞1ks сходится, если s > 1 и расходится, если s≤ 1 .
Для s = 1 получаем ∑k=1∞1k , ряд расходится.
При s < 1 получаем 1ks≥1k для k, натурального числа. Так как ряд является расходящимся ∑k=1∞1k , то предела нет. Следуя этому, последовательность ∑k=1∞1ks неограниченна. Делаем вывод, что выбранный ряд расходится при s < 1.
Необходимо предоставить доказательства, что ряд ∑k=1∞1ks сходится при s > 1.
Представим S2n-1-Sn-1 :
S2n-1-Sn-1=1+12s+13s+…+1(n-1)s+1ns+1(n+1)s+…+1(2n-1)s–1+12s+13s+…+1(n-1)s=1ns+1(n+1)s+…+1(2n-1)s
Допустим, что 1(n+1)s<1ns, 1(n+2)s<1ns, …, 1(2n-1)s<1ns , тогда S2n-1-Sn-1=1ns+1(n+1)s+…+1(2n-1)s<<1ns+1ns+…+1ns=nns=1ns-1
Представим уравнение для чисел, которые являются натуральными и четными n=2: S2n-1-Sn-1=S3-S1=12s+13s<12s-1n=4: S2n-1-Sn-1=S7-S3=14s+15s+16s+17s<14s-1=12s-12n=8: S2n-1-Sn-1=S15-S7=18s+19s+…+115s<18s-1=12s-13…
Получаем:
∑k=1∞1ks=1+12s+13s+14s+…+17s+18s+…+115s+…==1+S3-S1+S7-S3+S15+S7+…<<1+12s-1+12s-12+12s-13+…
Выражение 1+12s-1+12s-12+12s-13+… – это сумма геометрической прогрессии q=12s-1 . Согласно исходным данным при s>1, то0<q<1 . Получаем, ∑k=1∞<1+12s-1+12s-12+12s-13+…=11-q=11-12s-1 . Последовательность ряда при s > 1 увеличивается и ограничивается сверху 11-12s-1 . Представим, что есть предел и ряд является сходящимся ∑k=1∞1ks .
Ряд ∑k=1∞ak знакоположителен в том случае, если его члены >0 ak>0, k=1,2,… .
Ряд ∑k=1∞bk знакочередующийся, если знаки чисел отличаются. Данный пример представлен как∑k=1∞bk=∑k=1∞(-1)k·ak или ∑k=1∞bk=∑k=1∞(-1)k+1·ak , где ak>0, k=1,2, … .
Ряд ∑k=1∞bk знакопеременный, так как в нем множество чисел, отрицательных и положительных.
Второй вариант ряд – это частный случай третьего варианта.
Приведем примеры для каждого случая соответственно:
6+3+32+34+38+316+…6-3+32-34+38-316+…6+3-32+34+38-316+…
Для третьего варианта также можно определить абсолютную и условную сходимость.
Знакочередующийся ряд ∑k=1∞bk абсолютно сходится в том случае, когда ∑k=1∞bk также считается сходящимся.
Подробно разберем несколько характерных вариантов
Если ряды 6-3+32-34+38-316+… и 6+3-32+34+38-316+… определяются как сходящиеся, то верно считать, что 6+3+32+34+38+316+…
Знакопеременный ряд ∑k=1∞bk считается условно сходящимся в том случае, если ∑k=1∞bk – расходящийся, а ряд ∑k=1∞bk считается сходящимся.
Подробно разберем вариант ∑k=1∞(-1)k+1k=1-12+13-14+… . Ряд ∑k=1∞(-1)k+1k=∑k=1∞1k , который состоит из абсолютных величин, определяется как расходящийся. Этот вариант считается сходящимся, так как это легко определить. Из данного примера мы узнаем, что ряд ∑k=1∞(-1)k+1k=1-12+13-14+… будет считаться условно сходящимся.
Особенности сходящихся рядов
Проанализируем свойства для определенных случаев
- Если ∑k=1∞ak будет сходится, то и ряд ∑k=m+1∞ak также признается сходящимся. Можно отметить, что ряд без m членов также считается сходящимся. В случае, если мы добавляем к ∑k=m+1∞ak несколько чисел, то получившийся результат также будет сходящимся.
- Если ∑k=1∞ak сходится и сумма = S, то сходится и ряд ∑k=1∞A·ak , ∑k=1∞A·ak=A·S , где A –постоянная.
- Если ∑k=1∞ak и ∑k=1∞bk являются сходящимися , суммы A и B тоже, то и ряды ∑k=1∞ak+bk и ∑k=1∞ak-bk также сходятся . Суммы будут равняться A + B и A – B соответственно.
Определить, что ряд сходится ∑k=1∞23k·k3 .
Изменим выражение ∑k=1∞23k·k3=∑k=1∞23·1k43 . Ряд ∑k=1∞1k43 считается сходящимся, так как ряд ∑k=1∞1ks сходится при s > 1. В соответствии со вторым свойством, ∑k=1∞23·1k43 .
Определить, сходится ли ряд ∑n=1∞3+nn52 .
Преобразуем изначальный вариант ∑n=1∞3+nn52=∑n=1∞3n52+nn2=∑n=1∞3n52+∑n=1∞1n2 .
Получаем сумму ∑n=1∞3n52 и ∑n=1∞1n2 . Каждый ряд признается сходящимся согласно свойству. Так, как ряды сходятся, то исходный вариант тоже.
Вычислить, сходится ли ряд 1-6+12-2+14-23+18-29+… и вычислить сумму.
Разложим исходный вариант:
1-6+12-2+14-23+18-29+…==1+12+14+18+…-2·3+1+13+19+…==∑k=1∞12k-1-2·∑k=1∞13k-2
Каждый ряд сходится, так как является одним из членов числовой последовательности. Согласно третьему свойству, мы можем вычислить, что исходный вариант также является сходящимся. Вычисляем сумму: Первый член ряда ∑k=1∞12k-1 =1 , а знаменатель =0.5, за этим следует, ∑k=1∞12k-1=11-0.5=2 . Первый член ∑k=1∞13k-2=3, а знаменатель убывающей числовой последовательности=13. Получаем:∑k=1∞13k-2=31-13=92 .
Используем выражения, полученные выше, для того, чтобы определить сумму 1-6+12-2+14-23+18-29+…=∑k=1∞12k-1-2·∑k=1∞13k-2=2-2·92=-7
Необходимое условие для определения, является ли ряд сходящимся
Если ряд ∑k=1∞ak является сходящимся, то предел его k-ого члена =0: limk→+∞ak=0 .
Если мы проверим любой вариант, то нужно не забывать о непременном условии. Если оно не выполняется, то ряд расходится. Если limk→+∞ak≠0 , то ряд расходящийся.
Следует уточнить, что условие важно, но не достаточно. Если равенство limk→+∞ak=0 выполняется , то это не гарантирует, что ∑k=1∞ak является сходящимся.
Приведем пример. Для гармонического ряда ∑k=1∞1k условие выполняется limk→+∞1k=0 , но ряд все равно расходится.
Определить сходимость ∑n=1∞n21+n .
Проверим исходное выражение на выполнение условияlimn→+∞n21+n=limn→+∞n2n21n2+1n=limn→+∞11n2+1n=1+0+0=+∞≠0
Предел n-ого члена не равен 0. Мы доказали, что данный ряд расходится.
Как определить сходимость знакоположительного ряда.
Если постоянно пользоваться указанными признаками, придется постоянно вычислять пределы. Данный раздел поможет избежать сложностей во время решения примеров и задач. Для того, чтобы определить сходимость знакоположительного ряда, существует определенное условие.
Для сходимости знакоположительного ∑k=1∞ak, ak>0 ∀k=1,2,3,… нужно определять ограниченную последовательность сумм.
Как сравнивать ряды
Существует несколько признаков сравнения рядов. Мы сравниваем ряд, сходимость которого предлагается определить, с тем рядом, сходимость которого известна.
Первый признак
∑k=1∞ak и∑k=1∞bk – знакоположительные ряды. Неравенство ak≤bk справедливо для k = 1, 2, 3, … Из этого следует, что из ряда ∑k=1∞bk мы можем получить∑k=1∞ak . Так как ∑k=1∞ak расходится, то ряд∑k=1∞bk можно определить как расходящийся.
Данное правило постоянно используется для решения уравнений и является серьезным аргументом, которое поможет определить сходимость. Сложности могут состоять в том, что подобрать подходящий пример для сравнения можно найти далеко не в каждом случае. Довольно часто ряд выбирается по принципу, согласно которому показатель k-ого члена будет равняться результату вычитания показателей степеней числителя и знаменателя k-ого члена ряда. Допустим, что ak=k2+34k2+5 , разность будет равна 2 – 3 = -1. В данном случае можно определить, что для сравнения необходим ряд с k-ым членом bk=k-1=1k , который является гармоническим.
Для того, чтобы закрепить полученный материал, детально рассмотрим пару типичных вариантов.
Определить, каким является ряд ∑k=1∞1k-12 .
Так как предел =0 limk→+∞1k-12=0 , мы выполнили необходимое условие. Неравенство будет справедливым1k<1k-12 для k, которые являются натуральными. Из предыдущих пунктов мы узнали, что гармонический ряд ∑k=1∞1k – расходящийся. Согласно первому признаку, можно доказать, что исходный вариант является расходящимся.
Определить, является ряд сходящимся или расходящимся∑k=1∞1k3+3k-1 .
В данном примере выполняется необходимое условие, так как limk→+∞1k3+3k-1=0 . Представляем в виде неравенства 1k3+3k-1<1k3 для любого значения k. Ряд ∑k=1∞1k3 является сходящимся, так как гармонический ряд ∑k=1∞1ks сходится при s > 1. Согласно первому признаку, мы можем сделать вывод, что числовой ряд является сходящимся.
Определить, является каким является ряд ∑k=3∞1kln(ln k) .limk→+∞1kln(ln k)=1+∞+∞=0 .
В данном варианте можно отметить выполнение нужного условия. Определим ряд для сравнения. Например, ∑k=1∞1ks . Чтобы определить, чему равна степень, расммотрим последовательность {ln(ln k)}, k=3,4,5…. Члены последовательности ln (ln 3), ln (ln 4), ln (ln 5), … увеличивается до бесконечности. Проанализировав уравнение, можно отметить, что, взяв в качестве значения N = 1619, то члены последовательности >2. Для данной последовательности будет справедливо неравенство 1kln(ln k)<1k2 . Ряд ∑k=N∞1k2 сходится согласно первому признаку, так как ряд ∑k=1∞1k2 тоже сходящийся. Отметим, что согласно первому признаку ряд ∑k=N∞1kln(ln k) сходящийся. Можно сделать вывод, что ряд ∑k=3∞1kln(ln k) также сходящийся.
Второй признак
Допустим, что ∑k=1∞ak и ∑k=1∞bk – знакоположительные числовые ряды.
Если limk→+∞akbk≠∞ , то ряд ∑k=1∞bk сходится, и ∑k=1∞ak сходится также.
Если limk→+∞akbk≠0 , то так как ряд ∑k=1∞bk расходится, то ∑k=1∞ak также расходится.
Если limk→+∞akbk≠∞ и limk→+∞akbk≠0 , то сходимость или расходимость ряда означает сходимость или расходимость другого.
Рассмотрим ∑k=1∞1k3+3k-1 с помощью второго признака. Для сравнения ∑k=1∞bk возьмем сходящийся ряд∑k=1∞1k3 . Определим предел: limk→+∞akbk=limk→+∞1k3+3k-11k3=limk→+∞k3k3+3k-1=1
Согласно второму признаку можно определить, что сходящийся ряд∑k=1∞1k3 означается, что первоначальный вариант также сходится.
Определить, каким является ряд ∑n=1∞k2+34k3+5 .
Проанализируем необходимое условие limk→∞k2+34k3+5=0 , которое в данном варианте выполняется. Согласно второму признаку, возьмем ряд ∑k=1∞1k. Ищем предел: limk→+∞k2+34k3+51k=limk→+∞k3+3k4k3+5=14
Согласно приведенным выше тезисам, расходящийся ряд влечет собой расходимость исходного ряда.
Третий признак
Рассмотрим третий признак сравнения.
Допустим, что ∑k=1∞ak и _∑k=1∞bk – знакоположительные числовые ряды. Если условие выполняется для некого номера ak+1ak≤bk+1bk , то сходимость данного ряда∑k=1∞bk означает, что ряд ∑k=1∞ak также является сходящимся. Расходящийся ряд ∑k=1∞ak влечет за собой расходимость ∑k=1∞bk .
Признак Даламбера
Представим, что ∑k=1∞ak – знакоположительный числовой ряд. Если limk→+∞ak+1ak<1, то ряд является сходящимся, если limk→+∞ak+1ak>1 , то расходящимся.
Замечание 1
Признак Даламбера справедлив в том случае, если предел бесконечен.
Если limk→+∞ak+1ak=-∞ , то ряд является сходящимся, если limk→∞ak+1ak=+∞ , то расходящимся.
Если limk→+∞ak+1ak=1 , то признак Даламбера не поможет и потребуется провести еще несколько исследований.
Определить, является ряд сходящимся или расходящимся ∑k=1∞2k+12k по признаку Даламбера.
Необходимо проверить, выполняется ли необходимое условие сходимости. Вычислим предел, воспользовавшись правилом Лопиталя: limk→+∞2k+12k=∞∞=limk→+∞2k+1’2k’=limk→+∞22k·ln 2=2+∞·ln 2=0
Мы можем увидеть, что условие выполняется. Воспользуемся признаком Даламбера: limk→+∞=limk→+∞2(k+1)+12k+12k+12k=12limk→+∞2k+32k+1=12<1
Ряд является сходящимся.
Определить, является ряд расходящимся ∑k=1∞kkk! .
Воспользуемся признаком Даламбера для того, чтобы определить рассходимость ряда: limk→+∞ak+1ak=limk→+∞(k+1)k+1(k+1)!kkk!=limk→+∞(k+1)k+1·k!kk·(k+1)!=limk→+∞(k+1)k+1kk·(k+1)==limk→+∞(k+1)kkk=limk→+∞k+1kk=limk→+∞1+1kk=e>1
Следовательно, ряд является расходящимся.
Радикальный признак Коши
Допустим, что ∑k=1∞ak – это знакоположительный ряд. Еслиlimk→+∞akk<1 , то ряд является сходящимся, если limk→+∞akk>1 , то расходящимся.
Замечание 2
Данный признак будет считаться справедливым только в том случае, если предел бесконечен. Другими словами, если limk→+∞akk=-∞, то ряд сходится, если limk→+∞akk=+∞ , то ряд расходится.
Еслиlimk→+∞akk=1 , то данный признак не дает никакой информации – требуется проведение дополнительного анализа.
Данный признак может быть использован в примерах, которые легко определить. Случай будет характерным тогда, когда член числового ряда – это показательно степенное выражение.
Для того, чтобы закрепить полученную информацию, рассмотрим несколько характерных примеров.
Определить, является ли знакоположительный ряд ∑k=1∞1(2k+1)k на сходящимся.
Нужное условие считается выполненным, так как limk→+∞1(2k+1)k=1+∞+∞=0 .
Согласно признаку, рассмотренному выше, получаем limk→+∞akk=limk→+∞1(2k+1)kk=limk→+∞12k+1=0<1 . Данный ряд является сходимым.
Сходится ли числовой ряд ∑k=1∞13k·1+1kk2 .
Используем признак, описанный в предыдущем пункте limk→+∞13k·1+1kk2k=13·limk→+∞1+1kk=e3<1 , следовательно, числовой ряд сходится.
Интегральный признак Коши
Допустим, что ∑k=1∞ak является знакоположительным рядом. Необходимо обозначить функцию непрерывного аргумента y = f(x), которая совпадаетan= f(n) . Если y = f(x) больше нуля, не прерывается и убывает на [a; +∞) , где a≥1
, то в случае, если несобственный интеграл ∫a+∞f(x)dx является сходящимся, то рассматриваемый ряд также сходится. Если же он расходится, то в рассматриваемом примере ряд тоже расходится.
При проверке убывания функции можно использовать материал, рассмотренный на предыдущих уроках.
Рассмотреть пример ∑k=2∞1k·ln k на сходимость.
Условие сходимости ряда считается выполненным, так как limk→+∞1k·ln k=1+∞=0 . Рассмотрим y=1x·ln x . Она больше нуля, не прерывается и убывает на [2; +∞) . Первые два пункта доподлинно известны, а вот на третьем следует остановиться подробнее. Находим производную: y’=1x·ln x’=x·ln x’x·ln x2=ln x+x·1xx·ln x2=-ln x+1x·ln x2 . Она меньше нуля на [2; +∞) . Это доказывает тезис о том, что функция является убывающей.
Собственно, функция y=1x·ln x соответствует признакам принципа, который мы рассматривали выше. Воспользуемся им: ∫2+∞dxx·ln x=limA→+∞∫2Ad(ln x)ln x=limA→+∞ln(ln x)2A==limA→+∞(ln(ln A)-ln(ln 2))=ln(ln(+∞))-ln(ln 2)=+∞
Согласно полученным результатам, исходный пример расходится, так как несобственный интеграл является расходящимся.
Докажите сходимость ряда ∑k=1∞1(10k-9)(ln(5k+8))3 .
Так как limk→+∞1(10k-9)(ln(5k+8))3=1+∞=0 , то условие считается выполненным.
Начиная с k=4, верное выражение 1(10k-9)(ln(5k+8))3<1(5k+8)(ln(5k+8))3 .
Если ряд∑k=4∞1(5k+8)(ln(5k+8))3 будет считаться сходящимся, то, согласно одному из принципов сравнения, ряд ∑k=4∞1(10k-9)(ln(5k+8))3 также будет считаться сходящимся. Таким образом, мы сможет определить, что исходное выражение также является сходящимся.
Перейдем к доказательству ∑k=4∞1(5k+8)(ln(5k+8))3 .
Так как функция y=15x+8(ln(5x+8))3 больше нуля, не прерывается и убывает на [4; +∞) . Используем признак, описанный в предыдущем пункте:
∫4+∞dx(5x+8)(ln(5x+8))3=limA→+∞∫4Adx(5x+8)(ln(5x+8))3==15·limA→+∞∫4Ad(ln(5x+8)(ln(5x+8))3=-110·limA→+∞1(ln(5x+8))2|4A==-110·limA→+∞1(ln(5·A+8))2-1(ln(5·4+8))2==-110·1+∞-1(ln 28)2=110·ln 282
В полученном сходящемся ряде, ∫4+∞dx(5x+8)(ln(5x+8))3 , можно определить, что ∑k=4∞1(5k+8)(ln(5k+8))3 также сходится.
Признак Раабе
Допустим, что ∑k=1∞ak – знакоположительный числовой ряд.
Если limk→+∞k·akak+1<1 , то ряд расходится, еслиlimk→+∞k·akak+1-1>1 , то сходится.
Данный способ определения можно использовать в том случае, если описанные выше техники не дают видимых результатов.
Исследование на абсолютную сходимость
Для исследования берем ∑k=1∞bk . Используем знакоположительный ∑k=1∞bk . Мы можем использовать любой из подходящих признаков, которые мы описывали выше. Если ряд ∑k=1∞bk сходится, то исходный ряд является абсолютно сходящимся.
Исследовать ряд ∑k=1∞(-1)k3k3+2k-1 на сходимость ∑k=1∞(-1)k3k3+2k-1=∑k=1∞13k3+2k-1 .
Условие выполняется limk→+∞13k3+2k-1=1+∞=0 . Используем ∑k=1∞1k32 и воспользуемся вторым признаком: limk→+∞13k3+2k-11k32=13 .
Ряд ∑k=1∞(-1)k3k3+2k-1 сходится. Исходный ряд также абсолютно сходящийся.
Расходимость знакопеременных рядов
Если ряд ∑k=1∞bk – расходящийся, то соответствующий знакопеременный ряд ∑k=1∞bk либо расходящийся, либо условно сходящийся.
Лишь признак Даламбера и радикальный признак Коши помогут сделать выводы о ∑k=1∞bk по расходимости из модулей ∑k=1∞bk . Ряд ∑k=1∞bk также расходится, если не выполняется необходимое условие сходимости, то есть, если limk→∞+bk≠0 .
Проверить расходимость 17,272,-673,2474,12075-72076, … .
Модуль k-ого члена представлен как bk=k!7k .
Исследуем ряд ∑k=1∞bk=∑k=1∞k!7k на сходимость по признаку Даламбера: limk→+∞bk+1bk=limk→+∞(k+1)!7k+1k!7k=17·limk→+∞(k+1)=+∞ .
∑k=1∞bk=∑k=1∞k!7k расходится так же, как и исходный вариант.
Является ли ∑k=1∞(-1)k·k2+1ln(k+1) сходящимся.
Рассмотрим на необходимое условие limk→+∞bk=limk→+∞k2+1ln(k+1)=∞∞=limk→+∞=k2+1′(ln(k+1))’==limk→+∞2k1k+1=limk→+∞2k(k+1)=+∞ . Условие не выполнено, поэтому ∑k=1∞(-1)k·k2+1ln(k+1) ряд расходящийся. Предел был вычислен по правилу Лопиталя.
Признаки для условной сходимости
Признак Лейбница
Если величины членов знакочередующегося ряда убывают b1>b2>b3>…>… и предел модуля =0 при k→+∞ , то ряд ∑k=1∞bk сходится.
Рассмотреть ∑k=1∞(-1)k2k+15k(k+1) на сходимость.
Ряд представлен как ∑k=1∞(-1)k2k+15k(k+1)=∑k=1∞2k+15k(k+1) . Нужное условие выполняется limk→+∞=2k+15k(k+1)=0 . Рассмотрим ∑k=1∞1k по второму признаку сравнения limk→+∞2k+15k(k+1)1k=limk→+∞2k+15(k+1)=25
Получаем, что ∑k=1∞(-1)k2k+15k(k+1)=∑k=1∞2k+15k(k+1) расходится. Ряд ∑k=1∞(-1)k2k+15k(k+1) сходится по признаку Лейбница: последовательность2·1+15·1·11+1=310, 2·2+15·2·(2+1)=530, 2·3+15·3·3+1, … убывает и limk→+∞=2k+15k(k+1)=0 .
Ряд условно сходится.
Признак Абеля-Дирихле
∑k=1+∞uk·vk сходится в том случае, если {uk} не возрастает, а последовательность ∑k=1+∞vk ограничена.
Исследуйте 1-32+23+14-35+13+17-38+29+… на сходимость.
Представим
1-32+23+14-35+13+17-38+29+…=1·1+12·(-3)+13·2+14·1+15·(-3)+16·=∑k=1∞uk·vk
где {uk}=1, 12, 13, … – невозрастающая, а последовательность {vk}=1, -3 , 2, 1, -3, 2, … ограничена {Sk}=1, -2, 0, 1, -2, 0, … . Ряд сходится.
Содержание:
Числовые ряды:
При решении ряда математических задач, в том числе и в приложениях математики в экономике, приходится рассматривать суммы, составленные из бесконечного множества слагаемых. Из теории действительных чисел известно лишь, что означает сумма любого конечного числа чисел. Задача суммирования бесконечного множества слагаемых решается в теории рядов.
Основные понятия. Сходимость ряда
Определение. Числовым рядом называется бесконечная последовательность чисел 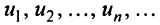
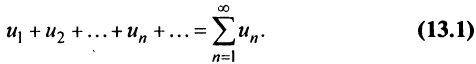
Числа 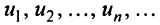 называются членами ряда, а член
называются членами ряда, а член 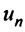 — общим или
— общим или 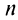 -м членом ряда.
-м членом ряда.
Ряд (13.1) считается заданным, если известен его общий член 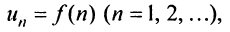 т.е. задана функция
т.е. задана функция 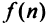 натурального аргумента. Например, ряд с общим членом
натурального аргумента. Например, ряд с общим членом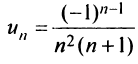 имеет вид
имеет вид
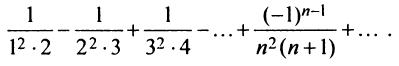
Более сложной является обратная задача: по нескольким первым членам ряда написать общий член. Эта задача имеет бесконечно много решений, но иногда удается найти самое естественное решение.
Пример:
Найти в простейшей форме общий член ряда:
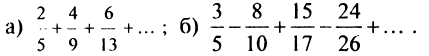
Решение:
Нетрудно убедиться, что для ряда а) общий член 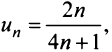 а для ряда б)
а для ряда б) 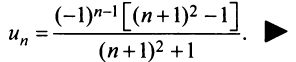
Рассмотрим суммы конечного числа членов ряда:
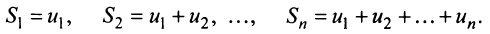
Сумма п первых членов ряда 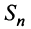 называется
называется 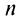 -й частичной суммой ряда.
-й частичной суммой ряда.
Определение. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.

Число 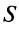 называется суммой ряда. В этом смысле можно записать
называется суммой ряда. В этом смысле можно записать
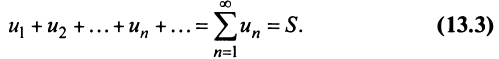
Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.
Пример:
Исследовать сходимость геометрического ряда, т.е. ряда, составленного из членов геометрической профессии
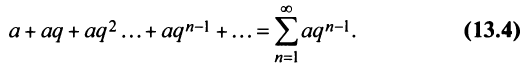
Решение:
Необходимо установить, при каких значениях знаменателя профессии  ряд (13.4) сходится и при каких — расходится.
ряд (13.4) сходится и при каких — расходится.
Из школьного курса алгебры известно, что сумма  первых членов геометрической профессии, т.е.
первых членов геометрической профессии, т.е. 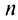 -я частичная сумма ряда при
-я частичная сумма ряда при 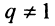 равна
равна 
Возможно несколько случаев:
1) если 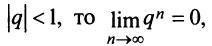
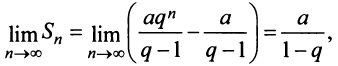 т.е. ряд сходится и его сумма
т.е. ряд сходится и его сумма 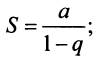
2) если 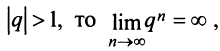 следовательно,
следовательно, 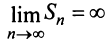 и ряд расходится;
и ряд расходится;
3) если 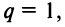 то ряд (13.4) примет вид
то ряд (13.4) примет вид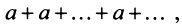 его
его 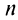 -я частичная сумма
-я частичная сумма 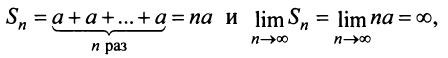 т.е. ряд расходится;
т.е. ряд расходится;
4) если 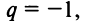 то ряд (13.4) примет вид
то ряд (13.4) примет вид 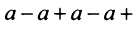
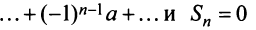 при
при 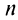 четном и
четном и 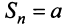 — при
— при 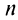 нечетном, следовательно,
нечетном, следовательно, 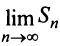 не существует, и ряд расходится.
не существует, и ряд расходится.
Таким образом, геометрический ряд сходится к сумме 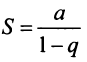 при
при 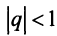 и расходится при
и расходится при 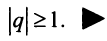
Пример:
Найти сумму ряда
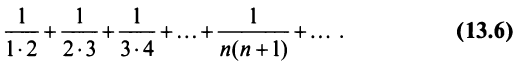
Решение:
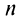 -я частичная сумма ряда
-я частичная сумма ряда
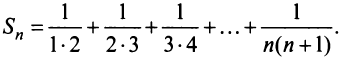 Учитывая, что
Учитывая, что 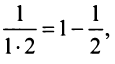
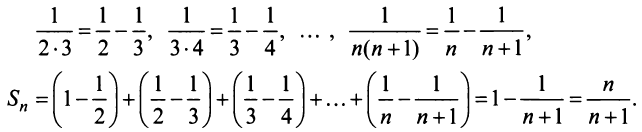 Отсюда
Отсюда 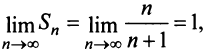 т.е. сумма ряда
т.е. сумма ряда 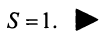
Свойства сходящихся рядов. 1. Если ряд  сходится и имеет сумму
сходится и имеет сумму 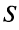 , то и ряд
, то и ряд 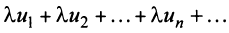 (полученный умножением данного ряда на число
(полученный умножением данного ряда на число 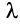 ) также сходится и имеет сумму
) также сходится и имеет сумму 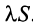 .
.
2. Если ряды 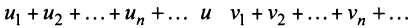 сходятся и их суммы соответственно равны
сходятся и их суммы соответственно равны 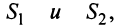 то и ряд
то и ряд 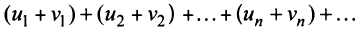 (представляющий сумму данных рядов) также сходится, и его сумма равна
(представляющий сумму данных рядов) также сходится, и его сумма равна 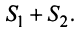
Свойства 1 и 2 непосредственно вытекают из свойств пределов числовых последовательностей.
3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.
Пусть в сходящемся ряде (13.1) отброшены 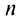 членов (в принципе можно отбрасывать члены с любыми номерами, лишь бы их было конечное число). Покажем, что полученный ряд
членов (в принципе можно отбрасывать члены с любыми номерами, лишь бы их было конечное число). Покажем, что полученный ряд
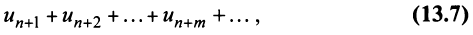
имеющий частичную сумму 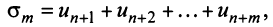 также сходится.
также сходится.
Очевидно, что 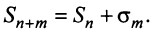 Отсюда следует, что при фиксированном
Отсюда следует, что при фиксированном 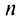 конечный предел
конечный предел 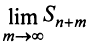 существует тогда и только тогда, когда существует конечный предел
существует тогда и только тогда, когда существует конечный предел 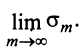 . А это и означает, что ряд (13.7) сходится. ■
. А это и означает, что ряд (13.7) сходится. ■
Ряд (13.7), полученный из данного отбрасыванием его первых 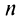 членов, называется
членов, называется 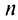 -м остатком ряда.
-м остатком ряда.
Если сумму 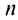 -го остатка ряда обозначить через
-го остатка ряда обозначить через 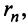 т.е.
т.е.
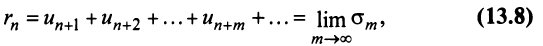
то сумму ряда (13.1) можно представить в виде

В результате мы подошли к свойству 4.
4. Для того чтобы ряд (13.1) сходился, необходимо и достаточно, чтобы при 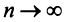 остаток ряда стремился к нулю, т.е. чтобы
остаток ряда стремился к нулю, т.е. чтобы 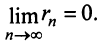
Это свойство вытекает из теоремы о связи бесконечно малых с пределами функций (см. § 6.3).
Установить сходимость (расходимость) ряда путем определения 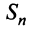 и вычисления
и вычисления 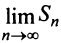 (как это сделано в примерах 13.2, 13.3) возможно далеко не всегда из-за принципиальных трудностей при нахождении
(как это сделано в примерах 13.2, 13.3) возможно далеко не всегда из-за принципиальных трудностей при нахождении 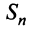 (суммировании
(суммировании 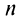 членов ряда). Проще это можно сделать на основании признаков сходимости, к изучению которых мы переходим.
членов ряда). Проще это можно сделать на основании признаков сходимости, к изучению которых мы переходим.
Необходимый признак сходимости. Гармонический ряд
Теорема (необходимый признак сходимости). Если ряд сходится, то предел его общего члена 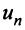 при
при 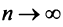 равен нулю, т.е.
равен нулю, т.е.
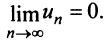
 Выразим
Выразим  -й член ряда через сумму его
-й член ряда через сумму его 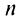 и
и 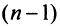 членов, т.е.
членов, т.е. 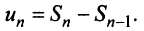 Так как ряд сходится, то
Так как ряд сходится, то 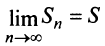 и
и 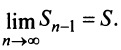 Поэтому
Поэтому
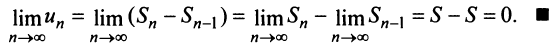
Пример №1
Проверить выполнение необходимого признака для ряда (13.6).
Решение:
Выше было доказано, что ряд (13.6) сходится, и действительно 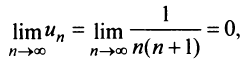 т.е. необходимый признак сходимости выполняется. ►
т.е. необходимый признак сходимости выполняется. ►
Следствие. Если предел общего члена ряда (13.1) при 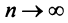 не равен нулю, т.е.
не равен нулю, т.е. 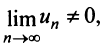 то ряд расходится.
то ряд расходится.
Предположим противное, т.е. ряд (13.1) сходится. Но в этом случае из приведенной выше теоремы следует 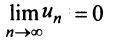 , что противоречит условию, заданному в следствии, т.е. ряд (13.1) расходится. ■
, что противоречит условию, заданному в следствии, т.е. ряд (13.1) расходится. ■
Пример №2
Исследовать сходимость ряда 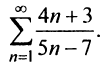
Решение:
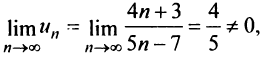 т.е. необходимый признак сходимости не выполняется, следовательно, ряд расходится. ►
т.е. необходимый признак сходимости не выполняется, следовательно, ряд расходится. ►
Замечание. Следует подчеркнуть, что рассмотренная теорема выражает лишь необходимый, но недостаточный признак сходимости ряда. Если 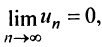 то из этого еще не следует, что ряд сходится.
то из этого еще не следует, что ряд сходится.
В качестве примера рассмотрим ряд
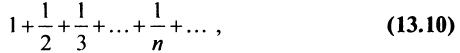
называемый гармоническим.
Необходимый признак сходимости выполнен: 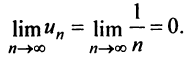 Докажем, что, несмотря на это, гармонический ряд расходится.
Докажем, что, несмотря на это, гармонический ряд расходится.
 Вначале получим вспомогательное неравенство. С этой целью запишем сумму первых
Вначале получим вспомогательное неравенство. С этой целью запишем сумму первых 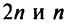 членов ряда:
членов ряда:
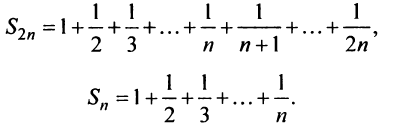
Найдем разность
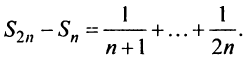
Заменяя в сумме каждое слагаемое наименьшим, равным 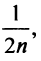 придем к вспомогательному неравенству
придем к вспомогательному неравенству
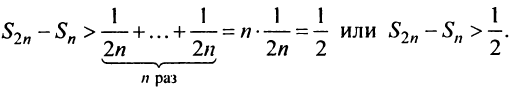
Предположим противное, т.е. что гармонический ряд сходится, тогда 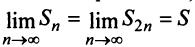 и, переходя к пределу в неравенстве (см. § 6.5), получим, что
и, переходя к пределу в неравенстве (см. § 6.5), получим, что 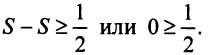
Мы пришли к противоречию, следовательно, наше предположение о сходимости гармонического ряда неверно, т.е. гармонический ряд расходится. ■
В следующих двух параграфах рассмотрим достаточные признаки сходимости.
Ряды с положительными членами
Теорема (признак сравнения). Пусть даны два ряда с положительными членами: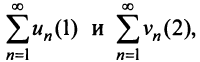 причем члены первого ряда не превосходят членов второго, т.е. при любом
причем члены первого ряда не превосходят членов второго, т.е. при любом 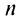

Тогда: а) если сходится ряд 2, то сходится и ряд 1; б) если расходится ряд 1, то расходится и ряд 2.
 а) Пусть частичные суммы рядов 1 и 2 соответственно равны
а) Пусть частичные суммы рядов 1 и 2 соответственно равны 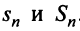 . По условию ряд 2 сходится, следовательно, существует
. По условию ряд 2 сходится, следовательно, существует 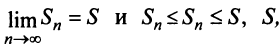 так как члены ряда 2 положительны. Рассмотрим последовательность частичных сумм
так как члены ряда 2 положительны. Рассмотрим последовательность частичных сумм 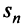 ряда 1. Эта последовательность является: возрастающей (так как с ростом
ряда 1. Эта последовательность является: возрастающей (так как с ростом 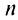 увеличивается сумма
увеличивается сумма 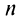 положительных слагаемых) и ограниченной (так как
положительных слагаемых) и ограниченной (так как 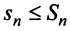 в силу условия (13.11), т.е.
в силу условия (13.11), т.е. 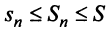 ).
).
Следовательно, на основании признака существования предела (см. § 6.5) последовательность 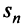 имеет предел, т.е. ряд 1 сходится.
имеет предел, т.е. ряд 1 сходится.
б) Применим метод доказательства от противного. Предположим, что ряд 2 сходится. Тогда согласно первой части теоремы сходится и ряд 1, что противоречит предположению; т.е. ряд 2 расходится. ■
Замечание. Так как сходимость ряда не изменяется при отбрасывании конечного числа членов ряда, то условие (13.11) не обязательно должно выполняться с первых членов рядов и только для членов с одинаковыми номерами  . Достаточно, чтобы оно выполнялось, начиная с некоторого номера
. Достаточно, чтобы оно выполнялось, начиная с некоторого номера  или чтобы имело место неравенство
или чтобы имело место неравенство 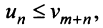 где
где 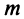 — некоторое целое число.
— некоторое целое число.
Пример №3
Исследовать сходимость ряда
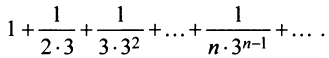
Решение:
Сравним данный ряд со сходящимся геометрическим рядом 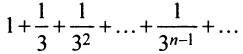 (его знаменатель
(его знаменатель 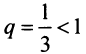 ).
).
Так как члены данного ряда, начиная со второго, меньше членов сходящегося геометрического ряда 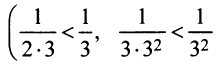 и вообще
и вообще 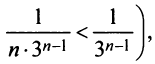 то на основании признака сравнения ряд сходится. ►
то на основании признака сравнения ряд сходится. ►
Пример №4
Исследовать сходимость ряда
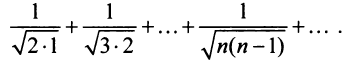
Решение:
Сравним данный ряд с гармоническим 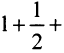
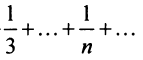 , мысленно отбросив его первый член, равный 1 (что, естественно, не повлияет на расходимость ряда). Так как
, мысленно отбросив его первый член, равный 1 (что, естественно, не повлияет на расходимость ряда). Так как 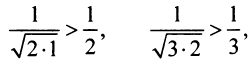 и вообще
и вообще 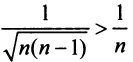 (ибо
(ибо 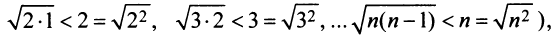 т.е. члены данного ряда больше членов расходящегося гармонического ряда, то на основании признака сравнения ряд расходится. ►
т.е. члены данного ряда больше членов расходящегося гармонического ряда, то на основании признака сравнения ряд расходится. ►
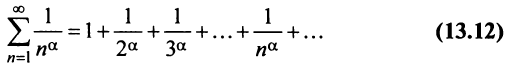
сходится при 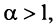 расходится при
расходится при 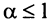 здесь же отметим, что при
здесь же отметим, что при 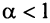 расходимость ряда (13.12) следует из признака сравнения, так как в этом случае члены ряда
расходимость ряда (13.12) следует из признака сравнения, так как в этом случае члены ряда 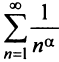 больше соответствующих членов гармонического ряда
больше соответствующих членов гармонического ряда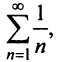 а в частном случае при
а в частном случае при 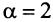 сходимость ряда (13.12) может быть доказана сравнением этого ряда со сходящимся (13.6)).
сходимость ряда (13.12) может быть доказана сравнением этого ряда со сходящимся (13.6)).
Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (13.11), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т.п.). В ряде случаев более простым оказывается предельный признак сравнения.
Теорема (предельный признак сравнения)
Теорема (предельный признак сравнения). Если 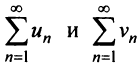 — ряды с положительными членами и существует конечный предел отношения их общих членов
— ряды с положительными членами и существует конечный предел отношения их общих членов 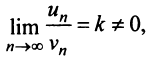 то ряды одновременно сходятся либо расходятся.
то ряды одновременно сходятся либо расходятся.
 Так как
Так как 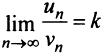 , то по определению предела числовой последовательности (см. § 6.1) для любого
, то по определению предела числовой последовательности (см. § 6.1) для любого 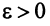 существует такой номер
существует такой номер 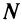 , что для всех
, что для всех 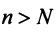 выполняется неравенство
выполняется неравенство
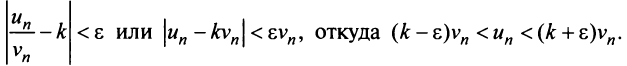
Если ряд  сходится, то сходится ряд
сходится, то сходится ряд 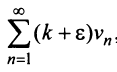 и в силу признака сравнения будет сходиться ряд
и в силу признака сравнения будет сходиться ряд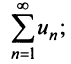 аналогично, если сходится ряд
аналогично, если сходится ряд 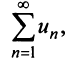 сходится ряд
сходится ряд 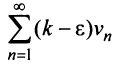 и сходится
и сходится 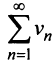 . Таким образом, из сходимости одного ряда следует сходимость другого. Утверждение теоремы о расходимости рядов доказывается аналогично.
. Таким образом, из сходимости одного ряда следует сходимость другого. Утверждение теоремы о расходимости рядов доказывается аналогично.
Пример №5
Исследовать сходимость ряда 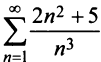
Решение:
Сравним данный ряд с расходящимся гармоническим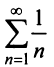 (выбор такого ряда для сравнения может подсказать то, что при больших
(выбор такого ряда для сравнения может подсказать то, что при больших 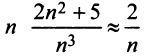 ). Так как
). Так как 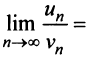
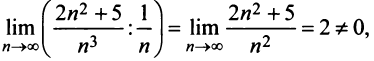 то данный ряд, так же как и гармонический, расходится. ►
то данный ряд, так же как и гармонический, расходится. ►
Весьма удобным на практике является признак Даламбера.
Теорема (признак Даламбера)
Теорема (признак Даламбера). Пусть для ряда 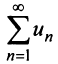 с положительными членами существует предел отношения
с положительными членами существует предел отношения 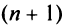 -го члена к
-го члена к 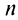 -му члену
-му члену 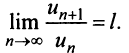 Тогда, если
Тогда, если 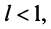 то ряд сходится; если
то ряд сходится; если 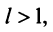 то ряд расходится; если
то ряд расходится; если 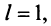 то вопрос о сходимости ряда остается нерешенным.
то вопрос о сходимости ряда остается нерешенным.
Из определения предела последовательности следует, что для любого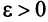 существует такой номер
существует такой номер 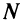 , что для всех
, что для всех 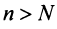 выполняется неравенство
выполняется неравенство 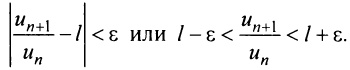 1) Пусть
1) Пусть 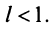 Выберем
Выберем 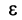 настолько малым, что число
настолько малым, что число
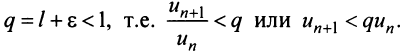
Последнее неравенство будет выполняться для всех 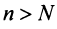 , т.е. для
, т.е. для 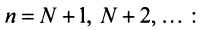
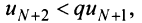
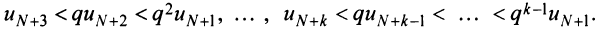
Получили, что члены ряда 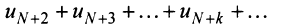 меньше соответствующих членов геометрического ряда
меньше соответствующих членов геометрического ряда 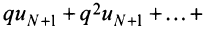
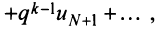 сходящегося при
сходящегося при 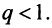 Следовательно, на основании признака сравнения этот ряд сходится, а значит, сходится и рассматриваемый ряд
Следовательно, на основании признака сравнения этот ряд сходится, а значит, сходится и рассматриваемый ряд 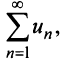 отличающийся от полученного на первые
отличающийся от полученного на первые 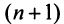 членов.
членов.
2) Пусть 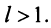 Возьмем
Возьмем 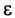 настолько малым, что
настолько малым, что 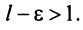 Тогда из условия
Тогда из условия 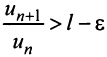 следует, что
следует, что 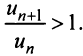 Это означает, что члены ряда возрастают, начиная с номера
Это означает, что члены ряда возрастают, начиная с номера 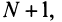 поэтому предел общего члена ряда не равен нулю, т.е. не выполнен необходимый признак сходимости, и ряд расходится. ■
поэтому предел общего члена ряда не равен нулю, т.е. не выполнен необходимый признак сходимости, и ряд расходится. ■
Пример №6
Исследовать сходимость рядов:
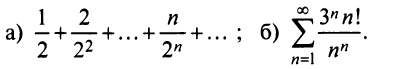
Решение:
а) Так как 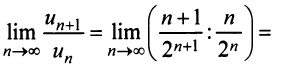
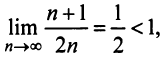 то по признаку Даламбера ряд сходится.
то по признаку Даламбера ряд сходится.
б) Так как 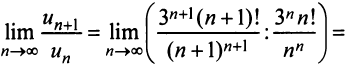
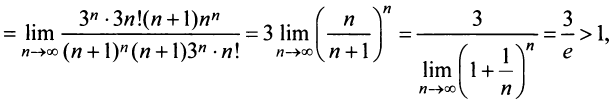 то по признаку Даламбера ряд расходится. ►
то по признаку Даламбера ряд расходится. ►
Замечание 1. Если 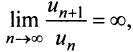 то ряд расходится.
то ряд расходится.
Замечание 2. Если 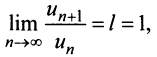 то, как отмечалось выше, признак Даламбера ответа о сходимости ряда не дает, и рекомендуется перейти к другим признакам сходимости.
то, как отмечалось выше, признак Даламбера ответа о сходимости ряда не дает, и рекомендуется перейти к другим признакам сходимости.
Теорема (интегральный признак сходимости)
Теорема (интегральный признак сходимости). Пусть дан ряд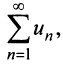 члены которого положительны и не возрастают, т.е.
члены которого положительны и не возрастают, т.е. а функция
а функция 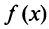 , определенная при
, определенная при 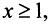 непрерывная и невозрастающая и
непрерывная и невозрастающая и
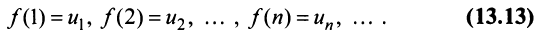
Тогда для сходимости ряда 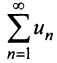 необходимо и достаточно, чтобы сходился несобственный интеграл
необходимо и достаточно, чтобы сходился несобственный интеграл 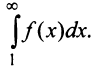
Рассмотрим ряд
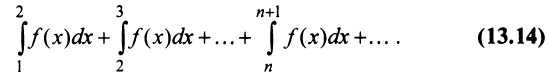
Его  -й частичной суммой будет
-й частичной суммой будет
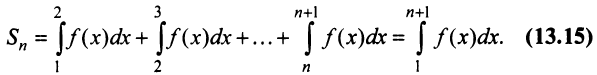
Сходимость ряда (13.14) означает существование предела последовательности его частичных сумм (13.15), т.е. сходимость несобственного интеграла 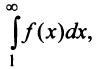 поскольку
поскольку 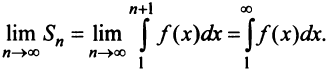 В силу монотонности функции
В силу монотонности функции 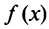 на любом отрезке
на любом отрезке 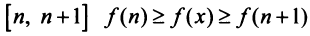 или, учитывая (13.13),
или, учитывая (13.13),

Интегрируя (13.16) на отрезке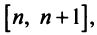 получим
получим
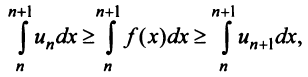
откуда
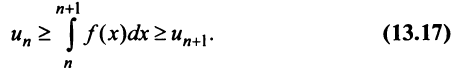
Если ряд 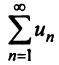 сходится, то по признаку сравнения рядов в силу первого неравенства (13.17) должен сходиться ряд (13.14), а значит, и несобственный интеграл
сходится, то по признаку сравнения рядов в силу первого неравенства (13.17) должен сходиться ряд (13.14), а значит, и несобственный интеграл 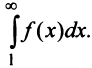 Обратно, если сходится J/(jc)c&, т.е. ряд (13.14), то согласно тому же признаку сравнения на основании второго неравенства (13.17) будет сходиться ряд
Обратно, если сходится J/(jc)c&, т.е. ряд (13.14), то согласно тому же признаку сравнения на основании второго неравенства (13.17) будет сходиться ряд 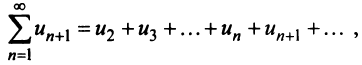 а следовательно, и данный ряд
а следовательно, и данный ряд 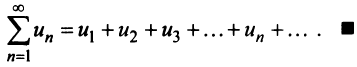
Пример №7
Исследовать сходимость обобщенного гармонического ряда 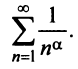
Решение:
Пусть 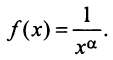 Функция
Функция 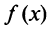 при
при 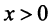 (а значит, и при
(а значит, и при 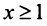 ) положительная и невозрастающая (точнее убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла
) положительная и невозрастающая (точнее убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла 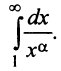 Имеем
Имеем 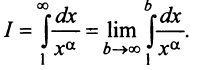 Если
Если 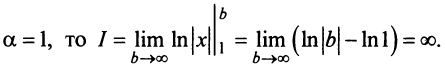
Если 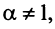 то
то
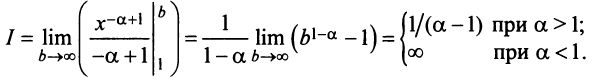 Итак, данный ряд сходится при
Итак, данный ряд сходится при 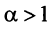 и расходится при
и расходится при 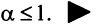
Ряды с членами произвольного знака
Знакочередующиеся ряды. Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны
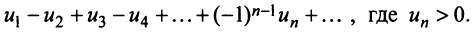
Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине 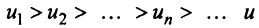 и предел его общего члена при
и предел его общего члена при 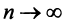 равен нулю, т.е.
равен нулю, т.е.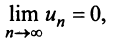 то ряд сходится, а его сумма не превосходит первого члена:
то ряд сходится, а его сумма не превосходит первого члена: 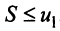 .
.
Рассмотрим последовательность частичных сумм четного числа членов при 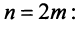
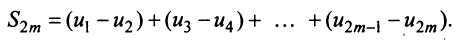
Эта последовательность возрастающая (так как с ростом  увеличивается число положительных слагаемых в скобках) и ограниченная (это видно из того, что
увеличивается число положительных слагаемых в скобках) и ограниченная (это видно из того, что  можно представить в виде
можно представить в виде
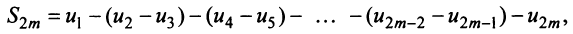
откуда следует, что 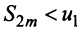 ). На основании признака существования предела (см. § 6.5) последовательность
). На основании признака существования предела (см. § 6.5) последовательность 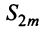 имеет предел
имеет предел 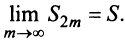
Попутно заметим, что, переходя к пределу в неравенстве 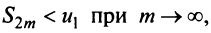 получим, что
получим, что 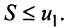
Теперь рассмотрим последовательность частичных сумм нечетного числа членов при 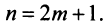 Очевидно, что
Очевидно, что 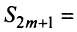
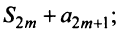 поэтому, учитывая необходимый признак сходимости ряда,
поэтому, учитывая необходимый признак сходимости ряда,
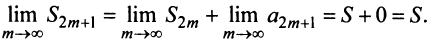
Итак, при любом  (четном или нечетном)
(четном или нечетном) 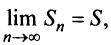 т.е. ряд сходится. Рис. 13.1 иллюстрирует сходимость
т.е. ряд сходится. Рис. 13.1 иллюстрирует сходимость 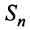 к числу
к числу 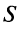 слева при четном
слева при четном 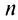 и справа при нечетном
и справа при нечетном 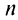 . ■
. ■
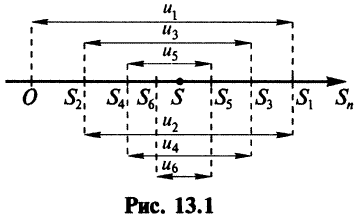
Из рис. 13.1 вытекает еще одна оценка для суммы  сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница: при любом
сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница: при любом 
Пример №8
Исследовать сходимость ряда
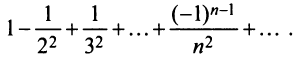
Решение:
Так как члены знакочередующегося ряда убывают по абсолютной величине 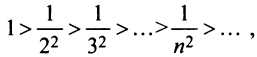 и предел общего члена
и предел общего члена 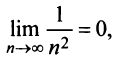 то по признаку Лейбница ряд сходится. ►
то по признаку Лейбница ряд сходится. ►
Замечание. В теореме Лейбница существенно не только условие 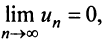 но и условие
но и условие 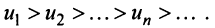 Так, например, для ряда ,
Так, например, для ряда ,
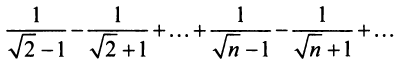 второе условие нарушено и, хотя
второе условие нарушено и, хотя 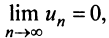 ряд расходится. Это видно, если данный ряд представить (после попарного сложения его членов) в виде
ряд расходится. Это видно, если данный ряд представить (после попарного сложения его членов) в виде 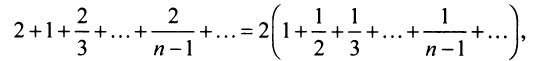
т.е. «удвоенного» гармонического ряда.
Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.
По формуле (13.9) сумму сходящегося ряда можно представить как сумму 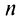 членов ряда и суммы
членов ряда и суммы 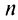 -гo остатка ряда, т.е.
-гo остатка ряда, т.е. 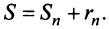 Полагая приближенно
Полагая приближенно 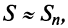 мы допускаем погрешность, равную
мы допускаем погрешность, равную 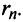 Так как при четном
Так как при четном 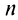
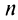 -й остаток знакочередующегося ряда
-й остаток знакочередующегося ряда 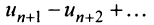 представляет ряд, удовлетворяющий условиям теоремы Лейбница, то его сумма
представляет ряд, удовлетворяющий условиям теоремы Лейбница, то его сумма 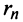 не превосходит первого члена
не превосходит первого члена 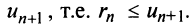 Так как при нечетном
Так как при нечетном 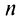 для
для 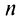 -го остатка ряда
-го остатка ряда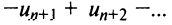 его сумма
его сумма 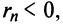 то, очевидно, что при любом
то, очевидно, что при любом 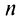

Пример №9
Какое число членов ряда 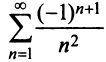 надо взять, чтобы вычислить его сумму с точностью до 0,001?
надо взять, чтобы вычислить его сумму с точностью до 0,001?
Решение:
По условию 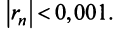 Учитывая следствие теоремы Лейбница (13.18), запишем более сильное неравенство
Учитывая следствие теоремы Лейбница (13.18), запишем более сильное неравенство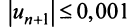 или
или 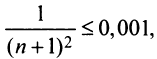 откуда
откуда 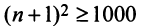 и
и 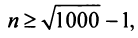 или
или 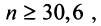 т.е. необходимо взять не менее 31 члена ряда. ►
т.е. необходимо взять не менее 31 члена ряда. ►
Знакопеременные ряды. Пусть  знакопеременный ряд (13.1), в котором любой его член
знакопеременный ряд (13.1), в котором любой его член 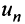 может быть как положительным, так и отрицательным.
может быть как положительным, так и отрицательным.
Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов данного ряда (13.1)
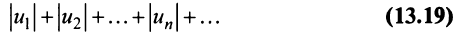
сходится, то сходится и данный ряд.
Обозначим 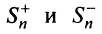 суммы абсолютных величин членов данного ряда (13.1), входящих в него со знаком «плюс» и «минус».
суммы абсолютных величин членов данного ряда (13.1), входящих в него со знаком «плюс» и «минус».
Тогда частичная сумма данного ряда 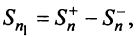 а ряда, составленного из абсолютных величин его членов,
а ряда, составленного из абсолютных величин его членов, 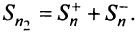 По условию ряд (13.19) сходится, следовательно, существует конечный предел
По условию ряд (13.19) сходится, следовательно, существует конечный предел 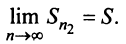
Последовательности 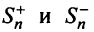 являются возрастающими (так как с увеличением
являются возрастающими (так как с увеличением 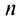 увеличиваются
увеличиваются 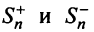 ) и ограниченными
) и ограниченными
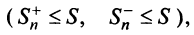 значит, существуют пределы
значит, существуют пределы 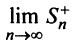 и
и 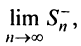 и соответственно предел частичной суммы данного ряда
и соответственно предел частичной суммы данного ряда
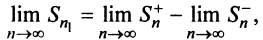 т.е. ряд (13.1) сходится. ■
т.е. ряд (13.1) сходится. ■
Следует отметить, что обратное утверждение неверно. Ряд (13.19) может расходиться, а ряд (13.1) сходиться. Например, ряд 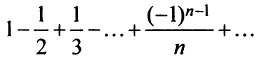 сходится по признаку Лейбница, а ряд из абсолютных величин его членов
сходится по признаку Лейбница, а ряд из абсолютных величин его членов 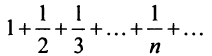 (гармонический ряд) расходится.
(гармонический ряд) расходится.
Поэтому введем следующие определения.
Определение 1. Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.
Определение 2. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Таким образом, рассмотренный выше ряд 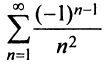 — абсолютно сходящийся, а ряд
— абсолютно сходящийся, а ряд 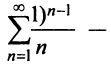 условно сходящимся.
условно сходящимся.
Грубо говоря, различие между абсолютно сходящимися и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся — в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.
Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.
Условно сходящиеся ряды такими свойствами не обладают.
Возьмем, например, ряд 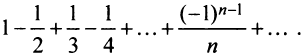 Переставим члены местами и сгруппируем их следующим образом:
Переставим члены местами и сгруппируем их следующим образом:
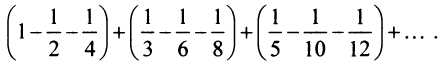
Перепишем ряд в виде:
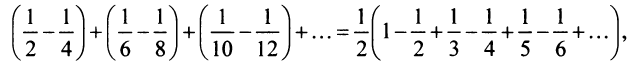
т.е. от перестановки членов ряда сумма его уменьшилась в 2 раза.
Можно показать (теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
Пример №10
Найти сумму ряда 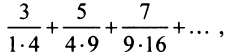 доказав его сходимость.
доказав его сходимость.
Решение:
Очевидно, что общий член ряда 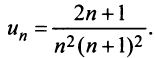
Представим сумму 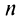 членов ряда в виде
членов ряда в виде 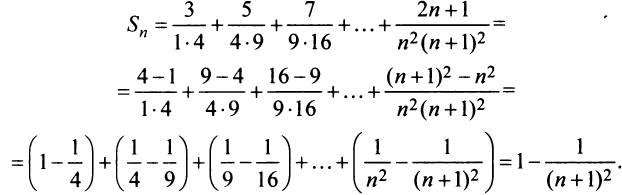 Так как при
Так как при 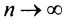 последовательность
последовательность 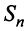 имеет конечный предел, то ряд сходится, и его сумма
имеет конечный предел, то ряд сходится, и его сумма
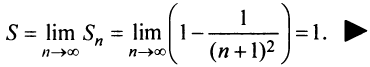
Пример №11
Исследовать сходимость ряда:
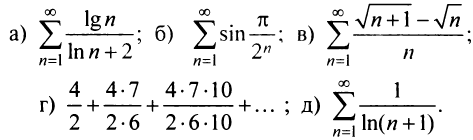
Решение:
а) Проверим выполнение необходимого признака сходимости, найдя предел общего члена:
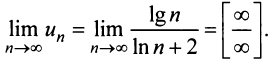
Для вычисления предела отношения двух бесконечно больших функций натурального аргумента правило Лопиталя непосредственно применять нельзя, ибо для таких функций не определено понятие производной. Поэтому применяя теорему о «погружении» дискретного аргумента  в непрерывный
в непрерывный 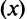 , получим
, получим 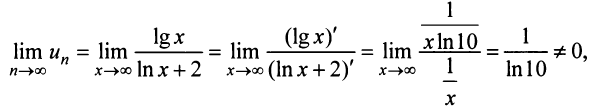
следовательно, ряд расходится.
б) Очевидно, что задан ряд с положительными членами, так как 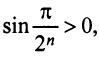 ибо аргумент синуса
ибо аргумент синуса 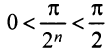 при любом
при любом 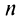 . Так как члены данного ряда меньше членов сходящегося геометрического ряда со знаменателем
. Так как члены данного ряда меньше членов сходящегося геометрического ряда со знаменателем
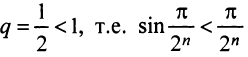 (ибо при
(ибо при 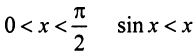 ), то данный ряд сходится.
), то данный ряд сходится.
в) Представим общий член ряда в виде
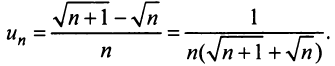 Применим предельный признак сравнения, сравнив данный ряд со сходящимся «эталонным» рядом (13.12) при
Применим предельный признак сравнения, сравнив данный ряд со сходящимся «эталонным» рядом (13.12) при 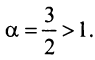 Так как предел отношения общих членов двух рядов
Так как предел отношения общих членов двух рядов
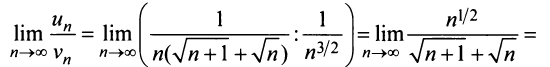
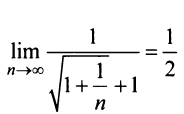
есть конечное число, не равное нулю, то данный ряд, так же как и «эталонный», сходится.
г) Применим признак Даламбера, заметив, что общий член ряда 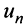 имеет вид
имеет вид 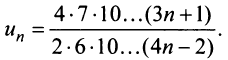
Тогда 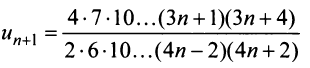 и
и 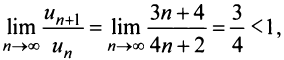 т.е. данный ряд сходится.
т.е. данный ряд сходится.
д) Применим признак Даламбера:
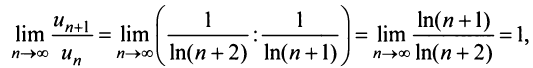
т.е. вопрос о сходимости ряда остается открытым. Проверим выполнение необходимого признака (с этого можно было начать исследование): 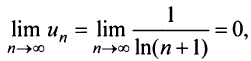 т.е. необходимый признак выполнен, но вопрос о сходимости ряда по-прежнему не решен.
т.е. необходимый признак выполнен, но вопрос о сходимости ряда по-прежнему не решен.
Применим признак сравнения в более простой предельной форме. Сравним данный ряд, например, с гармоническим.
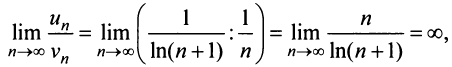 т.е. ответа о сходимости ряда нет. Аналогичная картина (
т.е. ответа о сходимости ряда нет. Аналогичная картина (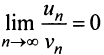 или
или 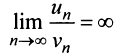 ) наблюдается и при использовании других «эталонных» рядов (см. § 13.3). Применим, наконец, признак сравнения в обычной форме. Сравним данный ряд с тем же гармоническим рядом, у которого отброшен первый член:
) наблюдается и при использовании других «эталонных» рядов (см. § 13.3). Применим, наконец, признак сравнения в обычной форме. Сравним данный ряд с тем же гармоническим рядом, у которого отброшен первый член:
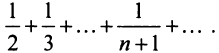 Так как члены рассматриваемого ряда больше членов расходящегося гармонического ряда
Так как члены рассматриваемого ряда больше членов расходящегося гармонического ряда 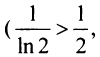
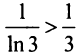 и вообще
и вообще
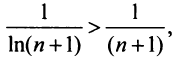 что вытекает из очевидного неравенства
что вытекает из очевидного неравенства 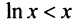 ), то данный ряд расходится. ►
), то данный ряд расходится. ►
Пример №12
Исследовать сходимость ряда:
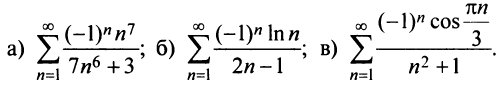
Решение:
а) Предел общего члена ряда 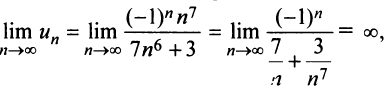 так как знаменатель дроби стремится к нулю, а числитель колеблется, принимая значения 1 (при четном
так как знаменатель дроби стремится к нулю, а числитель колеблется, принимая значения 1 (при четном  ) и —1 (при нечетном
) и —1 (при нечетном 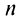 ). Следовательно, необходимый признак сходимости не выполнен, и ряд расходится.
). Следовательно, необходимый признак сходимости не выполнен, и ряд расходится.
б) Так как члены знакочередующегося ряда, начиная со второго, убывают по абсолютной величине —
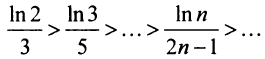
и предел общего члена 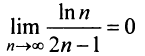 (это можно установить, например, с помощью правила Лопиталя), то по признаку Лейбница ряд сходится. Ряд
(это можно установить, например, с помощью правила Лопиталя), то по признаку Лейбница ряд сходится. Ряд 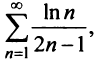 составленный из абсолютных величин членов данного ряда, расходится, так как его члены больше членов расходящегося гармонического ряда, умноженного на
составленный из абсолютных величин членов данного ряда, расходится, так как его члены больше членов расходящегося гармонического ряда, умноженного на 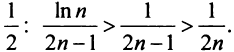 Следовательно, данный ряд условно сходящийся.
Следовательно, данный ряд условно сходящийся.
в) Ряд, составленный из абсолютных величин членов данного ряда, сходится, так как его члены меньше членов сходящегося ряда (13.12) при 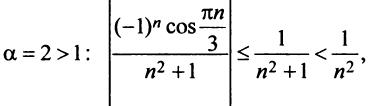 следовательно, данный ряд сходится и притом абсолютно. ►
следовательно, данный ряд сходится и притом абсолютно. ►
Определение ряда и его сходимость
Пусть

бесконечная последовательность чисел.
Определение 27.1.1. Выражение

называется числовым рядом, а элементы последовательности 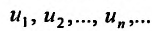 членами ряда.
членами ряда.
Поскольку выражение (27.1.2) рассматривается как единое целое, то для задания ряда необходимо задать каждый его член 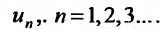 Обычно член ряда задается как некоторая функция от своего номера. Аналитическое выражение этой функции называют общим членом ряда. Например, общим членом ряда геометрической прогрессии
Обычно член ряда задается как некоторая функция от своего номера. Аналитическое выражение этой функции называют общим членом ряда. Например, общим членом ряда геометрической прогрессии 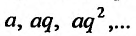 является
является 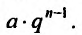
Припишем теперь определенный смысл выражению (27.1.2), т.е. введем определение.
Определение 27.1.2. Сумма n первых членов ряда (27.1.2) 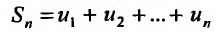 называется n-ой частичной суммой этого ряда.
называется n-ой частичной суммой этого ряда.
Ясно, что первая, вторая, третья и т.д. частичные суммы ряда 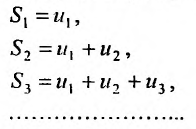
составляют бесконечную последовательность: 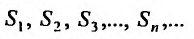
Определение 27.1.3. Ряд (27.1.2) называется сходящимся, если последовательность 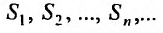 его частичных сумм имеет конечный предел:
его частичных сумм имеет конечный предел: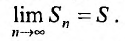
Значение S этого предела называется суммой ряда (27.1.2). Ряд (27.1.2) называется расходящимся, если последовательность его частичных сумм предела не имеет (например, если члены последовательности возрастают по модулю неограниченно).
Содержание теории числовых рядов состоит в установлении сходимости или расходимости тех или иных рядов и в вычислении сумм сходящихся рядов.
В принципе можно доказывать сходимость или расходимость каждого ряда, а также вычислять сумму сходящегося ряда, опираясь непосредственно на определения сходимости и суммы. Для этого в каждом случае составляется аналитическое выражение для n- ой частичной суммы ряда и находится предел этого выражения при возрастании n.
Пример:
Для ряда 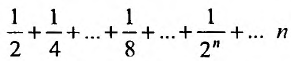 -я частичная сумма
-я частичная сумма 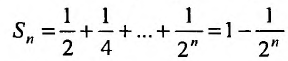 , и предел ее
, и предел ее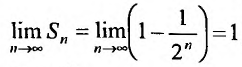 , поэтому этот ряд сходится и его сумма равна 1.
, поэтому этот ряд сходится и его сумма равна 1.
Пример:
Последовательность вида

называется геометрической прогрессией, где а – первый член, а
q – её знаменатель; выражение 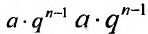 называется общим членом геометрической прогрессии.
называется общим членом геометрической прогрессии.
Числовой ряд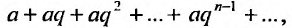 члены которого являются членами геометрической прогрессии, называется геометрическим рядом со знаменателем q .
члены которого являются членами геометрической прогрессии, называется геометрическим рядом со знаменателем q .
Если в прогрессии (27.1.3) имеется только конечное число членов, то прогрессия называется конечной; в противном случае, если за каждым членом прогрессии следует ещё хотя бы один член, то прогрессия называется бесконечной.
В случае конечной прогрессии 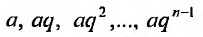 можно говорить о сумме всех её членов
можно говорить о сумме всех её членов 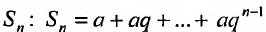 , которую можно назвать n- ой частичной суммой геометрического ряда.
, которую можно назвать n- ой частичной суммой геометрического ряда.
Известно, что при 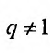 , эта сумма равна
, эта сумма равна 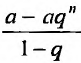 . Из определения 27.1.3 следует, что суммой геометрического ряда
. Из определения 27.1.3 следует, что суммой геометрического ряда
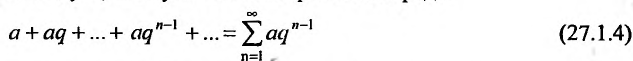
называется предел её частичных сумм 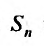 при неограниченном возрастании n:
при неограниченном возрастании n:
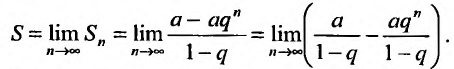
Так как а и q от n не зависят, то последнюю формулу представим в виде:

Если 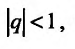 то предел
то предел 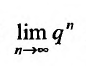 равен нулю, и мы получаем
равен нулю, и мы получаем
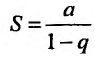 , т.е. при
, т.е. при 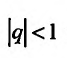 прогрессия (27.1.5) сходится. Следователь-
прогрессия (27.1.5) сходится. Следователь-
но, сходится и ряд (27.1.4). Если же 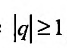 , то предел справа в равенстве (27.1.5) не существует и, следовательно, ряд (27.1.4) расходится.
, то предел справа в равенстве (27.1.5) не существует и, следовательно, ряд (27.1.4) расходится.
Итак, мы привели примеры, в которых исследование сходимости рядов проводили, применяя определение 27.1.3., т.е. вычисляли частичные суммы и находили предел их последовательностей. Ясно, что в общем случае, составление аналитического выражения для n- ой частичной суммы трудный вопрос. Кроме того, при исследовании рядов нередко значения сумм не представляют интереса, т.к. нужно определить только сходится ряд или нет. Поэтому представляют интерес методы анализа рядов, когда не требуется вычислять суммы рядов. Далее перейдем к изложению таких методов.
Свойства сходящихся рядов
Пусть дан ряд

Определение 27.2.1. Ряд 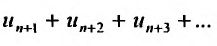 называется n-м остатком ряда (27.2.1.)
называется n-м остатком ряда (27.2.1.)
Очевидно, m- я частичная суммаn -го остатка ряда равна разности 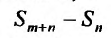 частичных сумм самого ряда. Кроме того,
частичных сумм самого ряда. Кроме того, 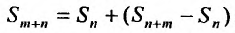 , откуда, переходя к пределу по m при
, откуда, переходя к пределу по m при 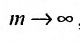 , получим
, получим 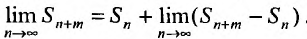
Предел слева есть сумма исходного ряда, а предел справа-сумма 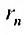 его n – го остатка:
его n – го остатка: 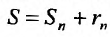 . Ясно, что из существования предела в левой части равенства следует существование другого предела в правой части и наоборот. Поэтому если сходится один из остатков ряда, то сходится и сам ряд. Точно так же из сходимости ряда следует сходимость каждого его остатка. Кроме того, справедлива следующая теорема.
. Ясно, что из существования предела в левой части равенства следует существование другого предела в правой части и наоборот. Поэтому если сходится один из остатков ряда, то сходится и сам ряд. Точно так же из сходимости ряда следует сходимость каждого его остатка. Кроме того, справедлива следующая теорема.
Теорема 27.2.1. Если ряд (27.2.1) сходится, то сумма его n-го остатка с ростом n стремится к нулю.
Доказательство. Выше показано, что 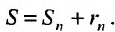 . Так как это равенство справедливо для любого n, то мы можем перейти в нем по n к пределу:
. Так как это равенство справедливо для любого n, то мы можем перейти в нем по n к пределу: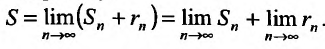
Но для сходящегося ряда 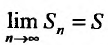 , поэтому
, поэтому 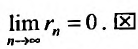
Рассмотрим теперь свойства сходящихся рядов, которые позволяют действовать с ними, как с конечными суммами.
Теорема 27.2.2. Если ряд

имеет сумму S, то ряд

полученный из предыдущего умножением всех членов на одно и тоже число a, имеет сумму aS.
Доказательство. Обозначим последовательность частичных сумм ряда (27.2.2) 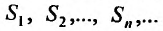 Тогда последовательность частичных сумм ряда (27.2.3) очевидно будет иметь вид:
Тогда последовательность частичных сумм ряда (27.2.3) очевидно будет иметь вид: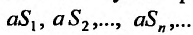 . И поэтому
. И поэтому 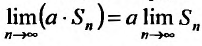 . Так как ряд
. Так как ряд
(27.2.2) сходится, то 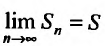 существует и, следовательно, существует предел
существует и, следовательно, существует предел 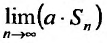 ив силу этого же равенства он равен aS.
ив силу этого же равенства он равен aS.
Теорема 27.2.3. Если ряды
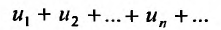 и
и 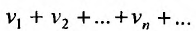 сходятся, а их суммы соответственно равны
сходятся, а их суммы соответственно равны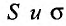 , то и ряд
, то и ряд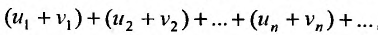 называемый суммой данных рядов, также сходится и его сумма равна сумме сумм данных рядов
называемый суммой данных рядов, также сходится и его сумма равна сумме сумм данных рядов 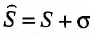 , другими словами, сходящиеся ряды можно почленно складывать.
, другими словами, сходящиеся ряды можно почленно складывать.
Доказательство. Пусть 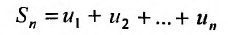 и
и
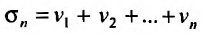 . Тогда n -ая частичная сумма
. Тогда n -ая частичная сумма 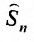 ряда
ряда
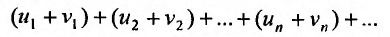 будет равна
будет равна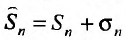 и так как
и так как 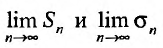 существуют, то
существуют, то
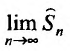 существует и равен
существует и равен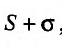 , т.е.
, т.е.
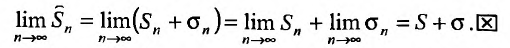
Следствие. Разность двух сходящихся рядов-ряд сходящийся.
Теорема 27.2.4. Свойства сходимости или расходимости ря-,ki не нарушается, если в ряде исключить или приписать к нему любое конечное число членов.
Доказательство. Пусть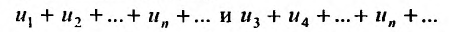 два ряда, причём второй получается из первого исключением первых двух членов. Тогда, если
два ряда, причём второй получается из первого исключением первых двух членов. Тогда, если 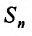 – n-я частичная сумма первого ряда, а
– n-я частичная сумма первого ряда, а 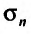 – n-я частичная сумма второго ряда, то, очевидно, что
– n-я частичная сумма второго ряда, то, очевидно, что
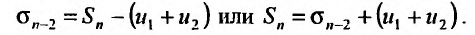
Из этого равенства следует, что, если 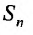 имеет предел, то
имеет предел, то 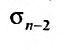 также имеет предел. Ясно, что эти пределы будут различны, а, именно
также имеет предел. Ясно, что эти пределы будут различны, а, именно 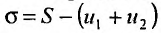 Если же
Если же 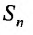 не имеет предела, то
не имеет предела, то 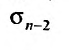 также не имеет предела.
также не имеет предела. 
Теорема 27.2.5. (Необходимое условие сходимости ряда). Если ряд 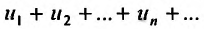 сходится, то его общий член стремится к нулю, т.е.
сходится, то его общий член стремится к нулю, т.е.

Доказательство. Пусть ряд 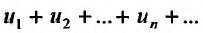 сходится и его сумма равна S. Из определения n -ой частичной суммы следует, что общий член ряда можно представить в виде разности и-ой частичной суммы и (n-1)-ой частичной суммы:
сходится и его сумма равна S. Из определения n -ой частичной суммы следует, что общий член ряда можно представить в виде разности и-ой частичной суммы и (n-1)-ой частичной суммы: 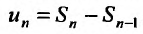 . Переходя к пределу в этом равенстве, получим утверждение теоремы:
. Переходя к пределу в этом равенстве, получим утверждение теоремы:
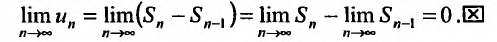
Отметим, что условие (27.2.4) не является достаточным, т.е. общий член может стремиться к нулю, но ряд все же может быть расходящимся. Но если общий член ряда не стремится к нулю, то ряд будет расходящийся.
- Заказать решение задач по высшей математике
Пример №13
Исследуем на сходимость гармонический ряд
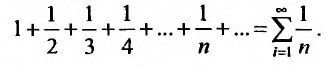
Решение:
Вначале находим предел общего члена: 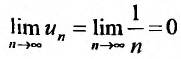 . Нетрудно, однако, показать, что сумма n первых членов гармонического ряда беспредельно возрастает. Для этого сгруппируем слагаемые, начиная со второго, в группы из 1, 2, 4, 8,… членов:
. Нетрудно, однако, показать, что сумма n первых членов гармонического ряда беспредельно возрастает. Для этого сгруппируем слагаемые, начиная со второго, в группы из 1, 2, 4, 8,… членов: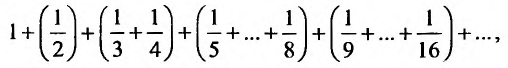 так что в k – ой группе будет
так что в k – ой группе будет 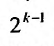 членов. Fx л и в каждой групп заменим все члены последним, то получим ряд:
членов. Fx л и в каждой групп заменим все члены последним, то получим ряд:
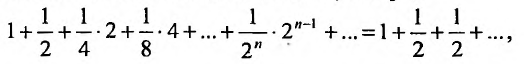 сумма n первых членов которого, равна
сумма n первых членов которого, равна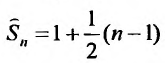 , очевидно, стремится к
, очевидно, стремится к 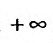 :
:
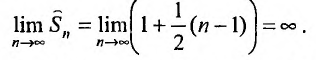 Но сумма n первых членов заданного гармонического ряда больше суммы n первых членов преобразованного ряда, т.е.
Но сумма n первых членов заданного гармонического ряда больше суммы n первых членов преобразованного ряда, т.е. 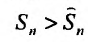 . Тогда
. Тогда 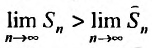 , что означает, что
, что означает, что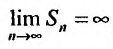 следовательно, гармонический ряд расходится.
следовательно, гармонический ряд расходится.
Пример №14
Найти формулу для общего члена ряда
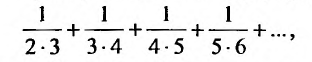
считая, что каждый его последующий член определяется по тому же закону, по которому образованы записанные члены, и найти ею сумму.
Решение:
Каждый член данного ряда представляет собой дробь, числитель которой равен 1, а знаменатель равен произведению двух последовательных натуральных чисел 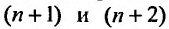 . Следовательно, искомая формула общего члена ряда имеет вид:
. Следовательно, искомая формула общего члена ряда имеет вид:
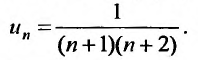
Для вычисления суммы ряда составим n -ую частичную сумму:
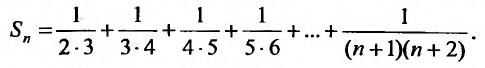
Представим выражение для общего члена в виде разности:
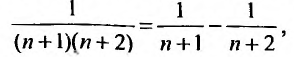
тогда
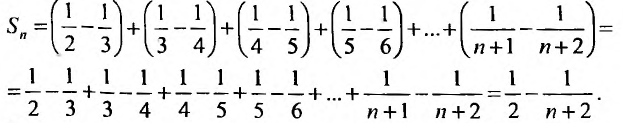
Переходя к пределу, получаем сумму ряда:
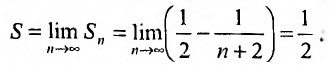
Пример №15
Исследовать сходимость ряда
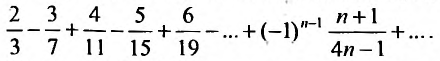
Решение:
Общий член ряда определяется формулой 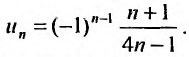
Вычислим предел модуля общего члена: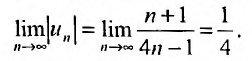
Так как предел общего члена не стремится к нулю, то ряд расходится.
Признаки сходимости числовых знакоположительных рядов
Рассмотрим числовые ряды с положительными членами. Существует много приёмов, называемых признаками сходимости, позволяющих установить сходимость или расходимость числовых рядов Так мы познакомились с методом исследования сходимости ряда на основании выяснения имеет ли предел последовательность частичных сумм. Стремление к нулю члена ряда по мерс роста его номера также является признаком сходимости, хотя только необходимым. Ниже мы приведём ряд достаточных признаков сходимости.
Признаки сравнения
Теорема 27.3.1. (I признак сравнения). Пусть 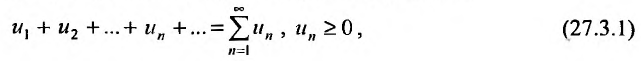
и
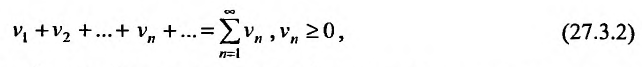
два ряда, причём члены первого ряда, начиная с некоторого номера k , не превосходят соответствующих членов второго

Тогда из сходимости ряда (27.3.2) следует сходимость ряда (27.3.1), а из расходимости ряда (27.3.1) следует расходимость ряда (27.3.2).
Доказательство. Так как исключение конечного числа членов ряда не влияет на его сходимость (теорема 27.2.4.), то достаточно доказать теорему для случая когда неравенства (27.3.3) выполняются для k = 1.
Пусть 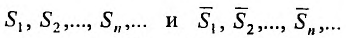 последовательности частичных сумм рядов (27.3.1) и (27.3.2) соответственно. Это возрастающие последовательности, так как члены рядов неотрицательные числа. В силу неравенств (27.3.3), имеем
последовательности частичных сумм рядов (27.3.1) и (27.3.2) соответственно. Это возрастающие последовательности, так как члены рядов неотрицательные числа. В силу неравенств (27.3.3), имеем 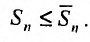
Пусть ряд (27.3.2) сходится. Тогда сходится соответствующая последовательность частичных сумм ряда (27.3.2), т.е.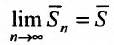
Поскольку выполняются неравенства (27.3.3), то члены последовательности частичных сумм ряда (27.3.1) удовлетворяют неравенству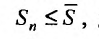 для всех т. Следовательно, последовательность
для всех т. Следовательно, последовательность 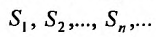 возрастает и ограничена:
возрастает и ограничена: 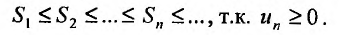
Поэтому, в силу признака Больцано-Всйсрштраса, последовательность частичных сумм ряда (27.3.1) сходится. По определению 27.1.3, сходится и ряд (27.3.1).
Пусть теперь ряд (27.3.1) расходится. Это значит, что его частичные суммы неограниченно возрастают. Но тогда, в силу неравенств (27.3.3), неограниченно возрастают и частичные суммы ряда (27.3.2), что означает, что этот ряд расходится.
Пример №16
Пусть дан ряд 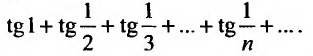
Исследуем его сходимость.
Решение:
Необходимый признак выполняется, т.е. 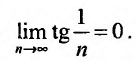
Для исследования сходимости заданного ряда применим 1 признак
сравнения (теорему 27.3.1). Сравним заданный ряд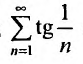 с гармоничсским рядом
с гармоничсским рядом 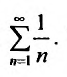 . Так как выполняются неравенства
. Так как выполняются неравенства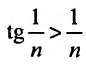 то ряд
то ряд 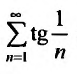 расходится, потому что расходится гармонический ряд.
расходится, потому что расходится гармонический ряд.
Пример №17
Исследовать сходимость ряда 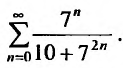
Решение:
Очевидно, что предел общего члена при возрастании т стремится к нулю.
Сравним данный ряд, общий член которого 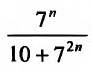 с гармоническим рядом
с гармоническим рядом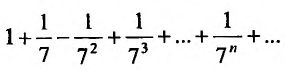 который сходится, так как
который сходится, так как 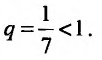
Поскольку 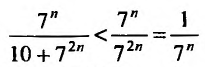 для
для 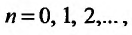 т.е. выполняются неравенства (27.3.3), то на основании первого признака сравнения заключаем, что исследуемый ряд также сходится.
т.е. выполняются неравенства (27.3.3), то на основании первого признака сравнения заключаем, что исследуемый ряд также сходится.
Теорема 27.3.2. (II признак сравнения). Если для рядов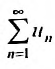 и
и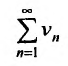 отношение общих членов
отношение общих членов 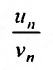 стремится к некоторому положительному и конечному пределу:
стремится к некоторому положительному и конечному пределу:

то ряды 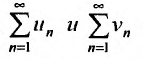 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Предельное соотношение (27.3.4), в силу определения 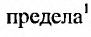 означает, что, начиная с некоторою номера N ,
означает, что, начиная с некоторою номера N ,
выполняется неравенство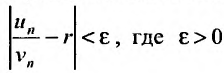 . Это неравенство равносильно неравенству:
. Это неравенство равносильно неравенству:
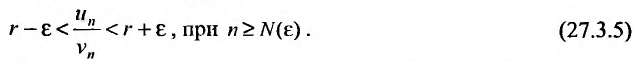
Обозначив 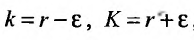 , неравенство (27.3.5) запишется в виде:
, неравенство (27.3.5) запишется в виде:
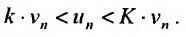
Предположим, что ряд 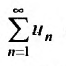 сходится. Поскольку выполняется неравенство
сходится. Поскольку выполняется неравенство 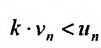 то, из первого признака сравнения, следует сходимость ряда
то, из первого признака сравнения, следует сходимость ряда 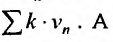 в силу теоремы 27.2.2, и ряда
в силу теоремы 27.2.2, и ряда 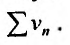 . Если же ряд
. Если же ряд 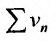 расходится, то расходится и ряд
расходится, то расходится и ряд 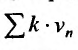 по теореме 27.2.2. Тогда, поскольку выполняется неравенство
по теореме 27.2.2. Тогда, поскольку выполняется неравенство 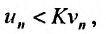 , расходится и ряд
, расходится и ряд 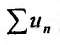 в силу I признака сравнения. Аналогично рассуждая можно показать, что из сходимости ряда
в силу I признака сравнения. Аналогично рассуждая можно показать, что из сходимости ряда 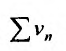 следует сходимость ряда
следует сходимость ряда 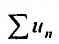 по I признаку сравнения с использованием теоремы 27.2.2. 13
по I признаку сравнения с использованием теоремы 27.2.2. 13
Последовательность 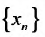 называется сходящейся, если существует такое вещественное число а , что для любого положительного числа
называется сходящейся, если существует такое вещественное число а , что для любого положительного числа 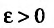 найдется номер
найдется номер 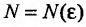 такой, что для всех
такой, что для всех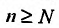 выполняется неравенство
выполняется неравенство 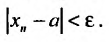
Пример №18
Исследовать сходимость ряда 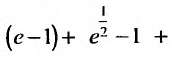
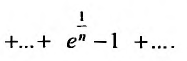
Решение:
Очевидно, что 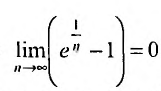 . Поэтому, воспользуемся признаком сравнения, сравнив заданный ряд с гармоническим. Найдем предел отношения общих членов исследуемого ряда и гармонического:
. Поэтому, воспользуемся признаком сравнения, сравнив заданный ряд с гармоническим. Найдем предел отношения общих членов исследуемого ряда и гармонического:
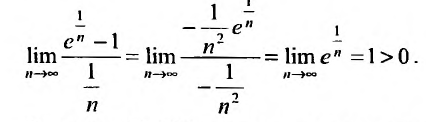
Теорема 27.3.2 выполняется, поэтому из расходимости гармонического ряда 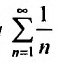 следует расходимость исследуемого ряда.
следует расходимость исследуемого ряда.
Признаки Д’Аламбсра и Коши
Иногда вместо признаков сравнения оказываются полезными некоторые специальные признаки сходимости ряда. Отметим среди них признаки Д’Аламбсра и Коши, непосредственно получающиеся из признаков сравнения, если в качестве ряда сравнения взять соответствующим образом выбранную геометрическую прогрессию.
Теорема 27.3.3. (признак Д’Аламбера). Если для ряда

с положительными членами существует такой номер 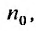 , начиная с которого, т.е. при
, начиная с которого, т.е. при 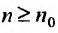 , отношение последующего члена к предыдущему удовлетворяет неравенству:
, отношение последующего члена к предыдущему удовлетворяет неравенству: 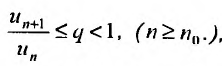 , то ряд (27.3.6) сходится. Если же существует номер
, то ряд (27.3.6) сходится. Если же существует номер 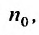 , начиная с которого, т.е. при
, начиная с которого, т.е. при 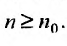 отношение последующего члена к предыдущему больше единицы:
отношение последующего члена к предыдущему больше единицы: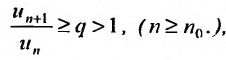 то ряд (27.3.6) расходится.
то ряд (27.3.6) расходится.
Доказательство. Пусть 0 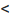 q
q 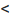 1 и пусть существует такой номер
1 и пусть существует такой номер 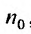 , что при
, что при 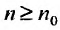 . выполняется неравенство:
. выполняется неравенство: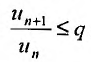 Перепишем это неравенство в виде:
Перепишем это неравенство в виде: 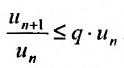 . Тогда, начиная с номера
. Тогда, начиная с номера 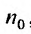 буду последовательно выполнятся неравенства:
буду последовательно выполнятся неравенства:
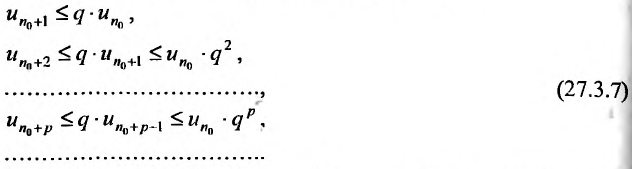
Ряд 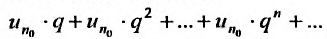 , являясь суммой член геометрической прогрессии со знаменателем
, являясь суммой член геометрической прогрессии со знаменателем 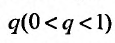 , сходите Из неравенств (27.3.7) следует, что по I признаку сравнения, сходится и ряд
, сходите Из неравенств (27.3.7) следует, что по I признаку сравнения, сходится и ряд 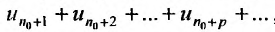 значит и весь ряд (27.3.6
значит и весь ряд (27.3.6
т.к. на сходимость ряда не влияет исключение конечного числа е^ членов.
Если же существует такое 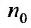 , что выполняется неравенств
, что выполняется неравенств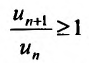 для всех
для всех 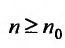 , то, переписав его в виде
, то, переписав его в виде 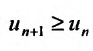 , можно для всех
, можно для всех 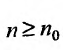 , последовательно записать следующие неравенство
, последовательно записать следующие неравенство
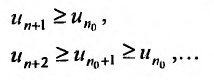
Так как по предположению 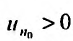 , то n-ный член ряда будучи ограниченным снизу положительной постоянной не стремится к нулю. Следовательно, не выполняется необходимое условие сходимости ряда, и поэтому ряд (27.3.6) расходится.
, то n-ный член ряда будучи ограниченным снизу положительной постоянной не стремится к нулю. Следовательно, не выполняется необходимое условие сходимости ряда, и поэтому ряд (27.3.6) расходится. 
Следствие 1. Пусть существует предел отношения последующего члена ряда (27.3.6) к предыдущему равный r :
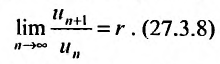
Тогда, если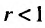 то ряд (27.3.6) сходится: если же
то ряд (27.3.6) сходится: если же 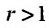 то ряд (21.3.6) расходится.
то ряд (21.3.6) расходится.
Доказательство. Воспользовавшись определением предела, для фиксированного 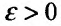 , можно утверждать, что начиная с некоторого номера
, можно утверждать, что начиная с некоторого номера 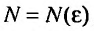 , для всех
, для всех 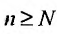 , все отношения
, все отношения 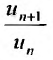 будут отличатся от значения предела r на число
будут отличатся от значения предела r на число 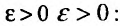
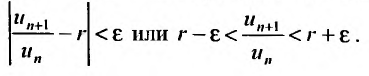
Рассмотрим правую часть двойного неравенства: 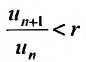 . Тогда сославшись на доказанную теорему 27.3.3, в случае если r
. Тогда сославшись на доказанную теорему 27.3.3, в случае если r 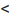 1, получаем сходимость ряда. Рассматривая левую часть неравенства
1, получаем сходимость ряда. Рассматривая левую часть неравенства
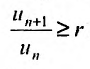 , получаем расходимость ряда приr > 1. Следствие доказано.
, получаем расходимость ряда приr > 1. Следствие доказано.
Пример №19
Рассмотрим ряд 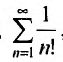 , сходимость которого исследуем, используя признак Даламбера, т.е. следствие 1.
, сходимость которого исследуем, используя признак Даламбера, т.е. следствие 1.
Решение:
Выпишем вначале значения 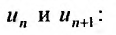
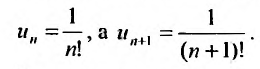
Затем вычислим предел отношения последующего члена ряда к предыдущему:
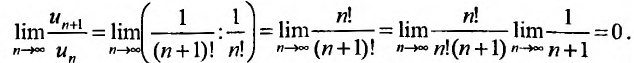
Так как этот предел меньше 1, то, в силу следствия 1, данный ряд сходится.
Заметим, что при исследовании сходимости ряда обычно (как правило, но не всегда) применяют следствие 1 из теоремы 27.3.3.
Теорема 27.3.4. (признак Kouiu). Если для ряда
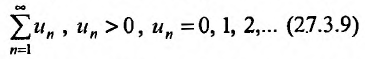
с положительными членами, начиная с некоторого номера 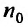 . выполняется неравенство
. выполняется неравенство 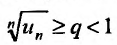 для всех
для всех 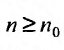 , то ряд (27.3.6) сходится. Если же существует такой номер
, то ряд (27.3.6) сходится. Если же существует такой номер 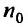 , начиная с которого выполняется неравенство
, начиная с которого выполняется неравенство 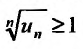 для всех
для всех 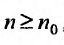 , то данный ряд расходится.
, то данный ряд расходится.
Доказательство. Пусть существует такой номер 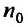 , что при всех
, что при всех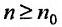 выполняется неравенство
выполняется неравенство 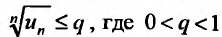 Тогда, возводя обе части неравенства в степень n, получим
Тогда, возводя обе части неравенства в степень n, получим 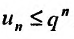 . Так как сходится геометрический ряд
. Так как сходится геометрический ряд 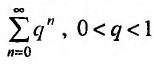 , то на основании признака сравнения, получаем, что ряд
, то на основании признака сравнения, получаем, что ряд 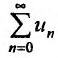 сходится. Если же существует номер
сходится. Если же существует номер 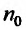 , такой что
, такой что 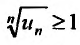 для всех
для всех 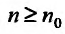 , то ясно, что
, то ясно, что 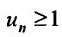 , и значит
, и значит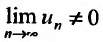 (не выполняется необходимый признак сходимости), поэтому ряд
(не выполняется необходимый признак сходимости), поэтому ряд 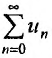 расходится.
расходится.
Следствие 2. Пусть существует предел корня n -ой степени из n-го члена ряда (27.3.9):

Тогда, если 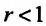 , то ряд (27.3.9) сходится, если же
, то ряд (27.3.9) сходится, если же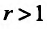 , то ряд (27.3.9) расходится.
, то ряд (27.3.9) расходится.
Доказательство. Из определения предела следует, что для фиксированного 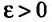 существует номер
существует номер 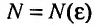 , начиная с которого выполняется неравенство
, начиная с которого выполняется неравенство 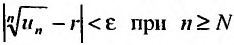 Это неравенство равносильно неравенству
Это неравенство равносильно неравенству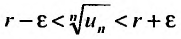 . Из правой части неравенства следует
. Из правой части неравенства следует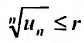 , поскольку
, поскольку 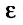 сколь угодно малое число. Тогда из теоремы 27.3.4, получаем сходимость ряда (27.3.9). Рассматривая левую часть неравенства
сколь угодно малое число. Тогда из теоремы 27.3.4, получаем сходимость ряда (27.3.9). Рассматривая левую часть неравенства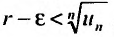 , получим
, получим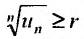 и если
и если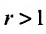 , то из теоремы 27.3.4 следует расходимость ряда (27.3.9). Следствие доказано.
, то из теоремы 27.3.4 следует расходимость ряда (27.3.9). Следствие доказано.
Пример №20
Рассмотрим ряд 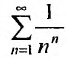 , сходимость которого исследуем по признаку Коши, т.е. применим следствие 2.
, сходимость которого исследуем по признаку Коши, т.е. применим следствие 2.
Решение:
Выпишем значение n-го члена ряда 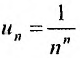 н вычислим предел корня n -ой степени:
н вычислим предел корня n -ой степени: 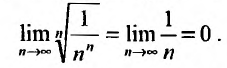
Так как этот предел меньше 1, то, согласно следствию 2, ряд сходится.
Замечание. Если пределы (27.3.8) и (27.3.10) равны 1, то для исследования сходимости ряда (27.3.9) нужно применять другие признаки, с которыми можно ознакомиться в [3].
Интегральный признак сходимости
Рассмотрим признак, достоинство которого состоит в исключительно высокой его чувствительности. Этим признаком проводится исследование сходимости там, где сформулированные признаки Д’Аламбсра и Коши «не работают».
Каждый член числового ряда 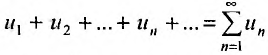 можно рассматривать как значение функции f от его номера:
можно рассматривать как значение функции f от его номера:
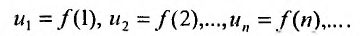
Эта функция определена пока только для целых положительных значений аргумента. Поэтому, доопределив значение функции f для всех нецелых значений аргумента, больших единицы, мы сможем, говорить о функции f(x), принимающей значения для любого 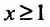 и при х = n, равные членам числового ряда. Теорема 27.3.5. Пусть дан ряд
и при х = n, равные членам числового ряда. Теорема 27.3.5. Пусть дан ряд

члены которого положительны и не возрастают 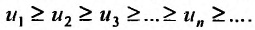 Если функция f, определённая для всех
Если функция f, определённая для всех 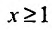 , неотрицательна и монотонно убывает, то ряд (27.3.11) сходится или расходится тогда и только тогда, когда сходится или
, неотрицательна и монотонно убывает, то ряд (27.3.11) сходится или расходится тогда и только тогда, когда сходится или
расходится интеграл 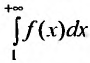
Доказательство. Пусть члены ряда (27.3.11) удовлетворяют условиям теоремы. Изобразим их графически, откладывая по оси Ох независимую переменную, а по оси Оу – соответствующие значения 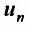 .
. 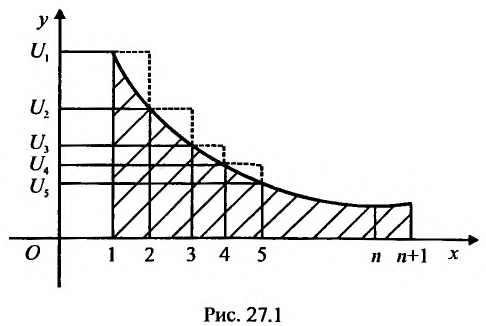
При таком графическом изображении сумма n первых членов ряда 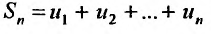 представляет сумму площадей описанных прямоугольников, которая заключает внутри себя площадь, ограниченной кривой
представляет сумму площадей описанных прямоугольников, которая заключает внутри себя площадь, ограниченной кривой  , осью Ох и прямыми
, осью Ох и прямыми 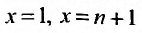 и поэтому будет выполняться неравенство:
и поэтому будет выполняться неравенство:

С другой стороны, криволинейная трапеция содержит сумму площадей вписанных прямоугольников, которая равна 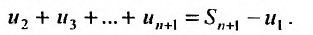 Поэтому, выполняется неравенство:
Поэтому, выполняется неравенство:

Из (27.3.12) и (27.3.13) следует неравенство:

Предположим, что несобственный интеграл 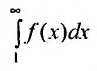 сходится. Это означает, что
сходится. Это означает, что 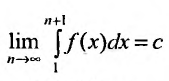 является конечным числом. Тогда из неравенства (27.3.14) следует, что последовательность частичных сумм
является конечным числом. Тогда из неравенства (27.3.14) следует, что последовательность частичных сумм 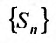 возрастающая и ограничена при всех n. Тогда в силу теоремы: “возрастающая последовательность, ограниченная сверху, сходится”, числовой ряд (27.3.11) сходится. Если же несобствснный интеграл
возрастающая и ограничена при всех n. Тогда в силу теоремы: “возрастающая последовательность, ограниченная сверху, сходится”, числовой ряд (27.3.11) сходится. Если же несобствснный интеграл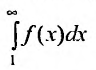 расходится, т.е.
расходится, т.е. 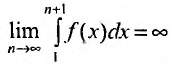 , то из неравенства (27.3.12) следует, что последовательность частичных сумм
, то из неравенства (27.3.12) следует, что последовательность частичных сумм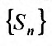 не ограничена. Тогда в силу определения 27.1.3 ряд будет расходящимся.
не ограничена. Тогда в силу определения 27.1.3 ряд будет расходящимся. 
Пример №21
Исследовать сходимость ряда 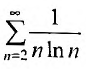
Решение:
Применим интегральный признак. Рассмотрим функцию 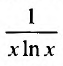 которая положительна и убывает при х> 2, и исследуем сходимость несобственного интеграла:
которая положительна и убывает при х> 2, и исследуем сходимость несобственного интеграла:
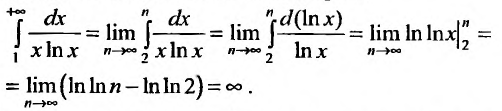
Так как несобственный интеграл расходится, то расходится и ряд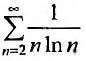 в силу инте1рального признака Коши.
в силу инте1рального признака Коши.
Замечание. Исследовать сходимость данного ряда при помощи следствий 1 и 2 не представляется возможным, так как соответствующие пределы равны 1.
Пример №22
Исследовать сходимость ряда Дирихле
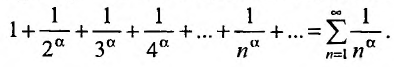
Решение:
Если 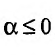 , то общий член ряда
, то общий член ряда 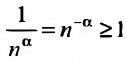 не стремится к нулю. На основании следствия из необходимого признака сходимости, следует расходимость ряда Дирихле при
не стремится к нулю. На основании следствия из необходимого признака сходимости, следует расходимость ряда Дирихле при 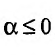 .
.
Пусть а > 0, тогда необходимый признак, очевидно, выполняется. Применим интегральный признак Коши. Введем функцию
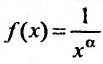 , которая положительная и не возрастает при
, которая положительная и не возрастает при  и исследуем сходимость несобственного интеграла
и исследуем сходимость несобственного интеграла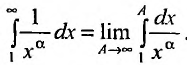
Вычислим определенный интеграл, записанный под знаком предела:
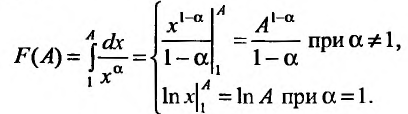
Если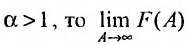 существует и равен
существует и равен 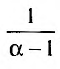 а при
а при 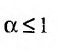 указанный предел не существует.
указанный предел не существует.
Таким образом, при a>1 несобственный интеграл 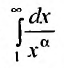 сходится, следовательно, сходится и ряд Дирихле, а при
сходится, следовательно, сходится и ряд Дирихле, а при 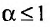 несобственный интеграл расходится, следовательно, расходится и ряд Дирихле.
несобственный интеграл расходится, следовательно, расходится и ряд Дирихле.
- Знакопеременные ряды
- Степенные ряды
- Элементы матричного анализа
- Уравнение линии
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
1.21. Основные понятия сходимости числовых рядов.
Числовым
рядом называется
выражение вида
![]() ,
,
где
![]()
являются членами
числового ряда
и представляют собой действительные
или комплексные числа.
Числовой
ряд задается с помощью формулы
общего члена ряда
![]() ,
,
описывающей зависимость члена ряда от
его номера.
Пример 1.Найти
общий член ряда
![]()
![]() .
.
Решение.
Последовательные числители образуют
арифметическую прогрессии. 1,3,5,7,…;
![]() й
й
член прогрессии находим по формуле![]()
Здесь
![]() ,
,
поэтому
![]() .
.
Последовательные знаменатели образуют
геометрическую прогрессии.
![]()
![]() -й
-й
член этой прогрессии
![]() .
.
Следовательно, общий член ряда
![]()
Пример 2.
Найти общий член ряда
![]()
Решение.
Показатель степени каждого члена
совпадает с номером этого члена, поэтому
показатель степени
![]() го
го
члена равен
![]() .
.
Числители дробей 2/3,3/7,4/11,5/15,… образуют
арифметическую прогрессию с первым
членом 2 и разностью 1. Поэтому
![]() -й
-й
числитель равен
![]() .
.
Знаменатели образуют арифметическую
прогрессию с первым членом 4 и разностью
4. Следовательно,
![]() -й
-й
знаменатель равен
![]() .
.
Итак, общим членом ряда является
![]()
Сумма
![]()
первых
![]()
членов ряда называется
![]() -й
-й
частичной суммой
ряда.
Рассмотрим последовательность частичных
сумм числового ряда:
![]() ,
,
![]() ,
,
![]() ,
,
…
Определение.
Если существует конечный предел
![]()
последовательности частичных сумм
ряда, то говорят, что числовой ряд
сходится.
Этот предел называют суммой
ряда
![]() .
.
Числовой
ряд называют расходящимся,
если
![]()
не существует или
![]() .
.
Пример
1.
Рассмотрим ряд 1/2+1/4+1/8+1/16+…+
С торона
торона
квадрата равна единице, следовательно
площадь 1/2+1/4+1/16+1/32+…. . . = 1
Пример
2.
Числовой ряд
![]()
является сходящимся. Это легко доказать,
рассмотрев последовательность частичных
сумм. Действительно,
![]() ,
,
![]() ,
,
![]() ,
,
…,
![]()
![]() .
.
Следовательно,
![]() ,
,
т.е. ряд сходится.
Пример 3.
Найти сумму ряда
![]() .
.
Решение.
Разлагаем общий член ряда на простейшие
дроби:
![]()
Выписываем несколько
членов ряда так, чтобы было видно, какие
слагаемые сокращаются при вычислении
частичной суммы ряда:
![]() .
.
Составляем
![]() ю
ю
частичную сумму ряда:
![]()
Вычисляем сумму ряда по формуле![]()
, получаем
![]()
![]() .
.
Ряд сходится и его сумма равна 1/2.
Пример 4.
Найти сумму ряда
![]() .
.
Решение. Разложим
общий член ряда
![]()
на простейшие дроби с помощью метода
неопределенных коэффициентов:
![]() .
.
Умножая на знаменатель левой части,
придем к тождеству
![]()
Полагая последовательно
![]()
находим: при
![]() :
:
1=2A; A=1/2; при
![]() :
:
![]()
при
![]()
![]()
Таким образом,
![]() ,
,
т.е.
![]() .
.
Выписываем несколько членов ряда, чтобы
было видно, какие слагаемые сокращаются
при вычислении частичной суммы ряда:
![]()
![]()
![]()
![]() .
.
Составляем
![]() ю
ю
частичную сумму ряда и сокращаем все
слагаемые, какие возможно:
Вычисляем сумму
ряда по формуле
![]() ,
,
получаем![]()
![]() .
.
Числовой
ряд
![]() расходится,
расходится,
так как последовательность частичных
сумм
![]()
![]()
не имеет предела.
Известным числовым
рядом является геометрическая прогрессия:
![]()
Сумма
первых
![]()
членов прогрессии находится по формуле
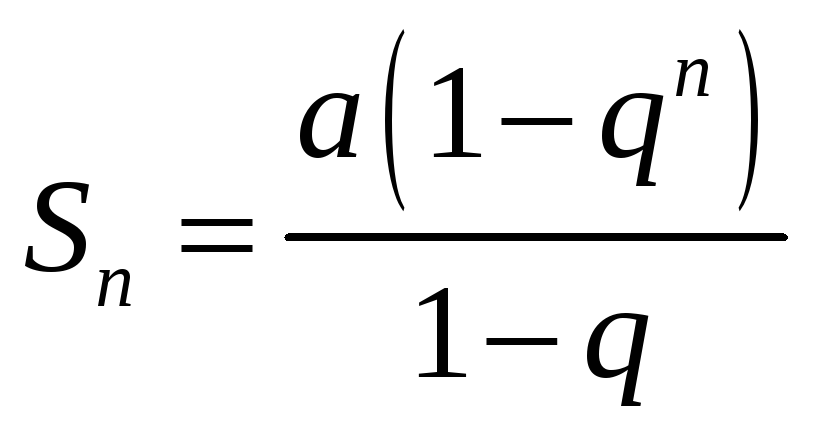 ,
,
![]() .
.
Предел этой суммы равен:
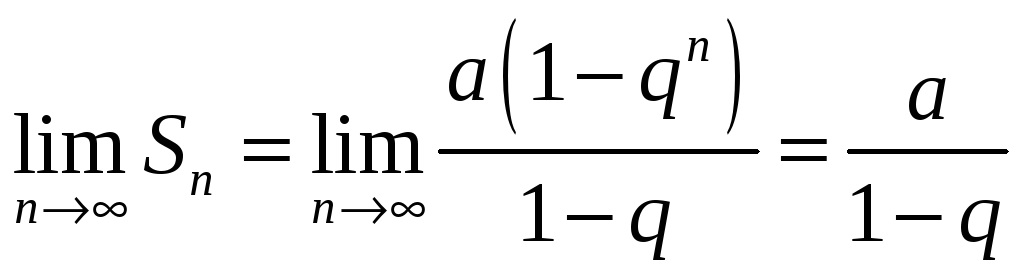 ,
,
если
![]() ,
,
так как
![]() .
.
Если
![]() ,
,
то
![]() ,
,
поэтому
![]() ,
,
ряд расходится. Если
![]() ,
,
то ряд принимает вид
![]() .
.
Последовательность частичных сумм
![]()
расходится,
![]() ,
,
следовательно, расходится и ряд. При
![]()
ряд принимает вид
![]()
– в этом случае
![]()
при четном
![]()
и
![]()
при нечетном
![]() .
.
Следовательно,
![]()
не существует, а ряд расходится.
Пример 5.
Исследовать сходимость ряда
![]() .
.
Решение.
Ряд составлен из членов бесконечно
убывающей геометрической прогрессии
и поэтому сходится. Найдем сумму ряда.
Здесь![]() (знаменатель
(знаменатель
прогрессии) Следовательно,
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.
Исследовать на сходимость числовой ряд
Числовой ряд в общем виде задаётся следующей формулой: $$sum_{n=1}^infty a_n.$$ Разберем из чего состоит ряд. $a_n$ – это общий член ряда. $n$ – это переменная суммирования, которая может начинаться с нуля или любого натурального числа. Таким образом ряд расписывается следующим образом: $$sum_{n=1}^infty a_n = a_1+a_2+a_3+…$$ Слагаемые $a_1,a_2,a_3,…$ называются членами ряда. Если они неотрицательные, то ряд называется положительными числовым рядом.
Ряд расходится, если сумма его членов равна бесконечности: $$sum_{n=1}^infty n^2+1 = 2+5+10+…$$Ряд сходится, если сумма его членов равна конечному числу. Например, бесконечно убывающая геометрическая прогрессия: $$sum_{n=0}^infty frac{1}{2^n} = 1+frac{1}{2} + frac{1}{4}+frac{1}{8}+…$$ Её сумма вычисляется по следующей формуле $S = frac{A}{1-q}$, где $A$ – первый член прогрессии, а $q$ – основание. В данном случае сумма равна $S = frac{1}{1 – frac{1}{2}} = 2$.
Стоит заметить, что вычислить сумму ряда в большинстве случаев просто так не получится. Поэтому используют признаки сходимости, выполнение которых достаточно для установления сходимости ряда. Например, признаки Коши и Даламбера. Зависит это от общего члена ряда.
Необходимый признак сходимости ряда
Необходимый признак сходимости ряда нужно применять мысленно перед тем, как использовать достаточные признаки. Именно благодаря ему, можно заранее установить, что ряд расходится и не тратить время на проверку достаточными признаками. Для этого, нужно найти предел общего члена ряда и в зависимости от его значения сделать вывод.
- Если ряд сходится, то $limlimits_{nto infty} a_n = 0$
- Если $limlimits_{nto infty} a_n neq 0$ или не существует, то ряд расходится
ЗАМЕЧАНИЕ ! Первый пункт не работает в обратную сторону и нужно использовать достаточный признак сходимости. То есть, если предел общего члена ряда равен нулю, то это ещё не значит, что ряд сходится! Требуется использовать один из достаточных признаков сходимости.
| Пример 1 |
| Проверить сходимость числового ряда $sum_{nto 1}^infty n^2 + 1$ |
| Решение |
| Применяем необходимый признак сходимости ряда $$lim_{ntoinfty} n^2+1 = infty$$Так как получили бесконечность, то значит ряд расходится и на этом исследование заканчивается. Если бы предел равнялся нулю, то действовали бы дальше применяя достаточные признаки. |
| Ответ |
| Ряд расходится |
| Пример 2 |
| Проверить сходимость $sum_{nto 1}^infty frac{1}{n^2+1}$ |
| Решение |
| Ищем предел общего члена ряда $$lim_{xtoinfty} frac{1}{n^2+1} = 0$$Так как предел получился равным нулю, то нельзя сказать сходится или расходится ряд. Нужно применить один из достаточных признаков сходимости. |
| Ответ |
| Требуется дополнительное исследование |
Признаки сравнения
Обобщенный гармонический ряд записывается следующим образом $ sum_{n=1} ^infty frac{1}{n^p} $.
- Если $ p = 1 $, то ряд $ sum_{n=1} ^infty frac{1}{n} $ расходится
- Если $ p leqslant 1 $, то ряд расходится. Пример,$ sum_{n=1} ^infty frac{1}{sqrt{n}} $, в котором $ p = frac{1}{2} $
- Если $ p > 1 $, то ряд сходится. Пример, $ sum_{n=1} ^infty frac{1}{sqrt{n^3}} $, в котором $ p = frac{3}{2} > 1 $
Этот ряд пригодится нам при использовании признаков сравнения, о которых пойдет речь дальше.
Признак сравнения
Пусть даны два знакоположительных числовых ряда $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$, причем второй ряд сходящийся. Тогда, если начиная с некоторого номера $n$ выполнено неравенство $a_n le b_n$, то ряд $sum_{n=1}^infty a_n$ сходится вместе с $sum_{n=1}^infty b_n$.
Предельный признак сравнения
Если предел отношения общих членов двух рядов $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$ равен конечному числу и отличается от нуля $$lim_{ntoinfty} frac{a_n}{b_n} = A,$$то оба ряда сходятся или расходятся одновременно.
ЗАМЕЧАНИЕ. Предельный признак удобно применять когда хотя бы один из общих членов ряда представляет собой многочлен.
| Пример 3 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^3+n^2+1}$$ |
| Решение |
|
Проверяем ряд на необходимый признак сходимости и убеждаемся в его выполнении $$lim_{ntoinfty} frac{1}{n^3+n^2+1} = 0.$$ Теперь данный ряд нужно сравнить с одним из гармонических рядов. В данном случае видим, что в знаменателе старшая степень $n^3$, значит подойдет гармонический ряд $frac{1}{n^3}$, а он как известно сходится. Но нужно дополнительно мысленно проверить, что выполняется неравенство $n^3 le n^3+n^2+1$. Убедившись в этом получаем, что $$frac{1}{n^3+n^2+1} le frac{1}{n^3}.$$Это означает, что $sum_{n=1}^infty frac{1}{n^3+n^2+1}$ сходится. |
| Ответ |
| Ряд сходится |
| Пример 4 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^2-2n}$$ |
| Решение |
| Воспользуемся предельным признаком сравнения. Сравним данный ряд со сходящимся рядом $sum_{n=1}^infty frac{1}{n^2}$. Найти предел отношения общих членов двух рядов $$lim_{ntoinfty} frac{frac{1}{n^2}}{frac{1}{n^2-2n}} = lim_{ntoinfty} frac{n^2-2n}{n^2} =$$Выносим за скобку $n^2$ и сокращаем на него числитель и знаменатель $$lim_{ntoinfty} frac{n^2(1-frac{2}{n})}{n^2} = lim_{ntoinfty} (1-frac{2}{n}) = 1.$$ Итак, получили конечное число отличное от нуля, значит оба ряда сходятся одновременно. |
| Ответ |
| Ряд сходится |
Признак Даламбера
Признак рекомендуется использовать, если в общем члене ряда есть:
- Число в степени. Например, $2^n, 3^{n+1}$
- Присутствует факториал. Например, $(n+1)!,(2n-3)!$
Для исследования сходимости ряда по признаку Даламбера нужно найти предел отношения двух членов ряда: $$lim_{ntoinfty} frac{a_{n+1}}{a_n} = L$$
В зависимости от значения предела делается вывод о сходимости или расходимости ряда:
- При $0 le L le 1$ ряд сходится
- При $L > 1$ или $L = infty$ ряд расходится
- При $L = 1$ признак не даёт ответа и нужно пробовать другой
| Пример 5 |
| Исследовать ряд на сходимость по признаку Даламбера $$sum_{n=1}^infty frac{2^{n+1}}{n!}$$ |
| Решение |
|
Общий член ряда $a_n = frac{2^{n+1}}{n!}$, тогда следующий член ряда будет $$a_{n+1} = frac{2^{(n+1)+1}}{(n+1)!} = frac{2^{n+2}}{(n+1)!}$$ Теперь находим предел предыдущего и последующего членов ряда $$L=lim_{ntoinfty} frac{a_{n+1}}{a_n} = lim_{ntoinfty} frac{frac{2^{n+2}}{(n+1)!}}{frac{2^{n+1}}{n!}} = lim_{ntoinfty} frac{2^{n+2} n!}{(n+1)! 2^{n+1}}$$ Выполняем сокращение на $2^{n+1}$ и $n!$ и находим значение предела $$L=lim_{ntoinfty} frac{2}{n+1} = 0$$ Так как предел равен нулю ($L=0$), то ряд сходится по признаку Даламбера. |
| Ответ |
| Числовой ряд сходится |
| Пример 6 |
| Исследовать сходимость ряда по признаку Даламбера $$sum_{n=1}^infty frac{3^{n+1}}{sqrt{2n+5}}$$ |
| Решение |
|
Начинаем с того, что выписываем общий член ряда $$a_n = frac{3^{n+1}}{sqrt{2n+5}}.$$ Подставляем в него $n = n + 1$ и раскрываем скобки $$a_{n+1} = frac{3^{(n+1)+1}}{sqrt{2(n+1)+5}} = frac{3^{n+2}}{sqrt{2n+7}}.$$ Находим отношение следующего общего члена к предыдущему и упрощаем $$frac{a_{n+1}}{a_n} = frac{frac{3^{n+2}}{sqrt{2n+7}}}{frac{3^{n+1}}{sqrt{2n+5}}} = frac{(3^{n+2})sqrt{2n+5}}{sqrt{2n+7}(3^{n+1})} = frac{3sqrt{2n+5}}{sqrt{2n+7}}$$ Теперь вычисляем предел последней дроби, чтобы проверить признаком Даламбера сходимость. Для этого сократим числитель и знаменатель на $n$ $$L = limlimits_{ntoinfty} frac{3sqrt{2n+5}}{sqrt{2n+7}} = 3limlimits_{ntoinfty} frac{sqrt{2+frac{5}{n}}}{sqrt{2+frac{7}{n}}} = 3frac{sqrt{2}}{sqrt{2}} = 3.$$ Так как получился $L > 0$, то по признаку Даламбера представленный ряд расходится. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Ряд расходится |
Радикальный признак Коши
Для установления сходимости ряда по радикальному признаку Коши нужно вычислить предел корня $n$ степени из общего члена ряда $$L = limlimits_{ntoinfty} sqrt[n]{a_n}.$$
- Если $L<1$, то ряд сходится,
- если $L>1$, то ряд расходится,
- если $L=1$, то признак не даёт ответа о сходимости.
Применяется данный признак в случаях, когда общий член ряда находится в степени содержащей $n$.
| Пример 7 |
| Исследовать ряд на сходимость $$sum_{n=1}^infty bigg(frac{3n+1}{2n+7}bigg)^{3n}.$$ |
| Решение |
|
Так как у общего члена есть тепень, в составе которой, присутствует $n$, то есть смысл попробовать применить радикальный признак сходимости Коши. Для этого, извлекаем корень $n$ степени из общего члена. $$sqrt[n]{bigg(frac{3n+1}{2n+7}bigg)^{3n}} = bigg(frac{3n+1}{2n+7}bigg)^3.$$ Теперь вычисляем предел полученного выражения. $$L = limlimits_{ntoinfty} bigg(frac{3n+1}{2n+7}bigg)^3 = limlimits_{ntoinfty}frac{(3n+1)^3}{(2n+7)^3}$$ Осталось вынести за скобки $n^3$ одновременно в числетеле и знаменателе. $$L=limlimits_{ntoinfty} frac{n^3(3+frac{1}{n})^3}{n^3(2+frac{7}{n})^3} = limlimits_{ntoinfty} frac{(3+frac{1}{n})^3}{2+frac{7}{n}} = frac{3}{2}.$$ Делаем вывод: так как $L > 1$, то представленный ряд расходится. |
| Ответ |
| Ряд расходится |
| Пример 8 |
| Исследовать сходимость ряда $$sum_{n=1}^infty frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n.$$ |
| Решение |
|
Выписываем общий член ряда и извлекаем из него корень $n$ степени. $$sqrt[n]{frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n} = frac{1}{3}frac{n}{n+1}$$ Вычисляем предел $$L = limlimits_{ntoinfty} frac{1}{3}frac{n}{n+1} = frac{1}{3} cdot 1 = frac{1}{3}.$$ Так как предел меньше единицы $L = frac{1}{3} < 1$, то данный ряд сходится. |
| Ответ |
| Ряд сходится |
Содержание:
- Ряды
- Числовые ряды – основные понятия и теоремы
- Необходимый признак сходящегося знакопостоянного ряда
- Достаточные условия сходимости знакопостоянного ряда
- Первый признак сравнения
- Второй признак сравнения
- Признак Даламбера
- Признак Коши
- Достаточный признак сходимости знакопеременного ряда. (признак Лейбница)
- Функциональные ряды
- Степенной ряд
- Признак сходимости степенного ряда (теорема Абеля)
- Свойства степенных рядов
- Разложение функции в степенной ряд. Ряд Маклорена
- Гармонические колебания
- Тригонометрический ряд. Ряд Фуре
- Теорема Дирихле
- Практический гармонический анализ
- Определение и решения рядов в высшей математике
- Числовой ряд и его сходимость. Ряд геометрической прогрессии
- Гармонический ряд
- Необходимый признак сходимости числового ряда
- Достаточные признаки сходимости числовых рядов с положительными членами
- Признак сравнения рядов
- Признак Даламбера
- Интегральный признак Коши
- Знакочередующиеся ряды. Признак сходимости Лейбница
- Абсолютная и условная сходимость ряда
- Понятие о степенном ряде и его сходимости
- Дифференцирование и интегрирование степенных рядов. Разложение некоторых функций в степенные ряды
- Разложение функции в ряд Маклорена
- Разложение функции в ряд Тейлора
- Применение степенных рядов к приближенным вычислениям
- Ряды и алгебра
- Что такое ряд
- Числовые ряды
- Свойства сходящихся рядов
- Свойства сходящихся рядов
- Функциональные ряды и их область сходимости
- Формула тейлора
- Ряды и методы их решения
- Признаки схождения рядов с положительными членами
- Признаки сравнения
- Радикальный признак Коши (теорема)
- Интегральный признак Коши схождение ряда
- Знакопеременные ряды
- Степенные ряды
- Разложение функции в ряды Тейлора и Маклорена
- Разложение функции в ряд Маклорена
- Использование рядов к приближенным вычислениям
- Ряды Фурье
- Разложение в ряд Фурье функции, что заданы на полупериоде
- Решение и определение рядов
- Числовой ряд и его сходимость
- Ряд геометрической прогрессии
- Гармонический ряд
- Свойства сходящихся рядов
- Необходимый признак сходимости ряда
- Достаточные условия сходимости числовых рядов
- Признак сравнения рядов с положительными членами
- Признак Даламбера
- Радикальный признак Коши
- Интегральный признак Коши
- Достаточный признак сходимости знакопеременного ряда
- Признак Лейбница сходимости знакопеременного ряда
- Функциональные ряды. Степенной ряд
- Область и радиус сходимости
- Свойства степенных рядов
- Степенные ряды Тейлора и Маклорена
- Разложение в ряд Маклорена основных элементарных функций
- Использование рядов в приближенных вычислениях
- Вычисления с помощью знакоперемежных рядов
- Вычисления с помощью знакододатних рядов
- Вычисление определенных интегралов
- Использование рядов при решении дифференциальных уравнений
- Ряды Фурье
- Тригонометрические ряды
- Тригонометрические ряды фурье
- Неполные ряды Фурье
- Ряд Фурье для функции с произвольным периодом
Ряды
Рядом в математике называют выражение вида

где  члены некоторой бесконечной последовательности. Член
члены некоторой бесконечной последовательности. Член  называют общим членом ряда.
называют общим членом ряда.
Три точки в конце выражения указывают на то, что последнего слагаемого нет, то есть ряд является бесконечной суммой.
Числовые ряды – основные понятия и теоремы
Если  числа, то ряд называют числовым. В зависимости от знака чисел ряды могут быть знакопостоянными и знакопеременными (знакочередующийся).
числа, то ряд называют числовым. В зависимости от знака чисел ряды могут быть знакопостоянными и знакопеременными (знакочередующийся).
Например, ряды:

являются знакопостоянными, а ряды

являются знакопеременными (знакочередующиеся).
Найти суммы бесконечного числа слагаемых непосредственным сложением не может ни человек, ни ЭВМ. Найти можно только сумму конечного числа слагаемых. Такие суммы называют частичными суммами ряда. Например,

А может ли существовать сумма бесконечного количества слагаемых? Рассмотрим пример: найти сумму ряда

Вычислим частичные суммы этого ряда:

Видим, что чем больше количество слагаемых, тем ближе Sn приближается к числу 2. Данный пример легко проиллюстрировать геометрически (рис. 1).

Не для каждого ряда последовательность частичных сумм при  приближается к конкретному числу.
приближается к конкретному числу.
Например, для ряда

частичные суммы Sn равны или 0, или 1; для ряда

частичная сумма  при
при 
Ряд, для которого существует предел последовательности частичных сумм при  называют сходящимся рядом, а число
называют сходящимся рядом, а число  суммой ряда. Если же
суммой ряда. Если же  либо не существует, то ряд называют расходящимся и ему не приписывают ни одного числового значения.
либо не существует, то ряд называют расходящимся и ему не приписывают ни одного числового значения.
При исследовании рядов основными являются два вопроса: будет ли данный ряд сходящимся и чему будет равна сумма ряда. Во многих практических задачах принципиальным является первый вопрос. Поэтому основное внимание уделим вопросу установлению является ли ряд сходящимся.
Необходимый признак сходящегося знакопостоянного ряда
Необходимый признак сходящегося знакопостоянного ряда: Если ряд  сходящийся, то его общий член
сходящийся, то его общий член  при неограниченном возрастании n стремится к нулю:
при неограниченном возрастании n стремится к нулю:

Пример 1. Дан общий член ряда:  Написать ряд в развёрнутом виде и проверить, выполняется ли необходимый признак сходящегося ряда.
Написать ряд в развёрнутом виде и проверить, выполняется ли необходимый признак сходящегося ряда.
Решение:
а) Находим  то есть
то есть 
Потому, что  , то необходимый признак сходящегося ряда не выполняется, следовательно ряд расходящийся.
, то необходимый признак сходящегося ряда не выполняется, следовательно ряд расходящийся.
б) Находим 
Записываем ряд: 
Необходимый признак сходимости ряда выполняется, так как 
Тем не менее, сделать вывод о сходимости ряде в данном случае невозможно. Для определения сходимости ряда необходимо проверить выполняются ли достаточные условия сходимости.
Достаточные условия сходимости знакопостоянного ряда
Основные вопросы, которые возникают при работе с числовым рядом:
1. Сходится ли он?
2. Если сходится, то какова его сумма?
Первый из этих вопросов можно выяснить не только по определению, но и с помощью, так называемых, признаков сходимости ряда.
Первый признак сравнения
Пусть дано два ряда  , причём
, причём  . Тогда а) из сходящего ряда (А) (с большими членами) вытекает сходимость ряда (В) (с меньшими членами); б) из расходящегося ряда (В) вытекает расхождение ряда (А).
. Тогда а) из сходящего ряда (А) (с большими членами) вытекает сходимость ряда (В) (с меньшими членами); б) из расходящегося ряда (В) вытекает расхождение ряда (А).
При использовании данного признака часто используют ряды, сходимость которых известна. Это может быть гармонический ряд  (расходящийся); обобщённый гармонический ряд
(расходящийся); обобщённый гармонический ряд  (который сходящийся при
(который сходящийся при  , расходящийся при
, расходящийся при  ); геометрическую прогрессию
); геометрическую прогрессию  (сходящийся при
(сходящийся при  ).
).
Пример 2. Используя первый признак сравнения, исследовать на сходимость ряд:

Решение: Для сравнения используем ряд  сходящуюся геометрическую прогрессию (так как
сходящуюся геометрическую прогрессию (так как  ). Справедливо неравенство
). Справедливо неравенство  , следовательно ряд
, следовательно ряд  сходится.
сходится.
Второй признак сравнения
Второй признак сравнения: Пусть дано два ряда  . Если
. Если  , где
, где  , то оба ряда ведут себя одинаково, то есть сходятся или расходятся одновременно.
, то оба ряда ведут себя одинаково, то есть сходятся или расходятся одновременно.
Пример 3. Исследовать на сходимость ряд  .
.
Решение: Здесь  . Для сравнения используем ряд
. Для сравнения используем ряд  с общим членом
с общим членом  сходящуюся геометрическую прогрессию. Отсюда:
сходящуюся геометрическую прогрессию. Отсюда:

Потому, что  , то оба ряда ведут себя одинаково и, значит, данный ряд сходящийся.
, то оба ряда ведут себя одинаково и, значит, данный ряд сходящийся.
Признак Даламбера
Пусть дан ряд  . Тогда, если существует
. Тогда, если существует  , то при
, то при  ряд сходящийся; при
ряд сходящийся; при  ряд расходящийся; при
ряд расходящийся; при  необходимо воспользоваться другим признаком.
необходимо воспользоваться другим признаком.
Пример 4. Исследовать на сходимость ряд:

Решение:

Признак Коши
Пусть дан ряд  . Тогда, если существует
. Тогда, если существует  , то при
, то при  ряд сходящийся; при
ряд сходящийся; при  ряд расходящийся; при
ряд расходящийся; при  необходимо воспользоваться другим признаком.
необходимо воспользоваться другим признаком.
Пример 5. Исследовать на сходимость ряд 
Решение: Найдём

Следовательно, ряд  — расходящийся.
— расходящийся.
Достаточный признак сходимости знакопеременного ряда. (признак Лейбница)
Если члены ряда  убывают по абсолютной величине и
убывают по абсолютной величине и  то ряд сходящийся.
то ряд сходящийся.
Для знакопеременных рядов вводят понятие абсолютной сходимости.
Знакопеременный (знакочередующийся) ряд  называется абсолютно сходящимся, если сходятся одновременно данный ряд и ряд, состоящий из абсолютных величин его членов. Если сходится только знакопеременный ряд, то его называют условно сходящимся рядом.
называется абсолютно сходящимся, если сходятся одновременно данный ряд и ряд, состоящий из абсолютных величин его членов. Если сходится только знакопеременный ряд, то его называют условно сходящимся рядом.
Пример 6. Исследовать на сходимость ряды:

Решение:
а) Потому, что 
то ряд  сходящийся по признаку Лейбница.
сходящийся по признаку Лейбница.
Но ряд  расходящийся, как гармонический и, отсюда, вывод, что данный знакопеременный ряд сходится условно.
расходящийся, как гармонический и, отсюда, вывод, что данный знакопеременный ряд сходится условно.
б) Данный знакопеременный ряд сходится абсолютно, так как ряд, составлен из модулей его членов:  , является обобщённо гармоническим, который при показателе степени большему чем единица сходится.
, является обобщённо гармоническим, который при показателе степени большему чем единица сходится.
Функциональные ряды
Если у ряда

члены последовательности  функции, то ряд называют функциональным.
функции, то ряд называют функциональным.
Например, функциональными будут ряды

Если в функциональный ряд подставить х=х0, то он преобразуется в числовой. Полученный при х=х0 числовой ряд может быть сходящимся, или расходящимся.
Точку х=х0, в которой функциональный ряд преобразуется в сходящийся числовой ряд, называют точкой сходимости ряда. Совокупность всех точек сходимости для данного функционального ряда называют областью сходимости.
Очевидно, что в точках сходимости  существуют значения сумм
существуют значения сумм  числовых рядов, и можно установить соответствие между точками сходимости и значениями сумм. Следовательно, суммой функционального ряда является некоторая функция f(х), область определения которой совпадает с областью сходимости функционального ряда. Говорят, что функциональный ряд сходится с функцией f(х), или что функция f(х) разлаживается на ряд. Имеем:
числовых рядов, и можно установить соответствие между точками сходимости и значениями сумм. Следовательно, суммой функционального ряда является некоторая функция f(х), область определения которой совпадает с областью сходимости функционального ряда. Говорят, что функциональный ряд сходится с функцией f(х), или что функция f(х) разлаживается на ряд. Имеем:

в области сходимости ряда.
Рассмотрим некоторые функциональные ряды.
Степенной ряд
Функциональный ряд вида

называют степенным рядом.
Здесь х – независимая переменная,  постоянные коэффициенты ряда, b – произвольное постоянное.
постоянные коэффициенты ряда, b – произвольное постоянное.
Если ввести замену х – b = z, то получим ряд

Следовательно, для изучения степенных рядов можно ограничиться рассмотрением ряда

Признак сходимости степенного ряда (теорема Абеля)
Если степенной ряд  сходящийся при
сходящийся при  , то он сходящийся, причём абсолютно, при всех х, для которых выполняется условие
, то он сходящийся, причём абсолютно, при всех х, для которых выполняется условие  . Если степенной ряд расходящийся при
. Если степенной ряд расходящийся при  , то он расходящийся для всех
, то он расходящийся для всех  .
.
Таким образом, из сходимости степенного ряда в одной точке  следует его сходимость в целом интервале
следует его сходимость в целом интервале  . Число
. Число  называют радиусом сходимости степенного ряда. радиус сходимости определяется из соотношений:
называют радиусом сходимости степенного ряда. радиус сходимости определяется из соотношений:

которые вытекают из признаков Даламбера и Коши для числовых рядов. Действительно, по признаку Даламбера ряд  будет сходиться, если
будет сходиться, если

Следовательно, при  будет абсолютно сходящимся. Аналогично доказывается и второе соотношение.
будет абсолютно сходящимся. Аналогично доказывается и второе соотношение.
Область сходимости степенного ряда может быть равна:
а) одной точки  ;
;
б) отрезку  ;
;
в) всей числовой оси.
Пример 7. Исследовать на сходимость степенной ряд  .
.
Решение: Здесь  , тогда радиус сходимости
, тогда радиус сходимости  , следовательно область сходимости
, следовательно область сходимости 
Исследуем сходимость ряда в предельных точках. При  степенной ряд будет иметь вид
степенной ряд будет иметь вид  . Оба этих ряда расходящиеся, так как для них не выполняется необходимый признак сходимости, следовательно область сходимости ряда (-2; 2).
. Оба этих ряда расходящиеся, так как для них не выполняется необходимый признак сходимости, следовательно область сходимости ряда (-2; 2).
Пример 8. Исследовать на сходимость ряд  .
.
Решение: Введём замену х-3=z, тогда

запишем:  .
.
Радиус сходимости

следовательно область сходимости ряда  , или
, или  .
.
Проверим сходимость ряда в предельных точках:  получим знакопостоянный ряд:
получим знакопостоянный ряд:

который является расходящимся (согласно второго признака сравнения с гармоническим рядом);
при  , получим знакопеременный ряд
, получим знакопеременный ряд

который сходящийся согласно признака Лейбница. Следовательно областью сходимости ряда является
 .
.
Свойства степенных рядов
Степенные ряды имеют ряд интересных свойств:
1. Суммой степенного ряда является непрерывная функция в области его сходимости.
2. Степенной ряд можно почленно интегрировать на любом отрезке из области его сходимости.
3. Степенной ряд можно почленно дифференцировать в любой точке из области его сходимости.
Разложение функции в степенной ряд. Ряд Маклорена
Пусть функция f(х) бесконечно дифференцирована в окрестности точки х=0 и разлаживается в степенной ряд

Коэффициенты  можно вычислить последовательно дифференцировав обе части ряда:
можно вычислить последовательно дифференцировав обе части ряда:

и т. д.
и подставляя х=0 в полученные выражения:

и т. д.
Полученные выражения для коэффициентов подставим в ряд; получим:

Такой ряд называют рядом Маклорена функции f(х), а функцию f(х) — порождающей для ряда Маклорена.
Приведённые рассуждения позволяют сделать важный вывод, который записывают в виде теоремы.
Теорема. Если бесконечно дифференцированная в окрестности точки х=0 функция f(х) может быть разложена в степенной ряд, то это будет ряд Маклорена этой функции.
Обратное утверждение, в общем говоря, неверно. Можно указать такие функции, для которых ряд Маклорена расходящийся при х=0, или же сумма ряда не совпадает с порождающей его функцией. Отметим, что для элементарных функций ряд Маклорена сходится к этим функциям в области своей сходимости.
Рассмотрим разложение в ряд Маклорена некоторых функций.
1. 
а) найдём производные функции и их значения в т. х=0:

б) запишем ряд Маклорена

в) вычислим область сходимости полученного ряда:

2. 
а) найдём производные функции и их значения в т. х=0:

(производные старших порядков повторяют предыдущие значения,  и т.д.)
и т.д.)
б) запишем ряд Маклорена

в) вычислим область сходимости полученного ряда:

следовательно, ряд сходящийся на промежутке  .
.
Аналогично:
 область сходимости
область сходимости  .
.
 область сходимости (-1; 1).
область сходимости (-1; 1).
 область сходимости (-1; 1);
область сходимости (-1; 1);
Данный ряд называют биноминальным рядом.
 область сходимости (-1; 1).
область сходимости (-1; 1).
Пример 9. Разложить функцию f(х) = 2х в ряд Маклорена.
Решение: Находим производные и вычисляем их значения при =х=0:

При разложении степенной ряд некоторых функций можно воспользоваться заменой и уже известные расклады.
Пример 10. Разложить в ряд функцию 
Решение: Пусть у = -х2, тогда

Пример 11. Разложить в ряд Маклорена функцию у=е5х.
Решение: Пусть z=5х, тогда

Разложение функции в степенной ряд часто используют для приближённого вычисления её значения.
Пример 12. Вычислить значения функции  при х=2 с точностью 0,001.
при х=2 с точностью 0,001.
Решение: Воспользуемся разложением функции  в ряд Маклорена
в ряд Маклорена

Ограничимся только первыми одиннадцатью членами, поскольку  , то есть следующие члены не влияют на точность вычисления.
, то есть следующие члены не влияют на точность вычисления.
Следовательно,  .
.
Использование свойств степенных рядов упрощает решение многих задач.
Пример 13.
а) Разложим в ряд функцию 
Известно, что

Проинтегрируем правую и левую части равенства

Использовав второе свойство, получим:

б) Найти разложение функции  . Представим функцию как сумму
. Представим функцию как сумму  . Потому, что
. Потому, что  получим согласно первого свойства
получим согласно первого свойства

Гармонические колебания
Общим признаком всех колебательных движений является то, что они периодически повторяются (или приближённо повторяются) через определённый промежуток времени. При изучении колебаний нас интересует, в основном, те признаки, которые характеризуют повторяемость движений. Это закон, по которому повторяется движение, время, через которое система снова вернётся в начальное положение, наибольшие отклонения, которых достигает движимое тело и т. д. Наиболее простыми процессами колебания являются движение маятника (при малых отклонениях), движение тела на пружине, напряжение и сила переменного тока. Имея разную физическую природу эти процессы математически описываются одним и тем же уравнением. Как пример, рассмотрим колебания материальной точки массой М вокруг положения равновесия (рис. 2). Неизвестным является закон движения х=х(t). Согласно закона Гука сила, которая действует на тело прямо пропорциональна отклонению точки от положения равновесия:

а согласно второму закону Ньютона эта сила равна:

где k — коэффициент жёсткости пружины, М — масса тела,  — ускорение движения тела.
— ускорение движения тела.
Для определения закона движения тела мы получили дифференциальное равенство:

Решим это равенство, разделив правую и левую части на М:

Это линейное однородное дифференциальное равенство II порядка с постоянными коэффициентами, его характеристическое равенство имеет вид

Решения составленного характеристического уравнения комплексно-сопряжённые


Решение показывает, что движение происходит по закону синуса (или косинуса). Такое движение носит название простого гармонического колебания. Поскольку  , то постоянная А определяет наибольшее отклонение точки от центра колебаний. Её называют амплитудой колебания. Величина
, то постоянная А определяет наибольшее отклонение точки от центра колебаний. Её называют амплитудой колебания. Величина  определяет начальное положение тела, её называют начальной фазой. Период колебания Т вычисляют по формуле
определяет начальное положение тела, её называют начальной фазой. Период колебания Т вычисляют по формуле

а величина v, обратная к периоду определяет число колебаний за одну секунду, её называют частотой колебаний

(Иногда частотой называют величину  Она выражает число колебаний за
Она выражает число колебаний за  секунду).
секунду).
Для построения графиков гармонических колебаний используют элементарные преобразования графика функции 
Равенство

называют равенством гармонических колебаний, или просто гармоникой.
Более сложные колебания, если это возможно, выгодно представлять как сумму нескольких гармонических колебаний с одинаковой частотой. Таким образом, возникает вопрос добавления гармонических колебаний. Сумма двух гармонических колебаний с одинаковыми частотами, но разными фазами и амплитудами , будет также гармоническим колебанием с той же частотой, но с новой фазой и амплитудой.
Если

то  , где
, где

Сумма двух колебаний с разной частотой не будет гармоническим колебанием. Для построения графика суммы двух гармонических колебаний с разной частотой используют графический метод, который заключается в суммировании ординат графиков в узловых точках.
Произвольный закон движения, или более обобщённо, произвольную функцию можно представить как бесконечную сумму простых гармоник, то есть в виде тригонометрического ряда.
Тригонометрический ряд. Ряд Фуре
периодическую функцию f(х) с периодом  можно представить как сумму ряда такого вида:
можно представить как сумму ряда такого вида:

где  постоянные величины.
постоянные величины.
Такой ряд называют тригонометрическим рядом, а постоянные  коэффициентами ряда. Говорят, что такая запись представляет собой разложение периодической функции f(х) в тригонометрический ряд. Положим
коэффициентами ряда. Говорят, что такая запись представляет собой разложение периодической функции f(х) в тригонометрический ряд. Положим  , тогда ряд приобретает вид:
, тогда ряд приобретает вид:

Как видим, все слагаемые ряда Т — тригонометрические функции с общим периодом  . Поэтому и сумма ряда Т будет периодической функцией с таким же периодом. В силу периодичности суммы ряда Т разложить в тригонометрический ряд непериодическую функцию можно только на отрезке, длина которого равна
. Поэтому и сумма ряда Т будет периодической функцией с таким же периодом. В силу периодичности суммы ряда Т разложить в тригонометрический ряд непериодическую функцию можно только на отрезке, длина которого равна  . В дальнейшем используется отрезок
. В дальнейшем используется отрезок  .
.
Перейдём к вопросу нахождения коэффициентов ряда. Формулы нахождения коэффициентов вводятся путём интегрирования левой и правой частей ряда (Т) и умножения на  или
или  . Запишем формулы:
. Запишем формулы:

Тригонометрический ряд, коэффициенты которого определены по приведённым формулам называют рядом Фурье функции f(х), а функцию f(х) — порождающей для ряда.
Из выше записанных формул легко можно показать, что если f(х) — чётная функция, то

(говорят, что функция разлаживается в ряд Фурье по косинусоидам);
если f(х) — нечётная функция, то 
(функция разлаживается в ряд Фурье по синусоидам).
Заметим, что записанный для функции f(х) ряд Фурье не всегда сходится именно к ней. приведём достаточное условие сходимости ряда Фурье к порождающей его функции.
Теорема. Если функция f(х) имеет конечное количество точек разрыва I рода на промежутке  , то её ряд Фурье является сходящимся к ней на этом промежутке.
, то её ряд Фурье является сходящимся к ней на этом промежутке.
Пример 13: Разложить в ряд Фурье периодическую функцию  с периодом
с периодом 
Решение:
а) Построим график данной функции с учётом периодичности:

б) Данная функция чётная, поэтому коэффициенты будем находить по формуле:

в) Вычислим коэффициенты ряда Фурье:

данный интеграл находим интегрированием частями:


г) Подставим найденные значения в формулу:

Пример 14. Разложить в ряд Фурье периодическую функцию 
Решение:
а) построим график данной функции с учётом периодичности:

б) Данная функция нечётная, следовательно 
в) Вычислим коэффициенты ряда

Здесь учтено, что  в зависимости от значений n.
в зависимости от значений n.
г) Подставим найденные значения в ряд Фурье, который в данном случае имеет вид

Пример 15. Разложить в ряд Фурье периодическую  функцию
функцию

Решение:
а) Построим график данной функции, учитывая периодичность:

б) Данная функция является не чётной, не нечётной, поэтому коэффициенты ряда Фурье будем вычислять по формулам:

в) Вычислим коэффициенты ряда:


г) Подставим найденные значения в общий вид ряда Фурье и получим:

Функции, которые мы разложили в ряд Фурье были непрерывными на  . Если же функция имеет точки разрыва на
. Если же функция имеет точки разрыва на  , или необходимо установить сходимость ряда Фурье на концах отрезка, то используют теорему Дирихле.
, или необходимо установить сходимость ряда Фурье на концах отрезка, то используют теорему Дирихле.
Теорема Дирихле
Если функция f(х) частично непрерывна на промежутке  (то есть имеет только конечное количество точек разрыва на этом промежутке) и имеет конечное число точек экстремума, то ряд Фурье этой функции сходится во всех точках данного промежутка, причём:
(то есть имеет только конечное количество точек разрыва на этом промежутке) и имеет конечное число точек экстремума, то ряд Фурье этой функции сходится во всех точках данного промежутка, причём:
а) в точках непрерывности функции его сумма равна f(х);
б) в точках разрыва функции f(х) его сумма равна  ;
;
в) на концах промежутка сумма ряда равна  .
.
Пример 16. Разложить в ряд Фурье периодическую  функцию
функцию

Решение:
а) Построим график данной функции

б) Данная функция является не чётной, не нечётной, и имеет разрыв в точке х=0 с промежутка  и на концах промежутка.
и на концах промежутка.
Согласно теореме Дирихле сумма рядов Фурье S1 в т. х=0 вычисляется по формуле

а сумма ряда S2 в т. х= вычисляется по формуле
вычисляется по формуле

в) Для нахождения коэффициентов ряда Фурье воспользуемся видом формулы. Вычислим коэффициенты ряда:


г) Запишем разложение данной функции в ряд Фурье, для точек из промежутков 

В точках х=0;  данный ряд сходится до числа 3/2.
данный ряд сходится до числа 3/2.
Практический гармонический анализ
Теория разложения функций в тригонометрические ряды носит название гармонического анализа. На практике гармоническим анализом называют представление функций, полученных при решении конкретных задач в виде ряда Фурье. Коэффициенты такого ряда Фурье, как правило, вычисляют приближённо. Если функции получены из экспериментальных данных, то они обычно имеют вид графиков или таблиц. В этих случаях коэффициенты ряда Фурье вычисляют с помощью приближённых методов интегрирования. Для приближённого вычисления интегралов

используем любой из методов приближённого интегрирования. Используем, например, формулу левых прямоугольников (п. 7.7). Отрезок  разделим на n равных частей, то есть шаг разделения возьмём равный
разделим на n равных частей, то есть шаг разделения возьмём равный  . Обозначим точки разделения отрезка через
. Обозначим точки разделения отрезка через  , а значения функции в точках деления через
, а значения функции в точках деления через  . Тогда
. Тогда

Для облегчения вычисления коэффициентов Фурье используют различные схемы и шаблоны, а в более сложных случаях вычисления проводят с помощью ЭВМ.
Пример 1. Найдите тригонометрический многочлен второго порядка для функции, график которой приведён на рис. 3

Решение: Разделим отрезок на 12 частей, получив шаг разделения. По графику функции непосредственным измерением ординат находим: 


Тогда по формулам приближённого вычисления коэффициентов ряда Фурье получим:

Для функций, заданных аналитически коэффициенты ряда Фурье находят согласно приведённых формул (п. 9.6).
Пример 2. Разложить в ряд Фурье кривую двухполупериодого выпрямленного синусоидального тока

Решение: Данную функцию можно представить в виде

Заменим  и продолжим функцию периодически на всю числовую ось (рис. 4).
и продолжим функцию периодически на всю числовую ось (рис. 4).

Полученная функция чётная, следовательно bn=0. Вычислим коэффициенты  :
:

При n нечётном  =0; при n чётном
=0; при n чётном  =
= 
Функция I(х) разложилась в ряд Фурье

а начальная функция i(t), соответственно, в ряд Фурье
 .
.
Пример 3. Разложить в ряд Фурье кривую однополупериодного выпрямленного синусоидального тока:

Решение: Пусть  , тогда:
, тогда:
 .
.
График функции представлен на рисунке 5.

Из предыдущего примера видим, что при n нечётной  , а при n чётной
, а при n чётной


Определение и решения рядов в высшей математике
Понятие суммы конечного количества чисел и ее свойства известны еще с древних времен. Ища сумму геометрической прогрессии, математик и механик Древней Греции Архимед столкнулся с бесконечными рядами.
Для детального изучения функции рядами систематически пользовались английский математик, механик, физик, астроном И. Ньютон и крупные немецкие ученые Г. Лейбниц и К. Гаусс.
Однако точная теория рядов, в основе которой лежали понятия предела последовательности, была построена в начале 19 в. французским математиком О. Коши. С этого времени ряды стали основным источником исследования в математике. Появились целые разделы математики, полностью построенные на теории рядов.
Методы этого раздела применяются для нахождения приближенных значений интегралов, которые часто встречаются в теории вероятностей и в страховом деле и не могут быть выражены элементарными функциями; при решении дифференциальных уравнений; при нахождении приближенных значений функций, которые используются при решении экономических задач.
Числовой ряд и его сходимость. Ряд геометрической прогрессии
Пусть задана бесконечная последовательность чисел u1, u2, u3, …, un, ….
Определение. Бесконечная сумма чисел вида u1 + u2 + u3 + …, + un +… называется числовым рядом, а u1, u2, u3, …, un — членами ряда.
Коротко ряд записывается так:  . Выражение для n-го члена ряда при произвольном натуральном n, называется общим членом этого ряда и обозначается un. Ряд считается заданным, если известно правило, согласно которому для произвольного номера n можно записать соответствующий член ряда. Общий член ряда можно задать формулой un = f (n), с помощью которой записывается произвольный член ряда.
. Выражение для n-го члена ряда при произвольном натуральном n, называется общим членом этого ряда и обозначается un. Ряд считается заданным, если известно правило, согласно которому для произвольного номера n можно записать соответствующий член ряда. Общий член ряда можно задать формулой un = f (n), с помощью которой записывается произвольный член ряда.
Например, если  , то ряд будет иметь соответственно вид
, то ряд будет иметь соответственно вид

Если ряд записано в виде  , то легко записать несколько его членов.
, то легко записать несколько его членов.
Например, если задан ряд  , то в другой форме он будет выглядеть
, то в другой форме он будет выглядеть 
Если известно несколько членов числового ряда, то поняв закономерность их образования, можно записать общий член ряда.
Например, задано четыре первых члена ряда

Как видим, числители каждого члена ряда являются натуральными числами. Знаменатель первого члена ряда 100 = 1. Каждый знаменатель следующего члена больше предыдущего в 10 раз. Таким образом, общий член ряда записываем  .
.
Пусть задано ряд u1 + u2 + u3 + …, + un +… (8.1)
Сумму n первых его членов обозначим через Sn:
Sn = u1 + u2 + u3 + …, + un (8.2)
и назовем n-й частной суммой ряда.
Образуем теперь последовательность частных сумм ряда:
S1 = u1,
S2 = u1 + u2 ,
…………………………………………………..
Sn = u1 + u2 + u3 + …, + un.
Определение. Если при n →  существует предел последовательности частных сумм Sn членов данного ряда
существует предел последовательности частных сумм Sn членов данного ряда  , то ряд называется сходящимся, а число S — его суммой.
, то ряд называется сходящимся, а число S — его суммой.
Записывают это так:
S = u1 + u2 + u3 + …, + un + …. (8.3)
Если последовательность частных сумм Sn не имеет предела, то ряд называется расходящимся.
Ряд может расходиться в двух случаях:
1) 
2) Последовательность Sn колеблется.
В качестве примера рассмотрим ряд бесконечной геометрической прогрессии:
a + aq + aq2 + … + aqn + …. (8.4)
Сумма n первых членов прогрессии равна 
Если  , то
, то  и поэтому
и поэтому

Итак, если  , то бесконечная геометрическая прогрессия образует сходящийся ряд, сумма которого
, то бесконечная геометрическая прогрессия образует сходящийся ряд, сумма которого 
Если  то
то  поэтому
поэтому  и ряд геометрической прогрессии разбегается.
и ряд геометрической прогрессии разбегается.
При q = 1 получим ряд a + a + a + a + … (a ≠ 0), который имеет частную сумму  и
и 
Если q = –1, получим ряд a – a + a – a + …
Его частные суммы приобретают следующие значения: S1 = a, S2 = 0, S3 = a, S4 = 0, … , то есть Sn — колеблющаяся последовательность, не имеющая предела.
Следствие. Если ряд (8.1) сходящийся, то разница между суммой S и его частной суммой Sn
 (8.5)
(8.5)
называется n-м остатком ряда.
Остаток Rn ряда представляет собой ту погрешность, которая получится, если вместо приближенного значения суммы ряда S взять сумму Sn первых n членов этого ряда. Но поскольку S является пределом переменной Sn, то очевидно

А потому, взяв достаточно большое число членов сходящегося ряда, можно сумму этого ряда вычислить с любой точностью.
Отсюда следует, что основной задачей теории рядов является исследование сходимости ряда.
В следующем примере покажем применение ряда бесконечно убывающей геометрической прогрессии в экономических исследованиях.
Пример. Пусть I0 — начальные инвестиции, вложенные в замкнутую экономическую систему, а q — доля национального дохода, которая идет на потребления, то в модели Кейнса [23] стоимость национального дохода Y выражается формулой
 (8.6)
(8.6)
Правая часть равенства (8.6) есть не что иное как сумма ряда бесконечно убывающей геометрической прогрессии со знаменателем q < 1 и
 (8.7)
(8.7)
Эта формула может быть использована для нахождения изменения стоимости национального дохода в зависимости от начальных инвестиций I0 и его судьбы q, что идет на потребление.
Гармонический ряд
Ряд
 (8.8)
(8.8)
называется гармоничным.
Докажем расхождение этого ряда. Воспользуемся тем, что переменная
 при неограниченном росте n стремится к неперовому числу e, оставаясь меньше своего предела. Поэтому при любом целом положительном n имеем
при неограниченном росте n стремится к неперовому числу e, оставаясь меньше своего предела. Поэтому при любом целом положительном n имеем
 .
.
Отсюда,  или
или  или
или 
Подставляя в последнее неравенство вместо n числа 1,2,3, … получим неравенства:

Добавив почленно эти неравенства, получим
 или
или 
Но  а потому и
а потому и  то есть ряд (8.8) расходится.
то есть ряд (8.8) расходится.
Необходимый признак сходимости числового ряда
ТЕОРЕМА. Если ряд
u1 + u2 + u3 + …, + un + …. (8.9),
совпадает, то его n-й член un при неограниченном росте номера n стремится к нулю.
Доказательство. Мы имеем Sn-1 = u1 + u2 + u3 + …, + un-1 и Sn = u1 + u2 + u3 + …, + un-1 + un.
Отсюда un = Sn – Sn-1. Поскольку данный ряд сходится, то  и
и  . Отсюда
. Отсюда
 что и требовалось доказать.
что и требовалось доказать.
Пример. Исследовать сходимость числового ряда
Решение. Общий член ряда  Найдем при n →
Найдем при n →  его предел:
его предел:

Следовательно, данный ряд расходится.
Отметим, что  является лишь необходимым условием сходимости числового ряда, но не достаточным. Это означает, что данное условие может выполняться, но соответствующий числовой ряд может быть расходящимся.
является лишь необходимым условием сходимости числового ряда, но не достаточным. Это означает, что данное условие может выполняться, но соответствующий числовой ряд может быть расходящимся.
Примером является гармонический ряд 
Как видим, необходимое условие для этого ряда выполняется:
 однако он расходится.
однако он расходится.
Существует несколько признаков, которые позволяют утверждать сходимость или расхождение числовых рядов.
Достаточные признаки сходимости числовых рядов с положительными членами
Признак сравнения рядов
ТЕОРЕМА. Если каждый член ряда
u1 + u2 + u3 + …, + un + …. (8.10)
с положительными членами меньше (или равен) соответствующего члена сходящегося ряда
v1 + v2 + v3 + …, + vn + …. (8.11)
с положительными членами, то ряд (8.10) сходится.
Если каждый член ряда (8.10) больше (или равен) соответствующего члена расходящегося ряда (8.11), то ряд (8.10) расходится.
Доказательство. Пусть un ≤ vn и ряд (8.11) сходится. Составим суммы первых n членов рядов (8.10) и (8.11):

Поскольку 
Ряд (8.11) совпадает, то  Отсюда следует, что
Отсюда следует, что  . При неограниченном возрастании номера n последовательность сумм
. При неограниченном возрастании номера n последовательность сумм 
как возрастающая последовательность и ограничена сверху числом S(2), имеет предел S(1) ≤ S(2), то есть  а потому ряд (8.10) также сходящийся.
а потому ряд (8.10) также сходящийся.
Пусть un ≥ vn и ряд (8.11) расходится. Тогда в силу неравенств  следует, что
следует, что  . Но поскольку,
. Но поскольку,  то
то  также будет неограниченно расти, то есть ряд будет расходиться.
также будет неограниченно расти, то есть ряд будет расходиться.
Пример 1. Исследовать сходимость ряда

Решение. Сравним данный ряд с бесконечно убывающей геометрической прогрессией

Поскольку  для произвольного n, а ряд бесконечно убывающей геометрической прогрессии является сходящимся рядом, то согласно признака сравнения рядов исходный ряд будет сходящимся.
для произвольного n, а ряд бесконечно убывающей геометрической прогрессии является сходящимся рядом, то согласно признака сравнения рядов исходный ряд будет сходящимся.
Пример 2. Исследовать сходимость ряда

Решение. Данный ряд сравним с гармоничным рядом. Для произвольного n выполняется неравенство 
Как было показано выше, гармонический ряд расходится, следовательно данный ряд расходится также.
Признак Даламбера
ТЕОРЕМА. Пусть все члены ряда u1 + u2 + u3 + …, + un + …. положительные и пусть при неограниченном росте номера n предел отношения (n + 1)-го члена к n-му существует и равен некоторому числу l, то есть 
Тогда:
1. Если l < 1, то ряд сходится.
2. Если l > 1, то ряд расходится.
3. Если l = 1, то признак не дает ответа на вопрос о схождении или расхождении ряда, то есть ряд в данном случае может как сходиться, так и расходиться.
Доказательство. Пусть имеем ряд
u1 + u2 + u3 + …, + un + …. (8.12)
составленный из положительных чисел, и пусть
 (8.13)
(8.13)
Тогда при достаточно большом n, то есть при n не меньше некоторого числа N имеем:
 , где ε — сколь угодно малое положительное число. Отсюда
, где ε — сколь угодно малое положительное число. Отсюда
 как только n ≥ N.
как только n ≥ N.
а) Пусть l < 1. Мы сможем выбрать число ε настолько малым, что l + ε также будет меньше единицы, тогда, положив l + ε = q, получим:
 и т. д.
и т. д.
Итак,

Отсюда следует, что члены ряда  которые представляют N-й остаток ряда (8.12), меньше соответствующих членов бесконечно убывающей геометрической прогрессии
которые представляют N-й остаток ряда (8.12), меньше соответствующих членов бесконечно убывающей геометрической прогрессии
 (знаменатель q < 1).
(знаменатель q < 1).
Этот ряд сходится, следовательно ряд (8.12) сходится.
б) Пусть l > 1. Тогда можно подобрать N таким, что при n ≥ N будет справедливо неравенство
 (8.14)
(8.14)
где ε выбирается настолько малым, чтобы величина q = l – ε оставалась большей 1. Тогда каждый последующий член ряда будет больше предыдущего, а это противоречит необходимому признаку сходимости ряда. Итак, ряд расходится.
в) В том случае, когда предел l = 1, признак Даламбера не дает ответы на вопросы о сходимости или расходимости ряда. Ряды могут быть как сходящимися так и расходящимися.
Пример 1. Исследовать сходимость ряда

Решение. Поскольку
 то
то  а значит,
а значит,


Здесь n! = 1⋅ 2 ⋅ 3 ⋅ … ⋅ n; 0! = 1! = 1; (n + 1)! = (n + 1) n!
Поскольку l = 0 < 1, то согласно признаку Даламбера данный ряд сходится.
Пример 2. Исследовать сходимость ряда

Решение. Здесь 
Поэтому

Поскольку l =  , то по признаку Даламбера числовой ряд расходится.
, то по признаку Даламбера числовой ряд расходится.
Пример 3. Исследовать сходимость ряда

Решение. Находим

Полученную неопределенность типа  раскроем по правилу Лопиталя:
раскроем по правилу Лопиталя:

Поэтому по признаку Даламбера сходимость исходного ряда установить невозможно. Если признак Даламбера не дает ответа на вопрос о сходимости ряда (при l = 1), нужно использовать другие признаки исследования сходимости данного ряда.
Интегральный признак Коши
ТЕОРЕМА. Пусть y = f (x) — непрерывная, монотонно убывающая и положительная в интервале [1,  ) функция, значение которой f (1), f (2), f (3), …, f (n) … совпадают с соответствующими положительными членами ряда
) функция, значение которой f (1), f (2), f (3), …, f (n) … совпадают с соответствующими положительными членами ряда
u1 + u2 + u3 + …, + un + …. (8.15)
Тогда для сходимости ряда необходимо и достаточно, чтобы несобственный
интеграл  имел конечную величину.
имел конечную величину.
Доказательство. Рассмотрим криволинейную трапецию, ограниченную линией y = f (x), с основанием от x = 1 до x = n, где n — произвольное целое положительное число (рис. 1)
Площадь фигуры, ограниченная данным линиями вычисляется по формуле
 (8.16)
(8.16)
Обозначим целые точки основания x = 1, x = 2, …, x = n – 1, x = n.
Рассмотрим две ступенчатые фигуры: одна из них (внутренняя) имеет площадь, равную f (2) + f (3) + …. + f (n) = Sn – u1, а вторая (внешняя) — площадь, равную f (1) + f (2) + …. + f (n – 1) = Sn – un , где Sn = u1 + u2 + u3 + …, + un.

Рис. 1.
Площадь первой фигуры меньше площади криволинейной трапеции, а площадь второй больше нее. Итак, имеем:
 (8.17)
(8.17)
Отсюда получим два неравенства:
 (8.18)
(8.18)
 (8.19)
(8.19)
Поскольку функция f (x) положительная, то интеграл In растет вместе с n.
Возможны два случая:
1) Несобственный интеграл сходится, то есть  существует. Тогда
существует. Тогда  и из неравенства (8.18) при произвольном n находим
и из неравенства (8.18) при произвольном n находим  Поскольку частные суммы Sn ограничены и возрастают с ростом n, то согласно известной теореме анализа, существует предел
Поскольку частные суммы Sn ограничены и возрастают с ростом n, то согласно известной теореме анализа, существует предел  , то есть ряд сходится.
, то есть ряд сходится.
2) Интеграл расходится. Тогда  , при
, при  и из неравенства (8.19) следует, что Sn также неограниченно растет, а это означает, что ряд расходится.
и из неравенства (8.19) следует, что Sn также неограниченно растет, а это означает, что ряд расходится.
Пример 1. Исследовать сходимость ряда

Решение. Функция  (ее вид устанавливаем из общего члена заменой n на x) принимает только положительные значения, монотонно убывает в интервале [1,
(ее вид устанавливаем из общего члена заменой n на x) принимает только положительные значения, монотонно убывает в интервале [1,  ). Значения
). Значения

совпадают с членами данного ряда. Итак, функция f (x) удовлетворяет условиям признака Коши.
Вопрос о сходимости данного ряда сводится к вопросу о сходимость несобственного интеграла 
Вычислим данный интеграл:



Несобственный интеграл сходится, а потому сходится и исходный ряд.
Пример 2. Исследовать сходимость гармонического ряда
.
Решение. Функция  удовлетворяет условиям признака Коши:
удовлетворяет условиям признака Коши:
а) принимает положительные значения и монотонно убывает на интервале [1,  );
);
б) значения 
совпадают с соответствующими членами гармонического ряда.
Вычисляем несобственный интеграл

Данный несобственный интеграл расходится, следовательно гармонический ряд тоже расходится.
Знакочередующиеся ряды. Признак сходимости Лейбница
Упомянутые признаки сходимости числовых рядов относились к рядам с положительными членами. Рассмотрим теперь ряды, часть членов которых положительная, а часть — отрицательная или равна нулю.
Если члены числового ряда имеют разные знаки, то ряд называется знакопеременным.
Если два подряд члена ряда имеют разные знаки, то знакопеременный ряд называют знакочередующимся. Он имеет вид

Числа u1, u2, u3, …, un, … — положительные. На вопрос о сходимости или расхождение такого ряда дает ответ признак Лейбница, который формулируется в виде теоремы.
ТЕОРЕМА. Если с ростом номера n члены ряда
 (8.20)
(8.20)
по абсолютной величине убывают, а общий член un стремится к нулю при n → ∞, то есть  то ряд (8.20) сходится.
то ряд (8.20) сходится.
Доказательство. Просуммируем четное число членов ряда (8.20):

Тогда 
Так как по условию теоремы  то
то  то есть с ростом n суммы с четными индексами также растут.
то есть с ростом n суммы с четными индексами также растут.
Запишем теперь частную сумму S2n в другом виде:

Поскольку согласно условию теоремы  при любом n, то из последнего равенства следует, что
при любом n, то из последнего равенства следует, что 
Таким образом, последовательность  возрастает с возрастанием n, и остается ограниченной, а потому стремится к определенному пределу, то есть
возрастает с возрастанием n, и остается ограниченной, а потому стремится к определенному пределу, то есть 
Теперь просуммируем нечетное число членов ряда (8.20)

Но так как по условию теоремы  , то
, то

Таким образом, доказано, что при данных условиях, ряд (8.20) сходится и 0 ≤ S ≤ u1 .
Следствие. Если ряд (8.20) сходится, то остаток ряда также представляет собой сходящийся ряд, и его сумма равна 
Остаток ряда, удовлетворяющий условиям только что доказанной теоремы, равен 
Отсюда  и ряд в правой части удовлетворяет условиям теоремы. Поэтому
и ряд в правой части удовлетворяет условиям теоремы. Поэтому  то есть
то есть 
Эта формула дает оценку величины погрешности в том случае, если вместо суммы ряда (8.20) берется сумма n первых его членов. Как видим, для знакопеременных рядов с убывающими членами эта погрешность не превышает абсолютной величины первого из отброшенных членов.
Пример 1. Исследовать сходимость ряда

Решение. Абсолютные величины членов знакочередующегося ряда убывают
 и предел общего члена равна нулю, то есть
и предел общего члена равна нулю, то есть 
Оба условия признака Лейбница выполняются, поэтому заданный ряд сходится.
Если хоть одно из условий признака Лейбница не выполняется, то знакочередующийся ряд будет расходящимся.
Пример 2. Исследовать сходимость ряда

Решение. Поскольку  то данный ряд расходится.
то данный ряд расходится.
Здесь не выполняется одно из условий признака Лейбница сходимости знакочередующегося ряда: 
Абсолютная и условная сходимость ряда
Рассмотрим знакопеременный ряд, в котором члены с положительными и отрицательными знаками не обязательно чередуются. Обозначим такой ряд u1 + u2 + u3 + …, + un + …. , где ui (i = 1, 2, 3, …, n) — числа как положительные, так и отрицательные.
Составляем ряд из абсолютных величин его членов:

Если ряд из абсолютных величин сходится, то знакопеременный ряд называется абсолютно сходящимся. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин, расходится, то знакопеременный ряд называется не абсолютно сходящимся (или условно сходящимся).
ТЕОРЕМА. Если ряд, составленный из абсолютных величин членов данного ряда, сходится, то сходится и данный ряд.
Доказательство. Обозначим через Sn сумму n первых членов ряда
u1 + u2 + u3 + …, + un + …. (8.21)
через  — сумму всех положительных членов, а через
— сумму всех положительных членов, а через  — сумму абсолютных
— сумму абсолютных
величин всех отрицательных членов среди первых n членов ряда.
Тогда  (8.22)
(8.22)
где 
Поскольку согласно условию σn имеет предел, то есть  а
а  и
и  — положительные и возрастающие функции от n, причем
— положительные и возрастающие функции от n, причем  и
и  , то и они имеют предел. А значит и
, то и они имеют предел. А значит и  при n →
при n →  стремится к пределу, что и требовалось доказать.
стремится к пределу, что и требовалось доказать.
Это достаточный признак, но не являющийся необходимым, то есть ряд  может сходиться и тогда, когда ряд
может сходиться и тогда, когда ряд  расходится.
расходится.
Пример 1. Исследовать сходимость ряда

Решение. Данный ряд называют рядом Лейбница.
Поскольку  nо данный ряд сходится (согласно признаку Лейбница). Ряд, составленный из абсолютных величин
nо данный ряд сходится (согласно признаку Лейбница). Ряд, составленный из абсолютных величин  является гармоническим, который, как известно, расходящийся. Следовательно, данный ряд Лейбница условно сходится.
является гармоническим, который, как известно, расходящийся. Следовательно, данный ряд Лейбница условно сходится.
Пример 2. Исследовать сходимость ряда

Решение. Составим ряд из абсолютных величин

Он сходится как ряд бесконечно убывающей геометрической прогрессии со знаменателем Итак, заданный ряд сходится абсолютно.
Итак, заданный ряд сходится абсолютно.
Понятие о степенном ряде и его сходимости
Ряд, членами которого являются функции переменной x, называется функциональным.
Это ряд вида
f1 (x) + f2 (x) + f3 (x) + … + fn (x) + … (8.23)
Если x приобретает любое числовое значение, то ряд (8.23) становится числовым.
Совокупность всех значений переменной x, при которых функциональный ряд сходится, называется областью сходимости этого ряда. Будем рассматривать ряды, областями сходимости которых служат различные интервалы оси Ox.
Если для всякого значения x из интервала (a, b) функциональный ряд сходится, то его сумма есть функция
f (x) = f1 (x) + f2 (x) + f3 (x) + … + fn (x) + … (8.24)
Иначе говоря, функция f (x) в интервале (a, b) раскладывается в ряд.
Степенным рядом называется функциональный ряд вида
 (8.25)
(8.25)
где a0, a1, a2 … an — постоянные числа.
Иногда рассматривают степенной ряд более общего вида:
 (8.26)
(8.26)
где a — некоторое постоянное число. Последний ряд легко приводится к предыдущему степенному ряду, если переобозначить x – a = x’.
Докажем важную теорему, на которой будет базироваться изучение степенных рядов.
ТЕОРЕМА Абеля. Если степенной ряд (8.25) сходится в точке x0 ≠ 0, то он сходится абсолютно в интервале  то есть при всяком x, удовлетворяющем условию
то есть при всяком x, удовлетворяющем условию
 .
.
Доказательство. Из сходимости ряда (8.25) в точке x0 следует, что его общий член  при n →
при n →  . А поэтому все члены этого ряда являются ограниченными, то есть существует такое постоянное положительное число M, что для всякого n имеет место неравенство
. А поэтому все члены этого ряда являются ограниченными, то есть существует такое постоянное положительное число M, что для всякого n имеет место неравенство
 (8.27)
(8.27)
Запишем ряд (8.25) так:
 (8.28)
(8.28)
и составим ряд из абсолютных величин членов этого ряда:
 (8.29)
(8.29)
В силу установленного неравенства (8.27) каждый член ряда (8.29) меньше соответствующего члена геометрической прогрессии со знаменателем 
 (8.30)
(8.30)
Если  то
то  и ряд (8.30) сходится; а потому сходится и ряд абсолютных величин (8.29), а значит, абсолютно сходится и сам ряд (8.25). Теорема доказана.
и ряд (8.30) сходится; а потому сходится и ряд абсолютных величин (8.29), а значит, абсолютно сходится и сам ряд (8.25). Теорема доказана.
Следствие. Если степенной ряд (8.25) расходится при x = x0, то он расходится и при всяком x, превышающем абсолютную величину x0, то есть при 
Таким образом можно утверждать, что для любого степенного ряда, который имеет как точки сходимости так и точки расхождения, существует такое положительное число R, что для всех x, по модулю меньших  ряд абсолютно сходится, а для всех x, по модулю больших R (| x |> R , ряд расходится. Число R называется радиусом сходимости степенного ряда (8.25). Интервал (-R, R) называется интервалом сходимости. Если R = 0, то интервал сходимости вырождается в точку, а при R =
ряд абсолютно сходится, а для всех x, по модулю больших R (| x |> R , ряд расходится. Число R называется радиусом сходимости степенного ряда (8.25). Интервал (-R, R) называется интервалом сходимости. Если R = 0, то интервал сходимости вырождается в точку, а при R =  — во всю числовую ось.
— во всю числовую ось.
Для степенных рядов (8.26) все сказанное выше остается в силе, только с той разницей, что теперь центр интервала сходимости будет лежать не в точке x = 0, а в точке x = x0. Следовательно, интервалом сходимости будет 
В следующей теореме будет дан способ отыскания радиуса сходимости степенного ряда.
ТЕОРЕМА. Если существует  то радиус сходимости степенного ряда находится по формуле
то радиус сходимости степенного ряда находится по формуле  (8.31)
(8.31)
Доказательство. Составим ряд с абсолютных величин членов ряда (8.25):  (8.32)
(8.32)
Из предыдущего параграфа известно, что если сходится ряд (8.32), то сходится ряд (8.25) абсолютно. Предположив, что n →  ,
,
получим 
Согласно признаку Даламбера, ряд (8.32) сходится, если
 то есть, если
то есть, если  и расходится, если
и расходится, если

Итак, степенной ряд (8.25) сходится, для всех значений x, для которых
 , и расходится для тех значений x, для которых
, и расходится для тех значений x, для которых 
Таким образом, для ряда (8.25), радиус сходимости находится по формуле

Пример 1. Найти интервал сходимости степенного ряда

и исследовать его сходимость на концах интервала.
Решение. Здесь

Находим радиус сходимости ряда


Итак, ряд сходится в интервале (-2, 2). Чтобы решить вопрос о сходимости степенного ряда на концах интервала, положим сначала х = 2. Получим гармонический ряд  который, как известно, расходится. При x = -2 получим знакопеременный ряд Лейбница:
который, как известно, расходится. При x = -2 получим знакопеременный ряд Лейбница:

Этот ряд сходится условно. Таким образом, степенной ряд сходится для x ∈ [-2; 2).
Пример 2. Найти интервал сходимости степенного ряда
 и исследовать его сходимость на концах интервала.
и исследовать его сходимость на концах интервала.
Несобственный интеграл сходится, значит, и числовой ряд тоже сходится, то есть правый конец входит в интервал сходимости.
При x = -1 получим числовой ряд  который сходится абсолютно, потому что выполняются условия признака Лейбница
который сходится абсолютно, потому что выполняются условия признака Лейбница  и сходится ряд, составленный из абсолютных величин. Таким образом, исходный степенной ряд абсолютно сходится на отрезку [- 1; 1].
и сходится ряд, составленный из абсолютных величин. Таким образом, исходный степенной ряд абсолютно сходится на отрезку [- 1; 1].
Пример 3. Найти интервал сходимости степенного ряда

Решение. Поскольку  то
то

Это означает, что ряд сходится только при x = 0 и расходится при других значениях.
Пример 4. Найти интервал сходимости степенного ряда

Решение. Здесь 

Значит, ряд сходится, если – 1 < x – 3 < 1, то есть интервал сходимости степенного ряда 2 < x < 4.
Исследуем сходимость степенного ряда на концах интервала сходимости. При x = 4 получим ряд  Данный ряд сходится, поскольку, согласно интегральному признаку Коши, несобственный интеграл
Данный ряд сходится, поскольку, согласно интегральному признаку Коши, несобственный интеграл

является сходящимся.
Если x = 2, то получим знакопеременный ряд
 .
.
Этот ряд сходится, поскольку выполняются условия признака Лейбница:
1)  2)
2)  .
.
Кроме этого, знакопеременный ряд сходится абсолютно, потому что совпадает ряд из абсолютных величин его членов.
Пример 5. Исследовать сходимость ряда

Решение. Поскольку  то
то

Это означает, что ряд сходится только при x – 10 = 0, то есть в точке x = 10.
Дифференцирование и интегрирование степенных рядов. Разложение некоторых функций в степенные ряды
Приведем две важные теоремы (без доказательства).
ТЕОРЕМА 1. Степенной ряд
 (8.33)
(8.33)
и полученный из него почленным дифференцированием ряд
 (8.34)
(8.34)
имеют один и тот же интервал сходимости (-R, R).
Сумма ряда (8.34) равна производной S’ (x) суммы S (x) ряда (8.33) при всех значениях x, для которых | x | < R.
ТЕОРЕМА 2. Степенной ряд
 (8.35)
(8.35)
и ряд
 (8.36)
(8.36)
полученный из ряда (8.35) почленным интегрированием, имеют одинаковый интервал сходимости. Сумма ряда (8.36) равна
 где S (x) — сумма ряда (8.35).
где S (x) — сумма ряда (8.35).
Для практики важно уметь данную функцию f (x) разложить в степенной ряд, то есть функцию f (x) представить в виде степенного ряда, что позволяет достаточно просто вычислять значения этой функции.
Сначала рассмотрим некоторые частные случаи. Рассмотрим степенной ряд
1 + x + x2 + … + xn + …. (8.37)
Этот ряд представляет собой ряд геометрической прогрессии со знаменателем x, который сходится при  и его сумма равна
и его сумма равна 
Следовательно, мы можем записать:
 (8.38)
(8.38)
На последнее равенство можно смотреть как на разложение функции  в степенной ряд. Из разложения (8.38) можно легко получить другие разложения функций.
в степенной ряд. Из разложения (8.38) можно легко получить другие разложения функций.
Разложение функции f (x) = ln (1 + x)
Заменив в разложении (8.38) x на (-у), будем иметь:
 (8.39)
(8.39)
Если  , то равенство (8.39), как было сказано в предыдущем параграфе, можно проинтегрировать почленно по у в пределах от 0 до x, то есть
, то равенство (8.39), как было сказано в предыдущем параграфе, можно проинтегрировать почленно по у в пределах от 0 до x, то есть 
Отсюда имеем 
Такое разложение справедливо также для x = 1 и соответственно ряд
 является сходящимся. Областью сходимости будет множество x∈ (- 1,1].
является сходящимся. Областью сходимости будет множество x∈ (- 1,1].
Разложение функции f (x) = arctg x
Положим в разложении (8.38) x = -y2.
 (8.40)
(8.40)
Умножив последнее равенство на dy и проинтегрировав почленно в пределах от 0 до x, где x < 1, получим:
 или
или

Поскольку arctg 0 = 0, то имеем:
 если x < 1. (8.41)
если x < 1. (8.41)
Можно доказать, что это разложение справедливо при x = –1 и x = 1.
При x = 1 имеем 
При x = -1 имеем 
Итак, областью сходимости данного степенного ряда будет отрезок [- 1; 1].
Мы видим, что некоторые функции, как, например ln (1 + x), arctg x и тому подобные, допускают разложение в степенной ряд относительно аргумента x. Естественно задать общий вопрос о разложении данной функции f (x) по растущим целым положительным степеням x. Этим вопросом мы займемся в следующем параграфе.
Разложение функции в ряд Маклорена
Предположим, что данная функция f (x) может быть разложена в степенной ряд (8.42)
(8.42)
где a0, a1, …, an, …. — неопределенные коэффициенты, причем интервал схождения (- R, R) не сводится к точке, то есть R > 0.
Как было сказано выше, степенной ряд (8.42) в его интервале сходимости можно дифференцировать почленно любое число раз, причем все полученные ряды будут совпадать и их суммы будут равны соответствующим производным от суммы данного ряда f (x).
Продифференцировав почленно ряд (8.42) n раз, получим:

Положив в этих равенствах, включая (8.42), х = 0 получим:

Отсюда 

Подставив значения коэффициентов a0, a1, …, an, … в (8.42), получим формулу Маклорена:
 (8.43)
(8.43)
где
 — остаточный член в форме Лагранжа.
— остаточный член в форме Лагранжа.
Число  можно записать в виде
можно записать в виде 
Если при неограниченном росте n, то есть при n → ∞
 (8.44)
(8.44)
то из формулы Маклорена получим разложение функции f (x) в ряд по степеням x, который называется рядом Маклорена:
 (8.45)
(8.45)
А условие (8.44) представляет собой необходимое и достаточное условие того, что ряд Маклорена для функции f (x), которая дифференцирована неограниченное число раз, сходится к этой функции.
Приведем примеры на применение ряда Маклорена к разложению некоторых элементарных функций в степенные ряды.
Разложение функции f (x) = ex
Пусть f (x) = ex. Тогда f'(x) = ex, f”(x) = ex … f (n) (x) = ex.
Положив x = 0, получим:
f (0) = e0 = 1; f'(0) = 1; f”(0) = 1 … f (n) (0) = 1.
Подставив эти значения в формулу Маклорена (8.43), получим:

где

Поскольку  — величина ограниченная при ограниченном x, то для того, чтобы доказать, что
— величина ограниченная при ограниченном x, то для того, чтобы доказать, что  , нужно показать, что
, нужно показать, что  . Для этого зафиксируем x и рассмотрим ряд
. Для этого зафиксируем x и рассмотрим ряд

Если он совпадает, то его общий член  при
при  стремится к нулю. Используем признак Даламбера к ряду абсолютных величин:
стремится к нулю. Используем признак Даламбера к ряду абсолютных величин:
и функция f (x) = ex разлагается в интервале  в следующий ряд Маклорена
в следующий ряд Маклорена
 (8.46)
(8.46)
Разложение функций f (x) = sin x, f (x) = соs x
Пусть f (x) = sin x; отсюда

Положив х = 0, имеем:

Подставив эти значения в формулу (8.45), получим:
 (8.47)
(8.47)
Можно легко убедиться, что ряд сходится для любого x ∈ 
Сделав аналогичные выкладки, можно найти разложение функции f (x) = соs x в ряд:
 для x ∈
для x ∈  (8.48).
(8.48).
Разложение бинома Ньютона f (x) = (1 + x) m
Пусть f (x) = (1 + x) m, где m — число целое или дробное, положительное или отрицательное.
Тогда имеем:

Положив x = 0 во всех этих формулах, получим:


Подставив выражения для f (0), f’ (0), … f (n) (0) в ряд Маклорена (8.45) будем иметь
 (8.49)
(8.49)
Пользуясь формулой
 найдем интервал сходимости (-R; R) ряда (8.49).
найдем интервал сходимости (-R; R) ряда (8.49).
Мы имеем:

Отсюда
 , и соответственно
, и соответственно
 (8.50)
(8.50)
Таким образом, биномиальный ряд сходится для x∈ (- 1,1) и расходится снаружи. Сходится ли этот ряд в точках x = –1 и x = 1, необходимо исследовать для каждого случая отдельно.
Разложение функции в ряд Тейлора
В некоторых случаях функция f (x) или ее производные теряют смысл в точке x = 0, как, например f (x) = ln x или  .
.
Такие функции не могут быть разложены в ряд Маклорена. Для разложения такого рода функций можно воспользоваться более общими степенными рядами, разложенными по степеням (x – a), где a — подобранное, в конкретном случае, постоянное число.
В разделе 4 было доказано, что если функция f (x) дифференцируема n раз в интервале (a, x), то имеет место формула Тейлора: (8.51)
(8.51)
где  , (a < c < x) — остаточный член в форме Лагранжа. Число с можно записать в виде с = a + θ (x – a), где 0 < θ < 1.
, (a < c < x) — остаточный член в форме Лагранжа. Число с можно записать в виде с = a + θ (x – a), где 0 < θ < 1.
Если при неограниченном росте n, то есть при n → ∞,
 (8.52)
(8.52)
то из формулы Тейлора получим разложение функции f (x) в ряд по степеням (x – a), который называется рядом Тейлора:
 (8.53)
(8.53)
Условие (8.52) служит необходимым и достаточным условием того, что ряд Тейлора для функции, неограниченное число раз дифференцируемой, сходится к этой функции.
Пример. Разложить в ряд по степеням (x – a) функцию

Решение. Продифференцируем функцию f (x):

Подставив x = a в предыдущие формулы, получим:

Используя ряд Тейлора (8.53), получим такое разложение функции f (x) по степеням (x – a):

Находим радиус сходимости данного ряда:
 Здесь
Здесь 
 при любом a ≠ 0.
при любом a ≠ 0.
Итак, область сходимости ряда будет  .
.
Применение степенных рядов к приближенным вычислениям
Полученные разложения некоторых функций в степенные ряды в §10, 11 дают возможность приближенно вычислять значения функции, определенные интегралы, пределы функции и т. д.
Пример 1. Вычислить  , ограничившись двумя членами разложения.
, ограничившись двумя членами разложения.
Решение. Используем формулу разложения cos х в ряд по возрастающим степеням x 
Переведем  в радианную меру:
в радианную меру: 
Тогда  . Подставив вместо π ≈ 3,14159, получим
. Подставив вместо π ≈ 3,14159, получим 
Пример 2. Вычислить число e.
Решение. Используем разложение функции ex в ряд Маклорена:

Положив x = 1, получим  Если за приближенное значение числа e взять сумму первых семи членов этого ряда
Если за приближенное значение числа e взять сумму первых семи членов этого ряда
 то получим e ≈ 2,718.
то получим e ≈ 2,718.
Пример 3. Вычислить  с точностью до 0,001.
с точностью до 0,001.
Решение. Используем формулу биномиального ряда

Если  то получим
то получим


Поскольку в знакочередующемся ряду с убывающими по абсолютной величине членами  то погрешность в наших вычислениях не превышает 0,0008, что обеспечивает необходимую точность.
то погрешность в наших вычислениях не превышает 0,0008, что обеспечивает необходимую точность.
Пример 4. Вычислить  ограничившись двумя членами разложения.
ограничившись двумя членами разложения.
Решение. Запишем число  в виде
в виде

В нашем случае, положив в биномиальном ряду 
 имеем:
имеем:
Пример 5. Вычислить ln 10, ограничившись тремя членами разложения.
Решение. Число ln 10 представим так:
 Положив в формуле
Положив в формуле
 значение
значение  получим
получим

Тогда ln 10 = 2,019 + 0,219 = 2,298.
Пример 6. Вычислить определенный интеграл  ограничившись четырьмя членами разложения функции sin x.
ограничившись четырьмя членами разложения функции sin x.
Решение. Поскольку неопределенный интеграл  может быть выражен в элементарных функциях и формулу Ньютона-Лейбница нельзя использовать, данный интеграл вычислим приближенно, используя теорию рядов. Разделим правую часть
может быть выражен в элементарных функциях и формулу Ньютона-Лейбница нельзя использовать, данный интеграл вычислим приближенно, используя теорию рядов. Разделим правую часть
разложения функции sin x в ряд
 на х и проинтегрируем полученное выражение:
на х и проинтегрируем полученное выражение:
.


Пример 7. Вычислить 
Решение. Заменив в равенстве 
x на “-x2” и проинтегрировав в пределах от 0 до 0,3, получим

Пример 8. Найти 
Решение. Поскольку 
 то
то


Пример 9. Найти решение дифференциального уравнения
y” + xy’ + y = x cos x, (8.54)
удовлетворяющего начальным условиям
y (0) = 0; y’ (0) = 1. (8.55)
Решение. Ищем решение y в виде ряда
 (8.56)
(8.56)
Найдя производную y’ и использовав (8.55), получим 
Тогда 
Продифференцировав разложение y два раза, получим:

Подставив y, y’, y” в (8.54) и заменив cos x его разложением (8.48), находим:

Приравняв коэффициенты при одинаковых степенях x, получим:

Отсюда следует, что a2 = a4 = a6 = a8 = … = 0;
 (8.57)
(8.57)
Подставив постоянные (8.57) в разложение (8.56) имеем:
 , что соответствует разложению функции y = sin x по степеням x.
, что соответствует разложению функции y = sin x по степеням x.
Проверка. Подставим y = sin x, y’ = cos x, y” = –sin x в уравнения (8.54):
–sin x + x cos x + sin x = x cos x, x cos x = x cos x.
Решение уравнения (8.54) найдено правильно.
Ряды и алгебра
В школьном курсе алгебры и начал анализа обычно рассматривают суммы, состоящие из конечного числа слагаемых. Единственным исключением является сумма бесконечно убывающей геометрической прогрессии,

где 
В курсе математического анализа изучаются суммы бесконечного множества слагаемых, или, как их называют, бесконечные ряды, которые являются действенным средством изучения функций и сильным вычислительным аппаратом, позволяющим находить с заданной точностью значения функций, вычислять приближенные значения интегралов и решать многие другие прикладные задачи.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Что такое ряд
Первоначально математики считали, что свойства бесконечных рядов аналогичны свойствам конечных сумм, и, не задумываясь, переставляли слагаемые, почленно дифференцировали и интегрировали бесконечные ряды, состоящие из функций, умножали один ряд на другой, так же, как перемножают многочлены, и т. д.
Но потом выяснилось, что столь беззаботное обращение с бесконечными рядами может привести к ошибочным результатам (см. примеры 8.9 и 8.10), и потому возникла необходимость в построении строгой теории бесконечных рядов, основными задачами которой являются:
- определение понятия суммы бесконечной последовательности слагаемых;
- установление признаков, по которым можно судить, имеет ли данный ряд сумму;
- выделение классов рядов, с которыми можно обращаться как с конечными суммами (например, переставлять члены ряда, почленно дифференцировать и интегрировать ряды, состоящие из функций, и т. д.);
- выведение формул, позволяющих представить заданные функции в виде сумм рядов, состоящих из сравнительно простых функций;
- изучение рядов, состоящих не только из действительных, но и из комплексных чисел.
Решению этих задач и посвящен курс «Теория рядов».
Возможно вам будут полезны данные страницы:
Числовые ряды
Определение 1.1. Числовым рядом с общим членом  называют последовательность чисел
называют последовательность чисел  соединенных знаком сложения, т. е. выражение вида:
соединенных знаком сложения, т. е. выражение вида:

Такой ряд записывают также в виде 
Примеры с решениями
Пример 1.1.
Если  то ряд имеет вид:
то ряд имеет вид:

или

Иногда при записи ряда выписывают только несколько его первых членов. Это делают лишь тогда, когда закономерность, характерная для членов ряда, легко усматривается.
Строго говоря, такой способ задания ряда не является математически корректным, так как получение формулы общего члена по нескольким первым членам ряда — задача, не имеющая однозначного решения.
Пример 1.2.
Напишем одну из возможных формул для общего члена ряда, зная его первые 4 члена:

Решение:
Рассмотрим сначала последовательность числителей 2, 5, 8, 11. Они образуют арифметическую прогрессию, первый член которой равен 2, а разность равна 3. Это позволяет в качестве общего выражения для числителя взять формулу общего члена арифметической прогрессии:  Знаменатели
Знаменатели  образуют геометрическую прогрессию с первым членом 2 и знаменателем 3. В качестве их общего выражения можно взять формулу общего члена геометрической прогрессии
образуют геометрическую прогрессию с первым членом 2 и знаменателем 3. В качестве их общего выражения можно взять формулу общего члена геометрической прогрессии  Итак, общий член ряда будет иметь следующий вид:
Итак, общий член ряда будет иметь следующий вид:

Следует отметить, что в качестве общего члена можно было бы принять и более сложное выражение

которое совпадает с написанным выше при 
Числа  могут быть как положительными, так и отрицатель ными. Иногда бывает целесообразно записать ряд
могут быть как положительными, так и отрицатель ными. Иногда бывает целесообразно записать ряд

в виде:

Сумма ряда. Сходящиеся и расходящиеся ряды. Поскольку сложение бесконечного множества чисел не определено, то надо выяснить смысл суммы бесконечного ряда. Для этого поставим в соответствие ряду  бесконечную последовательность чисел
бесконечную последовательность чисел  где
где  Мы будем называть число
Мы будем называть число  частичной суммой ряда
частичной суммой ряда  Очевидно, что
Очевидно, что  и потому
и потому

Определение 1.2. Числовой ряд называется сходящимся, если последовательность его частичных сумм имеет конечный предел, т. е. если существует  Значение
Значение  этого предела называется суммой ряда
этого предела называется суммой ряда  Если последовательность частичных сумм не имеет конечного предела, ряд называется расходящимся.
Если последовательность частичных сумм не имеет конечного предела, ряд называется расходящимся.
00
Будем условно писать  если
если  (соответственно
(соответственно  если
если 
В случае, когда числовой ряд  имеет сумму, будем иногда обозначать ее тем же символом
имеет сумму, будем иногда обозначать ее тем же символом  что и сам ряд.
что и сам ряд.
Пример 1.3.
Исследуем на сходимость бесконечную геометрическую прогрессию, т. е. ряд:

Решение:
Для этого ряда:

Если  то выполняется равенство
то выполняется равенство  а потому
а потому

Значит, при  исследуемая прогрессия сходится и ее сумма равна
исследуемая прогрессия сходится и ее сумма равна  ‘
‘
Если  то
то  а потому и
а потому и 
В этом случае последовательность частичных сумм не имеет конечного предела, т. е. ряд (1.1) расходится. Этот ряд расходится и при  В этом случае
В этом случае  а при
а при 
 Наконец, ряд (1.1) расходится и при
Наконец, ряд (1.1) расходится и при 
так как частичными суммами ряда  являются:
являются:

Последовательность  где
где  не имеет предела, а это и значит, что ряд расходится.
не имеет предела, а это и значит, что ряд расходится.
Пример 1.4.
Докажем, что ряд:

где  расходится.
расходится.
Решение:
Для этого ряда  Так как все члены этой суммы не меньше чем
Так как все члены этой суммы не меньше чем  она состоит из
она состоит из 
членов, то  Но при
Но при  имеем
имеем  и, значит,
и, значит,

Расходимость ряда П.2) доказана.
Пример 1.5.
Докажем, что ряд:

сходится, и найдем его сумму.
Решение:
Пользуясь известным тождеством 
 находим, что
находим, что

Так как

то ряд (1.3) сходится и его сумма равна 1.
Замечание. Рассмотрение примеров 1.3—1.5 может создать иллюзию, что и в общем случае исследование сходимости ряда можно провести таким же методом. В действительности это не так. Лишь в редких случаях (см. также упражнение 9) удается получить выражение для  содержащее ограниченное число слагаемых, и непосредственно найти
содержащее ограниченное число слагаемых, и непосредственно найти  Обычно используются различные признаки сходимости. Этот материал излагается во второй главе.
Обычно используются различные признаки сходимости. Этот материал излагается во второй главе.
Свойства сходящихся рядов
Необходимый признак сходимости ряда. Остаток ряда. При
определении суммы ряда мы писали  Если отбросить от последовательности
Если отбросить от последовательности  первых членов, то получившаяся последовательность
первых членов, то получившаяся последовательность  будет иметь тот же предел
будет иметь тот же предел  Это значит, что если существует
Это значит, что если существует 
то для любого  выполняется равенство
выполняется равенство

Теорема 2.1. Если ряд  сходится, то его общий член стремится к нулю.
сходится, то его общий член стремится к нулю.
Доказательство. Пусть  Тогда, как мы видели, и
Тогда, как мы видели, и  Но
Но  а потому
а потому

Отсюда и следует, что 
Из теоремы 2.1 непосредственно вытекает, что, например, ряд  расходится (его общий член не стремится к нулю). Следует иметь в виду, что стремление к нулю общего члена ряда является лишь необходимым признаком сходимости, но не является достаточным — общий член может стремиться к нулю и в некоторых расходящихся рядах. Например, ряд
расходится (его общий член не стремится к нулю). Следует иметь в виду, что стремление к нулю общего члена ряда является лишь необходимым признаком сходимости, но не является достаточным — общий член может стремиться к нулю и в некоторых расходящихся рядах. Например, ряд  при
при  расходится (см. пример 1.4), хотя
расходится (см. пример 1.4), хотя

Определение 2.1. Назовем  остатком ряда
остатком ряда  ряд, полученный отбрасыванием первых
ряд, полученный отбрасыванием первых  слагаемых, т. е. ряд
слагаемых, т. е. ряд

Если этот ряд сходится, то его сумму обозначают 
Теорема 2.2. Если ряд сходится, то сходится и каждый его остаток, причем выполняются равенства  где
где  — сумма ряда. Обратно: если хотя бы один остаток ряда сходится, то сходится и сам ряд.
— сумма ряда. Обратно: если хотя бы один остаток ряда сходится, то сходится и сам ряд.
Доказательство. Обозначим  частичную сумму ряда
частичную сумму ряда  через
через 

Ясно, что

Если ряд  сходится, то
сходится, то  где
где  — сумма этого ряда. Тогда имеем:
— сумма этого ряда. Тогда имеем:

Мы доказали, что последовательность  сходится к числу
сходится к числу  что сумма ряда
что сумма ряда  равна
равна  Таким образом,
Таким образом,  и тогда
и тогда 
Обратно: если ряд  сходится и его сумма равна
сходится и его сумма равна  то
то
 и потому
и потому  т. е. ряд сходится и его сумма равна
т. е. ряд сходится и его сумма равна 
Следствие. Если ряд  сходится, то
сходится, то 
В самом деле, в этом случае 
Пример 2.1.
Для ряда  найти величину
найти величину  и указать такое значение
и указать такое значение  чтобы при
чтобы при  имело место неравенство:
имело место неравенство: 
Решение:
Воспользуемся решением примера 1.5 (там рассматривался этот же ряд). Мы имели:

Следовательно,

Решим неравенство

Имеем:

В качестве  можно взять любое целое число, не меньшее чем 4999.
можно взять любое целое число, не меньшее чем 4999.
Свойства сходящихся рядов
Некоторые свойства числовых рядов непосредственно вытекают из соответствующих свойств числовых последовательностей:
а) Ряд не может иметь двух различных сумм.
Это следует из того, что последовательность частичных сумм не может иметь двух различных пределов.
б) Если данный ряд сходится, то и любой ряд, полученный из него группировкой слагаемых, сходится и имеет ту же сумму, что данный ряд.
В самом деле, пусть первая группа состоит из  слагаемых, вторая — из
слагаемых, вторая — из  слагаемых,
слагаемых,  из
из  слагаемых, …, т. е. пусть после группировки получается такой ряд:
слагаемых, …, т. е. пусть после группировки получается такой ряд:


где 
Тогда после группировки получится ряд, частичными суммами которого являются  В самом деле,
В самом деле,  частичная сумма ряда (2.1) состоит из скобок, в которые входят члены от первого до
частичная сумма ряда (2.1) состоит из скобок, в которые входят члены от первого до  до
до  Поэтому она равна
Поэтому она равна 
Таким образом, последовательность частичных сумм ряда к (2.1) является подпоследовательностью для  Отсюда следует, что если существует
Отсюда следует, что если существует  то и Последовательность частичных сумм ряда (2.1) сходится к тому же пределу
то и Последовательность частичных сумм ряда (2.1) сходится к тому же пределу  Свойство доказано.
Свойство доказано.
Отметим, что утверждение, обратное утверждению б), неверно, поскольку после группировки членов расходящегося ряда может получиться сходящийся ряд.
Пример 2.2.
Ряд  расходится, так как его общий член не стремится к нулю. Группируя члены этого ряда по два, получаем ряд из нулей
расходится, так как его общий член не стремится к нулю. Группируя члены этого ряда по два, получаем ряд из нулей

который, очевидно, сходится.
Решение:
Поскольку последовательности являются функциями натурального аргумента, их можно складывать, умножать и т. д. В связи с этим можно говорить о сумме рядов  т.е о ряде
т.е о ряде  об умножении всех членов ряда
об умножении всех членов ряда  на данное число
на данное число  и т- д. Докажем следующие теоремы.
и т- д. Докажем следующие теоремы.
Теорема 2.3. Пусть ряды  сходятся и имеют соответственно суммы
сходятся и имеют соответственно суммы  и
и  Тогда сходится и ряд
Тогда сходится и ряд
 причем его сумма
причем его сумма  равна
равна 
Доказательство. Найдем  частичную сумму ряда
частичную сумму ряда 

Переставляя слагаемые, получаем, что

где  частичная сумма ряда
частичная сумма ряда  а
а  частичная сумма ряда
частичная сумма ряда  В силу теоремы о пределе суммы существует
В силу теоремы о пределе суммы существует  причем
причем

Теорема 2.4. Если ряд  сходится и его сумма равна
сходится и его сумма равна  то сходится и ряд
то сходится и ряд  причем его сумма
причем его сумма  равна
равна 
Доказательство. Ясно, что  частичная сумма
частичная сумма  ряда
ряда  имеет вид:
имеет вид:

Поэтому

Разностью двух рядов  и
и  называют ряд
называют ряд 
 Отсюда как следствие теорем 2.3 и 2.4 вытекает, что разность двух сходящихся рядов является сходящимся рядом. При этом если
Отсюда как следствие теорем 2.3 и 2.4 вытекает, что разность двух сходящихся рядов является сходящимся рядом. При этом если  — сумма ряда
— сумма ряда 
 и
и  — суммы рядов
— суммы рядов  и
и  соответственно, то
соответственно, то  Ясно, что
Ясно, что 
Пример 2.3.
Докажем, что сумма сходящегося и расходящегося рядов является расходящимся рядом.
Доказательство проводим от противного. Пусть ряд  сходится, а ряд
сходится, а ряд  расходится. Допустим, что ряд
расходится. Допустим, что ряд  сходится. Тогда
сходится. Тогда  сходится как разность двух сходящихся рядов, что противоречит условию. Противоречие возникло из предположения, что ряд
сходится как разность двух сходящихся рядов, что противоречит условию. Противоречие возникло из предположения, что ряд  сходится, значит, такое предположение ложно. Итак, ряд
сходится, значит, такое предположение ложно. Итак, ряд  расходится.
расходится.
Исходя из этого примера, легко показать, что если разность  сходится, а один из рядов
сходится, а один из рядов  или
или  расходится, то и другой ряд также расходится.
расходится, то и другой ряд также расходится.
Заметим, что разность двух расходящихся рядов может сходиться.
Пример 2.4.
Ряды

расходятся, так как их общие члены не стремятся к нулю. Но ряд  сходится.
сходится.
Функциональные ряды и их область сходимости
Рассмотрим теперь ряды, членами которых являются не числа, а функции.
Определение 3.1. Пусть функции 
 заданы на одном и том же множестве
заданы на одном и том же множестве  Назовем функциональным рядом с общим членом
Назовем функциональным рядом с общим членом  выражение
выражение

Если заменять в этом выражении переменную  любым числом
любым числом  из
из  то получим числовой ряд:
то получим числовой ряд:

Таким образом, каждый функциональный ряд определяет множество числовых рядов, получаемых из него подстановкой вместо переменной ее значений. Эти числовые ряды могут сходиться при одних значениях аргументов и расходиться при других значениях. Например, как мы знаем, ряд

сходится, если  и расходится, если
и расходится, если 
Определение 3.2. Множество значений аргумента  при которых сходится функциональный ряд
при которых сходится функциональный ряд  называется областью сходимости этого ряда при
называется областью сходимости этого ряда при 
Тем самым в области сходимости ряда определена функция  называемая суммой этого ряда. Частичные суммы ряда будем обозначать
называемая суммой этого ряда. Частичные суммы ряда будем обозначать  а его остаток обозначим
а его остаток обозначим  Таким образом, в области сходимости имеем:
Таким образом, в области сходимости имеем:

Чаще всего используют функциональные ряды двух типов: степенные и тригонометрические.
1. Степенные ряды — это ряды вида:

Таким образом, степенной ряд является частным случаем функционального ряда, где  имеет вид:
имеет вид:

Частичная сумма степенного ряда является многочленом. Поэтому вычисление ее значения сводится к арифметическим операциям над значениями аргументов, числом  и коэффициентами ряда. При
и коэффициентами ряда. При  степенной ряд принимает вид:
степенной ряд принимает вид:

Формула тейлора
Представление функции  в виде суммы ряда вида
в виде суммы ряда вида  называется разложением этой функции в степенной ряд. Для разложения функций в степенные ряды применяется формула Тейлора, которую мы сейчас докажем.
называется разложением этой функции в степенной ряд. Для разложения функций в степенные ряды применяется формула Тейлора, которую мы сейчас докажем.
Теорема 4.1. Пусть функция  имеет на отрезке
имеет на отрезке  производные до
производные до  порядка включительно,
порядка включительно,
где  постоянные числа, причем
постоянные числа, причем  При
При  получаем тригонометрический ряд в форме
получаем тригонометрический ряд в форме

Из общего тригонометрического ряда с помощью замены 
получаем ряд вида (3.4). Отсюда следует, что если  область сходимости ряда (3.4), то ряд (3.3) сходится в области
область сходимости ряда (3.4), то ряд (3.3) сходится в области

Формула тейлора
Представление функции  в виде суммы ряда вида
в виде суммы ряда вида  называется разложением этой функции в степенной ряд. Для разложения функций в степенные ряды применяется формула Тейлора, которую мы сейчас докажем.
называется разложением этой функции в степенной ряд. Для разложения функций в степенные ряды применяется формула Тейлора, которую мы сейчас докажем.
Теорема 4.1. Пусть функция  имеет на отрезке
имеет на отрезке  производные до
производные до  порядка вклюнительно,
порядка вклюнительно,
причем  непрерывна на этом отрезке. Тогда для любого
непрерывна на этом отрезке. Тогда для любого  из этого отрезка выполняется равенство
из этого отрезка выполняется равенство

где

Равенство (4.1) называют формулой Тейлора,  остаточным членом этой формулы, а выражение (4.2) — интегральной формой остаточного члена формулы Тейлора. Отметим, что из существования на отрезке
остаточным членом этой формулы, а выражение (4.2) — интегральной формой остаточного члена формулы Тейлора. Отметим, что из существования на отрезке  производных функции
производных функции  до
до  порядка включительно вытекает непрерывность функций
порядка включительно вытекает непрерывность функций  на этом отрезке.
на этом отрезке.
Доказательство. Из формулы Ньютона — Лейбница следует, что  и потому
и потому

Поскольку переменной интегрирования является  мы считаем значение
мы считаем значение  постоянным. Но тогда
постоянным. Но тогда  Интегрируя по частям в формуле (4.3) и полагая
Интегрируя по частям в формуле (4.3) и полагая  получаем:
получаем:

Но при  выражение
выражение  обращается в нуль, и потому
обращается в нуль, и потому

Но при  выражение
выражение  обращается в нуль, и потому
обращается в нуль, и потому

Полученное выражение совпадает с (4.1), (4.2) при  Предположим теперь, что равенства (4.1), (4.2) доказаны при
Предположим теперь, что равенства (4.1), (4.2) доказаны при  т. е. что доказано соотношение
т. е. что доказано соотношение

Предполагая существование и непрерывность  положим
положим
 Так как
Так как


то получаем

Это и значит, что равенства (4.1), (4.2) верны при  Поскольку равенства (4.1), (4.2) верны при
Поскольку равенства (4.1), (4.2) верны при  и из их справедливости при
и из их справедливости при  следует, что они верны при
следует, что они верны при  то они верны для всех
то они верны для всех  Формулы (4.1), (4.2) доказаны.
Формулы (4.1), (4.2) доказаны.
Пример 4.1.
Применим к функции 
 формулу Тейлора при
формулу Тейлора при  и
и  и вычислим
и вычислим  с точностью до
с точностью до 
Решение:
Вычислим производные функции 

 при
при 
В точке  имеем:
имеем:

При  получим:
получим:

При 

При  получаем разложение функции
получаем разложение функции  по степеням
по степеням  поскольку
поскольку  тождественно обращается в нуль:
тождественно обращается в нуль:

Легко непосредственно проверить, что

Последнее слагаемое в разложении  при
при  равно
равно  Предыдущее слагаемое при
Предыдущее слагаемое при  равно
равно  Для вычисления с точностью
Для вычисления с точностью  в можно отбросить лишь последнее слагаемое. Имеем:
в можно отбросить лишь последнее слагаемое. Имеем:

с точностью до  В данном примере мы фактически знаем больше: истинное значение
В данном примере мы фактически знаем больше: истинное значение  превышает найденное на
превышает найденное на  (на ‘величину отброшенного члена).
(на ‘величину отброшенного члена).
Замечание. Использование формулы Тейлора для многочлена  степени при
степени при  дает разложение многочлена по степеням
дает разложение многочлена по степеням  так как
так как  в силу того, что
в силу того, что 
Пример 4.2.
Напишем формулу Тейлора при  и выражение остаточного члена для
и выражение остаточного члена для  при
при 
Дадим оценку  на отрезке
на отрезке 
Решение:
Имеем:

Отсюда:
 Искомая формула имеет вид:
Искомая формула имеет вид:

или

где
 Подынтегральная функция положительна и, кроме того,
Подынтегральная функция положительна и, кроме того,  ( так как
( так как  Следовательно,
Следовательно,
 Таким образом, вычисление функции
Таким образом, вычисление функции  на отрезке
на отрезке  по приближенной формуле
по приближенной формуле 
дает ее значение с избытком и ошибка не превышает величины 


Ряды и методы их решения
Пусть дана числовая последовательности  Выражение вида
Выражение вида

или, что то же самое, вида

Называют числовым рядом (или просто рядом). Числа 
 называются членами ряда,
называются членами ряда,  – первый член,
– первый член,  – второй член,
– второй член,  -нный или общий член ряда. Например, взяв
-нный или общий член ряда. Например, взяв

получим соответственно ряды:

С каждым рядом вида  будем связывать (ставить в соответствие) суммы
будем связывать (ставить в соответствие) суммы

которые называются частичными суммами этого ряда. Частичные суммы ряда образуют некоторую числовую последовательность его частичных сумм  Ряд
Ряд  сходится, если сходится последовательность его частичных сумм
сходится, если сходится последовательность его частичных сумм  то есть если существует ограниченная граница
то есть если существует ограниченная граница  Число
Число  при этом называют суммой ряда
при этом называют суммой ряда  и записывают
и записывают 
 или
или  При этом считают так же, что ряд
При этом считают так же, что ряд  сходится к числу
сходится к числу  . Если же последовательность частичных сумм
. Если же последовательность частичных сумм  ряда
ряда  расходится, то ряд
расходится, то ряд  называется расходящимся. В этом случае интеграл не имеет суммы
называется расходящимся. В этом случае интеграл не имеет суммы
Исследуем на сходимость ряды  Поскольку
Поскольку

то  – нную частичную сумму ряда
– нную частичную сумму ряда  можно преподнести в виде
можно преподнести в виде

Отсюда получилось, что ряд  сходится и имеет сумму, которая равна
сходится и имеет сумму, которая равна

Частичную сумму  ряда
ряда  запишем в виде
запишем в виде

Эта последовательность  – расходится, следует, расходится и ряд
– расходится, следует, расходится и ряд 
Частичная сумма  ряда
ряда  что равен
что равен

направляется к  при
при  Следует, и ряд
Следует, и ряд  расходится.
расходится.
Рассмотрим ряд, что сложен из элементов геометрической прогрессии. Такой ряд называют геометрическим рядом:

Число  – знаменатель геометрической прогрессии. Покажем, что геометрический ряд сходится тогда и только тогда, когда знаменатель прогрессии по модулю меньше от единиц. Обозначить через
– знаменатель геометрической прогрессии. Покажем, что геометрический ряд сходится тогда и только тогда, когда знаменатель прогрессии по модулю меньше от единиц. Обозначить через 
 – ую частичную сумму ряда
– ую частичную сумму ряда  получим:
получим:

отсюда

Если  то
то  Таким образом, если
Таким образом, если  то геометрическая прогрессия
то геометрическая прогрессия  сходится и ее сумма равна
сходится и ее сумма равна 
Если  то
то

Если  то
то

Если  то
то

и следует, последовательность  – расходится.
– расходится.
Таким образом, в трех других случаях геометрическая прогрессия расходится.
Ряд вида

называются гармоническим рядом. Доказано, что гармоничный ряд расходится.
Числовой ряд вида

называются обобщенным гармоническим рядом. Доказано, что при  обобщенный гармонический ряд расходится. а при
обобщенный гармонический ряд расходится. а при  этот ряд сходится. При
этот ряд сходится. При  получим гармонический ряд
получим гармонический ряд 
Необходимый признак схождения ряда. Если ряд  сходиться, то его
сходиться, то его  – нный член
– нный член  – направляется к нулю при
– направляется к нулю при 

Если  – нный член не направляется к нулю при
– нный член не направляется к нулю при  то ряд расходится.
то ряд расходится.
Например, ряд

– расходится, так как

Отметим, что рассмотренный признак является только необходимой, или не является достаточно, то есть из того, что  – нный член ряда направляется к нулю, не следует, что ряд сходится, ряд может и расходится.
– нный член ряда направляется к нулю, не следует, что ряд сходится, ряд может и расходится.
Например, гармонический ряд

расходится, не смотря на то, что

Решение примеров:
Пример 8.1
По заданному общему члену  записать ряд и найти его сумму.
записать ряд и найти его сумму.
Решение. Придавая  после значений
после значений  получим:
получим:

Для нахождения суммы ряда необходимо найти границу при 
 -нной частичной суммы заданного ряда:
-нной частичной суммы заданного ряда:

Для того, чтобы придать  более удобный вид, воспользуемся тождеством:
более удобный вид, воспользуемся тождеством:

Придавая последовательно  получим:
получим:

следует,

Очевидно, что в этой сумме слагаемые взаимно уничтожаются, кроме первого и последнего, получим:

Откуда 
То есть ряд сходится и его сумма равна 1.
Пример 8.2
Найти сумма ряда

Решение. Общий множитель  для каждого члена вынесем за скобки
для каждого члена вынесем за скобки

В скобках получили ряд, что представляет собой бесконечно спадающую геометрическую прогрессию, знаменатель которой  Сумма членов бесконечно спадающей геометрической прогрессии
Сумма членов бесконечно спадающей геометрической прогрессии

Следует сумма заданного ряда

Пример 8.3
Проверить, выполняется ли необходимое условие сходимости ряда 
Решение. Общий член заданного ряда –  Найдем границу общего члена
Найдем границу общего члена  при бесконечном возрастании его параметра
при бесконечном возрастании его параметра 

Для заданного ряда необходимо условие сходимости выполняется, вследствие чего ряд может сходиться или расходится. Это можно установить только после дополнительных исследований.
Пример 8.4
Проверить, выполняется ли необходимое условие сходимости ряда 
Решение. Общий член ряда – 
Найдем границу общего члена  при бесконечном возрастании его параметра
при бесконечном возрастании его параметра 

Необходимый признак сходимости заданного ряда не выполняется. Через это заданный ряд расходится.
Признаки схождения рядов с положительными членами
Ряд

называется положительным, если все его члены неотрицательные, то есть 

Признаки сравнения
Пусть имеет для ряда с положительными членами:

Для них справедливы следующие утверждения:
1. Если члены ряда  не больше соответственных членов ряда
не больше соответственных членов ряда  то есть
то есть  и ряд
и ряд  – сходится, то сходится и ряд
– сходится, то сходится и ряд  .
.
Пример 8.8.
Исследовать на схождение ряд 
Решение. Сравним заданный ряд

с рядом геометрической прогрессии, знаменатель которой 

Каждый член заданного ряда меньше соответственного члена ряда геометрической прогрессии, который сходится, потому, что 

Следует, заданный ряд сходится.
2. Если члены ряда  не меньше соответственных членов ряда
не меньше соответственных членов ряда  то есть
то есть  ряд
ряд  расходиться, то и ряд
расходиться, то и ряд  расходится.
расходится.
Пример 8.8
Исследовать на сходимость ряд 
Решение. Ряд

расходится, так как его члены, начиная со второго, больше соответственных членов гармонического ряда

который, как известно расходится.
3. Пусть  и
и  и пусть существует граница
и пусть существует граница

Если ряд  сходится при
сходится при  то и ряд
то и ряд  сходится. Если ряд
сходится. Если ряд  расходится при
расходится при  то и ряд
то и ряд  расходится.
расходится.
Пример 8.9
Исследовать на сходимость ряд 
Решение. Начиная с
 и
и 
найдем границу:

Поскольку ряд  будучи гармоническим рядом, расходится, то расходится и заданный ряд
будучи гармоническим рядом, расходится, то расходится и заданный ряд 
8.2.2 Признак Даламбера (теорема)
Если для ряда с положительными членами

соотношение  члена к
члена к  – нного имеют ограниченную границу
– нного имеют ограниченную границу  при
при  то есть
то есть

то: 1) ряд сходится, если 
2) ряд расходится, если 
(В случае  ответ на вопрос про схождение или расхождение ряда теорема не дает. Нужно использовать другой признак.)
ответ на вопрос про схождение или расхождение ряда теорема не дает. Нужно использовать другой признак.)
Пример 8.10
Исследовать на схождение числовой ряд 
Решение. Получим ряд

Тут 

Таким образом,  следует, заданный ряд сходится.
следует, заданный ряд сходится.
Пример 8.11
Исследовать на схождение числовой ряд 
Решение. Получим ряд

тут 


Таким образом,  и следует, заданный ряд сходятся
и следует, заданный ряд сходятся
Радикальный признак Коши (теорема)
Если для ряда с положительными членами

величина  имеет ограниченную границу
имеет ограниченную границу  при
при  то есть
то есть  то:
то:
то: 1) ряд сходится, если 
2) ряд расходится, если 
Пример 8.12
Исследовать на схождение ряд

Решение. Используем признак Коши:

Ряд сходиться.
Интегральный признак Коши схождение ряда
Пусть члены ряда

положительные и не возрастают, то есть

и пусть  – такая непрерывная не возрастающая функция, что
– такая непрерывная не возрастающая функция, что

Тогда справедливы следующие утверждение:
1) если несобственный интеграл  сходится, то сходится и ряд
сходится, то сходится и ряд 
2) если несобственный интеграл расходиться, то расходится и ряд 
Пример 8.13
Исследовать на схождение ряд 
Решение. Получим, что  Находим несобственный интеграл
Находим несобственный интеграл

Несобственный интеграл равен  (сходится), следует, сходиться и заданный ряд.
(сходится), следует, сходиться и заданный ряд.
Решение примеров:
Пример 8.14.
Воспользовавшись признаком сравнения исследовать на схождение следующие ряды:

Решение.
а) Имеем ряд  его общий член
его общий член 
Для сравнения возьмем гармонический ряд, который является расходящимся, и общий член которого  как так
как так 
Следует, заданный ряд расходится.
б) Задан ряд  его общий член
его общий член  Для сравнения выберем геометрический ряд
Для сравнения выберем геометрический ряд  который будет сходящимся. Общий член последнего ряда
который будет сходящимся. Общий член последнего ряда  Получим
Получим  так как
так как  Следует, заданный ряд сходится.
Следует, заданный ряд сходится.
в) Задан ряд  его общий член
его общий член  Используем граничную форму признака сравнения
Используем граничную форму признака сравнения

так как гармонический ряд  расходится, то и заданный ряд расходится.
расходится, то и заданный ряд расходится.
Пример 8.15.
Воспользовавшись признаком Даламбера, исследовать на схождение ряда:

Решение.
а) задан ряд  Тут
Тут  Найдем
Найдем 

Следует, ряд сходится.
б) Задан ряд  Найдем,
Найдем,

так, как  и через это ряд расходится.
и через это ряд расходится.
Пример 8.16.
Воспользовавшись признаком схождение рядов признака Коши:

Решение.
а) Для исследования заданного ряда  используем радикальный признак Коши
используем радикальный признак Коши

следует, ряд сходится.
б) Для исследования заданного ряда  используем радикальный признак Коши. Получим
используем радикальный признак Коши. Получим  Находим несобственный интеграл
Находим несобственный интеграл

несобственный интеграл расходится. Следует, расходится и заданный ряд.
Знакопеременные ряды
До этого мы изучали ряды, все члены которых были положительными. Теперь мы перейдем к рассмотрении рядов, которые содержат как положительные, так и отрицательные члены. Такие ряды называют знакопеременными. Приведем пример знакопеременного ряда:

Изучение знакопеременных рядов мы начнем с отдельного случая так называемых знакопеременных рядов, то есть рядов, в которых каждому положительному члену следует отрицательный, а отрицательному – положительный. Обозначить через абсолютные величины членов ряда и предположим, что первый член положительный, запишем знакопеременный ряд следующим образом:

Для знакопеременных рядов имеет место достаточный признак сходимости Лейбница.
Признак Лейбница. Если в знакопеременном ряду  абсолютные величины членов совпадают, то есть
абсолютные величины членов совпадают, то есть

и общий член направляется к нулю, то есть  то ряд сходиться, причем его сумма положительна и не превышает первого члена ряда.
то ряд сходиться, причем его сумма положительна и не превышает первого члена ряда.
Пример:
Исследовать на сходимость ряд

Решение. Этот ряд удовлетворяет условию признака Лейбница:


Следует, ряд сходится.
Перейдем теперь к рассмотрению общего вида знакопеременного ряду. Предположим, что в ряду

числа  может быть как положительными, как и отрицательными.
может быть как положительными, как и отрицательными.
Достаточный признак сходимости знакопеременного ряда. Если знакопеременный ряд такой, что ряд, сложенный из абсолютных величин его членов сходится, то и знакопеременный ряд также сходится. Исследование вопроса про сходимость знакопеременного ряда приводится ряда приводится в этом случае к исследованию ряда с положительными членами.
Пример:
Исследовать на схождение ряд

где  – любое число
– любое число
Решение. Наряду с данным рядом, рассмотрим ряды

и

Ряд  – сходится. Члены ряда
– сходится. Члены ряда  не более соответственных членов ряда
не более соответственных членов ряда  , следует ряд
, следует ряд  также сходится. Но тогда, в силу рассмотренного признака, данный знакопеременный ряд сходится.
также сходится. Но тогда, в силу рассмотренного признака, данный знакопеременный ряд сходится.
Подчеркнем, что признак схождения, которая рассмотрена выше, является только достаточным признаком схождения знакопеременного ряда, но не необходимым; существуют такие знакопеременные ряды, которые сами сходятся, но ряды, что сложены из абсолютных величин их членов, расходится. В связи с этим полезно ввести понятие про абсолютную и мнимую сходимость знакопеременного ряда и на основе этих понятий классифицировать знакопеременные ряды.
Знакопеременный ряд

называется абсолютно сходящимися, если сходится ряд, сложенный из абсолютных его членов:

Если же знакопеременный ряд  – сходится, а ряд
– сходится, а ряд  сложенный из абсолютных величин его членов, расходится, то данный знакопеременный ряд
сложенный из абсолютных величин его членов, расходится, то данный знакопеременный ряд  называется мнимой или не абсолютно сходящейся.
называется мнимой или не абсолютно сходящейся.
Примеры. Выяснить, какие из указанных рядов сходятся абсолютно, какие не абсолютно, какие расходятся.

Найдем 

Данный ряд сходится. Выясним как? Напишем ряд, сложенный из абсолютных величин данного ряда

Получили знакоположительный ряд. Используем признак Даламбера.


Следует, ряд  сходится абсолютно
сходится абсолютно

найдем 

Данный ряд сходится. Выясним как? Запишем ряд, сложенный из абсолютных величин членов данного ряда

Полученный ряд расходится. Следует, заданный ряд сходится условно.
Решение примеров:
Пример 8.20
Использовать. какие из заданных рядов сходятся абсолютно, какие условно, а какие расходятся.

Решение.
а) члены заданного знакопеременного ряда  спадают к абсолютному значению, направляясь к нулю:
спадают к абсолютному значению, направляясь к нулю:

и

Через это, согласно признаку Лейбница заданный ряд. Чтобы установить. сходиться он абсолютно или не абсолютно, исследуем ряд с положительными членами  сложенный из абсолютных значений членов данного ряда. Используем интегральный признак.
сложенный из абсолютных значений членов данного ряда. Используем интегральный признак.

Получили, что ряд с положительными членами, расходится. Следует, заданный ряд сходится не абсолютно.
б) Заданный ряд

удовлетворяет условием признака Лейбница, так как его члены спадают по абсолютному значению

и

Через это заданный ряд сходится. Выясним, как сходится. Исследуем ряд с положительными членами  что сложенный из абсолютных значений членов заданного ряда. Выясним интегральный признак
что сложенный из абсолютных значений членов заданного ряда. Выясним интегральный признак

Ряд с положительными членами сходится. Следует, заданный ряд сходиться абсолютно
в) члены заданного ряда

спадают по абсолютному значению

но

не удовлетворяет условию признака Лейбница. Следует, заданный ряд расходится.
Степенные ряды
Степенным рядом называют ряд вида

или

где  – действительные числа, которые называют коэффициентами степенного ряда,
– действительные числа, которые называют коэффициентами степенного ряда,  – некоторое постоянное число.
– некоторое постоянное число.
Теорема Абеля. Если ряд  сходиться при
сходиться при  то он сходится абсолютно для всех
то он сходится абсолютно для всех  что удовлетворяют неравенство
что удовлетворяют неравенство 
 Если ряд
Если ряд  расходится при
расходится при  то он расходится для всех
то он расходится для всех  что удовлетворяют неравенству
что удовлетворяют неравенству 
Область схождения степенного ряда. Теорема Абеля утверждает, что есть степенной ряд  сходится при
сходится при  то он сходится абсолютно при некотором
то он сходится абсолютно при некотором  из интервала
из интервала  Если же ряд расходится при
Если же ряд расходится при  то он расходится во всех точках, которые размещены за интегралом
то он расходится во всех точках, которые размещены за интегралом 
Радиусом схождения степенного ряда  называется неотрицательное число
называется неотрицательное число  такое, что при
такое, что при  ряд сходится, а при
ряд сходится, а при  расходиться. Интервалом сходимости ряда называется интервал
расходиться. Интервалом сходимости ряда называется интервал 
Найдем радиус схождения степенного ряда  через его коэффициенты. Для этого используем признаки Даламбера или признак Коши.
через его коэффициенты. Для этого используем признаки Даламбера или признак Коши.
Рассмотрим для каждого фиксированного  числовой ряд
числовой ряд  и предположим, что существует ограниченная граница
и предположим, что существует ограниченная граница

Тогда

Отсюда по признаку Даламбера ряд  сходится при
сходится при  и расходится при
и расходится при  Следует. если
Следует. если  то ряд
то ряд  сходится, а если
сходится, а если  то расходится. Таким образом радиус схождения степенного ряда определяется формулой
то расходится. Таким образом радиус схождения степенного ряда определяется формулой

Если к ряду используется признак Коши, то, рассуждая аналогично, получим следующую формулу

Формулами  и
и  выражается и радиус схождения ряда
выражается и радиус схождения ряда  . Интервалом схождения этого ряда –
. Интервалом схождения этого ряда – 
Таким образом, любой степенной ряд имеет радиус сходимости  и интервал сходимости
и интервал сходимости  При
При  ряд может или сходится или расходится. Этот вопрос решается для каждого конкретного ряда индивидуально. Следует, областью схождения степенного ряда
ряд может или сходится или расходится. Этот вопрос решается для каждого конкретного ряда индивидуально. Следует, областью схождения степенного ряда  является его интеграл схождения с возможным присоединением к него одной или двух точек в зависимости от того, как ведет себя ряд на концах интервала, то есть при
является его интеграл схождения с возможным присоединением к него одной или двух точек в зависимости от того, как ведет себя ряд на концах интервала, то есть при 
Решение примеров:
Пример 8.22
Найти область схождения ряда

Решение. По формуле  найдем радиус схождения
найдем радиус схождения

Следует. интегралом схождения ряда будет  Рассмотрим схождение ряда на концах интервала схождения. При
Рассмотрим схождение ряда на концах интервала схождения. При  получим ряд
получим ряд  Этот знакочередующий ряд с признаком Лейбница сходится не абсолютно. При
Этот знакочередующий ряд с признаком Лейбница сходится не абсолютно. При  получим ряд
получим ряд

который расходится. Следует, областью сходимости ряда является промежуток 
Пример 8.23.
Найти радиус и область сходимости ряда

Решение. Получим

В силу определения Даламбера заданный степенной ряд будет сходится для тех значений, для которых

то есть  Следует, радиус схождения
Следует, радиус схождения  а интервал схождения
а интервал схождения 
Теперь выясним поведение ряда на концах интервала сходимости. В левом конце, при  заданный степенной ряд преобразуется в числовой ряд
заданный степенной ряд преобразуется в числовой ряд

который сходится по признаку Лейбница. В правом конце, при  получим ряд
получим ряд

который сходиться.
Таким образом, заданный степенной ряд сходится на отрезке 
Пример 8.24
Найти область схождения степенного ряда 
Решение. Получим

Найдем

Откуда

Исследуем границы интервала. При  получим числовой знакопеременный ряд с общим членом
получим числовой знакопеременный ряд с общим членом  который сходится согласно признака Лейбница. При
который сходится согласно признака Лейбница. При  получим ряд с положительными членами
получим ряд с положительными членами  Исследуя его по интегральному признаку
Исследуя его по интегральному признаку

выясним, что он сходится. Следует, область сходимости заданного ряда является отрезок 
Разложение функции в ряды Тейлора и Маклорена
Рядом Тейлора для функции  при условии. что она определена около точки
при условии. что она определена около точки  и в этой точке имеет ограниченные производные любого порядка, называется степенной ряд вида:
и в этой точке имеет ограниченные производные любого порядка, называется степенной ряд вида:

Функция  будет суммой этого ряда только для тех значений
будет суммой этого ряда только для тех значений  при которых остаточный член
при которых остаточный член  где
где  формулы Тейлора
формулы Тейлора

имеют свою границу ноль, когда  то есть
то есть 
Коротко: необходимым и достаточным условием существования равенства

для значений  из некоторого промежутка является условие
из некоторого промежутка является условие  для всех
для всех  из этого промежутка. Формула
из этого промежутка. Формула  что верна при указанном условии, дает расклад в ряд Тейлора для рассмотренного
что верна при указанном условии, дает расклад в ряд Тейлора для рассмотренного  , если:
, если:
а)она имеет производные любого порядка,
б)граница остаточного члена при  равно нулю, то есть
равно нулю, то есть 
Для разложения заданной функции в ряд Тейлора необходимо:
1) записать ряд Тейлора для заданной функции,то есть вычислить значение этой функции и ее производные при  и подставить их в общее выражение ряда Тейлора
и подставить их в общее выражение ряда Тейлора  для заданной функции.
для заданной функции.
2) исследовать остаточный член  формулы Тейлора для заданной функции и обозначить совокупность значений
формулы Тейлора для заданной функции и обозначить совокупность значений  при которых полученный ряд сходится к заданной функции (то есть при которых
при которых полученный ряд сходится к заданной функции (то есть при которых  )
)
Для многих функций. которые используются в практических применениях математического анализа, интервал схождения ряда Тейлора совпадает с совокупностью тех значений  при которых соответственный остаточный член
при которых соответственный остаточный член  когда
когда  то есть для многих функций каждая точка
то есть для многих функций каждая точка  сходимости ряда Тейлора является и точкой схождения того ряда, который сложен для заданной функции. Через это при разложении многих функций в ряд Тейлора можно вместо исследования соответственного остаточного члена
сходимости ряда Тейлора является и точкой схождения того ряда, который сложен для заданной функции. Через это при разложении многих функций в ряд Тейлора можно вместо исследования соответственного остаточного члена  где в многих случаях сложно, исследовать сходимость самого ряда Тейлора, как случайного степенного ряда.
где в многих случаях сложно, исследовать сходимость самого ряда Тейлора, как случайного степенного ряда.
Разложение функции в ряд Маклорена
Если в ряде Тейлора  принять
принять  то получим ряд Маклорена:
то получим ряд Маклорена:

Рассмотрим разложение в степенной ряд (ряд Маклорена) некоторых элементарных функций.

Получим:

По формуле  сложим ряд Маклорена
сложим ряд Маклорена

найдем радиус схождения полученного ряда

следует, полученный ряд абсолютно сходится на всей числовой прямой. Он сходиться к функции  при любом
при любом  так как на любом отрезку функция
так как на любом отрезку функция  и ее производные ограничены одним и тем же числом, например
и ее производные ограничены одним и тем же числом, например 
Таким образом, при любом  имеет место разложение
имеет место разложение


Получим


По формуле  для функции
для функции  сложен ряд Маклорена:
сложен ряд Маклорена:

Легко показать, что ряд сходится абсолютно на всей числовой прямой, то есть  Так как
Так как  то полученный числовой ряд сходится к функции
то полученный числовой ряд сходится к функции  Следует, для любого
Следует, для любого  справедливо разложение:
справедливо разложение:


Аналогично, можно получит разложение функции  в ряд Маклорена, который справедливый при любом
в ряд Маклорена, который справедливый при любом 

Укажем разложение в ряд Маклорена и других функций, которые используются чаще.


Два степенных ряда можно по очереди складывать и умножать (по правилу умножения многочленов). При этом интервале схождении полученного нового степенного ряда будет совокупность всех точек, в которых одновременно сходятся оба ряда. Степенной ряд в интервале его схождения можно почленно интегрировать, а в середине интервала сходимости можно почленно дифференцировать.
Решение примеров:
Пример 8.26.
Разложить в ряд Тейлора  при
при 
Решение. Вычислим значение заданной функции и ее производных при 

Подставим эти значения в ряд Тейлора  для заданной функции, получим:
для заданной функции, получим:

Исследуем схождение полученного ряда с признаком Даламбера:

 если
если 
Решив это неравенство  находим интервал
находим интервал  Исследуем границы этого интервалу. Подставляя в ряд
Исследуем границы этого интервалу. Подставляя в ряд  а потом,
а потом,  получим числовые ряды
получим числовые ряды  и
и  которые расходятся, так как в них не выполняется необходимое условие сходимости ряда. Следует, интервал схождения полученного ряда Тейлора для заданной функции будет
которые расходятся, так как в них не выполняется необходимое условие сходимости ряда. Следует, интервал схождения полученного ряда Тейлора для заданной функции будет  Исследую остаточный член
Исследую остаточный член  формулы Тейлора для заданной функции, убедимся, что в указанном интервале полученный ряд сходится к заданной функции.
формулы Тейлора для заданной функции, убедимся, что в указанном интервале полученный ряд сходится к заданной функции.
Пример 8.27.
Разложить в ряд функцию 
Решение. Так как по 

то заменив  на
на  получим:
получим:

и наконец,

область схождения ряда 
Пример 8.28.
Разложить в ряд функцию 
Решение. В разложении

то заменив  на
на  получим:
получим:

Теперь

Область схождения ряда 
Пример 8.29.
Разложить в ряд Маклорена функцию 
Решение. Известно, что  Разложение функции
Разложение функции  ряд Маклорена можно получить, заменив в формуле
ряд Маклорена можно получить, заменив в формуле  на
на 

Получим, что

откуда:

область схождения полученного ряда 
Использование рядов к приближенным вычислениям
Степенные ряды имеют разное использование. С их помощью вычисляют с заданной степенью точности значения функции, обозначены интегралы, которые не выражаются через элементарные функции или не слишком удобные для вычислений, интегрируются дифференциальные уравнения. Для вычисления приближенных значений функции с заданной точностью удобно воспользоваться рядами в том случае, если соответственный ряд является знакопеременным. Для знакопеременного сходящегося ряда легко оценить погрешность приблизительногозначения суммы – она не превышает абсолютного значения первого из откинутых членов (признак Лейбница). В других случаях приближенное значение функции с заданной точностью вычисляется по формуле Тейлора (Маклорена).
Решение примеров:
Пример 8.37.
Вычислить  с точностью до 0,001.
с точностью до 0,001.
Решение. Используем ряд

Следует, в этом ряду необходимо взять  Получим знакопеременный ряд:
Получим знакопеременный ряд:

Если для вычисления взять  первых членов, то учитывая, что ряд знакопеременный, погрешность от откидывания прочие члены будут меньше абсолютной величины первого откинутого члена, то есть
первых членов, то учитывая, что ряд знакопеременный, погрешность от откидывания прочие члены будут меньше абсолютной величины первого откинутого члена, то есть  По условию должно быть получено число с точностью к 0,001, то есть общая погрешность от откидывания членов и округление должно быть меньше 0,0005. Если сохранить первые четыре члена, то погрешность от откидывания всех членов на основе признака Лейбница
По условию должно быть получено число с точностью к 0,001, то есть общая погрешность от откидывания членов и округление должно быть меньше 0,0005. Если сохранить первые четыре члена, то погрешность от откидывания всех членов на основе признака Лейбница  через это:
через это:

Вычислить с округлением нужно только остаточное дополнение. Если сохранить четыре десятичных знака, то погрешность округляется не больше 0,0005. Наивысшая граница общей погрешности равен 0,00021. Следует.

Пример 8.38.
Найти приблизительное значение  с точностью к 0,0001.
с точностью к 0,0001.
Решение. Переведем градусную меру в радиану 
Воспользуемся разложением  в степенной ряд
в степенной ряд

получим

этот ряд является рядом Лейбница, через это, приравняв к приблизительное значения  сумму первых двух членов разложения, выполним погрешность
сумму первых двух членов разложения, выполним погрешность  по абсолютной величиной меньше третьего члена
по абсолютной величиной меньше третьего члена

Таким образом,

С точность к 0,0001, с недостачей, так как третий член разложения положительный. Вычисляя сумму первых двух членов с точностью до  с остатком (для того, чтобы вычислить второй член с той же точностью с недостачей), получим абсолютную погрешность, то есть полную погрешность, меньшую 0,0001, соответственно с заданием ( такое как обе погрешности были меньше
с остатком (для того, чтобы вычислить второй член с той же точностью с недостачей), получим абсолютную погрешность, то есть полную погрешность, меньшую 0,0001, соответственно с заданием ( такое как обе погрешности были меньше  и имеют разные знаки). Следует,
и имеют разные знаки). Следует, 
Пример 8.39
Вычислить  с точностью до 0,001.
с точностью до 0,001.
Решение. Преобразуем заданный корень

Для вычисления  используем биномиальный ряд
используем биномиальный ряд

подставляя 

Чтобы обозначить, сколько необходимо взять первые члены этого знакопеременного ряда для вычисления  с точностью до 0,0001, вычислим несколько последовательных первых членов ряда:
с точностью до 0,0001, вычислим несколько последовательных первых членов ряда: 
 Согласно свойствам знакопеременного ряда, если ограничится суммой трех первых членов ряда, то погрешность искомого приблизительного значения корня будет меньшей
Согласно свойствам знакопеременного ряда, если ограничится суммой трех первых членов ряда, то погрешность искомого приблизительного значения корня будет меньшей  Следует,
Следует,

Пример 8.40
Вычислить интеграл  с точностью до 0,0001.
с точностью до 0,0001.
Решение. Неопределенный интеграл  не выражается через элементарные функции, через это при вычислении данного определенного интеграла формулу Ньютона – Лейбница использовать нельзя. Вычислим интеграл приблизительно. Разделим почленно ряд
не выражается через элементарные функции, через это при вычислении данного определенного интеграла формулу Ньютона – Лейбница использовать нельзя. Вычислим интеграл приблизительно. Разделим почленно ряд

на  получим:
получим:

Интегрируем этот ряд почленно:

так как

то по признаку Лейбница, чтобы исполнить заданную точность, нужно взять сумму первых двух членов:

Ряды Фурье
Разложение в ряды Фурье функции с периодом  :
:
Пусть  – функция с периодом
– функция с периодом  , что интегрируется на
, что интегрируется на 
Ряд вида:

называется тригонометрическом рядом функции  Числа
Числа 
 называется коэффициентом тригонометрического ряда. Этот ряд в укороченном виде может быть записан так:
называется коэффициентом тригонометрического ряда. Этот ряд в укороченном виде может быть записан так:

Тригонометрический ряд называется также рядом Фурье, коэффициенты которого обозначаются по формулам:

При этом пишут так:

Ряд Фурье функции  не всегда своей суммой имеет
не всегда своей суммой имеет  , если даже сходится. Простейшим достаточным признаком разложения функции в ряд Фурье будет:
, если даже сходится. Простейшим достаточным признаком разложения функции в ряд Фурье будет:
1) Если функция  с периодом
с периодом  имеет на отрезке
имеет на отрезке  оконченное число точек разрыва первого рода и абсолютно интегрирована на этом отрезке, то эта функция раскладывается в свой ряд Фурье в каждой точке, в которой она дифференцирована.
оконченное число точек разрыва первого рода и абсолютно интегрирована на этом отрезке, то эта функция раскладывается в свой ряд Фурье в каждой точке, в которой она дифференцирована.
2. Если функция с периодом  удовлетворяет условиям Дирихле на отрезке
удовлетворяет условиям Дирихле на отрезке  (если отрезок может быть разбит на оконченное число частей так, что в середине каждой части функция монотонна и ограничена), то эта функция раскладывается в свой ряд Фурье в каждой точке непрерывности, если же
(если отрезок может быть разбит на оконченное число частей так, что в середине каждой части функция монотонна и ограничена), то эта функция раскладывается в свой ряд Фурье в каждой точке непрерывности, если же  – точка разрыва, ряд Фурье сходится к числу:
– точка разрыва, ряд Фурье сходится к числу:

Ряд Фурье парной функции, то есть  не содержит членов с синусами; этот ряд имеет вид:
не содержит членов с синусами; этот ряд имеет вид:

где 

Ряд Фурье нечетной функции, то есть  не содержит произвольного члена и членов с косинусами; этот ряд имеет вид:
не содержит произвольного члена и членов с косинусами; этот ряд имеет вид:

где 
Решение примеров:
Пример 8.42.
Разложить в ряд Фурье функцию

Решение. Вычислим коэффициенты Фурье функции 

так как  то
то

Функция  удовлетворяет условиям Дирихле, а через это раскладывается в свой ряд Фурье. Следует, в каждой точке непрерывности:
удовлетворяет условиям Дирихле, а через это раскладывается в свой ряд Фурье. Следует, в каждой точке непрерывности:

Пример 8.43.
Разложить в ряд Фурье функцию 
Решение. Заданная функция удовлетворяет условиям Дирихле и через это может быть разложена в ряд Фурье. На интервале  функция
функция  – нечетная (см. рис. 8.1). Отсюда следует, что ряд Фурье этой функции будет содержать только синусы.
– нечетная (см. рис. 8.1). Отсюда следует, что ряд Фурье этой функции будет содержать только синусы.

найдем 


Следует, 
В развернутом виде, придавая  значения
значения  получим:
получим:

В интервале  эта функция имеет место в точках непрерывности функции
эта функция имеет место в точках непрерывности функции  то есть в данном случае во всех внутренних точках интервала
то есть в данном случае во всех внутренних точках интервала  По интервалу этот ряд изображает периодическое продолжение рассмотренной функции.
По интервалу этот ряд изображает периодическое продолжение рассмотренной функции.
В точках разрыва же, какими являются точки  сумма ряда равна среднему арифметическому ее левосторонней и правосторонней границы в этих точках.
сумма ряда равна среднему арифметическому ее левосторонней и правосторонней границы в этих точках.
Найдем эти границы. например, в точке 

Во всех точках разрыва этой функции получим то же самое. Таким образом, в точках разрыва сумма будет равны нулю. Следует, полученное разложение можно записать и так:

где  – любое целое число.
– любое целое число.
Пример 8.44. Разложить в ряд Фурье функцию 
Решение. Эта непрерывная функция с периодом  удовлетворяют условием разложения в ряд Фурье, она четная. Находим:
удовлетворяют условием разложения в ряд Фурье, она четная. Находим:


Следует,

Пример 8.45.
Разложить в ряд Фурье функцию  что задана на интервале
что задана на интервале 
Решение. На рис. 8.2 показан график заданной функции с ее периодическом продолжением. Аналитическое выражение функции совпадает с аналитическим выражением функции в задаче 8.43, но между ними получим существенное отличие. В задаче 8.43 функция  задавалась на интервале
задавалась на интервале  а в этой задаче на интервале
а в этой задаче на интервале  Их отличие можно увидеть из графиков функции. Функция
Их отличие можно увидеть из графиков функции. Функция  на интервале
на интервале  не принадлежит ни к классу четным, и ни к классу нечетных.
не принадлежит ни к классу четным, и ни к классу нечетных.

Если функция  задана не в интервале
задана не в интервале  а в интервале
а в интервале  также длиной
также длиной  то ее можно разложить в ряд Фурье того же вида, что и
то ее можно разложить в ряд Фурье того же вида, что и  но коэффициенты обозначаются формулами:
но коэффициенты обозначаются формулами:


В этом случае получим:

Подставляя полученные значения в формулу  получим:
получим:

Так как на интервале  функция
функция  непрерывна, то полученный ряд сходится к
непрерывна, то полученный ряд сходится к  всем точкам этого интервала. В точках
всем точкам этого интервала. В точках 
 какие являются точками разрыва функции ряд сходится к среднего арифметического левых и правых границ функций, то есть к числу
какие являются точками разрыва функции ряд сходится к среднего арифметического левых и правых границ функций, то есть к числу

Следует, в точках разрыва сумма ряда равна 
Разложение в ряд Фурье функции, что заданы на полупериоде
Функцию, что задана на полупериоде  можно разложить в ряд синусов или в ряд косинусов, продолжая на второй полупериод
можно разложить в ряд синусов или в ряд косинусов, продолжая на второй полупериод  соответственно четным или нечетным образом.
соответственно четным или нечетным образом.
а) Если нужно разложить такую функцию в ряд по косинусам, то из интервала  в соседний интервал
в соседний интервал  необходимо сделать четное продолжение функции, а потом за интервалом
необходимо сделать четное продолжение функции, а потом за интервалом  выполнить ее периодическое продолжение с периодом
выполнить ее периодическое продолжение с периодом 
Ряд будет иметь вид

а коэффициенты обозначаются по формуле:

б) Если же нужно функцию  что задано в интервале
что задано в интервале  разложить в ряд по синусам, то в соседний интервал
разложить в ряд по синусам, то в соседний интервал  нужно выполнить ее нечетное продолжение, а потом периодически продолжить ее с периодом
нужно выполнить ее нечетное продолжение, а потом периодически продолжить ее с периодом 
В этом случае, ряд будет иметь вид:

а коэффициенты  обозначается по формуле:
обозначается по формуле:

Решение примеров:
Пример 8.46
Функцию  разложить в ряд косинусов на интервале
разложить в ряд косинусов на интервале  .
.
Решение. Продолжая эту функцию четным образом, как показано на рис. 8.3 – пунктиром, получим:

Следует.

Разложение в ряд Фурье функции с периодом  :
:
Если период функции  равно не
равно не  а
а  то ее ряд Фурье имеет вид:
то ее ряд Фурье имеет вид:

а коэффициенты этого ряда  вычисляются формулами:
вычисляются формулами:

Если функция  на интервале
на интервале  четная, то все коэффициенты
четная, то все коэффициенты  ее разложение в ряд Фурье содержит только постоянную и косинусы и имеет вид:
ее разложение в ряд Фурье содержит только постоянную и косинусы и имеет вид:

Коэффициенты разложения  равны в этом случае:
равны в этом случае:

Если же на интервале  функция
функция  – нечетная, то
– нечетная, то  ее ряд Фурье содержит только синусы и имеет вид:
ее ряд Фурье содержит только синусы и имеет вид:

а коэффициенты

Решение примеров:
Пример 8.48
Разложить в ряд Фурье функцию

Решение. Воспользовавшись формулами  имея
имея  и разбивая интервал интегрирования
и разбивая интервал интегрирования  точкой
точкой  на две части, так как в каждый из них функцией задано разными формулами, получим:
на две части, так как в каждый из них функцией задано разными формулами, получим:

Если  четное:
четное:  и
и 
Если  нечетное:
нечетное:  и
и 
Если  по формуле
по формуле  получим:
получим:


Искомое разложение заданной функции имеет вид:

Это разложение справедливо на всей области определения данной функции: в интервале  сумма ряда
сумма ряда  а в интервале
а в интервале 
 В точке разрыва
В точке разрыва  где функция не определена
где функция не определена

Пример 8.48
Разложить в ряд Фурье функцию  на интервале
на интервале 
Решение. График функции изображен на рис. 8.5.

Находим коэффициенты Фурье, знач, что 


Кроме того,

Ряд Фурье для функции  имеет вид
имеет вид

Решение и определение рядов
Исследуя природные явления, ученые часто обращали внимание на существование определенных последовательностей и на их свойства. Эти последовательности казались такими привлекательными, что с их помощью пытались описывать законы природы. Одна из самых известных последовательностей образуют числа Фибоначчи, которые применяются сейчас, например, при торговле на рынке Форекс для определения уровня, которого может достичь цена.
Однако интересные свойства имеют не только сами последовательности, но и границы сумм бесконечного количества членов последовательностей. Такие суммы используются для приближенного вычисления значений всех элементарных функций и при составлении таблиц их значений, при вычислении интегралов, которые «не берутся», при решении некоторых типов дифференциальных уравнений и др. Бесконечные суммы, образованные из элементов последовательностей – тема данного раздела.
После изучения данной темы вы сможете:
- ● различать типы рядов;
- ● владеть методами исследования рядов на сходимость;
- ● применять ряды в приближенных вычислениях;
- ● понимать смысл величин, связанных с рядами, в задачах экономики;
- ● знать типы экономических задач, для решения которых целесообразно применять ряды.
Числовой ряд и его сходимость
Пусть задана бесконечная последовательность чисел  или последовательность функций
или последовательность функций 
Рассмотрим сначала числовую последовательность и введем понятие числового ряда. Последовательность функций является предметом рассмотрения в последующих главах.
Числовым рядом называется выражение вида:

Числа  называются членами ряда. Функция
называются членами ряда. Функция  которая дает возможность записать любой член ряда по его номеру n, называется общим членом ряда. Числовой ряд считается заданным, если известна формула его общего члена или любое другое правило, по которому можно найти произвольный член ряда.
которая дает возможность записать любой член ряда по его номеру n, называется общим членом ряда. Числовой ряд считается заданным, если известна формула его общего члена или любое другое правило, по которому можно найти произвольный член ряда.
Например, пусть общий член ряда задается формулой

Представим ряд в виде бесконечной суммы его членов, для чего последовательно подставим в указанную выше формулу для  значение
значение 
В результате получим:

Рассмотрим еще один ряд, общий член которого определяется формулой

Соответствующий ему ряд имеет вид:

Отметим, что в приведенных примерах по указанному общим членом образовывался ряд. Можно ставить в определенном смысле обратную задачу, а именно задачу о нахождении общего члена по нескольким заданным слагаемыми бесконечной суммы. Такая задача решается неоднозначно, поэтому стараются найти формулу общего члена ряда простейшего вида.
Например, чтобы записать формулу общего члена ряда

заданного в виде суммы первых четырех его членов, проанализируем закономерность образования этих чисел при росте номера слагаемого. Так, каждый член ряда имеет вид дроби с единицей в числителе, а знаменатель имеет вид произведения двух нечетных чисел, из которых второе число на шесть единиц больше первого. Поскольку знаки членов ряда чередуются, то общий член ряда можно записать в виде

Сумма первых  членов ряда называется частичной суммой ряда. Так, например,
членов ряда называется частичной суммой ряда. Так, например,  – суммы одного, двух, трех членов ряда, а в общем виде
– суммы одного, двух, трех членов ряда, а в общем виде

Последовательность частичных сумм может иметь конечную или бесконечную границу или не иметь границы вообще.
Числовой ряд называется сходящимся, если последовательность его частичных сумм совпадает, то есть существует конечное граница

при этом число  называется суммой ряда.
называется суммой ряда.
Ряд называется расходящимся, если граница частичных сумм не существует или равен бесконечности.
Если ряд сходится и его сумма равна  то записывают:
то записывают:

Установление факта сходимости или разногласия числового ряда называют исследованием ряда на сходимость.
Проведем исследование на сходимость числового ряда:

Данный ряд является бесконечной суммой членов арифметической прогрессии с первым членом  и разницей
и разницей  По определению (32.2) запишем сумму
По определению (32.2) запишем сумму  первых членов этого ряда:
первых членов этого ряда:

Следовательно, эту частичную сумму можно найти по формуле суммы n первых членов арифметической прогрессии:

тогда

то есть ряд расходится.
Доказать, что ряд сходится и найти его сумму:

Превратим общий член ряда по формуле:

Тогда частичная сумма равна:

Поэтому

есть ряд совпадает, а его сумма равна числу 1.
Исследовать на сходимость ряд

Образовав последовательность частичных сумм этого ряда, получим:

Ясно, что такая последовательность ограничена, но не имеет границы, следовательно, по определению ряд расходится.
Ряд геометрической прогрессии
Рассмотрим бесконечную геометрическую прогрессию. Известно, что общий член геометрической прогрессии описывается формулой  где
где  – первый член геометрической прогрессии, а
– первый член геометрической прогрессии, а  – ее знаменатель. Тогда числовой ряд, образованный из членов геометрической прогрессии, называют рядом геометрической прогрессии:
– ее знаменатель. Тогда числовой ряд, образованный из членов геометрической прогрессии, называют рядом геометрической прогрессии:

Частичная сумма такого ряда вычисляется по формуле

Исследуем предел последовательности частичных сумм 

в зависимости от знаменателя прогрессии 
10. Пусть  Граница частичной суммы ряда при
Граница частичной суммы ряда при  существует:
существует:

поскольку  Следовательно, ряд, построенный из членов бесконечно убывающей геометрической прогрессии, совпадает.
Следовательно, ряд, построенный из членов бесконечно убывающей геометрической прогрессии, совпадает.
20. Пусть  Граница частичной суммы ряда при
Граница частичной суммы ряда при  бесконечна, поскольку
бесконечна, поскольку  то есть
то есть

Следовательно, в этом случае ряд расходится.
30. Пусть  В этом случае частичная сумма ряда является суммой
В этом случае частичная сумма ряда является суммой  равных слагаемых:
равных слагаемых:  Итак,
Итак,  то есть соответствующий ряд расходится.
то есть соответствующий ряд расходится.
40. Пусть  Тогда частичную сумму ряда можно вычислить так:
Тогда частичную сумму ряда можно вычислить так:
 если
если  – четное,
– четное,
 если
если  – нечетное.
– нечетное.
Отсюда следует, что  не существует, а это означает, что соответствующий ряд расходится.
не существует, а это означает, что соответствующий ряд расходится.
Таким образом, мы доказали, что ряд геометрической прогрессии совпадает, если  и расходится, если
и расходится, если 
Гармонический ряд
Числовой ряд, который имеет вид

называется гармоничным рядом.
Исследуем этот ряд на сходимость. Сначала запишем ряд в таком виде:

Теперь создадим по данному ряда другой ряд, заменив слагаемые в скобках наименьшим из них. Получим вспомогательный ряд

Особенность такого ряда заключается в том, что каждая сумма дробей в скобках равна 1 февраля.
Вычислим частичную сумму  вспомогательного ряда, где
вспомогательного ряда, где  – количество слагаемых, выделенные скобками в частичной сумме вспомогательного ряда):
– количество слагаемых, выделенные скобками в частичной сумме вспомогательного ряда):

Если  Поскольку последовательность частичных сумм ограничено, то вспомогательный ряд расходится. Частичная сумма исходного ряда (гармоничного) при
Поскольку последовательность частичных сумм ограничено, то вспомогательный ряд расходится. Частичная сумма исходного ряда (гармоничного) при  больше частичную сумму вспомогательного, поэтому последовательность частичных сумм гармонического ряда также ограничено.
больше частичную сумму вспомогательного, поэтому последовательность частичных сумм гармонического ряда также ограничено.
Следовательно, гармонический ряд (32.7) также расходится.
Свойства сходящихся рядов
Ряд, полученный из ряда (32.1) отвержением первых  его членов, называть
его членов, называть  -м остатком (или просто остатком) числового ряда:
-м остатком (или просто остатком) числового ряда:

Первым членом  -го остатка ряда является член начального ряда, имеет номер
-го остатка ряда является член начального ряда, имеет номер 
Теорема 32.1. Если ряд (32.1) совпадает, то сходится и его остаток, и, наоборот, если совпадает остаток ряда, то совпадает и данный ряд.
Доказательство. Запишем частичную сумму  членов данного ряда:
членов данного ряда:

зафиксируем номер  и перейдем в равенстве (32.9) к пределу при
и перейдем в равенстве (32.9) к пределу при 

Граница левой части равенства существует, потому что по условию теоремы исходный ряд сходится, и равна сумме ряда  В правой части равенства граница первого слагаемого стала
В правой части равенства граница первого слагаемого стала  ибо число
ибо число  – фиксированное, тогда граница второго слагаемого существует и конечна (обозначим ее через
– фиксированное, тогда граница второго слагаемого существует и конечна (обозначим ее через  ), то есть остаток совпадает, а его сумма равна
), то есть остаток совпадает, а его сумма равна  . Таким образом,
. Таким образом,

Докажем обратное утверждение. Пусть остаток ряда совпадает, то есть существует конечное граница  Тогда существует граница правой части равенства, потому что
Тогда существует граница правой части равенства, потому что  стала, значит существует и граница левой части.
стала, значит существует и граница левой части.
С равенства (32.10) следует, что остаток ряда, совпадает, стремится к нулю при 

есть частичные суммы с увеличением номера  приближаются к сумме ряда
приближаются к сумме ряда 
Сходимость или расхождение ряда не нарушается, если исключить из него или добавить к нему конечное число членов.
Теорема 32.2. Если ряд  совпадает и имеет сумму
совпадает и имеет сумму  то совпадает и ряд
то совпадает и ряд  полученный из него умножением каждого члена на постоянное число
полученный из него умножением каждого члена на постоянное число  а сумма образованного ряда равен сумме данного, умноженной на
а сумма образованного ряда равен сумме данного, умноженной на 

Теорема 32.3. Если ряды с общими членами  и
и  совпадают и известные суммы для каждого ряда:
совпадают и известные суммы для каждого ряда:
 и
и 
то для произвольных чисел  и
и  ряд с общим членом
ряд с общим членом  является сходящимся, а его сумма равна
является сходящимся, а его сумма равна

Последние две теоремы легко доказываются на основе свойств границ.
Найдем сумму ряда 
Общий член этого ряда имеет вид:

Рассмотрим вспомогательные ряды с общими членами  и
и  Эти ряды совпадают, поскольку они определяются бесконечно убывающей геометрической прогрессии. Отсюда по теореме 32.3 исследуемый ряд сходится. Для нахождения его суммы сначала находим сумму каждого из вспомогательных рядов. Так, для первого ряда имеем:
Эти ряды совпадают, поскольку они определяются бесконечно убывающей геометрической прогрессии. Отсюда по теореме 32.3 исследуемый ряд сходится. Для нахождения его суммы сначала находим сумму каждого из вспомогательных рядов. Так, для первого ряда имеем:

Для второго ряда получим:
Теперь по формуле (32.12) находим сумму исследуемого ряда:

Необходимый признак сходимости ряда
Исследование числовых рядов на сходимость по определению достаточно сложная задача, потому что далеко не для каждого ряда можно найти общий член последовательности его частичных сумм. Поэтому в исключительной большинстве случаев вопрос о сходимости или расхождение ряда решают с помощью так называемых «признаков сходимости». Среди них выделяют необходимого признака сходимости, которая является единой для всех типов рядов, и достаточные признаки, использование которых зависят от типов рядов.
Теорема 32.4 (необходимый признак сходимости). Если ряд  совпадает, то граница общего члена ряда при
совпадает, то граница общего члена ряда при  равна 0, т.е.
равна 0, т.е.

Доказательство. Пусть ряд  сходится и его сумма равна
сходится и его сумма равна  Поскольку
Поскольку
 то можно записать
то можно записать 
Найдем границы левой и правой частей последнего равенства:

ведь при  и
и 
Соотношение (32.13) является необходимым признаком сходимости ряда.
Следует заметить, что когда необходимое условие сходимости не выполняется, то исследуемый ряд расходится. То есть условие

является достаточным признаком разногласия числового ряда.
Действительно, если бы ряд совпадал, то граница его общего члена равнялась бы нулю, что противоречит условию  Итак, ряд расходится.
Итак, ряд расходится.
Однако, если необходимый признак выполняется, то это еще не значит, что соответствующий ряд является сходящимся. То есть вопрос о сходимости ряда остается открытым и требует дальнейшего исследования. Например, для гармонического ряда необходимый признак сходимости выполняется, но анализ границы частичной суммы ряда показывает, что ряд расходится.
Исследовать, совпадает ли ряд 
Найдем границу общего члена ряда:

Итак, необходимый признак не выполняется, отсюда следует, что ряд расходится.
Исследовать ряд на сходимость 
Проверим выполнение необходимого признака сходимости. Согласно второй замечательной границы получим:

Это означает, что необходимый признак сходимости ряда не выполняется, следовательно, данный ряд расходится.
Исследовать на сходимость ряд 
Найдем границу общего члена ряда:

Выполнение необходимого признака сходимости по данному ряда определенного ответа не дает: ряд может совпадать, а может разбегаться. Но анализ общего члена ряда показывает, что ряд на бесконечности ведет себя как гармонический ряд, умноженный на

из чего следует, что исходный ряд расходится, потому что последовательность его частичных сумм не является ограниченной, поскольку ее члены крупнее членов последовательности частичных сумм расходящегося ряда.
Исследовать на сходимость ряд

Найдем границу общего члена ряда:

Выполнение необходимого признака сходимости определенного ответа не дает.
Если же общий член ряда представить в виде

и сравнить его с общим членом  сходящегося ряда
сходящегося ряда  то понятно, что
то понятно, что

то есть  Итак, частичные суммы исходного ряда меньше частичные суммы сходящегося ряда, а это значит, что их последовательность при
Итак, частичные суммы исходного ряда меньше частичные суммы сходящегося ряда, а это значит, что их последовательность при  имеет конечную границу, и заданный ряд сходится.
имеет конечную границу, и заданный ряд сходится.
В обоих предыдущих примерах исследования рядов на сходимость (при выполнении необходимого признака сходимости) свелось к их сравнению с рядами, «поведение» которых – сходимость или расхождение – известная. Такой подход к исследованию рядов является основой одной из достаточных признаков сходимости, которые рассматриваются в главе 33.
Достаточные условия сходимости числовых рядов
Рассмотрим сначала ряды, члены которых не меняют знак в зависимости от n, то есть знак каждого из них не зависит от номера. Такие ряды называют знакопостоянными. Ряд  называют рядом с положительными членами, если
называют рядом с положительными членами, если  для всех
для всех  Если все члены ряда отрицательные, то его исследования на сходимость сводится к исследованию ряда с положительными членами вынесением за скобки множителя
Если все члены ряда отрицательные, то его исследования на сходимость сводится к исследованию ряда с положительными членами вынесением за скобки множителя 
Признак сравнения рядов с положительными членами
Теорема 33.1. Пусть имеем два ряда

и

Если для всех членов этих рядов выполняются неравенства

то с сходимости ряда с общим членом  следует сходимость ряда с общим членом
следует сходимость ряда с общим членом  а с расхождения ряда с общим членом
а с расхождения ряда с общим членом  – расхождение ряду с общим членом
– расхождение ряду с общим членом 
Доказательство. Докажем сначала первое утверждение теоремы. Для этого рассмотрим частичные суммы
 и
и 
С сходимости ряда (33.2) следует существование конечной границы  причем
причем  поскольку по условию
поскольку по условию  Кроме того, если по условию
Кроме того, если по условию 
 и получается , что
и получается , что  Это значит, что последовательность частичных сумм
Это значит, что последовательность частичных сумм  монотонно возрастает и ограничена сверху. По теореме Вейерштрасса она имеет предел, то есть существует
монотонно возрастает и ограничена сверху. По теореме Вейерштрасса она имеет предел, то есть существует Итак, ряд с общим членом
Итак, ряд с общим членом  совпадает. Первая часть теоремы доказана.
совпадает. Первая часть теоремы доказана.
Для доказательства второй части предположим, что существует расходящийся ряд с общим членом  а ряд с общим членом
а ряд с общим членом  совпадает. Из первой части доказательства следует, что первый ряд также сходится, что противоречит сделанному предположению, следовательно, оно ошибочно. Значит, ряд с общим членом
совпадает. Из первой части доказательства следует, что первый ряд также сходится, что противоречит сделанному предположению, следовательно, оно ошибочно. Значит, ряд с общим членом  разбегается.
разбегается.
Эта теорема является базой для установления факта сходимости ряда по признаку сравнения.
Ряды, с которыми сравнивают исследуемые ряды, называются эталонными рядами (от фр. Etalon – образец меры). О таких ряды заранее известно, совпадают они или разбегаются.
При применении признака сравнения в роли эталонного ряда может выступать ряд бесконечно убывающей геометрической прогрессии качестве примера сходящегося ряда и гармонический ряд качестве примера расходящегося ряда.
При исследовании на сходимость рядов с положительными членами бывает удобнее использовать признак сравнения в предельной форме: если существует конечная, отличная от нуля граница

то оба ряда (33.1) и (33.2) или одновременно совпадают, либо одновременно разбегаются.
Действительно, если условие (33.4) выполняется, то можно доказать, что начиная с некоторого номера выполняется условие признаки сравнения.
Исследовать на сходимость ряд 
По очевидном неравенстве  правильной для
правильной для  получим неравенство
получим неравенство  и рассмотрим ряды с общими членами
и рассмотрим ряды с общими членами  и
и 
Ряд с общим членом  совпадает как ряд бесконечной геометрической прогрессии со знаменателем
совпадает как ряд бесконечной геометрической прогрессии со знаменателем  Итак, по признаку сравнения совпадает и ряд с общим членом
Итак, по признаку сравнения совпадает и ряд с общим членом 
Исследовать на сходимость ряд 
Для сравнения возьмем ряд с общим членом  то есть гармонический ряд, который разбегается. Применим признак сравнения рядов в предельной форме. поскольку
то есть гармонический ряд, который разбегается. Применим признак сравнения рядов в предельной форме. поскольку

то оба ряда ведут себя одинаково, а значит, исследуемый ряд тоже расходится.
Исследовать на сходимость ряд 
Запишем ряд в развернутой форме:

Сравним данный ряд с рядом, что является остатком гармонического ряда, а потому расходится:

Для этого проверим выполнение условия признака сравнения (теорема 33.1). имеем:

и в общем случае

Учитывая, что члены данного ряда крупнее соответствующие члены расходящегося ряда  то по признаку сравнения исследуемый ряд является рядом расходящимся.
то по признаку сравнения исследуемый ряд является рядом расходящимся.
Признак Даламбера
Теорема 33.2. Пусть для ряда с положительным общим членом  существует предел отношения последующего члена ряда
существует предел отношения последующего члена ряда  к предыдущему –
к предыдущему – 

Тогда:
1. Если  то ряд сходится.
то ряд сходится.
2. Если  то ряд расходится.
то ряд расходится.
3. Если  то информации недостаточно, чтобы сделать вывод о сходимости или расхождение ряда.
то информации недостаточно, чтобы сделать вывод о сходимости или расхождение ряда.
Доказательство.
1. Если  По определению предела последовательности для любого
По определению предела последовательности для любого  существует такое
существует такое  что для всех
что для всех  выполняется неравенство
выполняется неравенство

Обозначим  и выберем
и выберем  таким, чтобы выполнялось неравенство
таким, чтобы выполнялось неравенство  Тогда:
Тогда:

Отсюда имеем:

Построим ряд:

который является  -м остатком исследуемого ряда. Члены этого остатка меньше соответствующие члены бесконечно убывающей геометрической прогрессии с первым членом
-м остатком исследуемого ряда. Члены этого остатка меньше соответствующие члены бесконечно убывающей геометрической прогрессии с первым членом  и знаменателем
и знаменателем  поскольку
поскольку  поэтому по признаку сравнения
поэтому по признаку сравнения  -й остаток исследуемого ряда совпадает, следовательно, совпадает и данный ряд.
-й остаток исследуемого ряда совпадает, следовательно, совпадает и данный ряд.
2. Если  тогда
тогда  выберем настолько малым, чтобы для числа
выберем настолько малым, чтобы для числа  выполнялась неравенство
выполнялась неравенство  При достаточно больших
При достаточно больших  будем иметь:
будем иметь:

В этом случае каждый последующий член ряда больше, чем предыдущий. Поскольку все они положительные, то не может выполняться необходимое условие сходимости ряда. Следовательно, при  данный ряд расходится.
данный ряд расходится.
3. Если  то в этом случае ряд может оказаться как сходящимся, так и расходящимся
то в этом случае ряд может оказаться как сходящимся, так и расходящимся
Исследовать на сходимость ряд 
Выписываем общий член ряда  тогда
тогда 
Найдем отношение последующего члена ряда к предыдущему

и вычислим его границу. Получим:

Следовательно, ряд сходится по признаку Даламбера.
Исследовать на сходимость ряд 
По общему членом  находим следующий
находим следующий  член ряда:
член ряда:

Составляем отношение

вычисляем его границу и делаем соответствующий вывод:

Таким образом, ряд сходится по признаку Даламбера.
Исследовать на сходимость ряд 
Поскольку  тогда
тогда 
Найдем границу

а потому по признаку Даламбера ряд расходится.
Исследовать на сходимость по признаку Даламбера ряды
 и
и 
Рассмотрим предел отношения последующего члена к предыдущему для первого ряда:

Видно, что признак Даламбера не позволяет сделать вывод о сходимости или расхождение ряда, хотя именно об этом ряде мы знаем, что он сходится и его сумма равна числу 1.
Рассмотрим предел отношения последующего члена к предыдущему для второго ряда:

Признак Даламбера опять не дает возможности сделать вывод о сходимости или расхождение ряда, хотя именно об этом ряд мы знаем, что он расходится как гармонический ряд.
На этом примере мы убедились, что признак Даламбера в случае  не дает ответ на вопрос о сходимости или расхождение ряда, поскольку существуют как совпадающие, так и расходящиеся ряды, для которых условие
не дает ответ на вопрос о сходимости или расхождение ряда, поскольку существуют как совпадающие, так и расходящиеся ряды, для которых условие  выполняется.
выполняется.
Радикальный признак Коши
Теорема 33.3. Пусть для ряда с положительным общим членом  существует граница
существует граница

Тогда:
1. Если  то ряд сходится.
то ряд сходится.
2. Если  то ряд расходится.
то ряд расходится.
3. Если  то информации недостаточно, чтобы сделать вывод о сходимости или расхождение ряда.
то информации недостаточно, чтобы сделать вывод о сходимости или расхождение ряда.
Доказательство теоремы аналогичное доказательству теоремы 33.2.
Примеры исследования на сходимость рядов с положительными членами с помощью радикальной признаки Коши.
1. Находим границу корня
Находим границу корня  -й степени с
-й степени с  -го и делаем соответствующий вывод:
-го и делаем соответствующий вывод:
 ряд расходится.
ряд расходится.
2.  Аналогичным образом получаем:
Аналогичным образом получаем:
 ряд сходится.
ряд сходится.
Интегральный признак Коши
Теорема 33.4. Пусть  – неотъемлемая невозрастающая функция, непрерывная на промежутке
– неотъемлемая невозрастающая функция, непрерывная на промежутке  причем
причем 
Тогда:
1. Если несобственный интеграл  сходится, то и ряд
сходится, то и ряд  сходится.
сходится.
2. Если несобственный интеграл  расходится, то и ряд расходящийся.
расходится, то и ряд расходящийся.
Теорема примем без доказательства.
Рассмотрим применение интегральной признаки Коши на примерах.
Исследовать на сходимость ряд  где
где 
Этот ряд называют рядом Дирихле, или обобщенным гармоническим рядом. Для исследования этого ряда на сходимость применим интегральную признак Коши, вычислив интеграл

Следовательно, при  несобственный интеграл сходится, при
несобственный интеграл сходится, при  – расходящийся. Поэтому и ряд Дирихле сходится при
– расходящийся. Поэтому и ряд Дирихле сходится при  и расходится при
и расходится при  При
При  ряд Дирихле называют гармоничным рядом. Этот ряд был рассмотрен ранее:
ряд Дирихле называют гармоничным рядом. Этот ряд был рассмотрен ранее:

Отметим, что ряд Дирихле, как и гармонический ряд, используют в признаку сравнения рядов как эталонный ряд.
Исследовать на сходимость ряд 
Берем несобственный интеграл на промежутке  от функции
от функции

получаемой из общего члена ряда  подстановкой вместо натурального
подстановкой вместо натурального  непрерывной переменной
непрерывной переменной  и делаем соответствующий вывод:
и делаем соответствующий вывод:

Итак, несобственный интеграл совпадает, поэтому совпадает и данный ряд.
Исследовать на сходимость ряд 
Рассмотрим функцию  которая при натуральных
которая при натуральных  дает члены исследуемого ряда. Нетрудно убедиться с помощью производной, что данная функция является монотонно убывающей при
дает члены исследуемого ряда. Нетрудно убедиться с помощью производной, что данная функция является монотонно убывающей при  Поэтому найдем несобственный интеграл
Поэтому найдем несобственный интеграл

Поскольку несобственный интеграл сходится, то и данный ряд тоже сходится.
Достаточный признак сходимости знакопеременного ряда
Знакопеременным рядом называется ряд, членами которого являются действительные числа произвольного знака.
Достаточный признак сходимости знакопеременного ряда базируется на исследовании ряда, образованного из абсолютных величин членов данного ряда.
Теорема 33.5. Пусть имеем знакопеременный ряд

Если ряд, образованный из абсолютных величин его членов

совпадает, то совпадает и исходный ряд.
Доказательство. Обозначим n-на частичную сумму данного знакопеременного ряда через  Тогда
Тогда  где
где  – сумма всех положительных слагаемых, а
– сумма всех положительных слагаемых, а  – сумма абсолютных величин всех отрицательных слагаемых частичной суммы
– сумма абсолютных величин всех отрицательных слагаемых частичной суммы  Получим, что
Получим, что  -на частичная сумма ряда, образованного из абсолютных величин членов данного ряда, равно
-на частичная сумма ряда, образованного из абсолютных величин членов данного ряда, равно  По условию теоремы она существует, а потому существуют границы последовательностей
По условию теоремы она существует, а потому существуют границы последовательностей  и
и  – потому что каждая из них будет растущей и ограниченной сверху последовательностью.
– потому что каждая из них будет растущей и ограниченной сверху последовательностью.
Поскольку

то существование конечной границы  доказана. Следовательно, данный знакопеременный ряд является сходящимся рядом.
доказана. Следовательно, данный знакопеременный ряд является сходящимся рядом.
Этот признак является достаточным признаком сходимости, но она не является необходимой.
Существуют совпадающие знакопеременные ряды, для которых ряды, образованные из абсолютных величин членов исходного ряда, является расходящимися.
Знакопеременный ряд называется абсолютно сходящимся, если совпадает ряд, образованный из абсолютных величин его членов.
Если данный ряд сходится, а ряд, образованный из абсолютных величин его членов расходится, то такой ряд называется условно сходящимся.
Заметим, что для исследования сходящегося ряда на абсолютную или условную сходимость можно использовать признаки сходимости рядов с положительными членами, а именно: признаки сравнения, признак Даламбера, радикальную и интегральную признаки Коши. Если же поведение исходного ряда неизвестна, то на основе теоремы 33.5 можно сделать вывод о сходимости данного ряда только при условии сходимости ряда, составленного из абсолютных величин членов данного ряда. Если же ряд, составленный из абсолютных величин членов данного ряда разбегается, то на вопрос о сходимости или расхождение данного ряда теорема ответа не дает.
Проведем исследование на сходимость ряда 
Поскольку  В правой части последнего неравенства имеем общий член ряда Дирихле, для которого
В правой части последнего неравенства имеем общий член ряда Дирихле, для которого  Этот ряд сходится, поскольку
Этот ряд сходится, поскольку  Следовательно, по признаку сравнения рядов, ряд, образованный из абсолютных величин членов данного ряда, совпадает. Таким образом, исследуемый ряд сходится абсолютно.
Следовательно, по признаку сравнения рядов, ряд, образованный из абсолютных величин членов данного ряда, совпадает. Таким образом, исследуемый ряд сходится абсолютно.
Признак Лейбница сходимости знакопеременного ряда
Частным случаем знакопеременного ряда является ряд, у которого любые два соседние члены имеют разные знаки. Он называется знакопеременного ряда и имеет вид

Теорема 33.6 (признак Лейбница). Пусть для знакопеременного ряда (33.9) выполняются условия:

(Каждый последующий член ряда по абсолютной величине не больше предыдущего, и граница модуля общего члена ряда при  равна нулю.)
равна нулю.)
Тогда данный ряд сходится, а его сумма  неотъемлемая и не превышает модуля первого члена ряда, то есть
неотъемлемая и не превышает модуля первого члена ряда, то есть 
Доказательство. Рассмотрим случай, когда  то есть
то есть  является четным числом. тогда
является четным числом. тогда

Перепишем это равенство так:

С условия теоремы следует, что выражение в каждой дужке неотъемлемый.
Следовательно, сумма  и она растет с ростом
и она растет с ростом  Запишем эту сумму иначе:
Запишем эту сумму иначе:

Следовательно,  Таким образом, последовательность
Таким образом, последовательность  монотонно возрастает и ограничена сверху. Отсюда следует, что она имеет предел, то есть
монотонно возрастает и ограничена сверху. Отсюда следует, что она имеет предел, то есть

где число  принадлежит промежутку
принадлежит промежутку  (при исчислении границы учтено, что условие
(при исчислении границы учтено, что условие  влечет за собой условие
влечет за собой условие  ).
).
Докажем, что частичные суммы с нечетными номерами имеют своей границей то же число  Рассмотрим для этого сумму первых
Рассмотрим для этого сумму первых  членов ряда, где
членов ряда, где  Ее можно записать в виде:
Ее можно записать в виде:  Найдем границы левой и правой частей этого равенства при
Найдем границы левой и правой частей этого равенства при  а значит и при
а значит и при 

так как по условию теоремы Доказано, что
Доказано, что 
Следовательно, данный ряд сходится, потому произвольная (с четным или нечетным номером) частичная сумма  имеет одну и ту же конечную границу
имеет одну и ту же конечную границу  при
при 
Проверка выполнения условий (33.10) теоремы для знакоперемижного ряда является исследованием его на сходимость по признаку Лейбница.
Следствие. Если знакопеременных ряд совпадает, то сходится и его  -й остаток
-й остаток

а его сумма не превышает по абсолютной величине модуля первого члена ряда, то есть 
Справедливость последствия следует из того, что  -й остаток ряда, как и самый ряд, удовлетворяет условиям признаки Лейбница.
-й остаток ряда, как и самый ряд, удовлетворяет условиям признаки Лейбница.
Согласно следствием из признаки Лейбница, абсолютная погрешность при замене суммы  сходящегося знакоперемижного ряда (33.9) суммой первых
сходящегося знакоперемижного ряда (33.9) суммой первых  членов, то есть его частичной суммой
членов, то есть его частичной суммой  не превышает модуля первого из отброшенных членов ряда, то есть
не превышает модуля первого из отброшенных членов ряда, то есть

Исследовать на сходимость знакоперемижний ряд 
Проверим выполнение первой и второй требований по сходимости знакоперемижного ряда:

Оба условия выполняются, следовательно заданный знакоперемижний ряд совпадает по признаку Лейбница.
Ряд совпадает условно, так как ряд, составленный из абсолютных величин членов данного ряда  разбегается как гармоничный.
разбегается как гармоничный.
Исследовать на абсолютную и условную сходимость ряд 
Есть знакоперемижний ряд, который совпадает, потому выполняются оба условия признаки Лейбница. Проверим теперь, совпадает ли он абсолютно или условно. Для этого создадим ряд с абсолютных величин членов исследуемого ряда:

Этот ряд сходится как ряд Дирихле, у которого  Таким образом, исходный ряд совпадает, и к тому же абсолютно.
Таким образом, исходный ряд совпадает, и к тому же абсолютно.
Заметим, что для проверки первого условия признаки Лейбница  достаточно исследовать на монотонность функцию
достаточно исследовать на монотонность функцию  соответствующую общему члену ряда.
соответствующую общему члену ряда.
Проверку выполнения условий (33.10) можно начинать с любой из них.
Функциональные ряды. Степенной ряд
Понятие «функциональный ряд» является обобщением понятия «числовой ряд»: элементы такого ряда не стали, а переменные величины.
Ряд называется функциональным, если его членами являются функции переменной  которые определены и непрерывные на некотором множестве
которые определены и непрерывные на некотором множестве  то есть ряд вида
то есть ряд вида

где  – общий член ряда.
– общий член ряда.
Точка  называется точкой сходимости функционального ряда, если при подстановке ее в ряд образуется сходится числовой ряд.
называется точкой сходимости функционального ряда, если при подстановке ее в ряд образуется сходится числовой ряд.
Совокупность всех значений переменной  для которых ряд (34.1) совпадает, называется областью сходимости функционального ряда.
для которых ряд (34.1) совпадает, называется областью сходимости функционального ряда.
Сумма первых  членов ряда называется
членов ряда называется  -й частичной суммой ряда:
-й частичной суммой ряда:

Частичные суммы ряда в свою очередь образуют последовательность функций  определенных и непрерывных на некотором множестве, которую называют последовательностью частичных сумм ряда.
определенных и непрерывных на некотором множестве, которую называют последовательностью частичных сумм ряда.
В каждой точке x области сходимости функционального ряда существует конечная граница при неограниченном росте  последовательности его частичных сумм
последовательности его частичных сумм

которая называется суммой ряда (34.1). Сумма сходящегося ряда является функцией  определенной на области сходимости ряда.
определенной на области сходимости ряда.
Ряд, полученный из ряда (34.1) отвержением первых n ее членов, называется  -м остатком (или просто остатком) функционального ряда:
-м остатком (или просто остатком) функционального ряда:

Заметим, что по числовой ряд, функциональный ряд сходится тогда и только тогда, когда его остаток  для всех x из области сходимости при неограниченном росте
для всех x из области сходимости при неограниченном росте  стремится к нулю.
стремится к нулю.
Важными функциональными рядами с точки зрения приложений являются так называемые «степенные ряды».
Степенным рядом называется функциональный ряд, членами которого являются степенные функции  с растущими целыми положительными показателями степени, как правило, начиная с нуля:
с растущими целыми положительными показателями степени, как правило, начиная с нуля:

где действительные числа  – коэффициенты ряда, а выражение
– коэффициенты ряда, а выражение  – общий член степенного ряда.
– общий член степенного ряда.
Рассматривают также степенной ряд вида:

который называют степенным рядом по степеням разности  где
где  – постоянная. Этот ряд легко свести к предыдущему, если обозначить
– постоянная. Этот ряд легко свести к предыдущему, если обозначить 
Область и радиус сходимости
Отметим, что степенной ряд (34.2) всегда совпадает при  а степенной ряд (34.3) – при
а степенной ряд (34.3) – при 
Для нахождения области сходимости степенного ряда используется такая теорема.
Теорема 34.1 (теорема Абеля). Если степенной ряд сходится для некоторого значения  то он сходится абсолютно при каждом значении
то он сходится абсолютно при каждом значении  для которого выполняется условие
для которого выполняется условие

Если степенной ряд расходится для некоторого значения  то он р озбигаеться при каждом значении
то он р озбигаеться при каждом значении  для которого выполняется условие
для которого выполняется условие

Доказательство. Если при  степенной ряд (34.2)
степенной ряд (34.2)

совпадает, то по необходимым условием сходимости числового ряда его общий член стремится к нулю:  при
при  То есть числовая последовательность
То есть числовая последовательность  ограничено, поэтому найдется такое число
ограничено, поэтому найдется такое число  что для всех значений
что для всех значений  будет выполняться неравенство
будет выполняться неравенство 
На этом основании для любых  удовлетворяющие условие
удовлетворяющие условие  получаем такую оценку абсолютной величины общего члена ряда (34.2):
получаем такую оценку абсолютной величины общего члена ряда (34.2):

где  является знаменателем геометрической прогрессии с общим членом
является знаменателем геометрической прогрессии с общим членом 
Неравенство  значит, что члены ряда, составленного из модулей членов степенного ряда (34.2), не превышают членов сходящегося ряда геометрической прогрессии (ведь
значит, что члены ряда, составленного из модулей членов степенного ряда (34.2), не превышают членов сходящегося ряда геометрической прогрессии (ведь  ). По признаку сравнения заданный степенной ряд для всех
). По признаку сравнения заданный степенной ряд для всех  совпадает, и к тому же абсолютно.
совпадает, и к тому же абсолютно.
Докажем вторую часть теоремы. По условию теоремы в точке  степенной ряд (34.2) разбегается. Надо доказать, что ряд расходится для всех таких
степенной ряд (34.2) разбегается. Надо доказать, что ряд расходится для всех таких  что
что 
Предположим, что это не так. Пусть ряд будет сходящимся при некотором значении x1, для которого выполняется неравенство  или x x 0 1 <. Отсюда по доказанной частью теоремы ряд должен совпадать и в точке
или x x 0 1 <. Отсюда по доказанной частью теоремы ряд должен совпадать и в точке  что противоречит условию разногласия ряда в этой точке. Следовательно, предположение о существовании числа
что противоречит условию разногласия ряда в этой точке. Следовательно, предположение о существовании числа  ошибочно.
ошибочно.
Таким образом, для произвольного степенного ряда (34.2) имеем один из трех следующих случаев:
1) степенной ряд сходится для всех произвольных действительных значений  ;
;
2) степенной ряд расходится для всех произвольных действительных значений  , кроме случая
, кроме случая  ;
;
3) существуют такие значения  и
и  что ряд сходится при
что ряд сходится при  и расходится при
и расходится при  Тогда по теореме Абеля будет выполняться неравенство
Тогда по теореме Абеля будет выполняться неравенство  Это означает, что множество всех значений
Это означает, что множество всех значений  для которых степенной ряд будет сходящимся, ограничена сверху. Поэтому существует такое больше положительное число
для которых степенной ряд будет сходящимся, ограничена сверху. Поэтому существует такое больше положительное число  для всех
для всех  ряд совпадает, причем абсолютно (по теореме Абеля), а при
ряд совпадает, причем абсолютно (по теореме Абеля), а при  – разбегается. Такое число
– разбегается. Такое число  называется радиусом сходимости, а интервал
называется радиусом сходимости, а интервал  – интервалом сходимости степенного ряда.
– интервалом сходимости степенного ряда.
Понятно, что в первом из рассмотренных случаев  во втором –
во втором –  в третьем –
в третьем –  Заметим, что понятие интервала сходимости и понятия области сходимости степенного ряда являются близкими, но не тождественными, так как в области сходимости может принадлежать не только интервал сходимости, но и оба его конца, или же один из его концов.
Заметим, что понятие интервала сходимости и понятия области сходимости степенного ряда являются близкими, но не тождественными, так как в области сходимости может принадлежать не только интервал сходимости, но и оба его конца, или же один из его концов.
Теорему Абеля можно использовать для нахождения интервала и радиуса сходимости степенного ряда. Отметим, что согласно теореме Абеля интервалы сходимости ряда (34.2) и ряда, составленного из абсолютных величин членов данного ряда, совпадают.
Найдем интервал сходимости ряда

образованного из абсолютных величин членов данного степенного ряда при условии, что  Применим к этому ряду признак Даламбера:
Применим к этому ряду признак Даламбера:

Множество значений  для которых исходный ряд сходится абсолютно, и вместе с тем радиус сходимости ряда, найдем согласно признаку Даламбера при условии, что
для которых исходный ряд сходится абсолютно, и вместе с тем радиус сходимости ряда, найдем согласно признаку Даламбера при условии, что 

где  – радиус сходимости степенного ряда:
– радиус сходимости степенного ряда:

При всех значениях  для которых
для которых  ряд расходится.
ряд расходится.
Аналогично радиус сходимости ряда можно вычислить по формуле:
если применить к ряду (34.6) радикальную признак Коши.
Заметим, что формулы (34.7), (34.8) нельзя использовать, если показатель степени в общем члене ряда является функцией от  Например:
Например:  и так далее. Тогда нужно непосредственно применить признак Даламбера, как это было сделано выше.
и так далее. Тогда нужно непосредственно применить признак Даламбера, как это было сделано выше.
Исследование поведения числовых рядов, которые получают из степенного ряда (34.2) при то есть в точках
то есть в точках  нужно проводить отдельно.
нужно проводить отдельно.
Радиус сходимости степенного ряда (34.3) определяют по соотношениям (34.7), (34.8) после замены переменной:  Если радиус сходимости ряда с новой переменной найдено, то для исходного ряда получим:
Если радиус сходимости ряда с новой переменной найдено, то для исходного ряда получим:

то есть интервал сходимости ряда (34.3) имеет вид:
Исследования на сходимость ряда по степеням разности  в точках
в точках  так же проводят отдельно.
так же проводят отдельно.
Найти область сходимости степенного ряда 
Общий член этого ряда  тогда
тогда 
Составляем отношение модулей следующего и предыдущего членов ряда, находим его границу и сравниваем с единицей:

Последнее неравенство выполняется для любого  поэтому ряд совпадает на всей числовой оси:
поэтому ряд совпадает на всей числовой оси: 
Можно сразу найти радиус сходимости  по формуле (34.7), поскольку степенной ряд содержит все степени
по формуле (34.7), поскольку степенной ряд содержит все степени  (среди коэффициентов
(среди коэффициентов  форуме нулевых):
форуме нулевых):

Найти область сходимости степенного ряда 
В этом степенной ряде коэффициенты при парных степенях  равны нулю:
равны нулю:  и формулу (34.7) использовать невозможно. Однако непосредственное применение признаки Даламбера дает:
и формулу (34.7) использовать невозможно. Однако непосредственное применение признаки Даламбера дает:

Итак, ряд сходится при  и расходится при
и расходится при  интервал
интервал  – его интервал сходимости.
– его интервал сходимости.
Исследуем поведение степенного ряда на концах интервала сходимости.
Пусть  Подставим это значение в степенной ряд, в результате чего получим знакопостоянный числовой ряд с отрицательными членами
Подставим это значение в степенной ряд, в результате чего получим знакопостоянный числовой ряд с отрицательными членами

Возьмем расходящийся гармонический ряд как эталонный, тогда по признаку сравнения в предельной форме получим расхождение ряда с общим членом  Поскольку умножение ряда на
Поскольку умножение ряда на  не влияет на его расхождение, поэтому данный ряд также расходится.
не влияет на его расхождение, поэтому данный ряд также расходится.
При значении  степенной ряд превращается в числовой ряд
степенной ряд превращается в числовой ряд  Этот ряд, как мы уже выяснили, расходится.
Этот ряд, как мы уже выяснили, расходится.
Таким образом, областью сходимости исходного степенного ряда является интервал 
Найти область сходимости степенного ряда 
Обозначим  тогда
тогда  Для нахождения радиуса сходимости применим формулу (34.7):
Для нахождения радиуса сходимости применим формулу (34.7):

Таким образом, – интервал сходимости. Исследуем поведение ряда на концах полученного интервала.
– интервал сходимости. Исследуем поведение ряда на концах полученного интервала.
При  получим знакоперемижний числовой ряд
получим знакоперемижний числовой ряд  который совпадает по признаку Лейбница.
который совпадает по признаку Лейбница.
При  имеем знакосталий числовой ряд
имеем знакосталий числовой ряд  который совпадает как ряд Дирихле, поскольку
который совпадает как ряд Дирихле, поскольку 
Итак, областью сходимости степенного ряда будет промежуток 
Возвращаясь к переменной получим:
получим:

Таким образом, областью сходимости исходного степенного ряда является промежуток 
Свойства степенных рядов
Сформулируем (без доказательства) свойства сходящихся на интервале  степенных рядов, используемых при исследовании этих рядов.
степенных рядов, используемых при исследовании этих рядов.
1. Сумма членов степенного ряда является функцией, непрерывной во всех точках интервала сходимости.
2. Степенной ряд можно почленно дифференцировать в каждой точке интервала сходимости. Сумма этого нового ряда равна производной от суммы исходного ряда, а радиус сходимости нового ряда равен радиусу сходимости исходного ряда.
3. Степенной ряд можно почленно интегрировать на любом
промежутке  который принадлежит интервалу сходимости. Интеграл от суммы степенного ряда равен сумме ряда, образованного из интегралов от членов исходного ряда. Радиус сходимости нового ряда равен радиусу сходимости исходного ряда.
который принадлежит интервалу сходимости. Интеграл от суммы степенного ряда равен сумме ряда, образованного из интегралов от членов исходного ряда. Радиус сходимости нового ряда равен радиусу сходимости исходного ряда.
4. Степенные ряды можно почленно прибавлять и отнимать. Радиус сходимости полученного ряда не будет меньше наименьший из радиусов сходимости выходных рядов.
Проинтегрировать почленно ряд  при
при  и найти область сходимости образованного ряда.
и найти область сходимости образованного ряда.
Запишем ряд в развернутом виде:

Этот ряд на заданном промежутке собой ряд бесконечно убывающей геометрической прогрессии, а его сумма равна  на интервале
на интервале  он сходится, поэтому его можно почленно интегрировать (см. свойство 3).
он сходится, поэтому его можно почленно интегрировать (см. свойство 3).
Интегрируем почленно левую и правую части приведенной равенства в пределах от 0 до некоторого  принадлежащее интервалу сходимости:
принадлежащее интервалу сходимости:

Мы получили ряд, общий член которого  а сумма равна
а сумма равна  Согласно свойствами степенных рядов, интервалом сходимости этого ряда есть
Согласно свойствами степенных рядов, интервалом сходимости этого ряда есть  Исследуем поведение нового ряда на концах интервала сходимости.
Исследуем поведение нового ряда на концах интервала сходимости.
При  получим числовой ряд
получим числовой ряд  который расходится рядом.
который расходится рядом.
При  получим знакоперемижний числовой ряд
получим знакоперемижний числовой ряд  который является сходящимся по признаку Лейбница.
который является сходящимся по признаку Лейбница.
Итак, областью сходимости полученного после интегрирования степенного ряда является промежуток 
На этом примере мы увидели, что интегрирование степенного ряда может расширить его область сходимости.
Интегрировать в интервале  ряд и найти его область сходимости:
ряд и найти его область сходимости:

Как и в предыдущем примере, мы ряд, образованный членами
бесконечно убывающей геометрической прогрессии, для которого известны интервал сходимости:  и сумма
и сумма  в любой точке этого интервала.
в любой точке этого интервала.
С интегрируем почленно ряд в интервале сходимости и его сумму как функцию от 

Исследуем поведение полученного ряда на концах интервала сходимости.
Пусть  В этом случае общий член степенного ряда
В этом случае общий член степенного ряда
приобретает вид  то есть мы получили числовой знакоперемижний ряд, который является сходящимся по признаку Лейбница.
то есть мы получили числовой знакоперемижний ряд, который является сходящимся по признаку Лейбница.
Пусть  В этом случае также имеем знакоперемижний числовой ряд с общим членом
В этом случае также имеем знакоперемижний числовой ряд с общим членом  сходится по той же
сходится по той же
признаку.
Итак, областью сходимости образованного интегрированием степенного ряда является  Здесь интегрирование степенного ряда расширило область сходимости к замкнутому промежутку.
Здесь интегрирование степенного ряда расширило область сходимости к замкнутому промежутку.
Степенные ряды Тейлора и Маклорена
Степенные ряды часто используются в приближенных вычислениях при составлении таблиц элементарных функций, при вычислении интегралов, не выражаются через элементарные функции, при решении дифференциальных уравнений и др.
Если функция  на интервале
на интервале  является суммой степенного ряда
является суммой степенного ряда

говорится, что на заданном интервале функция разлагается в степенной ряд или ряд сходится к функции 
Поставим задачу нахождения коэффициентов ряда (34.8) для заданной функции 
Теорема 34.2 (о едином разложении функции в степенной ряд). Если функция  имеет производные любого порядка в окрестности точки
имеет производные любого порядка в окрестности точки  и разлагается в степенной ряд (34.8) в интервале его сходимости
и разлагается в степенной ряд (34.8) в интервале его сходимости  то это разложение можно осуществить единственным способом.
то это разложение можно осуществить единственным способом.
Доказательство. Так как по условию теоремы на интервале  ряд сходится и
ряд сходится и  является его суммой, то по свойству 2 степенных рядов этот ряд можно дифференцировать почленно на заданном промежутке сколько угодно раз. Совершив дифференцировки ряда
является его суммой, то по свойству 2 степенных рядов этот ряд можно дифференцировать почленно на заданном промежутке сколько угодно раз. Совершив дифференцировки ряда  раз, получим:
раз, получим:

Отсюда при  находим
находим  или
или

Таким образом, коэффициенты степенного ряда определяются формулами (34.9) однозначно, что и требовалось доказать. ■
Следовательно, если функция  разлагается в степенной ряд, то этот ряд имеет вид:
разлагается в степенной ряд, то этот ряд имеет вид:

и называется рядом Тейлора для функции  в окрестности точки
в окрестности точки 
Частным случаем ряда Тейлора при  есть ряд Маклорена:
есть ряд Маклорена:

Если привлечь к рассмотрению остаток ряда Тейлора (или ряда Маклорена)  то функцию
то функцию  можно записать как сумму первых
можно записать как сумму первых  членов ряда
членов ряда  и его
и его  -го остатка
-го остатка 

то есть

При дифференцированности функции  произвольное число раз ряд Тейлора можно получить с формулы Тейлора (15.39) при неограниченном росте номера
произвольное число раз ряд Тейлора можно получить с формулы Тейлора (15.39) при неограниченном росте номера  При этом остаточный член формулы Тейлора
При этом остаточный член формулы Тейлора  (15.40) удовлетворяет условию:
(15.40) удовлетворяет условию:

Теорема 34.3 (необходимое и достаточное условие сходимости ряда Тейлора). Ряд Тейлора сходится к функции  на интервале
на интервале  тогда и только тогда, когда остаточный член ее формулы Тейлора стремится к нулю при
тогда и только тогда, когда остаточный член ее формулы Тейлора стремится к нулю при  для всех x из этого интервала:
для всех x из этого интервала:

Доказательство. Запишем для функции  формулу Тейлора в виде:
формулу Тейлора в виде:
 или
или 
Пусть ряд (34.10) сходится к функции  в интервале
в интервале  то есть
то есть  при
при  Отсюда следует, что
Отсюда следует, что  при
при  в этом интервале, и наоборот. Если в интервале
в этом интервале, и наоборот. Если в интервале  выполняется условие
выполняется условие  при
при  то
то  при
при 
Замечания. Если  то ряд может быть сходящимся, однако его сумма не равна
то ряд может быть сходящимся, однако его сумма не равна  Примером такого ряда есть ряд Маклорена для функции
Примером такого ряда есть ряд Маклорена для функции 
Теорема 34.4 (достаточное условие сходимости ряда к функции  Если функция
Если функция  на некотором промежутке
на некотором промежутке  имеет производные всех порядков и существует число
имеет производные всех порядков и существует число  такое, что
такое, что  для всех
для всех  из
из  тогда во всех точках этого промежутка функцию
тогда во всех точках этого промежутка функцию  можно разложить в ряд Тейлора.
можно разложить в ряд Тейлора.
Доказательство. Запишем абсолютную величину остаточного члена формулы Тейлора (15.40) в форме Лагранжа и оценим его с учетом, что  и
и 

где  – промежуточная точка между
– промежуточная точка между  и
и 
Покажем, что  при
при  Для этого рассмотрим числовой ряд, общий член которого равен
Для этого рассмотрим числовой ряд, общий член которого равен  По признаку Даламбера ряд сходится, поэтому
По признаку Даламбера ряд сходится, поэтому  (по необходимым признаком сходимости числовых рядов).
(по необходимым признаком сходимости числовых рядов).
В неравенстве  переходим к пределу при
переходим к пределу при  и получим условие
и получим условие  Согласно теореме (34.3)
Согласно теореме (34.3)  разлагается в ряд Тейлора.
разлагается в ряд Тейлора.
Если исходная функция  является многочленом
является многочленом  -й степени, то все коэффициенты ряда Маклорена, начиная с
-й степени, то все коэффициенты ряда Маклорена, начиная с  -го равны нулю, и мы получим конечную сумму слагаемых – самый многочлен. Аналогичный результат получим при разложении многочлена в ряд Тейлора.
-го равны нулю, и мы получим конечную сумму слагаемых – самый многочлен. Аналогичный результат получим при разложении многочлена в ряд Тейлора.
Разложить в ряд Тейлора функцию  в окрестности точки
в окрестности точки 
Найдем значения функции и ее производных при 

Подставим эти значения в ряд (34.10), в результате чего получим:

или

Областью сходимости этого ряда, вырожденного в конечную сумму, есть вся числовая ось:  так же расклад – это тождественно запись многочлена по степеням разности
так же расклад – это тождественно запись многочлена по степеням разности 
Разложение в ряд Маклорена основных элементарных функций
Рассмотрим несколько важных примеров представление основных элементарных функций в виде ряда Маклорена, то есть разложение функции в ряд Маклорена.
Напомним, что ряд Маклорена

совпадает в интервале  к функции
к функции  (она является суммой ряда:
(она является суммой ряда:  если на этом интервале выполняется условие
если на этом интервале выполняется условие 
Аналогично ряд Тейлора

совпадает в интервале  к функции
к функции  если для ряда на этом интервале выполняется условие
если для ряда на этом интервале выполняется условие 
Рассмотрим разложение в ряд Маклорена некоторых элементарных функций. Алгоритм разложения функции в ряд предусматривает такие шаги:
а) нахождение коэффициентов ряда Маклорена для данной функции;
б) вычисления радиуса сходимости полученного ряда;
в) доказательства того, что полученный ряд сходится именно к функции 
Представим функцию  как ряд Маклорена. Для этого вычислим значение функции и ее производных при
как ряд Маклорена. Для этого вычислим значение функции и ее производных при 

Числовые коэффициенты ряда (35.1) имеют вид:

Подставляем найдены коэффициенты в ряд Маклорена:

Найдем радиус сходимости этого ряда:

Итак, ряд сходится в интервале 
Этот ряд сходится к функции  для любых значений
для любых значений  потому что на любом промежутке
потому что на любом промежутке  функция
функция  и ее производные по абсолютной величине ограничены числом
и ее производные по абсолютной величине ограничены числом 
Разложим в ряд Маклорена функцию 
Найдем значения функции и ее производных при 

Нетрудно заметить, что все производные четного порядка равны нулю:  а производные нечетного порядка по очереди равны числам 1 и
а производные нечетного порядка по очереди равны числам 1 и  где
где  Подставляем найдены коэффициенты в ряд Маклорена и получаем результат разложения функции
Подставляем найдены коэффициенты в ряд Маклорена и получаем результат разложения функции 

Найдем интервал сходимости этого ряда. По признаку Даламбера имеем:

Итак, ряд сходится на всей числовой оси: 
Этот ряд сходится к функции  потому модули функции и всех ее производных ограничены сверху единицей.
потому модули функции и всех ее производных ограничены сверху единицей.
Аналогично разложим в ряд Маклорена функцию 
Найдем значения функции и ее производных при 

Анализ значений производных показывает, что
Таким образом, получим:

Аналогично с предыдущим рядом область его сходимости  Ряд сходится к функции
Ряд сходится к функции  потому модули функции и всех ее производных ограничены сверху единицей.
потому модули функции и всех ее производных ограничены сверху единицей.
Обратим внимание, что функция sin x является нечетным, и она разложена в ряд по нечетным степеням переменной  – четная функция, поэтому ее расписание в ряд содержит только четные степени
– четная функция, поэтому ее расписание в ряд содержит только четные степени 
Разложим в ряд Маклорена степенную функцию 
 – бином с произвольным действительным показателем степени
– бином с произвольным действительным показателем степени 
Соответствующий ряд называют биномиальным.
Найдем значения функции и ее производных при 

Отсюда легко заметить общую закономерность – производные от данной функции в точке  является произведением с
является произведением с  множителей (по нисходящей), начиная с
множителей (по нисходящей), начиная с 

Подставим эти значения коэффициентов в ряд Маклорена и получим биномиальный ряд:

Найдем радиус сходимости этого ряда в случае, когда число  – положительное целое, функция
– положительное целое, функция  является многочленом, и радиус сходимости такого ряда бесконечный).
является многочленом, и радиус сходимости такого ряда бесконечный).
По признаку Даламбера и формулой для вычисления радиуса сходимости степенного ряда получим:

Следовательно,  – интервал сходимости этого ряда. В граничных точках при
– интервал сходимости этого ряда. В граничных точках при  и
и  ряд может совпадать или расходиться в зависимости от значения показателя степени m.
ряд может совпадать или расходиться в зависимости от значения показателя степени m.
Можно показать, что исследуемый ряд сходится на интервале  именно к функции
именно к функции  то есть сумма ряда равна
то есть сумма ряда равна  при
при 
Разложим в ряд Маклорена логарифмическую функцию: 

Для этого используем биномиальный ряд (35.6) при 
получим:

Учитывая, что степенной ряд можно почленно интегрировать в области его сходимости (свойство 4 степенных рядов), найдем интеграл от левой и правой частей данного ряда.

Определим радиус сходимости данного ряда:

то есть областью абсолютной сходимости ряда является интервал 
Исследуем сходимость ряда на концах интервала. При  получим числовой ряд с общим членом
получим числовой ряд с общим членом  Этот ряд расходится как гармонический ряд, умноженный на
Этот ряд расходится как гармонический ряд, умноженный на  При
При  получим знакопереминний числовой ряд с общим членом
получим знакопереминний числовой ряд с общим членом  Этот ряд сходится по признаку Лейбница.
Этот ряд сходится по признаку Лейбница.
Таким образом, областью сходимости ряда (35.7) является промежуток 
Разложим в ряд Маклорена функцию: 
Используем биномиальный ряд при  а вместо
а вместо  подставим
подставим 

Интегрируя ряд почленно на интервале сходимости  получим:
получим:

Можно убедиться, что этот ряд на концах интервала совпадает (как знакоперемижний ряд), и областью его сходимости является промежуток 
На практике приходится оперировать не только расписаниями в ряд основных элементарных функций, но и более сложных функций, в том числе и составленных. При развитии в ряд таких функций следует учитывать возможное изменение области сходимости ряда.
Найти расписание в степенной ряд интеграла 
Сначала запишем расписание в ряд функции  по формуле (35.5):
по формуле (35.5):

Составим отношение:

Выполняем почленное интегрирование:

Найдем область сходимости остатка этого ряда, полученного исключением первых двух слагаемых. По признаку Даламбера получим:

Ряд совпадает на всей числовой оси. Таким образом, формула

правильная везде, за исключением значения  так как логарифм нуля не существует.
так как логарифм нуля не существует.
Разложим в ряд Маклорена функцию  применяя ряд для
применяя ряд для  который совпадает на промежутке
который совпадает на промежутке 

Заменим 

и найдем область сходимости полученного ряда:

При  имеем:
имеем: Область сходимости
Область сходимости 
Разложим функцию  в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 
Находим значение функции и ее производных при 

и подставляем их в ряд (35.2):

По признаку Даламбера найдем интервал сходимости ряда:

Следовательно, при любом  граница
граница  меньше 1, а потому интервалом, и вместе с тем, областью сходимости ряда будет вся числовая ось:
меньше 1, а потому интервалом, и вместе с тем, областью сходимости ряда будет вся числовая ось: 
Ряд сходится к функции  для произвольных
для произвольных  так как в любом промежутке
так как в любом промежутке  функция и ее производные ограничены, например, числом
функция и ее производные ограничены, например, числом 
Заметим, что для разложения в ряд элементарных функций можно исходить из общих теоретических положений, но проще использовать установленные расписания (табл. 35.1) и свойства степенных рядов.
Основные расписания функций в степенной ряд Таблица 35.1

Использование рядов в приближенных вычислениях
В приближенных вычислениях степенные ряды играют чрезвычайно большую роль. С их помощью свое время был составлен таблицы тригонометрических функций, таблицы логарифмов, таблицы значений других функций, которые используются в различных областях знаний, например, в теории вероятностей и математической статистике. Кроме того, расписания функций в степенной ряд эффективно используются для их теоретического исследования.
Главным вопросом при применении степенных рядов в приближенных вычислениях вопрос оценки погрешности вычисления, возникающая при замене суммы ряда суммой первых  членов.
членов.
Вычисления с помощью знакоперемежных рядов
Пусть функция  разложена в степенной ряд. Если при вычислении значения функции для конкретного значения
разложена в степенной ряд. Если при вычислении значения функции для конкретного значения  получаем знакоперемежный числовой ряд, то за следствием из признаки Лейбница, заменив сумму ряда частичной суммой его первых
получаем знакоперемежный числовой ряд, то за следствием из признаки Лейбница, заменив сумму ряда частичной суммой его первых  членов, получим абсолютную погрешность, не превышающую модуля первого члена остатка этого ряда, то есть
членов, получим абсолютную погрешность, не превышающую модуля первого члена остатка этого ряда, то есть

Вычислить  с точностью до 0,0001. Для этого используем
с точностью до 0,0001. Для этого используем
ряд Маклорена (35.5) для  подставив значение угла в радианах:
подставив значение угла в радианах:

Если сравнить значения модулей первого и второго членов ряда с заданной погрешностью, получим:

Поскольку для третьего члена ряда получится:

то для вычисления  с заданной точностью достаточно оставить первые два члена ряда, поэтому
с заданной точностью достаточно оставить первые два члена ряда, поэтому

Полученное приближенное значение 0 9, 962 совпадает со значением  приведенным в справочных таблицах.
приведенным в справочных таблицах.
Вычислить  с точностью до 0,001.
с точностью до 0,001.
Превратим  до вида
до вида  где
где  чтобы можно было применить биномиальное ряд:
чтобы можно было применить биномиальное ряд:

Применим формулу биномиального ряда (35.6) 

Сравнивая последовательно члены ряда с допустимой погрешностью, видим, что  Итак, для приближенного вычисления числа
Итак, для приближенного вычисления числа  достаточно взять три члена ряда:
достаточно взять три члена ряда:

Вычисления с помощью знакододатних рядов
Рассмотрим примеры оценки погрешности при использовании ряда с положительными членами.
Вычислим число Эйлера  с точностью до
с точностью до 
Числовой ряд для приближенного подсчета e получим из разложения в ряд функции 

Оценим погрешность, возникающая при замене суммы ряда суммой первых его  членов. Заменим все сомножители факториалов, кроме единицы, двойками:
членов. Заменим все сомножители факториалов, кроме единицы, двойками:

Воспользуемся теоремой 34.4 – достаточным условием сходимости ряда к функции  – с учетом, что
– с учетом, что  и
и  где
где 


По условию задачи достаточно найти такое  чтобы выполнялось неравенство
чтобы выполнялось неравенство
 или
или 
Легко проверить, что это неравенство правильная при  так как
так как

Следовательно,

или

Вычислим  с точностью до 0,0001.
с точностью до 0,0001.
Для вычисления логарифмов, как правило, используется расписание в ряд функции:

Легко проверить, что этот ряд сходится на интервале 
Вычислим ln 2 с помощью ряда (35.11). Поскольку в данном примере 
 Таким образом,
Таким образом,

или

Для вычисления  с заданной точностью достаточно взять сумму первых четырех членов:
с заданной точностью достаточно взять сумму первых четырех членов:

Итак, отвергаем остаток

Оценим сделанную ошибку. Очевидно, что
 или
или 
Отсюда

Следовательно, окончательно получается:

Вычисление определенных интегралов
Рассмотрим приближенное вычисление определенных интегралов с помощью разложения в ряд подынтегральной функции.
Вычислить с точностью до 0,001 определенный интеграл 
Подынтегральная функция разложим в ряд Маклорена. Для этого в ряду (35.3) для функции  заменим
заменим 

Найдем интеграл от левой и правой частей этого ряда:

Полученный ряд является знакоперемежным, поэтому погрешность, возникающая при замене суммы ряда его частичной суммой, оценим по признаку Лейбница. Легко видеть, что при замене суммы ряда суммой первых пяти (по количеству) его членов, погрешность не превысит  (нумерация членов ряда начинается с нуля).
(нумерация членов ряда начинается с нуля).
Следовательно,

Отсюда окончательно с точностью до 0,001 получим:

Напомним, что первоначальная для функции  не выражается через конечное число элементарных функций.
не выражается через конечное число элементарных функций.
Вычислить приближенно  с точностью до 0,001.
с точностью до 0,001.
Для этого возьмем ряд Маклорена (35.5) для функции 

в котором заменим  на
на  Тогда получим:
Тогда получим:

Этот ряд сходится на всей числовой оси, в чем можно убедиться с помощью признака Даламбера и теоремы Абеля, как это уже делалось ранее. Интегрирование левой и правой частей последнего равенства в пределах от 0 до 1 дает:

По признаку Лейбница оценим погрешность, возникающая при замене суммы ряда суммой первых n его членов. Для этого вычислим последовательно члены ряда и сравним их значения с заданной погрешностью:

Следовательно, для вычисления интеграла с заданной точностью достаточно взять три члена ряда:

Использование рядов при решении дифференциальных уравнений
Если не удается интегрировать дифференциальное уравнение с помощью элементарных функций, то его решение во многих случаях можно найти в виде степенного ряда:

где коэффициенты  находят путем подстановки ряда в заданное уравнение и сравнением коэффициентов при одинаковых степенях разницы
находят путем подстановки ряда в заданное уравнение и сравнением коэффициентов при одинаковых степенях разницы  в левой и правой частях полученной равенства, то есть уже знакомым методом неопределенных коэффициентов.
в левой и правой частях полученной равенства, то есть уже знакомым методом неопределенных коэффициентов.
Можно также искать решение уравнения в виде ряда Тейлора

где для дифференциальных уравнений  -го порядка значение функции
-го порядка значение функции  и ее производных
и ее производных  в точке
в точке  определяются начальными условиями:
определяются начальными условиями:  а производные высших порядков
а производные высших порядков  последовательно находят с помощью дифференцирования левой и правой частей данного уравнения и подстановки вместо
последовательно находят с помощью дифференцирования левой и правой частей данного уравнения и подстановки вместо  числа
числа  Например, для дифференциальных уравнений 2-го порядка
Например, для дифференциальных уравнений 2-го порядка 

Найти частное решение уравнения 
Решение уравнения с учетом начального условия будем искать в виде:

поскольку 
Нужно определить только коэффициенты  так по условию
так по условию 
Найдем  почленно дифференцированием ряда на интервале сходимости:
почленно дифференцированием ряда на интервале сходимости:

и подставим ряды для  и
и  в исходное уравнение:
в исходное уравнение:

Приравниваем коэффициенты при одинаковых степенях  в левой и правой частях равенства и получим систему уравнений для нахождения коэффициентов:
в левой и правой частях равенства и получим систему уравнений для нахождения коэффициентов:

Итак, получили точное решение: 
Найти частное решение уравнения  при наличии начальных условий
при наличии начальных условий 
Решение уравнения будем искать в виде степенного ряда:
 поскольку
поскольку 
Теперь надо найти коэффициенты  воспользовавшись начальными условиями:
воспользовавшись начальными условиями: 
Дифференцируем степенной ряд:

Откуда находим:

Дифференцируем еще раз степенной ряд:

Подставляем в данное уравнение  получая равенство рядов:
получая равенство рядов:

Теперь приравниваем коэффициенты при одинаковых степенях 

Решая систему, получаем несколько первых неизвестных коэффициентов, а потом замечаем общую закономерность их образования:

Итак,

Ряды Фурье
В теории функциональных рядов важное место занимают ряды, которые названы именем французского математика и физика Фурье (1758-1830). Его «Аналитическая теория тепла»
(1822) стала началом теории тригонометрических рядов, получивших широкое применение в различных областях знаний, в которых рассматриваются колебательные процессы. Периодические функции, которые представляются в виде сумм тригонометрических рядов, применяют, например, при построении трендовых моделей для прогнозирования экономической динамики, а также для выявления скрытых периодических процессов, экономических циклов и др.
Тригонометрические ряды
Рассмотрим последовательность тригонометрических функций

Отметим, что последовательность (35.14) имеет следующие особенности:
1) функции этой последовательности являются периодическими с периодом 
2) функции этой последовательности являются ортогональными на отрезке  в том смысле, что интеграл на отрезке
в том смысле, что интеграл на отрезке  от произведения любых двух различных функций равна нулю, а интеграл на отрезке
от произведения любых двух различных функций равна нулю, а интеграл на отрезке  от квадрата любой функции отличен от нуля.
от квадрата любой функции отличен от нуля.
Действительно,


Аналогично находим

В случае, когда  получим:
получим:

Составим функциональный ряд, общий член которого имеет вид:

при этом для  возлагают
возлагают 
Тогда соответствующий функциональный ряд

или в сжатом виде

называется тригонометрическим рядом, а числа  называются коэффициентами тригонометрического ряда.
называются коэффициентами тригонометрического ряда.
Тригонометрический ряд, как и степенной, сходится к функции  , если существует граница
, если существует граница  -й частичной суммы
-й частичной суммы  которая равна
которая равна  :
:  В этом случае сумма ряда в точках его сходимости равен значению
В этом случае сумма ряда в точках его сходимости равен значению  , а относительно функции
, а относительно функции  говорят, что она разлагается в ряд, а именно:
говорят, что она разлагается в ряд, а именно:

Тригонометрические ряды фурье
Приведем условие единственности разложения и достаточные условия разложения функции  в тригонометрический ряд.
в тригонометрический ряд.
Теорема 35.1 (о единственности разложения функции в тригонометрический ряд). Если функция  является интегрированной на отрезке
является интегрированной на отрезке  и разлагается в тригонометрический ряд (35.18), который можно почленно интегрировать, то это расписание единственный.
и разлагается в тригонометрический ряд (35.18), который можно почленно интегрировать, то это расписание единственный.
Доказательство. Определим коэффициенты тригонометрического ряда (35.18).
С интегрируем равенство (35.18) на отрезке в результате получим:
в результате получим:

Для нахождения коэффициентов  при
при  домножим равенство (35.18) на
домножим равенство (35.18) на  и зинтегруемо на отрезке
и зинтегруемо на отрезке  левую и правую части этого равенства. Тогда, согласно второй свойством последовательности функций (35.14), получим:
левую и правую части этого равенства. Тогда, согласно второй свойством последовательности функций (35.14), получим:

Аналогично определяем коэффициенты  домножившы равенство (35.18) на
домножившы равенство (35.18) на 

Поскольку определенный интеграл – это определенное число, то коэффициенты ряда  определяются единственным образом.
определяются единственным образом.
Тригонометрический ряд (35.18) называется рядом Фурье, если его коэффициенты вычисляются по формулам (35.19) – (35.21).
Итак, для каждой из периодических интегрируемых функций можно вычислить коэффициенты Фурье  и формально построить ряд Фурье, но нельзя утверждать, что он совпадает, тем более к функции
и формально построить ряд Фурье, но нельзя утверждать, что он совпадает, тем более к функции  Заметим, что для коэффициентов ряда (35.18) можно выбрать любые числовые последовательности, а затем выяснить, где он совпадает и с которым функции.
Заметим, что для коэффициентов ряда (35.18) можно выбрать любые числовые последовательности, а затем выяснить, где он совпадает и с которым функции.
Приведем условия, которым должна удовлетворять функция  для ее ряд Фурье совпадал, и чтобы его сумма равна
для ее ряд Фурье совпадал, и чтобы его сумма равна  .
.
Теорема 35.2 (достаточные условия разложения функции в ряд Фурье). Если функция  на сегменте
на сегменте 
а) непрерывна или имеет конечное число точек разрыва первого рода;
б) монотонная или имеет конечное число экстремумов, то ряд Фурье совпадает. При этом:
1) в точках непрерывности функции  он сходится к самой функции, то есть его сумма
он сходится к самой функции, то есть его сумма 
2) в каждой точке разрыва  функции он сходится к полусуммы односторонних пределов функции слева и справа:
функции он сходится к полусуммы односторонних пределов функции слева и справа:

3) в обоих граничных точках промежутка  он сходится к полусуммы односторонних пределов функции
он сходится к полусуммы односторонних пределов функции 

Заметим, что теорему 35.2 называют теоремой Дирихле, а условия теоремы, по которым ряд Фурье сходится к функции  – условиями Дирихле.
– условиями Дирихле.
Теорема Дирихле применима и в случаях, когда на отрезке  задана произвольная функция
задана произвольная функция  , которая удовлетворяет ее условия, но не является периодической. Тогда строят функцию
, которая удовлетворяет ее условия, но не является периодической. Тогда строят функцию  определенную на всей числовой оси, периодом которой является промежуток
определенную на всей числовой оси, периодом которой является промежуток  при этом
при этом 
 Функцию
Функцию  называют периодическим продолжением функции
называют периодическим продолжением функции  с промежутка
с промежутка  на всю числовую ось.
на всю числовую ось.
Неполные ряды Фурье
Если функция  которая удовлетворяет условиям разложения в ряд Фурье на отрезке
которая удовлетворяет условиям разложения в ряд Фурье на отрезке  является четной, то коэффициенты Фурье вычисляются по формулам:
является четной, то коэффициенты Фурье вычисляются по формулам:

Ряд Фурье такой функции содержит только косинусы:

Если функция  которая разлагается в ряд Фурье, является нечетной, то коэффициенты Фурье будут такими:
которая разлагается в ряд Фурье, является нечетной, то коэффициенты Фурье будут такими:

Для нечетной функции ряд Фурье содержать только синусы:

Ряды (35.23) и (35.25) называют неполными.
Разложим в ряд Фурье функцию  с периодом
с периодом  что заданная так:
что заданная так:

График этой функции изображен на рис. 35.1.
Функция удовлетворяет условиям теоремы Дирихле, то есть разлагается в ряд Фурье. Она парная, поэтому коэффициенты ряда  Найдем
Найдем  и
и 
По формулам (35.22) имеем:

Для нахождения  применим формулу интегрирования по частям:
применим формулу интегрирования по частям:  для чего осуществляем разбиение подынтегрального выражения на части
для чего осуществляем разбиение подынтегрального выражения на части  и
и  Тогда
Тогда 

Рис. 35.1
Подсчитываем коэффициенты:

Таким образом,
 или
или

Ряд Фурье для функции с произвольным периодом
Рассмотрим функцию  которая является периодической с периодом
которая является периодической с периодом 

Период  называют стандартным. Положив
называют стандартным. Положив  каждую функцию
каждую функцию
с произвольным периодом сведем к функции со стандартным периодом. Расписание в ряд Фурье такой функции имеет вид:

а его коэффициенты определяются по формулам:

Рассмотрим также разложения в ряд Фурье функции  которая задана на отрезке
которая задана на отрезке  Такую функцию можно раскладывать (по желанию) в ряд, содержащий только синусы или только косинусы.
Такую функцию можно раскладывать (по желанию) в ряд, содержащий только синусы или только косинусы.
Если функция надо разложить в ряд по синусами, продолжаем ее на пивинтервал  так, чтобы
так, чтобы  В результате получаем нечетное функцию на интервале
В результате получаем нечетное функцию на интервале  Ряд Фурье в этом случае таков:
Ряд Фурье в этом случае таков:

Если функция надо разложить в ряд по косинусами, продолжаем ее на пивинтервал  так, чтобы
так, чтобы  В результате получаем парную функцию на интервале
В результате получаем парную функцию на интервале  Ряд Фурье в этом случае имеет вид:
Ряд Фурье в этом случае имеет вид:
 где
где 
Относительно сходимости рядов (35.29), (35.30) выполняется теорема, аналогичная теореме Дирихле, а именно: если функция  удовлетворяет условиям Дирихле, то ряды по синусами и косинусами совпадают. При этом: в точках, в которых функция непрерывна, суммы рядов равны
удовлетворяет условиям Дирихле, то ряды по синусами и косинусами совпадают. При этом: в точках, в которых функция непрерывна, суммы рядов равны  в точках разрыва функции
в точках разрыва функции  суммы равны среднему арифметическому левосторонней и правосторонней границ; на концах отрезка сумма ряда по косинусами совпадает со значением функции, а сумма ряда по синусами равна нулю.
суммы равны среднему арифметическому левосторонней и правосторонней границ; на концах отрезка сумма ряда по косинусами совпадает со значением функции, а сумма ряда по синусами равна нулю.

Рис. 35.2
Разложим в ряд Фурье по синусами функцию  заданную на промежутке
заданную на промежутке 
Чтобы получить расписание данной функции в ряд Фурье, имеет
только синусы, надо продлить ее на соседний слева интервал так, чтобы
так, чтобы  (рис. 35.2).
(рис. 35.2).
Находим коэффициенты Фурье:

Для вычисления  применим формулу интегрирования по частям
применим формулу интегрирования по частям

Таким образом,

Итак, получаем соотношение:

Заметим, что ряд (35.31) при  предоставляет разложения в ряд Фурье числа
предоставляет разложения в ряд Фурье числа 

Лекции:
- Найти общий интеграл дифференциального уравнения
- Алгебраические выражения
- Каноническое уравнение гиперболы
- Метод интервалов
- Обратная матрица примеры решения
- Кривизна и кручение пространственной кривой. Формулы Френе
- Исследовать ряд на условную сходимость
- Векторы в пространстве
- Основные геометрические фигуры
- Основные операции векторного анализа в криволинейных координатах
