Квадра́тное уравне́ние — алгебраическое уравнение второй степени с общим видом
в котором 



Корень уравнения 



Элементы квадратного уравнения имеют собственные названия[1]:
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент 
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.
Квадратное уравнение является разрешимым в радикалах, то есть его корни могут быть выражены через коэффициенты в общем виде.
Исторические сведения о квадратных уравнениях[править | править код]
Древний Вавилон[править | править код]
Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные уравнения[1]. Решение их в Древнем Вавилоне было тесно связано с практическими задачами, в основном такими, как измерение площади земельных участков, земельные работы, связанные с военными нуждами; наличие этих познаний также обусловлено развитием математики и астрономии вообще. Были известны способы решения как полных, так и неполных квадратных уравнений. Приведём примеры квадратных уравнений, решавшихся в Древнем Вавилоне, используя современную алгебраическую запись:
Правила решения квадратных уравнений во многом аналогичны современным, однако в вавилонских текстах не зафиксированы рассуждения, путём которых эти правила были получены.
Индия[править | править код]
Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.)[1]; Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: 

Корни квадратного уравнения на множестве действительных чисел[править | править код]
I способ. Общая формула для вычисления корней с помощью дискриминанта[править | править код]
Дискриминантом квадратного уравнения 

| Условие | 
|

|

|
| Количество корней | Два корня | Один корень кратности 2 (другими словами, два равных корня) |
Действительных корней нет |
| Формула |  (1) (1)
|

|
— |
Данный метод универсальный, однако не единственный.
II способ. Корни квадратного уравнения при чётном коэффициенте b[править | править код]
Для уравнений вида 

вместо формулы (1) для нахождения корней существует возможность использования более простых выражений[1].
Примечание: данные ниже формулы можно получить, подставив в стандартные формулы выражение b = 2k, через несложные преобразования.
| Дискриминант | Корни | |||
| неприведённое | приведённое | D > 0 | неприведённое | приведённое |
| удобнее вычислять значение
четверти дискриминанта: Все необходимые свойства при этом сохраняются. |
 . .
|

|

|
|
| D = 0 | 
|

|
III способ. Решение неполных квадратных уравнений[править | править код]
К решению неполных квадратных уравнений практикуется особый подход. Рассматриваются три возможных ситуации.
IV способ. Использование частных соотношений коэффициентов[править | править код]
Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.
Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту[править | править код]
Если в квадратном уравнении 



Доказательство
Способ 1. Сначала выясним, действительно ли такое уравнение имеет два корня (в том числе, два совпадающих):
.
Да, это так, ведь при любых действительных значениях коэффициентов 


Найдём эти корни:
.
В частности, если 

Способ 2.
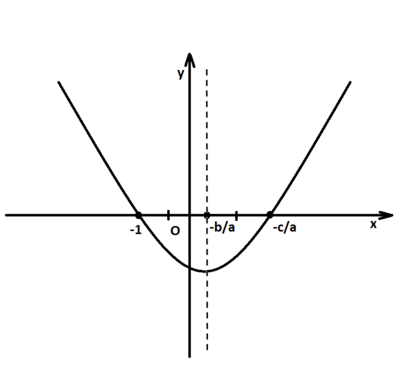
Геометрическая интерпретация: парабола, заданная аналитически указанной формулой, пересекает ось x в двух точках, абсциссами которых и являются корни, хотя бы один из которых равен -1
Используем геометрическую модель корней квадратного уравнения: их мы будем рассматривать как точки пересечения параболы 










- Отсюда следует, что перед решением какого-либо квадратного уравнения целесообразна проверка возможности применения к нему этой теоремы: сравнить сумму старшего коэффициента и свободного члена со вторым коэффициентом.
Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю[править | править код]
Если в квадратном уравнении сумма всех его коэффициентов равна нулю (


Доказательство
Способ 1. Прежде всего заметим, что из равенства 
Установим количество корней:
При любых значениях коэффициентов уравнение имеет хотя бы один корень: действительно, ведь при любых значениях коэффициентов 


Найдём эти корни:
что и требовалось доказать.
- В частности, если
, то уравнение имеет только один корень, которым является число
.
Способ 2. Пользуясь данным выше определением корня квадратного уравнения, обнаруживаем путём подстановки, что число 1 является таковым в рассматриваемом случае: 

- Отсюда следует, что перед решением уравнения стандартными методами целесообразна проверка применимости к нему этой теоремы, а именно сложение всех коэффициентов данного уравнения и установление, не равна ли нулю эта сумма.
V способ. Разложение квадратного трёхчлена на линейные множители[править | править код]
Если трёхчлен вида 





Рассматриваются некоторые частные случаи.
Использование формулы квадрата суммы (разности)[править | править код]
Если квадратный трёхчлен имеет вид 
Выделение полного квадрата суммы (разности)[править | править код]
Также названную формулу применяют, пользуясь методом, получившим названия «выделение полного квадрата суммы (разности)». Применительно к приведённому квадратному уравнению с введёнными ранее обозначениями, это означает следующее:
- прибавляют и отнимают одно и то же число:
.
- применяют формулу к полученному выражению, переносят вычитаемое и свободный член в правую часть:
- извлекают из левой и правой частей уравнения квадратный корень и выражают переменную:
Примечание: данная формула совпадает с предлагаемой в разделе «Корни приведённого квадратного уравнения», которую, в свою очередь, можно получить из общей формулы (1) путём подстановки равенства a = 1. Этот факт не просто совпадение: описанным методом, произведя, правда, некоторые дополнительные рассуждения, можно вывести и общую формулу, а также доказать свойства дискриминанта.
VI способ. Использование прямой и обратной теоремы Виета[править | править код]
Прямая теорема Виета (см. ниже) и обратная ей теорема позволяют решать приведённые квадратные уравнения устно, не прибегая к вычислениям по формуле (1).
Согласно обратной теореме, всякая пара чисел (число) 
- являются корнями уравнения
.
Подобрать устно числа, удовлетворяющие этим уравнениям, поможет прямая теорема. С её помощью можно определить знаки корней, не зная сами корни. Для этого следует руководствоваться правилом:
- 1) если свободный член отрицателен, то корни имеют различный знак, и наибольший по модулю из корней — знак, противоположный знаку второго коэффициента уравнения;
- 2) если свободный член положителен, то оба корня обладают одинаковым знаком, и это — знак, противоположный знаку второго коэффициента.
VII способ. Метод «переброски»[править | править код]
По своей сущности метод «переброски» является просто модификацией теоремы Виета.
Метод «переброски» — это сведение уравнения, которое нельзя привести так, чтобы все коэффициенты остались целыми, к приведённому уравнению с целыми коэффициентами:
- 1) умножаем обе части на старший коэффициент:
- 2) заменяем
Далее решаем уравнение относительно y по методу, описанному выше, и находим x = y/a.
Как можно заметить, в методе «переброски» старший коэффициент как раз «перебрасывается» к свободному члену.
Графическое решение квадратного уравнения[править | править код]
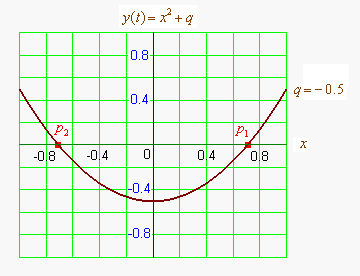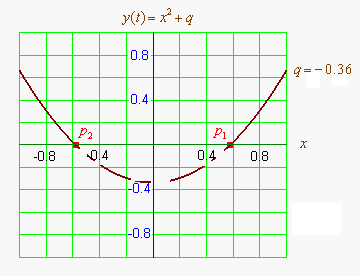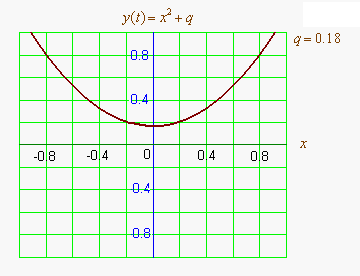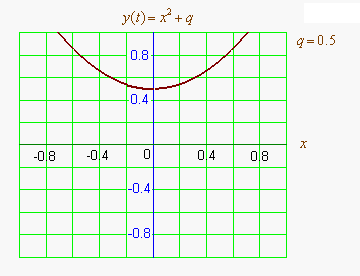
Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (в вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня (см. изображение справа.)
Если коэффициент 


Графический способ решения квадратных уравнений[править | править код]
Помимо универсального способа, описанного выше, существует так называемый графический способ. В общем виде этот способ решения рационального уравнения вида 


- Есть всего пять основных способов графического решения квадратных уравнений.
Приём I[править | править код]
Для решения квадратного уравнения 
и отыскиваются абсциссы точек пересечения такого графика с осью 
Приём II[править | править код]
Для решения того же уравнения этим приёмом уравнение преобразуют к виду
и строят в одной системе координат графики квадратичной функции 

Приём III[править | править код]
Данный приём подразумевает преобразование исходного уравнения к виду 





Приём IV[править | править код]
Квадратное уравнение преобразуют к виду 




Приём V[править | править код]
Квадратное уравнение преобразуют к особому виду:
затем
Совершив преобразования, строят графики линейной функции 


Решение квадратных уравнений с помощью циркуля и линейки[править | править код]
Описанные выше приёмы графического решения имеют существенные недостатки: они достаточно трудоёмки, при этом точность построения кривых — парабол и гипербол — низка. Указанные проблемы не присущи предлагаемому ниже методу, предполагающему относительно более точные построения циркулем и линейкой.
Чтобы произвести такое решение, нужно выполнить нижеследующую последовательность действий.
- Построить в системе координат
окружность с центром в точке
, пересекающую ось
в точке
.
- Далее возможны три случая:
Доказательство

Иллюстрация к доказательству.
Рассматриваемый способ предполагает построение окружности, пересекающей ось ординат в точках (точке), абсциссы которых являются корнями (или корнем) решаемого уравнения. Как нужно строить такую окружность? Предположим, что она уже построена. Окружность определяется однозначно заданием трёх своих точек. Пусть в случае, если корня два, это будут точки 









Итак, нами найдены необходимые для построения данные. Действительно, если мы построим окружность с центром в точке 

Корни квадратного уравнения на множестве комплексных чисел[править | править код]
Уравнение с действительными коэффициентами[править | править код]
Квадратное уравнение с вещественными коэффициентами 
Уравнение с комплексными коэффициентами[править | править код]
В комплексном случае квадратное уравнение решается по той же формуле (1) и указанным выше её вариантам, но различимыми являются только два случая: нулевого дискриминанта (один двукратный корень) и ненулевого (два корня единичной кратности).
Корни приведённого квадратного уравнения[править | править код]
Квадратное уравнение вида 

Мнемонические правила:
- Из «Радионяни»:
«Минус» напишем сначала,
Рядом с ним p пополам,
«Плюс-минус» знак радикала,
С детства знакомого нам.
Ну, а под корнем, приятель,
Сводится всё к пустяку:
p пополам и в квадрате
Минус прекрасное[2] q.
- Из «Радионяни» (второй вариант):
p, со знаком взяв обратным,
На два мы его разделим,
И от корня аккуратно
Знаком «минус-плюс» отделим.
А под корнем очень кстати
Половина p в квадрате
Минус q — и вот решенья,
То есть корни уравненья.
- Из «Радионяни» (третий вариант на мотив Подмосковных вечеров):
Чтобы x найти к половине p,
Взятой с минусом не забудь,
Радикал приставь с плюсом минусом,
Аккуратно, не как-нибудь.
А под ним квадрат половины p,
Ты, убавь на q и конец,
Будет формула приведенная,
Рассуждений твоих венец.
Будет формула приведенная,
Рассуждений твоих венец.
Теорема Виета [3][править | править код]
Формулировка для приведённого квадратного уравнения[править | править код]
Сумма корней приведённого квадратного уравнения 


С его помощью приведённые уравнения можно решать устно:
Для неприведённого квадратного уравнения[править | править код]
В общем случае, то есть для неприведённого квадратного уравнения 
На практике (следуя методу «переброски») для вычисления корней применяется модификация теорема Виета:
по которой можно устно находить ax1, ax2, а оттуда — сами корни:
Но у некоторых неприведённых уравнений корни можно устно угадать даже по стандартной теореме Виета:
Разложение квадратного трёхчлена на множители и теоремы, следующие из этого[править | править код]
Если известны оба корня квадратного трёхчлена, его можно разложить по формуле
(2)
Доказательство[править | править код]
Для доказательства этого утверждения воспользуемся теоремой Виета. Согласно этой теореме, корни 



В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.
- Из формулы (2) имеются два важных следствия:
Следствие 1[править | править код]
-
- Если квадратный трёхчлен раскладывается на линейные множители с вещественными коэффициентами, то он имеет вещественные корни.
Доказательство[править | править код]
Пусть 
.
Сопоставив полученное выражение с формулой (2), находим, что корнями такого трёхчлена являются 


Следствие 2[править | править код]
-
- Если квадратный трёхчлен не имеет вещественных корней, то он не раскладывается на линейные множители с вещественными коэффициентами.
Доказательство[править | править код]
Действительно, если мы предположим противное (что такой трёхчлен раскладывается на линейные множители), то, согласно следствию 1, он имеет корни в множестве 

Для квадратичной функции:
f (x) = x2 − x − 2 = (x + 1)(x − 2) действительной переменной x, x — координаты точки, где график пересекает ось абсцисс, x = −1 и x = 2, являются решениями квадратного уравнения: x2 − x − 2 = 0.
Уравнения, сводящиеся к квадратным[править | править код]
Алгебраические[править | править код]
Уравнение вида 
В общем случае оно решается методом введения новой переменной, то есть заменой 



Также при решении можно обойтись без замены, решив совокупность двух уравнений:
и
К примеру, если 
Такое уравнение 4-й степени называется биквадратным[4][1].
С помощью замены
к квадратному уравнению сводится уравнение
известное как возвратное или обобщённо-симметрическое уравнение[1].
Дифференциальные[править | править код]
Линейное однородное дифференциальное уравнение с постоянными коэффициентами второго порядка
подстановкой 
Если решения этого уравнения 

, где
и
— произвольные постоянные.
Для комплексных корней 
где A, B, C, φ — любые постоянные. Если решения характеристического уравнения совпадают 
Уравнения такого типа часто встречаются в самых разнообразных задачах математики и физики, например, в теории колебаний или теории цепей переменного тока.
Примечания[править | править код]
Литература[править | править код]
- Квадратное уравнение; Квадратный трёхчлен // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 133-136. — 352 с.
Ссылки[править | править код]
- Weisstein, Eric W. Quadratic Equation (англ.) на сайте Wolfram MathWorld.
- Вывод формулы корней полного квадратного уравнения. Решение приведённых квадратных уравнений и уравнений с чётным вторым коэффициентом Архивная копия от 28 января 2016 на Wayback Machine / Фестиваль педагогических идей «Открытый урок».
- Математические методы
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


на главную
Дискриминант
квадратного уравнения
Поддержать сайт![]()
Мы уже разобрали,
как решать квадратные уравнения.
Теперь давайте более подробно рассмотрим, что называют
дискриминантом квадратного уравнения.
Вернемся к нашей формуле для нахожденя корней квадратного уравнения.
Запомните!
![]()
Выражение «b2 − 4ac», которое находится под корнем,
принято называть дискриминантом и обозначать буквой «D».
По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:
x1;2 = , где «D = b2 − 4ac»
По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».
В зависимости от знака «D» (дискриминанта)
квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.
I случай
D > 0
(дискриминант больше нуля)
2x2 + 5x −7 = 0
D = b2 − 4ac
D = 52 − 4 · 2 · (−7)
D = 25 + 56
D = 81
D > 0
x1;2 =
x1;2 =
x1;2 =
| x1 = |
x2 = |
| x1 = |
x2 = |
| x1 = 1 |
x2 = −3 |
| x1 = 1 |
x2 = −3 |
Ответ: x1 = 1;
x2 = −3
Вывод: когда «D > 0» в квадратном уравнении два корня.
II случай
D = 0
(дискриминант равен нулю)
16x2 − 8x + 1 = 0
D = b2 − 4ac
D = (−8)2 − 4 · 16 · 1
D = 64 − 64
D = 0
x1;2 =
x1;2 =
x1;2 =
x =
x =
Ответ: x =
Вывод: когда «D = 0» в квадратном уравнении один корень.
III случай
D < 0
(дискриминант меньше нуля)
9x2 − 6x + 2 = 0
D = b2 − 4ac
D = (−6)2 − 4 · 9 · 2
D = 36 − 72
D = −36
D < 0
x1;2 =
x1;2 =
Ответ: нет действительных корней
Вывод: когда «D < 0» в квадратном уравнении нет корней.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Квадратные уравнения
Квадратным называется уравнение, содержащее переменную во второй степени.
В общем виде оно выглядит следующим образом:
(ax^{2} + bx + c = 0,) где (a neq 0, b, c) – некоторые числа.
ДИСКРИМИНАНТ:
Корни уравнения можно определить с помощью дискриминанта (D = b^{2} – 4ac) по формулам:
(leftlbrack begin{matrix} \ x_{1} = frac{- b + sqrt{D} }{2a} \ \ x_{1} = frac{- b – sqrt{D} }{2a} \ \ end{matrix} right. )
– Если дискриминант больше нуля – уравнение имеет два корня.
– Если дискриминант равен нулю – уравнение имеет один корень.
– Если дискриминант меньше нуля – корней нет.
Пример №1:
(x^{2} = 6x – 5)
-
Способ 1:
1. Преобразуем уравнение к стандартному виду, перенеся все слагаемые в левую часть:
(x^{2} – 6x + 5 = 0)
2. Определим дискриминант полученного уравнения:
(D = 6^{2} – 4 cdot 1 cdot 5 = 16 = 4^{2})
3. С помощью дискриминанта найдем корни по формулам:
(leftlbrack begin{matrix} \ x_{1} = frac{6 + 4 }{2} \ \ x_{1} = frac{6 – 4 }{2} \ \ end{matrix} right. ) (leftlbrack begin{matrix} x_{1} = 5 \ {text{ }x}_{2} = 1 \ end{matrix} right. )
Ответ: 5; 1.
СОКРАЩЁННЫЙ ДИСКРИМИНАНТ:
Существует второй способ решения квадратного уравнения. В случае, если коэффициент (b) – четное число, запишем его как (2k). Квадратное уравнение примет следующий вид:
(ax^{2} + 2kx + c = 0),( a neq 0, k, c) – некоторые числа.
Тогда вместо дискриминанта D будем использовать сокращённый дискриминант (frac{D}{4}), а формула его нахождения будет следующей:
(frac{D}{4} = k^{2} – ac)
Корни уравнения определим так же через сокращённый дискриминант:
(leftlbrack begin{matrix} \ x_{1} = frac{- k + sqrt{frac{D}{4}} }{a} \ \ x_{1} = frac{- k – sqrt{frac{D}{4}} }{a} \ \ end{matrix} right. )
-
Способ 2:
1. Преобразуем уравнение к стандартному виду, перенеся все слагаемые в левую часть:
(x^{2} – 6x + 5 = 0)
2. Выделим коэффициент k:
(x^{2} – 2 bullet 3x + 5 = 0)
(k = 3)
3. Определим сокращённый дискриминант полученного уравнения:
(frac{D}{4} = 3^{2} – 1 cdot 5 = 4 = 2^{2})
4. С помощью сокращённого дискриминанта найдем корни по формулам:
(leftlbrack begin{matrix} \ x_{1} = frac{3 + 2 }{1} \ \ x_{1} = frac{3 – 2 }{1} \ \ end{matrix} right. ) (leftlbrack begin{matrix} x_{1} = 5 \ {text{ }x}_{2} = 1 \ end{matrix} right. )
Ответ: 5; 1.
Как мы видим, ответ остался прежним, но числа, используемые при вычислениях, стали меньше. Это значит, что при работе с большими коэффициентами решение через сокращённый дискриминант уменьшает вероятность вычислительной ошибки.
ТЕОРЕМА ВИЕТА:
В некоторых случаях (например, (a = 1)) корни проще искать по теореме Виета, решая подбором систему уравнений:
(left{ begin{matrix} \ x_{1} cdot x_{2} = frac{c}{a} \ \ text{ x}_{1} + x_{2} = – frac{b}{a} \ \ end{matrix} right. )
Важно, что теорему Виета можно использовать при любом ненулевом коэффициенте а, формула представлена в общем виде. Однако если (a = 1,) то чаще всего нужно работать с целыми числами, а не с дробными, что упрощает подбор.
Следствия из теоремы Виета:
Используя теорему Виета, можно увидеть взаимосвязь между коэффициентами b и c и знаками корней уравнения.
Коэффициент c показывает, будут ли одинаковыми знаки корней:
-
Если( c > 0), то корни( x_{1}) и (x_{2} ) имеют одинаковый знак.
-
Если коэффициент (c < 0), корни (x_{1}) и (x_{2}) будут разных знаков.
Коэффициент b показывает, какой именно знак у корней, если он один, либо какой корень положительный, а какой отрицательный, если знаки разные.
-
Если (x_{1} + x_{2} = – b > 0) (т.е. сумма корней положительна), то возможны 2 варианта:
а) либо оба корня положительны;
б) либо модуль положительного корня больше модуля отрицательного.
-
Если( x_{1} + x_{2} = – b < 0) (т.е. сумма корней отрицательна), то опять же есть 2 варианта:
а) либо все корни отрицательны;
б) либо модуль положительного корня меньше модуля отрицательного.
Пример №2:
(x^{2} – 5x + 6 = 0)
1. Составим систему:
(left{ begin{matrix} \ x_{1} cdot x_{2} = 6 \ \ text{ }x_{1} + x_{2} = 5 \ \ end{matrix} right. )
Из следствий из т. Виета видим, что (c > 0), значит у корней одинаковые знаки.
Коэффициент (b > 0), значит оба корня положительные
2. Подберем (x_{1}, x_{2}) так, чтобы оба равенства выполнялись.
Видим, что произведение больше нуля, значит, либо оба числа отрицательные, либо оба положительные. Сумма положительна, значит, оба положительные.
Произведение корней раскладываем всеми способами на множители:
(6 = 2 cdot 3 = 1 cdot 6)
Через сумму делаем проверку:
(2 + 3 = 5)
(1 + 6 = 7)
В данном случае подходят числа
(x_{1} = 2, x_{2} = 3).
Ответ: 2; 3.
ЧАСТНЫЕ СЛУЧАИ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ:
-
Если (a + b + c = 0), то (x_{1} = 1, x_{2} = frac{c}{a})
Пример №3:
(x^{2} + 3x – 4 = 0)
1. Сложим все коэффициенты уравнения, чтобы проверить, является ли это уравнение примером частного случая. Действительно, коэффициенты в сумме дают 0:
(1 + 3 – 4 = 0)
2. Тогда по правилу: (x_{1} = 1, x_{2} = frac{c}{a}) получаем:
(leftlbrack frac{x_{1} = 1}{x_{2} = frac{–4}{1} = –4} right. )
Ответ: 1; -4.
-
Если (a + c = b), то (x_{1} = –1, x_{2} = – frac{c}{a})
Пример №4:
(x^{2} + 9x + 8 = 0)
1. Сложим коэффициенты a и c, чтобы проверить уравнение на соответствие второму частному случаю. Действительно (a + c = b):
(1 + 8 = 9)
2. Тогда по правилу: (x_{1} = –1, x_{2} = – frac{c}{a}) получаем:
(leftlbrack frac{x_{1} = –1}{x_{2} = – frac{8}{1} = –8} right. )
Ответ: – 1; – 8.
НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ
Неполное квадратное уравнение вида
(ax^{2} + bx = 0.)
Если отсутствует свободный член, то:
1.Раскладываем левую часть на множители:
(x(ax + b) = 0)
2. Приравниваем каждый из множителей к нулю:
(leftlbrack begin{matrix} \ begin{matrix} \ x = 0 \ ax + b = 0 \ \ end{matrix} \ end{matrix} right. )
3. Решаем каждое из полученных уравнений, получаем:
(leftlbrack begin{matrix} \ x = 0 \ x = – frac{b}{a} \ end{matrix} right. )
Неполное квадратное уравнение вида
(ax^{2} + c = 0.)
Если отсутствует слагаемое с переменной в первой степени, то:
1.Делим левую и правую часть на коэффициент (a neq 0.)
(x^{2} + frac{c}{a} = 0)
2. Смотрим на знак слагаемого без переменной.
Если (frac{c}{a} < 0), то раскладываем по формуле разности квадратов, приравниваем каждую из скобок к нулю и решаем полученные уравнения.
Если (frac{c}{a} = 0), то получаем единственное решение (x = 0.)
Если (frac{c}{a} > 0), то решений нет.

Общие сведения

Решение квадратных уравнений — одно из ключевых моментов в математике. Ещё древние вавилоняне и греки пытались найти закономерности при решении таких равенств. Но первым, кто описал методы нахождения дополнением квадрата, был индийский философ Будхаяма. Именно он предложил записывать уравнения в виде: ax 2 = c и ax 2 + bx = c. В дальнейшем способы усовершенствовались. Так, Евклид предложил метод геометрического вычисления ответа.
Но наиболее значимым стало открытие Буля. Изучая формулы различных уравнений, он пришёл к выводу, что выражения почти всегда можно упростить, заменив переменные другим набором, содержащим новые неизвестные. При этом, найдя их, определить первоначальные уже не составляет труда.
Такой способ был применён и к квадратному уравнению. Благодаря ему стало возможным упростить квадратичную форму с двумя переменными, используя дискриминант. Это понятие тесно связано с многочленом, имеющим следующий вид: d (m) = a 0 *mn + a 1 *mn-1 + a 2 *mn-2 + … + a n-1 *m + a n, где m — искомое неизвестное, a n, a n-1, a n-2, … a 1 и a 0 — числовые постоянные.
Термин «дискриминант» был придуман не математиками, но успешно стал ими использоваться при вычислении квадратичных функций. Произошёл он от латинского слова discriminans, что в дословном переводе означает «разделяющий». Важной величиной стало значение, придуманное Булем и имеющее вид b2 — 4ac. Учёный открыл, что после того как переменные линейно изменятся, дискриминант будет равняться первоначальному, умноженному на член, находимому из функции поведения неизвестных.
При решении равенств, содержащих формулу дискриминанта и его корней, используют формулу для быстрого определения количества возможных решений и их числового нахождения. Математически определение записывают следующим образом: p (x) = m + mx + ⋯ + mx, m ≠ 0, где: D (p) = m∏(m − m). То есть дискриминантом многочлена p (x) является сумма произведений корней на неизвестный коэффициент в основном поле их существования.
Смысл дискриминанта

Дискриминант — одно из эффективных решений квадратных выражений. С его помощью легко можно выявить, сколько корней имеет уравнение или установить, что их нет. Применять его можно как к полным квадратным равенствам, так и неполным. Но всё же во втором случае использовать дискриминант не нужно.
Эта тема изучается в седьмом и восьмом классе средней школы. Лучше понять смысл параметра поможет простой пример. Пусть имеется уравнение вида m2 + 2m — 8 = 0. Не имея понятие о дискриминанте, решение уравнения сводится к приведению его к формуле квадрата суммы m2 + 2m +1 — 1- 8 = 0. Добавление и вычитание единицы возможно, так как в итоге получается сложение с нулём.
Первые три члена представляют собой квадрат суммы, который можно свернуть по формуле сокращённого умножения до вида a2 +2ab + b2 = (a+b)2. Отсюда, применительно к рассматриваемому примеру, получится: (m + 1)2 — 1 — 8 = 0. После преобразований с переносом неизвестного в одну сторону (а известных — в другую) и раскрытием скобки получится равенство: (m + 1)2 = 9. То есть возможными решениями будут m = 2 для (m + 1) = 3 и m = -4 для (m + 1) = -3.
В общем виде все эти преобразования можно выполнить в следующей последовательности:

- Уравнение am2 + bm + c = 0 нужно переписать в приведённом виде, то есть разделить каждый член на первый коэффициент: m2 + bm / a + c / a = 0.
- Согласно формуле сокращённого умножения нужно добиться того, чтобы при неизвестном во втором члене стояло удвоенное произведение. Поэтому числитель и знаменатель нужно помножить на двойку: m2 + 2bm / 2a + c / a = 0.
- Полученное выражение стоит переписать в более наглядном виде m 2 + 2 m * (b /2 a) + c / a = 0. Это равенство являлось бы приведённым к формуле сокращённого умножения, если бы в последнем члене был квадрат.
- Ко второму члену следует прибавить и вычесть (b/2a)2. В итоге получится m2 + 2m * (b/2a) + (b/2a)2 — (b/2a)2 + c/a = 0.
- Первые три слагаемые — это классическая формула квадрата суммы. Применив её, получится: (m + b/2a)2 = (b/2a)2 — c/a.
- Затем нужно раскрыть скобки и привести к общему знаменателю. Получится конструкция вида (m + b/2a)2 = b 2 -4 ac /4 a 2.
- Умножив на 4a2 обе части. Выражение примет вид (2 am + b)2 = b 2 — 4 ac.
Многочлен b2 — 4ac было решено принять за дискриминант. Это выражение по сути и определяет возможность существования решений и количество корней. Выполнив его расчёт, фактически и находится ответ уравнения.
Взаимосвязь параметра

Объяснение дискриминанта имеет и графическое обоснование. Физически задача заключается в комплексном подходе установления взаимосвязи. Фактически это фиксирование нулей параболы уравнения, то есть точек, в которой она пересекает ось абсциссы. Знак при переменной в квадрате будет определять положение веток параболы. Они будут идти вверх при a > 0, и вниз, если a < 0.
Исходя из этого, дискриминант равняется отношению суммы или разности числового коэффициента, стоящего возле неизвестного в первой степени с корнем квадратным из b 2 — 4 ac к удвоенному произведению первого коэффициента в уравнениях x1 = (- b + √ b 2 — 4 ac) / 2a; x2 = (- b — √ b 2 — 4 ac) / 2a. Подкоренное выражение называют формулой сокращённого дискриминанта.
Дискриминант при нахождении корней уравнения может принимать три значения:

- Отрицательное. В случае, когда он меньше нуля, точный квадрат должен равняться числу с минусом, чего не может быть из-за свойств квадратной степени. Поэтому при таком положении вещей решений или действительных корней у уравнения нет. График уравнения не пересекает ось абсциссы.
- Равное нулю. Это состояние характеризуется уравнением вида: (2 am + b)2 = 0. Так как квадрат числа может быть равен нулю, только если это число нулевое, то рассматриваемое уравнение можно переписать как m = – b / 2a. Это и есть упрощённая формула при дискриминанте, равному 0. На графике существует лишь одна точка пересечения с осью абсциссы.
- Положительное. Это наиболее распространённый случай и самый тяжёлый для проведения расчётов. При нём из обеих частей уравнения теоремы (2 am + b) 2 = b 2 — 4 ac надо извлечь квадратный корень. В итоге получится 2am + b =± √D. Тут следует отметить следующее: минус возникает из-за того, что возводимое в квадрат число может быть как положительное, так и отрицательное. Например, 92 = 81 и -92 = 81. Из этого выражения можно выразить неизвестное. Оно будет равняться половинному значению m = (-b ± √D) / 2a. Парабола пересекает ось абсцисс в двух точках.
Последнее выражение является формулой корней квадратного уравнения. Именно с её помощью могут решаться равенства, в степени которых стоит двойка. Через дискриминант можно вычислять корни и уравнений больших порядков. Для этого используются приёмы понижения степени до квадратного. Но эти операции учащиеся начинают изучать на уроках в выпускном классе, когда проходят решение уравнений n-го порядка.
Типовые примеры
Даже зная правило поиска корней через дискриминант, научиться быстро вычислять корни уравнения не получится, если не практиковаться. Поэтому решение практических задач обязательно входит школьную в программу обучения:

- Дано равенство 6x2 — 13x +2 = 0. Нужно определить количество его корней, если они существуют, их числовые значения. В первую очередь нужно нарисовать таблицу, в которую выписаны все заданные коэффициенты. Так: a = 6; b = -13; c = 2. Эти значения нужно подставить в формулу дискриминанта и найти его: D = b2 — 4ac = (-13)2 — 4 * 6 *2 = 149 — 68 = 121. То есть D больше нуля. Значит, согласно правилу, уравнение будет иметь два корня. Теперь их нужно рассчитать: x1 = (13 + √126) / 2 * 6 = 2; x2 = (13 — √126) / 2 * 6 = 1/6. Задание решено.
-
Определить возможность решения уравнения 4m2 — 2m — 3 = 2. Для приведения к удобному виду двойку нужно перенести влево. В итоге получится 4m2 — 2m — 5 =0. Дискриминант равняется: D = 4 — 4 * 4 * (-5) = 4 + 80 = 84. Так как он больше нуля, то корней будет два. Тут сложность заключается в том, что нет целого числа, которое равнялось бы корню из √84. Однако, √84 = √4 * √21 = 2 √21. Используя формулы, получаем что m = (2 ± 2√21) / 2 * 4. Двойку можно вынести в числителе за скобки, получив тем самым удобную запись: m = (2 * (1 ±√21) / 2 * 4 = (1 ± √21) / 4. Это выражение и есть искомое решение.
-
Решить уравнение: x /3 — x2 / 4 + 1 /6 = 3x / 2 — 4x2 / 3. Для упрощения равенства нужно правую и левую сторону умножить на двенадцать: 12x / 3 — 12 * x2 / 4 + 12 /6 = (3 * 12x) / 2 — (4 * 12x2) / 3. Получится 4 x — 3 x 2 + 2 = 18 x — 16 x 2. Члены нужно привести к стандарту: 4 x — 3 x 2 + 2 — 18 x + 16 x 2 = 13 x 2 — 14 x + 2 = 0. Считаем дискриминант: D = (-14)2 — 4 * 13 * 2 = 92. Он больше нуля, поэтому есть смысл искать корни: X = (14 ± √ 92) / 2 * 13 = (14 ± 2 √ 23) / 2 * 13 = 2 (7±√23) / 2 *13 = (7± √23) /13.
Таким образом, любое выражение нужно стремиться переписать так, чтобы оно приняло классический вид. Это может быть умножение или деление на какое-либо число, поиск общего знаменателя. А уже после нужно искать дискриминант, по виду которого можно определить, есть ли смысл в дальнейшем нахождении корней уравнения.
Вычисления на онлайн-калькуляторе
Поиск решений уравнения через дискриминант — довольно простая тема. Необходимо запомнить всего две формулы и свойства, зависящие от значения дискриминанта. Но на практике попадаются примеры содержащие интегралы, логарифмы, экспоненциальные функции. При этом всё это может быть записано в виде сложных дробей.
Решая задания самостоятельно, даже имея большой опыт и знания, есть вероятность допущения ошибки. Поэтому при вычислении сложных примеров стоит использовать онлайн-калькуляторы.
Из сервисов, предлагающих такие услуги, можно отметить:
- Math.semestr;
- Kontrolnaya-rabota;
- Onlinemschool;
- Wpcalc;
- Webmath.

Эти российские сайты. Их интерфейс интуитивно понятен. Для выполнения вычислений не нужно указывать персональные данные или платить за услуги. От пользователя лишь требуется записать в предложенную форму квадратное уравнение или даже матрицу, состоящую из них. Программа автоматически выполнит нужный расчёт и предоставит пошаговое решение. Кроме того, на сайтах решателей уравнений содержится в кратком виде теоретический материал и типовые примеры с подробным решением.
Даже ничего не понимающий в дискриминантах человек, воспользовавшись онлайн-калькулятором несколько раз, сможет восполнить пробелы в знаниях, самостоятельно научиться решать примеры, узнает, как правильно должен писаться дискриминант. Использование онлайн-сайтов для математических решений позволяет сэкономить время и получить точный результат.
Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье “Решение неполных квадратных уравнений”.
Какие же квадратные уравнения называются полными? Это уравнения вида ах2 + b x + c = 0, где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.
D = b2 – 4ас .
В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.
Если дискриминант отрицательное число (D < 0),то корней нет.
Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),
тогда х1 = (-b – √D)/2a , и х2 = (-b + √D)/2a .
Например. Решить уравнение х2 – 4х + 4= 0.
D = 42 – 4 · 4 = 0
x = (- (-4))/2 = 2
Ответ: 2.
Решить уравнение 2х2 + х + 3 = 0.
D = 12 – 4 · 2 · 3 = – 23
Ответ: корней нет.
Решить уравнение 2х2 + 5х – 7 = 0.
D = 52 – 4 · 2 · (–7) = 81
х1 = (-5 – √81)/(2·2)= (-5 – 9)/4= – 3,5
х2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1
Ответ: – 3,5 ; 1.
Итак представим решение полных квадратных уравнений схемой на рисунке1.
По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида
Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида
ах2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х2 = 0, ошибочно можно решить, что
а = 1, b = 3 и с = 2. Тогда
D = 32 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).
Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах2, затем с меньшим – bx, а затем свободный член с.
При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.
Полное квадратное уравнение называется приведенным, если коэффициент при х2 равен единице и уравнение примет вид х2 + px + q = 0. Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а, стоящий при х2.
На рисунке 3 приведена схема решения приведенных квадратных уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.
Пример. Решить уравнение
3х2 + 6х – 6 = 0.
Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.
D = 62 – 4 · 3 · (– 6) = 36 + 72 = 108
√D = √108 = √(36 · 3) = 6√3
х1 = (-6 – 6√3 )/(2 · 3) = (6 ( -1- √(3)))/6 = –1 – √3
х2 = (-6 + 6√3 )/(2 · 3) = (6 ( -1+ √(3)))/6 = –1 + √3
Ответ: –1 – √3; –1 + √3
Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам , приведенным на схеме рисунка D1 = 32 – 3 · (– 6) = 9 + 18 = 27
√(D1) = √27 = √(9 · 3) = 3√3
х1 = (-3 – 3√3)/3 = (3 (-1 – √(3)))/3 = – 1 – √3
х2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3
Ответ: –1 – √3; –1 + √3. Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного  уравнения рисунок 3.
уравнения рисунок 3.
D2 = 22 – 4 · (– 2) = 4 + 8 = 12
√(D2) = √12 = √(4 · 3) = 2√3
х1= (-2 – 2√3)/2 = (2 (-1 – √(3)))/2 = – 1 – √3
х2= (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3
Ответ: –1 – √3; –1 + √3.
Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.










































