Как найти недостающее число в массиве

Let the given array be A with length N. Lets assume in the given array, the single empty slot is filled with 0.

We can find the solution for this problem using many methods including algorithm used in Counting sort. But, in terms of efficient time and space usage, we have two algorithms. One uses mainly summation, subtraction and multiplication. Another uses XOR. Mathematically both methods work fine. But programatically, we need to assess all the algorithms with main measures like

• Limitations(like input values are large(A[1...N]) and/or number of
  input values is large(N))
• Number of condition checks involved
• Number and type of mathematical operations involved

etc. This is because of the limitations in time and/or hardware(Hardware resource limitation) and/or software(Operating System limitation, Programming language limitation, etc), etc. Lets list and assess the pros and cons of each one of them.

Algorithm 1 :

In algorithm 1, we have 3 implementations.

1. Calculate the total sum of all the numbers(this includes the unknown missing number) by using the mathematical formula(1+2+3+...+N=(N(N+1))/2). Here, N=100. Calculate the total sum of all the given numbers. Subtract the second result from the first result will give the missing number.

   Missing Number = (N(N+1))/2) - (A[1]+A[2]+...+A[100])

2. Calculate the total sum of all the numbers(this includes the unknown missing number) by using the mathematical formula(1+2+3+...+N=(N(N+1))/2). Here, N=100. From that result, subtract each given number gives the missing number.

   Missing Number = (N(N+1))/2)-A[1]-A[2]-...-A[100]

   (Note:Even though the second implementation’s formula is derived from first, from the mathematical point of view both are same. But from programming point of view both are different because the first formula is more prone to bit overflow than the second one(if the given numbers are large enough). Even though addition is faster than subtraction, the second implementation reduces the chance of bit overflow caused by addition of large values(Its not completely eliminated, because there is still very small chance since (N+1) is there in the formula). But both are equally prone to bit overflow by multiplication. The limitation is both implementations give correct result only if N(N+1)<=MAXIMUM_NUMBER_VALUE. For the first implementation, the additional limitation is it give correct result only if Sum of all given numbers<=MAXIMUM_NUMBER_VALUE.)

3. Calculate the total sum of all the numbers(this includes the unknown missing number) and subtract each given number in the same loop in parallel. This eliminates the risk of bit overflow by multiplication but prone to bit overflow by addition and subtraction.

   //ALGORITHM
missingNumber = 0;
foreach(index from 1 to N)
{
missingNumber = missingNumber + index;
//Since, the empty slot is filled with 0,
//this extra condition which is executed for N times is not required.
//But for the sake of understanding of algorithm purpose lets put it.
if (inputArray[index] != 0)
missingNumber = missingNumber - inputArray[index];
}

In a programming language(like C, C++, Java, etc), if the number of bits representing a integer data type is limited, then all the above implementations are prone to bit overflow because of summation, subtraction and multiplication, resulting in wrong result in case of large input values(A[1...N]) and/or large number of input values(N).

Algorithm 2 :

We can use the property of XOR to get solution for this problem without worrying about the problem of bit overflow. And also XOR is both safer and faster than summation. We know the property of XOR that XOR of two same numbers is equal to 0(A XOR A = 0). If we calculate the XOR of all the numbers from 1 to N(this includes the unknown missing number) and then with that result, XOR all the given numbers, the common numbers get canceled out(since A XOR A=0) and in the end we get the missing number. If we don’t have bit overflow problem, we can use both summation and XOR based algorithms to get the solution. But, the algorithm which uses XOR is both safer and faster than the algorithm which uses summation, subtraction and multiplication. And we can avoid the additional worries caused by summation, subtraction and multiplication.

In all the implementations of algorithm 1, we can use XOR instead of addition and subtraction.

Lets assume, XOR(1...N) = XOR of all numbers from 1 to N

Implementation 1 => Missing Number = XOR(1...N) XOR (A[1] XOR A[2] XOR...XOR A[100])

Implementation 2 => Missing Number = XOR(1...N) XOR A[1] XOR A[2] XOR...XOR A[100]

Implementation 3 =>

//ALGORITHM
missingNumber = 0;
foreach(index from 1 to N)
{
    missingNumber = missingNumber XOR index;
    //Since, the empty slot is filled with 0,
    //this extra condition which is executed for N times is not required.
    //But for the sake of understanding of algorithm purpose lets put it.
    if (inputArray[index] != 0)
        missingNumber = missingNumber XOR inputArray[index];
}

All three implementations of algorithm 2 will work fine(from programatical point of view also). One optimization is, similar to

1+2+....+N = (N(N+1))/2

We have,

1 XOR 2 XOR .... XOR N = {N if REMAINDER(N/4)=0, 1 if REMAINDER(N/4)=1, N+1 if REMAINDER(N/4)=2, 0 if REMAINDER(N/4)=3}

We can prove this by mathematical induction. So, instead of calculating the value of XOR(1…N) by XOR all the numbers from 1 to N, we can use this formula to reduce the number of XOR operations.

Also, calculating XOR(1…N) using above formula has two implementations. Implementation wise, calculating

// Thanks to https://a3nm.net/blog/xor.html for this implementation
xor = (n>>1)&1 ^ (((n&1)>0)?1:n)

is faster than calculating

xor = (n % 4 == 0) ? n : (n % 4 == 1) ? 1 : (n % 4 == 2) ? n + 1 : 0;

So, the optimized Java code is,

long n = 100;
long a[] = new long[n];

//XOR of all numbers from 1 to n
// n%4 == 0 ---> n
// n%4 == 1 ---> 1
// n%4 == 2 ---> n + 1
// n%4 == 3 ---> 0

//Slower way of implementing the formula
// long xor = (n % 4 == 0) ? n : (n % 4 == 1) ? 1 : (n % 4 == 2) ? n + 1 : 0;
//Faster way of implementing the formula
// long xor = (n>>1)&1 ^ (((n&1)>0)?1:n);
long xor = (n>>1)&1 ^ (((n&1)>0)?1:n);

for (long i = 0; i < n; i++)
{
    xor = xor ^ a[i];
}
//Missing number
System.out.println(xor);

Учитывая массив n-1 различные целые числа в диапазоне от 1 до n, найти в нем пропущенное число за линейное время.

Например, рассмотрим массив {1, 2, 3, 4, 5, 7, 8, 9, 10} элементы которого различны и находятся в диапазоне от 1 до 10. Недостающее число — 6.

Потренируйтесь в этой проблеме

1. Использование формулы для суммы первых n Натуральные числа

Мы знаем, что сумма первых n натуральные числа можно вычислить по формуле 1 + 2 + … + n = n×(n+1)/2. Мы можем использовать эту формулу, чтобы найти пропущенное число.

Идея состоит в том, чтобы найти сумму целых чисел от 1 до n+1 используя приведенную выше формулу, где n размер массива. Также вычислите фактическую сумму целых чисел в массиве. Теперь недостающее число будет разницей между ними.

Этот подход демонстрируется ниже на C, Java и Python:

2. Использование оператора XOR

Мы знаем, что XOR двух одинаковых чисел отменяет друг друга. Мы можем воспользоваться этим фактом, чтобы найти недостающее число в массиве с ограниченным диапазоном.

Идея состоит в том, чтобы вычислить XOR всех элементов массива и вычислить XOR всех элементов от 1 до n+1, куда n размер массива. Теперь недостающее число будет XOR между ними.

Этот подход демонстрируется ниже на C, Java и Python:

Временная сложность обоих рассмотренных выше методов составляет O(n) и не требует дополнительного места, где n это размер ввода.

Если размер массива достаточно большой, а предполагаемое число пропущенных элементов не велико, можно еще и такой вариант.

$data = [1,2,5,6,9,11];

$prev = current($data);
$result = array_reduce($data, function($c, $item) use (&$prev){
                    if($item - $prev > 1){
                        $c = array_merge($c, range($prev + 1, $item - 1));
                    }
                    $prev = $item;
                    return $c;
                }, []);

А если специфика задачи такова, что у нас очень большой массив и получается очень много пропущенных значений (и не очень большом числе самих пропущенных интервалов), что использование функции range тратит не оправдано много памяти, то как по классическому примеру из справки по использованию генераторов можем сделать следующее:

$result =  function($data){
                $prev = current($data);
                $ranges = array_reduce($data, function($c, $item) use (&$prev){
                            if($item - $prev > 1)   $c[] = [$prev+1, $item -1];
                            $prev = $item;
                            return $c;
                          }, []);
                foreach($ranges as list($l, $h)){
                     while($l <= $h) yield $l++;
                }
            };

foreach($result($data) as $x) echo $x, "n";

в этом случае память будет тратится только на хранение пар значений, обозначающих края пропущенных отрезков.

Один из наиболее часто задаваемых вопросов на собеседованиях — найти пропущенное число в массиве на Java, C # или любом другом языке. Такого рода вопросы задаются не только в небольших стартапах, но и в некоторых крупнейших технических компаниях, таких как Google, Amazon, Facebook, Microsoft.

В простейшей версии этого вопроса надо найти недостающий элемент в массиве целых чисел, содержащем числа от 1 до 100. Это можно легко решить, вычислив предполагаемую сумму с помощью n (n + 1) /2 и отняв от нее сумму всех существующих элементов массива. Это также один из самых быстрых и эффективных способов, но его нельзя использовать, если массив содержит более одного пропущенного числа или если массив содержит дубликаты.

Это дает интервьюеру несколько хороших намеков, чтобы проверить, может ли кандидат применить свои знания в несколько иных состояниях или нет. Поэтому, если вы справитесь с первым подходом, вас попросят найти пропущенное число в массиве с дубликатами или с несколькими пропущенными числами. Это может быть более сложно, но вы скоро обнаружите, что другой способ найти пропущенное и повторяющееся число в массиве — это отсортировать его.

В отсортированном массиве вы можете сравнить, равно ли число ожидаемому следующему числу или нет.

Кроме того, вы также можете использовать BitSet в Java для решения этой проблемы — надо перебрать все записи и использовать набор битов, чтобы запомнить, какие числа установлены, а затем проверить на 0 бит. Запись с битом 0 является отсутствующим номером.

Найти пропущенное число в массиве: решение на Java

import java.util.Arrays;
import java.util.BitSet;
 
public class MissingNumberInArray {
 
    public static void main(String args[]) {

        // one missing number
        printMissingNumber(new int[]{1, 2, 3, 4, 6}, 6);
 
        // two missing number
        printMissingNumber(new int[]{1, 2, 3, 4, 6, 7, 9, 8, 10}, 10);
 
        // three missing number
        printMissingNumber(new int[]{1, 2, 3, 4, 6, 9, 8}, 10);
 
        // four missing number
        printMissingNumber(new int[]{1, 2, 3, 4, 9, 8}, 10);
 
        // Only one missing number in array
        int[] iArray = new int[]{1, 2, 3, 5};
        int missing = getMissingNumber(iArray, 5);
        System.out.printf("Missing number in array %s is %d %n",

                           Arrays.toString(iArray), missing);
    }

   /**
    * A general method to find missing values from an integer array in Java.
    * This method will work even if array has more than one missing element.
    */
    private static void printMissingNumber(int[] numbers, int count) {
        int missingCount = count - numbers.length;
        BitSet bitSet = new BitSet(count);
 
        for (int number : numbers) {
            bitSet.set(number - 1);
        }
 
        System.out.printf("Missing numbers in integer array %s, with total number %d is %n",
        Arrays.toString(numbers), count);
        int lastMissingIndex = 0;

        for (int i = 0; i < missingCount; i++) {
            lastMissingIndex = bitSet.nextClearBit(lastMissingIndex);
            System.out.println(++lastMissingIndex);
        }
 
    }

   /**
    * Java method to find missing number in array of size n containing

    * numbers from 1 to n only.
    * can be used to find missing elements on integer array of

    * numbers from 1 to 100 or 1 - 1000
    */
    private static int getMissingNumber(int[] numbers, int totalCount) {
        int expectedSum = totalCount * ((totalCount + 1) / 2);
        int actualSum = 0;
        for (int i : numbers) {
            actualSum += i;
        }
 
        return expectedSum - actualSum;
    }
 
}

Алгоритм с XOR

Мы можем использовать свойство XOR, чтобы получить решение этой проблемы, не беспокоясь о проблеме переполнения битов. Кроме того, XOR безопаснее и быстрее суммирования. Мы знаем свойство XOR, что XOR двух одинаковых чисел равен 0 ( A XOR A = 0). Если мы вычислим XOR всех чисел от 1 до N (это включает в себя неизвестное пропущенное число), а затем с этим результатом, XOR всех заданных чисел, общие числа будут отменены (так как A XOR A=0), и в конце мы получим пропущенное число. Если у нас нет проблемы переполнения битов, мы можем использовать как суммирование, так и алгоритмы на основе XOR, чтобы получить решение. Но алгоритм, использующий XOR, безопаснее и быстрее, чем алгоритм, который использует суммирование, вычитание и умножение. И мы можем избежать дополнительных забот, вызванных суммированием, вычитанием и умножением.

long n = 100;
long a[] = new long[n];

//XOR of all numbers from 1 to n
// n%4 == 0 ---> n
// n%4 == 1 ---> 1
// n%4 == 2 ---> n + 1
// n%4 == 3 ---> 0

//Slower way of implementing the formula
// long xor = (n % 4 == 0) ? n : (n % 4 == 1) ? 1 : (n % 4 == 2) ? n + 1 : 0;
//Faster way of implementing the formula
// long xor = (n>>1)&1 ^ (((n&1)>0)?1:n);

long xor = (n>>1)&1 ^ (((n&1)>0)?1:n);

for (long i = 0; i < n; i++)
{
   xor = xor ^ a[i];
}
//Missing number
System.out.println(xor);

Если вы нашли опечатку – выделите ее и нажмите Ctrl + Enter! Для связи с нами вы можете использовать info@apptractor.ru.

Время на прочтение
9 мин

Количество просмотров 9.8K

Добрый день. Сегодня хочется поговорить о том, как найти MEX (минимальное отсутствующие число во множестве).

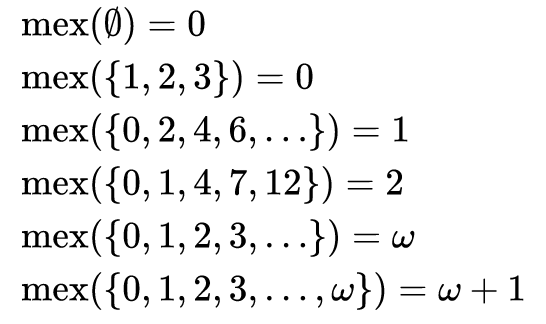
Мы разберем три алгоритма и посмотрим на их производительность.

Добро пожаловать под cut

Предисловие

Перед тем как начать, хотелось бы рассказать — почему я вообще за этот алгоритм взялся?
Всё началось с задачки на OZON.

Как видно из задачи, в математике результатом работы функции MEX на множестве чисел является наименьшим значением из всего набора, который не принадлежит этому множеству. То есть это минимальное значение набора дополнений. Название «MEX» является сокращением для «Minimum EXcluded» значение.

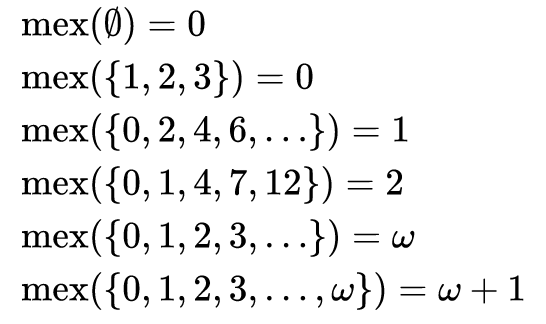
И покопавшись в сети, оказалось, что нет общепринятого алгоритма нахождения MEX…

Есть решения в лоб, есть варианты с дополнительными массивами, графами, но, как-то всё это раскидано по разным углам интернета и нет единой нормальной статьи по этому поводу. Вот и родилась идея — написать эту статью. В этой статье мы разберем три алгоритма нахождения MEX и посмотрим, что у нас получиться по скорости и по памяти.

Код будет на языке C#, но в целом там не будет специфичных конструкций.

Базовый код для проверок будет таким.

static void Main(string[] args)
        {
            //MEX = 2
            int[] values = new[] { 0, 12, 4, 7, 1 };
            
            //MEX = 5
            //int[] values = new[] { 0, 1, 2, 3, 4 };
            
            //MEX = 24
            //int[] values = new[] { 11, 10, 9, 8, 15, 14, 13, 12, 3, 2, 0, 7, 6, 5, 27, 26, 25, 4, 31, 30, 28, 19, 18, 17, 16, 23, 22, 21, 20, 43, 1, 40, 47, 46, 45, 44, 35, 33, 32, 39, 38, 37, 36, 58, 57, 56, 63, 62, 60, 51, 49, 48, 55, 53, 52, 75, 73, 72, 79, 77, 67, 66, 65, 71, 70, 68, 90, 89, 88, 95, 94, 93, 92, 83, 82, 81, 80, 87, 86, 84, 107, 106, 104 };
            
            //MEX = 1000
            //int[] values = new int[1000];
            //for (int i = 0; i < values.Length; i++) values[i] = i;
            
            //Импровизированный счетчик итераций
            int total = 0;
            int mex = GetMEX(values, ref total);
            Console.WriteLine($"mex: {mex}, total: {total}");
            Console.ReadKey();
        }

И еще один момент в статье я часто упоминаю слово «массив», хотя более правильным будет «множество», то заранее хочу извиниться перед теми, кому будет резать слух данное допущение.

Примечание 1 на основе комментариев: Многие придрались к O(n), мол все алгоритмы O(n) и по фигу, что «O» везде разное и не даёт фактически сравнить количество итераций. То для душевного спокойствия поменяем O на T. Где T более-менее понятная операция: проверка или присвоение. Так, как я понимаю, всем будет проще

Примечание 2 на основе комментариев: мы рассматриваем случай когда исходное множество НЕупорядоченное. Ибо сортировка это множества — тоже требует времени.

1) Решение в лоб

Как нам найти «минимальное отсутствующие число»? Самый простой вариант – сделать счетчик и перебирать массив до тех пор, пока не найдем число равное счетчику.

  static int GetMEX(int[] values, ref int total)
        {
            for (int mex = 0; mex < values.Length; mex++)
            {
                bool notFound = true;
                for (int i = 0; i < values.Length; i++)
                {
                    total++;
                    if (values[i] == mex)
                    {
                        notFound = false;
                        break;
                    }
                }
                if (notFound)
                {
                    return mex;
                }
            }
            return values.Length;
        }
    }

Максимально базовый случай. Сложность алгоритма составляет T(n*cell(n/2))… Т.к. для случая { 0, 1, 2, 3, 4 } нам нужно будет перебрать все числа т.к. совершить 15 операций. А для полностью заполного ряда из 100 числе 5050 операций… Так себе быстродейственность.

2) Просеивание

Второй по сложности вариант в реализации укладывается в T(n)… Ну или почти T(n), математики хитрят и не учитывают подготовку данных… Ибо, как минимум, — нам нужно знать максимальное число во множестве.

С точки зрения математики выглядит так.

Берется битовый массив S длинной m (где m – длина массива V) заполненный 0. И в один проход исходному множеству (V) в массиве (S) ставятся 1. После этого в один проход находим первое пустое значение. Все значения больше m можно просто игнорировать т.к. если в массиве «не хватает» значений до m, то явно будет меньше длины m.

static int GetMEX(int[] values, ref int total)
        {
            bool[] sieve = new bool[values.Length];
            for (int i = 0; i < values.Length; i++)
            {
                total++;
                var intdex = values[i];
                if (intdex < values.Length)
                {
                    sieve[intdex] = true;
                }
            }
            for (int i = 0; i < sieve.Length; i++)
            {
                total++;
                if (!sieve[i])
                {
                    return i;
                }
            }
            return values.Length;
        }

Т.к. «математики» – хитрые люди. То они говорят, что алгоритм T(n) ведь проход по исходному массиву всего один…

Вот сидят и радуются, что такой крутой алгоритм придумали, но правда такова.
Первое — нужно пройтись по исходному массиву и отметить это значение в массиве S T1(n)
Второе — нужно пройтись по массиву S и найти там первую попавшеюся свободную ячейку T2(n)
Итого, т.к. все операции в целом не сложные можно упростить все расчеты до T(n*2)

Но это явно лучше решения в лоб… Давайте проверим на наших тестовых данных:

1. Для случая { 0, 12, 4, 7, 1 }: В лоб: 11 итераций, просеивание: 8 итераций
2. Для случая { 0, 1, 2, 3, 4 }: В лоб: 15 итераций, просеивание: 10 итераций
3. Для случая { 11,…}: В лоб: 441 итерация, просеивание: 108 итерация
4. Для случая { 0,…,999}: В лоб: 500500 итераций, просеивание: 2000 итераций

Дело в том, что если «отсутствующее значение» является небольшим числом, то в таком случае — решение в лоб оказывается быстрее, т.к. не требует тройного прохода по массиву. Но в целом, на больших размерностях явно проигрывает просеиванию, что собственно неудивительно.
С точки зрения «математика» – алгоритм готов, и он великолепен, но вот с точки зрения «программиста» – он ужасен из-за объема оперативной памяти, израсходованной впустую, да и финальный проход для поиска первого пустого значения явно хочется ускорить.

Давайте сделаем это, и оптимизируем код.

static int GetMEX(int[] values, ref int total)
        {
            var max = values.Length;
            var size = sizeof(ulong) * 8;
            ulong[] sieve = new ulong[(max / size) + 1];
            ulong one = 1;
            for (int i = 0; i < values.Length; i++)
            {
                total++;
                var intdex = values[i];
                if (intdex < values.Length)
                {
                    sieve[values[i] / size] |= (one << (values[i] % size));
                }
            }

            var maxInblock = ulong.MaxValue;
            for (int i = 0; i < sieve.Length; i++)
            {
                total++;
                if (sieve[i] != maxInblock)
                {
                    total--;
                    for (int j = 0; j < size; j++)
                    {
                        total++;
                        if ((sieve[i] & (one << j)) == 0)
                        {
                            return i * size + j;
                        }
                    }
                }
            }
            return values.Length;
        }

Что мы тут сделали. Во-первых, в 64 раза уменьшили количество оперативной памяти, которая необходима.

var size = sizeof(ulong) * 8;
ulong[] sieve = new ulong[(max / size) + 1];

Во-вторых, оптимизировали финальную проверку: мы проверяем сразу блок на вхождение первых 64 значений: if (sieve[i] != maxInblock) и как только убедились в том, что значение блока не равно бинарным 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111, только тогда ищем уже вхождение на уровне блока: ((sieve[i] & (one << j)) == 0

В итоге алгоритм просеивание нам дает следующие результат:

1. Для случая { 0, 12, 4, 7, 1 }: просеивание: 8 итераций, просеивание с оптимизацией: 8 итераций
2. Для случая { 0, 1, 2, 3, 4 }: просеивание: 10 итераций, просеивание с оптимизацией: 11 итераций
3. Для случая { 11,…}: просеивание: 108 итерация, просеивание с оптимизацией: 108 итерации
4. Для случая { 0,…,999}: просеивание: 2000 итераций, просеивание с оптимизацией: 1056 итераций

Так, что в итоге в теории по скорости?

T(n*3) мы превратили в T(n*2) + T(n / 64) в целом, чуть увеличили скорость, да еще объём оперативной памяти уменьшили аж в 64 раза. Что хорошо)

3) Сортировка

Как не сложно догадаться, самый простой способ найти отсутствующий элемент во множестве – это иметь отсортированное множество.

Самый быстрый алгоритм сортировки — это «quicksort» (быстрая сортировка), которая имеет сложность в T1(n log(n)). И итого мы получим теоретическую сложность для поиска MEX в T1(n log(n)) + T2(n)

static int GetMEX(int[] values, ref int total)
        {
            total = values.Length * (int)Math.Log(values.Length);
            values = values.OrderBy(x => x).ToArray();
            for (int i = 0; i < values.Length - 1; i++)
            {
                total++;
                if (values[i] + 1 != values[i + 1])
                {
                    return values[i] + 1;
                }
            }
            return values.Length;
        }

Шикарно. Ничего лишнего.

Проверим количество итераций

1. Для случая { 0, 12, 4, 7, 1 }: просеивание с оптимизацией: 8, сортировка: ~7 итераций
2. Для случая { 0, 1, 2, 3, 4 }: просеивание с оптимизацией: 11 итераций, сортировка: ~9 итераций
3. Для случая { 11,…}: просеивание с оптимизацией: 108 итерации, сортировка: ~356 итераций
4. Для случая { 0,…,999}: просеивание с оптимизацией: 1056 итераций, сортировка: ~6999 итераций

Здесь указаны средние значения, и они не совсем справедливы. Но в целом: сортировка — не требует дополнительной памяти и явно позволяет упростить последний шаг в переборе.
Примечание: values.OrderBy(x => x).ToArray() – да я знаю, что тут выделилась память, но если делать по уму, то можно изменить массив, а не копировать его…

Вот у меня и возникла идея оптимизировать quicksort для поиска MEX. Данный вариант алгоритма я не находил в интернете, ни с точки зрения математики, и уж тем более с точки зрения программирования. То код будем писать с 0 по дороге придумывая как он будет выглядеть 😀

Но, для начала, давайте вспомним как вообще работает quicksort. Я бы ссылку дал, но нормальное пояснение quicksort на пальцах фактически нет, создается ощущение, что авторы пособий сами разбираются в алгоритме пока его рассказывают про него…

Так вот, что такое quicksort:
У нас есть неупорядоченный массив { 0, 12, 4, 7, 1 }
Нам потребуется «случайное число», но лучше взять любое из массива, — это называется опорное число (T).

И два указателя: L1 – смотрит на первый элемент массива, L2 смотрит на последний элемент массива.

0, 12, 4, 7, 1
L1 = 0, L2 = 1, T = 1 (T взял тупа последние)

Первый этап итерации:
Пока работам только с указателем L1
Сдвигаем его по массиву вправо пока не найдем число больше чем наше опорное.
В нашем случае L1 равен 8

Второй этап итерации:
Теперь сдвигаем указатель L2
Сдвигаем его по массиву влево пока не найдем число меньше либо равное чем наше опорное.
В данном случае L2 равен 1. Т.к. я взял опорное число равным крайнему элементу массива, а туда же смотрел L2.

Третей этап итерации:
Меняем числа в указателях L1 и L2 местами, указатели не двигаем.
И переходим к первому этапу итерации.
Эти этапы мы повторяем до тех пор, пока указатели L1 и L2 не будет равны, не значения по ним, а именно указатели. Т.е. они должны указывать на один элемент.

После того как указатели сойдутся на каком-то элементе, обе части массива будут всё еще не отсортированы, но уже точно, с одной стороны «обединённых указателей (L1 и L2)» будут элементы, которые меньше T, а со второй больше T. Именно этот факт нам и позволяет разбить массив на две независимые группы, которые можно сортировать в разных потоках в дальнейших итерациях.

Статья на wiki, если и у меня непонятно написанно

Напишем Quicksort

static void Quicksort(int[] values, int l1, int l2, int t, ref int total)
        {
            var index = QuicksortSub(values, l1, l2, t, ref total);
            if (l1 < index)
            {
                Quicksort(values, l1, index - 1, values[index - 1], ref total);
            }
            if (index < l2)
            {
                Quicksort(values, index, l2, values[l2], ref total);
            }
        }

        static int QuicksortSub(int[] values, int l1, int l2, int t, ref int total)
        {
            for (; l1 < l2; l1++)
            {
                total++;
                if (t < values[l1])
                {
                    total--;
                    for (; l1 <= l2; l2--)
                    {
                        total++;
                        if (l1 == l2)
                        {
                            return l2;
                        }
                        if (values[l2] <= t)
                        {
                            values[l1] = values[l1] ^ values[l2];
                            values[l2] = values[l1] ^ values[l2];
                            values[l1] = values[l1] ^ values[l2];
                            break;
                        }
                    }
                }
            }
            return l2;
        }

Проверим реальное количество итераций:

1. Для случая { 0, 12, 4, 7, 1 }: просеивание с оптимизацией: 8, сортировка: 11 итераций
2. Для случая { 0, 1, 2, 3, 4 }: просеивание с оптимизацией: 11 итераций, сортировка: 14 итераций
3. Для случая { 11,…}: просеивание с оптимизацией: 108 итерации, сортировка: 1520 итераций
4. Для случая { 0,…,999}: просеивание с оптимизацией: 1056 итераций, сортировка: 500499 итераций

Попробуем поразмышлять вот над чем. В массиве { 0, 4, 1, 2, 3 } нет недостающих элементов, а его длина равна 5. Т.е. получается, массив в котором нет отсутствующих элементов равен длине массива — 1. Т.е. m = { 0, 4, 1, 2, 3 }, Length(m) == Max(m) + 1. И самое главное в этом моменте, что это условие справедливо, если значения в массиве переставлены местами. И важно то, что это условие можно распространить на части массива. А именно вот так:
{ 0, 4, 1, 2, 3, 12, 10, 11, 14 } зная, что в левой части массива все числа меньше некого опорного числа, например 5, а в правой всё что больше, то нет смысла искать минимальное число слева.

Т.е. если мы точно знаем, что в одной из частей нет элементов больше определённого значения, то само это отсутствующие число нужно искать во второй части массива. В целом так работает алгоритм бинарного поиска.

В итоге у меня родилась мысль упростить quicksort для поиска MEX объединив его с бинарным поиском. Сразу скажу нам не нужно будет полностью отсортировывать весь массив только те части, в которых мы будем осуществлять поиск.

В итоге получаем код

static int GetMEX(int[] values, ref int total)
        {
            return QuicksortMEX(values, 0, values.Length - 1, values[values.Length - 1], ref total);
        }

        static int QuicksortMEX(int[] values, int l1, int l2, int t, ref int total)
        {
            if (l1 == l2)
            {
                return l1;
            }
            int max = -1;
            var index = QuicksortMEXSub(values, l1, l2, t, ref max, ref total);
            if (index < max + 1)
            {
                return QuicksortMEX(values, l1, index - 1, values[index - 1], ref total);
            }
            if (index == values.Length - 1)
            {
                return index + 1;
            }
            return QuicksortMEX(values, index, l2, values[l2], ref total);
        }

        static int QuicksortMEXSub(int[] values, int l1, int l2, int t, ref int max, ref int total)
        {
            for (; l1 < l2; l1++)
            {
                total++;
                if (values[l1] < t && max < values[l1])
                {
                    max = values[l1];
                }
                if (t < values[l1])
                {
                    total--;
                    for (; l1 <= l2; l2--)
                    {
                        total++;
                        if (values[l2] == t && max < values[l2])
                        {
                            max = values[l2];
                        }
                        if (l1 == l2)
                        {
                            return l2;
                        }
                        if (values[l2] <= t)
                        {
                            values[l1] = values[l1] ^ values[l2];
                            values[l2] = values[l1] ^ values[l2];
                            values[l1] = values[l1] ^ values[l2];
                            break;
                        }
                    }
                }
            }
            return l2;
        }

Проверим количество итераций

1. Для случая { 0, 12, 4, 7, 1 }: просеивание с оптимизацией: 8, сортировка MEX: 8 итераций
2. Для случая { 0, 1, 2, 3, 4 }: просеивание с оптимизацией: 11 итераций, сортировка MEX: 4 итераций
3. Для случая { 11,…}: просеивание с оптимизацией: 108 итерации, сортировка MEX: 1353 итераций
4. Для случая { 0,…,999}: просеивание с оптимизацией: 1056 итераций, сортировка MEX: 999 итераций

Итого

Мы получили разные варианты поиска MEX. Какой из них лучше — решать вам.

В целом. Мне больше всех нравится просеивание, и вот по каким причинам:
У него очень предсказуемое время выполнения. Более того, этот алгоритм можно легко использовать в многопоточном режиме. Т.е. разделить массив на части и каждую часть пробегать в отдельном потоке:

for (int i = minIndexThread; i < maxIndexThread; i++)
sieve[values[i] / size] |= (one << (values[i] % size));

Единственное, нужен lock при записи sieve[values[i] / size]. И еще — алгоритм идеален при выгрузке данных из базы данных. Можно грузить пачками по 1000 штук например, в каждом потоке и всё равно он будет работать.

Но если у нас строгая нехватка памяти, то сортировка MEX – явно выглядит лучше.

P.S.

Я начал рассказ с конкурса на OZON в котором я пробовал участвовать, сделав «предварительный вариант» алгоритма просеиванья, приз за него я так и не получил, OZON счел его неудовлетворительным… По каким именно причинам — он так и не сознался… Да и кода победителя я тоже не видел. Может у кого-то есть идеи как можно решить задачу поиска MEX лучше?