Одной из наиболее интересных тем школьной программы по физике является «сила трения». Она достаточно доступна в понимании учащихся и быстро поддается осмыслению, так как её наличие можно проверить, не отходя от парты.
Стоит начать с определения самого понятия. Сила трения — есть итог сопротивления движению физических тел. Иными словами, она появляется, когда происходит относительное перемещение между взаимодействующими телами.
Различают по его области:
- Внешнее — зарождается при непосредственном движении действующих друг на друга тел,
- Внутреннее — возникает между частями одного предмета.
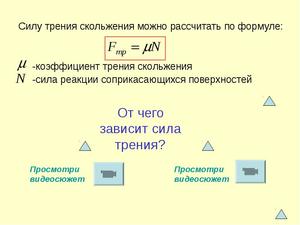
Основная формула силы трения
Ввиду отсутствия в природе абсолютно твердых тел сила трения существует постоянно, и его наличие разъясняют действием даже микроскопически шероховатых поверхностей между собой. Результат при умножении силы реакции опоры на коэффициент трения есть:
F тр.= N * k
В СИ (международная система единиц) измеряется F тр. в Ньютонах (Н).
Нужно знать, что противоположно ходу движения направлена F тр., а N против силы тяжести и перпендикулярно поверхности. Безразмерная величина k не зависит от площади соприкасания тел, а зависит от степени шероховатости и типа материалов трущихся тел.
Необходимо иметь полное представление о физических величинах, участвующих в основной формуле. В первую очередь, F тр. это векторная величина, то есть она имеет направление. Следовательно, нужно знать направление и точку ее приложения. Приложена она в области соприкосновения поверхностей, а направлена против движения объекта.
Из названия нормальной реакции опоры понятно, что она показывает реакцию самой опоры, а возникает на молекулярном уровне. Направлена против силы, с которой предмет давит на поверхность.
Коэффициент пропорциональности k является связующим звеном между F тр. и силой нормальной реакции. Если k соответствует наибольшей F тр. пок., то в большинстве своих случаев он больше коэффициента скольжения.

Коротко о типах трения
Отличают такие разновидности, как:
- покоя,
- скольжения,
- качения.
Прилагая минимум F тр. пок., объект начнет свое движение. Она не определяется достаточно точно и зависит от приложенного усилия. Поразительно, но именно оно разгоняет тела. F тр. пок. не исчезает бесследно, после того, как привела в движение предмет, она превращается в F тр. , а, следовательно, не может бесконечно увеличиваться — есть верхний максимальный предел, равный по величине F тр. скольжения.
В названии «сила трения качения» скрыта суть самого явления. Она намного меньше трения скольжения и возникает во время качения одного тела по-другому, скорости их соприкосновения в точках касания одинаковы по направлению и значению.
Типы трения скольжения различают по физике взаимодействия:
- Вязкое. Появляется, когда взаимодействующие тела разделены между собой слоем жидкости, газа или иного смазочного материала различного размера. F тр. пок. отсутствует. Абсолютная величина этой силы сопротивления зависит от скорости: прямо пропорциональна скорости при малых скоростях движение и прямо пропорциональна ее квадрату при больших.
- Сухое. Дополнительным смазочным материалом соприкасающиеся тела не разделены. Может возникать даже при отсутствии относительного движения предметов. Особый пример — F тр. покоя . Существует вид сухого взаимодействия с сухой смазкой, как пример, со слоем графитового порошка.
- Граничное. Одновременное содержание и слоев, и частей отличных по природе.
- Смешанное. Имеются участки частичной смазки.
Формула выглядит следующим образом:
F тр. скольж. = μN .
Использовались такие физические величины, как, μ — коэффициент трения скольжения, N — сила реакции опоры.
Также можно вывести формулу через массу:
F <> μmg,
где N = mg, g — свободного падения.

Формула коэффициента пропорциональности μ
В формуле, описывающей процесс приложения F тр. к любому телу, принимает участие коэффициент пропорциональности. Он выражается исключительно числами и почти при любых обстоятельствах меньше единицы. Это величина, зависящая от материала взаимодействующих объектов и от степени обработки их поверхностей.
μ =FN .
Данную формулу можно вывести через массу и ускорение свободного падения:
μ =Fmg, где замена N происходит ранее описанным способом.
Трение повинуется третьему закону Ньютона, так как является разновидностью взаимодействия. А конкретно, если F тр. действует на один из объектов, то такая же в точности сила по модулю, но устремленная противоположно оказывает воздействие и на второе тело. Все силы противодействия возникают как результат молекулярного и атомного взаимодействия трущихся тел.
В заключение приведены слова Шарля Гийом (1861−1938): «Вообразим, что трение может быть устранено совершенно. Тогда никакие тела, будь они величиною с каменную глыбу или малы, как песчинка, никогда не удержатся одно на другом: все будет скользить и катиться, пока не окажется на одном уровне. Не будь трения, Земля представляла бы шар без неровностей, подобно жидкому».
Видео
Это видео поможет вам понять, что такое сила трения.

{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения – зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу

mu = dfrac{F_{тр}}{mg}
Fтр – сила трения
m – масса тела
g – ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона

mu = tg(alpha)
α – угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Как найти силу трения скольжения
В школьных задачах по физике на определение силы трения скольжения в основном рассматривается прямолинейное равномерное или прямолинейное равноускоренное движение тела. Посмотрите, как можно найти силу трения в разных случаях зависимости от условий задачи. Чтобы правильно оценить воздействие сил и составить уравнение движения, всегда рисуйте чертеж.

Инструкция
Случай 1. Формула для силы трения скольжения: Fтр = мN, где м – коэффициент трения скольжения, N – сила реакции опоры, Н. Для тела, скользящего по горизонтальной плоскости, N = G = mg, где G – вес тела, Н; m – масса тела, кг; g – ускорение свободного падения, м/с2. Значения безразмерного коэффициента м для данной пары материалов даны в справочной литературе. Зная массу тела и пару материалов. скользящих друг относительно друга, найдите силу трения.
Случай 2. Рассмотрите тело, скользящее по горизонтальной поверхности и двигающееся равноускоренно. На него действуют четыре силы: сила, приводящее тело в движение, сила тяжести, сила реакции опоры, сила трения скольжения. Так как поверхность горизонтальная, сила реакции опоры и сила тяжести направлены вдоль одной прямой и уравновешивают друг друга. Перемещение описывает уравнение: Fдв – Fтр = ma; где Fдв – модуль силы, приводящей тело в движение, Н; Fтр – модуль силы трения, Н; m – масса тела, кг; a – ускорение, м/с2. Зная значения массы, ускорения тела и силы, воздействующей на него, найдите силу трения. Если эти значения не заданы прямо, посмотрите, есть ли в условии данные, из которых можно найти эти величины.
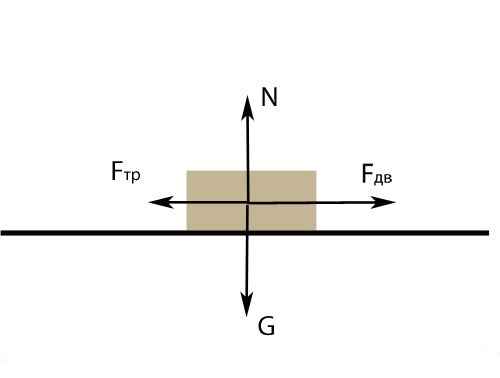
Пример задачи 1: на брусок массой 5 кг, лежащий на поверхности, воздействуют силой 10 Н. В результате брусок двигается равноускоренно и проходит 10 метров за 10 секунд. Найдите силу трения скольжения.
Уравнение для движения бруска:Fдв – Fтр = ma. Путь тела для равноускоренного движения задается равенством: S = 1/2at^2. Отсюда вы можете определить ускорение: a = 2S/t^2. Подставьте данные условия: а = 2*10/10^2 = 0,2 м/с2. Теперь найдите равнодействующую двух сил: ma = 5*0,2 = 1 Н. Вычислите силу трения: Fтр = 10-1 = 9 Н.
Случай 3. Если тело на горизонтальной поверхности находится в состоянии покоя, либо двигается равномерно, по второму закону Ньютона силы находятся в равновесии : Fтр = Fдв.
Пример задачи 2: бруску массой 1 кг, находящемуся на ровной поверхности, сообщили импульс, в результате которого он проехал 10 метров за 5 секунд и остановилось. Определите силу трения скольжения.
Как и в первом примере, на скольжение бруска влияют сила движения и сила трения. В результате этого воздействия тело останавливается, т.е. приходит равновесие. Уравнение движения бруска: Fтр = Fдв. Или: N*м = ma. Брусок скользит равноускоренно. Рассчитайте его ускорение подобно задаче 1: a = 2S/t^2. Подставьте значения величин из условия: а = 2*10/5^2 = 0,8 м/с2. Теперь найдите силу трения: Fтр = ma = 0,8*1 = 0,8 Н.
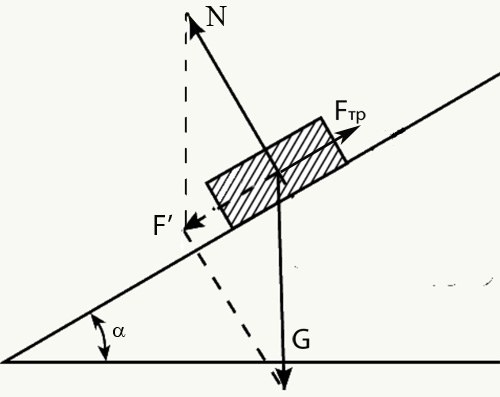
Случай 4. На тело, самопроизвольно скользящее по наклонной плоскости, действуют три силы: сила тяжести (G), сила реакции опоры (N) и сила трения (Fтр). Сила тяжести может быть записана в таком виде: G = mg, Н, где m – масса тела, кг; g – ускорение свободного падения, м/с2. Поскольку эти силы направлены не вдоль одной прямой, запишите уравнение движения в векторном виде.
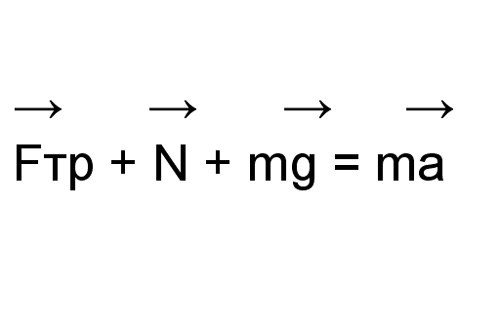
Сложив по правилу параллелограмма силы N и mg, вы получите результирующую силу F’. Из рисунка можно сделать выводы: N = mg*cosα; F’ = mg*sinα. Где α – угол наклона плоскости. Силу трения можно записать формулой: Fтр = м*N = м*mg*cosα. Уравнение для движения принимает вид: F’-Fтр = ma. Или: Fтр = mg*sinα-ma.
Случай 5. Если же к телу приложена дополнительная сила F, направленная вдоль наклонной плоскости, то сила трения будет выражаться: Fтр = mg*sinα+F-ma, если направление движения и силы F совпадают. Или: Fтр = mg*sinα-F-ma, если сила F противодействует движению.
Пример задачи 3: брусок массой 1 кг соскользнул с вершины наклонной плоскости за 5 секунд, пройдя путь 10 метров. Определите силу трения, если угол наклона плоскости 45о. Рассмотрите также случай, когда на брусок воздействовала дополнительная сила 2 Н, приложенная вдоль угла наклона по направлению движения.
Найдите ускорение тела аналогично примерам 1 и 2: а = 2*10/5^2 = 0,8 м/с2. Вычислите силу трения в первом случае: Fтр = 1*9,8*sin(45о)-1*0,8 = 7,53 Н. Определите силу трения во втором случае: Fтр = 1*9,8*sin(45о)+2-1*0,8= 9,53 Н.
Случай 6. Тело двигается по наклонной поверхности равномерно. Значит, по второму закону Ньютона система находится в равновесии. Если скольжение самопроизвольное, движение тела подчиняется уравнению: mg*sinα = Fтр.
Если же к телу приложена дополнительная сила (F), препятствующая равноускоренному перемещению, выражение для движения имеет вид: mg*sinα–Fтр-F = 0. Отсюда найдите силу трения: Fтр = mg*sinα-F.
Источники:
- скольжение формула
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Благодаря этой силе автомобили тормозят на светофоре, катер останавливается в воде, колесо буксует в яме. Как вы уже поняли, в этой статье мы будем разбираться, как решать задачи на силу трения.
Сила трения имеет электромагнитную природу. Это значит, что эта сила проявляется в результате взаимодействия частиц, из которых состоит вещество.
Хотите больше полезной и интересной информации по разным темам? Подписывайтесь на наш телеграм-канал.
Что нужно знать о силе трения, чтобы решать задачи
Трение – один из видов взаимодействия тел, которое возникает при их соприкосновении.
Сила трения всегда направлена в сторону, противоположную движению и по касательной к соприкасающимся поверхностям. Между твердыми телами возникает сухое трение, а при движении тел в жидкостях или газах говорят о вязком трении.
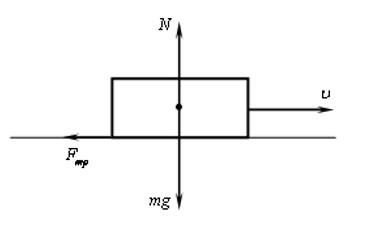
Природу этой силы мы уже установили. Помимо этого нужно знать, что бывают разные виды сил трения:
- трение покоя;
- трение скольжения;
- трение качения (при перекатывании тел друг по другу);
- сопротивление среды (для движения в жидкости).
Вот пример на виды силы трения: брусок лежит на столе, и никто его на трогает. В этом случае действуют только сила тяжести и сила нормальной реакции опоры. Если мы начнем толкать брусок, но так сильно, чтобы его сдвинуть, на него будет действовать сила трения покоя, по третьему закону Ньютона равная внешней силе, приложенной к бруску. Сила трения покоя имеет предельное значение. Если внешняя сила будет больше этого значения, брусок начнет скользить по столу. В этом случае говорят о силе трения-скольжения. А вот и простейшая формула для силы трения:
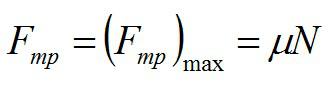
«Мю» – коэффициент трения скольжения. Это безразмерная величина, которая зависит от материалов взаимодействующих тел и от качества их поверхностей. Величина коэффициента трения не превышает единицы.
При решении простых физических задач силу трения скольжения часто принимают равной максимальной силе трения покоя.
Не забывайте также про нашу памятку и подборку полезных формул.
Вопросы по теме «Сила трения»
Вопрос 1. От чего зависит сила трения?
Ответ. Взглянем на формулу выше, и ответ придет сам. Сила трения зависит от свойств соприкасающихся тел, силы нормальной реакции опоры, скорости относительного движения тел.
Вопрос 2. Зависит ли сила трения от площади соприкасающихся поверхностей?
Ответ. Нет, площадь не влияет на силу трения.
Вопрос 3. Какими способами можно уменьшить или увеличить силу трения?
Ответ. Можно уменьшить коэффициент трения, сделав сухое трения вязким. Для увеличения силы трения необходимо увеличить давление на них.
Вопрос 4. Тело покоится на плоскости. Действует ли на него сила трения?
Ответ. Если на тело не действуют внешние силы, то сила трения покоя, по третьему закону Ньютона, равна нулю.
Вопрос 5. Какая из этих сил самая большая по модулю: сила трения покоя, сила трения качения или сила трения скольжения?
Ответ. Сила трения скольжения имеет самое большое значение.
Вопрос 6. Какие есть примеры полезного действия силы трения?
Ответ. Среди полезного использования силы трения можно выделить работу тормозов транспортных средств, добычу огня первобытными людьми.
Задачи на силу трения с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Нахождение силы трения
Условие
Брусок массой 5 килограмм скользит по горизонтальной поверхности. Сила трения скольжения равна 20 Н. Найдите силу трения, если масса бруска уменьшится в два раза, а коэффициент трения останется неизменным.
Решение
Применим формулы:
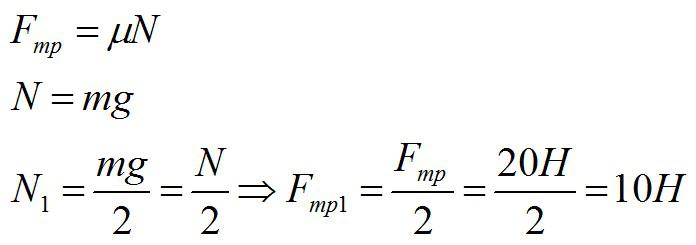
Ответ: 10 Н.
Задача №2. Нахождение коэффициента трения
Условие
Тело скользит по горизонтальной плоскости. Найти коэффициент трения, если сила трения равна 5 Н, а сила давления тела на плоскость – 20 Н.
Решение
Сила давления тела на плоскость равна силе нормальной реакции опоры.

Ответ: 0,25
Задача №3. Нахождение силы трения и коэффициента трения
Условие
Лыжник массой 60 кг, имеющий в конце спуска скорость 10 м/с, останавливается через 40 с после окончания спуска. Определите силу трения и коэффициент трения.
Решение
Сначала найдем ускорение, с которым движется лыжник. Затем по второму закону Ньютона найдем силу, которая действует на него:
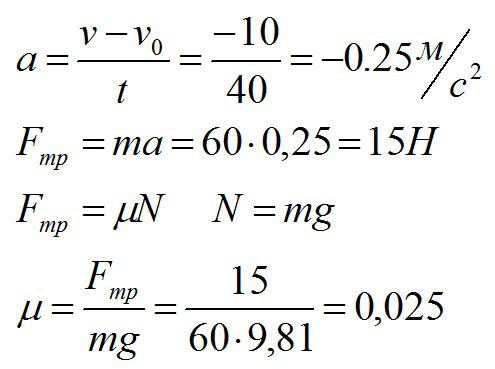
Ответ: 15 Н; 0,025.
Задача №4. Нахождение силы трения
Условие
Брусок массой 20 кг равномерно перемещается по горизонтальной поверхности под действием постоянной силы, направленной под углом 30° к поверхности и равной 75 Н. Каков коэффициент трения между бруском и плоскостью?
Решение
Сначала воспользуемся вторым законом Ньютона, учитывая, что ускорение равно нулю. Затем найдем проекции силы на вертикальную и горизонтальную оси:
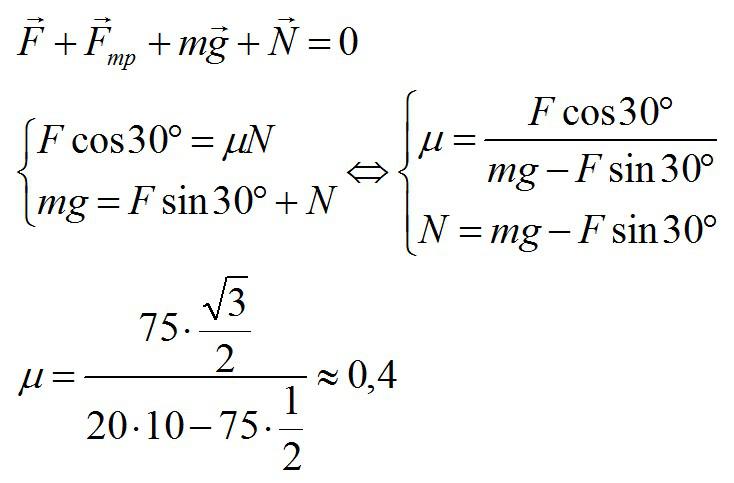
Ответ: 0,4
Задача №5. Нахождение силы трения покоя
Условие
Ящик массой 10 кг стоит на горизонтальном полу. Коэффициент трения между полом и ящиком равен 0,25. К ящику в горизонтальном направлении прикладывают силу 16 Н. Сдвинется ли он с места. Какова сила трения между ящиком и полом?
Решение
Вычислим максимальную силу трения покоя:
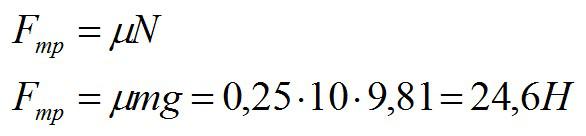
Так как приложенная сила по условию меньше, чем максимальная сила трения покоя, ящик останется стоять на месте. Сила трения между полом и ящиком, по третьему закону Ньютона, равна приложенной силе.
Ответ: 16 Н.
Нужна помощь в решении задач или других заданий? Обращайтесь за ней в профессиональный студенческий сервис.
Сила трения. Коэффициент трения
- Причины возникновения трения
- Трение покоя
- Трение скольжения
- Трение качения
- Задачи
- Лабораторная работа №8. Измерение коэффициента трения скольжения
п.1. Причины возникновения трения
При движении одного тела по поверхности другого всегда возникает сила, направленная противоположно направлению скорости и замедляющая движение. Эта сила называется силой трения.
По своей природе сила трения отличается от силы тяготения и силы упругости, которые были рассмотрены в предыдущих параграфах.
Причины возникновения силы трения можно разделить на два класса: 1) шероховатость поверхностей контактирующих тел; 2) взаимное притяжение молекул при контакте.
Неровности поверхностей проявляются на макроуровне и видны невооруженным глазом или в оптический микроскоп. Их влияние можно уменьшить, если отполировать поверхности или нанести смазку.
Взаимное притяжение молекул проявляется на микроуровне и приводит к тому, что даже на идеально отполированных поверхностях не удается избежать трения, когда частицы одного тела перемещаются относительно частиц другого.
Сила трения – это сумма межмолекулярных сил, возникающих при деформациях и изломах контактирующих поверхностей за счет разрыва межмолекулярных связей.
Сила трения направлена вдоль поверхностей контактирующих тел.
Как и сила упругости, сила трения имеет электромагнитную природу и связана с межмолекулярным взаимодействием.
Но в отличие от силы упругости, причиной силы трения является разрыв межмолекулярных связей. Кроме того, если сила упругости всегда направлена перпендикулярно поверхностям контактирующих тел, то сила трения всегда направлена вдоль этих поверхностей.
В зависимости от характера движения контактирующих тел различают трение покоя, трение скольжения и трение качения.
п.2. Трение покоя
Сила трения, возникающая при относительной скорости двух контактирующих тел равной нулю, называется силой трения покоя.
Сила трения покоя равна по модулю приложенной силе и направлена в сторону, противоположную возможному движению тела, параллельно контактирующим поверхностям.
Если параллельно поверхности контакта на тело не действует сила, сила трения покоя равна нулю. Максимальное значение силы трения, при котором тело все ещё неподвижно, называется максимальной силой трения покоя.
Пример изменения силы трения покоя
 |
Сила трения покоя равна приложенной силе, которая все ещё не приводит тело в движение. Допустим, что мы прикладываем к шкафу последовательно силу 100 Н, 200 Н, 300 Н, и он начинает равномерно двигаться только при 300 Н. Как только тело начинает скользить, на него уже действует сила трения скольжения. Получаем: |
||
| Приложенная сила, Н | Движение | Сила трения покоя, Н | Сила трения скольжения, Н |
| 100 | Нет | 100 | – |
| 200 | Нет | 200 | – |
| 300 | Есть, равномерное | – | 300 |
п.3. Трение скольжения
Силу трения, возникающую в результате движения одного тела по поверхности другого, называют силой трения скольжения.
Сила трения скольжения всегда направлена в сторону, противоположную перемещению тела («тормозит» движение).
 |
Если тело расположено на горизонтальной опоре, сила тяжести (mg), действующая на него, равна по величине силе реакции опоры (N) (см. §22 данного справочника). Сила трения направлена противоположно силе тяги. |
Сила трения скольжения прямо пропорциональна силе реакции опоры: $$ F_{text{тр}}=mu N $$ Коэффициент (mu) называют коэффициентом трения скольжения; величина (mu) зависит от материала трущихся тел и состояния их поверхностей.
Значения коэффициентов трения скольжения для различных поверхностей приводятся в справочных таблицах.
При проектировании и разработке машин и механизмов коэффициенты трения скольжения для отдельных узлов определяются в специальных лабораториях.
п.4. Трение качения
Сила трения, возникающая при качении одного тела по поверхности другого, называется силой трения качения.
Сила трения качения значительно меньше силы трения скольжения.
 |
Уменьшение трения за счет качения используется в шариковых и роликовых подшипниках. Первый подшипник качения был установлен в опоре ветряка, построенного в Англии в 1780 г. Этот подшипник состоял из двух литых чугунных дорожек качения, между которыми находилось 40 чугунных шаров. Сегодня подшипники являются незаменимой деталью во всех подвижных конструкциях; они уменьшают износ трущихся деталей и снижают потери энергии на нагрев из-за трения. |
п.5. Задачи
Задача 1. Найдите коэффициент трения между шинами автомобиля и дорогой, если при равномерном движении по прямолинейному участку двигатель развивает силу тяги, равную 30 кН. Масса автомобиля 6 т.
Дано:
(m=6 text{т}=6cdot 10^3 text{кг})
(F_{text{тяги}}=30 text{кН}=3cdot 10^4 text{Н})
(gapprox 10 text{м/с}^2)
__________________
(mu-?)

Коэффициент трения $$ mu=frac{F_{text{тр}}}{N}. $$ При равномерном движении скорость постоянна и ускорение (overrightarrow{a}=0). По второму закону Ньютона, равнодействующая горизонтальных сил равна нулю $$ overrightarrow{F_{text{тр}}}+ overrightarrow{F_{text{тяги}}}=0. $$ Значит, сила трения и сила тяги равны по модулю: $$ F_{text{тр}}=F_{text{тяги}}. $$ Сила реакции горизонтальной опоры равна силе тяжести, действующей на автомобиль: $$ n=mg. $$ Получаем: $$ mu=frac{F_{text{тр}}}{N}= frac{F_{text{тяги}}}{mg}, mu=frac{3cdot 10^4}{6cdot 10^3cdot 10}=0,5. $$ Ответ: 0,5
Задача 2. Деревянный брусок массой 3 кг равномерно тянут по горизонтальной деревянной доске с помощью динамометра. Жесткость пружины динамометра равна 3 Н/см, коэффициент трения дерева об дерево 0,3. На сколько сантиметров растянется пружина?
Дано:
(m=3 text{кг})
(k=3frac{text{Н}}{text{см}}=frac{3 text{Н}}{0,01 text{м}}=300frac{text{Н}}{text{м}})
(mu=0,3)
(gapprox 10 text{м/с}^2)
__________________
(Delta l-?)
Показания динамометра – это сила упругости, равная силе тяги. При равномерном движении сила тяги равна по модулю силе трения. Поэтому begin{gather*} F_{text{упр}}=kDelta l=F_{text{тр}}=mu N=mu mgRightarrow kDelta l=mu mg end{gather*} Получаем: $$ Delta l=frac{mu mg}{k}, Delta l=frac{0,3cdot 3cdot 10}{300}=0,03 (text{м})=3 (text{см}) $$ Ответ: 3 см.
Задача 3. Автомобиль движется по горизонтальному участку дороги со скоростью 72 км/ч. Рассчитайте время торможения и тормозной путь до полной остановки, если коэффициент трения колес о дорогу равен 0,4.
Дано:
(v_1=72frac{text{км}}{text{ч}}=20frac{text{м}}{text{с}})
(mu=0,4)
(v_2=0)
(gapprox 10 text{м/с}^2)
__________________
(t, s-?)
Автомобиль тормозит за счет силы трения. По второму закону Ньютона begin{gather*} F_{text{тр}}=ma. end{gather*} С другой стороны на горизонтальной дороге $$ F_{text{тр}}=mu N=mu mg. $$ Получаем: $$ ma=mu mgRightarrow a=mu g. $$ По определению ускорения $$ a=frac{v_2-v_1}{t}. $$ Т.к. (v_2=0), ускорение отрицательное.
Модуль ускорения $$ |a|=frac{v_1}{t}=mu gRightarrow t=frac{v_1}{mu g} $$ Время торможения прямо пропорционально скорости и обратно пропорционально коэффициенту трения. $$ t=frac{20}{0,4cdot 10}=5 (text{с}) $$ Найдем тормозной путь $$ s=v_1t+frac{at^2}{2}=v_1t+ left(frac{overbrace{v_2}^{=0}-v_1}{t}right)frac{t^2}{2}=v_1t -frac{v_1t}{2}=frac{v_1t}{2}=frac{v_1t}{2}cdot frac{v_1}{mu g}=frac{v_1^2}{2mu g} $$ Тормозной путь прямо пропорционален квадрату(!) скорости и обратно пропорционален коэффициенту трения. $$ s=frac{20^2}{2cdot 0,4cdot 10}=50 (text{м}) $$ Ответ: 5 с; 50 м.
п.6. Лабораторная работа №8. Измерение коэффициента трения скольжения
Цель работы
Научиться измерять силу трения скольжения и определять коэффициент трения скольжения. Изучить зависимость коэффициента трения скольжения от материалов соприкасающихся тел и от площади опоры движущегося тела.
Теоретические сведения
 |
При (v=const) (равномерное движение) получаем По вертикали (moverrightarrow{g}=-overrightarrow{N}). Модули этих сил равны По горизонтали (overrightarrow{F_{text{тр}}}=-overrightarrow{F_{text{тяги}}}). Модули этих сил равны $$ F_{text{тяги}}=F_{text{тр}}=mu N=mu mg $$ |
Если тело перемещать с помощью динамометра, то сила упругости, возникающая в пружине, будет равна силе тяги. Т.е., сила тяги непосредственно измеряется динамометром.
В работе используются стандартные лабораторные грузики массой 100 г.
Измерив силу тяги и зная массу перемещаемого тела, рассчитываем коэффициент трения: $$ mu=frac{F_{text{тяги}}}{mg} $$
Для расчетов используем стандартное значение (g=9,80665 text{м/с}^2).
Погрешность для прямых измерений (F_{text{тяги}}) определяется как половина цены деления динамометра. Погрешность для массы определяется по маркировке грузиков и бруска, (Delta m=2 text{г}) для (m=100 text{г}), т.е. (delta_m=2text{%}).
Погрешность эксперимента (delta_e) рассчитывается как средняя арифметическая по результатам измерений и вычислений.
Приборы и материалы
Лабораторный динамометр на 5 Н; набор грузиков по 100 г; деревянный брусок с крючком 100 г; деревянная доска; наждачная бумага.
Ход работы
1. Прикрепите динамометр к бруску, положите доску горизонтально, поставьте брусок самой большой по площади гранью слева на доску.
2. Перемещая брусок слева направо по доске, добейтесь равномерного скольжения (со стабильными показаниями динамометра). Снимите показания динамометра и запишите.
3. Повторите эксперимент, нагружая брусок одним, двумя, тремя и четырьмя грузиками.
4. Рассчитайте коэффициент трения дерева об дерево, определите относительную и абсолютную погрешности эксперимента.
5. Повторите эксперимент, перемещая брусок по доске, обмотанной наждачной бумагой. Найдите коэффициент трения дерева об наждак, определите относительную и абсолютную погрешности эксперимента.
6. Снимите наждачную бумагу и повторите эксперимент для трения дерева об дерево. Однако на этот раз брусок должен опираться на меньшую по площади грань. Рассчитайте коэффициент трения дерева об дерево в этом случае.
7. Сравните полученные коэффициенты трения, сделайте выводы о зависимости коэффициента трения от материала соприкасающихся поверхностей и от площади опоры движущегося тела.
Результаты измерений и вычислений
Цена деления динамометра (d=0,1 text{Н}).
Таблица для расчета коэффициента трения скольжения дерева об дерево
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,3 | 0,306 | 0,026 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,025 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,008 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,001 |
| 5 | Брусок + 4 грузика | 0,5 | 1,6 | 0,326 | 0,006 |
| Всего | – | – | 1,660 | 0,065 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,660}{5}=0,332 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,065}{5}=0,013 $$ Относительная погрешность begin{gather*} delta=frac{0,013}{0,332}cdot 100text{%}approx 3,9text{%}\[7pt] mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об наждак
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,6 | 0,612 | 0,039 |
| 2 | Брусок + 1 грузик | 0,2 | 1,1 | 0,561 | 0,012 |
| 3 | Брусок + 2 грузика | 0,3 | 1,7 | 0,578 | 0,005 |
| 4 | Брусок + 3 грузика | 0,4 | 2,2 | 0,561 | 0,012 |
| 5 | Брусок + 4 грузика | 0,5 | 2,7 | 0,551 | 0,022 |
| Всего | – | – | 2,862 | 0,090 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{2,862}{5}approx 0,572 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,090}{5}=0,018 $$ Относительная погрешность begin{gather*} delta=frac{0,018}{0,572}cdot 100text{%}approx 3,1text{%}\[7pt] mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об дерево (узкая грань)
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,35 | 0,357 | 0,011 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,011 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,006 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,015 |
| 5 | Брусок + 4 грузика | 0,5 | 1,7 | 0,347 | 0,000 |
| Всего | – | – | 1,732 | 0,043 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,732}{5}approx 0,346 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,043}{5}approx 0,009 $$ Относительная погрешность begin{gather*} delta=frac{0,009}{0,346}cdot 100text{%}approx 2,5text{%}\[7pt] mu ‘_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
В работе исследовалась зависимость коэффициента трения скольжения от поверхностей, из которых изготовлены соприкасающиеся тела.
Для скольжения дерева об дерево был получен коэффициент begin{gather*} mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Для скольжения дерева об наждак был получен коэффициент begin{gather*} mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%}\[7px] mu_{text{дн}}gt mu_{text{дд}} end{gather*}
Наждак является более шероховатой поверхностью и сила трения на ней больше.
Коэффициент трения скольжения сильно зависит от материалов соприкасающихся поверхностей.
Также в работе исследовалась зависимость коэффициента трения скольжения от площади опоры движущегося тела. Брусок выставлялся на более узкую грань, и изучалось скольжение дерева об дерево в этом случае. Был получен коэффициент begin{gather*} mu’_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*} Поскольку begin{gather*} 0,319le mu_{text{дд}}le 0,345 0,337le mu’_{text{дд}}le 0,355 end{gather*} Полученные отрезки значений перекрываются.
Таким образом, в рамках погрешности эксперимента коэффициент трения скольжения не зависит от площади опоры движущегося тела.
