Биссектриса треугольника – это отрезок, делящий любой угол треугольника на два равных угла. Для более
наглядного примера, если угол равняется 120°, то проведенная биссектриса создает уже пару углов по
60 °. В треугольнике можно провести максимум три биссектрисы, по одной из каждого угла. Точка
пересечения всех биссектрис является центром вписанной в треугольник окружности. Биссектриса
обладает особенными свойствами для некоторых видов треугольников, так, например, проведенная из
вершины равнобедренного треугольника будет являться одновременно и высотой, и медианой.
- Длина биссектрисы в треугольнике через две стороны и угол
между ними - Длина биссектрисы в треугольнике через все стороны
- Длина биссектрисы в треугольнике через две стороны и
отрезки - Длина биссектрисы в прямоугольном треугольнике через
катеты - Длина биссектрисы в прямоугольном треугольнике через
гипотенузу и угол - Длина биссектрисы из острого угла в прямоугольном
треугольнике через катет и угол - Длина биссектрисы из острого угла в прямоугольном
треугольнике через катет и гипотенузу - Длина биссектрисы в равнобедренном треугольнике через
боковую сторону и угол при основании - Длина биссектрисы в равнобедренном треугольнике через
основание и угол при основании - Длина биссектрисы в равнобедренном треугольнике через
боковую сторону и угол между боковыми сторонами - Длина биссектрисы в равнобедренном треугольнике через
основание и боковую сторону - Длина биссектрисы в равностороннем треугольнике через
сторону
Через две стороны и угол между ними
Нам дан некий треугольник, известно значение двух сторон и угла между ними. Нам нужно найти
биссектрису. Задача кажется невыполнимой, если не знать формулы:
L = (2bc · cos (α/2)) / b + c
где «L» это непосредственно длина, а «b» и «с» — стороны треугольника, «α» — угол между
ними.
Цифр после
запятой:
Результат в:
В нашем случае биссектриса равняется среднему двух сторон и угла, лежащего между ними.
Пример. Дан треугольник ABC. Известно, что стороны b = 6 см, а сторона c = 9 см.
Угол между двумя сторонами равен 65°. Нам нужно найти биссектрису. Подставив в формулу данные
значения, мы получаем ответ – биссектриса треугольника АВС равна 6 см. Решение легкое, ведь вам
нужно прибегнуть к обычному применению выведенной формулы. 2 × 6 × 9 × cos(65 ÷ 2) / 9 + 6 = 6 см.
Через две стороны и отрезки
Если вам известно 2 стороны треугольника и дано несколько отрезков на стороне, то вам нужно
руководствоваться следующей формулой:
L = √(b * c — a1 * a2)
где b, c — стороны, a1, a2 — длины отрезков, образованных на стороне.
Цифр после
запятой:
Результат в:
Пример. Есть треугольник АВС, у которого известны 2 стороны, 2 и 4 см
соответственно. Также дана пара отрезков на стороне, с показателем 2 см и 2 см. От нас просят найти
биссектрису треугольника АВС. Вместо b и c подставляем наши значения длин сторон, вместо а1 и а2 –
длины отрезков. Проводим вычисление и находим квадратный корень конечного результата. √(2 × 4 — 2 × 2) = 2 см.
Через все стороны
Чтобы отыскать длину биссектрисы треугольника, при известном значении каждой стороны фигуры, нужно
воспользоваться формулой ниже:
L = (√(bc (b + c + a)(b + c — a))) / (b + c)
где a, b, c — стороны.
Цифр после
запятой:
Результат в:
Пример. Нам дан некий треугольник АВС, известна каждая его сторона, допустим а = 10
см, b = 6 см, с = 8 см. Нам нужно отыскать биссектрису треугольника. Для этого подставляем все наши
известные значения в формулу. L = (√(6 * 8 * (6 + 8 + 10)(6 + 8 — 10))) / (6 + 8) = 4,8 см.
В прямоугольном треугольнике через гипотенузу и угол
Формула ниже слегка отличается от остальных, ведь тут использует понятие синуса и косинуса.
L = 2c / √2 * ((sin α * cos α) / (sin α + cos α))
где c — гипотенуза, sin α, cos α — угол.
Цифр после
запятой:
Результат в:
Именно данное вычисление поможет вам с поисками длины биссектрисы в прямоугольном треугольнике, если
вам известна одна гипотенуза и угол. «с» — гипотенуза, «а» — угол.
Пример. В прямоугольном треугольнике АВС известно значение гипотенузы и угла «а».
Пользуясь выведенной формулой, вы можете заметить, что от вас требуют синусы и косинусы угла «а».
Для того чтобы правильно посчитать, нужно воспользоваться специальной таблицей синусов и косинусов.
Далее решение не составит особого труда. Пусть гипотенуза c = 10 мм, угол α = 30 градусов,
тогда биссектриса L = 2* 10 / √2 * ((sin 30 * cos 30) / (sin 30 + cos 30)) = 4.48 мм.
В прямоугольном треугольнике через катеты
В прямоугольном треугольнике есть 2 катета и гипотенуза, как найти длину биссектрисы, если нам дано
только значение катетов треугольника. Для этого существует формула:
L = √2 * (ab / (a + b))
где «L» — искомая биссектриса, «а» и «b» — известное значение катетов прямоугольного
треугольника.
Цифр после
запятой:
Результат в:
Пример. Дан некий прямоугольный треугольник АВС, нам известна длина двух катетов,
5.5 см и 6 см. От нас просят найти длину биссектрисы треугольника АВС. √(2) × ((5.5 × 6) ÷ (5.5 + 6)) = 4,06 см.
Из острого угла в прямоугольном треугольнике через катет и угол
Если вам дан только катет и острый угол в прямоугольном треугольнике, используйте формулу:
L = b / cos β/2
где «b» — известный катет, а β — острый угол.
Цифр после
запятой:
Результат в:
Пример. Дан прямоугольный треугольник АВС. Известно, что катет «b» равен 9.7 см.,
угол β равен 45º. Нужно найти биссектрису. Нужно 9.7 поделить на косинус половины 45 град.
Подставляем значения в формулу: L = (9,7)/(cos(45)/(2)) = 10,5 см.
В равнобедренном треугольнике через боковую сторону и угол при основании
Для нахождения длины биссектрисы равнобедренного треугольника с помощью боковой стороны и угла при
основании можно воспользоваться данной формулой:
L = b * sin α
где b — боковая сторона, sin α — угол при основании.
Цифр после
запятой:
Результат в:
Пример. В условии дан равнобедренный треугольник. Известно, что боковая сторона
равна 12 см, а угол основания составляет 60 град. У нас есть все ключевые данные для решения, просто
подставляем их в формулу L = 12 * sin 60 = 10,4 см.
Из острого угла в прямоугольном треугольнике через катет и гипотенузу
Длину биссектрисы в прямоугольном треугольнике можно найти по формуле:
L = b * √(2c / b + c)
где «b» — гипотенуза, а «с» — катет.
Цифр после
запятой:
Результат в:
Пример. АВС –прямоугольный треугольник. Гипотенуза равна 8 см, а катет 3.5 см. L = 8 × √((2 × 3.5) ÷ (8 + 3.5)) = 4 см. Подставив значения в формулу,
мы получим результат, что биссектриса приблизительно равна 4 см.
В равнобедренном треугольнике через основание и угол при основании
Как и в предыдущих случаях, для данной задачи есть специальная формула:
L = a / 2 * tg α
где a — основание, tg α — угол при нижнем основании.
Цифр после
запятой:
Результат в:
Пример. Нам дан равнобедренный треугольник. В условии сказано, что основание «а»
равно 12 см, угол альфа – 60 град. Для решения поставим в формулу значения L = 12 ÷ 2 × tan(60) = 10.4 см
В равнобедренном треугольнике через основание и боковую сторону
Формула, по которой можно найти длину биссектрисы в равнобедренном треугольнике, если по условиям
дано основание и боковая сторона:
L = √(b² — a²/4)
где b и а — основание.
Цифр после
запятой:
Результат в:
Пример. В равнобедренном треугольнике АВС известно, что основание равно 9 см, а
боковая сторона 11 см. Нахождение биссектрисы происходит по формуле выше. L = √(9² — (11² ÷ 4)).
Следовательно, проведя сокращения, вычисления и округления у вас должен получится результат – 10 см.
Это и есть длина биссектрисы.
В равнобедренном треугольнике через боковую сторону и угол между боковыми сторонами
Как и все разы до этого, в данном случае применяется выведенная формула:
L = b * cos β/2
где b является боковой стороной, β – угол, который лежит между боковых сторон.
Цифр после
запятой:
Результат в:
Пример. Дан равнобедренный треугольник, боковая сторона которого равна 6.5 см.
Известно, что угол между боковыми сторонами равен 45 град. Нужно вычислить биссектрису. Используем
прямую формулу: L = 6.5 × cos(45 ÷ 2) = 6.005. После вычислений у нас
получается 6.005. Округляем до десятых и записываем в ответ 6 см.
В равностороннем треугольнике через сторону
Для нахождения длины биссектрисы в равностороннем треугольнике через сторону используйте формулу
ниже:
L = a√3 / 2
где а является стороной треугольника.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим равносторонний треугольник, сторона которого равна 5.8 см. Задача
заключается в нахождение биссектрисы. Для решения у нас есть все нужные данные. Подставим их в
формулу: L = (5.8 × √(3)) ÷ 2. Проведя вычисление, мы получаем ответ 5.02,
это и есть значение длины биссектрисы.
Решение задач по геометрии в школе предусматривает детально рассмотрение понятия биссектрисы и всех
ее свойств включительно. Выходя из некоторых особенностей данного отрезка можно решать задачи
высокого уровня. Главное знать все тонкости и нюансы такого элемента как биссектриса.
В данной публикации приведены примеры наиболее распространенных формул, используемых при вычислении
длины биссектрисы в треугольнике. Каждая формула по-своему уникальна, но не является сложной.
Выучить их все будет трудно, но иметь всегда с собой вполне реально.
Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.
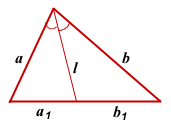
I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.
Утверждение 1
Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
![]()
![]()
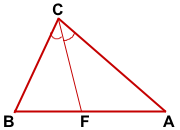 Дано:
Дано:
ΔABC,
СF — биссектриса ∠ABC
Доказать:
![]()
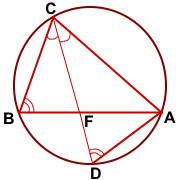 Доказательство:
Доказательство:
Опишем около треугольника ABC окружность и продлим биссектрису CF до пересечения с окружностью в точке D. Соединим точки A и D отрезком.
Рассмотрим треугольники BCF и DCA.
∠BCF=∠DCA (по условию);
∠CBF=∠CDA (как вписанные углы, опирающиеся на одну дугу AC).
Значит, треугольники BFC и DCA подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
![]()
![]()
По свойству пересекающихся хорд
![]()
Отсюда
![]()
![]()
![]()
Что и требовалось доказать.
II. Через три стороны треугольника
Утверждение 2
Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле
![]()
Доказательство:
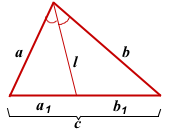 По свойству биссектрисы треугольника:
По свойству биссектрисы треугольника:
![]()
a1+b1=c, b1=c-a1, поэтому
![]()
![]()
![]()
![]()
![]()
Согласно утверждению 1,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
откуда
![Rendered by QuickLaTeX.com [ l = sqrt {frac{{ab}}{{(a + b)^2 }}(a + b + c)(a + b - c)} , ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-18591dd13191b4e7e6e02d8ea7855cc4_l3.png)
![]()
Что и требовалось доказать.
Аналогично,
![]()
![]()
III Через две стороны треугольника и угол между ними.
Утверждение 3
Длина биссектрисы треугольника через две стороны, образующие угол, из вершины которого исходит биссектриса, и угол между этими сторонами выражается по формуле
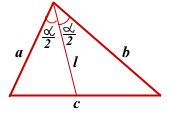
![]()
Доказательство:
Найдем площади треугольников BCF, ACF и ABC.
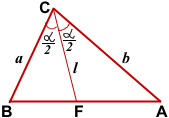
![]()
![]()
![]()
Так как
![]()
то
![]()
![]()
![]()
![]()
![]()
Что и требовалось доказать.

L– биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b – стороны треугольника
с – сторона на которую опущена биссектриса
d, e – отрезки полученные делением биссектрисы
γ – угол ABC , разделенный биссектрисой пополам
p – полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через стороны и отрезки d, e, (L):


Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
- Подробности
-
Опубликовано: 06 октября 2011
-
Обновлено: 13 августа 2021
Длина биссектрисы треугольника
Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.
I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.
Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
Дано:
СF — биссектриса ∠ABC
Доказательство:
Опишем около треугольника ABC окружность и продлим биссектрису CF до пересечения с окружностью в точке D. Соединим точки A и D отрезком.
Рассмотрим треугольники BCF и DCA.
∠BCF=∠DCA (по условию);
Значит, треугольники BFC и DCA подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
Что и требовалось доказать.
II. Через три стороны треугольника
Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле
По свойству биссектрисы треугольника:
Согласно утверждению 1,
Что и требовалось доказать.
III Через две стороны треугольника и угол между ними.
Длина биссектрисы треугольника через две стороны, образующие угол, из вершины которого исходит биссектриса, и угол между этими сторонами выражается по формуле
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).




Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
Формулы для вычисления длины биссектрисы треугольника

Формулы для вычисления длины биссектрисы треугольника
Можно вывести различные формулы, с помощью которых можно вычислить длину биссектрисы треугольника, если известны:

· длины прилежащих сторон и угол между ними


· длины прилежащих сторон и отрезки, на которые биссектриса разбивает противолежащую сторону


· длины трех сторон треугольника.

Докажем первую из формул.
Задача 1. Вычислить длину биссектрисы треугольника, если известны длинны двух прилежащих сторон треугольника и угол между ними.
Решение. Пусть в треугольнике АВС известно, что
 .
.

Обозначим биссектрису AD через la .


 .
.
Используя формулу синуса двойного угла, получаем:
 .
.

Ответ:  .
.
Выражение  называется средним гармоническим чисел а и с. Поэтому формулу
называется средним гармоническим чисел а и с. Поэтому формулу  можно запомнить следующим образом:
можно запомнить следующим образом:
биссектриса треугольника равна произведению среднего гармонического прилежащих сторон треугольника на косинус половинного угла между ними.
Доказательство остальных формул можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Задача 2. Вычислите биссектрису треугольника ABC, проведённую из вершины А, если ВС = 18, АС = 15, АВ = 12.
Решение. Воспользуемся формулой для вычисления биссектрисы угла, если известны три стороны треугольника: 


Задача 3. Определить площадь треугольника, если две его стороны равны 35 см и 14 см, а биссектриса угла между ними содержит 12 см.

Пусть в треугольнике АВС АС=35, АВ=14, AD – биссектриса, AD=12.
 ,
,
Вычислим  , получаем:
, получаем:
 ,
,  .
.
 (по основному тригонометрическому тождеству).
(по основному тригонометрическому тождеству).
Далее по формуле синуса двойного угла вычисляем
 .
.
Для вычисления площади треугольника воспользуемся формулой  .
.

Задача 4. . В равнобедренном треугольнике BCD с основанием BD
проведена биссектриса BE. Известно, что СЕ = 20 и DE = 10. Найдите BE.

Используя свойство биссектрисы угла треугольника (урок 4), получаем
 , то есть
, то есть  .
.
Таким образом, нам известны длины двух прилежащих сторон и отрезки, на которые биссектриса разбивает противолежащую сторону, поэтому 
Ответ : .
.
Задачи для самостоятельного решения
1. Дан треугольник со сторонами 4, 8, 9. Найти длину биссектрисы, проведенной к большей стороне.
2. В треугольнике ABC известно, что АВ = 10, АС = 15,  BAC = 120°. Найдите биссектрису AD.
BAC = 120°. Найдите биссектрису AD.
3. Катеты прямоугольного треугольника равны 6 и 8. Найдите биссектрису треугольника, проведённую из вершины прямого угла.
4. В равнобедренном треугольнике BCD с основанием BD проведена биссектриса BE. Известно, что СЕ = 18 и DE = 12. Найдите BE.
[spoiler title=”источники:”]
http://pandia.ru/text/78/654/11234.php
[/spoiler]
24
Ноя 2015
Категория: Справочные материалы
Формула длины биссектрисы через длины сторон треугольника
2015-11-24
2016-07-10
Докажем следующую теорему.
Пусть – стороны треугольника,
– биссектриса треугольника проведенная к стороне
.
Тогда
Доказательство:
Пусть – биссектриса треугольника
Пусть Пусть
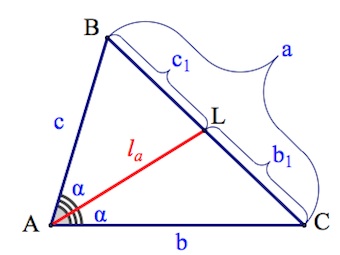
Распишем теорему Косинусов для треугольников
Откуда
(1)
По свойству биссектрисы треугольника
Или
Откуда
(2)
Тогда
(3)
Подставляем (2) и (3) в (1):
Что и требовалось доказать.
Автор: egeMax |
комментариев 5
