Как составить задачу на тему длина окружности – Сайт, где вы сможете решить свои вопросы

Длина окружности

Длина окружности
Задачи на длину окружности
Задачи на площадь круга

Длина окружности

Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):

Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:

C = πD = 2πR,

где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.

Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.

Задачи на длину окружности

Задача 1. Найти длину окружности, если её диаметр равен 5 см.

Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:

C ≈ 3,14 · 5 = 15,7 (см).

Ответ: 15,7 см.

Задача 2. Найти длину окружности, радиус которой равен 3,5 м.

Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:

D = 3,5 · 2 = 7 (м),

теперь найдём длину окружности, умножив π на диаметр:

C ≈ 3,14 · 7 = 21,98 (м).

Ответ: 21,98 м.

Задача 3. Найти радиус окружности, длина которой равна 7,85 м.

Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:

следовательно, радиус будет равен:

R	≈	7,85	=	7,85	= 1,25 (м).
2 · 3,14	6,28

Ответ: 1,25 м.

Задачи на площадь круга

Задача 1. Найти площадь круга, если его радиус равен 2 см.

Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:

S ≈ 3,14 · 2² = 3,14 · 4 = 12,56 (см²).

Ответ: 12,56 см².

Задача 2. Найти площадь круга, если его диаметр равен 7 см.

Решение: Сначала найдём радиус круга, разделив его диаметр на 2:

7 : 2 = 3,5 (см),

теперь вычислим площадь круга по формуле:

S = πr² ≈ 3,14 · 3,5² = 3,14 · 12,25 = 38,465 (см²).

Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:

S = π	D²	≈ 3,14 ·	7²	= 3,14 ·	49	=
4	4	4

=	153,86	= 38,465 (см²).
4

Ответ: 38,465 см².

Задача 3. Найти радиус круга, если его площадь равна 12,56 м².

Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:

r = √S : π ,

следовательно, радиус будет равен:

r ≈ √12,56 : 3,14 = √4 = 2 (м).

Ответ: 2 м.

Источник

Рассказываем, как решать задачи на нахождение длины окружности и площади круга. Приводим алгоритм и примеры решения.

Алгоритм решения задач на нахождение длины окружности и площади круга:

Выполняем краткую запись задачи;
Определяем способ и решаем задачу;
Выписываем полный ответ.

Определяем способ решения:

Задача 1. Найти площадь заштрихованной части, если радиус большего круга — 12 дм, а длина окружности меньшего радиуса равна 8π дм.

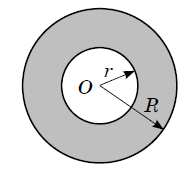
Краткая запись:

R-12 дм
C_r – 8π дм
S_з– ?

Решение:

(8π:2π=4) (дм) — r ((C=2πr, r = C:2π))
(π⋅42=π⋅16=16⋅π) (дм²) — Sм ((S_к= πR^2))
(π⋅122=π⋅144=144π) (дм²) — (S_б)
(144π-16π=128π) (дм²) — (S_з)

Ответ: площадь заштрихованной части равна 128π дм².

Источник

Инфоурок

›

Геометрия

›Другие методич. материалы›Задачи с решением по теме “Длина окружности и площадь круга”(9 класс)

Скачать материал (медленно)

Настоящий материал опубликован пользователем Чернакова Ирина Львовна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 8 лет и 6 месяцев
- Подписчики: 0
- Всего просмотров: 102865
- Всего материалов:
  
  40

Источник

Возьмем циркуль. Установим ножку циркуля с иглой в точку «O», а ножку циркуля с
карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую
линию. Такую замкнутую линию называют — окружность.

Рассмотрим более подробно окружность. Разберёмся, что называют центром,
радиусом и диаметром окружности.

$Окружность 6 класс. Центр, радиус и диаметр окружности$

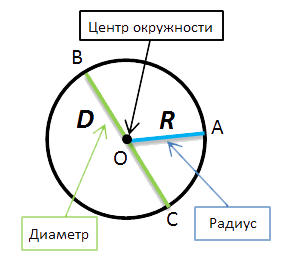
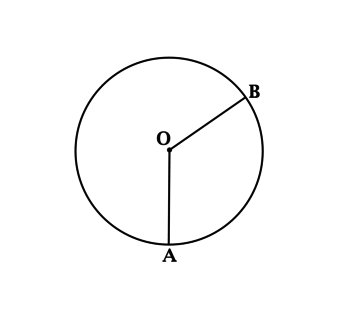
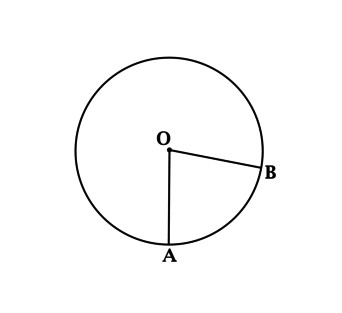
(·)O — называется центром окружности.
Отрезок, который соединяет
центр и любую точку окружности, называется радиусом окружности.
Радиус окружности обозначается буквой «R». На рисунке выше —
это отрезок «OA».
Отрезок, который соединяет
две точки окружности и проходит через её центр, называется
диаметром окружности.

Диаметр окружности обозначается буквой «D».
На рисунке выше — это отрезок «BC».

На рисунке также видно, что диаметр равен двум радиусам. Поэтому
справедливо выражение «D = 2R».

Число π и длина окружности

Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что
такое число π (читается как «Пи»), которое
так часто упоминают на уроках.

В далекие времена математики Древней Греции внимательно изучали окружность
и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.

Запомните!
$!$

Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
π ≈ 3,14…

Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π,

округленное до разряда сотых
π ≈ 3,14…

Теперь, зная, что такое число π, мы
можем записать формулу длины окружности.

Запомните!
$!$

Длина окружности
— это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С» (читается как «Це»).

C = πD
C = 2πR

, так как D = 2R

Как найти длину окружности

Чтобы закрепить полученные знания, решим задачу на окружности.

Разбор примера

Условие задачи:

Найдите длину окружности, радиус которой равен 24 см. Число
π
округлите до сотых.

Воспользуемся формулой длины окружности:

C = 2πR
≈ 2 · 3,14 · 24 ≈ 150,72 см

Разберем обратную задачу, когда мы знаем длину
окружности, а нас просят найти её диаметр.

Разбор примера

Условие задачи:

Определите диаметр окружности, если
её длина равна 56,52 дм.
(π ≈ 3,14).

Выразим из формулы длины окружности диаметр.

C = πD
D = С / π

D = 56,52 / 3,14 = 18 дм

Хорда и дуга окружности

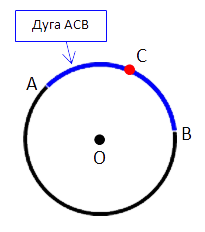
На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность
на две части, каждую из которых называют дугой.
Это синяя дуга «AB» и черная дуга «AB».
Точки «A» и «B» называют концами дуг.

Соединим точки «A» и «B» отрезком. Полученный отрезок называют
хордой.

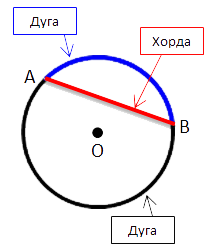
$Дуга и хорда окружности$

Важно!
$Галка$

Точки «A» и «B» делят окружность на две дуги. Поэтому важно
понимать, какую дугу вы имеете в виду, когда пишите дуга «AB».

Для того чтобы избежать путаницы, часто вводят дополнительную точку на
нужной дуге и обращаются к ней по трем точкам.

$Дуга по трем точкам$

Ваши комментарии

Важно!
$Галка$

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

$Пришелец пожимает плечами$

Оставить комментарий:

3 мая 2020 в 10:27

Владислав Заступневич
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Владислав Заступневич
Профиль
Благодарили: 0

Сообщений: 1

, Радиус одной окружности равен 12 см, а второй-36см.Чему равно отношения длины первой окружности к длине второй окружности?

0
Спасибо $thanks$
Ответить

6 мая 2020 в 15:48
Ответ для Владислав Заступневич

Галина Федотова
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Галина Федотова
Профиль
Благодарили: 0

Сообщений: 3

С=2πR
если длину одной окружности разделить на дилну другой, то 2π сократится, следовательно длины будут относится так же как радиусы, то есть 12:36=

0
Спасибо $thanks$
Ответить

22 сентября 2016 в 19:03

Вика Камалова
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Вика Камалова
Профиль
Благодарили: 0

Сообщений: 2

Помогите 2) чему равен деаметр если радиус равен а)12см б)10 децеметров
1) начертить окружность радиусом а)2 см пот буквой б)4см 5мм (начертиь!)
3)Чему равен радиус если деаметр равен а)6см б)9см в)12м
СРОЧНО СЕГОДНЯ! ПРОШУ!!!

0
Спасибо $thanks$
Ответить

23 сентября 2016 в 14:51
Ответ для Вика Камалова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Радиус равен половине диаметра. Обратно диаметр равен двум радиусам. Подробнее здесь.
1) а) 12см · 2=24см б)10дм · 2 = 20дм
2) ответил в теме.
3) а) 6см: 2 = 3см б) 9см: 2 = 4см 5 мм в)12м: 2 = 6м

0
Спасибо $thanks$
Ответить

22 сентября 2016 в 18:54

Вика Камалова
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Вика Камалова
Профиль
Благодарили: 0

Сообщений: 2

1)Начертить окружность радиусом а)2 см пот буквой б)4 см 5 мм
$cry$

0
Спасибо $thanks$
Ответить

23 сентября 2016 в 14:46
Ответ для Вика Камалова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Радиус окружности это расстояние от центра до любой точки окружности. Подробнее можно посмотреть вот здесь. На линейке циркулем отмеряем необходимый радиус и чертим окружность.

0
Спасибо $thanks$
Ответить

24 января 2016 в 13:45

Инна Шабрашина
(^-^)
Профиль
Благодарили: 0

Сообщений: 5

(^-^)
Инна Шабрашина
Профиль
Благодарили: 0

Сообщений: 5

Длина окружности и площадь круга.
Я не понимаю как найти площадь круга.

0
Спасибо $thanks$
Ответить

19 сентября 2016 в 10:56
Ответ для Инна Шабрашина

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

0
Спасибо $thanks$
Ответить

7 сентября 2015 в 21:08

Игорь Желтоновский
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Игорь Желтоновский
Профиль
Благодарили: 0

Сообщений: 1

радиус — 2,1 м.Найти длинну круга и его площадь(помогите плз)

0
Спасибо $thanks$
Ответить

2 сентября 2016 в 15:18
Ответ для Игорь Желтоновский

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Длина окружности(l) вычисляется по формуле: l=2?r
Площадь круга(S) вычисляется по формуле: S=?r²Подставляем значения и считаем, приняв ?=3,14
l=2 · 3,14 · 2,1 = 13,188
S = 3,14 · 2,1²=13,8474

Более подробно можно прочитать здесь: math-prosto.ru/index.php?page=pages/circle/square_of_circle.php

0
Спасибо $thanks$
Ответить

Источник

3. Геометрия на плоскости (планиметрия). Часть I

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Нахождение длины окружности и площади круга

(blacktriangleright) Длина окружности равна (large{C=2pi R}), а в градусной мере составляет (360^circ).

(blacktriangleright) Длина дуги окружности равна (large{C_{alpha}=dfrac{2pi R}{360}cdot alpha}), где (alpha) – угол в градусах, задающий данную дугу (центральный угол, опирающийся на дугу).

(blacktriangleright) Площадь круга равна (large{S=pi R^2}).

(blacktriangleright) Площадь сектора круга равна (large{S_{alpha}=dfrac{pi R^2}{360}cdot alpha}), где (alpha) – угол в градусах, задающий данный сектор.

Задание
1

#2953

Уровень задания: Равен ЕГЭ

На клетчатой бумаге нарисован круг площадью (2,8). Найдите площадь закрашенного сектора.

Заметим, что закрашенная фигура состоит из двух непересекающихся частей, равных (frac14) и (frac12) от (frac14) круга:

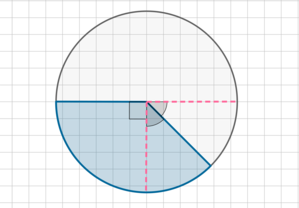
Таким образом, ее площадь равна [dfrac14S+dfrac12cdot left(dfrac14Sright)=dfrac38S=dfrac38cdot 2,8=1,05.]

Ответ: 1,05

Задание
2

#302

Уровень задания: Равен ЕГЭ

Длина окружности с центром в точке (O) равна 12. (angle AOB = 120^{circ}), точки (A) и (B) лежат на окружности и разбивают её на две дуги. Во сколько раз длина большей из получившихся дуг превосходит длину меньшей?

Длины дуг относятся так же, как их градусные меры. Так как (O) – центр окружности, то (angle AOB) – центральный.

Градусная мера дуги, меньшей, чем полуокружность, есть градусная мера центрального угла, который на неё опирается. Тогда градусная мера меньшей из дуг равна (120^{circ}), а большей из дуг (240^{circ}).

Градусная мера большей дуги в (240 : 120 = 2) раза больше, чем градусная мера меньшей дуги.

Ответ: 2

Задание
3

#1735

Уровень задания: Равен ЕГЭ

Найдите (angle AOB).

Длина всей окружности складывается из длин составляющих ее дуг (С = 1 + 2 + 5 + 10 = 18). Тогда (frac{C_{angle AOB}}{C} = frac{angle AOB}{360^circ}) (Rightarrow) (frac{5}{18} = frac{angle AOB}{360^circ}) (Rightarrow) (angle AOB = 100^circ).

Ответ: 100

Задание
4

#1791

Уровень задания: Равен ЕГЭ

Длина окружности с центром в точке (O) равна 18 см. Площадь сектора (AOB) равна (dfrac{18}{pi})см(^2). Найдите длину дуги (AB) этого сектора. Ответ дайте в сантиметрах.

Длина окружности равна (2pi R), где (R) – радиус этой окружности. Для данной окружности (2pi R = 18) см, тогда (R = dfrac{9}{pi}) см.

Площадь сектора, градусная мера дуги которого есть (alpha) равна (pi R^2 cdot dfrac{alpha}{360}).

Длина дуги с градусной мерой (alpha) равна (2pi Rcdot dfrac{alpha}{360}).

Из этих формул видно, что длина дуги с градусной мерой (alpha) получится из площади сектора, градусная мера дуги которого есть (alpha), при помощи умножения этой площади на (dfrac{2}{R}).

Длина дуги (AB) данного сектора равна (dfrac{18}{pi} cdot
dfrac{2pi}{9} = 4) см.

Ответ: 4

Задание
5

#304

Уровень задания: Равен ЕГЭ

Внутри большой окружности расположена маленькая, радиус которой в 2,5 раза меньше, чем радиус большой окружности. Найдите отношение площади зеленой области (U) к площади круга, ограниченного большой окружностью.

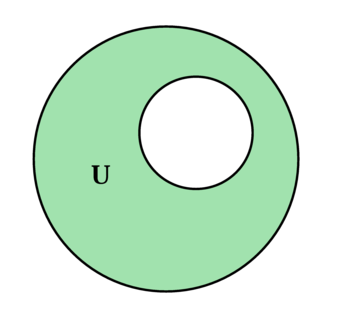
Обозначим радиус меньшей из окружностей за (r), тогда радиус большей окружности (2,5cdot r).
Площадь круга, ограниченного окружностью радиуса (R), равна (pi R^2).
Площадь меньшего круга равна (pi r^2), а площадь большего равна (pi cdot (2,5r)^2 = 6,25pi r^2).
Площадь области (U) равна разности площадей большего и меньшего кругов и равна (6,25pi r^2 – pi r^2 = 5,25pi r^2).
Искомое отношение площадей есть (dfrac{5,25pi r^2}{6,25pi r^2} = 0,84).

Ответ: 0,84

Задание
6

#1733

Уровень задания: Равен ЕГЭ

Две окружности касаются внутренним образом так, что один из радиусов большей окружности совпадает с диаметром меньшей окружности (смотри рисунок). Найдите радиус большей окружности, если площадь зеленой области равна (48pi).

Обозначим за (R) – радиус большей окружности и одновременно диаметр меньшей. Тогда площадь зеленой области (S) можно выразить через площади кругов следующим образом: (S = pi R^2 – frac{pi R^2}{4} = frac{3}{4}pi R^2). Т.к. (S = 48pi) (Rightarrow) (frac{3}{4}pi R^2 = 48pi) (Rightarrow) (R^2 = 64) (Rightarrow) (R = 8).

Ответ: 8

Задание
7

#1732

Уровень задания: Сложнее ЕГЭ

На рисунке изображены две окружности с общим центром (O), где радиусы (OB = 3) и (OA = 1), а угол (angle BOD = 90^circ). Найдите площадь фигуры (ABCDEFA) деленную на (pi).

Площадь сектора с углом (90^circ) в большой окружности равна (S_{big} = frac{picdot3^2}{360^circ}cdot90^circ = frac{9pi}{4}), а в маленькой (S_{small} = frac{picdot1^2}{360^circ}cdot90^circ = frac{pi}{4}). Тогда (frac{S_{ABCDEFA}}{pi} = frac{S_{big} – S_{small}}{pi} = 2).

Ответ: 2

Задачи на нахождение площади круга — обязательная часть ЕГЭ по математике. Как правило, этой теме отводится сразу несколько заданий в аттестационном испытании. Понимать алгоритм нахождения длины окружности и площади круга должны все старшеклассники, независимо от уровня их подготовки.

Если подобные планиметрические задачи вызывают у вас затруднения, рекомендуем обратиться к образовательному порталу «Школково». С нами вы сможете восполнить пробелы в знаниях.

В соответствующем разделе сайта представлена большая подборка задач на нахождение длины окружности и площади круга, подобных тем, которые включены в ЕГЭ. Научившись их правильно выполнять, выпускник сможет успешно справиться с экзаменом.

Основные моменты

Задачи, в которых требуется применить формулы площади, могут быть прямыми и обратными. В первом случае известны параметры элементов фигуры. При этом искомой величиной является площадь. Во втором случае, наоборот, площадь известна, а найти необходимо какой-либо элемент фигуры. Алгоритм вычисления правильного ответа в подобных заданиях различается только порядком применения базовых формул. Именно поэтому, приступая к решению таких задач, необходимо повторить теоретический материал.

На образовательном портале «Школково» представлена вся базовая информация по теме «Нахождение длины окружности или дуги и площади круга», а также по другим темам, например, «Центральный угол окружности». Ее наши специалисты подготовили и изложили в максимально доступной форме.

Вспомнив основные формулы, учащиеся могут приступить к выполнению задач на нахождение площади круга, подобных тем, которые включены в ЕГЭ, в режиме онлайн. Для каждого упражнения на сайте представлено подробное решение и дан правильный ответ. При необходимости любое задание можно сохранить в разделе «Избранное», чтобы в дальнейшем вернуться к нему и обсудить с преподавателем.

УСТАЛ? Просто отдохни

Источник

Длина окружности

Длина окружности

Задачи на длину окружности

Задачи на площадь круга

Число π и длина окружности

Как найти длину окружности

Разбор примера

Разбор примера

Хорда и дуга окружности

Ваши комментарии

Нахождение длины окружности и площади круга

Основные моменты

Вам также может понравиться

Как найти среднюю высоту дерева

Как найти градусную меру тупого угла параллелограмма

Как найти wifi direct на телефоне

Добавить комментарий Отменить ответ