Видеоурок: Строение атомного ядра. Ядерные силы
Лекция: Энергия связи нуклонов в ядре. Ядерные силы
Итак, из прошлой темы мы определились, что любое ядро состоит из нуклонов. Но благодаря чему ядра не распадаются? Казалось бы, в ядре всех элементов, кроме легкого водорода, содержится по несколько протонов. Как мы знаем, одноименные заряды отталкиваются, но этого не происходит в ядре. Более того, оно считается стабильным, а силы в нем самыми большими, в сравнении со всеми возможными. Можно предположить, что частицы держаться благодаря гравитационным силам. Все это можно проверить.
Предположим, что в ядре некоторого элемента содержится два протона (например, это гелий). Давайте определим, как относятся силы гравитационного взаимодействия к кулоновским силам. В формулах нам важно знать массу и величину заряда протона, а, как известно, это постоянные величины.


Судя из данных расчетов, электрические силы отталкивания во много раз больше гравитационных сил. А это значит, что существуют другие силы, позволяющие удерживать ядро целостным. Эти силы называются ядерными.
 Ядерные силы
Ядерные силы
До этого момента нами были изучены два вида сил: гравитационные и электромагнитные. Существует другое взаимодействие, которое называется сильным. Именно оно присутствует в ядре.
Свойства ядерных сил:
1. Данные силы имеются между всеми нуклонами в ядре (нейтронами и протонами).
2. Данные силы в 102 раз больше, чем электромагнитные. Не существует иных сил, которые превосходили бы ядерные силы.
3. Ядерные силы действуют на расстоянии не более 10-15м. Если расстояние увеличить, то силы гаснут, если же уменьшить, то они способствуют отталкиванию частиц.
 Атомная единица массы
Атомная единица массы
Достаточно неудобно рассчитывать ядерные массы в килограммах, поскольку масса любого ядра очень маленькая. Именно поэтому в качестве измерения массы ввели новую единицу, которая называется атомной единицей массы (а.е.м.). Именно данная величина указана в таблице Менделеева.
Точное значение а.е.м было принято за 1/12 величину массы углерода и оно равно:

Итак, всем нам известно, что любое покоящееся тело имеет энергию, которую можно рассчитать по формуле Е = mc2. Для упрощения счета некоторых величин, перемножим величину скорости света на 1 а.е.м. Энергия 1 а.е.м любого тела равна:

Чтобы не получать постоянно такие малые величины энергии, в ядерной физике используют другие единицы измерения, а именно электрон-вольты:

А это значит, что энергия 1 а.е.м. равна:

Для известных нам частиц можно так же рассчитать постоянное значение энергии:

 Дефект масс. Энергия связи
Дефект масс. Энергия связи
Существует огромное количество таблиц, в которых можно определить точное значение массы того или иного изотопа. Но Вы можете спросить, зачем они нужны, ведь можно просто взять и сложить массы всех частиц ядра и получить конечное его значение. До некоторого времени так и делали, пока не стало известно, что сумма масс всех нуклонов не совпадает с массой ядра. Масса ядра всегда меньше, чем сумма масс всех нуклонов. Разность этих масс называется дефектом масс.
Дефект масс находится по формуле:

Обратите внимание, в данной формуле М – это масса ядра. Однако, в таблице Менделеева и других таблицах указана масса всего атома. Поэтому из известного значения следует вычесть массу всех имеющихся электроном.
Например, давайте рассмотрим ядро Гелия и найдем для него дефект масс. Для начала найдем значение массы атома гелия и вычтем из нее массы двух имеющихся электронов:

Далее найдем массу всех нуклонов гелия:

В результате получим величину дефекта масс:

Разность энергий в таком случае находится следующим образом:

Данная разность называется энергией связи. Она определяется работой, которую прикладывают к ядру для расщепления его на составные единицы (нуклоны).
 Удельная энергия связи
Удельная энергия связи
Насколько прочное ядро характеризует удельная энергия связи. Эта величина показывает, какую работу следует приложить для отщепления одного нуклона из ядра. Находится данная величина по формуле:

Измеряется она в МэВ на нуклон.
На графике можно наблюдать зависимость величины удельной энергии от количества нуклонов в ядре:

Чем легче ядра и больше количество нуклонов, тем больше удельная энергия. Однако для тяжелых ядер данная зависимость является обратной.
Опытным путём было доказано, что масса ядра оказывается меньше, чем масса протонов и нейтронов, из которых состоит ядро. Разница между этими массами называется дефектом массы ядра.
Дефект массы ядра (
Δm
) — это разница между суммарной массой свободных нуклонов, из которых состоит ядро, и массой ядра.
Почему же масса нуклонов, связанных ядерными силами в ядро, оказывается меньше массы этих же нуклонов в свободном состоянии? Оказывается, что масса и энергия взаимосвязаны.
Всякое тело массой m обладает энергией, которая называется энергией покоя (
E0
):
, где c — скорость света в вакууме.
Впервые соотношение между энергией и массой вывел Альберт Эйнштейн, поэтому это выражение и получило название «уравнение Эйнштейна».
Уменьшение энергии покоя нуклонов в ядре вызвано наличием ядерных сил, которые удерживают протоны и нейтроны в ядре. Работа, которую необходимо совершить для разрыва ядерных сил и разъединения нуклонов, равна энергии, которая связывает нуклоны вместе. Эта энергия называется энергией связи (
Eсв
) ядра.
Энергия связи и дефект массы ядра связаны между собой уравнением Эйнштейна:
Удельной энергией связи ядра называют энергию связи, приходящуюся на (1) нуклон:
Удельная энергия равна средней энергии, необходимой для отрыва (1) нуклона от ядра.
Вычисления показали, что наибольшей удельной энергией связи обладают элементы, находящиеся в центре Периодической системы химических элементов. С увеличением порядкового номера начинает уменьшаться удельная энергия связи. Именно поэтому ядра элементов с порядковым номером больше (83) являются радиоактивными. Благодаря небольшой удельной энергии связи они способны самопроизвольно распадаться.
Единицы измерения энергии
В ядерной физике принято измерять энергию в мегаэлектронвольтах ((1) МэВ):
(1) МэВ (=)
106
эВ
≈1,6⋅10−13
Дж.
Для вычисления энергии связи удобно пользоваться переводным коэффициентом для массы и энергии.
Дефекту массы в (1) а. е. м. соответствует энергия, равная
кг
⋅(3⋅108
м/с
)2≈1,49⋅10−10
Дж
=931,5
МэВ.
Обрати внимание!
Для выражения изменения энергии системы в мегаэлектронвольтах нужно
изменение массы системы в атомных единицах массы умножить на переводной коэффициент (931,5) МэВ/а. е. м.
(1) а. е. м. (=) (931,5) МэВ.
Устойчивость атомных ядер основывается на действии неких колоссальных многократно превосходящих силы кулоновского отталкивания протонов сил, удерживающих нейтроны и протоны внутри ядра.
Приведенные выше силы, удерживающие нуклоны в ядре, носят название ядерных. Они представляют собой проявление самого интенсивного из всех известных в физике видов взаимодействия, то есть, так называемого сильного взаимодействия.
Ядерные силы превышают электростатические силы приблизительно в сотню раз и на десятки порядков обгоняют силы гравитационного взаимодействия нуклонов. Короткодействующий характер ядерных сил представляет собой их крайне важную особенность. Опыты Резерфорда, направленные на изучение рассеяния α-частиц показали, что обсуждаемый тип сил заметно проявляется только на расстояниях близких к размерам ядра, то есть на расстоянии в 10–12–10–13 см. На более протяженных расстояниях становится наблюдаемым действие сравнительно медленно спадающих кулоновских сил.
Основываясь на опытных данных, можно заявить, что протоны в ядре в отношении сильного взаимодействия ведут себя ровно так же, как и нейтроны. Из этого факта исходит вывод о том, что ядерные силы не имеют зависимости от наличия или отсутствия у частиц электрического заряда.
Дефект массы
Важнейшее место в ядерной физике занимает понятие энергии связи ядра.
Энергия связи атомного ядра эквивалентна минимальной необходимой для полного расщепления ядра на отдельные частицы энергии. Опираясь на закон сохранения энергии, можно сказать, что энергия связи равняется выделяющейся в процессе образования ядра из отдельных частиц энергии.
Энергия связи каждого ядра может быть определена при помощи точного измерения его массы. В наше время физики обладают знаниями, позволяющими им измерять массы частиц, будь то электроны, протоны, нейтроны, ядра или что-то подобное, с чрезвычайно высокой точностью.
Такие измерения доказывают, что масса каждого конкретного ядра Mя в любом случае меньше совокупности масс входящих в его состав протонов и нейтронов:
Mя<Zmp+Nmn.
Следующее выражение разности масс:
∆M=Zmp+Nmn-Mя .
Носит название дефекта массы.
Благодаря дефекту массы, используя формулу Эйнштейна E=mc2, можно высчитать энергию, выделившуюся при образовании приведенного ядра, то есть энергию связи ядра Eсв:
Eсв=∆Mc2=Zmp+Nmn-Mяс .
Данная энергия выделяется в процессе образования ядра в виде излучения γ-квантов.
Как пример высчитаем энергию связи ядра гелия He24, в чей состав входят пара протонов и два нейтрона. Масса ядра гелия Mя=4,00260 а. е. м. Сумма масс двух протонов с двумя нейтронами эквивалентна 2mp+2mn=4, 03298 а. е. м. Таким образом, дефект массы ядра гелия равняется ΔM=0,03038 а. е. м. Процесс расчета по формуле Eсв ΔMc2 приводит нас к следующему значению энергии связи ядра He24 : Eсв=28,3 МэВ. Это колоссальная величина. Образование всего 1 г гелия приводит к выделению энергии приближенной к 13,6 эВ. Приблизительно такая же энергия излучается в процессе сгорания практически целого вагона с каменным углем. Энергия связи ядра на много порядков превосходит энергию связи электронов с атомом. Для атома водорода H11 энергия ионизации равняется 13,6 эВ.
В таблицах обычно указана удельная энергия связи, то есть, энергия связи на один нуклон. Для ядра гелия удельная энергия связи примерно равна 7,1 МэВ/нуклон. На рисунке 6.6.1 проиллюстрирован график зависимости удельной энергии связи от массового числа A. Как мы можем наблюдать на графике, удельная энергия связи нуклонов у различных атомных ядер разнится. В случае легких ядер удельная энергия связи изначально резко увеличивается от 1,1 МэВ/нуклон у дейтерия до7,1 МэВ/нуклон у гелия He24. После ряда скачкообразных изменений удельная энергия медленно повышается до максимальной величины 8,7 МэВ/нуклон у элементов с массовым числом A=50–60, а затем все так же медленно падает у тяжелых элементов. К примеру, у урана U92238 она равняется 7,6 МэВ/нуклон.
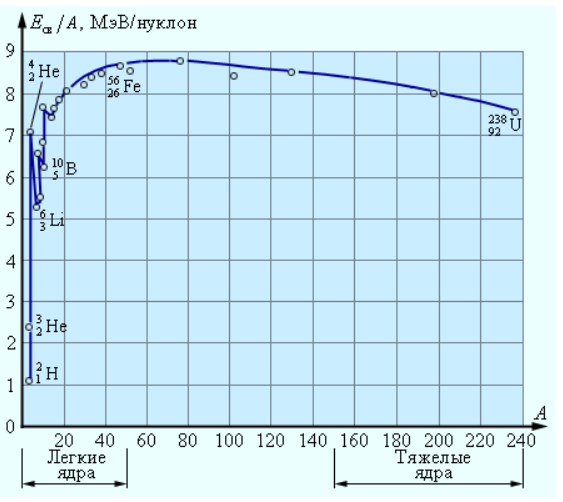
Рисунок 6.6.1. Удельная энергия связи ядер.
Понижение удельной энергии связи в процессе перехода к тяжелым элементам основывается на повышении энергии кулоновского отталкивания протонов. В тяжелых ядрах связь между нуклонами слабеет, вследствие чего структура ядер теряет значительную часть своей прочности. Числа протонов Z и нейтронов N выходят эквивалентными в случае стабильных легких ядер, когда роль кулоновского взаимодействия мала, в качестве примера можно привести He24, Li36, B510. Под воздействием ядерных сил формируются протон-нейтронные пары. Однако тяжелым ядрам, содержащим немалое число протонов, по причине увеличения энергии кулоновского отталкивания для обеспечения устойчивости необходимы дополнительные нейтроны. На рисунке 6.6.2 изображена диаграмма, демонстрирующая количество протонов и нейтронов в стабильных ядрах. У ядер, идущих следом за висмутом (Z>83), по причине большого числа протонов полная стабильность оказывается принципиально невозможной.
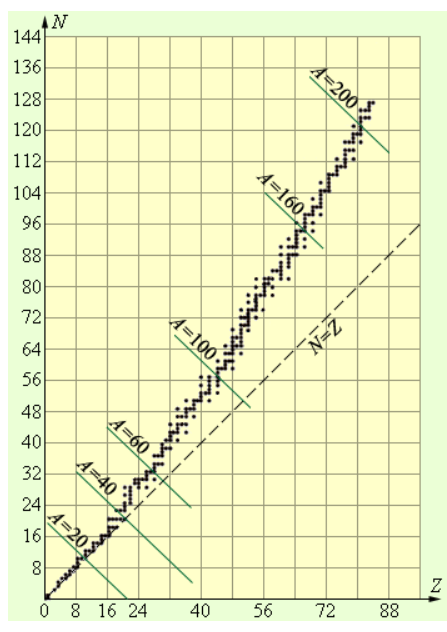
Рисунок 6.6.2. Количество протонов и нейтронов в стабильных ядрах.
Ядерные превращения
На рисунке 6.6.1 можно увидеть, что с энергетической точки зрения большей устойчивостью обладают ядра элементов из средней части системы Менделеева. Данный факт означает, что существуют две возможности получения положительного энергетического выхода в процессе ядерных превращений:
- Деление тяжелых ядер на более легкие.
- Слияние легких ядер в более тяжелые.
Оба приведенных процесса выделяют колоссальное количество энергии. В условиях современной физики, как деление тяжелых ядер на более легкие, так и слияние легких в тяжелые осуществлены на практике: реакции деления и термоядерные реакции.
Произведем некоторые оценки. Пускай, к примеру, ядро урана U92238 делится на два эквивалентных друг другу ядра с массовыми числами 119. У приведенных ядер, как видно из рисунка 6.6.1, удельная энергия связи около 8,5 МэВ/нуклон. Удельная энергия связи ядра урана 7,6 МэВ/нуклон. Соответственно, при делении ядра урана излучается энергия, равняющаяся 0,9 МэВ/нуклон или больше 200МэВ на один атом урана.
Исследуем следующий пример. Пускай в неких условиях два ядра дейтерия H12 формируют одно ядро гелия He24. Удельная энергия связи ядер дейтерия равняется значению 1,1 МэВ/нуклон, а удельная энергия связи ядра гелия 7,1 МэВ/нуклон. Соответственно, в процессе синтеза единого ядра гелия из двух ядер дейтерия произведется энергия, эквивалентная 6 МэВ/нуклон или 24 МэВ на атом гелия.
Стоит отметить, что в сравнении с делением тяжелых элементов синтез легких провоцирует излучение энергии на один нуклон большее примерно в шесть раз.
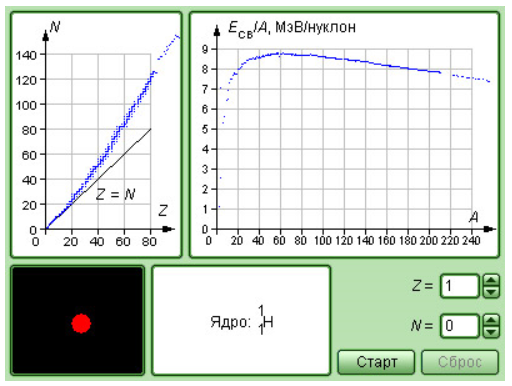
Рисунок 6.6.3. Модель энергии связи ядер.
