
{V= S cdot h}
На этой странице собраны формулы и калькуляторы для нахождения объема пирамиды. Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
Содержание:
- калькулятор объема пирамиды
- формула объема пирамиды
- объем правильной треугольной пирамиды
- объем правильной четырехугольной пирамиды
- объем правильной шестиугольной пирамиды
- объем правильной n-угольной пирамиды
- объем тетраэдра
- примеры задач
Формула объема пирамиды
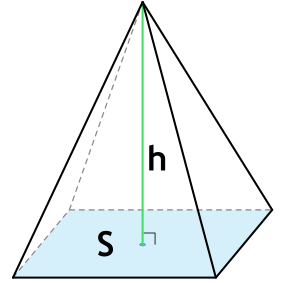
{V= dfrac{1}{3} S cdot h}
S – площадь основания пирамиды
h – высота пирамиды
Формула объема правильной треугольной пирамиды
Правильная треугольная пирамида – пирамида, в основании которой лежит равносторонний треугольник, а грани являются равнобедренными треугольниками.
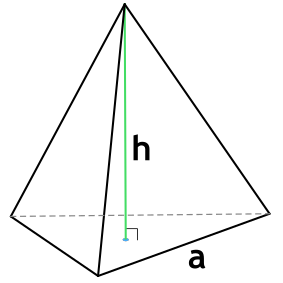
{V= dfrac{h cdot a^2}{4 sqrt{3}}}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной четырехугольной пирамиды
Правильная четырехугольная пирамида – пирамида, в основании которой лежит квадрат, а грани являются равнобедренными треугольниками.
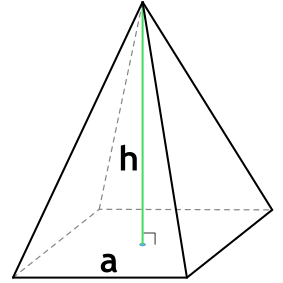
{V= dfrac{1}{3} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной шестиугольной пирамиды
Правильная шестиугольная пирамида – пирамида, в основании которой лежит правильный шестиугольник, а грани являются равнобедренными треугольниками.
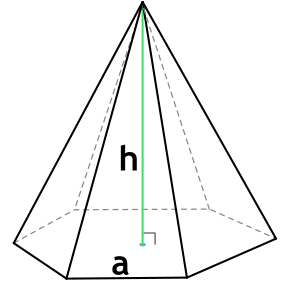
{V= dfrac{sqrt{3}}{2} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной n-угольной пирамиды
Правильная пирамида имеет в основании правильный многоугольник (все стороны и углы равны между собой), а высота проходит через центр этого основания.

{V= dfrac{n cdot h cdot a^2}{12 cdot tg(dfrac{180°}{n} )}}
a – длина стороны основания пирамиды
h – высота пирамиды
n – число сторон многоугольника в основании пирамиды
Формула объема тетраэдра
Тетраэдр – правильный многогранник (четырехгранник), имеющий четыре грани, каждая из которых является правильным треугольником. У тетраэдра кроме четырех граней также 4 вершины и 6 ребер.
{V= dfrac{sqrt{2} a^3}{12}}
a – длина стороны тетраэдра
Примеры задач на нахождение объема пирамиды
Задача 1
Найдите объем пирамиды с высотой 2м, а основанием ее служит квадрат со стороной 3м.
Решение
Так как в основании пирамиды лежит квадрат, то воспользуемся формулой объема правильной четырехугольной пирамиды и подставим в нее значения высоты и стороны основания.
V= dfrac{1}{3} cdot h cdot a^2 = dfrac{1}{3} cdot 2 cdot 3^2 = dfrac{1}{3} cdot 2 cdot 9 = dfrac{1}{3} cdot 18 = 6 : м^3
Ответ: 6 м³
Используем калькулятор для проверки полученного ответа.
Задача 2
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1см, а высота равна √3см.
Решение
Из условия следует, что пирамида правильная треугольная. Это значит, что для решения задачи необходимо воспользоваться формулой для правильной треугольной пирамиды. Подставим в нее значения и рассчитаем объем.
V= dfrac{h cdot a^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1}{4 sqrt{3}} = dfrac{sqrt{3}}{4 sqrt{3}} = dfrac{cancel{sqrt{3}}}{4 cancel{sqrt{3}}} = dfrac{1}{4} = 0.25 : м^3
Ответ: 0.25 см³
Для проверки с помощью калькулятора извлечем квадратный корень из 3: √3 = 1.73205. Теперь можем подставить значения в калькулятор и проверить полученный ответ.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 сентября 2022 года; проверки требуют 4 правки.

Пирами́да (от др.-греч. πυραμίς, род. п. πυραμίδος) — многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину[1]. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д.
Пирамида является частным случаем конуса[2].
История развития пирамиды в геометрии[править | править код]
Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Объём пирамиды был известен древним египтянам. Первым греческим математиком, кто установил, чему равен объём пирамиды, был Демокрит
[3], а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке (книга XI, определение 12[4]).
Элементы пирамиды[править | править код]

SO — высота
SF — апофема
OF — радиус вписанной в основание окружности
- вершина пирамиды — общая точка боковых граней, не лежащая в плоскости основания;
- основание — грань, которой не принадлежит вершина пирамиды;
- боковые грани — треугольные грани, сходящиеся в вершине;
- боковые рёбра — рёбра, являющиеся сторонами двух боковых граней (и, соответственно, не являющиеся сторонами основания);
- высота пирамиды — перпендикуляр из вершины пирамиды на её основание;
- апофема — высота боковой грани правильной пирамиды, проведённая из её вершины;
- диагональное сечение пирамиды — сечение пирамиды, проходящее через её вершину и диагональ основания.
Развёртка пирамиды[править | править код]

Развёртка правильной пятиугольной пирамиды:
1. в плоскости основания («звезда»)
2. в плоскости одной из боковых граней
Развёрткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).
Приступая к изучению развёртки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую плёнку. Некоторые из представленных таким образом поверхностей можно путём изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещён с плоскостью без разрывов и склеивания, то такую поверхность называют развёртывающейся, а полученную плоскую фигуру — её развёрткой.
Свойства[править | править код]
Если все боковые рёбра равны, то:
- вокруг основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;
- боковые рёбра образуют с плоскостью основания равные углы;
- также верно и обратное, то есть если боковые рёбра образуют с плоскостью основания равные углы, или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые рёбра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом, то:
- в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
- высоты боковых граней равны;
- площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.
Теоремы, связывающие пирамиду с другими геометрическими телами[править | править код]

Описание сферы вокруг правильной пирамиды:
SD — высота пирамиды.
AD — радиус окружности, описывающей основание.
В — середина ребра боковой грани
С — точка пересечения плоскостей проходящих через середину рёбер перпендикулярно им.
AC=CS — радиус сферы описывающей пирамиду

Сфера, вписанная в правильную пирамиду:
D — центр основания
SF — апофема
ASD — биссекторная плоскость угла между боковыми гранями
BCE — биссекторная плоскость угла между основанием и боковой гранью
С — точка пересечения всех биссекторных плоскостей
CK=CD — радиус сферы вписанной в пирамиду
Сфера[править | править код]
- около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие)[5]. Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им. Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу;
- в пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Конус[править | править код]
- Конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие);[6]
- Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые рёбра пирамиды равны между собой (необходимое и достаточное условие);
- Высоты у таких конусов и пирамид равны между собой.
Цилиндр[править | править код]
- Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.
- Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания пирамиды. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды — вписанный многоугольник (необходимое и достаточное условие).
Формулы, связанные с пирамидой[править | править код]
- Объём пирамиды может быть вычислен по формуле:
- где
— площадь основания и
— высота;[7]
- где
— объём параллелепипеда;
- Также объём треугольной пирамиды (тетраэдра) может быть вычислен по формуле[8]:
- где
— скрещивающиеся рёбра ,
— расстояние между
и
,
— угол между
и
;
- Боковая поверхность — это сумма площадей боковых граней:
- Полная поверхность — это сумма площади боковой поверхности и площади основания:
- Для нахождения площади боковой поверхности в правильной пирамиде можно использовать формулы:
- где
— апофема ,
— периметр основания,
— число сторон основания,
— боковое ребро,
— плоский угол при вершине пирамиды.
Особые случаи пирамиды[править | править код]
Правильная пирамида[править | править код]
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Тогда она обладает такими свойствами:
Прямоугольная пирамида[править | править код]
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
Тетраэдр[править | править код]
Тетраэдром называется треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды. Кроме того, существует большое различие между понятиями «правильная треугольная пирамида» и «правильный тетраэдр». Правильная треугольная пирамида — это пирамида с правильным треугольником в основании (грани же должны быть равнобедренными треугольниками). Правильным тетраэдром является тетраэдр, у которого все грани являются равносторонними треугольниками.
См. также[править | править код]
- Усечённая пирамида
- Бипирамида
Примечания[править | править код]
- ↑ Александров А. Д., Вернер А. Л. Геометрия. Учебник для 10—11 классов общеобразовательных учреждений. — 2-е изд. — М.: Просвещение, 2003. — 271 с. — ISBN 5-09-010773-4.
- ↑ Математика в понятиях, определениях и терминах. Ч. 1. Пособие для учителей. Под ред. Л. В. Сабинина. М., Просвещение, 1978. 320 с. С. 253.
- ↑ Б. Л. ван дер Варден. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. — 3-е изд.. — М.: КомКнига, 2007. — 456 с. — ISBN 978-5-484-00848-3.
- ↑ М. Е. Ващенко-Захарченко. Начала Евклида с пояснительным введением и толкованиями. — Киев, 1880. — С. 473. — 749 с.
- ↑ Саакян С. М., Бутузов В. Ф. Изучение геометрии в 10—11-х классах: книга для учителя. — 4-е изд., дораб.. — М.: Просвещение, 2010. — 248 с. — (Математика и информатика). — ISBN 978-5-09-016554-9.
- ↑ Погорелов А. В. Геометрия: Учебник для 10—11 классов общеобразовательных учреждений. — 8-е изд. — М.: Просвещение, 2008. — 175 с. — 60 000 экз. — ISBN 978-5-09-019708-3.
- ↑ Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, §357.
- ↑ Кушнир И. А. Триумф школьной геометрии. — К.: Наш час, 2005. — 432 с. — ISBN 966-8174-01-1.
- ↑ Готман Э. Свойства правильной пирамиды, вписанной в сферу Архивная копия от 22 января 2012 на Wayback Machine // Квант. — 1998. — № 4.
Литература[править | править код]
- Александров А. Д., Вернер А. Л. Геометрия. Учебник для 10—11 классов общеобразовательных учреждений. — 2-е изд. — М.: Просвещение, 2003. — 271 с. — ISBN 5-09-010773-4.
- Калинин А. Ю., Терешин Д. А. Стереометрия. 11 класс. — 2-е изд. — М.: Физматкнига, 2005. — 332 с. — ISBN 5-89155-134-9.
- А. П. Киселёв, Геометрия по Киселёву, arΧiv:1806.06942 [math.HO].
- Погорелов А. В. Геометрия: Учебник для 10—11 классов общеобразовательных учреждений. — 8-е изд. — М.: Просвещение, 2008. — 175 с. — 60 000 экз. — ISBN 978-5-09-019708-3.
Ссылки[править | править код]
- Бумажные модели пирамид Архивная копия от 4 января 2010 на Wayback Machine (англ.)
- «Начала» Евклида.
Как рассчитать объем пирамиды
На данной странице калькулятор поможет рассчитать объем пирамиды онлайн. Для расчета задайте площадь, высоту, сторону или количество сторон. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
Пирамида
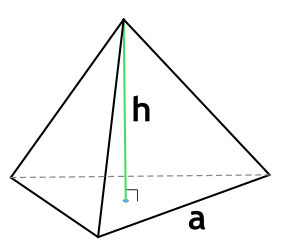
Формула объема пирамиды через высоту и площадь основания:
S – площадь основания; h – высота пирамиды.
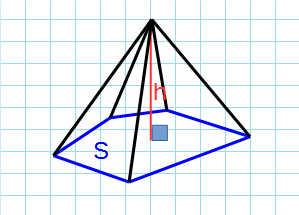
Правильная пирамида
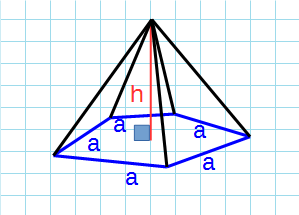
Правильная пирамида — пирамида, в основании которой лежит правильный многоугольник, а высота проходит через центр основания.
Формула объема правильной пирамиды через сторону основания, высоту и количество сторон:
a – сторона основания; h – высота пирамиды; n – количество сторон многогранника в основании.
Правильная треугольная пирамида
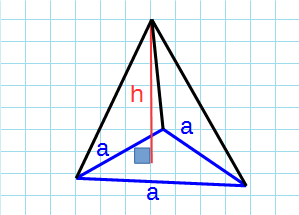
Правильная треугольная пирамида — пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.
Формула объема правильной треугольной пирамиды через сторону основания и высоту:
a – сторона основания; h – высота пирамиды.
Правильная четырехугольная пирамида
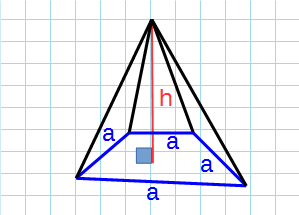
Правильная четырехугольная пирамида — пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.
Формула объема правильной четырехугольной пирамиды через сторону основания и высоту:
a – сторона основания; h – высота пирамиды.
Тетраэдр
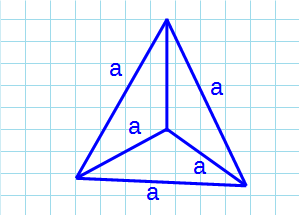
Тетраэдр — пирамида, у которой все грани равносторонние треугольники.
Формула объема тетраэдра:
a – ребро тетраэдра.






