Сила трения. Коэффициент трения
- Причины возникновения трения
- Трение покоя
- Трение скольжения
- Трение качения
- Задачи
- Лабораторная работа №8. Измерение коэффициента трения скольжения
п.1. Причины возникновения трения
При движении одного тела по поверхности другого всегда возникает сила, направленная противоположно направлению скорости и замедляющая движение. Эта сила называется силой трения.
По своей природе сила трения отличается от силы тяготения и силы упругости, которые были рассмотрены в предыдущих параграфах.
Причины возникновения силы трения можно разделить на два класса: 1) шероховатость поверхностей контактирующих тел; 2) взаимное притяжение молекул при контакте.
Неровности поверхностей проявляются на макроуровне и видны невооруженным глазом или в оптический микроскоп. Их влияние можно уменьшить, если отполировать поверхности или нанести смазку.
Взаимное притяжение молекул проявляется на микроуровне и приводит к тому, что даже на идеально отполированных поверхностях не удается избежать трения, когда частицы одного тела перемещаются относительно частиц другого.
Сила трения – это сумма межмолекулярных сил, возникающих при деформациях и изломах контактирующих поверхностей за счет разрыва межмолекулярных связей.
Сила трения направлена вдоль поверхностей контактирующих тел.
Как и сила упругости, сила трения имеет электромагнитную природу и связана с межмолекулярным взаимодействием.
Но в отличие от силы упругости, причиной силы трения является разрыв межмолекулярных связей. Кроме того, если сила упругости всегда направлена перпендикулярно поверхностям контактирующих тел, то сила трения всегда направлена вдоль этих поверхностей.
В зависимости от характера движения контактирующих тел различают трение покоя, трение скольжения и трение качения.
п.2. Трение покоя
Сила трения, возникающая при относительной скорости двух контактирующих тел равной нулю, называется силой трения покоя.
Сила трения покоя равна по модулю приложенной силе и направлена в сторону, противоположную возможному движению тела, параллельно контактирующим поверхностям.
Если параллельно поверхности контакта на тело не действует сила, сила трения покоя равна нулю. Максимальное значение силы трения, при котором тело все ещё неподвижно, называется максимальной силой трения покоя.
Пример изменения силы трения покоя
 |
Сила трения покоя равна приложенной силе, которая все ещё не приводит тело в движение. Допустим, что мы прикладываем к шкафу последовательно силу 100 Н, 200 Н, 300 Н, и он начинает равномерно двигаться только при 300 Н. Как только тело начинает скользить, на него уже действует сила трения скольжения. Получаем: |
||
| Приложенная сила, Н | Движение | Сила трения покоя, Н | Сила трения скольжения, Н |
| 100 | Нет | 100 | – |
| 200 | Нет | 200 | – |
| 300 | Есть, равномерное | – | 300 |
п.3. Трение скольжения
Силу трения, возникающую в результате движения одного тела по поверхности другого, называют силой трения скольжения.
Сила трения скольжения всегда направлена в сторону, противоположную перемещению тела («тормозит» движение).
 |
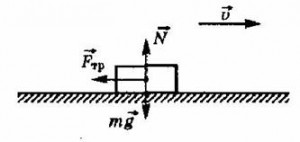
Если тело расположено на горизонтальной опоре, сила тяжести (mg), действующая на него, равна по величине силе реакции опоры (N) (см. §22 данного справочника). Сила трения направлена противоположно силе тяги. |
Сила трения скольжения прямо пропорциональна силе реакции опоры: $$ F_{text{тр}}=mu N $$ Коэффициент (mu) называют коэффициентом трения скольжения; величина (mu) зависит от материала трущихся тел и состояния их поверхностей.
Значения коэффициентов трения скольжения для различных поверхностей приводятся в справочных таблицах.
При проектировании и разработке машин и механизмов коэффициенты трения скольжения для отдельных узлов определяются в специальных лабораториях.
п.4. Трение качения
Сила трения, возникающая при качении одного тела по поверхности другого, называется силой трения качения.
Сила трения качения значительно меньше силы трения скольжения.
 |
Уменьшение трения за счет качения используется в шариковых и роликовых подшипниках. Первый подшипник качения был установлен в опоре ветряка, построенного в Англии в 1780 г. Этот подшипник состоял из двух литых чугунных дорожек качения, между которыми находилось 40 чугунных шаров. Сегодня подшипники являются незаменимой деталью во всех подвижных конструкциях; они уменьшают износ трущихся деталей и снижают потери энергии на нагрев из-за трения. |
п.5. Задачи
Задача 1. Найдите коэффициент трения между шинами автомобиля и дорогой, если при равномерном движении по прямолинейному участку двигатель развивает силу тяги, равную 30 кН. Масса автомобиля 6 т.
Дано:
(m=6 text{т}=6cdot 10^3 text{кг})
(F_{text{тяги}}=30 text{кН}=3cdot 10^4 text{Н})
(gapprox 10 text{м/с}^2)
__________________
(mu-?)

Коэффициент трения $$ mu=frac{F_{text{тр}}}{N}. $$ При равномерном движении скорость постоянна и ускорение (overrightarrow{a}=0). По второму закону Ньютона, равнодействующая горизонтальных сил равна нулю $$ overrightarrow{F_{text{тр}}}+ overrightarrow{F_{text{тяги}}}=0. $$ Значит, сила трения и сила тяги равны по модулю: $$ F_{text{тр}}=F_{text{тяги}}. $$ Сила реакции горизонтальной опоры равна силе тяжести, действующей на автомобиль: $$ n=mg. $$ Получаем: $$ mu=frac{F_{text{тр}}}{N}= frac{F_{text{тяги}}}{mg}, mu=frac{3cdot 10^4}{6cdot 10^3cdot 10}=0,5. $$ Ответ: 0,5
Задача 2. Деревянный брусок массой 3 кг равномерно тянут по горизонтальной деревянной доске с помощью динамометра. Жесткость пружины динамометра равна 3 Н/см, коэффициент трения дерева об дерево 0,3. На сколько сантиметров растянется пружина?
Дано:
(m=3 text{кг})
(k=3frac{text{Н}}{text{см}}=frac{3 text{Н}}{0,01 text{м}}=300frac{text{Н}}{text{м}})
(mu=0,3)
(gapprox 10 text{м/с}^2)
__________________
(Delta l-?)
Показания динамометра – это сила упругости, равная силе тяги. При равномерном движении сила тяги равна по модулю силе трения. Поэтому begin{gather*} F_{text{упр}}=kDelta l=F_{text{тр}}=mu N=mu mgRightarrow kDelta l=mu mg end{gather*} Получаем: $$ Delta l=frac{mu mg}{k}, Delta l=frac{0,3cdot 3cdot 10}{300}=0,03 (text{м})=3 (text{см}) $$ Ответ: 3 см.
Задача 3. Автомобиль движется по горизонтальному участку дороги со скоростью 72 км/ч. Рассчитайте время торможения и тормозной путь до полной остановки, если коэффициент трения колес о дорогу равен 0,4.
Дано:
(v_1=72frac{text{км}}{text{ч}}=20frac{text{м}}{text{с}})
(mu=0,4)
(v_2=0)
(gapprox 10 text{м/с}^2)
__________________
(t, s-?)
Автомобиль тормозит за счет силы трения. По второму закону Ньютона begin{gather*} F_{text{тр}}=ma. end{gather*} С другой стороны на горизонтальной дороге $$ F_{text{тр}}=mu N=mu mg. $$ Получаем: $$ ma=mu mgRightarrow a=mu g. $$ По определению ускорения $$ a=frac{v_2-v_1}{t}. $$ Т.к. (v_2=0), ускорение отрицательное.
Модуль ускорения $$ |a|=frac{v_1}{t}=mu gRightarrow t=frac{v_1}{mu g} $$ Время торможения прямо пропорционально скорости и обратно пропорционально коэффициенту трения. $$ t=frac{20}{0,4cdot 10}=5 (text{с}) $$ Найдем тормозной путь $$ s=v_1t+frac{at^2}{2}=v_1t+ left(frac{overbrace{v_2}^{=0}-v_1}{t}right)frac{t^2}{2}=v_1t -frac{v_1t}{2}=frac{v_1t}{2}=frac{v_1t}{2}cdot frac{v_1}{mu g}=frac{v_1^2}{2mu g} $$ Тормозной путь прямо пропорционален квадрату(!) скорости и обратно пропорционален коэффициенту трения. $$ s=frac{20^2}{2cdot 0,4cdot 10}=50 (text{м}) $$ Ответ: 5 с; 50 м.
п.6. Лабораторная работа №8. Измерение коэффициента трения скольжения
Цель работы
Научиться измерять силу трения скольжения и определять коэффициент трения скольжения. Изучить зависимость коэффициента трения скольжения от материалов соприкасающихся тел и от площади опоры движущегося тела.
Теоретические сведения
 |
При (v=const) (равномерное движение) получаем По вертикали (moverrightarrow{g}=-overrightarrow{N}). Модули этих сил равны По горизонтали (overrightarrow{F_{text{тр}}}=-overrightarrow{F_{text{тяги}}}). Модули этих сил равны $$ F_{text{тяги}}=F_{text{тр}}=mu N=mu mg $$ |
Если тело перемещать с помощью динамометра, то сила упругости, возникающая в пружине, будет равна силе тяги. Т.е., сила тяги непосредственно измеряется динамометром.
В работе используются стандартные лабораторные грузики массой 100 г.
Измерив силу тяги и зная массу перемещаемого тела, рассчитываем коэффициент трения: $$ mu=frac{F_{text{тяги}}}{mg} $$
Для расчетов используем стандартное значение (g=9,80665 text{м/с}^2).
Погрешность для прямых измерений (F_{text{тяги}}) определяется как половина цены деления динамометра. Погрешность для массы определяется по маркировке грузиков и бруска, (Delta m=2 text{г}) для (m=100 text{г}), т.е. (delta_m=2text{%}).
Погрешность эксперимента (delta_e) рассчитывается как средняя арифметическая по результатам измерений и вычислений.
Приборы и материалы
Лабораторный динамометр на 5 Н; набор грузиков по 100 г; деревянный брусок с крючком 100 г; деревянная доска; наждачная бумага.
Ход работы
1. Прикрепите динамометр к бруску, положите доску горизонтально, поставьте брусок самой большой по площади гранью слева на доску.
2. Перемещая брусок слева направо по доске, добейтесь равномерного скольжения (со стабильными показаниями динамометра). Снимите показания динамометра и запишите.
3. Повторите эксперимент, нагружая брусок одним, двумя, тремя и четырьмя грузиками.
4. Рассчитайте коэффициент трения дерева об дерево, определите относительную и абсолютную погрешности эксперимента.
5. Повторите эксперимент, перемещая брусок по доске, обмотанной наждачной бумагой. Найдите коэффициент трения дерева об наждак, определите относительную и абсолютную погрешности эксперимента.
6. Снимите наждачную бумагу и повторите эксперимент для трения дерева об дерево. Однако на этот раз брусок должен опираться на меньшую по площади грань. Рассчитайте коэффициент трения дерева об дерево в этом случае.
7. Сравните полученные коэффициенты трения, сделайте выводы о зависимости коэффициента трения от материала соприкасающихся поверхностей и от площади опоры движущегося тела.
Результаты измерений и вычислений
Цена деления динамометра (d=0,1 text{Н}).
Таблица для расчета коэффициента трения скольжения дерева об дерево
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,3 | 0,306 | 0,026 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,025 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,008 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,001 |
| 5 | Брусок + 4 грузика | 0,5 | 1,6 | 0,326 | 0,006 |
| Всего | – | – | 1,660 | 0,065 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,660}{5}=0,332 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,065}{5}=0,013 $$ Относительная погрешность begin{gather*} delta=frac{0,013}{0,332}cdot 100text{%}approx 3,9text{%}\[7pt] mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об наждак
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,6 | 0,612 | 0,039 |
| 2 | Брусок + 1 грузик | 0,2 | 1,1 | 0,561 | 0,012 |
| 3 | Брусок + 2 грузика | 0,3 | 1,7 | 0,578 | 0,005 |
| 4 | Брусок + 3 грузика | 0,4 | 2,2 | 0,561 | 0,012 |
| 5 | Брусок + 4 грузика | 0,5 | 2,7 | 0,551 | 0,022 |
| Всего | – | – | 2,862 | 0,090 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{2,862}{5}approx 0,572 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,090}{5}=0,018 $$ Относительная погрешность begin{gather*} delta=frac{0,018}{0,572}cdot 100text{%}approx 3,1text{%}\[7pt] mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об дерево (узкая грань)
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,35 | 0,357 | 0,011 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,011 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,006 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,015 |
| 5 | Брусок + 4 грузика | 0,5 | 1,7 | 0,347 | 0,000 |
| Всего | – | – | 1,732 | 0,043 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,732}{5}approx 0,346 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,043}{5}approx 0,009 $$ Относительная погрешность begin{gather*} delta=frac{0,009}{0,346}cdot 100text{%}approx 2,5text{%}\[7pt] mu ‘_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
В работе исследовалась зависимость коэффициента трения скольжения от поверхностей, из которых изготовлены соприкасающиеся тела.
Для скольжения дерева об дерево был получен коэффициент begin{gather*} mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Для скольжения дерева об наждак был получен коэффициент begin{gather*} mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%}\[7px] mu_{text{дн}}gt mu_{text{дд}} end{gather*}
Наждак является более шероховатой поверхностью и сила трения на ней больше.
Коэффициент трения скольжения сильно зависит от материалов соприкасающихся поверхностей.
Также в работе исследовалась зависимость коэффициента трения скольжения от площади опоры движущегося тела. Брусок выставлялся на более узкую грань, и изучалось скольжение дерева об дерево в этом случае. Был получен коэффициент begin{gather*} mu’_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*} Поскольку begin{gather*} 0,319le mu_{text{дд}}le 0,345 0,337le mu’_{text{дд}}le 0,355 end{gather*} Полученные отрезки значений перекрываются.
Таким образом, в рамках погрешности эксперимента коэффициент трения скольжения не зависит от площади опоры движущегося тела.
Как определить коэффициент трения
Трение – это процесс взаимодействия твердых тел при их относительном движении, либо при движении тела в газообразной или жидкой среде. Коэффициент трения зависит от материала трущихся поверхностей, качества их обработки и других факторов. В физических задачах наиболее часто определяется коэффициент трения скольжения, так как сила трения качения значительно меньше.

Вам понадобится
- Сила трения, ускорение тела, угол наклона плоскости
Инструкция
Рассмотрим для начала случай, когда одно тело скользит по горизонтальной поверхности другого. Предположим, что оно скользит по неподвижной поверхности. В этом случае сила реакции опоры, действующая на скользящее тело, направлена перпендикулярно плоскости скольжения.
По механическому закону Кулона сила трения скольжения равна F = kN, где k – коэффициент трения, а N – сила реакции опоры. Так как сила реакции опоры направлена строго вертикально, то N = Fтяж = mg, где m – масса скользящего тела, g – ускорение свободного падения. Это условие следует из неподвижности тела относительно вертикального направления.
Таким образом, коэффициент трения можно найти по формуле k = Fтр/N = Fтр/mg. Для этого необходимо знать силу трения скольжения. Если тело движется равноускоренно, то силу трения можно найти, зная ускорение a. Пусть на тело действует движущая сила F и направленная противоположно ей сила трения Fтр. Тогда по второму закону Ньютона (F-Fтр)/m = a. Выражая отсюда Fтр и подставляя в формулу для коэффициента трения, получим: k = (F-ma)/N.
Из этих формул видно, что коэффициент трения является безразмерной величиной.
Рассмотрим более общий случай, когда тело соскальзывает с наклонной плоскости, например, с закрепленного блока. Такие задачи очень часто встречаются в школьном курсе физики в разделе «Механика».
Пусть угол наклона плоскости равен φ. Сила реакции опоры N будет направлена перпендикулярно наклонной плоскости. На тело также будут действовать сила тяжести и сила трения. Оси направим вдоль и перпендикулярно наклонной плоскости.
Согласно второму закону Ньютона можно записать уравнения движения тела: N = mg*cosφ, mg*sinφ-Fтр = mg*sinφ-kN = ma.
Подставив первое уравнение во второе и сократив массу m, получим: g*sinφ-kg*cosφ = a. Отсюда, k = (g*sinφ-a)/(g*cosφ).
Рассмотрим важный частный случая соскальзывания по наклонной плоскости, когда a = 0, то есть тело движется равномерно. Тогда уравнение движения имеет вид g*sinφ-kg*cosφ = 0. Отсюда, k = tgφ, то есть для определения коэффициента скольжения достаточно знать тангенс угла наклона плоскости.
Видео по теме
Обратите внимание
Следует не путать закон Кулона в механике с законом Кулона в электростатике!
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Эта статья отвечает на вопрос: как найти коэффициент трения? Все мы знаем, что самые гладкие поверхности также имеют некоторые неровности, но мы их не видим.
Если мы их не видим, то как мы будем измерять уровень шероховатости на поверхности? Ответ на этот вопрос кроется в свойстве поверхности, называемом коэффициентом трения. Это дает нам меру того, насколько шероховатая поверхность. В этой статье мы обсудим нахождение коэффициента трения в различных ситуациях.
Что такое трение?
Все мы знаем о трении и его влиянии на нашу жизнь. Противодействующая сила или сопротивление, которое мы чувствуем, толкая что-то вперед, называется трением.
Трение не обязательно плохо. Без трения наша жизнь не была бы такой легкой, если бы не было трения. В этой статье мы узнаем о трении, коэффициенте трения, его использовании и его негативном влиянии на нашу жизнь.
Что такое коэффициент трения?
Коэффициент трения — это свойство поверхности, которое говорит нам о том, насколько она шероховатая.
Мы не можем наблюдать шероховатости невооруженным глазом просто потому, что неровности очень мелкие по своей природе. Нам нужно свойство, которое определяет эти неровности. Это свойство называется коэффициентом трения.
Положительные эффекты трения
Трение часто считают плохим и нежелательным. Это верно во многих областях, но в то же время трение играет очень важную роль и в нашей жизни.
Положительные эффекты трения или преимущества трения приведены в списке ниже:
- тормоза – Тормоза полностью используют трение, чтобы остановить движение автомобиля. Тормоза позволяют шинам сцепляться с неровностями дорожного покрытия. Таким образом, автомобиль перестанет двигаться. Без трения было бы трудно ездить по дорогам, и аварии происходили бы чаще.

Кредиты изображений: анонимные, Дисковый тормоз, CC BY-SA 3.0
- Прогулки – Простая задача, такая как ходьба, также нуждается в помощи трения. Учитывая поверхность с меньшим трением, по которой можно ходить, человек просто соскользнет, если начнёт идти. Это потому, что он не имеет должного сцепления с полом. Подходящей поверхностью для ходьбы является та поверхность, которая не скользкая и имеет лучшее сцепление с дорогой.
- Бег – Бег – это преемник ходьбы. Бег также требует трения, так как трение меньше, а скользкий пол просто приведет к несчастным случаям. Несчастные случаи, которые также могут быть фатальными.
- Зубчатое зацепление – Шестерни имеют зубья, выступающие за пределы колес, которые входят в зацепление с зубьями других шестерен. Зубчатые колеса передают движение одного колеса другому, таким образом, зубчатые колеса выполняют свою функцию с помощью трения.
- Вождение – Вождение автомобиля или велосипеда требует трения, так как трение обеспечивает лучшее сцепление и силу прямой реакции на колеса. Все мы видели, как трудно управлять автомобилем на скользкой дороге, потому что вода смазывает дорогу, делая ее менее скользкой.
- Держа книгу – Держите книгу или, скажем, любой предмет, который нужно держать. Это сцепление обеспечивается трением. Сцепление — это не что иное, как неровности, сцепляющиеся друг с другом.
- Держа карандаш – Подобно тому, как вы держите книгу, держите карандаш – прекрасный пример использования силы трения.
- Катание мяча– Если мяч катится, это не значит, что он будет катиться вечность. Мяч приходит в состояние покоя через некоторое время. Это возможно из-за наличия трения в системе.
Негативные последствия трения
Мы все думаем, что трения нежелательны. Это верно, когда речь идет о местах, где мы требуем от системы максимальной работы. Места, где трение действует как люфт, приведены ниже:
- Выделение тепла при торможении – Выделение тепла в шинах приведет к износу резины, находящейся в шинах. Шины станут плоскими и потребуют обслуживания. Выделение тепла нежелательно в жаркую погоду, так как ущерб будет больше.
- Выделение тепла при работе машин – Выработка тепла в машинах означает, что некоторое количество топлива используется для выработки бесполезного тепла. Следовательно, особое внимание уделяется смазке деталей машин, так как тепло может повредить машины, а также увеличить стоимость эксплуатации.
- Замедление объектов из-за трения – Иногда мы склонны толкать объект на большее расстояние, но трение заставляет его остановиться, прежде чем он достигнет места назначения. Следовательно, нам нужно прикладывать больше усилий при толкании объекта, чтобы он набрал достаточную скорость, чтобы достичь места назначения без каких-либо остановок.
- Трубный поток– Жидкость в трубе замедляется из-за трения между поверхностью трубы и жидкостью. Это приводит к большим потерям в насосах, поскольку им необходимо проталкивать воду с большей силой, чтобы она покрывала потери из-за трения.
Как найти коэффициент трения с массой и силой
Масса объекта отвечает за вес, то есть масса в сочетании с гравитационным притяжением дает вес. Сила трения действует на предмет в силу его шероховатости.
Для расчета коэффициента трения с помощью этих величин используется следующее уравнение:
u= П/С
Где F – сила трения
N — нормальная сила реакции, равная весу тела.
Как рассчитать коэффициент трения с ускорением
Ускорение объекта возникает только при движении объекта. Когда объект движется, в игру вступает кинетическое трение.
Кинетическое трение является постоянной величиной и не может изменяться при любом изменении скорости объекта. Даже если тело движется с ускорением, величина кинетического трения, действующая на тело, будет такой же. Если бы величина кинетического трения также увеличивалась, то ускорение было бы невозможно. Объект не сможет ускориться. Математически кинетическое трение определяется как:
u= F/N= ma/mg= a/g
Здесь сила равна силе, необходимой для того, чтобы объект продолжал двигаться.
Как найти коэффициент трения между двумя материалами
Коэффициент трения можно рассчитать по той же формуле, что и F/N. Чтобы найти коэффициент трения между двумя материалами, мы выполняем следующие шаги:
- Пусть два предмета трутся друг о друга. Этими двумя объектами являются объект A и объект B.
- Когда эти два объекта трутся друг о друга, они приобретают определенную скорость, давайте рассмотрим объект B неподвижным, а объект A движущимся.
- Чтобы заставить объект А двигаться с этой скоростью, требуется сила F.
- Из-за веса объекта на объект B действует сила реакции, обозначаемая как R.
- Чтобы найти коэффициент трения между этими материалами, мы делим силу F на силу реакции R.
Таким образом рассчитывается коэффициент трения между двумя материалами.
Как рассчитать коэффициент трения со скоростью и расстоянием
Мы можем найти значение коэффициента трения, используя скорость и расстояние.
Совершенная работа определяется Fs
Сила, необходимая для совершения работы = F = сила трения = umg
Следовательно, сила, необходимая для остановки объекта = umg.s
Это равно кинетической энергии, то есть KE = O,5 mv^2.
Следовательно, и = (v^2/2g)
Как найти коэффициент трения между двумя поверхностями
Ни одна поверхность не бывает идеально гладкой. В нем будет некоторая шероховатость. Чтобы найти величину шероховатости, нам нужно определить свойство, называемое коэффициентом трения.
Коэффициент трения между двумя поверхностями можно найти, используя тот же метод, который мы обсуждали для нахождения коэффициента трения для двух материалов. Основная формула коэффициента трения остается той же, то есть u = F/N.
Как найти коэффициент трения с энергией
Мы уже обсуждали в предыдущем разделе, что кинетическую энергию можно приравнять к работе, необходимой для остановки движения объекта.
Из вышеприведенного равенства можно найти значение коэффициента трения. Давайте еще раз посмотрим, как мы нашли коэффициент трения с помощью энергии.
Кинетическая энергия- 1/2 мВ^2
Работа, необходимая для того, чтобы объект не двигался — umg.s
Приравнивая обе части, получаем u = v^2/2g
Как найти коэффициент трения с центростремительной силой
Центростремительная сила определяется выражением Fc = mv^2/r
Наблюдения и советы этой статьи мы подготовили на основании опыта команды сила трения действие на объект определяется как – umg
Приравняв обе стороны получим,
и = v ^ 2 / г
Как найти коэффициент трения только по углу
Когда объект движется со наклонная плоскость. Эффект угла вступает в игру. Для наклонной плоскости мы разделяем силы на горизонтальные силы и вертикальные силы.
Коэффициент трения определяется выражением u = F/N
После разрешения получаем u = mgsinA/mgcosA
А – угол, под которым наклонена плоскость.
После решения получаем, u = tanA
Таким образом, мы можем найти коэффициент трения, используя только угол.
Коэффициент трения скольжения — отношение силы трения к нормальной составляющей внешних сил, действующих на поверхности тела.
![]()
Коэффициент трения скольжения выводится из формулы силы трения скольжения
![]()
Так как сила реакции опоры, это масса умножить на ускорение свободного падения, то формула коэффициента получается:
![]()
Ниже приведена таблица коэффициентов трения скольжения для некоторых материалов:

В Формуле мы использовали :
![]() — Коэффициент трения скольжения
— Коэффициент трения скольжения
![]() — Сила трения скольжения
— Сила трения скольжения
![]() — Сила нормальной реакции опоры
— Сила нормальной реакции опоры
![]() — Масса тела
— Масса тела
![]() — Ускорение свободного падения
— Ускорение свободного падения

{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения – зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу

mu = dfrac{F_{тр}}{mg}
Fтр – сила трения
m – масса тела
g – ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона

mu = tg(alpha)
α – угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
