Четырехугольники
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.
 Определение
Определение
Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.
 На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь
На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь 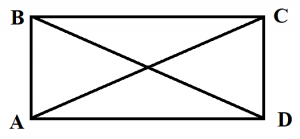
- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
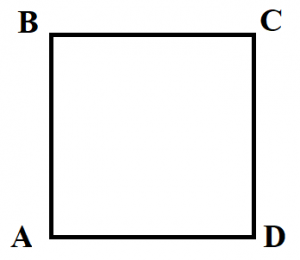 Свойства квадрата
Свойства квадрата
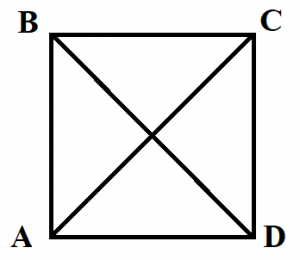
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Ромб – это параллелограмм, у которого все стороны равны.

Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.

Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.

углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
math4school.ru
Четырёхугольники
Основные определения и свойства
Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.
Сумма углов выпуклого четырёхугольника равна 360°:
Не существует четырёхугольников, у которых все углы острые или все углы тупые.
Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов:
Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон:
Площадь произвольного выпуклого четырёхугольника равна:
Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины.
Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет.
Площадь произвольного выпуклого четырёхугольника:
Если M , N , P , Q – середины сторон выпуклого четырёхугольника ABCD , а R , S – середины его диагоналей, то четырёхугольники MNPQ , MRPS , NSQR являются параллелограммами и называются параллелограммами Вариньона.
Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD . Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны;
Отрезки MP , NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника.
В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Для других четырёхугольников средние линии – отрезки.
Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам:
MG=GP , NG=GQ , RG=GS .
Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей:
MP 2 + NQ 2 + RS 2 = ¼ (AB 2 +BC 2 +CD 2 +AD 2 +AC 2 +BD 2 ).
Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь:
Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости.
Описанные четырёхугольники
Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной.
Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны:
Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно:
Площадь описанного четырёхугольника:
где r – радиус вписанной окружности, p – полупериметр четырёхугольника.
Площадь описанного четырёхугольника:
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника:
AK = AN , BK = BL , CL = CM , DM = DN .
Если O – центр окружности, вписанной в четырёхугольник ABCD, то
∠AOB+∠COD = ∠BOC+∠AOD =180°.
Для описанного четырёхугольника ABCD со сторонами AB = a , BC = b , CD = c и AD = d верны соотношения:
Вписанные четырёхугольники
Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника.
Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°:
Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Радиус окружности, описанной около четырёхугольника:
Площадь вписанного четырёхугольника:
Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами.
Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов.
У вписанного четырёхугольника любые два связанных угла равны.
Если четырёхугольник одновременно является описанным и вписанным, то его площадь:
Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение:
Параллелограмм
Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны:
У параллелограмма противолежащие стороны равны и противолежащие углы равны:
Сумма любых двух соседних углов параллелограмма равна 180°:
∠A +∠ B =∠ B +∠ C =∠ C +∠ D =∠ A +∠ D =180°.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам:
Каждая диагональ делит параллелограмм на два равных треугольника:
∠ ABC =∠ CDA ; ∠ ABD =∠ CDB .
Две диагонали параллелограмма делят его на четыре равновеликих треугольника:
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
e 2 +f 2 = a 2 +b 2 +a 2 +b 2 = 2(a 2 +b 2 ).
- Если у четырёхугольника противолежащие стороны попарно равны, то этот четырёхугольник – параллелограмм.
- Если у четырёхугольника две противолежащие стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
- Четырёхугольник, диагонали которого в точке пересечения делятся пополам – параллелограмм.
- Если у четырёхугольника противолежащие углы попарно равны, то этот четырёхугольник – параллелограмм.
Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне:
Площадь параллелограмма можно определить:
- через его сторону и высоту, проведённую к ней:
- через две его стороны и угол между ними:
Ромбом называется параллелограмм, у которого все стороны равны:
Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов:
∠ ABD =∠ CBD =∠ ADB =∠ CDB ; ∠ BAC =∠ DAC =∠ BCA =∠ DCA .
В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей.
Радиус окружности, вписанной в ромб, можно вычислить:
- через диагонали ромба и сторону:
- через отрезки, на которые делит сторону ромба точка касания:
Площадь ромба можно определить:
- через сторону и угол ромба:
- через сторону и радиус вписанной окружности:
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые:
Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка:
Площадь прямоугольника можно определить:
- через диагонали и угол между ними:
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали:
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны:
Диагонали квадрата равны и перпендикулярны.
Сторона и диагональ квадрата связаны соотношениями:
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей.
Радиус описанной окружности:
Радиус вписанной окружности:
Трапеция
Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны:
Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции:
Средняя линия трапеции параллельна её основаниям и равна их полусумме:
При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ:
Δ AED ∼ Δ BEC , k = AD / BC .
Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ:
Δ AОD ∼ Δ CОВ , k = AD / BC .
Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны:
Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон:
Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности:
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон:
Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств:
Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом:
Радиус вписанной в трапецию окружности можно определить:
- через отрезки, на которые делится боковая сторона точкой касания:
Равнобокой называется трапеция, у которой боковые стороны равны:
У равнобокой трапеции:
- углы при основании равны:
- сумма противолежащих углов равна 180?:
Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
Стороны и диагональ равнобокой трапеции связаны соотношением:
Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.
Площадь трапеции можно определить:
- через полусумму оснований (первую среднюю линию) и высоту:
- через диагонали и угол между ними:
Дельтоид
Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон.
Дельтоид может быть выпуклым или невыпуклым.
Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом.
В любом дельтоиде углы между соседними неравными сторонами равны.
Площадь любого дельтоида можно определить:
- через две соседние неравные стороны и угол между ними:
В любой выпуклый дельтоид можно вписать окружность.
Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида.
Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины.
Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°.
Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:
Ортодиагональные четырёхугольники
Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом.
Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий:
- для сторон четырёхугольника верно: a²+c² = b²+d ²;
- для площади четырёхугольника верно: S = ½ef ;
- параллелограмм Вариньона с вершинами в серединах сторон четырёхугольника является прямоугольником.
Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности:
Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны:
Если ABCD – ортодиагональный четырёхугольник, описанный около окружности с центром в точке О , то верны соотношения:
Многоугольник. Нахождение диагоналей вписанного четырехугольника. Теорема Птоломея.
Обозначим стороны вписанного четырехугольника ABCD через a, b, с, d и его диагонали через x и y .Проведем AK ^ BС и СL ^ AD.
Так как сумма противоположных углов вписанного четырехугольника равна 2d, то, если угол B острый, угол D должен быть тупым.
Поэтому из треугольников ABС и ADС можем написать:
x 2 = a 2 + b 2 – 2b . BK [1];
x 2 = с 2 + d 2 + 2d . DL [2].
Прямоугольные треугольники ABK и СDL подобны, т.к. они содержат по равному острому углу (углы B и СDL равны, потому что каждый из них служит дополнением до 2d к углу ADС).
Из их подобия выводим:
откуда BK . с = DL . a [3].
Таким образом, мы получим три уравнения с тремя неизвестными x, BK и DL.
Чтобы исключить BK и DL , уравняем в первых двух уравнениях последние члены, для чего умножим уравнение [1] на сd , а уравнение [2] на ab .
Сложив затем результаты и, приняв во внимание уравнение [3], найдем:
(ab + сd)x 2 = a 2 сd + b 2 сd + с 2 ab + d 2 ab =aс(ad + bс) + bd(bс+ad)=(aс + bd)(ad+bс),
.
Заметим, что в числителе подкоренной величины первый множитель – сумма произведений противоположных сторон, а второй – сумма произведений сторон, сходящихся в концах определяемой диагонали, знаменатель же представляет сумму произведений сторон, сходящихся в концах другой диагонали.
После этого мы можем, по аналогии, написать следующую формулу для диагонали y:
.
Следствие 1.
Произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон.
Действительно, перемножив выражения, выведенные для x и для y, получим:
.
Это предложение известно под именем теоремы Птоломея.
Следствие 2.
Отношение диагоналей вписанного четырехугольника равно отношению суммы произведений сторон, сходящихся в концах первой диагонали, к сумме произведений сторон, сходящихся в концах второй диагонали.
Действительно, разделив те же два равенства, найдем:
.
Эти два следствия удобны для запоминания. Из них можно обратно вывести формулы для x и y (перемножением или делением равенств, определяющих xy и x/y).
[spoiler title=”источники:”]
http://math4school.ru/chetyrehugolniki.html
http://www.calc.ru/Mnogougolnik-Nakhozhdeniye-Diagonaley-Vpisannogo-Chetyrekhug.html
[/spoiler]
 В этой статье мы рассмотрим все основные свойства и признаки четырехугольника.
В этой статье мы рассмотрим все основные свойства и признаки четырехугольника.
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Четырехугольники бывают выпуклые, если они расположены в одной полуплоскости относительно прямой, которая содержит одну из его сторон (ABCD) и невыпуклые (A1B1C1D1).
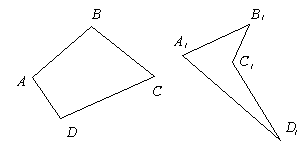
Если любые две противолежащие точки выпуклого четырёхугольника соединить между собой отрезком, то весь отрезок будет лежать внутри многоугольника. Для невыпуклого четырёхугольника это не выполняется (рисунок ниже).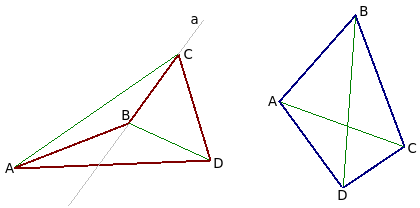
Диагонали выпуклого четырёхугольника лежат внутри него и пересекаются. Одна из диагоналей невыпуклого четырёхугольника лежит снаружи, а другая внутри него, и эти диагонали не пересекаются.
Определения для четырехугольника
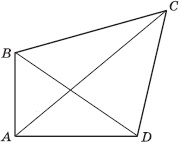 Данный четырёхугольник обозначается ABCD.
Данный четырёхугольник обозначается ABCD.- Точки A, B, C, D называются его вершинами, а отрезки AB, BC, CD, DA – его сторонами.
- Смежные стороны – соседние стороны, имеющие общую вершину. Пары смежных сторон: AB и AD, AB и BC, BC и CD, CD и AD.
- Противолежащие стороны – несмежные стороны, не имеющие общих вершин. Пары противолежащих сторон: AB и CD, BC и AD.
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. AC и BD – диагонали четырехугольника ABCD.
Виды четырехугольников:
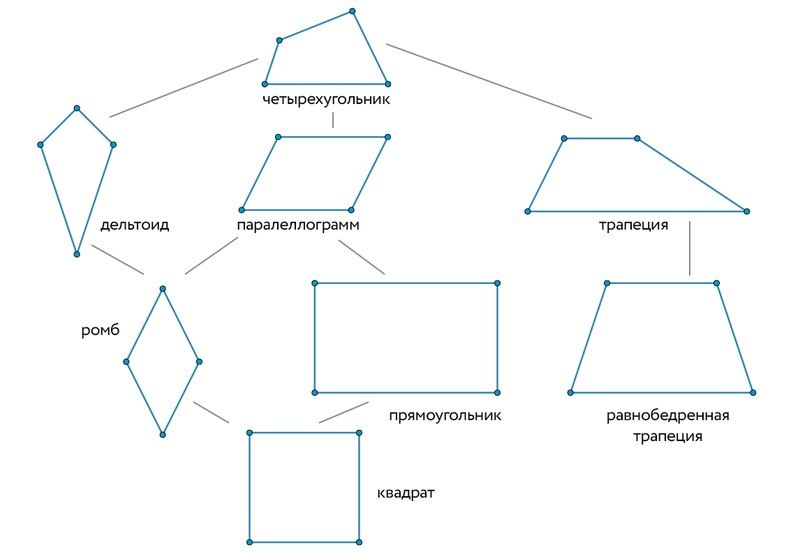
Если рассмотреть схему, то каждый следующий четырехугольник обладает всеми свойствами предыдущего. Поэтому запоминать надо совсем немного.
Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны. Трапеции бывают: произвольная, равносторонняя, прямоугольная.
Параллелограмм — это четырехугольник у которого противолежащие стороны параллельны. В параллелограмме:
— противоположные стороны и противоположные углы равны.
— диагонали параллелограмма делятся точкой пересечения пополам.
Соответственно, если четырехугольник обладает этими свойствами, то он является параллелограммом.
Прямоугольник — это параллелограмм, у которого все углы прямые. Прямоугольник является частным случаем параллелограмма, поэтому обладает всеми его свойствами.
Ромб — это параллелограмм, у которого все стороны равны. Ромб является частным случаем параллелограмма, поэтому обладает всеми его свойствами. В ромбе:
— противоположные углы равны,
— диагонали точкой пересечения делятся пополам,
— диагонали взаимно перпендикулярны,
— диагонали ромба являются биссектрисами углов.
Квадрат — это прямоугольник, у которого все стороны равны. Квадрат является частным случаем прямоугольника и частным случаем ромба, поэтому обладает всеми их свойствами. В квадрате:
— все углы равны 90 градусов,
— диагонали точкой пересечения делятся пополам,
— диагонали взаимно перпендикулярны,
— диагонали являются биссектрисами углов,
— диагонали равны.
Свойства углов четырехугольника
- Сумма углов четырёхугольника равна 360°
- Сумма внешних углов четырехугольника, взятых по одному при каждой вершине, равна 360°.
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
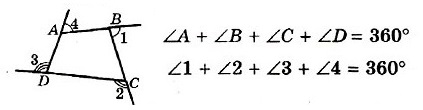
Свойства сторон четырехугольника
- Каждая сторона четырехугольника меньше суммы всех его других сторон.
- Сумма диагоналей меньше его периметра.
Четырехугольник и окружность
Четырехугольник вокруг окружности.
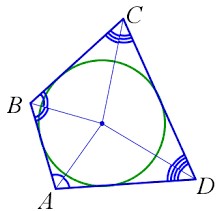
- Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
- В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны (AB+CD=AD+BC).
- Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырехугольник внутри окружности.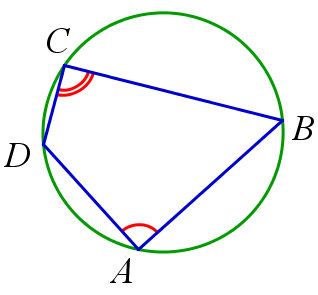
- Вписанный четырёхугольник — это четырёхугольник, все вершины которого лежат на одной окружности. Эта окружность называется описанной.
- Вокруг четырёхугольника можно описать окружность, если сумма двух его противоположных углов равна 180°.
- Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
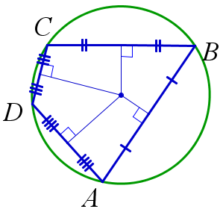
- Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон (AC*BD=AB*CD+AD*BC).
Частные случаи:
- Параллелограмм, вписанный в окружность – это прямоугольник, центр окружности совпадает с точкой пересечения диагоналей.
- Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
- Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной.
Диагонали четырехугольника
- Диагонали выпуклого четырёхугольника пересекаются в одной точке.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
Периметр и площадь четырехугольника
Периметр четырёхугольника равен сумме длин всех его сторон: ![]() где a, b, c, d – длины сторон четырёхугольника.
где a, b, c, d – длины сторон четырёхугольника.
Площадь произвольного выпуклого четырёхугольника можно найти по формуле: ![]() где d1 и d2— диагонали четырёхугольника, a — угол между диагоналями.
где d1 и d2— диагонали четырёхугольника, a — угол между диагоналями.
Площадь вписанного четырёхугольника может быть вычислена по формуле: 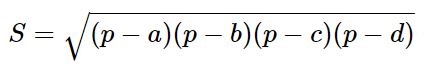 где a, b, c, d – длины сторон четырёхугольника, p=(a+b+c+d)/2 – его полупериметр.
где a, b, c, d – длины сторон четырёхугольника, p=(a+b+c+d)/2 – его полупериметр.
Площадь описанного четырёхугольника равна произведению его полупериметра на радиус вписанной окружности: ![]()

Как найти диагональ четырехугольника
Четырехугольником называется фигура, состоящая из четырех сторон и углов, прилежащих к ним. К числу таких фигур относятся прямоугольник, трапеция, параллелограмм. В ряде задач по геометрии требуется найти диагональ одной из этих фигур.
Инструкция
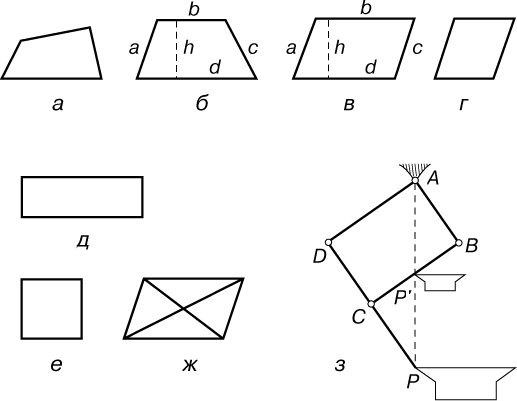
Диагональю четырехугольника называется отрезок, соединяющий его противоположные углы. У четырехугольника имеются две диагонали, которые между собой пересекаются в одной точке. Диагонали иногда бывают равными, как у прямоугольника и квадрата, а иногда имеют различную длину, как, например, у трапеции. Способ нахождения диагонали зависит от фигуры.Постройте прямоугольник со сторонами a и b и двумя диагоналями d1 и d2. Из свойств прямоугольника известно, что его диагонали между собой равны, пересекаются в одной точке и делятся в ней пополам. Если известны две стороны прямоугольника, то его диагонали найдите следующим образом: d1=√a^2+b^2=d2.Частным случаем прямоугольника является квадрат, у которого диагональ равна a√2. Кроме того, диагональ можно найти, зная площадь квадрата. Она равна: S = d^2/2.Отсюда длину диагонали вычислите по формуле: d = √2S.
Несколько иным образом решайте задачу, когда дан не прямоугольник, а параллелограмм. У этой фигуры, в отличие от прямоугольника или квадрата, равны между собой не все углы, а только противоположные. Если в условии задача присутствует параллелограмм со сторонами a и b и заданным между ними углом, как показано на рисунке к шагу, то диагональ найдите, используя теорему косинусов: d^2 = a^2+b^2-2ab*cosα.Параллелограмм, имеющий равные стороны, называется ромбом. Если по условиям задачи необходимо найти диагональ этой фигуры, то потребуются значения его второй диагонали и площади, поскольку диагонали этой фигуры неравны. Формула площади ромба выглядит следующим образом: S = d1*d2/2.Отсюда d2 равна удвоенной площади фигуры, деленной на d1: d2 = 2S/d1.
При вычислении площади трапеции придется воспользоваться тригонометрической функцией синуса. Если данная фигура является равнобочной, то, зная ее первую диагональ d1 и угол между двумя диагоналями AOD, как показано на рисунке к шагу, найдите вторую по следующей формуле: d2 = 2S/d1*sinφ. В данном случае рассматриваем трапецию ABCD.Существует также прямоугольная трапеция, диагональ которой найти несколько проще. Зная длину боковой стороны этой трапеции, совпадающей с ее высотой, а также нижнее основание, найдите ее диагональ, пользуясь обычной теоремой Пифагора. А именно сложите квадраты этих величин, а затем из результата извлеките квадратный корень.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти диагональ четырехугольника
Многоугольник. Нахождение диагоналей вписанного четырехугольника. Теорема Птоломея.
Обозначим стороны вписанного четырехугольника ABCD через a, b, с, d и его диагонали через x и y .Проведем AK ^ BС и СL ^ AD.
Так как сумма противоположных углов вписанного четырехугольника равна 2d, то, если угол B острый, угол D должен быть тупым.
Поэтому из треугольников ABС и ADС можем написать:
x 2 = a 2 + b 2 – 2b . BK [1];
x 2 = с 2 + d 2 + 2d . DL [2].
Прямоугольные треугольники ABK и СDL подобны, т.к. они содержат по равному острому углу (углы B и СDL равны, потому что каждый из них служит дополнением до 2d к углу ADС).
Из их подобия выводим:
откуда BK . с = DL . a [3].
Таким образом, мы получим три уравнения с тремя неизвестными x, BK и DL.
Чтобы исключить BK и DL , уравняем в первых двух уравнениях последние члены, для чего умножим уравнение [1] на сd , а уравнение [2] на ab .
Сложив затем результаты и, приняв во внимание уравнение [3], найдем:
(ab + сd)x 2 = a 2 сd + b 2 сd + с 2 ab + d 2 ab =aс(ad + bс) + bd(bс+ad)=(aс + bd)(ad+bс),
.
Заметим, что в числителе подкоренной величины первый множитель — сумма произведений противоположных сторон, а второй — сумма произведений сторон, сходящихся в концах определяемой диагонали, знаменатель же представляет сумму произведений сторон, сходящихся в концах другой диагонали.
После этого мы можем, по аналогии, написать следующую формулу для диагонали y:
.
Следствие 1.
Произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон.
Действительно, перемножив выражения, выведенные для x и для y, получим:
.
Это предложение известно под именем теоремы Птоломея.
Следствие 2.
Отношение диагоналей вписанного четырехугольника равно отношению суммы произведений сторон, сходящихся в концах первой диагонали, к сумме произведений сторон, сходящихся в концах второй диагонали.
Действительно, разделив те же два равенства, найдем:
.
Эти два следствия удобны для запоминания. Из них можно обратно вывести формулы для x и y (перемножением или делением равенств, определяющих xy и x/y).
Как вычислить диагональ четырёхугольника? Например : стороны четырёхугольника — 5, 7, 8 и 11 см. Чему равна диагональ ?

держи: Четырехугольником называется фигура, состоящая из четырех сторон и углов, прилежащих к ним. К числу таких фигур относятся прямоугольник, трапеция, параллелограмм. В ряде задач по геометрии требуется найти диагональ одной из этих фигур.
Как найти диагональ четырехугольника
Инструкция
1
Диагональю четырехугольника называется отрезок, соединяющий его противоположные углы. У четырехугольника имеются две диагонали, которые между собой пересекаются в одной точке. Диагонали иногда бывают равными, как у прямоугольника и квадрата, а иногда имеют различную длину, как, например, у трапеции. Способ нахождения диагонали зависит от фигуры. Постройте прямоугольник со сторонами a и b и двумя диагоналями d1 и d2. Из свойств прямоугольника известно, что его диагонали между собой равны, пересекаются в одной точке и делятся в ней пополам. Если известны две стороны прямоугольника, то его диагонали найдите следующим образом: d1=√a^2+b^2=d2.Частным случаем прямоугольника является квадрат, у которого диагональ равна a√2. Кроме того, диагональ можно найти, зная площадь квадрата. Она равна: S = d^2/2.Отсюда длину диагонали вычислите по формуле: d = √2S.
2
Несколько иным образом решайте задачу, когда дан не прямоугольник, а параллелограмм. У этой фигуры, в отличие от прямоугольника или квадрата, равны между собой не все углы, а только противоположные. Если в условии задача присутствует параллелограмм со сторонами a и b и заданным между ними углом, как показано на рисунке к шагу, то диагональ найдите, используя теорему косинусов: d^2 = a^2+b^2-2ab*cosα.Параллелограмм, имеющий равные стороны, называется ромбом. Если по условиям задачи необходимо найти диагональ этой фигуры, то потребуются значения его второй диагонали и площади, поскольку диагонали этой фигуры неравны. Формула площади ромба выглядит следующим образом: S = d1*d2/2.Отсюда d2 равна удвоенной площади фигуры, деленной на d1: d2 = 2S/d1.
3
При вычислении площади трапеции придется воспользоваться тригонометрической функцией синуса. Если данная фигура является равнобочной, то, зная ее первую диагональ d1 и угол между двумя диагоналями AOD, как показано на рисунке к шагу, найдите вторую по следующей формуле: d2 = 2S/d1*sinφ. В данном случае рассматриваем трапецию ABCD.Существует также прямоугольная трапеция, диагональ которой найти несколько проще. Зная длину боковой стороны этой трапеции, совпадающей с ее высотой, а также нижнее основание, найдите ее диагональ, пользуясь обычной теоремой Пифагора. А именно сложите квадраты этих величин, а затем из результата извлеките квадратный корень.
Одна из основных фигур курса математики – прямоугольник.
Впервые о нем заговорили еще в Древнем Египте, а позже и в
Древней Греции. Именно свойства его диагоналей помогают
решить многие задания учебного курса. Подход, который
сейчас используется в геометрии разработал Евклид. Формулы,
представленные в данной статье, пригодятся как при решении
домашних упражнений, так и на ЕГЭ. Именно такие задачки
помогают набрать недостающие баллы, поэтому ими не стоит пренебрегать.
- Диагональ прямоугольника через его стороны
- Диагональ прямоугольника через площадь и известную сторону
- Диагональ прямоугольника через периметр и сторону
- Диагональ прямоугольника через диаметр описанной окружности
- Диагональ прямоугольника через радиус описанной окружности
- Диагональ прямоугольника через площадь и острый угол между диагоналями
- Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
- Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
- Что такое диагональ прямоугольника, когда требуется ее вычисление
Диагональ прямоугольника через его стороны
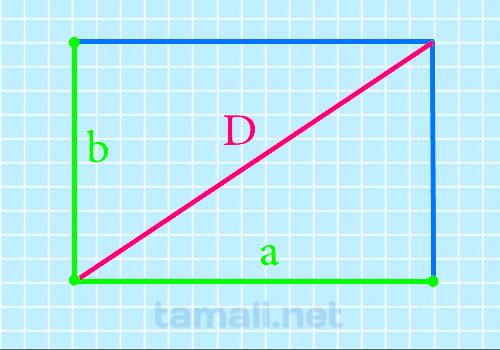
Если заданы хотя бы 2 стороны, то вычислить линию, соединяющую противоположные вершины, будет довольно просто. Применяется классическая теорема Пифагора. Достаточно подставить приведенные в дано числовые параметры в виде суммы квадратов под корнем:
![]()
Где a, b – это стороны, а d – прямая, которую мы ищем.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через площадь и известную сторону
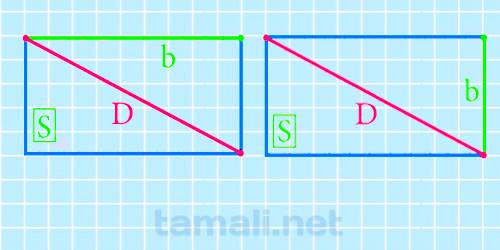
Когда в дано есть S и одна сторона, то узнать искомое значение можно используя следующее равенство:
![]()
Где D – это прямая, которую необходимо найти, a и b – любая заданная сторона, а S – площадь.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через периметр и сторону
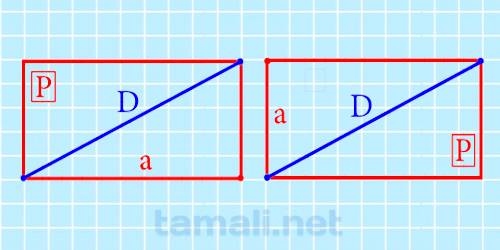
Когда задан периметр (сумма сторон) и, хотя бы одна сторона, отрезок, соединяющий несмежные точки высчитывают так:
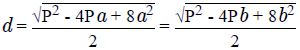
Где P – сумма сторон, a и b – любая заданная сторона.
Рассчитать искомый отрезок можно и через соотношение сторон и площадь.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через диаметр описанной окружности
Поиск отрезка через описанную окружность еще более прост, здесь даже не придется проводить расчеты: D = d
Где d – это обозначенный диаметр.
Различить вписанную/описанную окружность легко. Когда геометрическое тело вписано куда-то, то оно всегда будет находиться в другой фигуре. Когда окружность описана, то она находится снаружи, она как бы описывает другое геометрическое тело. Описанные фигуры задевают собой точки, а вписанные – касаются сторон.
Цифр после запятой:
Результат в:
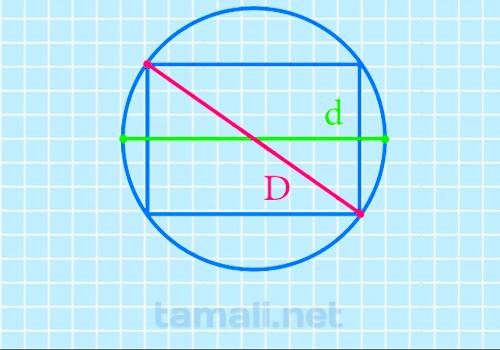
Диагональ прямоугольника через радиус описанной окружности
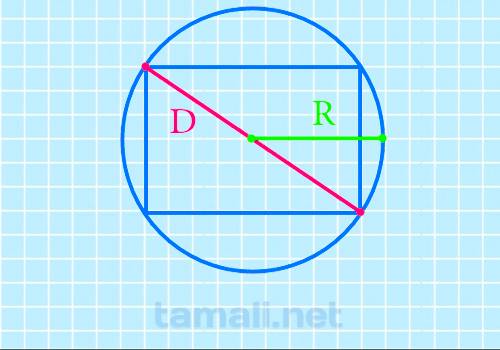
Для расчета искомого отрезка через описанную окружность нужно провести вычисления, где: D = 2R
Где R – это заданный радиус.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через площадь и острый угол между диагоналями
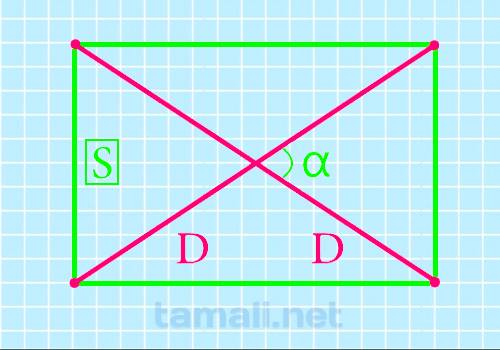
Если необходимо узнать прямую, соединяющую вершины 4-хугольника, это можно осуществить с помощью двух диагоналей. Для получения ответа к задаче понадобится sin β между ними и S (произведение длины и ширины).
Расчет проводится с равенством:
![]()
Где соответственно S – это площадь, а sin β – это острый угол, расположенный внутри фигуры (меж пересекающимися прямыми).
Если в 4-хугольнике расчертить 2 отрезка, объединяющие несмежные вершины, то они будут равны меж собой (все 4 отрезка), а точка пересечения разделит их пополам.
Пересечение всегда происходит в геометрическом центре самой фигурки. Этот же центр является центром описанной окружности.
Площадь (S):
Цифр после запятой:
Результат в:
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
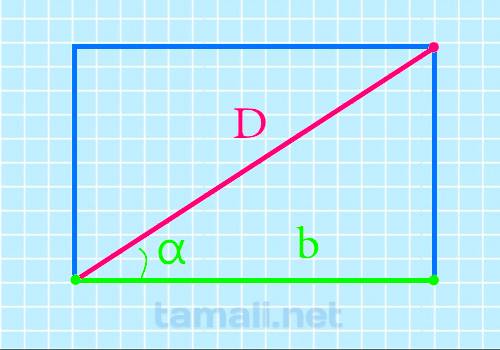
Когда одна из сторон 4-хугольника прилегает к углу, то просчитать отрезок, соединяющий вершины тоже возможно:
![]()
Где b – это сторона, прилегающая к углу, а cos a – это тот самый угол.
Косинус угла в треугольнике с прямым углом рассчитывается по формуле – длина соседней стороны, разделенная на гипотенузу. Синус – это противолежащий катет, разделенный на гипотенузу. Либо можно поступить еще проще, подсмотрев в таблицу Брадиса.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
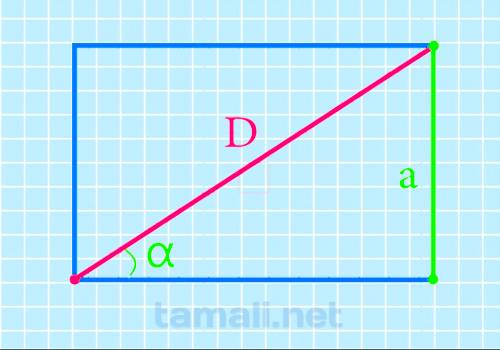
Чтобы найти нужный отрезок внутри четырехугольника, должен быть задан угол, прилегающий к искомому отрезку и сторона, противоположная углу:
![]()
Где a – это сторона четырехугольника, а sin a – это прилегающий угол.
Длинная сторона 4-хугольника– это длина, а короткая – его ширина. Помните, что каждая сторона одновременно является высотой.
Цифр после запятой:
Результат в:
Что такое диагональ прямоугольника, когда требуется ее вычисление
Прямоугольник – это частный случай параллелограмма. Иначе 4-хугольник с попарно равными сторонами, параллельными друг другу, а также равными прямыми углами по 90⁰. Сумма углов четырехугольника составляет 360⁰.
Диагональ разделяет фигуру на два новых элемента – треугольники с прямым углом. Это прямая, объединяющая противоположные вершины. Имея 2 прямоугольных треугольника, отрезок уже можно рассчитать по теореме Пифагора. По теореме гипотенуза – это квадрат из суммы катетов (обозначенных сторон треугольника), возведенных в квадрат.
Линии, соединяющие противоположные точки в четырехугольнике всегда пересекаются друг с другом.
Отрезок обозначают как d или D. Если названы все точки, то его можно называть в соответствии с ними – AC или BD.
Знания о линии, проходящей через несмежные точки 4-хугольника может понадобиться в легких геометрических упражнениях, так и в более сложных многоуровневых задачках, которые появляются на ЕГЭ. Свойства данного отрезка помогают находить важные параметры прямоугольника. Зная данные обеих линий, соединяющих противоположные углы, можно рассчитать S геометрического тела.
Перед решением любой геометрической задачки рекомендуется сделать чертеж и обозначить всю заданную информацию. Так будет значительно проще сосредоточиться на искомом значении.
Если регулярно решать тесты по геометрии, то формулы легче запомнятся, а их применение будет доведено до автоматизма.
