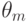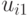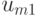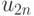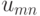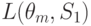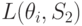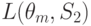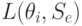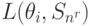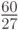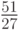Основные критерии применяемые в процессе принятия решений в условиях неопределённости и риска, а также в игре с природой
Критерий среднего выигрыша
Формула критерия среднего выигрыша
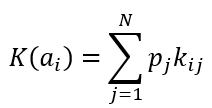
Формула оптимального решения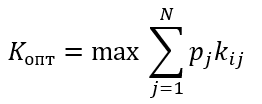
Пример

Пусть даны вероятности, p1=0.2 p2=0.1 p3=0.3 p4=0.2, тогда получаем
K(a1)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.4=0.3
K(a2)=0.2*0.3+0.1*0.2+0.3*0.3+0.2*0.5=0.27
K(a3)=0.2*0.6+0.1*0.3+0.3*0.3+0.2*0.2=0.28
K(a4)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.3=0.25
Kопт=max{0.27; 0.48; 0.43; 0.51}=0.51
В итоги оптимальным вариантом выбора программы по критерию среднего выигрыша является вариант первой программы.
Критерий Вальда или пессимизма
Формула критерия Вальда или максимина
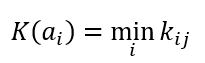
Формула оптимального решения по критерию Лапласа
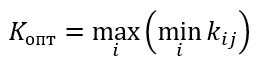
Пример

K(a1)=min(0.4;0.5;0.3;0.4)=0.3
K(a2)=min(0.3;0.2;0.3;0.5)=0.2
K(a3)=min(0.6;0.3;0.3;0.2)=0.2
K(a4)=min(0.4;0.5;0.2;0.3)=0.2
Kопт=max{0.3; 0.2; 0.2; 0.2}=0.3
По критерию Вальда оптимальным решением является выбор первой программы.
Критерий максимакса или оптимизма
Формула критерия максимакса
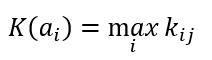
Формула оптимального решения по критерию максимакса
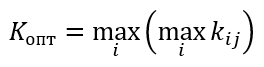
Пример

K(a1)=max(0.4;0.5;0.3;0.4)=0.5
K(a2)= max (0.3;0.2;0.3;0.5)=0.5
K(a3)= max (0.6;0.3;0.3;0.2)=0.6
K(a4)= max (0.4;0.5;0.2;0.3)=0.5
Kопт=max{0.5; 0.5; 0.6; 0.5}=0.6
По критерию максимакса оптимальным решением является выбор третьей программы.
Критерий Лапласа
Формула критерия Лапласа
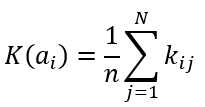
Формула оптимального решения по критерию Лапласа

Пример

Решение
K(a1)=0.25*(0.4+0.5+0.3+0.4)=0.4
K(a2)=0.25*(0.3+0.2+0.3+0.5)=0.325
K(a3)=0.25*(0.6+0.3+0.3+0.2)=0.35
K(a4)=0.25*(0.4+0.5+0.2+0.3)=0.35
Kопт=max{0.4; 0.325; 0.35; 0.35}=0.4
По критерию Лапласа оптимальным решением является выбор первой программы.
Критерий Гурвица
Пример

Формула критерия Гурвица
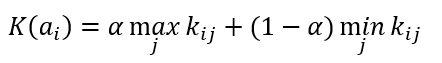
Формула оптимального решения по Гурвица критерию

Коэффициент α принимает значения от 0 до 1. Если α стремится к 1, то критерий Гурвица приближается к критерию Вальда, а при α стремящемуся к 0, то критерий Гурвица приближается к критерию максимакса.
Пусть α=0.7
K(a1)= 0.7* 0.5+(1-0.7)*0.3=0.44
K(a2)= 0.7* 0.5+(1-0.7)*0.2=0.41
K(a3)= 0.7* 0.6+(1-0.7)*0.2=0.48
K(a4)= 0.7* 0.5+(1-0.7)*0.2=0.41
Kопт=max{0.44; 0.41; 0.48; 0.41}=0.48
По критерию Гурвица оптимальным решением является выбор третьей программы.
Критерий Сэвиджа или минимакса (критерий потерь)
Формула критерия Сэвиджа для построения матрицы потерь

Формула для выбора максимального значения из матрицы потерь

Формула оптимального решения по критерию Сэвиджа
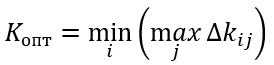
Для примера

Строим матрицу потерь по столбцам выбираем максимальное значение и поочередно вычитаем значения каждой ячейки соответствующего столбца согласно формуле, в итоге получим матрицу вида

K(a1)= max{0.2; 0; 0; 0.1}=0.2
K(a2)= max{0.3; 0.3; 0; 0}=0.3
K(a3)= max{0; 0.2; 0; 0.3}=0.3
K(a4)= max{0.2; 0; 0.1; 0.2}=0.2
Kопт=min{0.2; 0.3; 0.3; 0.2}=0.2
По критерию Сэвиджа оптимальным решением является выбор первой или четвёртой программы.
Таким образом, в соответствии со всеми приведёнными критериями большинство решений указывает на выбор первой программы.
Матрица потерь
|
|
|
|||
|
|
|
|
|
|
|
|
0,1 |
0 |
0,3 |
0,2 |
|
|
0 |
0 |
0,2 |
0 |
|
|
0,1 |
0,1 |
0 |
0,1 |
Тогда
К(а1)
=max(0,1; 0; 0,3; 0,2) =0,3;
К(а2)
= mах(0; 0,2; 0,2; 0) = 0,2;
К(а3)
= mах(0,1; 0,1; 0; 0,1) = 0,1.
Оптимальное
решение— система а1 .
Критерий минимального риска отражает
сожаление по поводу того, что выбранная
система не оказалась наилучшей при
определенном состоянии обстановки.
Так, если произвести выбор системы а1,
а состояние обстановки в действительности
n3, то сожаление, что
не выбрана наилучшая из систем (а3),
составит 0,3. О критерии Сэвиджа можно
сказать, что он, как и критерий Вальда,
относится к числу осторожных критериев.
По сравнению с Критерием Вальда в нем
придается несколько большее значение
выигрышу, чем проигрышу. Основной
недостаток критерия — не выполняется
требование 4.
Таким образом,
эффективность систем в неопределенных
операциях может оцениваться по целому
ряду критериев. На выбор того или иного
критерия оказывает влияние ряд факторов:
-
природа конкретной
операции и ее цель (в одних операциях
допустим риск, в других — нужен
гарантированный результат); -
причины
неопределенности (одно дело, когда
неопределенность является случайным
результатом действия объективных
законов природы, и другое, когда она
вызывается действиями разумного
противника, стремящегося помешать в
достижении цели); -
характер лица,
принимающего решение (одни люди склонны
к риску в надежде добиться большего
успеха, другие предпочитают действовать
всегда осторожно).
Выбор какого-то
одного критерия приводит к принятию
решения по оценке систем, которое может
быть совершенно отличным от решений,
диктуемых другими критериями. Это
наглядно подтверждают результаты оценки
эффективности систем применительно к
примеру 2.2 по рассмотренным критериям
(табл. 2.13).
Таблица
2.13
Сравнительные результаты оценки систем
|
|
|
|
||||||||
|
|
|
|
|
Среднего выигрыша |
Лапласа |
Вальда |
Макимакса |
Гурвица |
Сэвиджа |
|
|
|
0,1 |
0,5 |
0,1 |
0,2 |
0,21 |
0,224 |
0,1 |
0,5 |
0,34 |
0,3 |
|
|
0,2 |
0,3 |
0,2 |
0,4 |
0,28 |
0,275 |
0,2 |
0,4 |
0,32 |
0,2 |
|
|
0,1 |
0,4 |
0,4 |
0,3 |
0,25 |
0,300 |
0,1 |
0,4 |
0,28 |
0,1 |
Тип критерия для
выбора рационального варианта должен
быть оговорен на этапе анализа систем,
согласован с заказывающей организацией
и в последующих задачах синтеза
информационных и других сложных систем
предполагается заданным. Процесс выбора
вида критерия для учета неопределенности
достаточно сложен. Устойчивость
выбранного рационального варианта
можно оценить на основе анализа по
нескольким критериям. Если существует
совпадение, то имеется большая уверенность
в правильности выбора варианта.
В случаях, когда
системы, выбранные по различным критериям,
конкурируют между собой за право быть
окончательно выбранными, могут применяться
процедуры, основанные на мажоритарной
обработке результатов оценки по простому
большинству голосов. Особенностью
мажоритарной обработки является
опасность выбора системы, не являющейся
лучшей, на основе многоэтапного выбора
при группировке альтернатив в коалиции.
Такая ситуация отражена на рис. 2.12, где
8 из 27 систем по разным критериям были
оценены как худшие. Однако при группировке
в коалиции и организации двухэтапной
процедуры мажоритарной обработки в
качестве лучшей была выбрана одна из
худших систем.

В любом случае при
выделении множества предпочтительных
систем по разным критериям окончательный
выбор системы должен осуществляться
лицом, принимающим решение. При этом в
операциях, которым в зависимости от
характера соответствует либо пороговая,
либо монотонная функция полезности,
эффективность систем правомочно
оценивать непосредственно по показателям
исходов. Для детерминированных операций
критерием эффективности будет служить
сам показатель, для вероятностных —
либо, вероятность получения допустимого
значения показателя (при пороговой
функции полезности), либо математическое
ожидание значения показателя (при
линейной функции полезности).
Оценка эффективности
систем на основе показателей исходов
в других случаях может приводить к
неправильному выбору, поэтому переход
к оценке эффективности систем без
введения функции полезности должен
всегда сопровождаться обоснованием.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обоснование статистических решений при фиксированных экспериментах
Часто встречаются ситуации, когда на выбор решения существенное влияние оказывают факторы, информация о которых отсутствует или является недостаточно полной. Обоснование решений в этих условиях оказывается весьма эффективным с помощью статистических решений.
Сущность задач статистических решений состоит в том, что нужно сделать выбор из множества действий  , эффективность каждого из которых зависит от того, какое из состояний “природы”
, эффективность каждого из которых зависит от того, какое из состояний “природы”  имеет место. Поэтому каждая пара
имеет место. Поэтому каждая пара 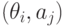 , состоящая из действия и состояния “природы”, имея тот или иной исход, характеризуется значением критерия эффективности
, состоящая из действия и состояния “природы”, имея тот или иной исход, характеризуется значением критерия эффективности  . Последнее приводит к
. Последнее приводит к 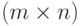 матрице (таблица 11.1), на основании которой нужно выбрать действие, являющееся оптимальным согласно некоторому критерию. Подобная матрица представляет стохастическую модель конфликтной ситуации, в которой одним из противников является “природа” (обстановка боевых действий, — Абчук В.А., Емельянов Л.А., Матвейчук Ф.А., Суздаль В.Г. Введение в теорию выработки решений. М., Военное издательство, 1972.). Обычно в теории статистических решений оперируют с критерием эффективности, характеризующим те или иные потери. Поэтому получаемую матрицу называют матрицей потерь.
матрице (таблица 11.1), на основании которой нужно выбрать действие, являющееся оптимальным согласно некоторому критерию. Подобная матрица представляет стохастическую модель конфликтной ситуации, в которой одним из противников является “природа” (обстановка боевых действий, — Абчук В.А., Емельянов Л.А., Матвейчук Ф.А., Суздаль В.Г. Введение в теорию выработки решений. М., Военное издательство, 1972.). Обычно в теории статистических решений оперируют с критерием эффективности, характеризующим те или иные потери. Поэтому получаемую матрицу называют матрицей потерь.
| Состояние “природы” | Действие | |||||
|---|---|---|---|---|---|---|
 |
 |
… | 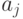 |
… | 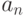 |
|

. . .
. . .
|

. . .
. . .
|
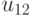
. . .
. . .
|
…
… … … |

. . .
. . .
|
…
… … … |

. . .
. . .
|
Поясним сказанное на следующем примере.
Предположим, что ракетная подводная лодка для нанесения удара по береговой цели должна занять огневую позицию в одном из трех районов. Каждый район огневых позиций  в зависимости от состояния моря
в зависимости от состояния моря  характеризуется математическим ожиданием числа непопадающих ракет
характеризуется математическим ожиданием числа непопадающих ракет  , величины которых определяются таблицей 11.2.
, величины которых определяются таблицей 11.2.
| Состояние “природы” | Действие | ||
|---|---|---|---|
| Район №1 | Район №2 | Район №3 | |
| Море 2 балла
Море 5 |
0
5 |
1
3 |
3
2 |
Очевидно, если вероятности состояний “природы”  известны и равны соответственно
известны и равны соответственно  , где
, где  , то за критерий можно принять среднюю (ожидаемую) эффективность действия
, то за критерий можно принять среднюю (ожидаемую) эффективность действия 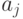 . Тогда выбирается действие, которое минимизирует данный критерий, и принимается , что это действие является оптимальным при данном априорном распределении вероятностей.
. Тогда выбирается действие, которое минимизирует данный критерий, и принимается , что это действие является оптимальным при данном априорном распределении вероятностей.
Так, если в рассматриваемом примере все состояния равновероятны, то следует выбрать действие  (район №2), поскольку в этом случае средняя эффективность будет равна
(район №2), поскольку в этом случае средняя эффективность будет равна  , тогда как при выборе
, тогда как при выборе  (района №1) или
(района №1) или  (района №3) она составит
(района №3) она составит  соответственно.
соответственно.
Таким образом, допущение априорного распределения вероятностей дает довольно простой метод выбора оптимального решения. Однако на практике истинное распределение вероятностей состояний “природы”, как правило, неизвестно. В связи с этим целесообразно поставить эксперимент для оценки состояния “природы”.
Предположим, что в рассматриваемом примере таким экспериментом является измерение атмосферного давления.
Пусть 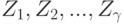 — множество возможных исходов, и известна вероятность
— множество возможных исходов, и известна вероятность  каждого исхода для каждого истинного состояния природы. Допустим
каждого исхода для каждого истинного состояния природы. Допустим 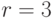 и примем значения вероятности
и примем значения вероятности  , равным приведенным в таблице 11.3.
, равным приведенным в таблице 11.3.
| Состояние “природы” | Наблюдение | ||
|---|---|---|---|
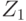 |
 |
 |
|

|
0,60
0,20 |
0,25
0,30 |
0,15
0,50 |
Теперь в зависимости от результатов эксперимента можно перечислить все возможные стратегии выбора района огневых позиций. Так, например, одной из стратегий может быть следующий план: выбрать район №1 (действие  ), если результат эксперимента
), если результат эксперимента 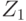 ; район №2 (действие
; район №2 (действие  ), если результат эксперимента
), если результат эксперимента  ; район №3, если результат эксперимента
; район №3, если результат эксперимента  .
.
Каждая такая стратегия представляет систему:
 |
( 11.1) |
,
где 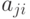 — действие, предпринимаемое при наблюдении
— действие, предпринимаемое при наблюдении 
 — номер действия
— номер действия  ;
;
 — номер стратегии
— номер стратегии 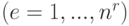 ;
;
 — номер эксперимента
— номер эксперимента  .
.
Иными словами, стратегия – это функция, определенная на пространстве выбора эксперимента  , значения которой суть действия
, значения которой суть действия 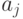 . Поскольку каждому исходу эксперимента соответствует
. Поскольку каждому исходу эксперимента соответствует  возможных действий, при
возможных действий, при  возможных исходных имеется
возможных исходных имеется  возможных стратегий. Для рассматриваемого примера
возможных стратегий. Для рассматриваемого примера 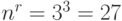 (таблица 11.4).
(таблица 11.4).
| Наблюдение | Стратегия | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
 |
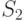 |
 |
 |
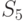 |
 |
 |
 |
 |
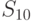 |
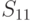 |
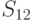 |
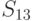 |
 |

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|
|
|
 |
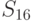 |
 |
 |
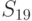 |
 |
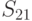 |
 |
 |
 |
 |
 |
 |
|

|

|

|

|

|

|

|

|

|

|

|

|

|
Из анализа таблицы видно, что некоторые из стратегий совершенно не учитывают исход эксперимента, например,  ; другие — учитывают в определенной степени и так далее. Однако каждая стратегия в зависимости от истинного состояния “природы” приводит к тем или иным результатам. Для вычисления этого результата с учетом эксперимента определим его вероятность
; другие — учитывают в определенной степени и так далее. Однако каждая стратегия в зависимости от истинного состояния “природы” приводит к тем или иным результатам. Для вычисления этого результата с учетом эксперимента определим его вероятность  как вероятность того, что, когда истинное состояние “природы” есть
как вероятность того, что, когда истинное состояние “природы” есть 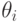 , эксперимент
, эксперимент  приводит к исходу, с которым стратегия
приводит к исходу, с которым стратегия 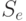 связывает действие
связывает действие 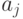 . Очевидно, что
. Очевидно, что  . Так, например, из описания стратегии
. Так, например, из описания стратегии 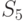 (таблица 11.4) видно, что если результатом эксперимента будет
(таблица 11.4) видно, что если результатом эксперимента будет 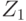 , то выбирается действи
, то выбирается действи  , если
, если  или
или  , — действие
, — действие  . Для состояния природы
. Для состояния природы  исход эксперимента
исход эксперимента 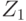 возможен с вероятностью 0.60 (таблица 11.3), а
возможен с вероятностью 0.60 (таблица 11.3), а  или
или  — с вероятностью 0,40. Следовательно,
— с вероятностью 0,40. Следовательно,
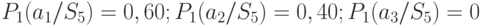 .
.
Аналогично для состояния “природы” 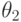 получим:
получим:
 .
.
Теперь можно определить средние потери для каждой стратегии 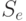 , когда истинное состояние “природы” есть
, когда истинное состояние “природы” есть 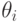 .
.
Так как следствием пары  являются результаты
являются результаты  , а вероятность пар “действие – состояние”
, а вероятность пар “действие – состояние”  равны
равны  , то средние потери для стратегии
, то средние потери для стратегии 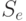 будут:
будут:
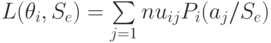 |
( 11.2) |
,
где  — потери при выборе действия
— потери при выборе действия 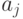 и истинном состоянии “природы”
и истинном состоянии “природы” 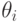 .
.
На основании (11.2.) можно вычислить матрицу средних потерь.
| Состояние “природы” | Стратегия | |||||
|---|---|---|---|---|---|---|
 |
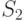 |
… | 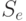 |
… |  |
|

. . .
. . .
|

. . .
. . .
|
L(theta_1,S_2)
. . .
. . .
|
…
… … … |

. . .
. . .
|
…
… … … |
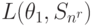
. . .
. . .
|
Для условий рассматриваемого примера вычисление средних потерь по формуле (11.2.) приводит к таблице 11.6.
| Состояние “природы” | Стратегия | ||||||||
|---|---|---|---|---|---|---|---|---|---|
 |
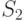 |
 |
 |
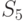 |
 |
 |
 |
 |
|

|
0,00
5,00 |
0,15
4,00 |
0,45
3,50 |
0,25
4,40 |
0,40
3,40 |
0,70
2,90 |
0,75
4,10 |
0,90
3,10 |
1,20
2,60 |
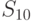 |
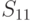 |
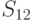 |
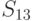 |
 |
 |
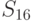 |
 |
 |
|

|
0,60
4,60 |
0,75
3,60 |
1,05
3,10 |
0,85
4,00 |
1,00
3,00 |
1,30
2,50 |
1,35
3,70 |
1,50
2,70 |
1,80
2,20 |
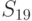 |
 |
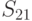 |
 |
 |
 |
 |
 |
 |
|

|
1,80
4,40 |
1,95
3,40 |
2,25
2,90 |
2,05
3,80 |
2,20
2,80 |
2,50
2,30 |
2,55
3,50 |
2,70
2,50 |
3,00
2,00 |
Матрица средних потерь (табл. 11.5) представляет собой модель конфликтной ситуации при фиксированных экспериментах. В связи с этим первоначальная задача статического решения модифицируется, сводясь к выбору одной из стратегий  для состояний “природы”
для состояний “природы”  .
.
Предположим теперь, что даны априорные вероятности состояний “природы” 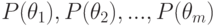 . После постановки эксперимента, исход которого зависит от истинного состояния “природы”, значения вероятностей состояний изменяются и по формуле Байеса будут равны
. После постановки эксперимента, исход которого зависит от истинного состояния “природы”, значения вероятностей состояний изменяются и по формуле Байеса будут равны
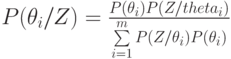 |
( 11.3) |
,
где  — апостериорная вероятность состояния
— апостериорная вероятность состояния 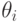 ;
;
 — вероятность исхода
— вероятность исхода  для истинного состояния
для истинного состояния 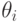 .
.
Если теперь принять, что  и
и 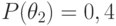 , то апостериорные вероятности состояний примут значения, приведенные в таблице 11.7.
, то апостериорные вероятности состояний примут значения, приведенные в таблице 11.7.
В результате приходим к первоначальной задаче оптимального выбора действия, когда вероятности состояний “природы” известны и равны  .
.
На основании этого можно определить средние потери для действия 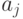 с учетом эксперимента
с учетом эксперимента  по формуле
по формуле
 |
( 11.4) |
,
где  — потери пары “действие – состояние”
— потери пары “действие – состояние”  .
.
Оптимальным в этом случае будет действие, дающее наименьшие потери. Для нашего примера расчеты, выполненные по формуле 11.4., сведены в таблицу 11.8.
| Эксперимент | Действие | ||
|---|---|---|---|
 |
 |
 |
|
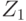
|

|

|

|
Из таблицы 11.8 видно, что в случае исхода 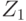 оптимальным является действие a_1, исхода
оптимальным является действие a_1, исхода  — действие
— действие  и исхода
и исхода  — действие
— действие  .
.
Таким образом, получено правило, в соответствии с которым каждому исходу эксперимента  соответствует действие
соответствует действие  , дающее минимальные потери. Это правило называется правилом Байеса относительно априорного распределения вероятностей состояний природы, а действие — байесовым. Так, для рассматриваемого примера, если исход эксперимента
, дающее минимальные потери. Это правило называется правилом Байеса относительно априорного распределения вероятностей состояний природы, а действие — байесовым. Так, для рассматриваемого примера, если исход эксперимента 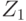 , байесовым действием является действие
, байесовым действием является действие  , если исход
, если исход  — действие
— действие  и если исход
и если исход  — действие
— действие  .
.
Байесовое действие входит в байесовую стратегию, которая минимизирует среднее взвешенное
 |
( 11.5) |
и соответствует вероятности  .
.
В этом можно убедиться, если по формуле (11.4.) произвести вычисление, используя данные таблицы 11.5 – 11.7, и выбрать стратегию, для которой 
будет минимальным. Такой байесовой стратегией окажется  . Из описания стратегии
. Из описания стратегии  видно, что если исход эксперимента
видно, что если исход эксперимента 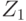 , то выбирается действие
, то выбирается действие  , если
, если  , то действие
, то действие  , и если
, и если  , то действие
, то действие  , то есть байесовые действия.
, то есть байесовые действия.
Таким образом, задаваясь априорным распределением вероятностей состояния природы, возможно их уточнить путем постановки эксперимента и определения апостериорных вероятностей.
Теорема Байеса. Пусть  — взаимоисключающие события. Объединение всех
— взаимоисключающие события. Объединение всех  образует достоверное событие, полную группу событий. Тогда теорема Байеса гласит: вероятность того, что событие
образует достоверное событие, полную группу событий. Тогда теорема Байеса гласит: вероятность того, что событие  наступит при условии, что событие E уже наступило, определяется выражением
наступит при условии, что событие E уже наступило, определяется выражением
 |
( 11.15) |
.
LossMatrix: Loss Matrix
Description
A loss matrix is useful in Bayesian decision theory for selecting the
Bayes action, the optimal Bayesian decision, when there are a discrete
set of possible choices (actions) and a discrete set of possible
outcomes (states of the world). The Bayes action is the action that
minimizes expected loss, which is equivalent to maximizing expected
utility.
Usage
LossMatrix(L, p.theta)
Arguments
L
This required argument accepts a (S times A)
matrix or (S times A times N) array of losses,
where (S) is the number of states of the world, (A) is the
number of actions, and (N) is the number of samples. These
losses have already been estimated, given a personal loss
function. One or more personal losses has already been estimated
for each combination of possible actions
(a=1,dots,A) and possible states
(s=1,dots,S).
p.theta
This required argument accepts a
(S times A) matrix or
(S times A times N) array of state prior
probabilities, where (S) is the number of states of the world,
(A) is the number of actions, and (N) is the number of
samples. The sum of each column must equal one.
Value
The LossMatrix function returns a list with two components:
This is a numeric scalar that indicates the action
that minimizes expected loss.
This is a vector of expected losses, one for each
action.
Details
Bayesian inference is often tied to decision theory (Bernardo and
Smith, 2000), and decision theory has long been considered the
foundations of statistics (Savage, 1954).
Before using the LossMatrix function, the user should have
already considered all possible actions (choices), states of the world
(outcomes unknown at the time of decision-making), chosen a loss
function (L(theta, alpha)), estimated loss, and
elicited prior probabilities (p(theta | x)).
Although possible actions (choices) for the decision-maker and
possible states (outcomes) may be continuous or discrete, the loss
matrix is used for discrete actions and states. An example of a
continuous action may be that a decision-maker has already decided to
invest, and the remaining, current decision is how much to invest.
Likewise, an example of continuous states of the world (outcomes) may
be how much profit or loss may occur after a given continuous unit of
time.
The coded example provided below is taken from Berger (1985, p. 6-7)
and described here. The set of possible actions for a decision-maker
is to invest in bond ZZZ or alternatively in bond XXX, as it is called
here. A real-world decision should include a mutually exhaustive list
of actions, such as investing in neither, but perhaps the
decision-maker has already decided to invest and narrowed the options
down to these two bonds.
The possible states of the world (outcomes unknown at the time of
decision-making) are considered to be two states: either the chosen
bond will not default or it will default. Here, the loss function is
a negative linear identity of money, and hence a loss in element
L[1,1] of -500 is a profit of 500, while a loss in
L[2,1] of 1,000 is a loss of 1,000.
The decision-maker’s dilemma is that bond ZZZ may return a higher
profit than bond XXX, however there is an estimated 10% chance, the
prior probability, that bond ZZZ will default and return a substantial
loss. In contrast, bond XXX is considered to be a sure-thing and
return a steady but smaller profit. The Bayes action is to choose the
first action and invest in bond ZZZ, because it minimizes expected
loss, even though there is a chance of default.
A more realistic application of a loss matrix may be to replace the
point-estimates of loss with samples given uncertainty around the
estimated loss, and replace the point-estimates of the prior
probability of each state with samples given the uncertainty of the
probability of each state. The loss function used in the example is
intuitive, but a more popular monetary loss function may be
(-log(E(W | R))), the negative log of the
expectation of wealth, given the return. There are many alternative
loss functions.
Although isolated decision-theoretic problems exist such as the
provided example, decision theory may also be applied to the results
of a probability model (such as from
IterativeQuadrature, LaplaceApproximation,
LaplacesDemon, PMC), or
VariationalBayes, contingent on how
a decision-maker is considering to use the information from the
model. The statistician may pass the results of a model to a client,
who then considers choosing possible actions, given this
information. The statistician should further assist the client with
considering actions, states of the world, then loss functions, and
finally eliciting the client’s prior probabilities (such as with the
elicit function).
When the outcome is finally observed, the information from this
outcome may be used to refine the priors of the next such decision. In
this way, Bayesian learning occurs.
References
Berger, J.O. (1985). “Statistical Decision Theory and Bayesian
Analysis”, Second Edition. Springer: New York, NY.
Bernardo, J.M. and Smith, A.F.M. (2000). “Bayesian Theory”. John
Wiley & Sons: West Sussex, England.
Savage, L.J. (1954). “The Foundations of Statistics”. John Wiley &
Sons: West Sussex, England.
See Also
elicit,
IterativeQuadrature,
LaplaceApproximation,
LaplacesDemon,
PMC, and
VariationalBayes.
Examples
Run this code
# NOT RUN {
library(LaplacesDemon)
### Point-estimated loss and state probabilities
L <- matrix(c(-500,1000,-300,-300), 2, 2)
rownames(L) <- c("s[1]: !Defaults","s[2]: Defaults")
colnames(L) <- c("a[1]: Buy ZZZ", "a[2]: Buy XXX")
L
p.theta <- matrix(c(0.9, 0.1, 1, 0), 2, 2)
Fit <- LossMatrix(L, p.theta)
### Point-estimated loss and samples of state probabilities
L <- matrix(c(-500,1000,-300,-300), 2, 2)
rownames(L) <- c("s[1]: Defaults","s[2]: !Defaults")
colnames(L) <- c("a[1]: Buy ZZZ", "a[2]: Buy XXX")
L
p.theta <- array(runif(4000), dim=c(2,2,1000)) #Random probabilities,
#just for a quick example. And, since they must sum to one:
for (i in 1:1000) {
p.theta[,,i] <- p.theta[,,i] / matrix(colSums(p.theta[,,i]),
dim(p.theta)[1], dim(p.theta)[2], byrow=TRUE)}
Fit <- LossMatrix(L, p.theta)
Fit
### Point-estimates of loss may be replaced with samples as well.
# }
Run the code above in your browser using DataCamp Workspace