Как найти погрешность коэффициента вязкости

Как найти погрешность коэффициента вязкости

Министерство
здравоохранения Российской Федерации

Государственное
образовательное учреждение

высшего
профессионального образования

«Тверская
государственная медицинская академия
Министерства здравоохранения Российской
Федерации»

кафедра
медбиофизики и информатики

ИССЛЕДОВАНИЕ
ВЯЗКОСТИ ЖИДКОСТИ

Методические
указания
для лабораторной работы № 1

(для
фармацевтического факультета)

Тверь
2007

Методические
указания составлены кафедрой медбиофизики
ТГМА и предназначены в помощь студентам
фармацевтического факультета при
подготовке и выполнении лабораторной
работы.

Лабораторная
работа №1

ИССЛЕДОВАНИЕ
ВЯЗКОСТИ ЖИДКОСТИ

ЦЕЛЬ
РАБОТЫ:

  1. Теоретически
    изучить явление вязкости жидкости
    (внутреннего трения) и методы определения
    коэффициента вязкости.

  2. Экспериментально
    освоить метод Стокса.

  3. Используя
    метод Стокса, определить вязкость
    глицерина, рассчитать величину
    погрешности величины вязкости.

ПРИБОРЫ И
ПРИНАДЛЕЖНОСТИ:

стеклянный
цилиндр с исследуемой жидкостью
(глицерин), штангенциркуль, секундомер,
шарики.

ЛИТЕРАТУРА:

  1. Ремизов
    А.Н. Медицинская
    и биологическая физика    .
    М.: Высшая школа, 1996. (см. § 3.2 – 3.4).

  2. Лекции
    по теории вероятности и математической
    статистики (II семестр).

  3. Морозов
    Ю.В., Основы
    высшей математики и статистики    .
    М.: Медицина, 1998. (см. п. 9.4).

  4. Павлушков
    И.В. и др., Основы
    высшей математики и математической
    статистики    .
    М.: Геотар-Мед., 2003. (см. п. 8.2.2, 8.2.3).

КРАТКАЯ
ТЕОРИЯ

Движение
неидеальной жидкости сопровождается
потерей её механической энергии
(переходом части механической энергии
в тепловую), вследствие чего падает
давление внутри жидкости и уменьшается
скорость течения. Основная причина
перехода механической энергии в тепло
– взаимодействие молекул, движущихся
поступательно в одну сторону, но с
разными скоростями, сопровождаемое
передачей импульса – вязкость. Нужно
различать скорость течения жидкости
(скорость течения слоя жидкости) и
скорость молекул (внутри слоя жидкости).
В результате импульс передается стенкам
сосуда, приводя к нагреву последних, и
уменьшению поступательной скорости
молекул. Явление вязкости количественно
характеризуется величиной вязкости
(
– читается
“эта”). Таким образом, вязкость есть
одно из явлений переноса. В данном случае
переноса импульса.

Явление
вязкости можно смоделировать следующим
образом. Мысленно разобьём жидкости на
очень тонкие слои так, что бы поступательная
скорость молекул внутри слоя (скорость
слоя жидкости) была одинаковой. Тогда
явление вязкости будет представлять
собой трение между слоями жидкости,
часто называемое внутренним трением.
Сила трения между слоями жидкости
описывается формулой Ньютона:

(1),

где
F
– сила трения
между слоями жидкости (Н), S
– площадь
соприкосновения слоев (м2),

– градиент скорости, т.е. быстрота
изменения скорости в направлении,
перпендикулярном направлению движения
слоя (с-1),

– коэффициент
вязкости (Пас).
Для многих жидкостей
зависит лишь от природы жидкости и
температуры. Такие жидкости называются
ньютоновскими, в отличие от неньютоновских,
в которых вязкость также зависит от
режима течения. Для последних вводят
условный коэффициент вязкости.

Для
характеристики вязкости на практике
часто пользуются понятием относительной
вязкости отн:

(2),

где
0
= 110
-3
(Пас)
– вязкость воды при 200
С.

Строго
говоря, вести речь о слоях жидкости
можно лишь тогда, когда жидкость движется
не перемешиваясь (нет перемешивания
слоёв). Такое движение называется
ламинарным в отличие от турбулентного,
при котором образуются завихрения и
происходит перемешивание жидкости. Вид
течения жидкости для прямой круглой
трубы можно определить по числу
Рейнольдса:

(3),

где

–
плотность жидкости (кг/м3),

–
коэффициент вязкости (Пас),
r
–
радиус трубы (м), v
–
скорость течения (м/с). Если Re
<
1000 –
течение ламинарное, если Re
>
1500 – турбулентное,
1000 
Re

1500 –
течение нестабильно и может изменяться
случайным образом от ламинарного к
турбулентному и наоборот.

Кровь
– неоднородная жидкость, представляющая
собой суспензию форменных элементов в
белковом растворе
–
плазме. Строго говоря, кровь следует
отнести к неньютоновским жидкостям, но
обычно этим пренебрегают. Относительная
вязкость крови в норме составляет
от 4,2 до 6.
Она может снижаться до
2 ÷ 3
(например, при анемии) и повышаться до
15
÷
20
(при полицитемии). Относительная вязкость
сыворотки крови в норме
1,64 ÷ 1,69
и при патологии 1,5
÷ 2,0.
Относительная вязкость крови
–
важный диагностический показатель
состояния.

На
практике вязкость жидкости определяется
с помощью прибора
–
капиллярного вискозиметра,
основанного на законе Гагена-Пуазейля.

(4),

где
Р1,
Р2
– давление (Па) в начале и конце трубы
длины
l
(м);
r
–
радиус трубы (м); vcp–
средняя скорость течения жидкости
(м/с). Из закона Гагена-Пуазейля следует,
что объем вязкой жидкости V
=
vcp

S
(где
S
– площадь поперечного сечения трубы,
м2),
протекающей по тонкой трубке в единицу
времени, обратно пропорционален вязкости
жидкости .
Измеряя V,
можно
определить .
Схему капиллярного вискозиметра и
принцип действия подробно смотрите в
учебнике.

Течение
крови в сосудистой системе в нормальных
условиях имеет в основном ламинарный
характер. Оно может переходить в
турбулентное при сужении просвета
сосуда, при разветвлениях. Подобное
явление происходит место при дефекте
митральных или аортальных клапанов.
При этом появляются звуки, называемые
сердечными шумами, которые являются
одним из признаков этого явления.
Прослушивание звуков, сопровождающих
турбулентное течение при прохождении
крови по искусственно
сжатой артерии, используется при
измерении артериального давления.
Знание свойств крови, в частности
вязкости, позволяет рассчитывать
движение крови по сосудам, создавать
модель кровообращения, результатом
которых может служить аппарат
искусственного кровообращения.

ТЕОРИЯ
МЕТОДА СТОКСА И ОПИСАНИЕ УСТАНОВКИ

К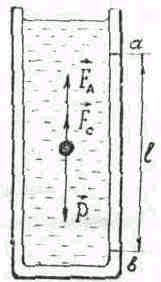
оэффициент
вязкости может быть определён методом
падающего шарика в вязкой среде (метод
Стокса). Рассмотрим падение шарика в
вязкой покоящейся жидкости (рис. 1). На
движущийся шарик действуют следующие
силы:

Рис.
1

Сила
тяжести:

P
= mg или P
=4/3r31g (5),

где
r
–радиус
шарика (м); 1
– плотность
шарика (кг/м3);
g
–
ускорение свободного падения (9,8 м/с2).

Выталкивающая
сила (сила Архимеда):

FA=4/3r32g (6),

где
2
–
плотность жидкости.

Сила
сопротивления движению (сила Стокса)

FС=6rv (7),

где

– коэффициент вязкости, v
– скорость шарика.

Подчеркнем,
что здесь играет роль не трение шарика
о жидкость, а трение отдельных слоев
жидкости друг о друга, так как при
соприкосновении твердого тела с жидкостью
к поверхности тела тотчас же прилипают
молекулы жидкости. Тело обволакивается
слоями жидкости, связанными с ним
межмолекулярными силами. Непосредственно
прилегающий к телу слой жидкости движется
вместе с ним со скоростью движения тела.
Этот слой увлекает в своём движении
соседние слои жидкости, которые на
некоторый период времени приходят в
плавное безвихревое движение (при малых
скоростях и малых размерах шарика), т.е.
наблюдается явление вязкости. Направление
этих сил показано на рисунке 1.

Равнодействующая
сил, действующих на шарик, в векторной
форме:

(8).

В
скалярной форме с учётом направления
сил, если направление силы тяжести
принять за положительное (ось системы
координат направлена вниз):

R
= P
– (FA
+
FC) (9).

В
начале скорость движения шарика (10)
будет возрастать, так как сила тяжести
в этот момент больше суммы сил в скобках
(9).

(10).

Но
по мере увеличения скорости также будет
возрастать сила сопротивления и наступит
такой момент, когда сила тяжести Р
будет уравновешена суммой FA
и FC

и
равнодействующая сила станет равной
нулю, т.е.:

P
– (FA
+
FC)
= 0 (11).

Время
от начала движения в жидкости до
установления равномерного движения
определяется соотношением:

(12).

При
t
>>
движение шарика становится равномерным
со скоростью
v
= v0.

Подставляя
в уравнение (11) соответствующие значения
Р,
FA
и
FC
и
считая движение жидкости относительно
шарика ламинарным,
получим для коэффициента вязкости
выражение:

(13).

Соотношение
(13) и используется в методе Стокса для
определения вязкости жидкости.
Следовательно, чтобы рассчитать значение
вязкости, нужно предварительно определить
r,
v0,
1
и 2.
Значение 1
и 2
даны (см.
на установку), r
или d
(диаметр шарика) шарика определяется с
помощью штангенциркуля с точностью до
0,1
мм и погрешностью
х
= 0,05
мм, скорость шарика определяется
экспериментально, как v0=,
t
– время движения шарика в жидкости по
секундомеру. Соотношение (13) можно
упростить и рассчитать
как:

(14),

где

(15).

ОПРЕДЕЛЕНИЕ
ПОГРЕШНОСТЕЙ

Расчетные
значения должны округляться согласно
точности используемых приборов. Так
точность измерения штангенциркуля
равна 0,1 мм, погрешность 0,05 мм; секундомера
0.01 с; линейки 1 см и погрешность 0,5 см с
сантиметровыми делениями или 1 мм и
погрешность 0,5 мм для линейки с
миллиметровыми делениями. Следовательно,
при переводе всех значений в систему
СИ величина вязкости будет иметь только
две значащие цифры после запятой. Число
значащих цифр определяется наиболее
грубым измерением в выбранной системе
единиц, в данном случае или секундомером
или линейкой с сантиметровыми делениями.

Предполагая,
что все определённые числовые значения
величин распределены по нормальному
закону, рассчитаем экспериментальные
погрешности. Для определения абсолютной
погрешности косвенных измерений вязкости
сначала требуется найти частные
производные по всем переменным (16).

(16)

или
косвенная абсолютная погрешность одного
определения вязкости равна

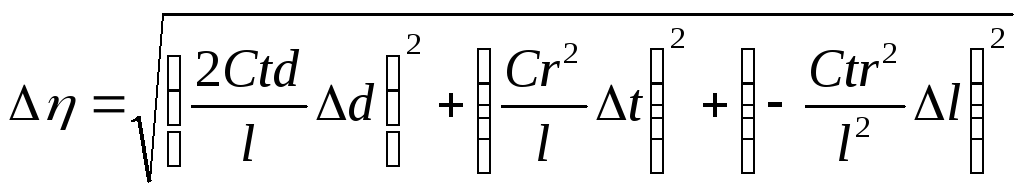(17).

Абсолютные
погрешности прямых измерений х
некоторой величины х
определяют по соотношению (18)

(18),

если
х
оказывается меньше погрешности
используемого измерительного прибора,
то в качестве абсолютной погрешности
х
используется погрешность данного
прибора (см. выше). Здесь k
– количество измерений, t,k-1
– коэффициент Стьюдента (берется из
соответствующих таблиц).

Если
проводится несколько опытов определения
величины i
и в каждом
рассчитывается абсолютная погрешность
i,
то погрешность среднего арифметического
ср
искомой величины
не может быть меньше

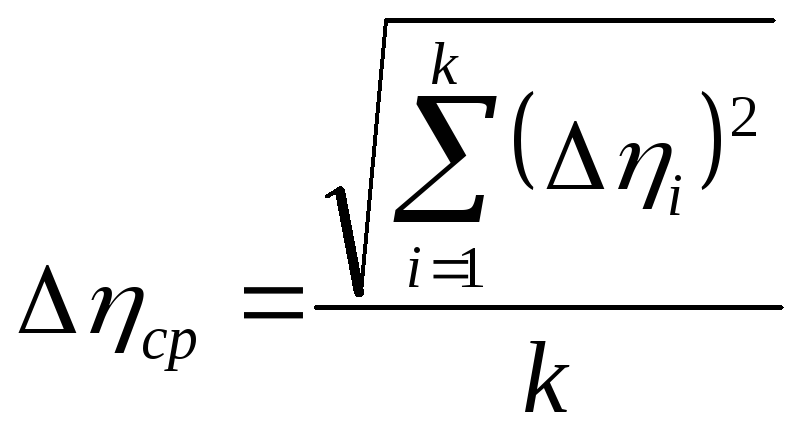(19)

Относительная
ошибка (погрешность) эксперимента равна

(20).

ИЗМЕРЕНИЕ
И ОБРАБОТКА
РЕЗУЛЬТАТОВ

  1. Измерить
    диаметр шарика штангенциркулем три
    раза в разных местах и записать среднее
    значение dcp
    в таблицу 1, в расчетах использовать
    среднее значение диаметра.

  2. Опустить
    шарик в жидкость как можно ближе к оси
    цилиндра (глаз наблюдателя должен быть
    при этом установлен против верхней
    метки а
    так, чтобы она сливалась в одну линию),
    в момент прохождения шариком верхней
    метки а
    включить секундомер, в момент прохождения
    нижней метки
    b
    –
    остановить. Наблюдение прохождение
    шариком метки «b»
    аналогично описанному выше. Время
    t
    прохождения шариком пути l
    между метками «а»
    и «b»
    занести в таблицу 1.

  3. Провести
    не менее десяти опытов.

  4. Измерить
    линейкой расстояние l
    между метками «а»
    и «b».

  5. Показать
    полученные результаты преподавателю.

  6. В
    каждом опыте рассчитать значение
    вязкости i
    и абсолютную ошибку вязкости i
    согласно (15) и (17), в качестве абсолютных
    погрешностей (d,
    t,
    l)
    используются погрешности приборов.

  7. Рассчитать
    абсолютную ошибку среднего арифметического
    опытов cp
    по соотношению (19).

  8. Рассчитать
    абсолютную ошибку среднего арифметического
    опытов cp
    по соотношению (18), взяв
    .

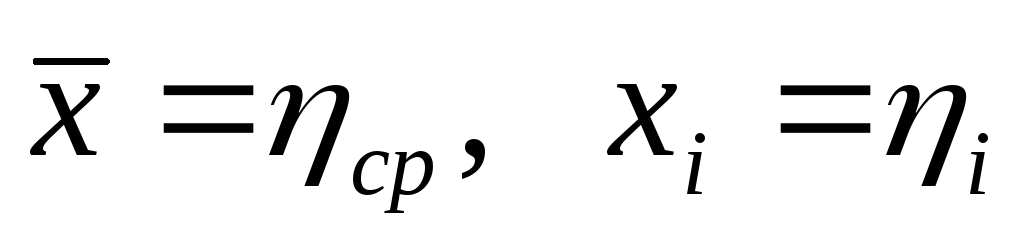  9. За
    абсолютную ошибку величины cp
    принять наибольшую из величин пунктов
    7 и 8.

  10. Определить
    относительную погрешность .

  11. Занести
    все полученные значения в таблицу 1.

  12. В
    каждом опыте определить число Рейнолдса,
    приняв за r
    средний радиус шарика, а за плотность
    глицерина cp.
    Определите характер течения жидкости
    вокруг шарика.

  13. Сделать
    вывод. Записать ответ.

Таблица
1.

№

dcp,

м

t,

с

l,

м

v0,

м/с

Пас

cp

Пас



Пас

cp

Пас

(см.
пункт 7)

cp

Пас

(см.
пункт 8)

,
%

Re

1

…

10

КОНТРОЛЬНЫЕ
ВОПРОСЫ

  1. Напишите
    и объясните условие неразрывности
    струи.

  2. Напишите
    уравнение Бернулли для течения идеальной
    жидкости.

  3. Напишите
    уравнение зависимости величины скорости
    от оси круглой трубы.

  4. Написать
    и объяснить формулу Ньютона для силы
    внутреннего трения (вязкость жидкости).
    Что называется турбулентным и ламинарным
    течением? Для чего служит число
    Рейнольдса?

  5. Что
    называется явлением вязкости? В каких
    единицах измеряется величина вязкости?

  6. Что
    такое относительная вязкость?
    Кинематическая вязкость?

  7. Какой
    характер имеет течение крови по сосудам
    и чем сопровождается турбулентное
    течение крови? От чего зависит коэффициент
    вязкости крови и какова относительная
    вязкость крови в норме?

  8. От
    чего зависит коэффициент вязкости
    различных жидкостей? Что такое
    относительная вязкость жидкости?

  9. Пояснить
    закон Гагена-Пуазейля. Нарисовать, как
    зависит скорость течения крови в сосуде
    от расстояния до стенок сосуда.

  10. Что
    называется гидравлическим сопротивлением?
    Как определит объёмную скорость
    жидкости?

  11. Изменится
    ли значение коэффициента вязкости,
    получаемое в вашем эксперименте, если
    вместо свинцового шарика, использовать,
    например, стеклянный? Можно ли в вашем
    эксперименте за верхнюю риску принять
    поверхность жидкости?

  12. Расскажите
    метод Стокса по измерению вязкости
    жидкости.

  13. Как
    рассчитать абсолютную и относительную
    погрешность величины при прямых
    измерениях?

  14. Как
    рассчитать абсолютную и относительную
    погрешность величины при косвенных
    измерениях?

  15. Что
    принимается за абсолютную ошибку
    вязкости? Как рассчитать абсолютную
    ошибку вязкости?

ЗАДАЧИ

1.Площадь
соприкосновения слоев текущей жидкости
10-3
м2,
относительная
вязкость жидкости равна 1, а возникающие
силы трения между слоями равны 10-3
Н. Чему равен градиент скорости (в с-1).

Ответ;
1000 с-1

2.
Пользуясь капиллярным вискозиметром,
коэффициент вязкости определяют по
формуле
= 0
,
где 0
– коэффициент вязкости дистиллированной
воды при данной температуре, t0
– время истечения дистиллированной воды
через капилляр определенного объема,
0
– плотность
дистиллированной воды при данной
температуре,
и t
–
соответственно плотность исследуемой
жидкости и время ее истечения через
капилляр того же объема.

а)
определить вязкость раствора белка в
(Паc),
если он через капилляр вискозиметра
вытекает за
30 с, а вода
– за 15 с.
Коэффициент вязкости воды равен 10-3
Пас,
плотность раствора белка 103
кг/м3,
плотность воды 103
кг/м3.
Ответ дать в системе СИ.

Ответ:
210-3
Пас.

б)
Определить время протекания крови через
капилляр вискозиметра в (с) при следующих
данных: коэффициент вязкости воды равен
10-3 Пас,
крови
– 510-3
Пас,
плотность воды – 103
кг/м3,
крови – 1,05103
кг/м3,
время протекания воды через капилляр
5 с.

Ответ;
23,8 с.

3.
Вычислить горизонтальную силу, действующую
на площадь S
= 2 м2
дна русла, если по нему перемещается
поток воды высотой 2 м. Скорость от дна
вверх увеличивается линейно и у верхнего
слоя воды v
= 0,3 м/с. Коэффициент вязкости воды равен
10-3 Пас.

Ответ:
310–4
Н.

4.
Определить характер течения крови через
аорту диаметром 0,02 м, если скорость
течения крови через аорту 0,4 м/с, плотность
крови – 1,05103
кг/м3,
а вязкость крови – 510-3
Пас.

Ответ:
ламинарный; т.к. Re
= 840.

5.
Определить объёмную скорость кровотока
через аорту, если диаметр аорты 0,02 м. а
скорость течения крови 0,5 м/с.

Ответ:

0,00016 м3/c.

6.
Определить максимальное количество
крови (массу), которое может пройти через
аорту за 1 с. Диаметр аорты 0,02 м, скорость
течения крови в аорте 0,4 м/с, плотность
крови – 1,05103
кг/м3.
Ответ дать в системе СИ.

Ответ:

0,13 кг.

7.
Определить относительную вязкость
крови, если коэффициент вязкости крови
– 510-3
Пас,
коэффициент вязкости воды – 10-3
Пас.

Ответ:
5.

Соседние файлы в предмете Физика

  • #
  • #
Источник

Рис.
2

1) 
сила тяжести Р,
направленная вертикально вниз и равная

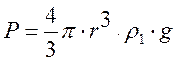        (1)

(где r – радиус шарика,  –
плотность материала шарика при данной температуре; g – ускорение свободного падения).

2) 
сила Архимеда FA, направленная вертикально вверх и равная весу
жидкости, вытесненной шариком,

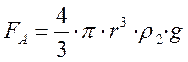          (2)

(где  – плотность
жидкости при данной температуре).

3) 
сила внутреннего трения Fтрнаправлена в сторону, обратную скорости движения (в
нашем случае вертикально вверх); ее можно рассчитать по формуле Стокса:

           (3)

(где V–
скорость равномерного движения шарика;  –
коэффициент внутреннего трения).

Силы
Pи
FA постоянны, а Fтррастет с
увеличением скорости шарика. Это происходит до тех пор, пока равнодействующая
всех сил не станет равной нулю:

.       (4)

Начиная
с этого момента шарик движется равномерно.

Подставляя
(1), (2) и (3) в уравнение (4), получим условие равномерного движения шарика в
виде:

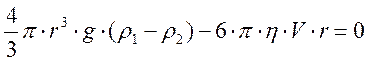
Заменив
в полученном соотношении радиус шарика на его диаметр ,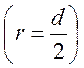
а скорость установившегося движения шарика по отношению пройденного пути l
к затраченному на его прохождение времени ,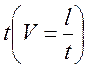
получаем окончательное выражение для расчета коэффициента вязкости жидкости:

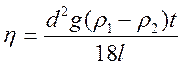     (5)

Уравнение (5) справедливо для случая, когда шарик
падает в безграничной среде. Если шарик движется вдоль оси трубки, то
необходимо учитывать влияние стенок трубки. Это влияние обусловлено тем, что
молекулы слоя жидкости, прилегающие к внутренним стенкам трубки, «прилипают» к
ней и не перемещаются.

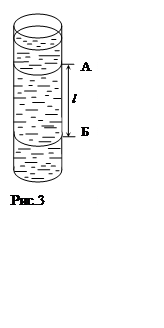Вискозиметр, используемый в данной работе (рис.3),
представляет собою стеклянный цилиндрический сосуд, закрепленный в держателе и
расположенный строго вертикально. Нижний конец сосуда запаян, а на верхнем
имеется воронка с отверстием строго по осевой линии цилиндра, предназначенная
для зарядки вискозиметра исследуемой жидкостью и для придания направления
движения твердых шариков, опускаемых в жидкость. На цилиндре имеются две метки
(А и Б), способные перемещаться вдоль него. Внутренний диаметр вискозиметра
значительно превосходит диаметр маленьких твердых шариков, поэтому влиянием
вискозиметра на их движение можно пренебречь.

Наблюдая за характером равномерного движения шарика в
жидкости и используя соотношение (5), можно определить коэффициент внутреннего
трения жидкости.

Порядок работы
и обработки результатов измерений

1. 
Отобрать для опыта пять шариков;

2. 
Измерить диаметр каждого шарика
три раза в различных направлениях и данные измерений занести в табл. 1;

3.  Измерить расстояние между метками на вискозиметре с
точностью до 1 мм;

Таблица 1

Номер

шарика

Диаметр шарика d, см.

Средний диаметр шарика dср, см

1

2

3

1

2

3

4

5

4. 
Опустить шарик в вискозиметр через
воронку и измерить время его движения между метками;

            Измерение повторить для каждого из пяти
шариков. Данные опыта занести в таблицу 2.

Таблица 2

Номер шарика

dср, см

l,
см.

t, с.

h,

Па·с

1

2

3

4

5

hср=

5. 
Вычислить коэффициент внутреннего
трения по результатам каждого опыта. Определить среднее значение этого
коэффициента.

П
р и м е ч а н и е.  При проведении
опытов фиксируются: наименование жидкости, ее плотность, температура окружающей
среды и плотность материала шарика.

Оценить
абсолютную погрешность измерения коэффициентов вязкости по методу Стьюдента.

Для
этого необходимо найти

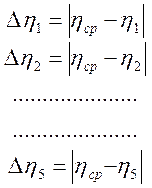
и вычислить вспомогательную
величину

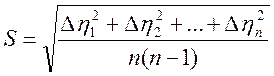
где
n – число измерений коэффициента вязкости.

Затем
вычислить абсолютную погрешность по формуле

где
а – коэффициент Стьюдента, равный 2.8 для доверительной вероятности =0.95 при n=5.

Окончательный
результат записать в виде

Контрольные вопросы.

  1. В
    чем заключается физическая природа вязкости?
  2.  При
    каких условиях сила внутреннего трения пропорциональна скорости?
  3. Объясните
    характер зависимости коэффициента внутреннего трения от температуры?
  4. Напишите
    размерность коэффициента трения.
  5. Каков
    характер изменения скорости и ускорения шарика на всем пути его движения?
  6. Как
    изменяется скорость падения парашютиста при затяжном прыжке?

Литература

  1. Савельев
    И.В. Курс общей физики, т.2..М.: Наука, 1987
  2. Матвеев
    А.Н. Молекулярная физика. М.: Высшая школа, 1981
  3. Кикоин
    А.К. Молекулярная физика. М.: Наука, 1982

Содержание

Цель
работы………………………………………………..

3

Введение……………………………………………………

3

Описание установки и
методика измерения……………..

5

Порядок выполнения работы и
результаты измерений…

8

Контрольные
вопросы…………………………………….

10

Литература…………………………………………………

10

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

Источник

Лабораторная работа № 9

Определение коэффициента внутреннего трения жидкости по методу Стокса.

Цель
работы: 1.Изучить явление внутреннего трения в
жидкостях. 2.Освоить метод определения вязкости жидкости – метод Стокса.
3.Определить температурную зависимость коэффициента вязкости глицерина.

Принадлежности:
Стеклянный цилиндр с исследуемой жидкостью (глицерин); термостат; секундомер;
измерительный микроскоп; масштабная линейка; мелкие свинцовые или стальные
шарики.

Литература:

1. А. Н. Матвеев. Молекулярная физика; М.: Высшая
школа; 1987- с.360

2. Я. И. Френкель. Кинетическая теория жидкостей; Л.:
Наука; 1975- с.221 – 229

3. И. К. Кикоин, А. К. Кикоин. Молекулярная физика;
М.: Наука; 1976 §§ 48, 49, 97

4. Л. Л. Гольдин. Руководство к лабораторным занятиям
по физике; 1973, с.140

5. В.М. Гзогян, Ю.П. Полыгалов. Ключевые вопросы
молекулярной физики; Кемерово 2003

Краткая теория

          Явление внутреннего трения (вязкость) состоит в возникновении сил трения
между слоями газа и жидкости при их относительном перемещении. Сила трения
выражается формулой Ньютона:

                                         
(1)

где
 – коэффициент динамической вязкости:    величина, показывающая, как быстро
изменяется скорость жидкости или газа в направлении,
перпендикулярном направлению движения слоев. Эта величина называется градиентом
скорости;  –
элементарная площадка поверхности соприкосновения слоев.

Из формулы (1) очевиден физический смысл коэффициента
вязкости. Он численно равен силе трения между
слоями площади при градиенте скорости, равном единице.

Надпись: Рис.1         Вязкость жидкостей (газов) обуславливает
сопротивления движению в них твердых тел. Стокс установил, что сила
сопротивления пропорциональна коэффициенту динамической вязкости, скорости движения тела v относительно жидкости
и характерному размеру тела r. Коэффициент пропорциональности зависит
от  формы тела и для шара он   равен 6.
Следовательно , сила сопротивления движению шарика в жидкости при небольших
скоростях в соответствии с формулой Стокса равна:

                                           
(2)

    
На небольшой шарик, падающий вертикально в жидкости или газе, действует три
силы:

1. сила тяжести
 (– радиус
шарика, – его плотность), направленная вниз;  2. выталкивающая (Архимедова) сила  (– 
плотность жидкости или газа), направленная вверх;  3. сила сопротивления,
направленная в сторону, противоположную движению, т.е. вверх (рис. 1). основной закон динамики в этом
случае запишется так:

                                                       
(3)

      
Из этих трех сил одна является переменной – это сила сопротивления, быстро
возрастающая с ростом  скорости. Но с течением времени, по мере возрастания
скорости, ускорение уменьшается и наступает такой момент, когда оно становится
равным нулю. Начиная с этого момента, тело будет двигаться равномерно с
постоянной скоростью, которая называется установившейся. Тогда уравнение (3) запишется так:

                                   
(4)

          Это выражение можно использовать для определения коэффициента вязкости:

                                            
(5)

          При движении шарика в среде, помещенной в каком-либо сосуде, необходимо
в (5) внести поправку, учитывающую
размеры тела (радиус сосуда) и окончательно эта формула имеет вид:

                                          (6)

где
– радиус сосуда, в котором происходит
падение шарика.

          При выводе формулы Стокса предполагается, что обтекание шарика жидкостью
имеет ламинарный характер. Как известно, характер обтекания определяется
значением числа Рейнольдса.

                                                 
(7)

          Обтекание
является ламинарным лишь при небольшом значении. По
результатам опыта следует вычислить числа Рейнольдса для различных температур
жидкости.

Описание установки

          Для
измерений используется стеклянный цилиндрический сосуд, наполненный глицерином
и имеющий двойные стенки, между которыми циркулирует вода из термостата. На
стенках сосуда устанавливают две метки на некотором расстоянии  друг от друга. Верхняя метка должна располагаться
ниже уровня жидкости с таким расчетом, чтобы скорость шарика к моменту
прохождения этой метки успела установиться. Измеряя расстояние между метками
линейкой, а время падения секундомером, определяют скорость шарика.

          Радиусы шариков измеряются с
помощью измерительного микроскопа, снабженного окулярной шкалой, цена деления
которой 0,05 мм.. Для каждого шарика рекомендуется измерить несколько различных
диаметров и вычислить среднее значение. Такое усреднение целесообразно
поскольку в работе используются шарики, форма которых может несколько
отличаться от сферической. Плотность шариков определяется из таблиц или
находится по весу и объему.

          Опыты
по определению коэффициента внутреннего трения жидкости проводятся при
нескольких температурах в интервале от комнатной температуры до 500
С.

          Общий
вид прибора для измерения коэффициента вязкости по методу Стокса показан на рис. 2.

Рис. 2.  Схема установки для определения
коэффициента вязкости жидкости по методу Стокса.

А – сосуд с глицерином; Т1 – контактный термометр; Т2 – контрольный термометр; Н – нагреватель; Д – насос – мешалка; Э –
электродвигатель.

          Для
установления необходимой температуры служит термостат с контактным термометром.
Термостат представляет собой водяную ванну с нагревателем, который
автоматически включается контактным термометром и служит для поддержания
постоянной температуры.

          Контактный
термометр, показанный на рис. 2 ,
представляет собой ртутный термометр, в капиллярной трубке которого может
перемещаться вольфрамовая нить. Нижний конец нити устанавливается на требуемом
делении шкалы термометра. От баллончика со ртутью и от нити сделаны выводы к
наружным клеммам термометра, с помощью которого он включается в цепь
электрического реле.

          Схема
включения контактного термометра КТ,
реле Р и нагревателя Н, показана на рис. 3.

Рис. 3. Электрическая схеме термостата.

          При
повышении температуры столбик ртути поднимается по капилляру до нижнего конца
вольфрамовой нити и замыкает цепь реле. Реле срабатывает и размыкает цепь
нагревателя Н. При понижении температуры
нагреватель вновь включается в сеть.

          Настройка терморегулятора на
требуемую температуру производится с помощью постоянного магнита,
расположенного в головке контактного термометра. Вращая магнит в ту или другую
сторону, приводят во вращение винт, перемещающий вольфрамовую нить в капилляре.
Для контроля за температурами исследуемой  жидкости и воды в термостате служит
ртутный контрольный термометр.

          При
каждом значении температуры необходимо повторить опыт с 5-ю шариками. Плотность
жидкости для каждого значения температуры следует взять из графика,
прилагаемого к работе. По полученным данным следует построить график
зависимости коэффициента вязкости от температуры.

Измерения

1.                
Отберите 5 шариков и с помощью
микроскопа измерьте их средние диаметры.

2.                
Измерьте комнатную температуру глицерина, для которой, пользуясь
графиком, прилагаемом в работе, найдите плотность глицерина.

3.                
Включите тумблер “сеть” на секундомере, дайте ему прогреться
1-2 минуты нажмите кнопку “сброс”. Для пуска и остановки секундомера
пользуйтесь тумблером “пуск” и “стоп”.

4.                
Опустите один из измеренных шариков в сосуд с глицерином и
как только шарик пересечет верхнюю метку, включите секундомер, а когда шарик
пройдет нижнюю метку, остановите его.

5.                
Измерьте расстояние L между метками,
соответствующее измеренному времени t.

6.                
Повторите опыт для остальных четырех шариков.

7.                
Рассчитайте скорость движения шарика.
Величины L, t, занесите в таблицу.

8.                
По формуле (6) вычислите значение коэффициента вязкости и относительную
погрешность.

№

R (см)

сосуда

(г/см3)

шарика

(г/см3)

глицерин

r (см)

шарика

L

см

t

с

 v

см/с

  

г/cм с

г/см с

%

9.                
Включите термостат. Для этого поставьте переключатель “сеть”
и тумблер “мотор” в положение “вкл.”. На контактном термометре установите
температуру 300 С, при этом должна загореться сигнальная лампочка на
панели термостата. При достижении заданной температуры лампочка начнет мигать,
при этом отключать прибор не требуется. Далее необходимо выждать некоторое
время для того, чтобы в системе установилось термодинамическое равновесие.

10.            
При достижении температурного равновесия проведите эксперимент
по определению скорости движения шариков в жидкости и вычислите коэффициент
вязкости для данной температуры. Повторите опыты для температуры 400С,
500С.

11.            
Постройте график зависимости коэффициента внутреннего трения
от температуры.

12.            
 Вычислите для каждой температуры число Рейнольдса Re по формуле (7)
и сделайте вывод о применении формулы Стокса в каждом эксперименте.

Контрольные вопросы

1.     Объясните
причину возникновения внутреннего трения между двумя слоями жидкости или газа,
движущимися с различными скоростями. С переносом какой физической величины
связано внутреннее трение?

2.     Получите формулы
переносимой величины и коэффициента вязкости среды (газа).

3.     Как зависит
коэффициент вязкости газа от температуры и давления (рассмотрите область
нормальных давлений)?

4.     Изобразите
графики зависимостей средней длины свободного пробега молекул, коэффициентов
диффузии, теплопроводности и вязкости в зависимости от давления газа (охватывая
область от низких до высоких давлений).

5.     Какое условие
нужно обеспечить, чтобы можно было говорить о вакууме внутри сосуда? Почему
понятие вакуума имеет относительный характер?

6.     Изобразите
примерный график зависимости скоростей от расстояний при движении шарика в
жидкости.

7.     Как зависит сила
трения от скорости тела (при больших и малых скоростях)?

8.     Выведите рабочую
формулу метода Стокса. При каких условиях она справедлива?

9.     Что такое
“радиометрический эффект”, какими причинами вызывается этот эффект?
(см. Сивухин Д.В. “Молекулярная физика”,1979, с.362).

10. Как зависит результат
измерения коэффициента вязкости от материала шарика?

11. Какие факторы могут повлиять
на результаты измерений, если движение шарика будет происходить вблизи стенки
сосуда?

12. Из каких соображений верхняя
метка должна устанавливаться ниже уровня жидкости?

13. Будет ли зависеть результата
измерения коэффициента вязкости, если шарик бросить в жидкость со скоростью?

14. Сравните порядок измеренных
Вами величин коэффициентов вязкости жидкости и газа при комнатной температуре.
Объясните причину различия.

15. Определите относительную
погрешность измерения коэффициента вязкости жидкости.

Источник

    Определение вязкости. Коэффициент динамической вязкости определялся при помош,и стеклянного капиллярного вискозиметра [2] при трех температурах. Погрешность определения 0,2% (см. табл. 3). [c.70]

    Вычисленнее значение динамического коэффициента вязкости равно 0,01768 сП. Экспериментально найдено 0,01778 сП. Погрешность расчета —0,56%.. [c.74]

    Кривая течения для турбулентного потока (см. рис. П-44) имеет резкий перелом. Точки перелома будут разными при различных диаметрах труб. Существует два способа определения размеров трубопровода. По первому способу подсчитывают обобщенное число Рейнольдса [уравнение (П-110)], из рис. П-25 находят коэффициент трения, а затем по з равнению (П-52) определяют падение давления “. По второму способу находят турбулентную вязкость , используя падение давления в турбулентной области (рис. П-44) и зависимость коэффициента трения от числа Рейнольдса (рис. П-25). Это делается следующим образом по значениям >Др/4 и О определяют коэффициент трения f из уравнения (П-52), по значению f получают соответствующую величину Re (рис. П-25) и, исходя из того, что Re=Dup/ lx, подсчитывают значение турбулентной вязкости Ат, которое затем можно применить при расчете труб других диаметров. Используемое при этом способе значение падения давления должно определяться с погрешностью до 25% Теоретический анализ турбулентного течения неньюТоновских жидкостей можно найти в литературе  [c.158]

    Исследование течения расплавов ПБХ композиций с помощью капиллярных вискозиметров затрудняется тем, что материал, находясь длительное время в загрузочной камере прибора, подвергается значительным термическим воздействиям. Это вносит дополнительные погрешности в определение коэффициента эффективной вязкости расплава. Результаты измерений показателя текучести расплава (ПТР), полученные с помощью широко распространенного прибора измерения индекс расплава термопластов (ИИРТ), также по мнению авторов [45] неоднозначно характеризуют реологические свойства ПБХ композиций. С большим успехом этот показатель может применяться для оценки из термомеханической предыстории. [c.188]

    При расчетах печей динамический коэффициент вязкости влажного воздуха с нормальной влажностью = 10 г/кг можно принимать с допустимой погрешностью таким же, что и для сухого воздуха. [c.152]

    При эксплуатации УУСН необходимо по возможности обеспечивать узкий диапазон расходов через измерительные линии, особенно при высокой вязкости жидкости. Наиболее благоприятным для турбинных преобразователей расхода является диапазон 40-80 % от верхнего предела. Для уменьшения погрешности измерения объема жидкости и расширения диапазона расходов рекомендуется применять электронные преобразователи, блоки обработки информации, позволяющие корректировать коэффициент преобразования ТПР по расходу. [c.38]

    Экспериментально найденное значение динамического коэффициента вязкости окиси углерода при < = 50 °С и р = 1 ат равно 186 мкП. Погрешность расчета 1,9%. [c.96]

    Определение динамического коэффициента вязкости для жидкостей (т1к,Лх). Бретшнайдер [69], отмечая относительно большие погрешности в определении динамического коэффициента вязкости жидкостей по эмпирическим формулам, включающим структурные группы атомов, предлагает для расчетов использовать формулы Саудерса или Томаса. Первая из них дает хорошее совпадение с экспериментальными данными для органических жидкостей, вторая — для жидкостей в температурном интервале, в котором приведенная температура Гпр не превышает 0,7. Формула Саудерса имеет следующий вид  [c.78]

    ЭП Дельта-2 позволяет вводить в память градуировочную характеристику ТПР во всем диапазоне и исключить систематическую погрешность, обусловленную нелинейностью градуировочной характеристики. Также предусмотрена коррекция значений коэффициента преобразования ТПР по вязкости жидкости. [c.50]

    Необходимо отметить, что количество УУН, на которых вязкость непостоянна, невелико по сравнению с общим количеством УУН. Причем, закон изменения вязкости на таких УУН может быть различным. От характера изменения вязкости жидкости зависит способ введения поправки. Если период изменения вязкости велик, например, сезонные изменения, то исключить влияние вязкости можно уменьшением межповерочного интервала и изменением коэффициента преобразования на вторичных приборах. Если вязкость изменяется часто или непрерывно, то её влияние можно исключить только автоматическим введением поправок в результаты измерений. Поэтому для решения вопроса об исключении влияния вязкости нефти на погрешность определения ее количества в первую очередь необходимо исследовать закон изменения вязкости на УУН. [c.106]

    Вычисление динамического коэффициента вязкости 1 с небольшой погрешностью возможно, когда известно хотя бы одно экспериментально найденное значение этого коэффициента при любых произвольных условиях (температуре и давлении). Во всех других случаях приходится пользоваться либо трудоемкими и неточными методами, описанными в предыдущем разделе, либо менее трудоемкими, однако тоже неточными методами, основанными на примеиении правила аддитивности к некоторым физикохимическим свойствам. [c.302]

    Для тех типов ТПР, которые не проходили государственные испытания, при метрологической аттестации первых головных образцов должны быть определены допускаемые пределы изменения вязкости жидкости ДУд Эти пределы определяются по результатам измерений, произведенных для получения функции влияния вязкости, из условия, что изменение коэффициента преобразования ТПР при изменении вязкости в пределах Ауд пренебрежимо мало, то есть не превышает 0,35 основной погрешности. Это условие может быть записано следующим образом [c.107]

    Применение образцового счетчика для поверки ТПУ основано на том, что некоторые счетчики, например, турбинные, имеют очень высокую стабильность показаний при постоянных расходах, вязкости и температуре. Счетчик, поверенный по специальной методике в стабильных условиях, может быть использован в таких же условиях как образцовое средство измерения для поверки ТПУ. Для поверки образцового счетчика применяются образцовые мерники или ТПУ. При этом определяются коэффициент преобразования и погрешность счетчика. [c.168]

    При теоретическом описании закономерностей ламинарного и турбулентного потоков было принято постоянство физических свойств жидкостей (плотности, вязкости) это условие предполагают также приведенные выше эмпирические формулы для расчета коэффициента X. Между тем в химической технологии часто встречаются потоки, которые подвергаются нагреванию или охлаждению по всей своей длине (неизотермические потоки). Если зависимостью плотности жидкости от температуры Т можно большей частью практически пренебречь, то игнорирование изменения вязкости ц с температурой может привести к значительной погрешности расчета. Эта погрешность возрастает по мере увеличения абсолютного значения р,. Напомним, что вязкость жидкостей падает, а вязкость газов возрастает с увеличением температуры, причем эта зависимость сильнее у жидкостей, чем у газов. [c.55]

    Повышенные значения коэффициентов вариации у неньютоновских систем указывают на меньшую точность измерения предельного динамического напряжения сдвига, эффективной вязкости пластовых нефтей при напряжениях меньше критического напряжения сдвига, градиента динамического давления сдвига и коэффициента подвижности при фильтрации неньютоновской нефти в образцах пород при градиентах, меньше критического. Чтобы избежать этого, или по крайней мере, снизить погрешности определения этих параметров, опыты следует вести после предварительного разрушения структуры. [c.27]

    Так как суммарная максимальная абсолютная погрешность в определении коэффициента вязкости равна  [c.65]

    При анализе течений с учетом выталкивающей силы, проведенном в предыдущих главах, предполагалось, что теплофизические свойства жидкости постоянны с тем лишь исключением, что учитывалась переменность плотности в члене с объемными силами, входящем в уравнение движения. Это изменение играет существенную роль для описания выталкивающей силы. Однако уравнение неразрывности использовалось для несжимаемой среды. Такой подход позволяет анализировать течения жидкости с постоянными свойствами. Однако теплофизические свойства большинства жидкостей зависят от температуры и, если в окружающей среде создаются большие градиенты температуры, теплофизические свойства, как правило, существенно изменяются. Пренебрежение подобными изменениями может во многих случаях привести к серьезным погрешностям при расчете тепловых потоков. Теплофизические свойства, входящие в основные уравнения, включают термодинамические параметры и характеристики переноса. Термодинамические параметры определяются из равновесного состояния системы. К ним относятся температура, плотность и удельная теплоемкость жидкости. К характеристикам переноса относятся различные коэффициенты, определяющие скорости процессов, например коэффициент теплопроводности или вязкость. Опубликовано большое количество данных, позволяющих найти зависимость этих характеристик от температуры для различных жидкостей, представляющих практический интерес. Можно рекомендовать работу [32]. [c.474]

    При превышении вязкости жидкости значения 0,05 Па-с погрешность расчетов по уравнению (II. 2) превышает 15—25%, поэтому в него необходимо вводить экспериментально определенные поправочные коэффициенты [109]. [c.53]

    Прямая зависимость эффективного коэффициента диффузии Дт от понижения активности воды в бинарных растворах сохраняется в широкой области концентраций (см табл 3 15) Максимальное отклонение вычисленных по формуле (3 30) значений коэффициентов диффузии от опытных составляет – 2,5%, что лежит в пределах погрешностей эксперимента при определении коэффициентов диффузии, вязкости и активности воды, используемых в расчетах [c.409]

    Зависимость вязкости газа от давления показана на обобщенных диаграммах Карра (рис. 1-13) [110]. Средняя погрешность определения по этим диаграммам вязкости газа хр при некотором давлении Р составляет 2%, максимальная 10%. Обе диаграммы представляют собой варианты одной и той же зависимости с перестановкой величин на параметрических кривых и осях координат. Это дает возможность осуществить более точное интерполирование коэффициентов вязкости. Например, если известно, что приведенная температура 7 пр=1,67 и приведенное давление Япр = =23, то с помощью рис. 1-13, а можно найти значения Hp/Hi при Рпр=23, 7 пр = 1,6 и Т р—1,75 (это позволяет обойтись без построения изотермы 1,67, которая иа диаграмме не показана). Затем, построив по двум найденным значениям изобару Рпр = 23 на [c.29]

    При определении погрешности измерения коэффициента динамической вязкости исходным является расчетное уравнение (102)  [c.63]

    При эксплуатации форсунок рассмотренных конструкций необходимо следить за сохранением производительности форсунки при неизменном давлении, за вязкостью мазута, отсутствием закоксовывания, поддержанием минимального коэффициента избытка воздуха. Нарушение производительности форсунки при неизменных давлении перед ней и вязкости мазута наблюдается при нарушении заданной точности изготовления и недостаточно тщательной сборке при ремонте. Погрешности изготовления оказывают тем большее влияние, чем меньше расчетная производительность форсунки. Небрежная сборка форсунок может привести к снижению. производительности до уровня 40% номинальной, а также способствует закоксовыванию форсунки. [c.61]

    Для проверки гипотез о природе наблюдаемых релаксационных явлений были проведены исследования сдвиговых вязкоупругих свойств некоторых из перечисленных выше растворов методом измерения комплексного коэффициента отражения поперечной звуковой волны от границы раздела жидкость — твердая среда [16]. Так как теории акустического поглощения и динамических вязкоупругих свойств растворов полимеров основаны на одной и той же модели гауссовых субцепей, то согласно теоретическим представлениям следует ожидать, что релаксация сдвиговой и объемной вязкостей должна иметь место на одних и тех же частотах. Однако измерения показали [17] (рис. 1), что динамическая сдвиговая вязкость растворов ПС и ПИБ не зависит от частоты в интервале от 30 до 150 МГц, и ее значение в пределах погрешности эксперимента совпадает с высокочастотным предельным значением Дг оо,  [c.188]

    Эта формула является точной при Ке <С 1 и, как показывают расчеты, выполняется с погрешностью не более 5% при Ке 100 (см. табл. 1.1). Формулу (1.50) можно использовать ц при более высоких значениях Ке. Это иллюстрируется данными рис. 1.7, где приведена зависимость коэффициента сопротивления от Ке для твердой сферы, газового пузырька и капли с соотношением вязкостей х = 1. В области значений 100 < Ке < 400 кривые I и 3 достроены по формулам (1.46) и (1.47) соответственно, а для построения кривой 2 использована формула (1.50). На рисунках нанесены также экспериментальные точки для системы четыреххлористый углерод —вода (р, =1,01) по данным работы [32], [c.23]

    На рис. 3.6 дана зависимость относительных коэффициентов подачи т, напора к, к. п. д. п от относительной вязкости жидкости I (с известной погрешностью вязкость воды Vh прИНИМалаСЬ постоянной и равной Vh = М с). [c.53]

    Счетчики НОРД-М комплектуются электронным блоком НОРД-ЭЗМ и магнитоиндукционными датчиками Н0РД-И1У без предусилителя, Н0РД-И2У с предусилителем или электронными преобразователями (ЭП) и датчиками Дельта-2 . НОРД-ЭЗМ позволяет вводить только постоянное значение коэффициента преобразования в диапазоне расходов. Фактическое значение погрешности при этом зависит от диапазона расходов и вязкости продукта. При вязкости 20 мм /с она составляет 1-1,5 % в диапазоне расходов 20-100 %. Поэтому такие счетчики использовались в основном для оперативного учета нефти. [c.49]

    Основные функциональные возможности ПИК интегрирование по времени частотных сигналов ТПР не менее чем одновременно по шести каналам (включая ТПР в БКН) аппроксимация градуировочных характеристик до пяти ТПР во всем рабочем диапазоне в виде функции К = Ф [ у) или К = Ф(/) с погрешностью не более 0,05 %, где/-частота выходного сигнала ТПР V – вязкость жидкости преобразование частотного сигнала плотномера 8сЬ1ишЬег ег 7835 в цифровой код автоматическая коррекция коэффициента преобразования ТПР в соответс вии с функциональной зависимостью К = = Ф [ у) или К = Ф(/) ручной ввод с клавиатуры значений плотности, избыточного давления в БИЛ и в БКН, температуры нефти (там же), влагосодержания, содержания солей магния (мг/л), содержания примесей (%) массы для осуществления вычислений при отсутствии или выходе приборов из строя, а также для определения массы нефти нетто ручной ввод с клавиатуры уставок предельных значений (нижнего и верхнего уровня расхода по каждой измерительной линии, верхнего и нижнего значений избыточного давления в БИЛ, верхнего и нижнего значений температуры в БИЛ (катушке К ), верхнего и нижнего значений плотности, разницы показаний плотномеров, нижнего и верхнего уровня избыточного давления в БКН, перепада давлений на блоках фильтров, нижнего уровня расхода в БКН, нижнего уровня температуры жидкости, содержание газа в нефти) вычисление мгновенного и мгновенного суммарного расходов по каждой линии и по установке в целом, соответственно сравнение показаний параллельно работающих плотномеров и выдачу данных расхождения вычисление средних значений плотности (при текущей температуре и 20 °С), температуры, давления, влажности партии перекачиваемой нефти с начала текущей смены, двухчасовки, относительной погрешности вычисления суммарного объема, массы брутто нефти, объемного расхода – не более 0,05 %. [c.70]

    Градуировочная характеристика и характеристики погрешности ТПР, определенные при поверке, соответствуют только условиям поверки. При эксплуатации ТПР в условиях, отличных от условий поверки, или при изменении условий эксплуатации фактическое значение коэффициента ТПР будет отличаться от определенного при поверке. При этом возникают дополнительные систематические погрешности, которые при определенных условиях могут значительно превышать основную погрешность ТПР. Например, для ТПР типа Турбоквант изменение коэффициента преобразования (следовательно, возможна дополнительная погрешность) составляет 0,6-1,0 % на каждые 10 мм /с. Таков же порядок дополнительной погрешности для других ТПР, не снабженных устройствами компенсации влияния вязкости ( НОРД и др.). Поэтому дополнительные погрешности, обусловленные влиянием условий эксплуатации, должны быть исключены путем введения поправок в результаты измерений или другими методами. Наиболее полное исключение дополнительных погрешностей достигается поверкой ТПР на месте эксплуатации и обеспечением таких условий эксплуатации, при которых дополнительные погрешности не превышают установленных пределов. Всякая поверка в условиях, отличных от рабочих, особенно демонтаж ТПР и поверка его на стендах или других УУН, всегда сопровождается невыяв-ленными погрешностями. Наиболее существенными и трудно поддающимися нормированию и контролю являются изменение коэффициента преобразования ТПР от влияния вязкости и изменение его во времени. Трудность определения функции влияния вязкости на коэффициент преобразования ТПР вызвана двумя причинами  [c.105]

    Моделирование на основе приведенной зависимости является приближенным. Однако погрешность, возникающая за счет пренебрежения влиянием критерия Fr, невелика и приемлема для технических целей. В рассматриваемом случае задача экспериментального исследования сводится к установлению для объектов заданной формы (Г/= onst) явного вида зависимости Eu = /(Re). Такое исследование на модели можно проводить с той же жидкостью, что и в прототипе, изменяя соответственно скорость. Для моделирования необходимо равенство значений Re и Г , относящихся к образцу и модели. Из равенства значений Re вытекает условие, что поля скоростей в образце и модели должны быть связаны соотношением w jw” = t”v )l l v”). Следовательно, вязкости жидкостей, используемых в образце и модели, и скорости их движения должны находиться в определенных соотношениях, зависящих от размеров образца и модели. Если модель является 0,01 частью натуры [I jl” — 100), то при одинаковых скоростях w — w кинематический коэффициент вязкости жидкости в модели должен быть в 100 раз меньше, чем в образце, а при использовании одной и той же жидкости (v =v”) скорость в модели должна быть в 100 раз больше, чем в образце. Такие условия не всегда могут быть выполнены точно, поэтому часто моделирование является приближенным. [c.75]

    Точность расчета по последнему уравнению того же порядка, что и по уравнению (У11-24) (средняя погрешность равна 4,47о)-Подобную формулу вывел также Гамбилл [20]. Однако другие уравнения для расчета динамического коэффициента вязкости, например (УИ-ЗО) и (УИ-31), удобнее и по точности не уступают формулам Шейбеля или Гамбилла. [c.230]

    Будденберг и Уилк применили формулу (УП-89) для определения вязкости многокомпонентной смеси. При этом в состав знаменателей слагаемых отдельных компонентов расширенного уравнения входили коэффициенты диффузии Dj, 2, 3, Do, , D2, з, D2,i и т. д. Расширенная формула тоже дает хорошие результаты [60]. Например, авторы вычислили вязкость смеси, содержащей (в мольных долях) СО2 — 0,104 СО — 0,285 Пг — 0,016 N2 — 0,595. Вычисленная вязкость смеси была равна 171,8 мкпз (экспериментально найдено 173,8 мкпз). Погрешность расчета составляла—1,1%- [c.266]

    Рид И Шервуд [4] приводят другие расчеты, когда для 36 жидкостей (при 128 температурах) средняя погрешность была равна 217о, а максимальная 90% (спирты, кислоты). При вычислении коэффициента вязкости ароматических (за исключением бензола) моногалогенпроизводных, углеводородов с большими молекулами (предельных углеводородов нормального строения) и эфиров ио-грешность была меньше 157о- Гамбилл [39] считает метод Томаса наиболее универсальным и точным методом аддитивного расчета вязкости, когда неизвестно ни одного экспериментального значения ц. [c.306]

    Коэффициент расхода для решетки С является функцией числа Рейнольдса для решетки Re= Do.puplaii (где />о.р—характерный линейный размер отверстия решетки, м р — плотность среды, кг м ц — вязкость среды, н-сек м ). Для решеток с прямоугольной сеткой на Т)ис. П-41 приведена кривая зависимости С от Re. Погрешность результатов, получаемых по кривой, находится в пределах 20%. Значения С>1 указывают на то, что происходит частичное [c.155]

    Хотя погрешность определения вязкости методом катящегося шарика и оценивается авторами, применившими его, йорядка 5—6%, все же следует отметить, что достаточно точных значений коэффициентов вязкости для газообразного состояния этим методом пока получить не удалось. На это указывают, во-первых, большой разброс экспериментальных точек у каждого исследователя, во-вторых, значительные расхождения в данных различных исследователей, работавших по этому методу и, в-третьих, большие расхождения со значениями, полученными наиболее надежным и точным в настоящее время методом капилляра. [c.27]

    Кестин и соавторы получили очень хорошую воспроизводимость измерений (в среднем 0,05%), которую и приняли за основу при оценке погрешности коэффициентов вязкости. Однако, как известно, в.оспронзводимость определяет собой [c.34]

    Величина коэффициента динамической вязкости в каждом случае относится к определенному состоянию исследуемого вещества (температуре и давлению). И хотя температура и давление не входят в расчетное уравнение, тем не менее погрешность их измерения, называемая погрешностью отнесения, влияет на точность определения коэффициейта вязкости. Максимальная относительная погрешность при этом определится  [c.66]

    Преимущество метода пористого электрода состоит в чрезвычайной простоте способа введения анализируемого раствора в источник излучения. При благоприятных условиях [4] можно достичь относительной погрешности 2—4%, а иногда даже еще лучшей. Например, магний в литейном железе определяли в интервале концентраций 0,01—0,16% [9] с коэффициентом вариации 1,8%. Фракционирование в пористом электроде-чашке наблюдалось только при высоких концентрациях. Это ограничение не являлось единственным при выборе внутреннего стандарта. Раствор не должен содержать взвешенных частиц. Однако значительно труднее поддерживать постоянную скорость просачивания раствора через электрод, поскольку она сильно зависит от качества и постоянства пористости угля, а также от вязкости раствора. Кроме того, необходимо исключить опасность загрязнения за счет элект-рододержателя, так как раствор просачивается и через боковые стенки электрода. Поэтому электрододержатели должны быть покрыты защитной пленкой из золота или платины. Другой метод защиты — применение соответствующих покрытий из лака на боковых стенках электродов. [c.161]

    Но если теплота и работа диссоциации вычисляются из констант, отягощенных внетермодинамическими допущениями, то и сами эти величины будут содержать систематические погрешности. Поэтому в справочнике не приводятся значения термодинамических функций процесса ассоциации. В разделе 7 помещены только величины Ка, Хо и а, а в разделе 6 — коэффициенты вязкости, которые могут понадобиться для расчета констант. [c.16]

    Погрешности расчета по формуле (2.19) в среднем такие же, как по описанным выше формулам. При расчете вязкости по методу Андруссова необходима предварительная обработка экспериментальных данных по вязкости методами регрессионного анализа для получения необходимых коэффициентов, что затрудняет широкое применение метода. Погрешности расчета по методу Дина и Стила [формула (2.20)] при Г/7п. кр 1,5 больше, чем по формулам (2.17), (2.18) и (2.19). Погрешности увеличиваются при расчете вязкости смесей с полярными газами. По методу Дина и Стила [формула (2.21)] при Г/Гп. кр> 1,5 получаются малые погрешности для некоторых смесей. Для смесей с водородом и некоторыми полярными газами погрешности расчета вязкости возрастают. [c.28]

    Максимальная погрешность аппроксимации в узловых точках 6мах<0,2%. Коэффициент вязкости газообразного хлора ЦС1, (О при нормальном давлении принят по [112] в Па-с  [c.140]

Источник

Добавить комментарий