Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
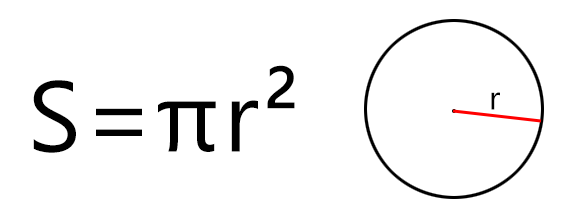
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d – диаметр, а π – константа, равная 3,1415…):
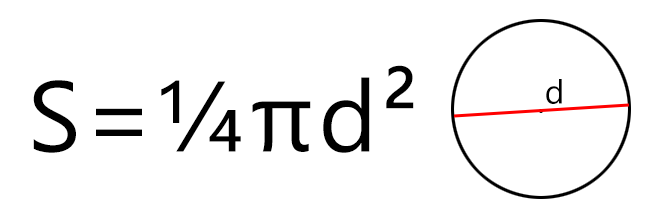
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L – длина окружности, а π – константа, равная 3,1415…):
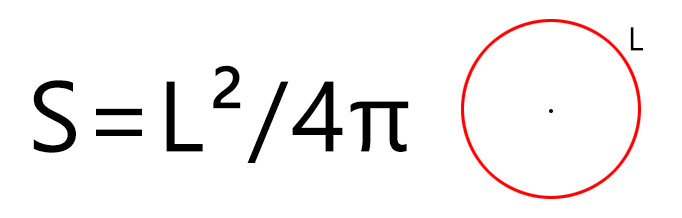
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
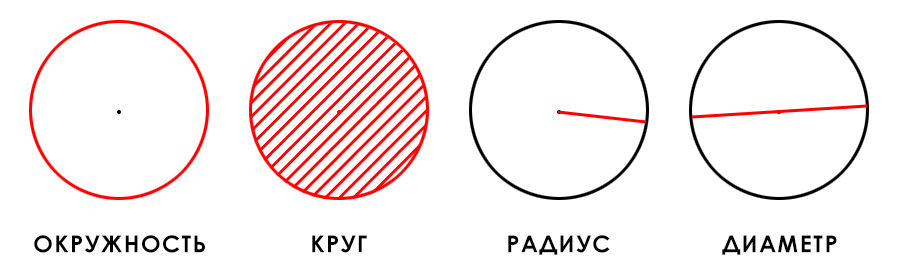
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:

Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
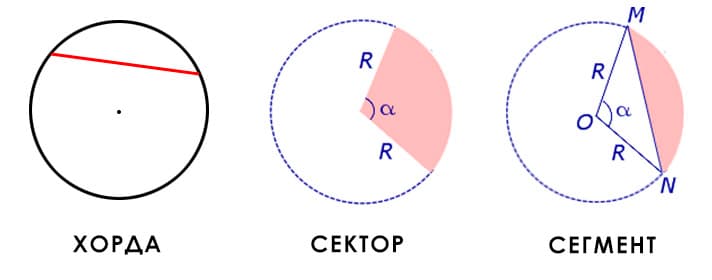
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Площадь круга через Диаметр
S – площадь круга,
d – диаметр круга,
π ≈ 3,141592653589
Площадь круга через Радиус
S – площадь круга,
r – радиус круга,
π ≈ 3,141592653589
Площадь круга через Длину Окружности
S – площадь круга,
l – длина окружности,
π ≈ 3,141592653589
Определения и термины
Круг – множество точек плоскости, расстояние до которых от данной точки (центра круга) не превышает заданного расстояния (радиуса круга).
Радиус круга – отрезок, соединяющий центр круга с любой точкой, которая лежит на внешней окружности круг
Диаметр круга – отрезок, соединяющий любые две точки, лежащие на внешней окружности круга, и проходящий через центр круга
Окружность – замкнутая плоская кривая состоящия из всех точек полскости равноудаленных от заданной точки (центра окружности)
Число Пи (π) – математическая константа, которая выражает отношение длины окружности к её диаметру.
Равно приблизительно 3,141592653589…
Площадь окружности
Окружность, по своей сути, является границей круга – замкнутой плоской кривой. Из определения следует, что площади окружности не существует,
а существует Площадь круга.
На странице собраны калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного многоугольника по стороне и количеству сторон, а также зная радиус вписанной и описанной окружностей.
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Содержание:
- калькулятор площади правильного многоугольника
- формула площади правильного многоугольника через длину стороны
- формула площади правильного многоугольника радиус вписанной окружности
- формула площади правильного многоугольника радиус описанной окружности
- пример задачи
Формула площади правильного многоугольника через длину стороны и число сторон
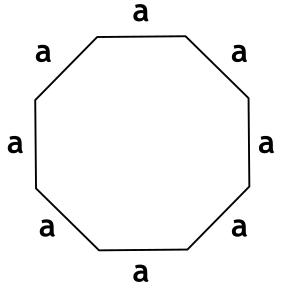
S = dfrac{na^2}{4} cdot ctg dfrac{180°}{n}
a – длина стороны многоугольника
n – число сторон многоугольника
Формула площади правильного многоугольника через радиус вписанной окружности
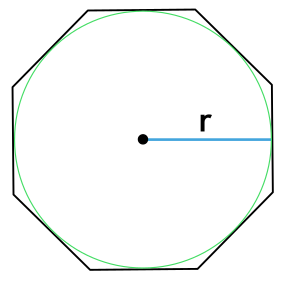
S = nr^2 tg dfrac{180°}{n}
r – радиус вписанной в многоугольник окружности
n – число сторон многоугольника
Формула площади правильного многоугольника через радиус описанной окружности

S = dfrac{nR^2}{2} cdot sin dfrac{360°}{n}
R – радиус описанной в многоугольник окружности
n – число сторон многоугольника
Пример задачи на нахождение площади правильного многоугольника
Задача 1
Найдите площадь правильного n-угольника, если n = 6, r = 9 см, где r – радиус вписанной окружности.
Решение
Чтобы решить эту задачу мы используем вторую формулу.
S = nr^2 tg dfrac{180°}{n} = 6 cdot 9^2 cdot tg dfrac{180°}{6} = 6 cdot 81 cdot tg 30° = 486 cdot tg 30° = 486 cdot 0.57735027 approx 280.59223 : см^2
Ответ: 486 cdot tg 30° approx 280.59223 : см^2
Чтобы проверить ответ воспользуемся калькулятором .
Круг – это геометрическая фигура; множество точек на плоскости, которые лежат внутри окружности.
-
Формула вычисления площади
- По радиусу
- По диаметру
- Примеры задач
Формула вычисления площади
По радиусу
Площадь круга (S) равняется произведению числа π и квадрата его радиуса.
S = π ⋅ r 2
Радиус круга (r) – это отрезок, соединяющий его центр и любую точку на окружности.

Примечание: для расчетов значение числа π округляется до 3,14.
По диаметру
Площадь круга равняется одной четвертой произведения числа π и квадрата его диаметра:


Диаметр круга (d) равняется двум радиусам (d = 2r). Это отрезок, который соединяет две противоположные точки на окружности.
Примеры задач
Задание 1
Найдите площадь круга, радиус которого равен 9 см.
Решение:
Используем формулу, в которой задействован радиус:
S = 3,14 ⋅ (9 см)2 = 254,34 см2.
Задание 2
Найдите площадь круга, диаметр которого равняется 8 см.
Решение:
Применим формулу, в которой фигурирует диаметр:
S = 1/4 ⋅ 3,14 ⋅ (8 см)2 = 50,24 см2.
|
Как найти площадь круга?С помощью какой формулы можно найти площадь круга?
Две шутливые запоминалки. Одну, как учитель математики я часто рассказывала ученикам. Анекдот. Вопрос.
Второй вариант – метод от противного. Произведение знаменитого пародиста Иванова. « – Площадь круга, площадь круга?
(ЦПР – церковно приходская школа). Так как Иванов пародировал очередного «умника», то формула «2 пи эр» не правильная – это ДЛИНА окружности, а ПЛОЩАДЬ круга – это «пи эр квадрат». К слову, число пи можно тоже запомнить стишком. «Надо только постараться и запомнить все как есть Три, четырнадцать пятнадцать девяносто два и шесть». Вывод. Площадь круга это произведение числа пи и радиуса круга эр возведенного в квадрат. автор вопроса выбрал этот ответ лучшим
Алексис 11 лет назад Длину радиуса (половина диаметра) возвести в квадрат (перемножить на себя) и умножить на магическое число пи (оно равно 3,14), получится площадь круга в квадратных единицах, в которых Вы задали радиус.
Площадь круга находится по формуле: S = П * R2, где S – площадь определяемого вами круга, П – число «пи», константа равная примерно 3,1415 R – радиус круга, в котором вы определяете радиус Если вам, например нужно определить площадь круга имея диаметр, то вышеизложенная формула будет иметь вид: S = П * D2/4, где S – площадь определяемого вами круга, П – число «пи», константа равная примерно 3,14 D – диаметр круга, в котором вы определяете радиус elena-kh 10 лет назад Площадь круга можно найти. Из курса геометрии, насколько я помню, ищут ее через радиус. Радиус – это половина диаметра круга. Его Вы можете найти, проведя линию от центра круга до любой грани круга. Радиус в квадрате умножьте на “пи”. Площадь круга измеряется в квадратных метрах, сантиметрах, миллиметрах и т.д. На самом деле, это очень простая формула, которую знают многие ещё со школы. Звучит она так: площадь круга равна произведению числа П на радиус в квадрате. То есть для вычисления площади круга необходимо знать только радиус фигуры, ведь число П всегда нам известно.
Блондинка 10 лет назад
Для тех, кто обычно забывает площадь круга (стыдно, но я именно к таким отношусь). Тогда когда нужно быстро узнать значение чуть меньше площади квадрата. Так же как вариант площадь круга равна “Пи” умноженное на диаметр возведенный в квадрат, деленное на четыре.
alexey92719 9 лет назад Площадь круга равна произведению полуокружности на радиус .S=? r2 Равные отрезки , соединяющие центр с точками окружности , называются центром окружности .Окружность есть геометрическое место точек плоскости , равноудалённых от точек плоскости.
Площадь круга вычисляется по формуле S= П*R*R. А именно радиус в квадрате умножен на число пи, которое ровняется 3,1415. Так-же вместо радиуса можно подставить диаметр, тогда будет произведение пи на диаметр в квадрате деленное на четыре. chela 10 лет назад Как найти площадь круга если радиус и диаметр не известны? Найдем площадь круга, если известна длина его окружности: S=L(в квадрате)/4пи, где L длина окружности Длина окружности в квадрате, разделенная на четыре пи, будет площадью круга. Площадь круга находят по следующей формуле.
Где S- это площадь, n-число пи=3,1415…(отношение длины окружности к ее диаметру, величина которая остается постоянной), г – радиус, D – диаметр. Вывод этой формулы показан на видео. Видео.
Galina7v7 7 лет назад Площадь круга всегда найдём,если знаем только один параметр круга ,или окружности: его радиус R.Тогда площадь круга Sкр. S кр.= pi*R^2=3,14*R^2.А так как радиус окружности равен половине его диаметра,то ` Sкр.=3,14 *d^2/4.
gematogen 9 лет назад Площадь круга равна Пи(r*r) Пи-это не изменяемое число которое равно 22/7 или если записать десятичной дробью то это 3.1415…. r-это радиус окружности. Пиэрквадрат (по-простому).S=ПR*R (учебник в мое время, вроде 5-го класса) Знаете ответ? |



