Необходимо построить развертку поверхностей и перенести линию пересечения поверхностей на развертку. В основе данной задачи рассматриваются поверхности (конуса и цилиндра) с их линией пересечения, приведенные в предыдущей задаче 8.
Для решения таких задач по начертательной геометрии необходимо знать:
— порядок и методы построения разверток поверхностей;
— взаимное соответствие между поверхностью и ее разверткой;
— частные случаи построения разверток.
Порядок решения задачи
1. Отметим, что разверткой называется фигура, получаемая в
результате разреза поверхности по какой-либо образующей и постепенного разгибания ее до полного совмещения с плоскостью. Отсюда развертка, прямого кругового конуса — сектор с радиусом, равным длине образующей, и основанием, равным длине окружности основания конуса. Все развертки строятся только из натуральных величин.
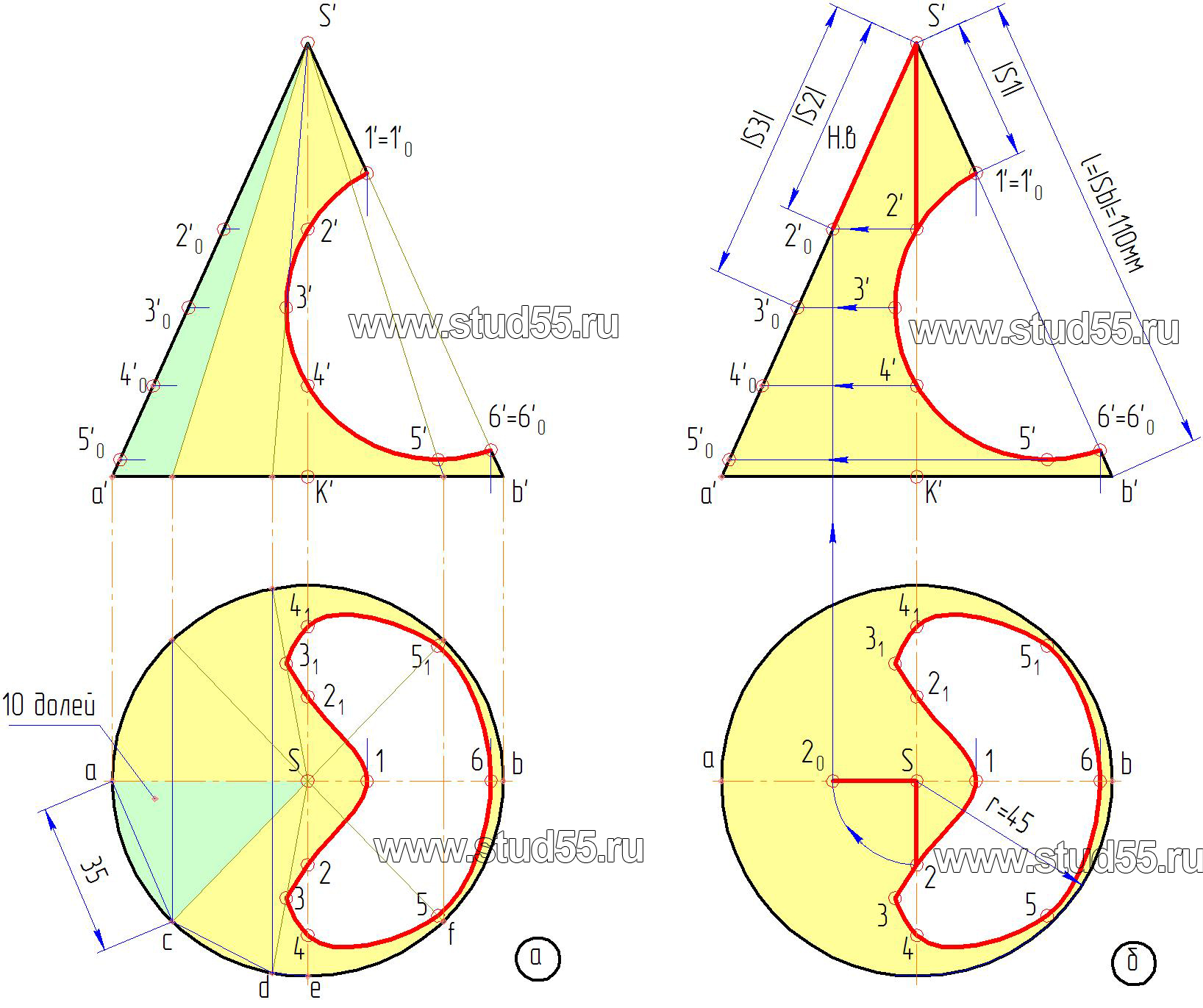
Рис.9.1
— длину окружности основания конуса, выраженную в натуральной величине делим на ряд долей: в нашем случае — 10, от количества долей зависит точность построения развертки (рис.9.1.а);
— откладываем полученные доли, заменяя их хордами, на длине
дуги, проведенной радиусом, равным длине образующей конуса l=|Sb|. Начало и конец отсчета долей соединяем с вершиной сектора — это и будет развертка боковой поверхности конуса.
Второй способ:
— строим сектор с радиусом, равным длине образующей конуса.
Заметим, что как в первом, так и во втором случае за радиус берется крайняя правая или левая образующие конуса l=|Sb|, т.к. они выражены в натуральной величине;
— при вершине сектора откладываем угол а, определяемый по формуле:

Рис.9.2
где r — величина радиуса основания конуса;
l — длина образующей конуса;
360 — постоянная переводная в градусы величина.
К сектору-развертке строим основание конуса радиуса r.
2. По условиям задачи требуется перенести линию пересечения
поверхностей конуса и цилиндра на развертку. Для этого используем свойства взаимной однозначности между поверхностью и ее разверткой, в частности, отметим, что каждой точке на поверхности соответствует точка на развертке и каждой линии на поверхности соответствует линия на развертке.
Отсюда вытекает последовательность перенесения точек и линий
с поверхности на развертку.
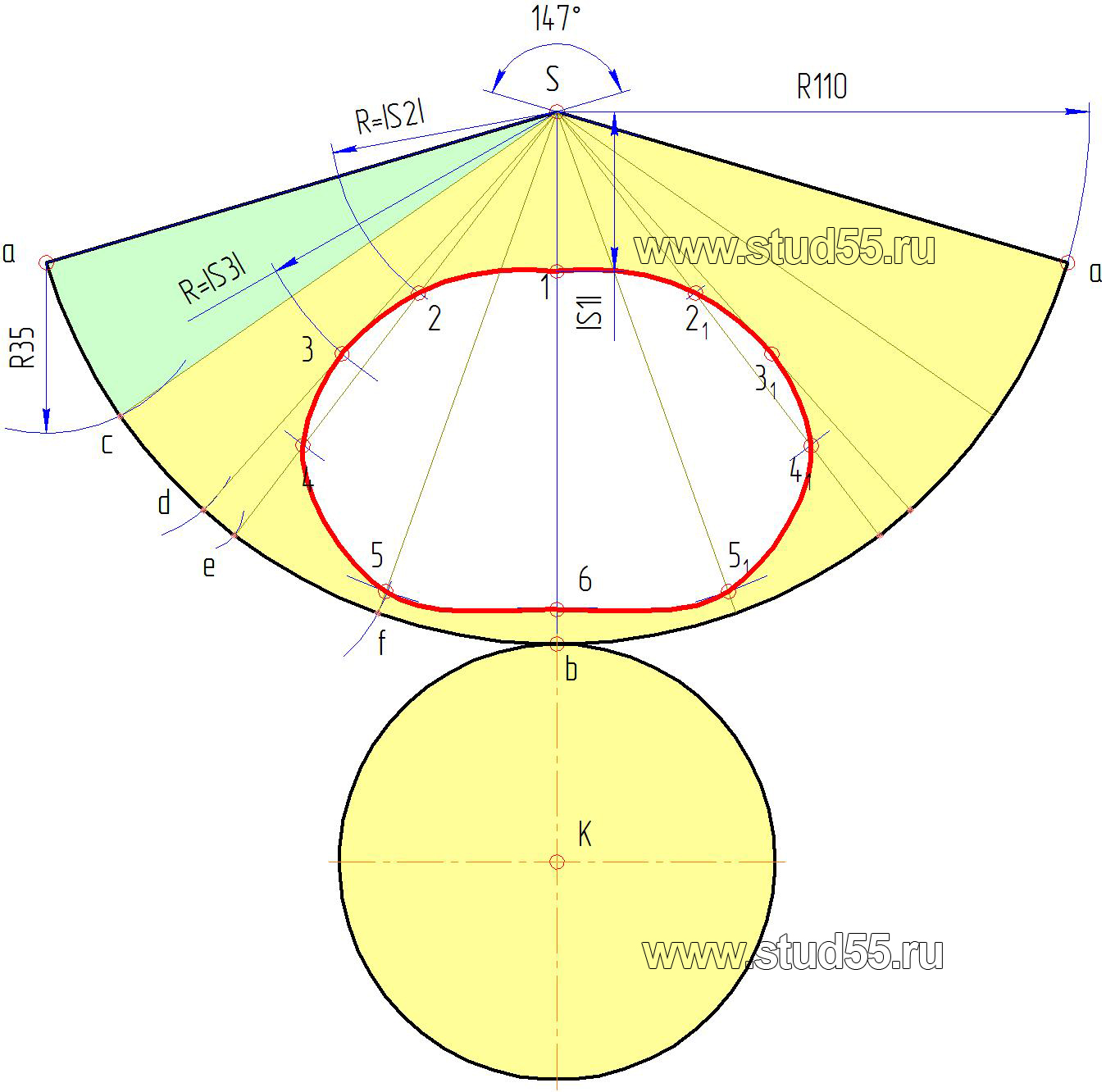
Рис.9.3
Для развертки конуса. Условимся, что разрез поверхности конуса произведен по образующей S’a’. Тогда точки 1, 2, 3,…6
будут лежать на окружностях (дугах на развертке) с радиусами соответственно равными величинам расстояний, взятым по образующей S’A’ от вершины S’ до соответствующей секущей плоскости с точками 1’, 2’, 3’…6’ -|S1|, |S2|, |S3|….|S6| (рис.9.1.б).
Положение точек на этих дугах определяется расстоянием, взятым с горизонтальной проекции от образующей Sa, по хорде до соответствующей точки, например до точки с, ас=35 мм (рис.9.1.а). Если расстояние по хорде и дуге сильно разнятся, то для уменьшения погрешности можно разделить большее количество долей и отложить их на соответствующие дуги развертки. Таким способом переносятся любые точки с поверхности на ее развертку. Полученные точки соединятся плавной кривой по лекалу (рис.9.3).
Для развертки цилиндра.
Развертка цилиндра есть прямоугольник с высотой, равной высоте образующей, и длиной, равной длине окружности основания цилиндра. Таким образом, для построения развертки прямого кругового цилиндра необходимо построить прямоугольник с высотой, равной высоте цилиндра, в нашем случае 100мм, и длиной, равной длине окружности основания цилиндра, определенной по известным формулам: C=2R=220мм, или делением окружности основания на ряд долей, как было указано выше. К верхней и нижней части полученной развертки пристраиваем основание цилиндра.
Условимся, что разрез произведен по образующей AA1 (A’A’1; AA1). Заметим, что разрез следует производить по характерным (опорным) точкам для более удобного построения. Учитывая, что длина развертки есть длина окружности основания цилиндра C, от точки A’=A’1 разреза фронтальной проекции берем расстояние по хорде (если расстояние большое, то необходимо его разделить на доли) до точки B’ (в нашем примере — 17мм) и откладываем его на развертке (по длине основания цилиндра) от точки А. Из полученной точки В проводим перпендикуляр (образующую цилиндра). Точка 1 должна находиться на этом перпендикуляре) на расстоянии от основания, взятого с горизонтальной проекции до точки. В нашем случае точка 1 лежит на оси симметрии развертки на расстоянии 100/2=50мм (рис.9.4).
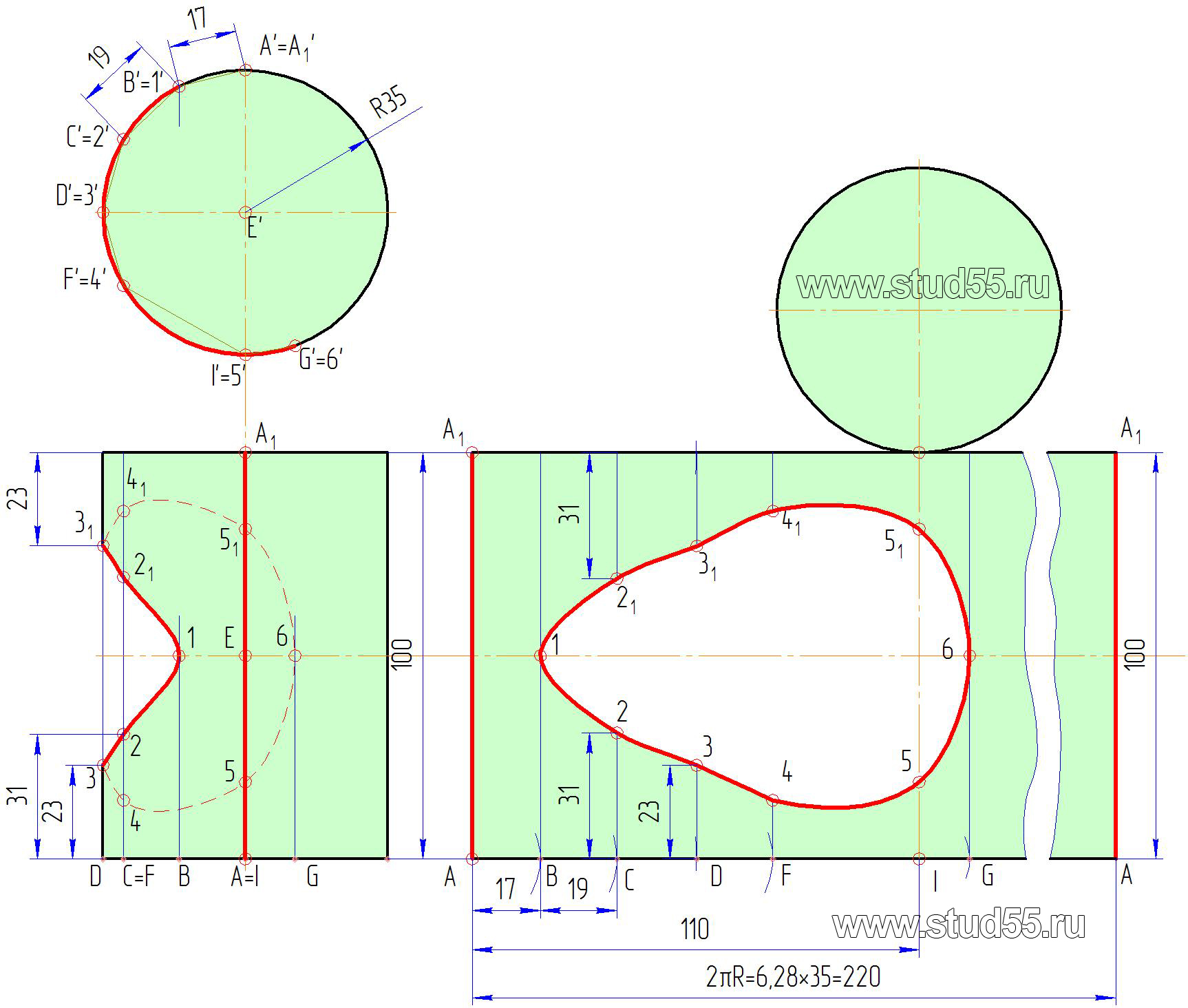
Рис.9.4
И так поступаем для нахождения на развертке всех других точек.
Подчеркнем, что расстояние по длине развертки для определения положения точек берется с фронтальной проекции, а расстояние по высоте — с горизонтальной, что соответствует их натуральным величинам. Полученные точки соединяем плавной кривой по лекалу (рис.9.4).
В вариантах задач, когда линия пересечения распадается на несколько ветвей, что соответствует полному пересечению поверхностей, способы построения (перенесения) линии пересечения на развертку аналогичны, описанным выше.
Раздел: Начертательная геометрия /
- Рекомендуем
- Комментарии
- Наши товары
Боковая поверхность
цилиндра представляет собой прямоугольник
со сторонами Н и πD. Основания цилиндра
на горизонтальной плоскости проекций
изображаются в натуральную величину.
Для построения развертки цилиндра
(рисунок 22) нужно на свободном поле
чертежа провести две параллельные
прямые, расстояние между ними равно
высоте цилиндра – Н.
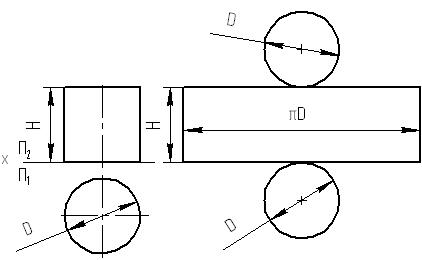
Рисунок 22
На этих прямых от
произвольно выбранной точки отложить
расстояние, равное длине окружности –
πD. Построенный прямоугольник является
разверткой боковой поверхности цилиндра.
Остается пристроить окружности –
основания цилиндра.
Если на фигуру
развертки необходимо нанести линию
пересечения, то лучше воспользоваться
вторым способом (рисунок 23).
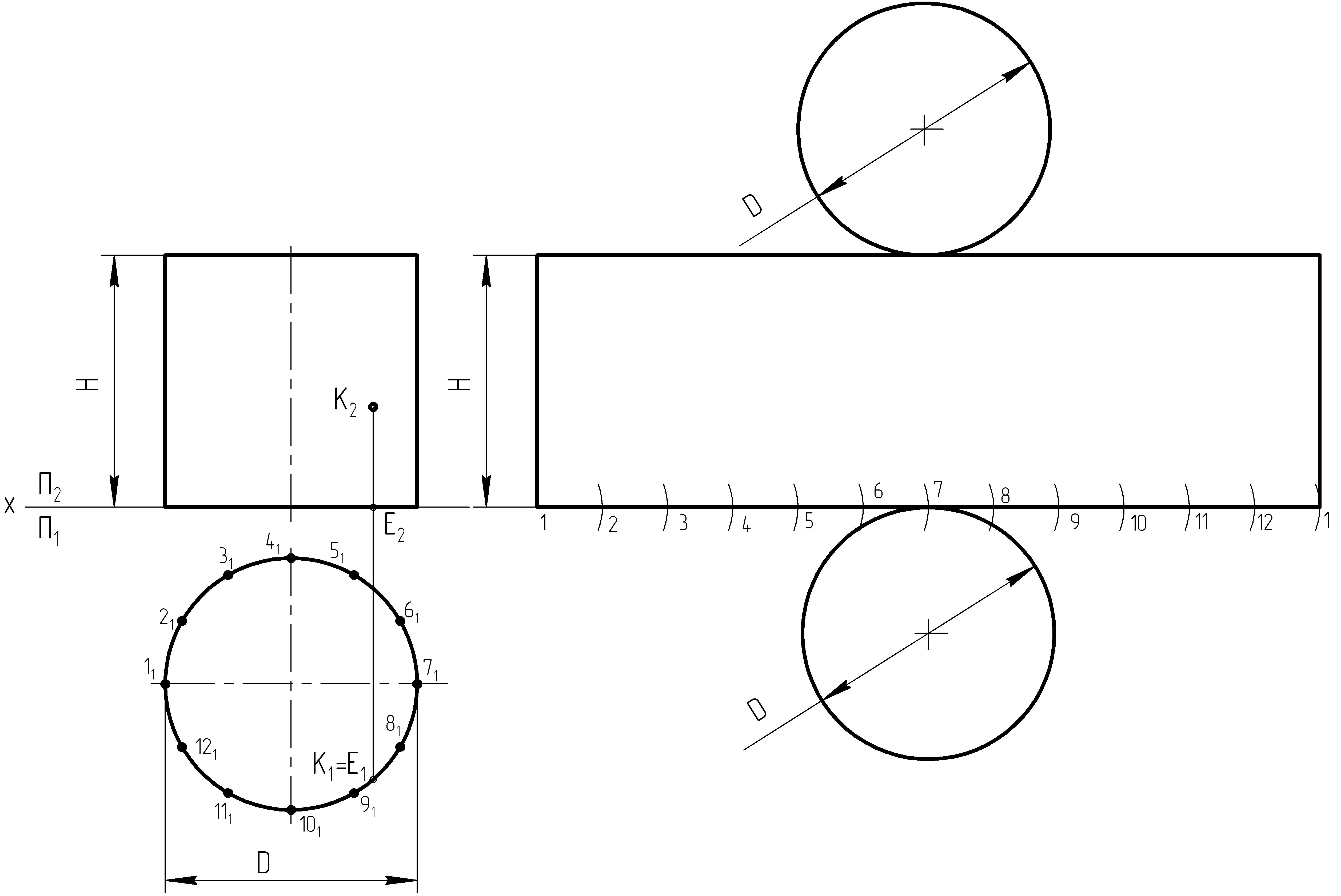
Рисунок 23
Разделим основание
цилиндра на 12 частей, как показано на
рисунке 18, затем на свободном поле
чертежа проведем две параллельные
прямые, расстояние между которыми равно
высоте цилиндра. На одной из прямых
отложим с помощью циркуля 12 раз 1/12 часть
окружности, построили контур развертки
боковой поверхности цилиндра. Как
построить основания ясно из рисунка.
На
развертке цилиндра найдем положение
точки К (рисунок 24). Для этого циркулем
измерим расстояние от т.81
(или 91)
до т.Е1,
затем на развертке найдем т.8 (или т.9) и
из нее как из центра проведем дугу
радиусом равным измеренному расстоянию,
получим т.Е. Далее через т.Е нужно провести
образующую, на которой отложить расстояние
|Е2К2|,
искомая точка К построена.
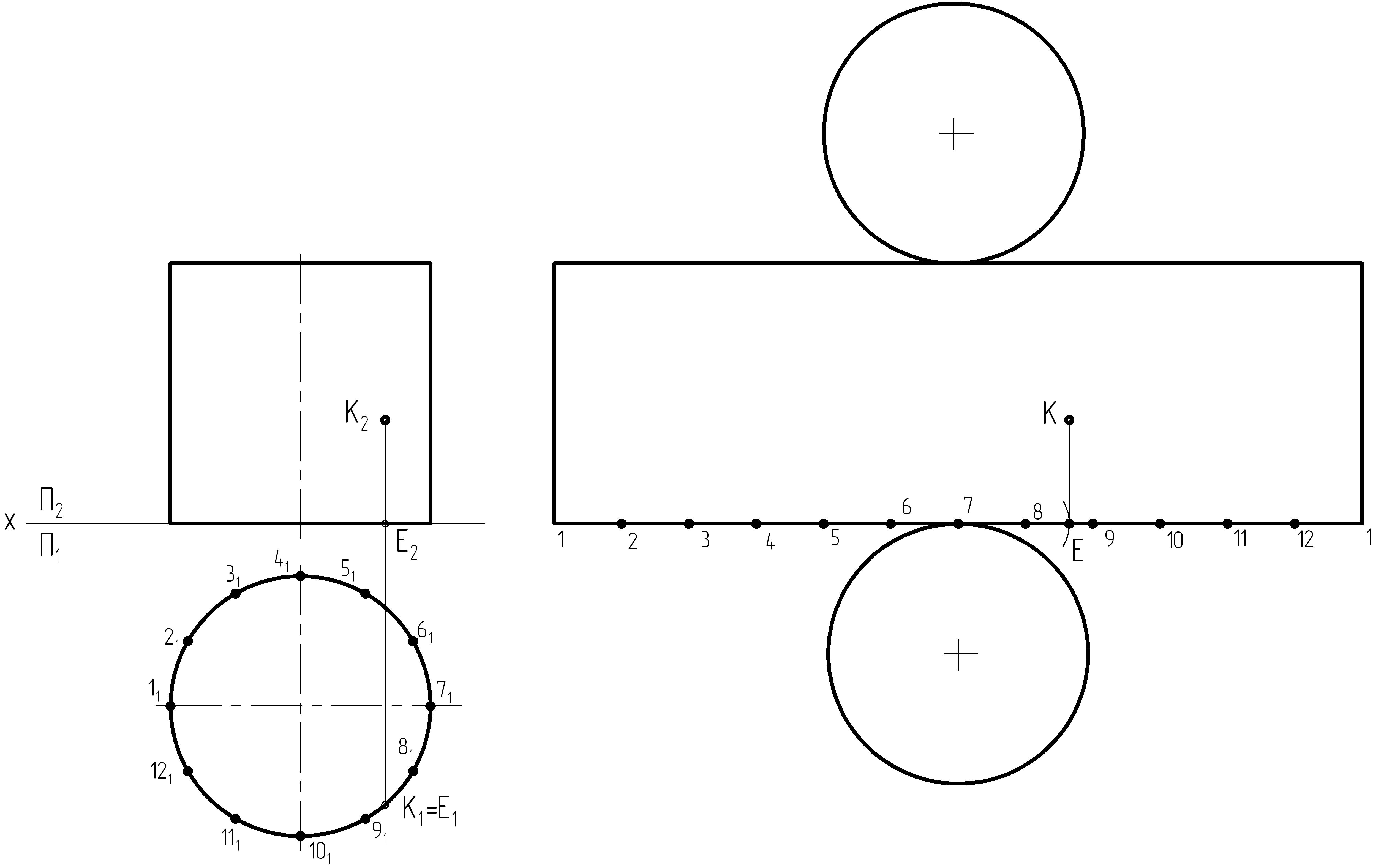
Рисунок 24
ПРИЛОЖЕНИЕ
3
Формы основной надписи для оформления графических работ
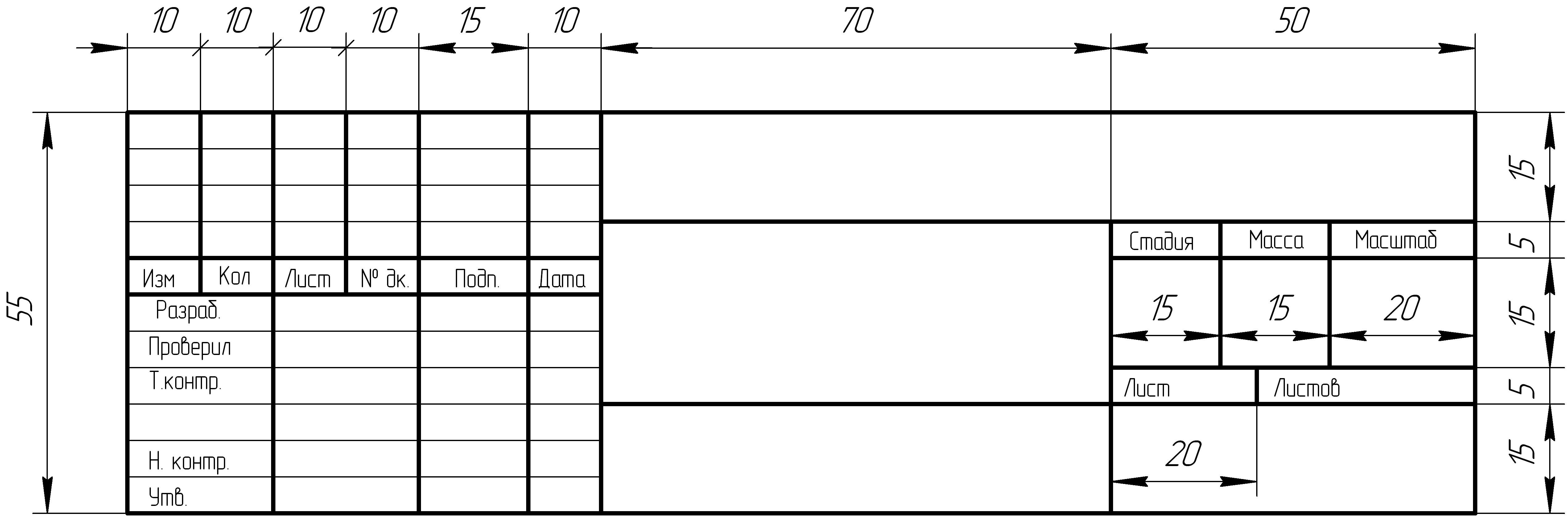
Основная
надпись для оформления графических
работ (факультет ПГС)

Основная
надпись для оформления графических
работ (факультет МСХ)
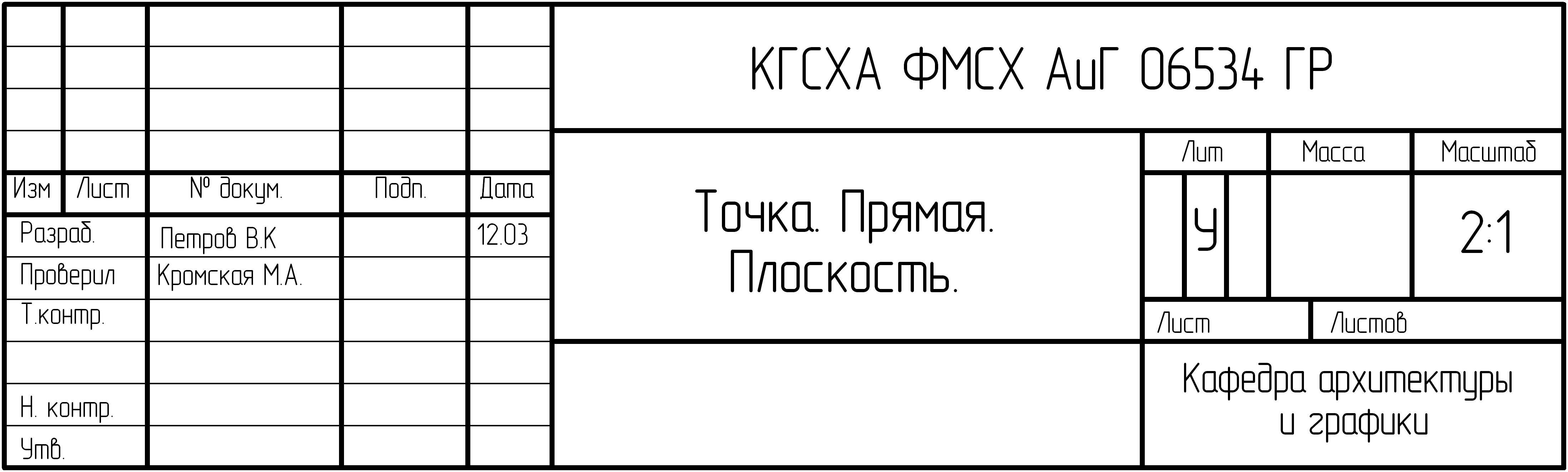
Пример
заполнения основной надписи (факультет
МСХ)
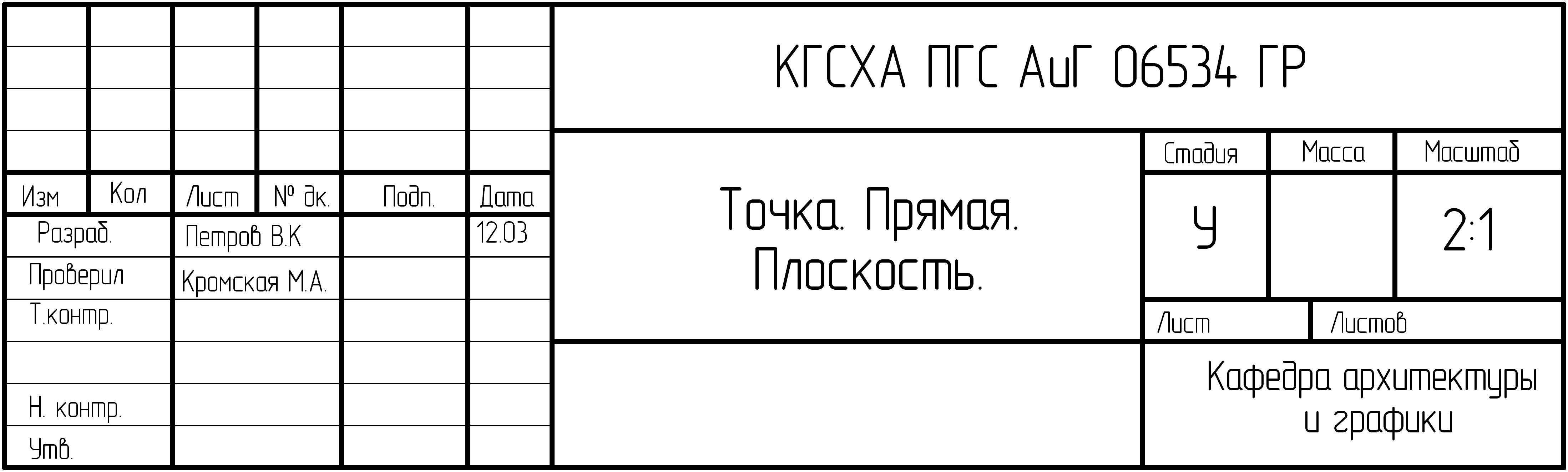
Пример
заполнения основной надписи (факультет
ПГС)
ПРИЛОЖЕНИЕ
4
Общие правила оформления чертежей Форматы (гост 2.301 – 68*)
Данный
ГОСТ устанавливает пять основных
форматов:
А4
210 х 297 А2
420 х 594
А0
841 х 1189
А3
297 х 420 А1
594 х 841
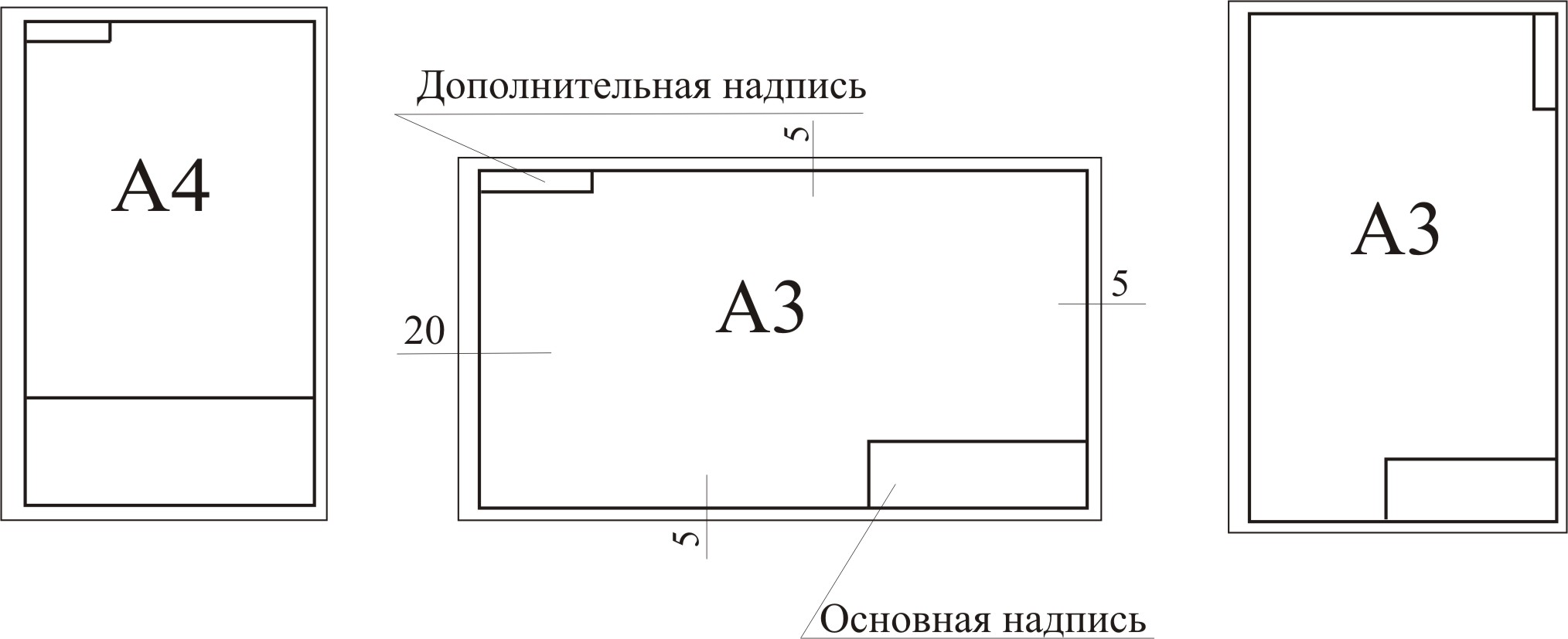
При
оформлении чертежа следует помнить:
-
Формат
А4 располагается только
вертикально, остальные
могут располагаться как вертикально
так и горизонтально; -
Рамка основной
надписи выполняется сплошной основной
линий (от левого края формата отступается
20 мм (поле для подшивки), с других сторон
по 5 мм).
Масштабы (гост 2.302 – 68*)
Детали на
чертеже в зависимости от их сложности
и размеров могут изображаться в
натуральную величину либо с увеличением
или уменьшением.
Масштабом
называется отношение линейных размеров
изделия на чертеже к его действительным
размерам.
Масштабы:
▪ уменьшения 1:2 1:2,5 1:4 1:5 1:10 1:15 1:20
1:25 1:40 1: 50 и т.д.
▪ натуральный
1:1
▪ увеличения
2:1 2,5:1 4:1 5:1 10:1 15:1 20:1 25:1 40:1 50:1 и
т.д.
Замечания:
▪ угловые размеры при масштабировании
не изменяются;
▪ какой
бы ни был масштаб, размеры наносятся
действительные;
▪ масштаб
изображения, отличающийся от указанного
в основной надписи, указывают в скобках
рядом с обозначением. Например:
А (2:1) В
– В (1:4)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Оцените запись
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Развертка прямого кругового цилиндра.
Цилиндр диаметром D и высотой H показан на рис. 1. Развертка представляет собой прямоугольник длиной с = πD и высотой Н.
Прямой круговой цилиндр, усеченный плоскостью, параллельной его оси, показан на рис. 2. Развертка представляет собой прямоугольник высотой Н и длиной L = b + k, где b = πDᵠ/360° и k = 2 √((D/2)2 – a2) = 2a tg (ᵠ/2).
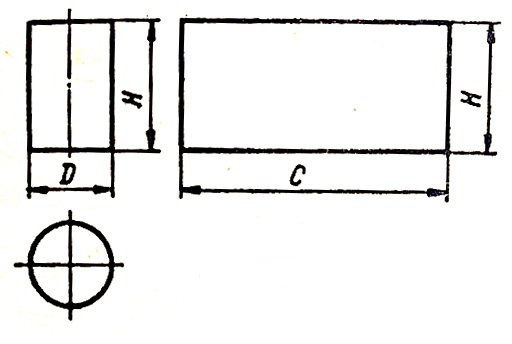
Рис. 1.
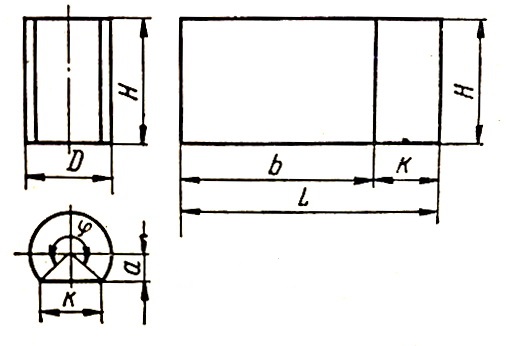
Рис. 2.
Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
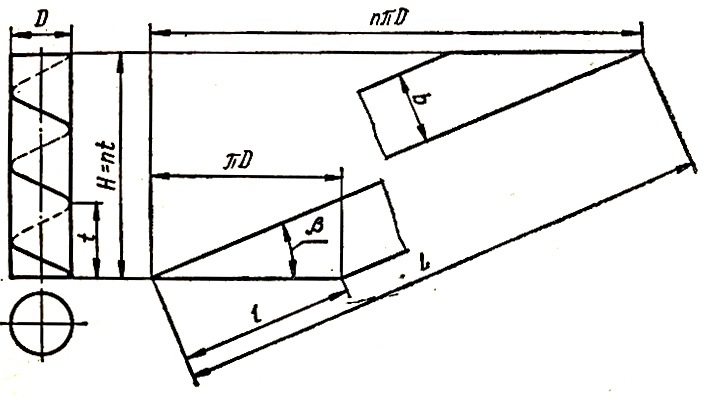
Рис. 3.
Цилиндр показан на рис. 3. При определении развертки можно использовать следующие зависимости:
где
D — диаметр цилиндра;
t — шаг винтовой линии;
n — число полных витков на общей длине цилиндра H, Н = nt;
b — ширина ленты;
L — общая длина ленты;
I — длина скоса.
Развертка усеченного цилиндра.
Цилиндр показан на рис. 4.

Рис. 4.
Для получения развертки горизонтальная проекция цилиндра делится на равные части и точки деления нумеруются (в данном случае от 0 до 12). Из точек деления проводятся вертикали до пересечения верхнего основания в точках 0′1, 1′1…, 6′1. На продолжении прямой 0’6′ откладывается отрезок длиной с = πD, который делится на принятое число равных частей. Из точек деления 00, 10, …, 60 строятся перпендикуляры до их пересечения с соответствующими горизонтальными линиями в точках 001, 101, …, 601. Полученные точки соединяются плавной кривой. Ввиду симметричности остальные точки кривой находит аналогичным путем.
Линию развертки можно определить и таким способом. На расстоянии h1 = (h + H)/2 от линии 00120 проводится параллельная прямая. Из центра S, лежащего на прямой, описывается полуокружность радиусом А. Полуокружность делится на равные части, число которых равно половине точек деления развертки (в данном случае на шесть). Через точки деления 0ꞋꞋ, 1ꞋꞋ, …, 6ꞋꞋ проводятся горизонтальные прямые до пересечения вертикалей, проходящих через 00, 10, … , 120. Полученные точки 001, 101, …, 1201 соединяются плавной кривой.
Верхнее основание цилиндра представляет собой эллипс с полуосями a = D/2 cos α = 0′13′1 и b = D/2.

Рис. 5.
При аналитическом определении координат точек кривой развертки цилиндра, усеченного плоскостью под углом α (рис. 5), могут быть использованы следующие зависимости:
xk = kx1 = πD/2 kε/180°; yk = D/2 tg α sin kε = A sin kε = A sin ᵠi,
где х1 = πD/ (2n) = πD/2 ε/180° — длина дуги окружности основания цилиндра, разделенная на 2n равных частей; ε = 360°/2n — центральный угол, соответствующий одному делению; k — порядковый номер точки; A = (H — h)/2 = (D/2) tg α — амплитуда синусоиды; ᵠi= kε.
Значения sin kε для наиболее часто употребляемых значений 2n приведены в табл. 1.
Таблица 1. Значения sin kε и sin2 kε
| 2n | sin kε | sin2 kε | 2n | sin kε | sin2 kε | ||||||
| 8 | 16 | 32 | 64 | 12 | 24 | 48 | 96 | ||||
| — | — | — | 1 | 0,09802 | 0,00961 | — | — | — | 1 | 0,06540 | 0,00428 |
| — | — | 1 | 2 | 0,19509 | 0,03806 | — | — | 1 | 2 | 0,13053 | 0,01704 |
| — | — | — | 3 | 0,29028 | 0,08426 | — | — | — | 3 | 0,19509 | 0,03806 |
| — | 1 | 2 | 4 | 0,38268 | 0,14645 | — | 1 | 2 | 4 | 0,25882 | 0,06699 |
| — | — | — | 5 | 0,47139 | 0,22221 | — | — | — | 5 | 0,32144 | 0,10332 |
| — | — | 3 | 6 | 0,55557 | 0,30866 | — | — | 3 | 6 | 0,38268 | 0,14645 |
| — | — | — | 7 | 0,63439 | 0,40245 | — | — | — | 7 | 0,44229 | 0,19562 |
| 1 | 2 | 4 | 8 | 0,70711 | 0,50000 | 1 | 2 | 4 | 8 | 0,50000 | 0,25000 |
| — | — | — | 9 | 0,77301 | 0,59754 | — | — | — | 9 | 0,55557 | 0,30866 |
| — | — | 5 | 10 | 0,83147 | 0,69134 | — | — | 5 | 10 | 0,60876 | 0,37059 |
| — | — | — | 11 | 0,88192 | 0,77778 | — | — | — | 11 | 0,65935 | 0,43474 |
| — | 3 | 6 | 12 | 0,92388 | 0,85355 | — | 3 | 6 | 12 | 0,70711 | 0,50000 |
| — | — | — | 13 | 0,95694 | 0,91573 | — | — | — | 13 | 0,75184 | 0,56526 |
| — | — | 7 | 14 | 0,98079 | 0,96194 | — | — | 7 | 14 | 0,79335 | 0,62941 |
| — | — | — | 15 | 0,99518 | 0,99039 | — | — | — | 15 | 0,83147 | 0,69134 |
| 2 | 4 | 8 | 16 | 1,00000 | 1,00000 | 2 | 4 | 8 | 16 | 0,86617 | 0,75000 |
| — | — | — | 17 | 0,89687 | 0,80438 | ||||||
| — | — | 9 | 18 | 0,92388 | 0,85355 | ||||||
| — | — | — | 19 | 0,94693 | 0,89668 | ||||||
| — | 5 | 10 | 20 | 0,96600 | 0,93301 | ||||||
| — | — | — | 21 | 0,98079 | 0,96194 | ||||||
| — | — | 11 | 22 | 0,99144 | 0,98296 | ||||||
| — | — | — | 23 | 0,99786 | 0,99572 | ||||||
| 3 | 6 | 12 | 24 | 1,00000 | 1,00000 |
Примечание: Значения sin kε и sin2 kε даны для одной четверти окружности. В остальных четвертях они повторяются.
Ввиду симметричности синусоиды достаточно определить координаты точек одной четверти окружности, например от у0 до у3. Остальные координаты имеют соответственно равные значения. Например: у4 — у2, …, у11 = — у1 и т. д.

Ну, что такое цилиндр, все представляют ))
Цилиндр – это, к примеру, консервная банка из-под зелёного горошка. Если мы открывашкой по кругу вскроем до конца оба донышка, а потом то, что осталось, – боковину – разрежем по вертикали и распрямим на плоскости, то как раз и получится развёртка цилиндра – развёрнутые в прямоугольник боковые стенки и два донышка-кругляшка.

Если же развёртку нужно делать из бумаги, поступаем следующим образом. Строим с помощью циркуля два круга одинакового радиуса R. Это будут основания цилиндра. Затем строим боковую поверхность цилиндра. Она, как мы уже знаем из опыта с банкой, представляет собой прямоугольник. Длина этого прямоугольника будет такой же, как длина окружности оснований L. А длина окружности, согласно формуле, будет равна: L = 2πR, где R – радиус оснований, а π=3,14. Высота прямоугольника будет равна высоте нашего цилиндра – обозначим её как h.
Развёрточка готова.
Если требуется реальная выкройка для склеивания цилиндра, то вдоль сторон L боковой поверхности делаем припуск на склейку в виде полос, которые вырезаем зубцами, для приклеивания донышек. А вдоль одной стороны h делаем припуск в виде сплошной полосы для склеивания боковой поверхности цилиндра.
Ну, а если мы уже разучились чертить с помощью циркуля и прочих старинных инструментов, можно всё вышеперечисленное выполнить на компьютере, скажем, в программе Autocad.
Цилиндр – это одна из пространственных фигур, которая является объектом изучения стереометрии. Важная характеристика любой фигуры – это площадь ее поверхности. В данной статье рассмотрим, что собой представляет развертка цилиндра, а также покажем, как вычислить ее площадь.
Цилиндр как фигура геометрии
Предположим, что у нас имеется некоторая плавная кривая. Это может быть круг, эллипс, парабола и так далее. Возьмем отрезок произвольной длины, который не лежит в плоскости кривой, и опишем с помощью него поверхность, следуя направлению кривой и транслируя отрезок параллельно самому себе. Полученная поверхность называется цилиндрической или просто цилиндром. Отмеченная кривая называется директрисой (направляющей), а отрезок – генератрисой (образующей).
Если к цилиндрической поверхности добавить еще две плоские одинаковые фигуры, ограничивающие эту поверхность с торцов, то полученное тело также называется цилиндром. Оно состоит из двух равных оснований и цилиндрической поверхности.
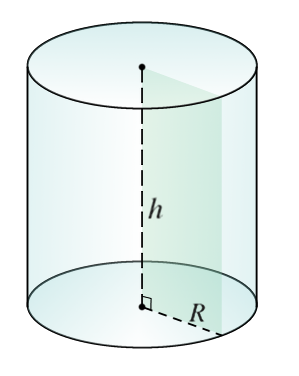
Для наглядного представления описанной фигуры ниже приведен рисунок. На нем изображен эллиптический цилиндр, имеющий полуоси a и b и высоту h (дистанция между основаниями).
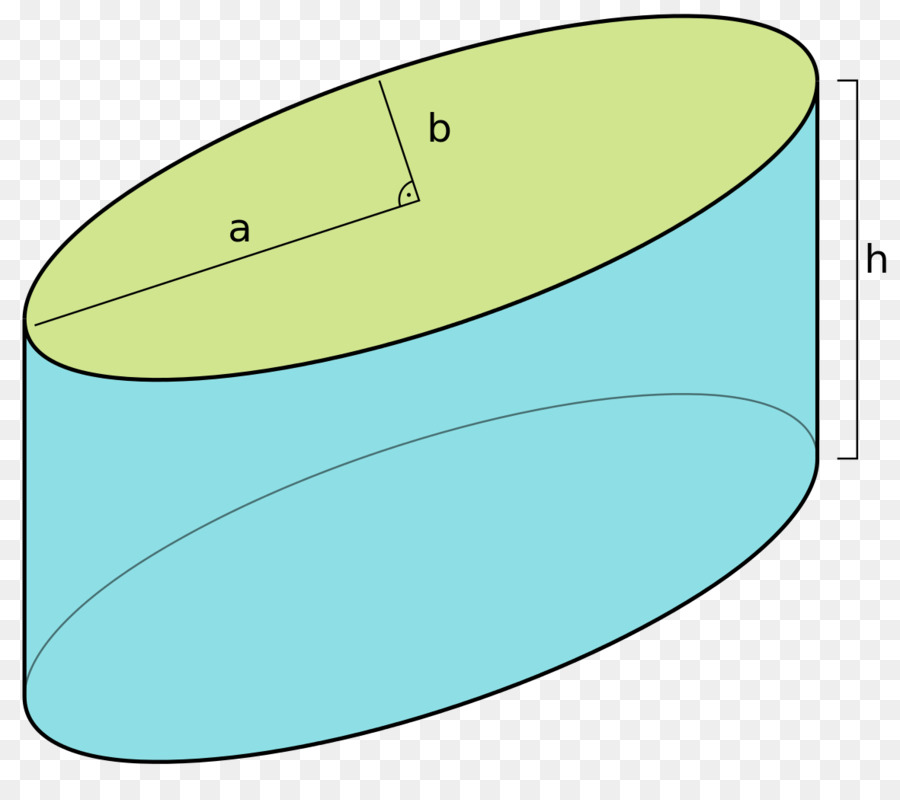
Круглый прямой цилиндр
Пусть директрисой будет окружность некоторого радиуса. Тогда образованная генератрисой фигура будет называться круглым цилиндром. Тем не менее генератриса относительно плоскости, ограниченной директрисой, может быть направлена произвольным образом. Поэтому в общем случае говорят о наклонном круглом цилиндре. Если же генератриса будет перпендикулярна плоскостям основания, то цилиндр называется прямым. Он показан на рисунке ниже.
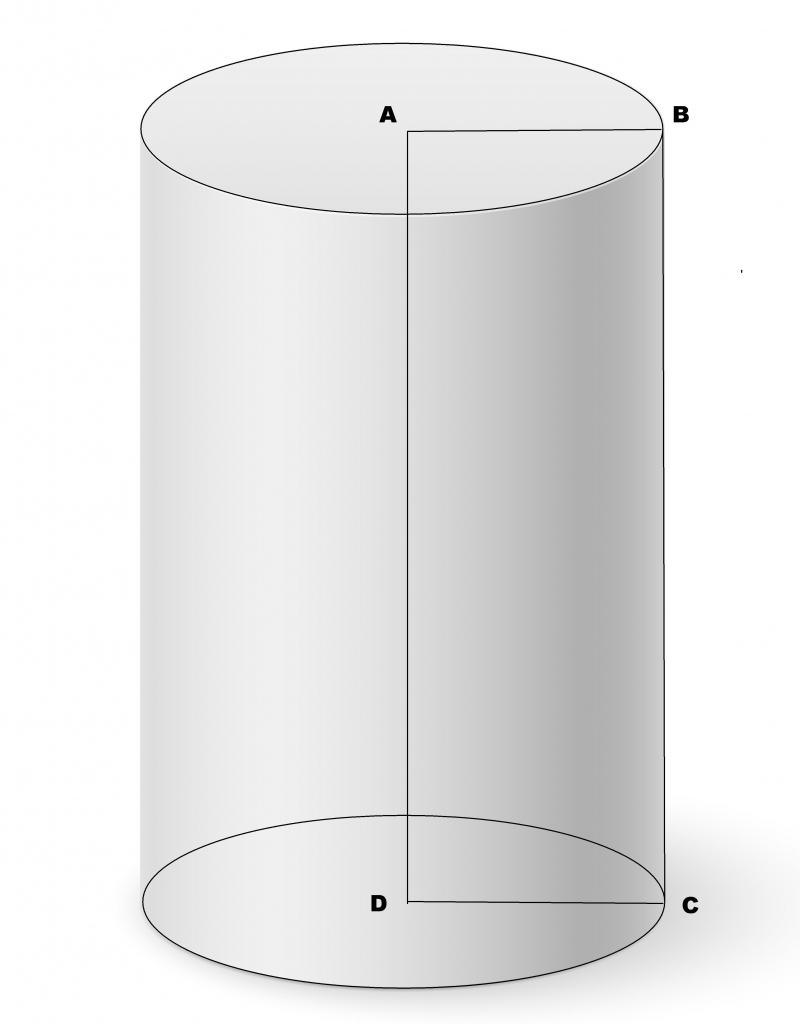
Здесь AB = DC – радиус цилиндра, AD = BC = h – высота фигуры. Для прямого цилиндра высота всегда равна длине образующей. Отрезок AD обозначает ось цилиндра – прямая, соединяющая две центральные точки оснований. От оси цилиндра все точки боковой поверхности лежат на одном расстоянии, равном радиусу фигуры.
Далее в статье будем рассматривать развертку поверхности цилиндра, круглого и прямого.
Развертка круглого прямого цилиндра
Когда говорят о развертке цилиндра, то подразумевают общую площадь его поверхности, представленную плоскими фигурами. Круглый прямой цилиндр образован двумя кругами, имеющими одинаковые радиусы, и одной боковой поверхностью, которая эти круги соединяет друг с другом.

На рисунке показан бумажный цилиндр. Как осуществляется построение развертки цилиндра? Возьмем воображаемые ножницы и отрежем одно основание вдоль окружности. Затем проделаем аналогичные действия со вторым основанием. Боковую поверхность разрежем вдоль генератрисы, то есть параллельно оси фигуры, и развернем ее. Таким образом, мы получили развертку, которая показана на рисунке ниже.
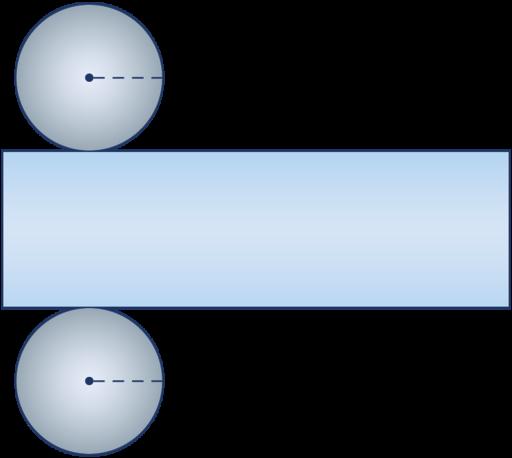
Очевидно, что она состоит из двух одинаковых кругов. Что касается цилиндрической поверхности, то в разрезанном виде она представлена прямоугольником. Развертку удобно использовать при определении площади поверхности рассматриваемой фигуры.
Площадь развертки цилиндра
Выше мы показали, как можно получить развертку фигуры. Чтобы рассчитать ее площадь, необходимо сложить площади для всех ее частей, то есть для двух круглых оснований и одного прямоугольника.
Обозначим радиус основания буквой r, а высоту фигуры – буквой h. Площадь одного основания равна площади круга, то есть:
So = pi*r2
Здесь pi – число Пи, приблизительно равное 3,14.
Чтобы вычислить площадь прямоугольника, представляющего боковую поверхность фигуры в развернутом виде, необходимо знать две его стороны. Одна из них равна высоте h. Вторая, как можно догадаться, соответствует длине директрисы, то есть длине окружности. Обозначим ее l. Тогда можно записать следующие равенства:
l = 2*pi*r;
Sb = l*h = 2*pi*r*h
Здесь Sb – площадь прямоугольника, равная площади цилиндрической поверхности.
Учитывая, что фигура имеет два основания, складываем рассчитанные величины, получаем общую площадь развертки цилиндра:
S = 2*So + Sb = 2*pi*r2 + 2*pi*r*h = 2*pi*r*(r + h)
Площадь S фигуры однозначно определяется через ее радиус и высоту.
Покажем, как использовать это равенство для решения геометрической задачи.
Задача на нахождение радиуса фигуры
Известно, что общая поверхность круглого прямого цилиндра составляет 60 см2. Чему равен радиус основания цилиндра, если его высота равна 7 см, а фигура имеет лишь одно основание.
Описанный в условии задачи цилиндр представляет собой бочку без крышки, поэтому площадь его поверхности образована не двумя, а одним основанием.

Если учесть названный факт, тогда формула для площади фигуры запишется в следующем виде:
S = pi*r2 + 2*pi*r*h
Подставим все известные из условия величины в это равенство, получим:
60 = 3,14*r2 + 43,96*r =>
3,14*r2 + 43,96*r – 60 = 0
Мы получили классическое полное квадратное уравнение. Его решение даст искомое значение радиуса r. Решаем через дискриминант:
D = 43,962 – 4*3,14*(- 60) ≈ 2686,08;
r = (-43,96±√2686,08)/(2*3,14) = 1,25 см
При решении уравнения отрицательный корень был отброшен, в виду его нефизического значения.
Таким образом, параметры открытого цилиндра из условия задачи составляют 7 см в высоту и 2,5 см в диаметре.
