Как найти сумму всех 3 значных чисел

Лично я подобные задачки решаю на компьютере. Тут требуется элементарная по простоте программка.

Например на бейсике она может выглядеть так:

s = 0

For x = 100 To 999

s = s + x

Next x

Print s

Если её запустить, получается результат: 494550.

Стал я смотреть дальше на закономерности, учитывая ручной способ сложения по два.

И пришёл к интересным выводам.

Если наш диапазон чисел 900. Это числа: 100,101,…,999. Всего их 900. (999-100+1=900 )

Это 899 чисел (от 101 до 999) и 900 – е число – это число 100.

То если решать методом сумм по 2, то нужно 450 сложений.

Число 450 получается из числа 900: 900/2=450.

Теперь получается интересный эффект.

Если попробовать поделить полученный результат 494550 на наше число 450, то получается число 1099.

А что такое число 1099?

Это сумма чисел из нашего условия: 100+999=1099.

Получается, зная это с самого начала, не нужно было бы делать 450 сложений.

Нужно просто перемножить 450 на 1099 и получишь 494550.

Получается вот такая формула для решения данной задачки:

Summa =(100+999)*(999-100+1)/2=1099*450=494550.

Не знаю, насколько годится данная формула для решения других задачек (особенно для нечётного диапазона чисел), это ещё надо проверять, но результат получился интересный.

Как найти сумму всех трехзначных чисел

Набор из всех трехзначных чисел с точки зрения математики представляет собой арифметическую прогрессию, то есть последовательность чисел, каждое из которых (кроме самого первого) получается прибавлением к предыдущему одного и того же числа (шага прогрессии). Поэтому задачу нахождения суммы трехзначных чисел можно сформулировать как вычисление суммы некоторого количества первых членов арифметической прогрессии.

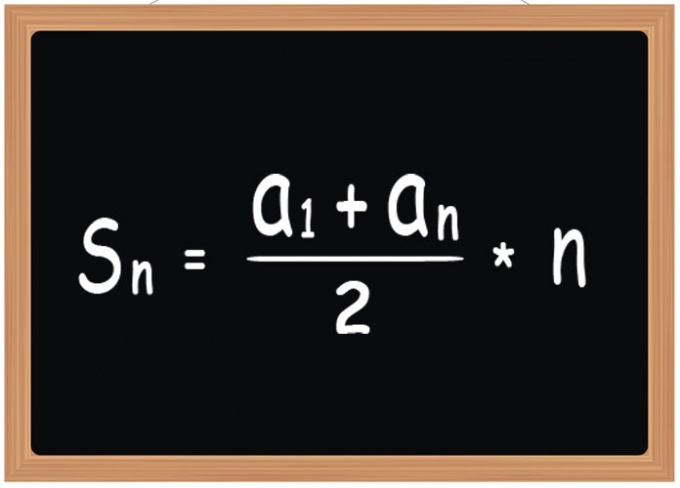
Инструкция

Выделите из условий задачи параметры арифметической прогрессии. Самое меньшее из трехзначных чисел – это 100, значит, именно с него и начинается прогрессия. Каждое последующее число прогрессии больше предыдущего на единицу – значит, шаг (приращение) равен одному. Последнее из трехзначных чисел – это 999, значит, нужно найти сумму первых 900 (999-100+1=900) чисел прогрессии.

Используйте формулу, согласно которой сумма N первых членов арифметической прогрессии равна полусумме первого и N-ного ее членов, умноженной на количество суммируемых чисел (N). В нашем случае первый член равен 100, последний равен 999, а количество суммируемых чисел равно 900. То есть расчет надо производить таким образом: (100+999)/2∗900.

Воспользуйтесь каким-либо калькулятором, если есть затруднения с вычислениями «в уме». Например, это могут быть калькуляторы, встроенные в поисковые системы Google или Nigma. Перейдя на сайт Google, введите запрос (100+999)/2*900 и получите ответ, даже не нажимая кнопки отправки запроса на сервер. Калькулятор Nigma не сможет сам определить правильную последовательность операций умножения и деления, поэтому вам надо самостоятельно расставить скобки: ((100+999)/2)*900. Обе поисковые системы выдадут одинаковый результат вычисления суммы всех трехзначных чисел, который будет равен 494550.

Посчитайте результат с помощью стандартного калькулятора, встроенного в ОС Windows, если нет возможности использовать интернет. Он запускается несколькими способами, наиболее простой из которых заключается в нажатии сочетания клавиш WIN + R с последующим вводом команды calc и нажатием клавиши Enter. Интерфейс калькулятора очень прост, и последовательность из операций сложения чисел 100 и 999, деления результата пополам и умножения его на 900 не должна вызвать затруднений.

Источники:

• Среди двузначных чисел найти те, которые делятся на число

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Подсказываю, выписываем ряд трехзначных чисел в прямом и в обратном порядке

Обращаем внимание, что сумма каждой пары чисел 1099
всего таких пар 900.
Итак два раза просуммированный ряд = 1099х900. Половина этого произведения и будет искомой суммой всех трехзначных чисел.

Вообще это частный случай арифметической прогрессии.

А помнишь, а выкладывала задачку, которую Эшли придумала на Ряды Гаусса, когда ей лет 7-8 было? Я ее тогда с ее слов записала и сохранила.

Вот как-то учительница и говорит: «Сегодня мы идём в Парк аттракционов! Но сначала скажите мне, кто сегодня отсутствует». Выяснилось, что 1-го и 2-го нет. Ладно, значит в классе сейчас 21 ученик.

Пришли они в Парк. А контролер говорит,что вместо входных билетиков сегодня надо решить маленькую задачку, причем устно! Надо сказать сумму всех чисел, которые написаны на футболках. Опечалились ребята, трудно ведь сложить все числа,да еще и устно.

Но учительница попросила всех встать в РЯД по порядку: 3,4,5. 22,23. Потом хотела построить всех парами, но ведь 21-го человека парами не поставишь. Пришлось ей ученика номер 3 попросить отойти в сторонку. Стоит 3-й там и грустно наблюдает за остальными ребятами.

А учительница оставшихся 20 человек построила парами, да причем так хитро. 4-го и 23-го, 5-го и 22-го, 6-го и 21-го.То есть последнего из ряда и первого. Пар получилось 10 (20:2) и в каждой паре сумма была 27 (23+4, 22+5. )

Конечно весь класс пригласили пройти в Парк. И ребята катались на всех горках и каруселях целый день!

О Карле Гауссе:
Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 50 х 101 = 5050.

Источник

Как найти сумму всех трехзначных чисел?

Последовательность трёхзначных чисел можно представить как конечную арифметическую прогрессию, в которой первый член равен 100, последний член равен 999, а разность равна 1.

Соответственно нам нужно найти сумму этой прогрессии.

Формула суммы арифметической прогрессии давно известна:

a1 — первый член; an — последний член; n — количество членов.

a1 и an нам известны, они равны соответственно 100 и 999.

Остаётся найти n. Оно равно 999 – 100 + 1 = 900.

Подставляем всё в формулу:

S = (a1 + an)* n/2 = (100 + 999) * 900/2 = 1099 * 900/2 = 989100/2 = 494550.

Лично я подобные задачки решаю на компьютере. Тут требуется элементарная по простоте программка.

Например на бейсике она может выглядеть так:

Если её запустить, получается результат: 494550.

Стал я смотреть дальше на закономерности, учитывая ручной способ сложения по два.

И пришёл к интересным выводам.

Если наш диапазон чисел 900. Это числа: 100,101. 999. Всего их 900. (999-100+1=900 )

То если решать методом сумм по 2, то нужно 450 сложений.

Число 450 получается из числа 900: 900/2=450.

Теперь получается интересный эффект.

Если попробовать поделить полученный результат 494550 на наше число 450, то получается число 1099.

А что такое число 1099?

Это сумма чисел из нашего условия: 100+999=1099.

Получается, зная это с самого начала, не нужно было бы делать 450 сложений.

Нужно просто перемножить 450 на 1099 и получишь 494550.

Получается вот такая формула для решения данной задачки:

Не знаю, насколько годится данная формула для решения других задачек (особенно для нечётного диапазона чисел), это ещё надо проверять, но результат получился интересный.

Я не занимаюсь составлением программ и помнить формулы прогрессий тоже не в состоянии. Однако найти сумму всех трехзначных чисел не сложно. надо просто скомбинировать их правильным образом. Для начала отбросим число 100 и 550, которые пригодятся на последнем этапе подсчета. Потом обратим внимание, что 101+999 = 1100. Такая же сумма будет у всех остальных пар чисел до 549+551. Остается определить, сколько же пар чисел мы имеем 549-100 = 449. Теперь просто умножаем 449 на 1100, и добавляем к этому произведению отброшенные ранее числа 100 и 550. Получается 494550.

всё просто сумма чисел от 100 до 999 расчитывается так 1000+101, потом 999+102 итд до 550+551 всего таких пар 450 поэтому расчет идет так 1101*450+100-1000=494550

А ещё можно написать программу на на каком-нибудь языке программирования с помощью цикла. Например, если писать на Паскале, то программа будет иметь вид:

for i:=100 to 999 do

Программа выведет число 494450. Можете сами проверить результат программы.

Задача в школе, которую продвинутые в математике родители предлагают решить по методу Гаусса.

Составляем в ряд комбинации (100 + 999) + (101 + 998) + (102 + 997) и так далее. И далее считаем

1099 умножить 900 деленное на 2 будет равно 494 550. Это и есть сумма всех трехзначных чисел.

Вы все правильно написали, только чисел из одинаковых цифр, не одно, а 9: 11, 22, 33, 44, 55, 66, 77, 88, 99.

И у всех сумма цифр, естественно, четная.

Но решение обеих задач

«Почему чисел с четной суммой цифр нечетное количество» и «Почему чисел с нечетной суммой цифр нечетное количество»

намного проще, чем вы расписываете.

Очевидно, что числа с четной и нечетной суммой цифр идут через одно.

Поэтому их одинаковое количество. А так как всего двузначных чисел ровно 90, то чисел каждого вида по 45.

Перевод из двоичной системы в десятичную осуществляется по формуле:

1*2^0+0*2^1+0*2^2+­ 1*2^3+1*2^4+1*2^5+1*2­ ^6=1+8+16+32+64=121

Числа используются для количественной характеристики объектов (вес, стоимость, время и т.п.). Именно в количественных характеристиках легко можно сравнить объекты между собой, но только в одинаковых единицах измерения или их нужно с помощью стандартизации или пересчета в темпах роста и т.п. привести в соизмеримые значения. Именно наличие числовых значений помогают провести анализ объектов и событий и принять обоснованные решения на текущий момент или спрогнозировать значения показателей на будущие периоды. Имея числовые характеристики, можно контролировать многие процессы (в бизнесе, государственном секторе, медицине, личной жизни (например, хронометраж времени и выявление хронофагов (поглотителей времени) и т.п.)

Для перевода двоичного числа 1110001 в десятичную систему используем формулу:

Математическая запись этого преобразования выглядит так:

Если нужно перевести число 1100001 из двоичной системы счисления в десятичную систему можно использовать формулу:

Математическая запись этого преобразования выглядит так:

Источник

Войти

Задать вопрос

Алгебра

Германыч

7 июля, 05:26

Найти сумму всех трехзначных чисел

+3

Ответы (1)

1. 

   Витяся
   
   7 июля, 06:17

   
   0
   

   Самое наименьшее 3-значное 100 наибольшее-999 всего их 900

   считаем (100+999) * 900/2

   1099*450

   494550

   • Комментировать
   • Жалоба
   • Ссылка

Знаешь ответ?

Не уверен в ответе?

Найди верный ответ на вопрос ✅ «Найти сумму всех трехзначных чисел …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Новые вопросы по алгебре

Периметр прямоугольника 6,6 дм. Одна сторона больше другой на 0,9 дм. найдите площадь прямоугольника.

Ответы (1)

Как решить систему уровнений x-y=17 3x-4y=-12

Ответы (1)

x (x+2) (5x-1) = 0

Ответы (1)

Турист проплыл по течению 240 км, затратив на этот путь 12 часов, при этом скорость течения равнялась 3 км/ч. Далее он продолжил путь по озеру, затратив на весь путь по нему 4 часа. Найдите расстояние, которое турист проплыл по озеру.

Ответы (2)

Решите систему уравнений 5y-6x=4 7x-4y=-1

Ответы (1)

Главная » Алгебра » Найти сумму всех трехзначных чисел

Задача по математике -5класс

Подсказываю, выписываем ряд трехзначных чисел в прямом и в обратном порядке

100 101 102 . 998 999 далее в обратном
999 998 997 . 101 100

Обращаем внимание, что сумма каждой пары чисел 1099
всего таких пар 900.
Итак два раза просуммированный ряд = 1099х900. Половина этого произведения и будет искомой суммой всех трехзначных чисел.

Вообще это частный случай арифметической прогрессии.

А помнишь, а выкладывала задачку, которую Эшли придумала на Ряды Гаусса, когда ей лет 7-8 было? Я ее тогда с ее слов записала и сохранила.

В волшебной стране Математика, в маленьком городке Ряды Гаусса жили-были в одном классе дети, у которых вместо имен были . номера! И было в этом классе 23 ученика.У них и футболки были с номерами: 1-й,2-й,3-й. 22-й,23-й.

Вот как-то учительница и говорит: «Сегодня мы идём в Парк аттракционов! Но сначала скажите мне, кто сегодня отсутствует». Выяснилось, что 1-го и 2-го нет. Ладно, значит в классе сейчас 21 ученик.

Пришли они в Парк. А контролер говорит,что вместо входных билетиков сегодня надо решить маленькую задачку, причем устно! Надо сказать сумму всех чисел, которые написаны на футболках. Опечалились ребята, трудно ведь сложить все числа,да еще и устно.

Но учительница попросила всех встать в РЯД по порядку: 3,4,5. 22,23. Потом хотела построить всех парами, но ведь 21-го человека парами не поставишь. Пришлось ей ученика номер 3 попросить отойти в сторонку. Стоит 3-й там и грустно наблюдает за остальными ребятами.

А учительница оставшихся 20 человек построила парами, да причем так хитро. 4-го и 23-го, 5-го и 22-го, 6-го и 21-го.То есть последнего из ряда и первого. Пар получилось 10 (20:2) и в каждой паре сумма была 27 (23+4, 22+5. )

» У нас получилось 270! » — закричали радостно ребята. И тут все заметили грустного 3-го, который уже собирался плакать. «Нет, ребята. Наша сумма 273!» — сказала учительница и обняла 3-го. (270+3)

Конечно весь класс пригласили пройти в Парк. И ребята катались на всех горках и каруселях целый день!

О Карле Гауссе:
Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 50 х 101 = 5050.

Источник

Найти наиболее удобным способом сумму всеx треxзначныx чисел.. пожалуйста

Все вам правильно ответили, но вы еще сможете блеснуть своей эрудицией.
Был такой величайший немецкий математик Карл Фридрих Гаусс (Gauss) родился 30 апреля 1777 года в Брауншвейге. Умер — 23 февраля 1855 года в Геттингене.
Родился в семье водопроводчика.
С детства проявил способности к математике. В 10-летнем возрасте решил задачу о суммировании чисел от 1 до 100, чем обратил на себя внимание учителя.
По известным данным, во времена его обучения в одной группе были собраны по нашим меркам несколько классов. Учитель, чтобы объяснить, что-то старшеклассникам, должен был чем-то занять учеников младших классов. Он дал им задачу найти сумму чисел от 1 до 100, в надежде что они за этим занятием проведут очень много времени (калькуляторов как вы понимаете тогда не было) . Но учителя постигло разочарование, когда буквально через 2-3 минуты, маленький Карл сказал, что он справился с задачей и назвал число — 5050. Учитель был поражен и спросил как он это вычислил. Карл объяснил. Вот ряд чисел 1, 2, 3, 4 . 97, 98, 99, 100. Пара чисел 1+100 = 101, 2+99 = 101, 3+98 =101 и т. д
То есть сумма пары чисел первого и последнего, второго и предпоследнего дают в сумме 101 таких пар 50. Тогда если одна пара дает в сумме 101 то 50 пар дадут 50*101 = 5050. Вот что значит гениальные люди.
После этого учитель начал дополнительно заниматься с этим учеником.
Аналогично, поступили и те, кто дал вам ответ на ваш вопрос.
Вот вам еще некоторые данные из биографии величайшего ученого.

В 1795-98 учился в Геттингенском ун-те.
С 1807 — профессор математики и астрономии Геттингенского ун-та и одновременно директор обсерватории. К концу учебы в ун-те подготовил фундаментальную работу по теории чисел и высшей алгебре «Арифметические исследования» (издана в 1801).
30 марта 1796 решил задачу о построении правильного 17-угольника, что явилось поворотным пунктом в жизни Гаусса, он решает посвятить себя не филологии, а исключительно математике.
Мировую известность Гаусс приобрел после разработки им метода вычисления эллиптической орбиты планеты по трем наблюдениям. Применение этого метода к малой планете Церера дало возможность вновь найти ее на небе после того, как она была утеряна вскоре после ее открытия Дж. Пиацци в 1801. В фундаментальной работе «Теория движения небесных тел» (1809) Гаусс изложил методы вычисления планетных орбит, с небольшими усовершенствованиями используемые и в настоящее время.
Иностранный почетный член Петербургской АН (1824). Его имя занесено на карту Луны.
Желаю вам тоже достичь таких же сияющих вершин. Удачи.

Источник

Определить сумму всех трехзначных чисел, которые без остатка делятся на 3 (проверить правильность кода)

Определить сумму всех трехзначных чисел, которые без остатка делятся на 3

Мой код,правильный ли он?)

Сколько существует трехзначных чисел, которые делятся на 3 без остатка
Сколько существует трехзначных чисел, составленных из цифр 1, 2, 3, 4, 5 и 6 (цифры могут.

Для N целых чисел, которые вводятся с клавиатуры, определить сумму и кол-во положительных чисел, которые делятся на 6 без остатка
Наро плизз вот такие задачки: 1. Для N целыых чисел, которые вводятся с клавиатуры, определить.

Определить сумму и количество положительных чисел, которые делятся на 6 без остатка.
Вот задача: Пользователь вводит количество чисел, определить сумму и количество положительных.

Решение

Правильно, но можно проще:

Решение

Catstail, да я не об этом. Ну ладно, Бог с ними, с решениями определённых интегралов методом трапеций, или тригонометрическими функциями разложением в ряд. Будь хотябы последовательность из произвольных чисел — ну да, в цикле каждый элемент проверять на делимость на три и прибавлять к сумме, если делится. Но сумму арифметической прогрессии циклом считать — занятие как минимум подозрительное.

Это один из ответов на очень-очень старый тест, который предлагался при приеме на работы в IBM. Задача формулировалась так: «Дана целая переменная i. Если ее значение = 1, присвоить ей значение 2. Если же значение i равно двум, присвоить i единицу» В решении допущена умышленная некорректность (вполне очевидная) и правильным решением признавалось вот это:

А решение, которое приведено выше, считается хотя и коротким, но неправильным. И не потому, что оно не учитывает возможную некорректность, а потому, что оно не соотносится с постановкой.

Что я, собственно, и пытаюсь доказать.

Для N целых чисел определить сумму и количество положительных чисел, которые делятся на 6 без остатка
вот эта «задача»: Для N целых чисел определить сумму и количество положительных чисел, которые.

Посчитать произведение чисел из 5 заданных, которые делятся без остатка на 3 и не делятся без остатка на 5
Написать программу, которая введет 5 значений и посчитает произведение чисел, которые делятся без.

Определение всех нечётных чисел, которые делятся на 3 без остатка
Для введенной последовательности целых чисел признаком конца которой является -990, определить всех.

Найти сумму чисел от 1 до A которые делятся на 3 без остатка
Пользователь пишет число A. Нужно найти все числа от 0 до А, которые делятся без остатка на 3. А.

Среди всех двухзначных чисел вывести те, которые делятся на 3 без остатка
Напишите, как сделать деление на 3 без остатка. А ещё, почему не работает? Выдает ошибку C2061 на.

Среди всех двузначных чисел вывести те, которые делятся на 8 без остатка
здравствуйте, помогите пожалуйста решить задание , очень вас об этом прошу!! мне надо создать три.

Источник