Как найти постоянная планка фотоэффект – Сайт, где вы сможете решить свои вопросы

Квантовая механика
Введение^[en] История^[en] Математические основы
Основа Классическая механика Постоянная Планка Интерференция Бра и кет Гамильтониан Старая квантовая теория
Фундаментальные понятия Квантовое состояние Квантовая наблюдаемая Волновая функция Квантовая суперпозиция Квантовая запутанность Смешанное состояние Измерение Неопределённость Принцип Паули Дуализм Декогеренция Симметрия Теорема Эренфеста Туннельный эффект
Эксперименты Опыт Дэвиссона — Джермера Опыт Франка — Герца Опыт Штерна — Герлаха Опыт Юнга Квантовый ластик Квантовый ластик с отложенным выбором Проверка неравенств Белла Фотоэффект Эффект Комптона
Формулировки Представление Шрёдингера Представление Гейзенберга Представление взаимодействия Представление фазового пространства Матричная квантовая механика Интегралы по траекториям Диаграммы Фейнмана
Уравнения Шрёдингера Паули Клейна — Гордона Дирака Швингера — Томонаги фон Неймана Блоха Линдблада Гейзенберга
Интерпретации Копенгагенская Теория скрытых параметров Локальная^[en] Многомировая Теория де Бройля — Бома
Развитие теории Квантовая теория поля Квантовая электродинамика Теория Глэшоу — Вайнберга — Салама Квантовая хромодинамика Стандартная модель Квантовая гравитация
Сложные темы Релятивистская квантовая механика Квантовая теория поля Квантовая гравитация Теория всего
Известные учёные Планк Эйнштейн Шрёдингер Гейзенберг Йордан Бор Паули Дирак Фок Борн де Бройль Ландау Фейнман Бом Эверетт
См. также История возникновения Глоссарий^[en] ЭПР-парадокс
См. также: Портал:Физика

Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии кванта электромагнитного излучения с его частотой, так же как и вообще величину кванта энергии любой линейной колебательной физической системы с её частотой. Связывает энергию и импульс с частотой и пространственной частотой, действие с фазой. Является квантом момента импульса. Впервые упомянута Максом Планком в работе, посвящённой тепловому излучению, и потому названа в его честь. Обычное обозначение — латинское $h$ .

С 2019 года значение постоянной Планка считается зафиксированным и точно равным величине $h$ = 6,626 070 15⋅10⁻³⁴ кг·м²·с⁻¹ (Дж·с).

Широко используется также приведённая постоянная Планка, равная постоянной Планка, делённой на 2 π и обозначаемая как $hbar$ («h с чертой»):

$hbar equiv {frac {h}{2pi }}=1{,}054 571 800(13)times 10^{{-34}}$ Дж·c = ${displaystyle 6{,}582 119 514(40)cdot 10^{-16}}$ эВ·с

Физический смысл[править | править код]

В волновой квантовой механике каждой частице ставится в соответствие волновая функция, при этом характеристики этой волны связаны с характеристиками частицы: волновой вектор ${vec k}$ — с импульсом ${vec p}$ , частота ${displaystyle omega =2pi nu }$ — с энергией $E$ , фаза $varphi$ — c действием $S$ . Постоянная Планка является коэффициентом, связывающим эти величины между собой:

${displaystyle {vec {p}}=hbar {vec {k}},,,(left|{vec {p}}right|=h/lambda ),}$

${displaystyle E=hnu =hbar omega ,}$

${displaystyle S=hbar varphi .}$

В теоретической физике часто для упрощения внешнего вида формул используется система единиц, в которой $hbar = 1$ , тогда эти соотношения принимают вид:

${displaystyle {vec {p}}={vec {k}},,,(left|{vec {p}}right|=2pi /lambda ),}$

${displaystyle E=omega ,}$

${displaystyle S=varphi ,}$

${displaystyle (hbar =1).}$

Величина постоянной Планка определяет и границы применимости классической и квантовой физики. В сравнении с величиной характерных для рассматриваемой системы величин действия или момента импульса, или произведений характерного импульса на характерный размер, или характерной энергии на характерное время, — постоянная Планка показывает, насколько применима к данной физической системе классическая механика. А именно, если $S$ — действие системы, а $L$ — её момент импульса, то при $Sgg hbar$ или ${displaystyle Lgg hbar }$ поведение системы обычно может с хорошей точностью быть описано классической механикой.

Эти оценки следуют из соотношений неопределённости Гейзенберга. В квантовой физике измеряемым физическим величинам ставятся в соответствие операторы, алгебра которых отличается от алгебры действительных чисел главным образом тем, что операторы могут не коммутировать, то есть величина ${displaystyle {hat {C}}={hat {A}}{hat {B}}-{hat {B}}{hat {A}}}$ , называемая коммутатором, может быть не равна нулю. Обычно коммутатор операторов физических величин имеет величину порядка постоянной Планка. Если коммутатор двух операторов квантовой механики не равен нулю, то соответствующие им величины не могут быть измерены одновременно с произвольно большой точностью. Это приводит к возникновению волновых явлений при рассмотрении соответствующих физических систем. Таким образом, постоянная Планка определяет пределы применимости классической физики.

История открытия[править | править код]

Формула Планка для теплового излучения[править | править код]

Формула Планка — выражение для спектральной плотности мощности ${displaystyle u_{nu }(nu ,T)}$ равновесного теплового излучения абсолютно чёрного тела, которое было получено Максом Планком после того, как стало ясно, что формула Вина удовлетворительно описывает излучение только в области коротких волн, но не работает при высоких температурах и в инфракрасной области. В 1900 году Планк предложил формулу, которая хорошо согласовывалась с экспериментальными данными. При выводе этой формулы, однако, Планку пришлось прибегнуть к гипотезе квантования энергии при излучении и поглощении электромагнитных волн. Причём величина кванта энергии оказалась связана с частотой волны:

${displaystyle varepsilon =hnu .}$

Коэффициент пропорциональности в этой формуле и получил название постоянной Планка.

При этом Планк полагал, что использованная им гипотеза является не более чем удачным математическим трюком, но не является отражением непосредственно физического процесса. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с частотой излучения^{[источник не указан 511 дней]}^[a].

Фотоэффект[править | править код]

Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.

Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии при представлении света в виде частиц (фотонов) следует формула Эйнштейна для фотоэффекта:

${displaystyle hbar omega =A_{out}+{frac {mv^{2}}{2}},}$

где $A_{out}$ — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества),

${frac {mv^{2}}{2}}$ — кинетическая энергия вылетающего электрона,

$omega$ — частота падающего фотона с энергией ${displaystyle hbar omega ,}$

$hbar$ — постоянная Планка.

Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества, то есть на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.

Эффект Комптона[править | править код]

Переопределение[править | править код]

На XXIV Генеральной конференции по мерам и весам (ГКМВ) 17—21 октября 2011 года была единогласно принята резолюция^[2], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить единицы измерений СИ таким образом, чтобы постоянная Планка была равной точно 6,62606X⋅10⁻³⁴ Дж·с, где Х заменяет одну или более значащих цифр, которые будут определены в дальнейшем на основании наиболее точных рекомендаций CODATA^[3]. В этой же резолюции предложено таким же образом определить как точные значения постоянную Авогадро, элементарный заряд и постоянную Больцмана.

XXV ГКМВ, состоявшаяся в 2014 году, приняла решение продолжить работу по подготовке новой ревизии СИ, включающей привязку основных единиц СИ к точному значению постоянной Планка, и предварительно наметила закончить эту работу к 2018 году с тем, чтобы заменить существующую СИ обновлённым вариантом на XXVI ГКМВ^[4]. В 2019 году постоянная Планка получила фиксированное значение как и постоянная Больцмана, постоянная Авогадро и другие^[5].

Значения постоянной Планка[править | править код]

Ранее постоянная Планка была экспериментально измеряемой величиной, точность известного значения которой постоянно повышалась. В результате изменений СИ 2019 года было принято фиксированное точное значение постоянной Планка:

h = 6,626 070 15 × 10⁻³⁴ Дж·c^[6];

h = 6,626 070 15 × 10⁻²⁷ эрг·c;

h = 4,135 667 669… × 10⁻¹⁵ эВ·c^[6].

Это значение является составной частью определения Международной системы единиц.

Часто применяется величина ${displaystyle hbar equiv {frac {h}{2pi }}}$ :

ħ = 1,054 571 817… × 10⁻³⁴ Дж·c^[6];

ħ = 1,054 571 817… × 10⁻²⁷ эрг·c;

ħ = 6,582 119 569… × 10⁻¹⁶ эВ·c^[6],

называемая редуцированной (иногда рационализированной или приведённой) постоянной Планка или постоянной Дирака. Применение этого обозначения упрощает многие формулы квантовой механики, так как в эти формулы традиционная постоянная Планка часто входит в виде деленной на константу ${2pi}$ .

В ряде естественных систем единиц является единицей измерения действия^[7]. В планковской системе единиц, также относящейся к естественным системам, служит в качестве одной из основных единиц системы.

Методы измерения[править | править код]

Использование законов фотоэффекта[править | править код]

При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:

${displaystyle K_{max}=hnu -A,}$

где ${displaystyle K_{max}}$ — максимальная кинетическая энергия вылетевших с катода фотоэлектронов,

$nu$ — частота падающего света,

$A$ — т. н. работа выхода электрона.

Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой ${displaystyle nu _{1}}$ , при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:

${displaystyle hnu _{1}=A+eU_{1},}$

где $e$ — заряд электрона.

Затем тот же фотоэлемент облучают монохроматическим светом с частотой ${displaystyle nu _{2}}$ и точно так же запирают его с помощью напряжения ${displaystyle U_{2}:}$

${displaystyle hnu _{2}=A+eU_{2}.}$

Почленно вычитая второе выражение из первого, получаем:

${displaystyle h(nu _{1}-nu _{2})=e(U_{1}-U_{2}),}$

откуда следует:

${displaystyle h={frac {e(U_{1}-U_{2})}{(nu _{1}-nu _{2})}}.}$

Анализ спектра тормозного рентгеновского излучения[править | править код]

Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,

${displaystyle h{frac {c}{lambda }}=eU,}$

где $c$ — скорость света,

$lambda$ — длина волны рентгеновского излучения,

$e$ — заряд электрона,

$U$ — ускоряющее напряжение между электродами рентгеновской трубки.

Тогда постоянная Планка равна:

${displaystyle h={frac {{lambda }{Ue}}{c}}.}$

См. также[править | править код]

Планковские единицы
Рациональная система единиц

Примечания[править | править код]

Комментарии[править | править код]

↑ Значение постоянной Планк нашел, вручную подбирая энергию пакетов и добиваясь наилучшего совпадения с экспериментальными данными^[1]

Источники[править | править код]

↑ Каку, 2022, с. 69.
↑ On the possible future revision of the International System of Units, the SI. Архивная копия от 4 марта 2012 на Wayback Machine Resolution 1 of the 24th meeting of the CGPM (2011).
↑ Agreement to tie kilogram and friends to fundamentals — physics-math — 25 October 2011 — New Scientist. Дата обращения: 28 октября 2017. Архивировано 3 ноября 2011 года.
↑ On the future revision of the International System of Units, the SI (англ.). Resolution 1 of the 25th CGPM (2014). BIPM. Дата обращения: 6 июля 2017. Архивировано 14 мая 2017 года.
↑ The International System of Units – making measurements fundamentally better. BIPM. Дата обращения: 22 мая 2019. Архивировано из оригинала 24 мая 2019 года.
↑ ¹ ² ³ ⁴ Fundamental Physical Constants — Complete Listing. Дата обращения: 19 июня 2011. Архивировано 8 декабря 2013 года.
↑ Tomilin K. A. Natural Systems of Units: To the Centenary Anniversary of the Planck System (англ.). Proc. of the XXII Internat. Workshop on high energy physics and field theory (июнь 1999). Дата обращения: 22 декабря 2016. Архивировано 12 мая 2016 года.

Литература[править | править код]

Митио Каку. Уравнение Бога. В поисках теории всего = Michio Kaku. The God Equation: The Quest for a Theory of Everything. — М.: Альпина нон-фикшн, 2022. — 246 с. — ISBN 978-5-00139-431-0.
John D. Barrow. The Constants of Nature; From Alpha to Omega — The Numbers that Encode the Deepest Secrets of the Universe. — Pantheon Books, 2002. — ISBN 0-37-542221-8.
Steiner R. History and progress on accurate measurements of the Planck constant // Reports on Progress in Physics. — 2013. — Vol. 76. — P. 016101.

Ссылки[править | править код]

Planck constant The NIST Reference on Constants, Units and Uncertainty.
New Measurement Will Help Redefine International Unit of Mass (англ.). News. NIST (30 июня 2017). Дата обращения: 6 июля 2017.
Measurement of the Planck constant at the National Institute of Standards and Technology from 2015 to 2017.
Земцов Ю. К. Курс лекций по атомной физике, анализ размерностей.

Источник

Материал
из свободной русской энциклопедии «Традиция»

Значения h	Единицы
6,626 070 040(81) • 10⁻³⁴	Дж∙c
4,135 667 662(25) • 10⁻¹⁵	эВ∙c
6,626 070 040(81) • 10⁻²⁷	эрг∙c

Постоя́нная Пла́нка, обозначаемая как h, является физической постоянной,
используемой для описания величины кванта действия в квантовой механике. Данная
постоянная впервые появилась в работах М. Планка, посвящённых тепловому
излучению, и потому названа в его честь. Она присутствует как коэффициент между
энергией E и частотой
ν фотона в формуле Планка:

Скорость
света c связана с частотой ν и длиной волны λ соотношением:

$~nu = frac{c}{lambda}.$

С учётом этого
соотношение Планка записывается так:

$~E = frac{hc}{lambda}.$

Часто
применяется величина

$~hbar equiv {frac {h}{2pi }}=1,054 571 800(13)times 10^{{-34}}$ Дж•c,

$~hbar =1,054 571 800(13)times 10^{{-27}}$ эрг•c,

$~hbar =6,582 119 514(40)times 10^{{-16}}$ эВ•c,

называемая
редуцированной (или рационализированной) постоянной Планка или постоянной
Дирака.

Постоянную
Дирака удобно использовать тогда, когда применяется угловая частота ω, измеряемая в радианах за секунду,
вместо обычной частоты ν,
измеряемой количеством циклов за секунду. Так как ω = 2πν,
то справедлива формула:

Согласно
гипотезе Планка, впоследствии подтверждённой, энергия атомных состояний
является квантованной. Это приводит к тому, что нагретое вещество излучает
электромагнитные кванты или фотоны определённых частот, спектр которых зависит
от химического состава вещества.

В Юникоде
постоянная Планка занимает позицию U+210E (h), а постоянная Дирака U+210F (ħ).

Содержание

1 Величина
2 Происхождение
постоянной Планка

2.1 Излучение
чёрного тела
2.2 Фотоэффект
2.3 Структура
атома
2.4 Принцип
неопределённости
2.5 Спектр
тормозного рентгеновского излучения

3 Физические
константы, связанные с постоянной Планка

3.1 Масса
покоя электрона
3.2 Постоянная
Авогадро
3.3 Элементарный
заряд
3.4 Магнетон
Бора и ядерный магнетон

4 Определение
из экспериментов

4.1 Постоянная
Джозефсона
4.2 Баланс
мощности
4.3 Магнитный
резонанс
4.4 Постоянная
Фарадея
4.5 Рентгеновская
плотность кристалла

5 Постоянная
Планка в системе единиц СИ
6 Постоянная
Планка в теории бесконечной вложенности материи
7 См.
также
8 Ссылки
9 Литература
10 Внешние
ссылки

Величина

Постоянная
Планка имеет размерность энергии, умноженной на время, как и размерность
действия. В международной системе единиц СИ постоянная Планка выражается в
единицах Дж•с. Такую же размерность имеет произведение импульса на расстояние в
виде Н•м•с, а также момент импульса.

Значение
постоянной Планка равно:^[1]

$h=6,626070040(81)times 10^{{-34}}$ Дж•с $=4,135667662(25)times 10^{{-15}}$ эВ•с.

Две цифры
между скобками обозначают неопределённость в двух последних цифрах значения
постоянной Планка (данные обновляются приблизительно каждые 4 года).

Происхождение
постоянной Планка

Излучение
чёрного тела

Основная статья: Формула Планка

Интенсивность света, излучаемая чёрным телом в зависимости от длины
волны. Кривые обозначены разным цветом и построены для разных температур тела.
Планк был первым, кто объяснил форму этих кривых

В конце
19 века Планк исследовал проблему излучения абсолютно чёрного тела, которую за
40 лет до этого сформулировал Кирхгоф. Нагретые тела светятся тем сильнее, чем
выше их температура и больше внутренняя тепловая энергия. Теплота
распределяется между всеми атомами тела, приводя их в движение друг
относительно друга и к возбуждению электронов в атомах. При переходе электронов
к устойчивым состояниям излучаются фотоны, которые могут снова поглощаться
атомами. При каждой температуре возможно состояние равновесия между излучением
и веществом, при этом доля энергии излучения в общей энергии системы зависит от
температуры. В состоянии равновесия с излучением абсолютно чёрное тело не
только поглощает всё падающее на него излучение, но и излучает само то же самое
количество энергии, по определённому закону распределения энергии по частотам.
Закон, связывающий температуру тела с мощностью общей излучаемой энергии с
единицы поверхности тела, носит название закон Стефана-Больцмана и был
установлен в 1879–1884 гг.

При
нагревании увеличивается не только общее количество излучаемой энергии, но
меняется и состав излучения. Это видно по тому, что меняется цвет нагреваемых
тел. Согласно закону смещения Вина 1893 г., основанному на принципе
адиабатического инварианта, для каждой температуры можно вычислить длину волны
излучения, при которой тело светится наиболее сильно. Вин сделал достаточно
точную оценку формы энергетического спектра чёрного тела при высоких частотах,
но не смог объяснить ни форму спектра, ни его поведение при низких частотах.

Планк
предположил, что поведение света подобно движению набора множества одинаковых
гармонических осцилляторов. Он изучал изменение энтропии этих осцилляторов в
зависимости от температуры, пытаясь обосновать закон Вина, и нашёл подходящую
математическую функцию для спектра чёрного тела. ^[2]

Однако
вскоре Планк понял, что кроме его решения возможны и другие, приводящие к
другим значениям энтропии осцилляторов. В результате он был вынужден
использовать вместо феноменологического подхода отвергаемую им ранее
статистическую физику, ^[2] что он
описывал как “акт отчаяния … Я был готов пожертвовать любыми моими
предыдущими убеждениями в физике.”^[3]
Одним из новых принятых Планком условий было:

интерпретировать
U_N (энергия колебаний N осцилляторов) не как
непрерывную неограниченно делимую величину, а как дискретную величину,
состоящую из суммы ограниченных равных частей. Обозначим каждую такую часть в
виде элемента энергии через ε;^[2]

С этим
новым условием Планк фактически вводил квантованность энергии осцилляторов,
говоря, что это “чисто формальное предположение … на самом деле я не думал
об этом глубоко…”,^[4] однако это привело к
настоящей революции в физике. Применение нового подхода к закону смещения Вина
показало, что “элемент энергии” должен быть пропорционален частоте
осциллятора. Это было первой версией того, что сейчас называется “формула
Планка”:

Планку
удалось вычислить значение h из
экспериментальных данных по излучению чёрного тела: его результат был 6,55 • 10⁻³⁴
Дж•с, с точностью 1,2 % от принятого сейчас значения.^[2] Он также смог впервые определить постоянную Больцмана k_B из тех же данных и своей теории.^[5]

До теории
Планка предполагалось, что энергия тела может быть любой, являясь непрерывной
функцией. Это эквивалентно тому, что элемент энергии ε (разность между
дозволенными уровнями энергии) равен нулю, следовательно должна быть равна нулю
и h. Исходя из этого следует
понимать утверждения о том, что “постоянная Планка равна нулю в
классической физике” или что “классическая физика является пределом
квантовой механики при устремлении постоянной Планка к нулю”. Вследствие
малости постоянной Планка она почти не проявляется в обычном человеческом опыте
и до работ Планка была незаметна.

Проблема
чёрного тела была пересмотрена в 1905 г., когда Рэлей и Джинс с одной стороны,
и Эйнштейн с другой стороны, независимо доказали, что классическая
электродинамика не может обосновать наблюдаемый спектр излучения. Это привело к
так называемой “ультрафиолетовой катастрофе”, обозначенной таким
образом Эренфестом в 1911 г. Усилия теоретиков (вместе с работой Эйнштейна по
фотоэффекту) привели к признанию того, что постулат Планка о квантовании
уровней энергии является не простым математическим формализмом, а важным элементом
представлений о физической реальности. Первый Сольвеевский конгресс в 1911 г.
был посвящён “теории радиации и квантов”.^[6]
Макс Планк в 1918 г. получил Нобелевскую премию по физике “за признание
заслуг в развитии физики и открытие кванта энергии”.

Фотоэффект

Основная статья: Фотоэффект

Фотоэффект
заключается в эмиссии электронов (называемых фотоэлектронами) с поверхности при
освещении её светом. Впервые он наблюдался Беккерелем в 1839 г., хотя обычно
упоминается Генрих Герц, ^[7] который
опубликовал в 1887 г. обширное исследование на эту тему. Столетов в 1888–1890
гг. сделал несколько открытий в области фотоэффекта, в том числе вывел первый
закон внешнего фотоэффекта. Другое важное исследование фотоэффекта опубликовал
Ленард в 1902 г. ^[8] Хотя Эйнштейн не
проводил сам экспериментов по фотоэффекту, но его работа 1905 г. ^[9] рассматривала эффект на основе световых квантов. Это
принесло Эйнштейну нобелевскую премию в 1921 г.^[7],
когда его предсказания были подтверждены экспериментальной работой Милликена. ^[10] В это время теория фотоэффекта Эйнштейна
рассматривалась как более значительная, чем его теория относительности.

До работы
Эйнштейна каждое электромагнитное излучение рассматривалось в виде набора волн,
обладающих своей “частотой” и “длиной волны”. Энергия,
переносимая волной за единицу времени, называется интенсивностью. Аналогичные
параметры имеют и другие виды волн, например звуковая волна или волна на воде.
Однако перенос энергии, связанной с фотоэффектом, не согласуется с волновой
картиной света.

Кинетическая
энергия фотоэлектронов, появляющихся в фотоэффекте, может быть измерена.
Оказывается, что она не зависит от интенсивности света, ^[8] но зависит линейно от частоты.^[10] При этом увеличение интенсивности света
приводит не к увеличению кинетической энергии фотоэлектронов, а к увеличению их
количества.^[8] Если же частота слишком мала
и кинетическая энергия фотоэлектронов порядка нуля, то фотоэффект исчезает,
несмотря на значительную интенсивность света.^[10]

Согласно
объяснению Эйнштейна, в данных наблюдениях проявляется квантовая природа света;
энергия света переносится малыми “пакетами” или квантами, а не в виде
непрерывной волны. Величина этих “пакетов” энергии, которые позже
назвали фотонами, была той же самой, что и у “элементов энергии”
Планка. Это привело к современному виду формулы Планка для энергии фотона:

Постулат
Эйнштейна был доказан экспериментально: постоянная пропорциональности между
частотой света ν и энергией
фотона E оказалась равной
постоянной Планка h.^[10]

Структура
атома

Основная статья: Постулаты Бора

Схематическая модель Бора атома водорода. Показан переход электрона с
уровня n=3 на уровень n=2, приводящий к возникновению кванта
видимого света с длиной волны 656 нм (красный), в соответствии с
предсказаниями модели

Нильс Бор
представил первую квантовую модель атома в 1913 г., пытаясь избавиться от затруднений
классической модели атома Резерфорда. ^[11]
Согласно классической электродинамике, точечный заряд при вращении вокруг
неподвижного центра должен излучать электромагнитную энергию. Если такая
картина справедлива для электрона в атоме при его вращении вокруг ядра, то с
течением времени электрон потеряет энергию и упадёт на ядро. Для преодоления
этого парадокса Бор предложил считать, аналогично тому, как это имеет место у
фотонов, что электрон в водородоподобном атоме должен иметь квантованные
энергии E_n:

$~E_n = -frac {h Z^2 c R_infty } {n^2},$

где R_∞ есть экспериментально
определённая константа ( постоянная Ридберга в единицах обратной длины), с – скорость света, n – целое число (n = 1, 2, 3, …), Z – порядковый номер химического элемента
в таблице Менделеева, равный единице для атома водорода. Электрон, попавший на
нижний энергетический уровень (n =
1), находится в основном состоянии атома и уже не может, в силу пока не
определённых в квантовой механике причин, уменьшить свою энергию. Такой подход
позволил Бору прийти к формуле Ридберга, эмпирически описывающей спектр
излучения атома водорода, и вычислить значение постоянной Ридберга R_∞ через другие фундаментальные
константы.

Бор также
ввёл величину h/2π, известную как редуцированная постоянная
Планка или постоянная Дирака ħ, как квант
момента импульса. Бор предполагал, что ħ определяет модуль момента импульса
каждого электрона в атоме. Но это оказалось неточным, несмотря на улучшения
теории Бора Зоммерфельдом и другими. Более корректной оказалась квантовая
теория, в виде матричной механики Гейзенберга в 1925 г. и в виде уравнения
Шрёдингера в 1926 г. При этом постоянная Дирака осталась фундаментальным
квантом момента импульса. Если J
есть общий момент импульса системы с инвариантностью вращения, и J_z есть момент импульса,
измеряемый вдоль выделенного направления, то эти величины могут иметь только
следующие значения: 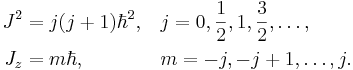$begin{align} J^2 = j(j+1) hbar^2,quad & j = 0, frac{1}{2}, 1, frac{3}{2}, ldots, \ J_z = m hbar, qquadquadquad & m = -j, -j+1, ldots, j. end{align}$

Принцип
неопределённости

Постоянная
Планка содержится также в выражении для принципа неопределённости Вернера
Гейзенберга. Если брать большое количество частиц в одном и том же состоянии,
то неопределённость в их положении Δx
, и неопределённость в их импульсе (в том же самом направлении), Δp, подчиняются соотношению:

$~ Delta x, Delta p ge begin{matrix}frac{1}{2}end{matrix} hbar,$

где
неопределённость задаётся как среднеквадратическое отклонение измеряемой
величины от её математического ожидания. Существуют и другие подобные пары
физических величин, для которых справедливо соотношение неопределённостей.

В
квантовой механике постоянная Планка входит в выражение для коммутатора между
оператором положения и оператором импульса :

$~[hat{p}_i, hat{x}_j] = -i hbar delta_{ij},$

где δ_ij
есть символ Кронекера.

Спектр
тормозного рентгеновского излучения

При
взаимодействии электронов с электростатическим полем атомных ядер возникает
тормозное излучение в виде рентгеновских квантов. Известно, что частотный
спектр тормозного рентгеновского излучения имеет точную верхнюю границу,
называемую фиолетовой границей. Её существование вытекает из квантовых свойств
электромагнитного излучения и закона сохранения энергии. Действительно,

$~hfrac{c}{lambda}=eU,$

где – скорость
света,

–
длина волны рентгеновского излучения,

– заряд
электрона,

–
ускоряющее напряжение между электродами рентгеновской трубки.

Тогда
постоянная Планка будет равна:

$~h=frac{{lambda}{Ue}}{c}.$

Физические
константы, связанные с постоянной Планка

Список
констант, указанных ниже, основан на данных 2014 CODATA. ^[12]. Приблизительно 90 % неточности в этих
константах связаны с неточностью определения постоянной Планка, как это видно
из квадрата коэффициента корреляции Пирсона (r² >
0,99, r > 0,995). Если
сравнивать с другими константами, постоянная Планка известна с точностью
порядка $u_{r}=1,2cdot 10^{{-8}}$ при неопределённости измерения 1σ. Эта
точность значительно лучше, чем у гравитационной
постоянной или у универсальной газовой постоянной.

Масса покоя
электрона

Как
правило, постоянная Ридберга R_∞
(в единицах обратной длины) определяется через массу электрона
m_e и другие физические константы:

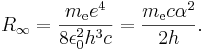
$~R_infty = frac{m_{rm e} e^4}{8 epsilon_0^2 h^3 c} = frac{m_{rm e} c alpha^2}{2 h}.$

Постоянная
Ридберга может быть определена очень точно ( $u_r=6,6 cdot 10^{-12}$ )
из спектра атома водорода, тогда как для массы электрона нет прямого способа
измерения. Поэтому для определения массы электрона используется формула:

$~m_{rm e} = frac{2 R_{infty} h}{c alpha^2},$

где c есть скорость света и α есть постоянная
тонкой структуры. Скорость света достаточно точно определяется в системе
единиц СИ, как и постоянная тонкой структуры ( $u_r=6,8 cdot 10^{-10}$ ).
Поэтому неточность определения массы электрона зависит только от неточности
постоянной Планка (r² >
0,999).

Постоянная Авогадро

Основная статья: Число Авогадро

Число
Авогадро N_A
определяется как отношение массы одного моля электронов к массе одного
электрона. Для её нахождения нужно взять массу одного моля электронов в виде
“относительной атомной массы” электрона A_r(e), измеряемой в ловушке Пеннинга ( $u_r=4,2 cdot 10^{-10}$ ),
умноженной на единицу молярной массы M_u,
которая в свою очередь определяется как 0,001 кг/моль. В результате
получается:

$~N_{rm A} = frac{M_{rm u} A_{rm r}({rm e})}{m_{rm e}} = frac{M_{rm u} A_{rm r}({rm e}) c alpha^2}{2 R_{infty} h}.$

Зависимость
числа Авогадро от постоянной Планка (r² >
0,999) повторяется и для других постоянных, связанных с количеством вещества,
например, для атомной единицы массы. Неопределённость в значении постоянной
Планка ограничивает значения атомных масс и частиц в единицах системы СИ, то
есть в килограммах. В то же время отношения масс частиц известны с лучшей
точностью.

Элементарный
заряд

Зоммерфельд
первоначально определял постоянную тонкой структуры α так:

$~alpha = frac{e^2}{hbar c 4 pi epsilon_0} = frac{e^2 c mu_0}{2 h},$

где e есть элементарный электрический заряд, ε₀ – электрическая постоянная (называемая также
диэлектрической проницаемостью вакуума), μ₀
– магнитная постоянная или магнитная проницаемость вакуума. Последние две
постоянные имеют фиксированные значения в системе единиц СИ. Значение α может быть определено экспериментально
путём измерения g-фактора электрона g_e
и последующего сравнения со значением, вытекающим из квантовой электродинамики.

В
настоящее время наиболее точное значение элементарного электрического заряда
получается из приведённой выше формулы:

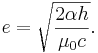
$~e = sqrt{frac{2alpha h}{mu_0 c}}.$

Магнетон
Бора и ядерный магнетон

Основные статьи: Магнетон Бора , Ядерный магнетон

Магнетон
Бора и ядерный магнетон являются единицами, используемыми для описания
магнитных свойств электрона и атомных ядер соответственно. Магнетон Бора есть
магнитный момент, который ожидается у электрона, если бы он вёл себя как
вращающаяся заряженная частица согласно классической электродинамике. Его
значение выводится через постоянную Дирака, элементарный электрический заряд и
массу электрона. Все эти величины выводятся через постоянную Планка,
результирующая зависимость от h^½
(r² > 0,995)
может быть найдена с учётом формулы:

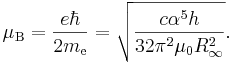
$~mu_{rm B} = frac{e hbar}{2 m_{rm e}} = sqrt{frac{c alpha^5 h}{32 pi^2 mu_0 R_{infty}^2}}.$

Ядерный магнетон
имеет похожее определение, с той разницей, что протон значительно массивнее
электрона. Отношение электронной относительной атомной массы к протонной
относительной атомной массе может быть определено с большой точностью ( $u_r=4,3 cdot 10^{-10}$ ).
Для связи между обоими магнетонами можно записать:

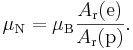
$~mu_{rm N} = mu_{rm B} frac{A_{rm r}({rm e})}{A_{rm r}({rm p})}.$

Определение
из экспериментов

Метод	Значение h, 10^–34Дж∙с	Точность определения	Ссылка
Баланс мощности	6,626 068 89(23)	3,4∙10^–8	^[1^3] ^[1^4][1^5]
Рентгеновская плотность кристалла	6,626 074 5(19)	2,9∙10^–7	^[1^6]
Постоянная Джозефсона	6,626 067 8(27)	4,1∙10^–7	^[1^7] ^[1^8]
Магнитный резонанс	6,626 072 4(57)	8,6∙10^–7	^[1^9] ^[^20]
Постоянная Фарадея	6,626 065 7(88)	1,3∙10^–6	^[2^1]
CODATA 2010 принятое значение	6,626 069 57(29)	4,4∙10^–8	^[^22]
Для пяти различных методов указаны девять недавних измерений постоянной Планка. В случае, если имеется более одного измерения, указывается средневзвешенное значение h согласно методике CODATA.

Постоянная
Планка может быть определена из спектра излучающего чёрного тела или
кинетической энергии фотоэлектронов, как это было сделано в начале двадцатого
века. Однако данные методы не самые точные. Значение h согласно CODATA основано на базе трёх измерений методом
баланса мощностей произведения величин K_J²R_K и одного межлабораторного
измерения молярного объёма кремния,^[22] в
основном методом баланса мощностей до 2007 г. в США в National Institute of
Standards and Technology (NIST).^[15] Другие
измерения, указанные в таблице, не повлияли на результат из-за недостаточной
точности.

Имеются
как практические, так и теоретические трудности при определении h. Так, наиболее точные методы баланса
мощности и рентгеновской плотности кристалла не полностью согласуются друг с
другом по своим результатам. Это может быть следствием переоценки точности в
этих методах. Теоретические трудности вытекают из того, что все методы, кроме рентгеновской
плотности кристалла, основаны на теоретической базе эффекта Джозефсона и
квантового эффекта Холла. При некоторой возможной неточности этих теорий
возникнет и неточность в определении постоянной Планка. При этом полученное
значение постоянной Планка уже не может использоваться как тест для проверки
этих теорий во избежание замкнутого логического круга. Положительным моментом
является то, что имеются независимые статистические способы проверки этих
теорий.^[22]

Постоянная Джозефсона

Основная статья: Эффект Джозефсона

Постоянная
Джозефсона K_J
связывает разность потенциалов U,
возникающую в эффекте Джозефсона в “контактах Джозефсона”, с частотой
ν микроволнового излучения. Из
теории достаточно строго следует выражение:

$~K_{rm J} = Unu = 2e/h.$

Постоянная
Джозефсона может быть измерена путём сравнения с разностью потенциалов,
возникающей в батарее контактов Джозефсона. Для измерения разности потенциалов
используется компенсация электростатической силы силой гравитации. Из теории
следует, после замены электрического заряда e
на его значение через фундаментальные постоянные (см. выше Элементарный заряд), выражение для
постоянной Планка через K_J:

$~h = frac{8alpha}{mu_0 c K_{rm J}^2}.$

Баланс
мощности

В данном
методе осуществляется сравнение двух видов мощности, одна из которых измеряется
в системе единиц СИ в ваттах, а другая измеряется в условных
электрических единицах. Из определения условного
ватта W₉₀, он даёт
меру для произведения K_J²R_K в единицах СИ, где R_K есть постоянная Клитцинга,
появляющаяся в квантовом эффекте Холла. Если теоретическая трактовка эффекта
Джозефсона и квантового эффекта Холла верна, тогда R_K = h/e², и измерение K_J²R_K приводит к определению
постоянной Планка:

$~h = frac{4}{K_{rm J}^2 R_{rm K}}.$

Магнитный
резонанс

Основная статья: Гиромагнитное отношение

Гиромагнитное
отношение γ является
коэффициентом пропорциональности между частотой ν ядерного магнитного резонанса (или электронного
парамагнитного резонанса для электронов), и приложенным магнитным полем B: ν =
γB. Хотя имеется трудность в
определении гиромагнитного отношения из-за неточности измерения B, для протонов в воде при 25 °C она
известна с лучшей точностью, чем 10^–6. Протоны частично
“экранируются” от приложенного магнитного поля электронами молекул
воды. Такой же эффект приводит к химическому сдвигу в ядерно-магнитной спектроскопии, и
обозначается штрихом у символа гиромагнитного отношения, γ′_p. Гиромагнитное отношение
связано с магнитным моментом экранированного протона μ′_p, спиновым квантовым числом S (S=1/2
для протонов) и постоянной Дирака:

$~gamma^{prime}_{rm p} = frac{mu^{prime}_{rm p}}{S hbar} = frac{2 mu^{prime}_{rm p}}{hbar}.$

Отношение
магнитного момента экранированного протона μ′_p
к магнитному моменту электрона μ_e
может быть измерено независимо с высокой точностью, поскольку неточность
магнитного поля на результате сказывается мало. Значение μ_e, выраженное в магнетонах
Бора, равно половине электронного g-фактора g_e.
Следовательно,

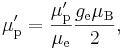
$~mu^{prime}_{rm p} = frac{mu^{prime}_{rm p}}{mu_{rm e}} frac{g_{rm e} mu_{rm B}}{2},$

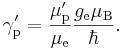
$~gamma^{prime}_{rm p} = frac{mu^{prime}_{rm p}}{mu_{rm e}} frac{g_{rm e} mu_{rm B}}{hbar}.$

Дальнейшее
усложнение связано с тем, что для измерения γ′_p
необходимо измерение электрического тока. Этот ток независимо измеряется в условных амперах, поэтому для перевода в
амперы системы СИ требуется коэффициент пересчёта. Символом Γ′_p-90 обозначается измеряемое
гиромагнитное отношение в условных электрических единицах (разрешённое
использование данных единиц началось с начала 1990 г.). Эта величина может
измеряться двумя способами, методом “слабого поля” и методом
“сильного поля”, и коэффициент пересчёта в этих случаях получается
различным. Обычно для измерения постоянной Планка используется метод сильного
поля и значение Γ′_p-90(hi):

$~gamma^{prime}_{rm p} = frac{K_{rm J-90} R_{rm K-90}}{K_{rm J} R_{rm K}} Gamma^{prime}_{rm p-90}({rm hi}) = frac{K_{rm J-90} R_{rm K-90} e}{2} Gamma^{prime}_{rm p-90}({rm hi}).$

После
замены получается выражение для постоянной Планка через Γ′_p-90(hi):

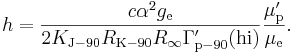
$~h = frac{c alpha^2 g_{rm e}}{2 K_{rm J-90} R_{rm K-90} R_{infty} Gamma^{prime}_{rm p-90}({rm hi})} frac{mu_{rm p}^{prime}}{mu_{rm e}}.$

Постоянная Фарадея

Основная статья: Постоянная Фарадея

Постоянная
Фарадея F есть заряд одного моля
электронов, равный числу Авогадро N_A,
умноженному на элементарный электрический заряд e. Она может быть определена при тщательных экспериментах по
электролизу, путём измерения количества серебра, перемещённого с одного
электрода на другой за данное время при заданном электрическом токе. На
практике она измеряется в условных электрических единицах, и обозначается F₉₀. Подставляя значения N_A и e, и переходя от условных электрических единиц к единицам
СИ, получают соотношение для постоянной Планка:

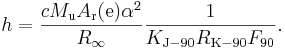
$~h = frac{c M_{rm u} A_{rm r}({rm e})alpha^2}{R_{infty}} frac{1}{K_{rm J-90} R_{rm K-90} F_{90}}.$

Рентгеновская
плотность кристалла

Метод рентгеновской
плотности кристалла является основным методом измерения постоянной Авогадро N_A, а через неё и постоянной
Планка h. Для нахождения N_A берётся отношение между
объёмом элементарной ячейки кристалла, измеряемой методом рентгеноструктурного
анализа, и молярным объёмом вещества. Используются кристаллы кремния, поскольку
они доступны с высоким качеством и чистотой благодаря технологии, развитой при
производстве полупроводников. Объём элементарной ячейки вычисляется из
пространства между двумя кристаллическими плоскостями, обозначаемыми d₂₂₀. Молярный объём V_m(Si) вычисляется через
плотность кристалла и атомный вес используемого кремния. Постоянная Планка
даётся выражением:

$~h = frac{M_{rm u} A_{rm r}({rm e}) c alpha^2}{R_{infty}} frac{sqrt{2}d^3_{220}}{V_{rm m}({rm Si})}.$

Постоянная Планка в системе единиц СИ

Основная статья: Килограмм

Как было
указано выше, численное значение постоянной Планка зависит от используемой
системы единиц. Её значение в системе единиц СИ известно с точностью 1,2∙10^–8,
хотя в атомных (квантовых) единицах она определяется точно (в атомных единицах путём выбора единиц энергии и
времени можно добиться того, чтобы постоянная Дирака как редуцированная
постоянная Планка равнялась 1). Такая же ситуация имеет место в условных
электрических единицах, где постоянная Планка (записывается h₉₀ в отличие от обозначения в
СИ) даётся выражением:

$~h_{90} = frac{4}{K_{J-90}^2 R_{K-90}},$

где K_J–90 и R_K–90 являются точно
определёнными постоянными. Атомные единицы и условные электрические единицы
удобно использовать в соответствующих областях, так как неопределенности в окончательном
результате зависят только от неопределённостей измерений, не требуя
дополнительного и вносящего неточность коэффициента пересчёта в систему СИ.

Существует
ряд предложений по модернизации значений существующей системы базовых единиц СИ
с помощью фундаментальных физических констант.^[23]
Это уже было сделано для метра, который определяется через заданное значение
скорости света. Возможной следующей единицей для пересмотра является килограмм,
чьё значение фиксируется с 1889 г. массой малого цилиндра из платиноиридиевого
сплава, хранящегося под тремя стеклянными колпаками. Имеется порядка 80 копий
таких стандартов массы, которые периодически сравниваются с международной
единицей массы. Точность вторичных эталонов изменяется со временем за счёт их использования,
вплоть до значений в десятки микрограммов. Это приблизительно соответствует
неточности в определении постоянной Планка.

На 24-й
Генеральной конференции по мерам и весам 17—21 октября 2011 года была
единогласно принята резолюция, ^[24] в
которой, в частности, предложено в будущей ревизии Международной системы единиц
(СИ) переопределить единицы измерений СИ таким образом, чтобы постоянная Планка
была равной точно 6,62606X• 10⁻³⁴ Дж•с, где Х заменяет одну или
более значащих цифр, которые будут определены в дальнейшем на основании
наиболее точных рекомендаций CODATA. ^[25]. В этой
же резолюции предложено таким же образом определить как точные значения
постоянную Авогадро, элементарный заряд и постоянную Больцмана.

Постоянная
Планка в теории бесконечной вложенности материи

В отличие от атомизма, в теории бесконечной вложенности
материи отсутствуют материальные объекты – частицы с минимальной
массой или размерами. Вместо этого предполагается бесконечная делимость материи
на всё более уменьшающиеся структуры, и одновременно существование множества
объектов, по размерам значительно превышающих нашу Метагалактику. При этом
материя организуется в отдельные уровни по массам и размерам, для которых
возникает подобие уровней материи,
проявляется масштабное измерение и
осуществляется квантованность параметров
космических систем.

Так же
как постоянная Больцмана и ряд других констант, постоянная Планка отражает
свойства, присущие уровню элементарных частиц (в первую очередь нуклонам и электронам, составляющим вещество). С одной
стороны, постоянная Планка связывает энергию фотонов и их частоту; с другой
стороны, она с точностью до небольшого численного коэффициента 2π, в виде постоянной Дирака ħ задаёт единицу орбитального
момента электрона в атоме. Такая связь не случайна, поскольку при излучении из
атома электрон уменьшает свой орбитальный момент импульса, передавая его фотону
за период существования возбуждённого состояния. За один период обращения электронного
облака вокруг ядра фотон получает такую долю энергии, которая соответствует
доле переданного электроном момента импульса. Средняя частота фотона близка к
частоте вращения электрона вблизи уровня энергии, куда электрон переходит при
излучении, поскольку мощность излучения электрона быстро нарастает при
приближении к ядру.

Математически
это можно описать так. Уравнение вращательного движения имеет вид:

$~K =frac{dL}{dt},$

где K – момент
силы, L
– момент импульса. Если умножить это соотношение на приращение угла вращения и
учесть, что есть изменение энергии вращения электрона, а $omega =frac{d varphi }{dt}$ есть угловая частота орбитального
вращения, то будет:

В этом
соотношении энергию dE
можно трактовать как приращение энергии излучаемого фотона при приращении им
момента импульса на величину dL. Для полной энергии фотона E и полного момента импульса фотона
величину ω следует понимать как
усреднённую угловую частоту фотона. ^{[26] [27]}

В
дополнение к корреляции свойств излучаемых фотонов и атомных электронов через
момент импульса, атомные ядра также обладают моментами импульса, выражаемыми в
единицах ħ. Можно поэтому предположить, что постоянная Планка описывает
вращательное движение элементарных частиц (спин
нуклонов, ядер и электронов, орбитальное движение электронов в атоме), и
преобразование энергии вращения и колебаний заряженных частиц в энергию
излучения. Кроме этого, основываясь на идее корпускулярно-волнового дуализма, в
квантовой механике всем частицам приписывается сопутствующая им материальная
волна де Бройля. Эта волна рассматривается в виде волны амплитуды вероятности
нахождения частицы в той или иной точке пространства. Как и для фотонов,
постоянные Планка и Дирака в таком случае становятся коэффициентами
пропорциональности для квантовой частицы, входя в выражения для импульса
частицы , для энергии E и для действия S:

где –
волновой вектор, λ и ν –
длина и частота соответствующей волны, ω – угловая
частота волны, φ – фаза волны.

Если
теперь перейти к другим уровням материи, то для них также можно определить
характерные моменты импульса и соответствующие постоянные. Используя
коэффициенты подобия между уровнями материи и SPФ-симметрию,
для уровня вырожденных звёздных объектов типа нейтронных звёзд было найдено,
что h’_s = h’_s
= h ∙ Ф’ ∙ S’ ∙ Р’ = 3,5∙10⁴² Дж∙с (здесь Ф’ ∙ S’ ∙ Р’
– коэффициенты подобия по массе, скоростям
процессов и размерам соответственно). ^[28] ^[29]Величина h’_s называется звёздная постоянная
Планка. С помощью коэффициентов подобия могут быть определены
аналогичные постоянные для каждого уровня материи, как характерные моменты
импульса и действия типичных объектов на этих уровнях.

См. также

Спин
Введение в квантовую
механику
Планковские единицы
Квант
Корпускулярно-волновой
дуализм
Принцип неопределённости Гейзенберга
Бесконечная вложенность материи
Подобие уровней материи
SPФ-симметрия
Квантованность параметров космических
систем
Звёздные постоянные
Звёздная постоянная Планка
Звёздная постоянная Дирака
Дискретность параметров звёзд
Водородная система
Длина
волны де Бройля

Ссылки

Fundamental Physical Constants
— Complete Listing.
^а ^б ^в ^г Planck, Max (1901), “Ueber das Gesetz der
Energieverteilung im Normalspectrum”, Ann. Phys. Vol. 309 (3), P. 553–63,
doi:10.1002/andp.19013090310, English translation: “On the Law of
Distribution of Energy in the Normal Spectrum”.
Kragh, Helge (1 December 2000), Max Planck: the reluctant revolutionary, PhysicsWorld.com.
Kragh, Helge (1999), Quantum Generations: A History
of Physics in the Twentieth Century, Princeton University Press, p. 62, ISBN
0691095523.
Planck, Max (2 June 1920), The Genesis and Present State
of Development of the Quantum Theory (Nobel Lecture).
Previous Solvay Conferences on
Physics, International Solvay Institutes, 12 декабря 2008 г.
^а ^б Arrhenius, Svante (10 December 1922), Presentation speech of the 1921
Noble Prize for Physics.
^а ^б ^в Lenard, P. (1902), “Ueber die
lichtelektrische Wirkung”, Ann. Phys. Vol. 313 (5), P. 149–98,
doi:10.1002/andp.19023130510
Einstein, Albert (1905), “Über einen die Erzeugung
und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt”, Ann. Phys. Vol. 17, P.
132–48, doi:10.1002/andp.19053220607.
^а ^б ^в ^г Millikan, R. A. (1916), “A Direct
Photoelectric Determination of Planck’s h”, Phys. Rev. 7: 355–88,
doi:10.1103/PhysRev.7.355.
Bohr, Niels (1913), “On the Constitution of
Atoms and Molecules” Phil. Mag., Ser. 6, Vol. 26, P. 1–25.
Mohr, Peter J.; Newell,
David B.; Taylor, Barry N. (2015). “CODATA recommended values of the
fundamental physical constants: 2014”. Zenodo. arXiv: 1507.07956. doi: 10.5281/zenodo.22826.
Kibble, B. P.; Robinson, I. A.; Belliss, J. H.
(1990), “A Realization of the SI Watt by the NPL Moving-coil
Balance”, Metrologia, Vol. 27 (4), p.173–92,
doi:10.1088/0026-1394/27/4/002.
Steiner, R.; Newell, D.; Williams, E. (2005), “Details of the 1998 Watt
Balance Experiment Determining the Planck Constant”, J. Res. Natl. Inst. Stand.
Technol. Vol. 110 (1), P. 1–26.
^а ^б Steiner, R. L.; Williams, E. R.; Liu, R.;
Newell, D. B. (2007), “Uncertainty Improvements of the NIST
Electronic Kilogram”, IEEE Trans. Instrum. Meas. Vol. 56 (2), P.
592–96, doi:10.1109/TIM.2007.890590.
Fujii, K.; Waseda, A.; Kuramoto, N.; Mizushima,
S.; Becker, P.; Bettin, H.; Nicolaus, A.; Kuetgens, U.; Valkiers, S.; Taylor,
P.; De Bievre, Paul; Mana, G.; Massa, E.; Matyi, R.; Kessler, E.G., Jr.;
Hanke, M. (2005), “Present state of the avogadro constant
determination from silicon crystals with natural isotopic
compositions”, IEEE Trans. Instrum. Meas. Vol. 54 (2), P. 854–59,
doi:10.1109/TIM.2004.843101.
Sienknecht, Volkmar; Funck, Torsten (1985),
“Determination of the SI Volt at the PTB”, IEEE Trans. Instrum.
Meas. Vol. 34 (2), P. 195–98, doi:10.1109/TIM.1985.4315300. Sienknecht,
V.; Funck, T. (1986), “Realization of the SI Unit Volt by Means of a
Voltage Balance”, Metrologia Vol. 22 (3), P. 209–12,
doi:10.1088/0026-1394/22/3/018. Funck, T. (1991), “Determination of
the volt with the improved PTB voltage balance”, IEEE Trans. Instrum.
Meas. Vol. 40 (2), P. 158–61, doi:10.1109/TIM.1990.1032905.
Clothier, W. K.; Sloggett, G. J.; Bairnsfather,
H.; Currey, M. F.; Benjamin, D. J. (1989), “A Determination of the
Volt”, Metrologia, Vol. 26 (1), P. 9–46,
doi:10.1088/0026-1394/26/1/003.
Kibble, B. P.; Hunt, G. J. (1979), “A
Measurement of the Gyromagnetic Ratio of the Proton in a Strong Magnetic
Field”, Metrologia, Vol. 15 (1), P. 5–30,
doi:10.1088/0026-1394/15/1/002.
Liu, R.; Liu, H.; Jin, T.; Lu, Z.; Du, X.; Xue,
S.; Kong, J.; Yu, B.; Zhou, X.; Liu, T.; Zhang, W. (1995), “A Recent
Determination for the SI Values of γ′p and 2e/h at NIM”, Acta Metrol.
Sin. Vol. 16 (3), P. 161–68.
Bower, V. E.; Davis, R. S. (1980), “The
Electrochemical Equivalent of Pure Silver: A Value of the Faraday
Constant”, J. Res. Natl. Bur. Stand. Vol. 85 (3), P. 175–91.
^а ^б ^в P.J. Mohr, B.N. Taylor, and D.B. Newell (2011), “The 2010
CODATA Recommended Values of the Fundamental Physical Constants” (Web
Version 6.0). This database was developed by J. Baker, M. Douma, and S.
Kotochigova. Available: http://physics.nist.gov
[Thursday, 02-Jun-2011 21:00:12 EDT]. National Institute of Standards and
Technology, Gaithersburg, MD 20899.
94th Meeting of the International Committee for
Weights and Measures (2005). Recommendation 1: Preparative steps
towards new definitions of the kilogram, the ampere, the kelvin and the
mole in terms of fundamental constants.
On the possible future revision
of the International System of Units, the SI. Resolution
1 of the 24th meeting of the CGPM (2011).
Agreement to tie kilogram and
friends to fundamentals — physics-math — 25 October 2011 — New Scientist.
Федосин С.Г. Физические
теории и бесконечная вложенность материи, Пермь, 2009, 844 стр., Табл.
21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0 .
Fedosin S.G. The
substantial model of the photon. Journal of Fundamental and Applied
Sciences, Vol. 9, No. 1, pp. 411-467 (2017). http://dx.doi.org/10.4314/jfas.v9i1.25.
// Субстанциональная модель фотона.
Федосин С. Г. Физика
и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, 544
стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
Комментарии
к книге: Федосин С.Г. Физические теории и бесконечная вложенность
материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN
978-5-9901951-1-0.

Литература

Barrow, John D. (2002). The Constants of Nature; From
Alpha to Omega – The Numbers that Encode the Deepest Secrets of the
Universe. Pantheon Books. ISBN 0-375-42221-8.

Внешние
ссылки

История уточнения
постоянной Планка
The NIST Reference on Constants, Units and
Uncertainty
Quantum of Action and Quantum of Spin –
Numericana

Источник

Физика, 11 класс

Урок 22. Фотоэффект

Перечень вопросов, рассматриваемых на уроке:

предмет и задачи квантовой физики;
гипотеза М. Планка о квантах;
опыты А.Г. Столетова;
определение фотоэффекта, кванта, тока насыщения, задерживающего напряжения, работы выхода, красной границы фотоэффекта;
уравнение Эйнштейна для фотоэффекта;
законы фотоэффекта.

Глоссарий по теме:

Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.

Фотоэффект – это вырывание электронов из вещества под действием света.

Квант – (от лат. quantum — «сколько») — неделимая порция какой-либо величины в физике.

Ток насыщения – некоторое предельное значение силы фототока.

Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.

Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. которую нужно сообщить электрону, для того чтобы он мог преодолеть силы, удерживающие его внутри металла.

Красная граница фотоэффекта – это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.

Основная и дополнительная литература по теме урока:

1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 259 – 267.

2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. – С. 153 – 158.

3. Элементарный учебник физики. Учебное пособие в 3 т./под редакцией академика Ландсберга Г. С.: Т.3. Колебания и волны. Оптика. Атомная и ядерная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 422 – 429.

4. Тульчинский М. Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 157.

Теоретический материал для самостоятельного изучения

В начале 20-го века в физике произошла величайшая революция. Попытки объяснить наблюдаемые на опытах закономерности распределения энергии в спектрах теплового излучения оказались несостоятельными. Законы электромагнетизма Максвелла неожиданно «забастовали». Противоречия между опытом и практикой были разрешены немецким физиком Максом Планком.

Гипотеза Макса Планка: атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями – квантами. Энергия Е каждой порции прямо пропорциональна частоте ν излучения света: E = hν.

Коэффициент пропорциональности получил название постоянной Планка, и она равна:

h = 6,63 ∙ 10^-34Дж∙с.

После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.

Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.

Поведение всех микрочастиц подчиняется квантовым законам. Но впервые квантовые свойства материи были обнаружены именно при исследовании излучения и поглощения света.

В 1886 году немецкий физик Густав Людвиг Герц обнаружил явление электризации металлов при их освещении.

Явление вырывания электронов из вещества под действием света называется внешним фотоэлектрическим эффектом.

Законы фотоэффекта были установлены в 1888 году профессором московского университета Александром Григорьевичем Столетовым.

Схема установки для изучения законов фотоэффекта

Первый закон фотоэффекта: фототок насыщения – максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, – прямо пропорционален интенсивности падающего излучения.

Зависимость силы тока от приложенного напряжения

Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.

Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.

Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.

hν_min= A_в

где А_в– работа выхода электронов;

h – постоянная Планка;

ν_min – частота излучения, соответствующая красной границе фотоэффекта;

с – скорость света;

λкр – длина волны, соответствующая красной границе_.

Фотоэффект практически безынерционен: фототок возникает одновременно с освещением катода с точностью до одной миллиардной доли секунды.

Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.

Для большинства веществ фотоэффект возникает только под действием ультрафиолетового облучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.

Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, “затрудняющее” вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.

Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.

Задерживающее напряжение

Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:

где – максимальная кинетическая энергия электронов;

Е – заряд электрона;

– задерживающее напряжение.

Теорию фотоэффекта разработал Альберт Эйнштейн. На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии:

В 1921 году Альберт Эйнштейн стал обладателем Нобелевской премии, которая, согласно официальной формулировке, была вручена «за заслуги перед теоретической физикой и особенно за открытие закона фотоэлектрического эффекта».

Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны – фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.

Примеры и разбор решения заданий

1. Монохроматический свет с длиной волны λ падает на поверхность металла, вызывая фотоэффект. Фотоэлектроны тормозятся электрическим полем. Как изменятся работа выхода электронов с поверхности металла и запирающее напряжение, если уменьшить длину волны падающего света?

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Работа выхода	Запирающее напряжение

Решение:

Работа выхода – это характеристика металла, следовательно, работа выхода не изменится при изменении длины волны падающего света.

Запирающее напряжение – это такое минимальное напряжение, при котором фотоэлектроны перестают вылетать из металла. Оно определяется из уравнения:

Следовательно, при уменьшении длины волны падающего света, запирающее напряжение увеличивается.

Ответ:

Работа выхода	Запирающее напряжение
не изменится	увеличится

2. Красная граница фотоэффекта для вещества фотокатода λ₀ = 290 нм. При облучении катода светом с длиной волны λ фототок прекращается при напряжении между анодом и катодом U = 1,5 В. Определите длину волны λ.

Решение.

Запишем уравнение для фотоэффекта через длину волны:

Условие связи красной границы фотоэффекта и работы выхода:

Запишем выражение для запирающего напряжения – условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:

Решая систему уравнений (1), (2), (3), получаем формулу для вычисления длины волны λ:

Подставляя численные значения, получаем: λ ≈ 215 нм.

Ответ: λ ≈ 215 нм.

Источник

В 1887 году Г. Герцем был открыт фотоэлектрический эффект, а продолжить его исследования довелось А.Г. Столетову. Ф. Леонард в 1900 году серьезно занялся данным проектом. К тому времени был открыт электрон. Это говорило о том, что фотоэффект состоял в вырывании электронов из вещества под действием падающего на него света.

Данное исследование законов Столетова изображено на рисунке 5.2.1.

Фотоэффект. Фотоны

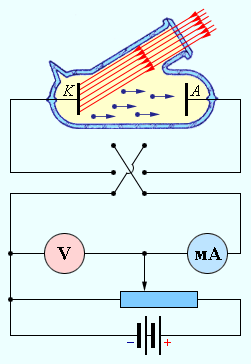
Рисунок 5.2.1. Схема экспериментальной установки для изучения фотоэффекта.

В лабораторных условиях применили стеклянный вакуумный баллон с двумя металлическими электродами с очищенной поверхностью. К ним прикладывали напряжение U с возможностью изменения полярности с помощью ключа. Катод освещали монохроматическим светом с длиной волны λ через кварцевое окошко. Так как световой поток оставался неизменным, то зависимость силы тока I от напряжения ослабевала. Рисунок 5.2.2. наглядно демонстрирует кривые зависимости при интенсивном свете, попадающем на катод.

Фотоэффект. Фотоны

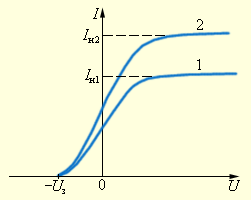
Рисунок 5.2.2. Зависимость силы фототока от приложенного напряжения. Кривая 2 соответствует большей интенсивности светового потока. Iн1 и Iн2 – токи насыщения, Uз – запирающий потенциал.

По графику видно, что при подаче большого напряжения фототок анода А достигает насыщения, потому как при вырывании светом из катода они в состоянии достичь его.

Ток насыщения. Закономерности фотоэффекта

Определение 1

Ток насыщения Iнпрямо пропорционален интенсивности падающего света.

При наличии отрицательного напряжения на аноде, электрическое поле, находящееся между катодом и анодом, тормозится электронами. К аноду могут добраться электроны, у которых кинетическая энергия превышает значение |eU|. При наличии напряжения меньше, чем –Uз, происходит прекращение фототока. После измерения –Uзопределяется максимальная кинетическая энергия фотоэлектронов:

mυ22max=eU3.

Из формулы видно, что оно не зависит от интенсивности падающего света. После глубоких исследований стало ясно, что при возрастании запирающего потенциала происходит линейное увеличение частоты света ν.

Ток насыщения. Закономерности фотоэффекта

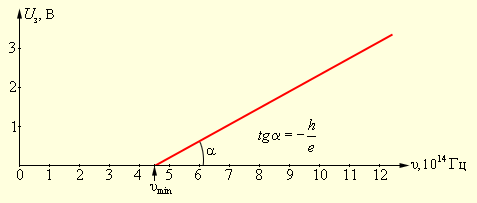
Рисунок 5.2.3. Зависимость запирающего потенциала Uз от частоты ν падающего света.

Определение 2

После многочисленных экспериментов были установлены закономерности формул фотоэффекта:

При увеличении частоты света ν происходит возрастание кинетической энергии, независящей от ее интенсивности.
Наименьшей частотой νminс внешним фотоэффектом называют красную границу фотоэффекта каждого вещества.
Количество фотоэлектронов за 1 с вырывания из катода прямо пропорционально интенсивности света.
Фотоэффект возникает после освещения катода с условием, что ν>νmin_.

Данные закономерности не соответствовали представлениям классической физики о взаимодействии света с веществом. Исходя из волновых представлений, взаимодействие световой волны с электроном должно действовать по принципу постепенного накапливания энергии. Чтобы он смог вылететь из катода, необходимо иметь достаточное количество энергии, накапливаемой за определенный промежуток времени, не зависящий от интенсивности света.

Появление фотоэлектронов происходит сразу после освещения катода. Данная модель не давала четкого представления нахождения красной границы фотоэффекта. Волновая теория света не могла дать объяснение независимости энергии фотоэлектронов от интенсивности светового потока и пропорциональности максимальной кинетической энергии частоты света. Поэтому электромагнитная теория была не способна объяснить эти изменения.

В 1905 году А. Эйнштейн дает теоретическое объяснение наблюдаемых закономерностей фотоэффекта, основываясь на гипотезе М. Планка.

Постоянная Планка. Уравнение Эйнштейна

Определение 3

Излучение и поглощение света происходит определенными порциями, где она определяется формулой E=hν, h принято называть постоянной Планка.

Основной шаг в развитии квантовых представлений относится к Эйнштейну:

Определение 4

Свет обладает прерывистой структурой. Электромагнитная волна состоит из порций, называемых, кварками, спустя время которые зафиксировали как фотоны.

После взаимодействия с веществом фотон передает свою энергию hν одному электрону, одна часть которой рассеивается при столкновениях с атомами, а другая затрачивается на преодоление потенциального барьера на границе металл-вакуум. Для этого ему необходимо совершить работу выхода А, зависящую от свойств материала катода.

Определение 5

Наибольшую кинетическую энергию, вылетевшую из катода фотоэлектроном, определяют законом сохранения энергии:

mν22max=eUe=hν-A.

Формула получила название уравнения Эйнштейна для фотоэффекта.

Благодаря ему, закономерности внешнего явления фотоэффекта могут быть объяснены.

Линейная зависимость максимальной кинетической энергии от частоты и независимость от интенсивности света, существование красной границы, безынерционность фотоэффекта следуют из данного выражения.

Определение 6

Общее количество фотоэлектронов, которые покидают поверхность катода в течение 1 с, пропорционально числу фотонов, падающих на поверхность. Можно сделать вывод, что ток насыщения должен быть прямо пропорционален интенсивности светового потока.

Определение 7

По уравнению фотоэффекта Эйнштейна тангенс угла наклона прямой, выражающий зависимость запирающего потенциала Uз от частоты ν, равняется отношению постоянной Планка h к заряду электрона e:

tg α=he.

Формула позволяет вычислить значение постоянной Планка.

Определение 8

Р. Милликенн проводил измерения в 1914 году, после чего смог определить работу выхода А:

A=hνmin=hcλкр,

где c – скорость света, λкр– длина волны, которая соответствует красной границе фотоэффекта.

Большинство металлов имеет работу выхода А и составляет несколько электрон-вольт (1 эВ = 1,602·10–19 Дж).

Определение 9

Квантовая физика использует электрон-вольт как энергетическую единицу измерения. Тогда значение постоянной Планка равняется

h=4,136·10-15 эВ·с.

Наименьшая работа выхода наблюдается у щелочных элементов. Натрий при A=1,9 эВ соответствует красной границе фотоэффекта λкр≈680 нм. Такие соединения применяют для создания катодов в фотоэлементах, используемых для регистрации видимого света.

Определение 10

Законы фотоэффекта говорят о том, что при пропускании и поглощении свет ведет себя подобно потоку частиц, называемых фотонами или световыми квантами.

Определение 11

Энергия фотонов записывается в виде формулы E=hν.

Определение 12

При движении в вакууме фотон обладает скоростью с, а его масса m=0. Общее соотношение теории относительности, связывающее энергию, импульс и массу любой частицы, записывается как E2=m2c4+p2c2.

Отсюда следует, что фотон обладает импульсом, значит:

p=Ec=hνc.

Можно сделать вывод, что учение о свете вернулось к представлениям о световых частицах – корпускулах. Но это не расценивается как возврат к корпускулярной теории Ньютона. В XX было известно о двойственной природе света. Когда он распространялся, то проявлялись его волновые свойства (интерференция, дифракция, поляризация), при его взаимодействии с веществом – корпускулярные, то есть явление фотоэффекта. Это и получило название корпускулярно-волнового дуализма.

Спустя время, данная теория была подтверждена у других элементарных частиц. Классическая физика не дает наглядную модель сочетаний волновых и корпускулярных свойств микрообъектов. Их движениями управляют законы квантовой механики. В основе этой науки лежит теория абсолютно черного тела, доказанная М. Планком, и квантовая, предложенная Эйнштейном.

Постоянная Планка. Уравнение Эйнштейна

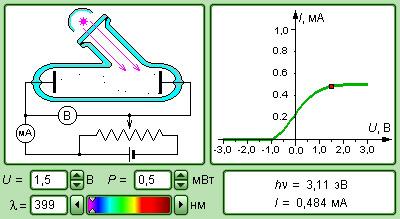
Рисунок 5.2.4. Модель фотоэффекта

Источник

Фотоэффект. Определение постоянной планка и работы выхода электронов

Цель
работы: ознакомление с явлением внешнего
фотоэффекта и определение постоянной
Планка и работы выхода электронов из
металла.

Электромагнитное
излучение обладает двойственной
природой. При взаимодействии с веществом
оно проявляет себя как поток частиц –
фотонов с энергией Е и импульсом Р,
равными

Е = hν, Р = kh/2π.
(1)

Под действием
электромагнитного излучения электроны
могут вылетать из вещества. Это явление
называют фотоэффектом.

С точки зрения
квантовой теории света взаимодействие
света с электронами вещества можно
рассматривать как неупругое столкновение
фотона с электроном. При таком столкновении
фотон поглощается, а его энергия
передается электрону. Таким образом, в
результате единичного акта столкновения
электрон приобретает дополнительную
энергию.

Кинетическая энергия электрона частично
тратится на совершение выхода А против
задерживающих сил, действующих в
поверхностном слое вещества, а оставшаяся
часть кинетической энергии есть
максимальная кинетическая энергия
вылетевшего фотоэлектрона. Уравнение
Эйнштейна, описывающее баланс энергии
для взаимодействия фотона с электроном
имеет вид

hν
= А + Е_max,
(2)

где
hν – энергия поглощенного фотона, А –
работа выхода электрона, Е_max
– максимальная
кинетическая энергия вылетевшего
фотоэлектрона. Здесь предполагается,
что кинетическая энергия электрона в
веществе до поглощения фотона много
меньше энергии фотона.

При
экспериментальном изучении фотоэффекта
используется двухэлектродная лампа-диод.
Один из электродов – катод, освещается
светом определенной частоты. Вылетающие
фотоэлектроны достигают анода. При
фиксированной частоте и постоянной
мощности падающего света типичная
зависимость силы фототока I от приложенного
напряжения U между катодом и анодом
приведена на рис.1.

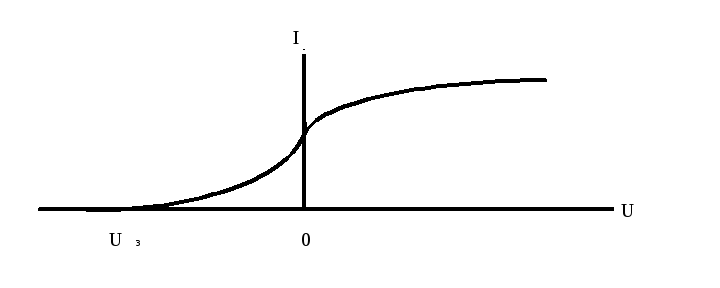
Рис.1

При
некотором отрицательном напряжении
U_з,
называемом запирающим
напряжением,
фототок обращается в нуль. Это связано
с тем, что максимальной кинетической
энергии вылетающих фотоэлектронов Е_max
недостаточно для совершения работы
eU_з
против тормозящих сил электрического
поля между катодом и анодом ( e – заряд
электрона). Согласно уравнению Эйнштейна
(1), величина U_з
для определенного фотокатода прямо
пропорциональна частоте ν падающего
света

eU_з
= Е_max=
hν – А. (3)

Для
каждого вещества существует минимальная
частота ν_min,
при превышении которой может наблюдаться
фотоэффект. Она определяется из условия
Е_max
= 0 и описывается формулой

ν_min
= А/h. (4)

Соответствующая
длина волны, называемая красной
границей фотоэффекта,
равна

λ_max
= c /ν_min,
(5)

где
с – скорость света.

В
данной работе осуществляется
экспериментальная проверка уравнения
Эйнштейна (2) для фотоэффекта и измеряются
значения постоянной Планка h и работы
выхода электронов А для материала
катода.

Соседние файлы в предмете Физика

Источник

Физический смысл[править | править код]

История открытия[править | править код]

Формула Планка для теплового излучения[править | править код]

Фотоэффект[править | править код]

Эффект Комптона[править | править код]

Переопределение[править | править код]

Значения постоянной Планка[править | править код]

Методы измерения[править | править код]

Использование законов фотоэффекта[править | править код]

Анализ спектра тормозного рентгеновского излучения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Комментарии[править | править код]

Источники[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Содержание

Величина

Происхождение постоянной Планка

Излучение чёрного тела

Фотоэффект

Структура атома

Принцип неопределённости

Спектр тормозного рентгеновского излучения

Физические константы, связанные с постоянной Планка

Масса покоя электрона

Постоянная Авогадро

Элементарный заряд

Магнетон Бора и ядерный магнетон

Определение из экспериментов

Постоянная Джозефсона

Баланс мощности

Магнитный резонанс

Постоянная Фарадея

Рентгеновская плотность кристалла

Постоянная Планка в системе единиц СИ

Постоянная Планка в теории бесконечной вложенности материи

См. также

Ссылки

Литература

Внешние ссылки

Ток насыщения. Закономерности фотоэффекта

Постоянная Планка. Уравнение Эйнштейна

Фотоэффект. Определение постоянной планка и работы выхода электронов

Вам также может понравиться

Гта 4 как исправить пьяную камеру

Сайт как можно найти солдата

Как найти среднюю налоговую ставку

Добавить комментарий Отменить ответ

Происхождение
постоянной Планка

Излучение
чёрного тела

Структура
атома

Принцип
неопределённости

Спектр
тормозного рентгеновского излучения

Физические
константы, связанные с постоянной Планка

Масса покоя
электрона

Элементарный
заряд

Магнетон
Бора и ядерный магнетон

Определение
из экспериментов

Баланс
мощности

Магнитный
резонанс

Рентгеновская
плотность кристалла

Постоянная
Планка в теории бесконечной вложенности материи

Внешние
ссылки