Работа силы упругости


4.4
Средняя оценка: 4.4
Всего получено оценок: 465.
4.4
Средняя оценка: 4.4
Всего получено оценок: 465.
В повседневной жизни часто приходится встречаться с таким понятием как работа. Что это слово означает в физике и как определить работу силы упругости? Ответы на эти вопросы вы узнаете в статье.
Механическая работа
Работа – это скалярная алгебраическая величина, которая характеризует связь между силой и перемещением. При совпадении направления этих двух переменных она вычисляется по следующей формуле:
A=FS
Где:
- F – модуль вектора силы, которая совершает работу;
- S – модуль вектора перемещения.
Не всегда сила, которая действует на тело, совершает работу. Например, работа силы тяжести равна нулю, если ее направление перпендикулярно перемещению тела.
Если вектор силы образует отличный от нуля угол с вектором перемещения, то для определения работы следует воспользоваться другой формулой:
A=FScosα
Где:
α – угол между векторами силы и перемещения.
Значит, механическая работа – это произведение проекции силы на направление перемещения и модуля перемещения, или произведение проекции перемещения на направление силы и модуля этой силы.
Знак механической работы
В зависимости от направления силы относительно перемещения тела работа A может быть:
- положительной (0°≤ α<90°);
- отрицательной (90°<α≤180°);
- равной нулю (α=90°).
Если A>0, то скорость тела увеличивается. Пример – падение яблока с дерева на землю. При A<0 сила препятствует ускорению тела. Например, действие силы трения скольжения.
Единица измерения работы в СИ (Международной системе единиц) – Джоуль (1Н*1м=Дж). Джоуль – это работа силы, значение которой равно 1 Ньютону, при перемещении тела на 1 метр в направлении действия силы.
Работа силы упругости
Работу силы можно определить и графическим способом. Для этого вычисляется площадь криволинейной фигуры под графиком Fs(x).
Так, по графику зависимости силы упругости от удлинения пружины, можно вывести формулу работы силы упругости.
Она равна:
A=kx2/2
Где:
- k – жесткость;
- x – абсолютное удлинение.

Что мы узнали?
Механическая работа совершается при действии на тело силы, которая приводит к перемещению тела. В зависимости от угла, который возникает между силой и перемещением, работа может быть равна нулю или иметь отрицательный или положительный знак. На примере силы упругости вы узнали о графическом способе определения работы.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Саша Волков
5/5
-

Николай Топченский
5/5
-

Катя Пу
5/5
Оценка доклада
4.4
Средняя оценка: 4.4
Всего получено оценок: 465.
А какая ваша оценка?
Сила упругости, как и
сила тяжести, является консервативной. Напомним, что консервативная сила —
это такая сила, работа которой при движении тела по замкнутому контуру, равна
нулю. В одном из уроков мы уже убедились, что работу силы упругости нельзя
вычислить, пользуясь общей формулой для работы силы. Дело в том, что сила
упругости изменяется с изменением растяжения или сжатия пружины. Поэтому нам
необходимо будет воспользоваться графиком зависимости силы упругости от
удлинения.
Поскольку сила упругости
линейно зависит от удлинения, нам не составит труда найти площадь под графиком
функции силы упругости. Эта площадь и будет являться работой. На графике
зависимости силы упругости от удлинения обозначим два произвольных значения
силы: F1
и F2.
Этим значениям будут соответствовать значения удлинения х1 и х2.
Как видно из графика, чтобы найти работу, нам нужно вычислить площадь трапеции.
Площадь трапеции равна произведению полусуммы оснований и высоты. Очевидно, что
основания — это F1
и F2,
а высота равна х1 − х2. Тогда,
используя формулу для силы упругости, мы можем вывести окончательное выражение
для работы силы упругости:
Напомним, что изучая
работу силы, мы пришли к выводу, что работа равна изменению кинетической
энергии. В данном случае мы видим, что работа силы упругости равна изменению
потенциальной энергии пружины. Но о потенциальной энергии мы поговорим
немного позже.
Итак, мы выяснили, что работа
силы упругости, так же, как и работа силы тяжести, не зависит от траектории
движения.
Пример решения задачи.
Задача.
Когда пружину, изначально находящуюся в расслабленном состоянии, растянули на 2
см, сила упругости составила 5 Н. Найдите работу силы упругости при растяжении этой
пружины на 8 см.
Работа силы упругости — работа, совершаемая силой упругости при изменении деформации пружины от некоторого начального значения x1 до конечного значения x2
![]()
Коэффициент жесткости пружины k называется жесткостью тела, он зависит от материала, из которого тело изготовлено, а также от его геометрических размеров и формы. Жесткость выражается в ньютонах на метр (Н/м).
Сила упругости зависит только от изменения расстояний между взаимодействующими частями данного упругого тела. Работа силы упругости не зависит от формы траектории и при перемещении по замкнутой траектории равна нулю. Поэтому силы упругости являются потенциальными силами.
Обозначения:
A — Работа силы упругости
k — Коэффициент упругости пружины
x — Деформация пружины
Работа силы упругости — работа, совершаемая силой упругости при изменении деформации пружины от некоторого начального значения x1 до конечного значения x2
![]()

Вывод формулы работы силы упругости ( через интеграл )

Коэффициент жесткости пружины k называется жесткостью тела, он зависит от материала, из которого тело изготовлено, а также от его геометрических размеров и формы. Жесткость выражается в ньютонах на метр (Н/м). Сила упругости зависит только от изменения расстояний между взаимодействующими частями данного упругого тела. Работа силы упругости не зависит от формы траектории и при перемещении по замкнутой траектории равна нулю. Поэтому силы упругости является потенциальными силами.
В формуле мы использовали :
![]() — Работа силы упругости
— Работа силы упругости
![]() — Коэффициент упругости пружины
— Коэффициент упругости пружины
![]() — Деформация пружины
— Деформация пружины
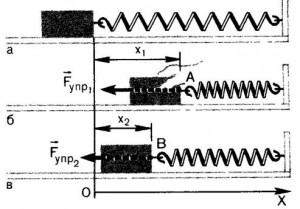
Сила упругости, как мы знаем, возникает при деформации тел. По своему абсолютному значению она пропорциональна величине деформации (удлинению), а направлена в сторону, противоположную направлению смещения точек тела при деформации.

рис. 1
На рисунке 1, а показана пружина в ее естественном, недефор-мнрованном состоянии. Правый конец пружины закреплен, а к левому прикреплено тело. Если пружину сжать, сместив левый ее конец на расстояние $x_{1}$ (рис. 1, б), то возникнет сила упругости, действующая со стороны пружины на тело, равная:
$F_{1упр} = – kx_{1}$,
где $k$ – жесткость пружины.
При перемещении витков пружины сила упругости совершит работу. Какова величина этой работы?
Предположим, что левый конец пружины переместился из положения $A$ в положение $B$ (рис. 1, в). В этом положении деформа ция пружины равна уже не $x_{1}$, а $x_{2}$. Значит, конец пружины переместился на расстояние $x_{2} – x_{1}$. Чтобы вычислить работу, нужно это перемещение умножить на силу. Но сила упругости в отличие от силы тяжести вблизи поверхности Земли при движении тела изменяется от точки к точке. Если в начальной точке она была равна $- kx_{1}$, то в конечной точке (в точке $B$) она стала равной $-kx_{2}$.
Для того чтобы вычислить работу силы упругости, нужно взять среднее значение силы упругости и умножить его на перемещение $x_{2} – x_{1}$ (см. §75).
Сила упругости пропорциональна деформации пружины. Поэтому среднее значение силы упругости можно найти, используя метод, который был использован при нахождении среднего значения скорости при равноускоренном движении.
Для среднего значения скорости при равноускоренном движении мы получили формулу
$v_{ср} = frac{v_{1} + v_{0} }{2}$,
где $v_{0}$ – начальное и $v_{1}$ – конечное значение скорости. Подобно этому среднее формуле значение силы упругости можно определить по
$F_{упр.ср} = – k frac{x_{1} + x_{2} }{2}$.
На это-то значение силы упругости и нужно умножить перемещение $x_{2} – x_{1}$, чтобы получить работу этой силы:
$A = – k frac{x_{1} + x_{2} }{2} (x_{2} – x_{1})$.
Так как $(x_{1} + x_{2}) (x_{2} – x_{1}) = x_{2}^{2} – x_{1}^{2}$, то формула для работы принимает вид:
$A = frac{k}{2} (x_{1}^{2} – x_{2}^{2} )$.
Работа силы упругости равна половине произведения жесткости упругого тела на разность квадратов его начального и конечного удлинений.
Если конечное удлинение пружины равняется нулю ($x_{2} = 0$), т. е. пружина приходит в недеформированное состояние, то она совершает работу
$A = frac{kx^{2} }{2}$,
где $x$ – начальное удлинение пружины.
Интересно, что работа силы упругости имеет некоторое сходство с работой силы тяжести. Если сравнить выражения для работы этих двух сил:
$A = mg (h_{1} – h_{2})$
и $A = frac{k}{2} (x_{1}^{2} – x_{2}^{2} )$,
то можно заметить, что в обоих случаях работа зависит от начального и конечного положений тела. В первой формуле высота $h$ определяет положение тела, на которое действует сила тяжести (например, относительно поверхности Земли). Во второй формуле удлинение $x$ определяет положение одного конца пружины относительно другого ее конца.
Работа как силы упругости, так и силы тяжести зависит не от формы, или длины пути, а только от начального и конечного положений движущегося тела.
Задача. При столкновении вагонов их буфера (по два на каждом вагоне) сжались на 5 см. Какая работа была при этом совершена силами упругости пружин, если известно, что при сжатии буфера на 1 см возникает сила упругости в 10 000 Н?
Решение. Вычислим сначала работу одной из четырех пружин. Для этого воспользуемся формулой
$A = frac{k}{2} (x_{1}^{2} – x_{2}^{2} )$.
Подставив сюда приведенные в условии задачи значения, получим:
$A = frac{10^{2} Н/м}{2} [0 – (0,05 м)^{2}] = – 1 250 Дж$.
Так как у сталкивающихся вагонов четыре пружины, то общая работа сил упругости равна – 5000 дж. Знак «минус» означает, что сила упругости пружин направлена против направления перемещения вагонов.
