Определение натуральной величины сечения
Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.
Дано: чертеж «Сечение комбинированной поверхности плоскостью».
Задание: Построить натуральную величину сечения, применив для этого любой способ преобразования чертежа.
Решение задачи по начертательной геометрии на определение натуральной величины сечения:
Все способы преобразования чертежа представлены в виде практических видеоуроков по НГ/Автокад в разделе «Способы преобразования чертежа».
В этом видеоуроке мы будем использовать способ перемены плоскостей проекций. Мы уже решили несколько задач по начертательной геометрии, используя способ перемены плоскостей проекций, вот некоторые из них:
- Построение натуральной величины сечения.
- Способ замены (перемены) плоскостей проекций для нахождения натуральной величины сечения цилиндра.
Алгоритм решения задачи с использованием способа замены (перемены) плоскостей проекции
- Вводим новую плоскость, которая будет располагаться параллельно отрезка, в который проецируется сечение комбинированной поверхности на горизонтальной плоскости проекции.
- Строим линии связи.
- На линиях проекционной связи откладываем координаты Z точек сечения цилиндра.
Повторим специальную команду Выровнять в Автокад, которая ускорит построение натуральной величины сечения в 3 раза.
Более подробно в видеоуроке по начертательной геометрии в Автокад.
Видео “Определение натуральной величины сечения – Способ перемены плоскостей проекций”

7.1. Общие понятия и определения. 7.2. Сечения многогранников и тел вращения плоскостями частного положения. Определение натуральной величины сечения. 7.3. Сечения многогранников и тел вращения плоскостями общего положения. Определение натуральной величины сечения
7.1. Общие понятия и определения
Сечением называется плоская фигура, полученная в результате пересечения геометрического тела секущей плоскостью и содержащая точки, принадлежащие поверхности тела и плоскости.
Сечение ограничивается замкнутой ломаной линией, если плоскостью пересекается гранная поверхность, и замкнутой кривой линией, если плоскостью пересекается кривая поверхность.
Построение линии сечения в общем случае сводится к определению точек пересечения ребер многогранника или образующих кривой поверхности с секущей плоскостью. Следовательно, построение линии сечения сводится к множественной задаче определения точек пересечения прямой с плоскостью.
7.2. Сечения многогранников и тел вращения плоскостями частного положения. Определение натуральной величины сечения
Сечение поверхностей гранных геометрических тел плоскостями частного положения. Сечением многогранника плоскостью является плоский многоугольник, вершины которого принадлежат ребрам, а стороны — граням многогранника. В зависимости от вида гранной поверхности и положения секущей плоскости сечение может принимать различные геометрические фигуры. Например, при пересечении поверхностей прямых правильных призмы и пирамиды плоскостями возможно образование геометрическихфигур, показанныхнарис. 88 и89.
Рис. 88. Сечение прямой призмы плоскостями частного положения
101
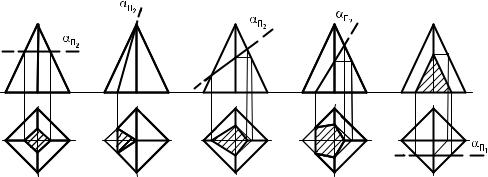
Рис. 89. Сечение прямой пирамиды плоскостями частного положения
Построение линии пересечения многогранника плоскостью сводится к многократному решению задачи на определение точек пересечения ребер многогранника с секущей плоскостью. Определение натуральной величины сечения гранной поверхности плоскостью определяют любым известным способом, например, способом совмещения секущей плоскости с плоскостью проекций, способом вращения, способом замены плоскостей проекций и т. д.
Рассмотрим некоторые примеры.
З а д а ч а 19
Дано: прямая шестигранная пирамида ABCDEFS с вершиной в точке S и фронтально-проецирующая плоскость α (рис. 90).
Выполнить: 1) построить линию пересечения пирамиды плоскостью; 2) определить натуральную величину сечения пирамиды плоскостью.
Порядок выполнения:
1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α
обладает собирательным свойством (любой геометрический элемент, принадлежащий фронтально-проецирующей плоскости, в т. ч. и линия пересечения пирамиды плоскостью, будет проецироваться в ее фронтальный след). Следовательно, пересечение фронтального следа αΠ2 с ребрами пирамиды образует фронтальную проекцию сечения
геометрического тела плоскостью 122232425262.
2.Горизонтальную проекцию сечения геометрического тела плос-
костью 112131415161 определяют из условия принадлежности точки прямой.
3.Натуральную величину сечения пирамиды плоскостью в данной задаче определяют способом вращения, совмещая секущую плоскость
сгоризонтальной плоскостью проекций, однако допустимо применение и любого другого способа.
102
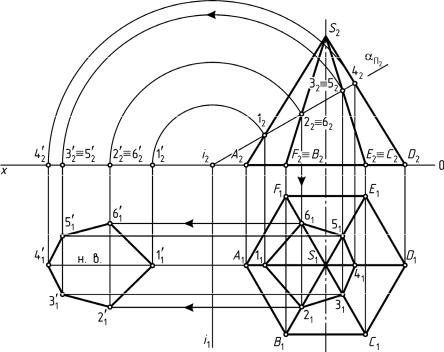
Рис. 90. Пересечение прямой пирамиды плоскостью частного положения
З а д а ч а 20 Дано: прямая шестигранная призма и фронтально-проецирующая
плоскость α (рис. 91).
Выполнить: 1) построить линию пересечения призмы плоскостью; 2) определить натуральную величину сечения призмы плоскостью.
Порядок выполнения:
1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α
обладает собирательным свойством (любой геометрический элемент, принадлежащий фронтально-проецирующей плоскости, будет проецироваться в ее фронтальный след). Следовательно, пересечение фронтального следа αΠ2 с ребрами призмы образует фронтальную проек-
цию сечения геометрического тела плоскостью 122232425262.
2.Призматическая поверхность является горизонтально-проеци- рующей, поэтому горизонтальную проекцию сечения геометрического
тела плоскостью 112131415161 определяют из этого условия и условия принадлежности точки прямой.
3.Натуральную величину сечения призмы плоскостью в данной задаче определяют способом вращения, совмещая секущую плоскость
сгоризонтальной плоскостью проекций, однако допустимо применение и любого другого способа.
103
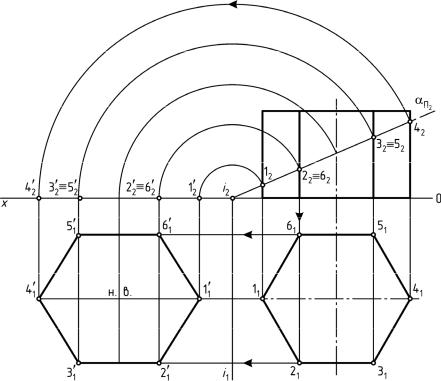
Рис. 91. Пересечение прямой призмы плоскостью частного положения
З а д а ч а 21
Дано: наклонная пирамида ABCDS с вершиной в точке S и горизон- тально-проецирующая плоскость α (рис. 92).
Выполнить: 1) построить линию пересечения пирамиды плоскостью; 2) определить натуральную величину сечения пирамиды плоскостью.
Порядок выполнения:
1. Горизонтальный след αΠ1 горизонтально-проецирующей плос-
кости α обладает собирательным свойством (любой геометрический элемент, принадлежащий горизонтально-проецирующей плоскости, в т. ч. и линия пересечения пирамиды плоскостью, будет проецироваться в ее горизонтальный след). Следовательно, пересечение следа αΠ1 с поверхностью наклонной пирамиды образует горизонтальную
проекциюсечениягеометрическоготелаплоскостью11213141.
2.Фронтальную проекцию сечения геометрического тела плоскостью 12223242 определяют из условия принадлежности точки прямой.
3.Натуральная величина сечения пирамиды плоскостью в данной задаче определена способом плоскопараллельного перемещения и вынесена за пределы графических построений.
104
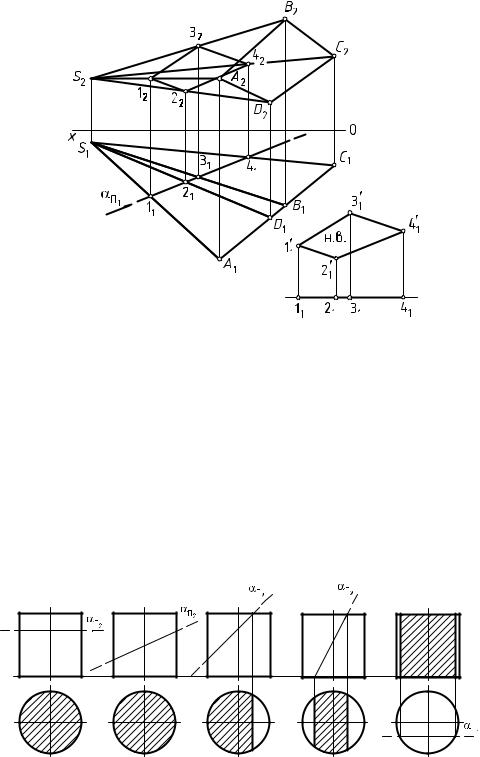
Рис. 92. Пересечение наклонной пирамиды плоскостью частного положения
Сечение поверхностей геометрических тел вращения плоско-
стями частного положения. Сечением тел вращения плоскостью является плоская кривая линия. В зависимости от вида поверхности вращения и положения секущей плоскости сечение может принимать различные геометрические фигуры. Так, при пересечении поверхности прямого кругового цилиндра плоскостью возможно образование следующих геометрических фигур:
окружности, если секущая плоскость перпендикулярна оси цилиндра, такое сечение называют нормальным (рис. 93, а);
эллипса, если секущая плоскость наклонена к оси цилиндра и пересекает все его образующие (рис. 93, б);
|
а |
б |
в |
г |
д |
|
Рис. 93. Пересечение прямого цилиндра плоскостями частного положения |
105
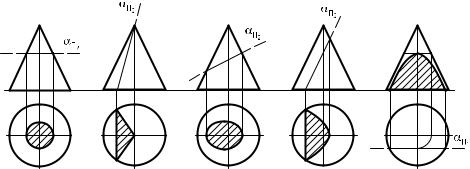
усеченного эллипса, если секущая плоскость наклонена к оси цилиндра и пересекает одно или оба его основания (рис. 93, в и г);
прямоугольника, если секущая плоскость параллельна оси цилинд-
ра (рис. 93, д).
При пересечении поверхности прямого кругового конуса плоскостью возможно образование следующих геометрических фигур:
окружности, если секущая плоскость перпендикулярна оси конуса
(рис. 94, а);
треугольника, если секущая плоскость пересекает конус через его вершину по двум образующим (рис. 94, б);
эллипса, если секущая плоскость наклонена к оси конуса и пересекает все его образующие (рис. 94, в).
параболы, если секущая плоскость параллельна одной из образующих конуса (рис. 94, г);
гиперболы, если секущая плоскость параллельна оси конуса или параллельна двум его образующим (рис. 94, д).
а б в г д
Рис. 94. Пересечение прямого конуса плоскостями частного положения
Построение линии пересечения тел вращения плоскостью сводится к многократному решению задачи на определение точек пересечения образующих кривой поверхности с секущей плоскостью.
Рассмотрим некоторые примеры. З а д а ч а 22
Дано: прямой круговой цилиндр и фронтально-проецирующая плоскость α (рис. 95, а).
Выполнить: 1) построить линию пересечения цилиндра плоскостью; 2) определить натуральную величину сечения цилиндра плоскостью.
Порядок выполнения:
1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α
обладает собирательным свойством. Следовательно, пересечение фронтального следа αΠ2 с поверхностью цилиндра образует фрон-
106

тальную проекцию сечения геометрического тела плоскостью
А21222D23242B25262C27282.
2.Цилиндрическая поверхность является горизонтально-проецирую- щей, поэтому горизонтальную проекцию сечения геометрического тела плоскостью А11121D13141B15161C17181 определяют из этого условия
иусловия принадлежности точки прямой.
3.Натуральную величину сечения цилиндра плоскостью в данной задаче определяют способом замены плоскостей проекций.
Рис. 95. Пересечение геометрических тел плоскостью частного положения
З а д а ч а 23 Дано: сфера и фронтально-проецирующая плоскость α (рис. 95, б).
Выполнить: 1) построить линию пересечения сферы плоскостью; 2) определить натуральную величину сечения сферы плоскостью.
Порядок выполнения:
1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α
обладает собирательным свойством. Следовательно, пересечение фронтального следа αΠ2 с поверхностью сферы образует фронтальную про-
екцию сечения геометрического тела плоскостью 1222426282725232.
107

2.Горизонтальную проекцию сечения геометрического тела
плоскостью 1121416181715131 определяют из условия принадлежности точки прямой.
3.Натуральную величину сечения сферы плоскостью в данной задаче определяют способом замены плоскостей проекций, однако допустимо применение и любого другого способа.
З а д а ч а 24 Дано: прямой круговой конус и фронтально-проецирующая плос-
костьα (рис. 96).
Выполнить: 1) построить линию пересечения конуса плоскостью; 2) определить натуральную величину сечения конуса плоскостью.
Рис. 96. Пересечение прямого конуса плоскостью частного положения
Порядок выполнения:
1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α
обладает собирательным свойством. Следовательно, пересечение фронтального следа αΠ2 с поверхностью конуса образует фронталь-
ную проекцию сечения геометрического тела плоскостью
128242621022292523272.
2. Горизонтальную проекцию сечения геометрического тела плоскостью 118141611012191513171 определяют из условия принадлежности точки прямой.
108
3. Натуральную величину сечения конуса плоскостью в данной задаче определяют способом вращения, совмещая секущую плоскость с горизонтальной плоскостью проекций, однако допустимо применение и любого другого способа.
З а д а ч а 25 Дано: наклонный цилиндр и горизонтально-проецирующая плос-
кость α (рис. 97).
Рис. 97. Пересечение наклонного цилиндра плоскостью частного положения
Выполнить: 1) построить линию пересечения цилиндра плоскостью; 2) определить натуральную величину сечения цилиндра плоскостью.
109
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
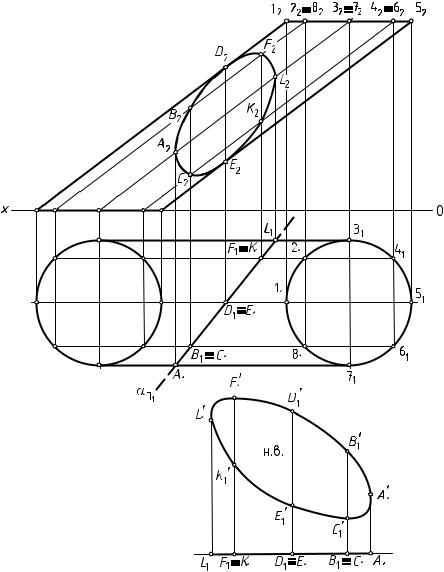
Сечение поверхности конуса плоскостью общего положения
При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.
Ниже мы рассмотрим задачу, в которой требуется построить проекции и натуральную величину сечения конуса ω плоскостью α . Начальные данные представлены на рисунке ниже.

Содержание
- Определение высшей и низшей точки сечения. Границы видимости
- Построение промежуточных точек и проекций эллипса
- Построение натуральной величины сечения методом совмещения
Определение высшей и низшей точки сечения. Границы видимости
Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.
Через ось конической поверхности проведем вспомогательную плоскость γ, параллельную П2. Она пересекает конус ω по двум образующим, а плоскость α по фронтали fγ. Точки 1 и 2 пересечения fγ с образующими являются граничными точками. Они делят сечение на видимую и невидимую части.

Определим высшую и низшую точки линии пересечения. Для этого через ось конуса перпендикулярно h0α введем дополнительную секущую плоскость β. Она пересекает коническую поверхность по образующим SL и SK, а плоскость α по прямой MN. Искомые точки 3 = SL ∩ MN и 4 = SK ∩ MN определяют большую ось эллипса. Его центр находится в точке O, которая делит отрезок 3–4 пополам.
Определение промежуточных точек и построение проекций эллипса
Чтобы построить проекции сечения наиболее точно, найдем ряд дополнительных точек. В случае с эллипсом целесообразно определить величину его малого диаметра. Для этого через центр O проводим вспомогательную горизонтальную плоскость δ. Она пересекает коническую поверхность по окружности диаметром AB, а плоскость α – по горизонтали hδ. Строим горизонтальные проекции окружности и прямой hδ. Их пересечение определяет точки 5′ и 6′ малого диаметра эллипса.
Для построения промежуточных точек 7 и 8 вводим вспомогательную горизонтальную плоскость ε. Проекции 7′ и 8′ определяются аналогично 5′ и 6′, как это показано на рисунке.

Соединив найденные точки плавной кривой, мы получили контур эллиптического сечения. На рисунке он обозначен красным цветом. Фронтальная проекция контура меняет свою видимость в точках 1 и 2, как это было отмечено выше.
Построение натуральной величины сечения методом совмещения
Чтобы найти натуральную величину сечения, повернем плоскость α до совмещения её с горизонтальной плоскостью. В качестве оси вращения будем использовать след h0α. Его положение в процессе преобразований останется неизменным.

Построение начинается с определения направления фронтального следа f1α. На прямой f0α возьмем произвольную точку E и определим её проекцию E’. Из E’ опустим перпендикуляр к h0α. Пересечение данного перпендикуляра с окружностью радиусом XαE” определяет положение точки E’1. Через Xα и E’1 проводим f1α.
Строим проекцию горизонтали h’1δ ∥ h0α, как это показано на рисунке. Точки O’1 и 5′1, 6′1 лежат на пересечении h’1δ с прямыми, проведенными перпендикулярно h0α из O’ и 5′, 6′. Аналогично на горизонтали h’1ε находим 7′1 и 8′1.
Строим проекции фронталей f’1γ ∥ f1α, f’3 ∥ f1α и f’4 ∥ f1α. Точки 1′1, 2′1, 3′1 и 4′1 лежат на пересечении этих фронталей с перпендикулярами, восстановленными к h0α из 1′, 2′, 3′ и 4′ соответственно.
Наверх

В статье рассмотрим вопрос: «Как чертится натуральная величина сечения конуса»
Первоначально необходимо начертить сечение конуса, полученное в результате секущей плоскости, и отобразить на трех видовых проекциях.
Определение точек сечения определяется с помощью секущих плоскостей.

1.) Отмеряем размер от оси Х до осевой линии вида сверху и откладывается от точки до оси строящегося сечения;

2.) Также как и в 1 пункте отмеряем длину от оси Х до оси вида сверху;

3.) Чертим центральную ось сечения под углом 900;

4.) Отмеряют расстояние согласно рисунку;
5.) Подобным образом переносятся остальные точки;

6.) Соединяем и обводим полученное сечение.

Вы также можете ознакомиться с построение в видео.
Просмотрели 424
Как найти натуральную величину сечения
Свойствами фигур в пространстве занимается такой раздел геометрии, как стереометрия. Основным методом для решения задач в стереометрии является метод сечения многогранников. Он позволяет правильно строить сечения многогранников и определять вид этих сечений.

Инструкция
Определение вида сечения какой-либо фигуры, то есть натуральной величины этого сечения, часто подразумевается при формулировке задач на построение наклонного сечения. Наклонное сечение правильнее называть фронтально-проецирующей секущей плоскостью. И для построения его натуральной величины достаточно выполнить несколько действий.
С помощью линейки и карандаша начертите фигуру в 3х проекциях – вид спереди, вид сверху и вид сбоку. На главной проекции на виде спереди покажите путь, по которому проходит фронтально-проецирующая секущая плоскость, для чего начертите наклонную прямую.
На наклонной прямой отметьте главные точки: точки вхождения сечения и выхода сечения. Если фигурой является прямоугольник, то точек вхождения и выхода будет по одной. Если фигурой является призма, то количество точек удваивается. Две точки определяют вхождение в фигуру и выход. Две другие определяют точки на боках призмы.
На произвольном расстоянии проведите прямую, параллельную фронтально-проецирующей секущей плоскости. Затем из точек, расположенных на оси главного вида, проведите вспомогательные линии перпендикулярно наклонной прямой, пока они не пересекутся с параллельной осью. Тем самым вы получите проекции полученных точек фигуры в новой координатной системе.
Чтобы определить ширину фигуры, опустите прямые из точек главного вида на фигуру вида сверху. Обозначьте соответствующими индексами проекции точек при каждом пересечении прямой и фигуры. Например, если точка А принадлежит главному виду фигуры, то точки А’ и А” принадлежат проецирующим плоскостям.
Отложите в новой координатной системе расстояние, которое образуется между вертикальными проекциями основных точек. Фигура, которая получается в результате построения, и является натуральной величиной наклонного сечения.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

