что такое вертикальная составляющая скорости в физике?
Елена Сотникова
Мастер
(1225),
закрыт
12 лет назад
Palemon
Мыслитель
(5062)
12 лет назад
Скорость – есть вектор, а вектор можно разложить на составляющие, т. е. спроецировать его на оси координат. Для удобства можно взять плоскую систему координат. Тогда проекция вектора скорости на ось “у” и будет являться вертикальной составляющей. Соответственно если вектор скорости будет направлен параллельно оси “ох”, то вертикальная составляющая равна нулю.
ХеХе
Мастер
(1953)
12 лет назад
Скорость подъёма-опускания.
Елена СотниковаМастер (1225)
12 лет назад
тогда чем она просто от скорости отличается? или это аналогичные понятия?
ХеХе
Мастер
(1953)
Ну может же ещё присутствовать и горизонтальная составляющая.
Например, тело движется, грубо говоря, по наклонной линии. Вверх, и в вперёд. С какой скоростью оно поднимается – вертикальная составляющая, с какой продвигается вперёд – горизонтальная. А реальная его скорость (по траектории движения) – по теореме Пифагора 🙂
Там ниже про векторы всё верно пишут…
Движение горизонтально брошенного тела:
Рассмотрим движение шара, движущегося прямолинейно по поверхности стола с высотой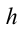 
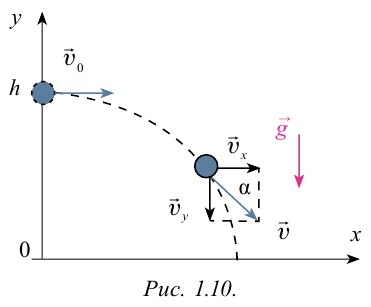
При достаточно малом сопротивлении воздуха, которым можно пренебречь, тело будет двигаться в горизонтальном направлении равномерно со скоростью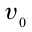 
. Поэтому перемещение
в горизонтальном направлении в любой момент времени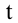 
, или длина полета, определяется следующей формулой:
Проекции скорости тела на оси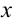 
и 
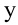определятся следующими соотношениями:
В вертикальном же направлении, двигаясь равноускоренно без начальной скорости, тело будет свободно падать с высоты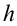 
. Следовательно, положение тела в вертикальном направлении после произвольного времени 
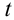будет определяться формулой:
Из соотношений (1.21) и (1.22) уравнение траектории движения горизонтально брошенного тела на плоскости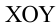 
будет иметь следующий вид:
Выражение (1.24) является уравнением параболы. Значит, горизонтально брошенное тело будет двигаться по параболической линии. Время полета тела, брошенного горизонтально с высоты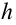 
, определяется выражением:
В этом случае формула для расчета длины полета тела будет иметь вид:
Горизонтально брошенное тело, одновременно двигаясь в горизонтальном направлении равномерно и в вертикальном направлении равноускоренно, свободно падает. К концу движения (после истечения времени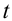 
) скорости в горизонтальном и вертикальном направлении будут 
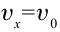и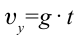 
соответственно. Таким образом, скорость тела при падении на землю определяется выражением:
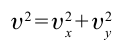
или
Перемещение и траектория тела при криволинейном движении неравны между собой. Модуль вектора и направление движения горизонтально брошенного тела на протяжении движения меняются непрерывно.
Образец решения задачи:
Тело брошено горизонтально на высоте 35 м со скоростью 30м/с. Найти скорость тела при падении на землю.
Дано:
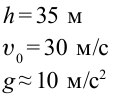
Найти:
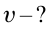
Формула:
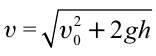
Решение:
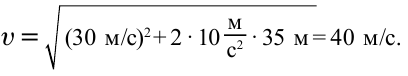
Ответ: 40 м/c.
Движение тела, брошенного горизонтально и под углом к горизонту
Если материальная точка участвует одновременно в нескольких движениях, то такое движение называют сложным.
Примером сложного движения является движение под действием силы тяжести в том случае, если падающему телу сообщена начальная скорость, непараллельная вектору ускорения свободного падения.
Рассмотрим движение тела, брошенного горизонтально со скоростью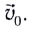 
Выберем систему координат так, что ее начало находится на поверхности Земли, направив ось Ох горизонтально, а ось Оу — вертикально (рис. 23).
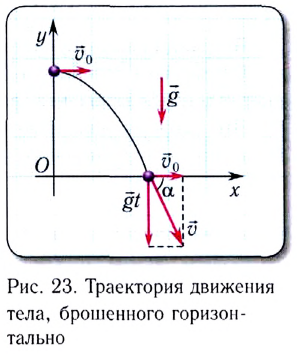
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного с постоянной скоростью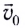 
вдоль горизонта (оси Ох) и свободного падения в вертикальном направлении с ускорением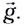 
Движение тела в горизонтальном направлении будет описываться уравнением
а в вертикальном — уравнением
Здесь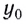 
— координата тела по оси Оу в начальный момент времени 
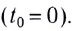Если тело брошено с высоты 
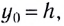то время падения 
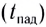определяется из
условия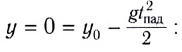 
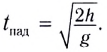
Для получения уравнения траектории движения у(х) необходимо исключить время из уравнений движения (1) и (2). Из уравнения (1) выражаем время t и подставляем в уравнение (2). Получаем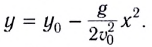 
Это уравнение параболы, ветви которой направлены вниз, так как коэффициент перед множителем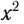 
отрицательный.
Скорость вдоль направления оси Ох остается неизменной и равной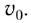 
Вдоль оси Оу движение равноускоренное. В начальный момент времени вертикальная составляющая скорости равна нулю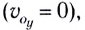 
поэтому мгновенная скорость вдоль оси Оу находится из соотношения 
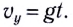Модуль мгновенной скорости определяется по теореме Пифагора (см. рис. 23):
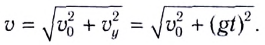
Угол между начальной скоростью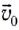 
и мгновенной скоростью и в момент времени t можно найти из соотношения
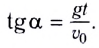
В приведенных формулах сопротивление воздуха не учитывается.
Рассмотрим теперь движение тела, брошенного со скоростью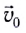 
под некоторым углом 
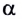к горизонту (рис. 24).
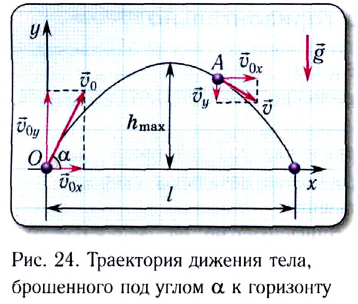
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного в горизонтальном направлении со скоростью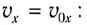 
и равноускоренного в вертикальном направлении с ускорением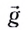 
и начальной
скоростью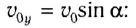 
В том случае, если система координат выбрана так, что начальные координаты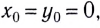 
уравнение траектории движения имеет вид
Как и при движении тела, брошенного горизонтально, траектория представляет собой параболу, ветви которой направлены вниз, поскольку коэффициент перед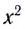 
отрицателен. Вершина параболы при этом имеет координаты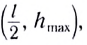 
где l — дальность полета тела,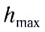 
— максимальная высота его подъема в процессе полета.
Модули горизонтальной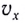 
и вертикальной 
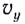составляющих мгновенной скорости 
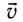движения определяются из следующих соотношений:
Мгновенную скорость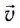 
и движения тела в произвольной точке Л траектории можно найти как векторную сумму горизонтальной 
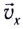и вертикальной 
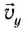мгновенных скоростей движения (см. рис. 24).
Время подъема тела можно найти из условия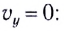 
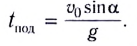
Если сопротивление воздуха при движении не учитывается, то время подъема равно времени падения: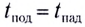 
(докажите это самостоятельно).
Таким образом, время полета тела можно найти как
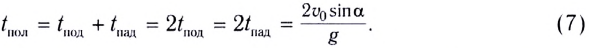
Определив вертикальную составляющую скорости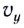 
в искомый момент времeни, по формуле 
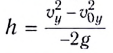можно найти высоту, на которой находится тело.
Максимальная высота подъема тела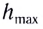 
легко определяется из условия, что вертикальная составляющая скорости в этой точке равна пулю 
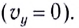Тогда
Дальность полета l — расстояние, пройденное телом за время полета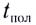 
вдоль оси Ох с постоянной скоростью 
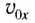(см. рис. 24). Она определяется по формуле
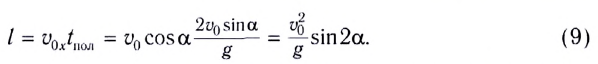
Таким образом, дальность полета определяется модулем начальной скорости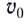 
тела и углом его бросания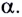 
Заметим, что согласно формуле (9) при неизменном модуле начальной скорости тела максимальная дальность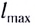 
полета достигается при 
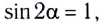т. е. при угле бросания 
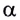= 45°.
- Движение тела, брошенного под углом к горизонту
- Принцип относительности Галилея
- Движение в гравитационном поле
- Зависимость веса тела от вида движения
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Взаимная передача вращательного и поступательного движения
Когда объект падает с определенной высоты, сила тяжести в значительной степени влияет на его достижение. скорость. Итак, ясно, что высота — это сущность, влияющая на движение.
Свободно падающий объект сначала достигает нуля скорость, и когда он начинает двигаться вниз, он набирает скорость. Предположим, мы знаем единственную высоту падающего объекта, как найти скорость с высотой, а также вместе с высотой, как другие объекты влияют на скорость, объясняется в этом посте.
Как найти скорость по высоте?
Рассмотрим книгу, которую держат на столе на высоте h от земли. Когда книга падает со стола, скорость падения книги на землю определяется скоростью. Поскольку книга находится на высоте h, как найти скорость с высотой?
Мы знаем, что скорость можно вычислить, зная расстояние, пройденное телом, и время, затрачиваемое им на преодоление этого расстояния. Математически это можно записать как,
В приведенном выше примере нам предоставлена высота h. высота тела связана с потенциалом энергия. Таким образом, основное уравнение неверно.
Учитывая потенциальную энергию, которой обладает книга до того, как она упадет, выражение можно записать в виде
PE = мгч.
Но книга находится в движении; следовательно, потенциальная энергия теперь превращается в кинетическую энергию, как
Таким образом, потенциальная энергия и кинетическая энергия равны по закону сохранения энергии. Следовательно, уравнение можно записать в виде
Преобразовав уравнение, мы получим скорость как
v2 = 2гх
В приведенном выше уравнении g — это ускорение свободного падения. Любой объект, падающий с определенной высоты, находится под влиянием гравитации и постоянно ускоряется из-за гравитации.
Как найти скорость через ускорение и высоту?
Мы знаем, как найти скорость с ускорением и расстоянием из предыдущей статьи. Но мы дали с ускорением и высотой, тогда как найти скорость с ускорением и высотой вместо расстояния?
Ускорение и скорость пропорциональны друг другу, поскольку производная скорости по времени есть ускорение. Если у нас есть средства ускорения, при интегрировании ускорения мы можем получить скорость. Но в данном случае у нас есть ускорение и высота. Обсудим, как найти скорость с высотой, если задано ускорение.
Предположим, что мяч находится на определенной высоте над землей. Мяч падает с высоты «h», и он начинает ускоряться на «а» в направлении ускорения под действием силы тяжести; это означает, что мяч падает с высоты h в направлении силы тяжести.
Поскольку и ускорение, и ускорение свободного падения имеют одно и то же направление, общее ускорение тела равно сумме обоих ускорений тела и ускорения свободного падения A = g+a. Теперь скорость мяча можно рассчитать, используя уравнение движения.
Мы знаем из кинематического уравнения движения, что расстояние, пройденное телом, можно записать в терминах математического уравнения как
Но у нас есть высота мяча и ускорение. Расстояние можно записать через высоту как
Начальное положение мяча, когда он начинает двигаться, и конечное положение мяча определяют расстояние.
Следовательно, x = h – 0, т. е. x=h, можно сказать, что расстояние по вертикали – это высота. Теперь подставив x = h, мы получим уравнение вида
Преобразовывая приведенное выше уравнение, мы имеем
Уравнение, полученное выше, дает скорость мяча с учетом ускорения и высоты.
Приведем другой пример, если снаряд движется к земле с высоты h и его ускорение больше, чем ускорение свободного падения, так как снаряд преодолевается за счет трения о воздух, то уравнение скорости будет вычисляться как
В уравнениях кинематики скорость определяется выражением
v2 = 2Ах
Где х – расстояние. Но здесь х = h, тогда
v2 = 2Ач
Рассмотрим другой случай; если подбросить мяч в воздух, то после достижения высоты h мяч начнет ускоряться вниз под действием силы тяжести; движение называется движение снаряда; как в этой ситуации найти скорость через ускорение и высоту? Движение мяча в воздухе показано на рисунке ниже.
Из приведенного выше рисунка высота объекта равна h, а расстояние — это не высота, но у нас есть высота в терминах расстояния с использованием уравнения движения снаряда. Связь между расстоянием и высотой можно записать как
Подставив значение расстояния в уравнение движения, получим
Преобразовывая уравнение, мы получаем скорость как
Как найти начальную скорость, зная ускорение и высоту?
Начальная скорость может быть получена из ускорения и высоты, учитывая уравнение движения.
Тело ускоряется, значит, должно быть изменение скорости тела в данном случае, что также говорит о том, что изначально тело имеет некоторую скорость, которая продолжает меняться со временем. Таким образом, чтобы найти Начальная скорость, нам нужно знать конечную скорость тела.
Когда мы подбрасываем мяч в воздух, он достигает определенной высоты h с определенной скоростью и приобретает ускорение а. Изначально; мяч движется со скоростью vi. Наконец, скорость будет vf. Уравнение начальной скорости запишем с помощью уравнения движения мяча, которое можно рассчитать следующим образом.
Скорость может быть
Конечная скорость мяча определяется как vf, следовательно, из средней скорости.
Но на высоте h мяч приобретает нулевую конечную скорость, падая обратно на землю под действием силы тяжести.
Но мы не знаем, сколько времени потребуется мячу, чтобы достичь высоты h, поэтому мы можем использовать ускорение. Первоначально мяч ускоряется против силы тяжести; его ускорение станет отрицательным.
Мы знаем, конечная скорость равно нулю, то
Таким образом, мы получаем фактор времени как
Подставляя в уравнение средней начальной скорости, получаем
Преобразовывая уравнение, получаем
Мы можем вычислить начальную скорость, когда конечная скорость отлична от нуля. Рассмотрим уравнение
В приведенном выше уравнении подставив значение t как
т = (vf+vi) / а
Получаем уравнение в виде
(vf+vi) (вf-vi) = 2ah
Приведенное выше уравнение можно записать как
vf2-vi2 = 2ah
Переставляя условия, чтобы получить начальную скорость как
vi2 = Vf2– 2 часа
Как рассчитать скорость по высоте и времени?
При вертикальном движении путь, пройденный телом, равен высоте, с которой тело начинает движение.
Скорость можно рассчитать, используя высоту и время. Расстояние, пройденное телом с время всегда описывает скорость тела. Физические объекты, такие как ускорение и высота, также способствуют нахождению скорости.
Мы можем вычислить скорость по высоте и времени тремя способами.
- При вертикальном движении тела
- При метательном движении тела
- График зависимости роста от времени
При вертикальном движении тела
Если баскетбольный мяч падает из корзины на высоте h и ускоряется в направлении силы тяжести, то скорость можно определить как
Но ускорение задается
Подставляя значение a и заменяя член расстояния высотой h, мы получаем
При перестановке членов скорость с высотой и временем равна
По движению снаряда
Рассмотрим другой пример; баскетболист бросает мяч в корзину, стоящую на расстоянии d от корзины. Мяч делает движение снаряда добраться до корзины; то мы можем рассчитать скорость следующим образом:
Общее выражение скорости дается выражением
Мяч проходит расстояние d на высоте h; если пренебречь трением, расстояние можно записать как
Подставляя значение x в общее уравнение скорости, получаем
График зависимости роста от времени
Если мы построим график с высотой по оси y и временем по оси x, график называется графиком высота-время.
Мы можем рассчитать скорость по графику высота-время. Наклон графика высота-время дает скорость тела.
Из приведенного выше графика наклон определяется выражением
Из графика AB параллелен высоте h, а BC параллелен времени t; следовательно, мы можем сказать, что
АВ = h и ВС = t;
Из определения скорости мы можем сказать, что наклон есть не что иное, как скорость. Таким образом, наклон равен скорости.
Как найти скорость по высоте и массе?
Хотя масса не влияет на скорость, она вносит энергию и силу, необходимые телу для достижения определенной скорости.
Высота и масса — это объекты, связанные с объектом. потенциальная энергия. Масса также вносит вклад в кинетическую энергию, приобретаемую объектом при движении. Зная массу, давайте поймем, как найти скорость с высотой.
Объект на определенной высоте обладает потенциалом, который заставляет тело двигаться, и он равен кинетической энергии тела при движении.
Поскольку и потенциальная энергия, и кинетическая энергия равны, мы можем их приравнять.
Ep= Ek
Кинетическая энергия тела равна
Преобразовывая уравнение, получаем
В начале мы сказали, что потенциальная энергия = кинетическая энергия,
Поэтому уравнение можно переписать как
В общем случае потенциальная энергия равна Е.p= мгх.
Ответ, который мы получили из потенциальной энергии, можно подставить в приведенное выше уравнение, чтобы получить скорость тела.
Как найти скорость с учетом высоты и силы тяжести?
Когда вы бросаете камень в воздух, он падает на землю под действием силы тяжести. Это общий процесс. Но заметили ли вы, что скорость мяча? Скорость камня при движении вниз немного меньше скорости того же камня при падении назад.
Приведенное выше утверждение поясняет, что скорость может меняться и под действием силы тяжести. Гравитация вступает в действие, когда тело находится на определенной высоте; поскольку гравитация является силой притяжения, она пытается поднять тело на высоту к земле, поэтому, основываясь на этих данных, как найти скорость через высоту и расстояние?
В предыдущем разделе обсуждался один из способов нахождения скорость с высотой и силой тяжести. Обсудим, как найти скорость по высоте и расстоянию, рассматривая кинематическое уравнение движения.
Высота всегда равна расстоянию из кинематического уравнения расстояния. Следовательно, мы можем рассматривать расстояние как высоту. Таким образом, уравнение будет
Если камень движется в направлении силы тяжести, то ускорение происходит только благодаря силе тяжести; следовательно, уравнение можно переписать как
Переставив члены, уравнение будет
Приведенное выше уравнение дает скорость с высотой и силу тяжести с временным фактором. Если тело движется с ускорением против силы тяжести, то
г = -г
Как найти скорость по высоте и углу?
Когда тело начинает падать с некоторой высоты на поверхность, оно образует с точкой падения некоторый угол θ. Угол, создаваемый объектом, помогает нам найти ответ на вопрос, как найти скорость с высотой.
Компания смещение тела в вертикальном положении – высота. Вертикальную составляющую скорости можно записать как
v = v sinθ
Если тело вырабатывает некоторые горизонтальное смещение, то скорость
v = v cos θ
Из уравнения движения вертикальную и горизонтальную скорости можно записать как
vx = v cosθ
vy = v sinθ-gt; где g – ускорение свободного падения
На максимальной высоте vy= 0 = v sinθ –gt
v sinθ = gt
Когда тело падает под углом θ и движется со скоростью v, его дальность действия определяется выражением
Поэтому, используя значение R,
Следовательно, скорость можно переписать как
Решенные задачи о том, как рассчитать скорость с высотой
Задача 1) Мяч падает с высоты 15 м и достигает земли с определенной скоростью. Вычислите скорость мяча.
Решение:
Нам предоставляется только высота h = 15м.
Поскольку мяч движется к земле, движение происходит за счет ускорения силы тяжести g. Величина ускорения свободного падения g = 9.8 м/с.2. Скорость мяча
Подставляя значения h и g;
v = 17.14 м / с.
Задача 2) Вычислите начальную скорость камня, падающего с высоты 3 м, и его ускорение 2 м/с.2, и, следовательно, найти время, за которое камень достигнет земли.
Решение:
Приведенные данные: Высота h = 3м
Ускорение камня a = 2 м/с2.
Скорость камня определяется выражением
v = 3.46 м / с.
Время, необходимое камню, чтобы достичь земли, определяется уравнением
t = 1.79 с.
Задача 3) Тело массой 3 кг падает с высоты 7 м, ускоряясь под действием силы тяжести. Вычислите скорость объекта.
Решение:
Даны данные – масса объекта m = 3кг.
Высота, с которой упал предмет, h = 7 м.
Ускорение свободного падения g = 9.8 м/с.2.
Поскольку движение объекта обусловлено массой, высотой и гравитацией, то совершаемая работа равна потенциальной энергии. это дано
Ep = мгх
Объект движется, поэтому объект обладает кинетической энергией; это представлено формулой,
Из закона сохранения энергии, когда объект начинает двигаться, его потенциальная энергия теперь называется кинетической энергией.
Поэтому Еp = Ek
Потенциальная энергия Еp = 3 × 9.8 × 7
Ep = 205.8 Дж
Подставив Ep = Ek = 205.8 Дж.
v2 = 137.2
v = 11.71 м / с.
Задача 4) Спортсмен стреляет толканием ядра в воздух в вертикальном направлении, и ему требуется время 3 секунды, чтобы упасть на землю вертикально с высоты 7 м от земли. Рассчитайте скорость, с которой толкатель ядра возвращается на землю.
Решение:
Приведенные данные – высота от земли h = 7 м.
Время, необходимое для достижения земли = 3 секунды.
Скорость определяется выражением
v = 2.33 м / с.
Задача 5) Тело массой 4 кг падает с высоты 11 м над землей под углом 20°. Вычислите скорость тела. (Примите ускорение свободного падения равным 10 м/с.2)
Решение:
Приведены данные – масса тела m = 4 кг.
Высота h = 11 м.
Угол θ = 20°.
Ускорение свободного падения g = 10 м/с.2.
Скорость определяется выражением
v = 43.45 м / с.
Движение тела, брошенного горизонтально
При решении задач с телом, брошенным горизонтально, очень важно помнить, что это движение состоит из двух: тело летит горизонтально, и его скорость постоянна, и одновременно тело падает, и движение в вертикальной плоскости является равноускоренным. Если всегда помнить про этот факт – не проблема решить любую задачу.
Задача 1.
Горизонтально летящая пуля последовательно пробивает два вертикальных листа бумаги, расположенных на расстоянии 30 м друг от друга. При этом пробоина на втором листе оказывается на мм ниже, чем на первом. С какой скоростью подлетела пуля к первому листу? 1.240
Итак, пуля летела горизонтально с неизменной скоростью. Одновременно пуля падала в вертикальной плоскости и успела «упасть» на 2 мм. Тогда, зная путь, пройденный ею в вертикальной плоскости, можно найти время падения:
Не забываем переводить величины в систему СИ, м:
Получили время падения пули, или время движения между листами. Найти скорость пули можем теперь по хорошо известной нам формуле:
Ответ: м/с
Задача 2.
С вертолета, летящего горизонтально со скоростью на высоте
, сброшен груз. На какой высоте
скорость груза будет направлена под углом
к горизонту? Найти радиус кривизны траектории
на данной высоте. Чему равно расстояние
между грузом и самолетом в момент падения груза на землю?
На последний вопрос задачи отвечаем элементарно: ведь мы помним, что горизонтально направленная составляющая скорости остается постоянной, то есть тело летело сначала в вертолете, а потом его выбросили и оно продолжает лететь с той же самой скоростью, просто оно теперь начинает еще и падать. Да, по вертикали расстояние между телом и самолетом растет, но при этом тело все время находится под брюхом самолета, просто с каждой секундой все ниже и ниже. Так что в момент падения между самолетом и грузом будет расстояние .
Груз падает с вертолета
Так как в процессе падения тело будет набирать вертикальную составляющую скорости под действием ускорения свободного падения, то в какой-то момент времени скорость тела, а это векторная сумма вертикальной и горизонтальной составляющих, будет образовывать угол с горизонтом. Сделаем чертеж:
Тогда угол
Найдем . Движение равноускоренное, без начальной скорости, поэтому
, где
– находим его так же, как и в предыдущей задаче про пулю.
Возведем все в квадрат:
Осталось найти радиус кривизны траектории. Он входит в формулу центростремительного ускорения:
Выражаем радиус:
Скорость тела – векторная сумма горизонтальной и вертикальной составляющих:
Можно выразить косинус угла через ускорения:
Или, записывая нормальное ускорение
Ответ: ,
,
.
Задача 3.
Тело брошено горизонтально. Через время 5 с после броска угол между скоростью и ускорением стал . Определить скорость тела
в этот момент. В какой момент времени
после броска скорость тела будет в два раза больше его начальной скорости?
К задаче 3
Нарисуем картинку. Сразу становится понятным, что угол между скоростью и ускорением – это угол между скоростью и вертикальной составляющей скорости, так как она направлена вертикально вниз, как и ускорение . А значит, угол между скоростью и горизонтальной составляющей равен
. Тогда составляющие скорости равны, и можно вычислить вертикальную, зная время, а потом найти и скорость тела.
Делаем!
Тело падало в течение 5 с, поэтому м/с. Горизонтальная составляющая
м/с. Скорость тела будет равна:
Горизонтальная составляющая скорости неизменна, и раз нам удалось ее определить – неважно, для какого момента полета тела – значит, она будет иметь такое значение всегда, от начала полета и до его конца. Это и есть начальная скорость тела. По условию, в некоторый момент скорость тела больше его начальной вдвое, поэтому .
Тогда можем найти вертикальную составляющую скорости для этого момента:
Теперь, найдя вертикальную составляющую, найдем и момент времени:
Ответ: м/с,
c.
Задача 4.
Камень брошен горизонтально со склона горы, образующего угол с горизонтом. Чему равна начальная скорость
камня, если он упал на склон на расстоянии 50 м от точки бросания?
К задаче 4
Так как склон образует с горизонтом угол , то можно определить, какие расстояния камень пролетел по горизонтали и по вертикали – это будут катеты треугольника, а расстояние 50 м вдоль склона – гипотенуза. Тогда
Это дает нам в руки ключ к решению: ведь по вертикали камень падал, и можно узнать, сколько времени:
Мы выяснили, что время падения камня 2,68 с – но ведь это же время он двигался и по горизонтали, причем с постоянной скоростью, и пролетел м. Тогда его горизонтальная составляющая скорости (она же – начальная скорость) равна
м/с.
Ответ: м/с.
Задача 5.
Тело брошено горизонтально с горы, высота которой 80 м, с начальной скоростью м/с. Найти перемещение и угол, который составляет перемещение с горизонтом, между двумя точками полета тела, в которых скорости соответственно
м/с и
м/с.
Определим сначала, в какие моменты времени тело окажется в указанных точках. Для этого найдем вертикальные составляющие его скорости и для первого, и для второго моментов времени:
Тогда моменты времени, в которых у тела были соответствующие скорости, равны:
За начало отсчета и точку старта теперь принимаем время – координаты тела в данный момент времени примем за
. Тогда по горизонтали тело пролетит расстояние:
А по вертикали расстояние можно определить как разность расстояний, пройденных телом за время и
:
Модуль перемещения будет равен:
Угол, который перемещение составляет с горизонтом, определим как арктангенс отношения: :
Ответ: ,
.
Кинематика
Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Содержание
- Механическое движение и его виды
- Относительность механического движения
- Правило сложения перемещений
- Правило сложения скоростей
- Относительная скорость
- Скорость
- Ускорение
- Равномерное движение
- График скорости (проекции скорости)
- График перемещения (проекции перемещения)
- Прямолинейное равноускоренное движение
- Свободное падение (ускорение свободного падения)
- Движение тела по вертикали
- Движение тела, брошенного горизонтально
- Движение тела, брошенного под углом к горизонту (баллистическое движение)
- Движение по окружности с постоянной по модулю скоростью
- Основные формулы по теме «Кинематика»
Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
3. по скорости
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
4. по ускорению
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):
Определим скорость второго тела относительно первого ( v_{21} ):
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — ( v ), единицы измерения — м/с (км/ч).
Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:
Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:
Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — ( a ), единица измерения — м/с2.
В векторном виде:
где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:
где ( a_n ) – нормальное ускорение, ( a_{tau} ) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:
Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:
Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.
Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: ( x=x(t) ).
График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:
Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:
При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:
При разгоне (в проекциях на ось ОХ):
При торможении (в проекциях на ось ОХ):
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:
График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
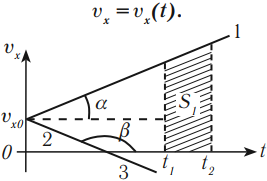
График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) > 0.
График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,
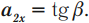
График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ( t_2-t_1 ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:
Перемещение в ( n )-ую секунду при равноускоренном движении рассчитывается по формуле:
Координата тела при равноускоренном движении рассчитывается по формуле:
Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – ( g ), единицы измерения – м/с2.
Важно! ( g ) = 9,8 м/с2, но при решении задач считается, что ( g ) = 10 м/с2.
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:
Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:
Тело брошено вверх:
Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью ( v_0=v_{0x} );
- равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_{0y}=0 ).
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Дальность полета:
Угол между вектором скорости и осью ОХ:
Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Время подъема на максимальную высоту:
Максимальная высота подъема:
Время полета:
Максимальная дальность полета:
Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ), с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ), под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:
Это облегчает решение задач:
Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.
Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_{цс} ), единицы измерения – м/с2.
Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ), единицы измерения – с.
где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ), единицы измерения – с–1 (Гц).
Период и частота – взаимно обратные величины:
Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ), единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:
Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ), единицы измерения – рад/с .
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:
Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:
Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:
Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ), и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.
Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ), мгновенная скорость точки ( (p) ), лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.
Основные формулы по теме «Кинематика»
Кинематика
3 (59.69%) 130 votes
