Содержание
- Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
- Функции МАКС и МИН в Excel по условию
- Функции Excel 2016 МАКСЕСЛИ (MAXIFS) и МИНЕСЛИ (MINIFS)
- Формула Excel MAX IF, чтобы найти наибольшее значение с условиями
- Формула Excel МАКС ЕСЛИ
- Как работает эта формула
- Формула MAX IF с несколькими критериями
- Как работают эти формулы
- МАКС. ЕСЛИ без массива
- Как работает эта формула
- Формула Excel MAX IF с логикой ИЛИ
- Как работают эти формулы
- MAXIFS — простой способ найти максимальное значение с условиями
Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
history 14 января 2021 г.
Пусть дана функция с несколькими переменными F(x1, x2, . )=a1*x1+a2*x2+. Также даны граничные условия в виде b1*x1+b2*x2+. файл примера ).

Переменные (выделено зеленым) . В качестве переменных модели, очевидно, выступают x1, x2, x3, x4. Эта задача хороша тем, что переменные задаются однозначно, не требуется осмысливать житейскую задачу, например как с оптимизацией затрат . Хотя математически — это эквивалентные задачи, только количество переменных разное.
После запуска Поиск решения будет методично (последовательно) по своему алгоритму подставлять в зеленые ячейки числовые значения и вычислять функцию F (красная ячейка).
Ограничения (выделено серым) . Ограничения модели — это ограничения на область изменения переменных. Они могут задаваться как простыми выражениями для одной переменной, например х1>=0, так и для некой комбинации переменных 5*x1+4*x2-x3-2*x4 =0 ограничения можно ввести прямо в окне Поиска решения (будет показано ниже), для более сложных зависимостей удобно подготовить вспомогательную таблицу (С26:Е29).
Составить модель, особенно первую, непросто. Может помочь такой подход: считать, что переменные (зеленые ячейки) уже содержат некие значения, пусть даже не оптимальные. Так легче составлять огграничения. В нашем случае ограниечение 5*x1+4*x2-x3-2*x4 можно записать с помощью формулы = СУММПРОИЗВ($D$19:$D$22;C26:C29) . В диапазоне D19:D22 содержатся коэффициенты 5; 4; -1; -2. Кроме того, если значения переменных заданы, то и значение целевой функции также автоматически рассчитано (тоже не оптимальное пока, до запуска Поиска решения).
Целевая функция (выделено красным) . Целевая функция — это то, что требуется оптимизировать, т.е. F. Формула для ее вычисления задана в явном виде — не нужно догадываться из условий обычной задачи как ее подсчитать. Это не всегда очевидно (см., например, статью про пропускную способность трубопровода ).
Ниже приведено окно Поиска решения с заполненными полями: целевая функция, переменные и ограничения.

После запуска Поиска решения ответ будет вычислен за доли секунды: F=3.
Источник
Функции МАКС и МИН в Excel по условию
Подсчет максимального и минимального значения выполняется известными функциями МАКС и МИН. Бывает, что вычисления нужно произвести по группам или в зависимости от условия, как в СУММЕСЛИ.
Долгое время в Excel не было аналога СУММЕСЛИ или СРЗНАЧЕСЛИ для расчета максимального и минимального значения, поэтому использовали формулу массивов.
Пусть имеются данные
![]()
Нужно подсчитать максимальное значение в указанной группе. Название группы (критерий) введем в отдельную ячейку (D2). Пусть для начала это будет группа Б. Рядом введем следующую формулу:
Это формула массивов, поэтому ввести ее нужно комбинацией Ctrl + Shift + Enter.
![]()
Теперь, меняя название группы, можно без всяких фильтров и сводных таблиц видеть максимальное значение внутри этой группы.
Как это работает? Очень просто. Первым делом нужно указать диапазон, который будет использоваться в качестве аргумента функции МАКС, то есть только те ячейки, которые соответствуют указанной группе. Так как мы заранее позаботились об удобстве использования функции, то название группы указали не внутри формулы, а в отдельной ячейке (гораздо легче менять группу). Тогда формула для нужного диапазона выглядит так.
Указанное выражение отбирает только те значения, для которых название группы совпадает с условием в ячейке D2. Вот, как это видит Excel
![]()
На следующем этапе укажем функцию МАКС, аргументом которой выступает полученный выше массив. Excel воспринимает примерно так.
![]()
Видно, что максимальное значение внутри массива равно 31. Его и мы и увидим в ячейке с формулой. Нужно только не забыть итоговую функцию ввести комбинацией клавиш Ctrl + Shift + Enter, иначе ничего не получится. В строке формул формула массива отображается внутри фигурных скобок. Добавляются сами, специально дорисовывать не нужно.
Если функцию МАКС заменить на МИН, то по указанному условию (названию группы) будет выдаваться минимальное значение.
Функции Excel 2016 МАКСЕСЛИ (MAXIFS) и МИНЕСЛИ (MINIFS)
В MS Excel добавили новые статистические функции — МАКСЕСЛИ и МИНЕСЛИ. Обе функции имеют возможность учитывать несколько условий и некоторое время в их названиях в конце были буквы -МН. Потом убрали, хотя в скриншотах ниже используется вариант названий с -МН.
Есть ряд значений, каждое из которых входит в некоторую группу. Нужно рассчитать максимальное значение по группе А. Используем формулу МАКСЕСЛИ.
![]()
Все очень просто. Как и у СУММЕСЛИМН вначале указываем диапазон, где находится искомое максимальное значение (колонка В), затем диапазон с критериями (колонка А) и далее сам критерий (в ячейке D2). Можно указать сразу несколько условий. Таким же способом легко рассчитать минимальное значение по условию. Найдем, к примеру, минимум внутри группы Б.
![]()
Ниже показан ролик, как рассчитать максимальное и минимальное значение по условию.
Источник
Формула Excel MAX IF, чтобы найти наибольшее значение с условиями
В статье показано несколько различных способов получить максимальное значение в Excel на основе одного или нескольких указанных вами условий.
В нашем предыдущем руководстве мы рассмотрели распространенное использование функции MAX, которая предназначена для возврата наибольшего числа в наборе данных. Однако в некоторых ситуациях вам может потребоваться углубиться в свои данные, чтобы найти максимальное значение на основе определенных критериев. Это можно сделать с помощью нескольких различных формул, и в этой статье объясняются все возможные способы.
Формула Excel МАКС ЕСЛИ
До недавнего времени в Microsoft Excel не было встроенной функции МАКС. ЕСЛИ для получения максимального значения в зависимости от условий. С введением MAXIFS в Excel 2019 мы можем легко выполнять условное максимальное значение.
В Excel 2016 и более ранних версиях вам все равно придется создавать собственную формулу массива, комбинируя функцию MAX с оператором IF:
<=МАКС(ЕСЛИ(критерии_диапазонзнак равнокритерии, максимальный_диапазон))>
Чтобы увидеть, как эта общая формула MAX IF работает с реальными данными, рассмотрим следующий пример. Предположим, у вас есть таблица с результатами прыжков в длину нескольких учеников. В таблицу включены данные по трем раундам, и вы ищете лучший результат конкретного спортсмена, скажем Якова. С именами учащихся в A2:A10 и расстояниями в C2:C10 формула принимает следующий вид:
Помните, что формулу массива всегда нужно вводить, одновременно нажимая клавиши Ctrl + Shift + Enter. В результате он автоматически обрамляется фигурными скобками, как показано на скриншоте ниже (набор фигурных скобок вручную не работает!).
В реальных рабочих листах критерий удобнее вводить в какую-то ячейку, чтобы можно было легко изменить условие, не меняя формулу. Итак, набираем нужное имя в F1 и получаем следующий результат:
=МАКС(ЕСЛИ(A2:A10=F1, C2:C10))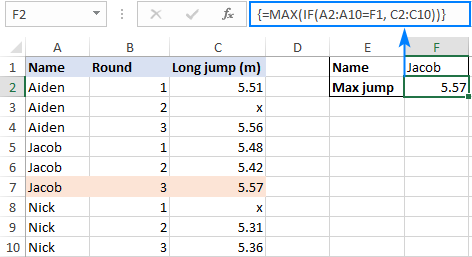
Как работает эта формула
В логическом тесте функции ЕСЛИ мы сравниваем список имен (A2:A10) с целевым именем (F1). Результатом этой операции является массив значений ИСТИНА и ЛОЖЬ, где значения ИСТИНА представляют имена, совпадающие с целевым именем (Джейкоб):
Для значение_ если_истина аргумент, мы предоставляем результаты длинного перехода (C2:C10), поэтому, если логический тест оценивается как TRUE, возвращается соответствующее число из столбца C. значение_ если_ложь аргумент опущен, то есть будет иметь значение FALSE, если условие не выполняется:
Этот массив передается функции MAX, которая возвращает максимальное число, игнорируя значения FALSE.
Кончик. Чтобы просмотреть внутренние массивы, описанные выше, выберите соответствующую часть формулы на листе и нажмите клавишу F9. Чтобы выйти из режима оценки формулы, нажмите клавишу Esc.
Формула MAX IF с несколькими критериями
В ситуации, когда вам нужно найти максимальное значение на основе более чем одного условия, вы можете:
Используйте вложенные операторы IF, чтобы включить дополнительные критерии:
<=МАКС(ЕСЛИ(критерии_диапазон1знак равнокритерии1ЕСЛИ(критерии_диапазон2знак равнокритерии2, максимальный_диапазон)))>
Или обработайте несколько критериев, используя операцию умножения:
<=МАКС(ЕСЛИ((критерии_диапазон1знак равнокритерии1) * (критерии_диапазон2знак равнокритерии2), максимальный_диапазон))>
Допустим, у вас есть результаты юношей и девушек в одной таблице и вы хотите найти самый длинный прыжок среди девушек в 3 туре. Для этого вводим первый критерий (женский) в G1, второй критерий (3) в G2 и используйте следующие формулы для определения максимального значения:
=МАКС(ЕСЛИ(B2:B16=G1, ЕСЛИ(C2:C16=G2, D2:D16)))
Поскольку обе формулы являются формулами массива, не забудьте нажать Ctrl + Shift + Enter, чтобы заполнить их правильно.
Как показано на снимке экрана ниже, формулы дают одинаковый результат, поэтому какую из них использовать, зависит от ваших личных предпочтений. Для меня формулу с булевой логикой легче читать и строить — она позволяет добавлять сколько угодно условий без вложения дополнительных функций ЕСЛИ.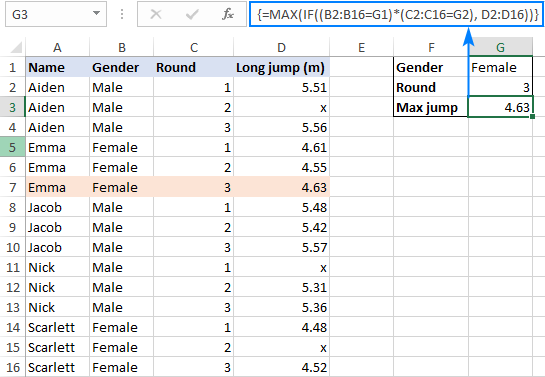
Как работают эти формулы
Первая формула использует две вложенные функции ЕСЛИ для оценки двух критериев. В логической проверке первого оператора IF мы сравниваем значения в столбце «Пол» (B2:B16) с критерием в G1 («Женский»). Результатом является массив значений TRUE и FALSE, где TRUE представляет данные, соответствующие критерию:
Аналогичным образом вторая функция ЕСЛИ проверяет значения в столбце округления (C2:C16) на соответствие критерию в G2.
Для значение_если_истина аргумент во втором операторе IF, мы предоставляем результаты прыжка в длину (D2:D16), и таким образом мы получаем элементы, которые имеют TRUE в первых двух массивах в соответствующих позициях (т. е. элементы, где пол «женский» и круглые равно 3):
Этот последний массив передается функции MAX, и она возвращает наибольшее число.
Вторая формула оценивает одни и те же условия в рамках одного логического теста, а операция умножения работает как оператор И:
Когда значения TRUE и FALSE используются в любой арифметической операции, они преобразуются в 1 и 0 соответственно. А поскольку умножение на 0 всегда дает ноль, результирующий массив имеет 1 только тогда, когда все условия ИСТИННЫ. Этот массив оценивается в логической проверке функции ЕСЛИ, которая возвращает расстояния, соответствующие элементам 1 (ИСТИНА).
МАКС. ЕСЛИ без массива
Многие пользователи Excel, в том числе и я, предвзято относятся к формулам массивов и стараются по возможности избавиться от них. К счастью, в Microsoft Excel есть несколько функций, которые изначально обрабатывают массивы, и мы можем использовать одну из таких функций, а именно СУММПРОИЗВ, как своего рода «оболочку» вокруг MAX.
Общая формула MAX IF без массива выглядит следующим образом:
=СУММПРОИЗВ(МАКС((критерии_диапазон1знак равнокритерии1) * (критерии_диапазон2знак равнокритерии2) * максимальный_диапазон))
Естественно, при необходимости вы можете добавить больше пар диапазон/критерий.
Чтобы увидеть формулу в действии, мы будем использовать данные из предыдущего примера. Цель состоит в том, чтобы получить максимальный прыжок спортсменки в раунде 3:
=СУММПРОИЗВ(МАКС(((B2:B16=G1) * (C2:C16=G2) * (D2:D16))))
Эта формула заменяется обычным нажатием клавиши Enter и возвращает тот же результат, что и формула массива MAX IF:
Присмотревшись к приведенному выше снимку экрана, вы можете заметить, что недопустимые переходы, отмеченные знаком «x» в предыдущих примерах, теперь имеют 0 значений в строках 3, 11 и 15, и в следующем разделе объясняется, почему.
Как работает эта формула
Как и в случае с формулой МАКС. ЕСЛИ, мы оцениваем два критерия, сравнивая каждое значение в столбцах «Пол» (B2:B16) и «Округление» (C2:C16) с критериями в ячейках G1 и G2. Результатом являются два массива значений TRUE и FALSE. Умножение элементов массивов в одинаковых позициях преобразует ИСТИНА и ЛОЖЬ в 1 и 0 соответственно, где 1 представляет элементы, соответствующие обоим критериям. Третий умноженный массив содержит результаты прыжков в длину (D2:D16). И поскольку умножение на 0 дает ноль, выживают только элементы, имеющие 1 (ИСТИНА) в соответствующих позициях:
В случае максимальный_диапазон содержит любое текстовое значение, операция умножения возвращает ошибку #ЗНАЧ, из-за которой вся формула не работает.
Функция MAX берет его отсюда и возвращает наибольшее число, удовлетворяющее заданным условиям. Результирующий массив, состоящий из одного элемента <4.63>, поступает в функцию СУММПРОИЗВ и выводит максимальное число в ячейке.
Примечание. Из-за своей специфической логики формула работает со следующими оговорками:
- Диапазон, в котором вы ищете наибольшее значение, должен содержать только числа. Если есть какие-либо текстовые значения, #VALUE! возвращается ошибка.
- Формула не может оценить условие «не равно нулю» в отрицательном наборе данных. Чтобы найти максимальное значение без учета нулей, используйте либо формулу МАКС. ЕСЛИ, либо функцию МАКС.
Формула Excel MAX IF с логикой ИЛИ
Чтобы найти максимальное значение при выполнении любого из указанных условий, используйте уже знакомую формулу массива МАКС ЕСЛИ с булевой логикой, но сложите условия, а не перемножайте их.
<=МАКС(ЕСЛИ((критерии_диапазон1знак равнокритерии1) + (критерии_диапазон2знак равнокритерии2), максимальный_диапазон))>
Кроме того, вы можете использовать следующую формулу без массива:
=СУММПРОИЗВ(МАКС(((критерии_диапазон1знак равнокритерии1) + (критерии_диапазон2знак равнокритерии2)) * максимальный_диапазон))
Для примера вычислим лучший результат в раундах 2 и 3. Обратите внимание, что в языке Excel задача формулируется иначе: вернуть максимальное значение, если раунд либо 2, либо 3.
С раундами, перечисленными в B2:B10, результатами в C2:C10 и критериями в F1 и H1, формула выглядит следующим образом:
=МАКС(ЕСЛИ((B2:B10=F1) + (B2:B10=H1), C2:C10))
Введите формулу, нажав комбинацию клавиш Ctrl + Shift + Enter, и вы получите такой результат:
Максимальное значение с теми же условиями также можно найти с помощью этой формулы без массива:
=СУММПРОИЗВ(МАКС(((B2:B10=F1) + (B2:B10=H1)) * C2:C10))
Однако в этом случае нам нужно заменить все значения «x» в столбце C нулями, потому что СУММПРОИЗВ МАКС работает только с числовыми данными:
Как работают эти формулы
Формула массива работает точно так же, как МАКС. ЕСЛИ с логикой И за исключением того, что вы соединяете критерии, используя операцию сложения вместо умножения. В формулах массива сложение работает как оператор ИЛИ:
Сложение двух массивов ИСТИНА и ЛОЖЬ (которые получаются в результате проверки значений в B2:B10 по критериям в F1 и H1) дает массив из 1 и 0, где 1 представляет элементы, для которых любое условие является ИСТИННЫМ, а 0 представляет элементы. для которого оба условия ЛОЖНЫ. В результате функция ЕСЛИ «сохраняет» все элементы в C2:C10 (значение_если_истина), для которого любое условие ИСТИННО (1); остальные элементы заменяются на FALSE, потому что значение_если_ложь аргумент не указан.
Формула без массива работает аналогичным образом. Разница в том, что вместо логического теста IF вы умножаете элементы массива 1 и 0 на элементы массива результатов прыжка в длину (C2:C10) в соответствующих позициях. Это аннулирует элементы, которые не соответствуют ни одному условию (имеют 0 в первом массиве), и сохраняет элементы, которые соответствуют одному из условий (имеют 1 в первом массиве).
MAXIFS — простой способ найти максимальное значение с условиями
Пользователи Excel 2019, 2021 и Excel 365 избавлены от необходимости приручать массивы для создания собственной формулы MAX IF. Эти версии Excel предоставляют долгожданную функцию MAXIFS, которая упрощает поиск наибольшего значения в условиях детской игры.
В первом аргументе MAXIFS вы вводите диапазон, в котором должно быть найдено максимальное значение (в нашем случае D2:D16), а в последующих аргументах вы можете ввести до 126 пар диапазон/критерий. Например:
=МАКСЕСЛИ(D2:D16, B2:B16, G1, C2:C16, G2)
Как показано на снимке экрана ниже, у этой простой формулы нет проблем с обработкой диапазона, содержащего как числовые, так и текстовые значения: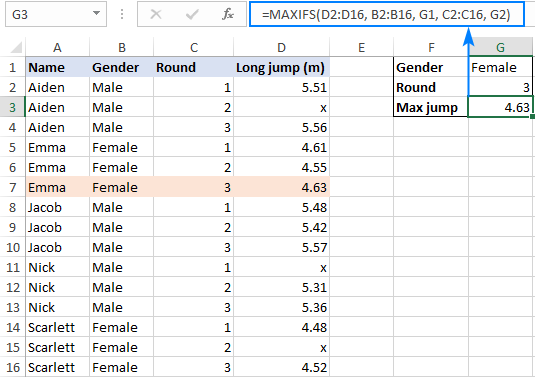
Подробную информацию об этой функции см. в разделе Функция MAXIFS в Excel с примерами формул.
Вот как вы можете найти максимальное значение с условиями в Excel. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Источник
history 14 января 2021 г.
- Группы статей
- Надстройка “Поиск решения”
Пусть дана функция с несколькими переменными F(x1, x2, …)=a1*x1+a2*x2+… Также даны граничные условия в виде b1*x1+b2*x2+…<=c (несколько условий). Нужно найти экстремум функции F (минимум или максимум). Это классическая задача для Поиска решения MS EXCEL, кроме того это линейная модель. Сделаем удобную форму для таких задач и покажем как настроить Поиск решения.
Задача
Пусть дана явная функция с 4 переменными:

Также даны несколько (семь) граничных условий (англ: restrictions, constraints):

Требуется найти максимум функции F.
Создание модели
Решим задачу с помощью инструмента MS EXCEL
Поиск решения
, хотя можно ее решить и другим способом, например аналитически.
На рисунке ниже приведена модель, созданная для решения задачи (см.
файл примера
).

Переменные (выделено зеленым)
. В качестве переменных модели, очевидно, выступают x1, x2, x3, x4. Эта задача хороша тем, что переменные задаются однозначно, не требуется осмысливать житейскую задачу, например как с
оптимизацией затрат
. Хотя математически – это эквивалентные задачи, только количество переменных разное.
После запуска Поиск решения будет методично (последовательно) по своему алгоритму подставлять в зеленые ячейки числовые значения и вычислять функцию F (красная ячейка).
Ограничения (выделено серым)
. Ограничения модели – это ограничения на область изменения переменных. Они могут задаваться как простыми выражениями для одной переменной, например х1>=0, так и для некой комбинации переменных 5*x1+4*x2-x3-2*x4<=-3. В первом случае х1>=0 ограничения можно ввести прямо в окне Поиска решения (будет показано ниже), для более сложных зависимостей удобно подготовить вспомогательную таблицу (С26:Е29).
Составить модель, особенно первую, непросто. Может помочь такой подход: считать, что переменные (зеленые ячейки) уже содержат некие значения, пусть даже не оптимальные. Так легче составлять огграничения. В нашем случае ограниечение 5*x1+4*x2-x3-2*x4 можно записать с помощью формулы =
СУММПРОИЗВ($D$19:$D$22;C26:C29)
. В диапазоне D19:D22 содержатся коэффициенты 5; 4; -1; -2. Кроме того, если значения переменных заданы, то и значение целевой функции также автоматически рассчитано (тоже не оптимальное пока, до запуска Поиска решения).
Целевая функция (выделено красным)
.
Целевая функция – это то, что требуется оптимизировать, т.е. F. Формула для ее вычисления задана в явном виде – не нужно догадываться из условий обычной задачи как ее подсчитать. Это не всегда очевидно (см., например, статью про
пропускную способность трубопровода
).
Ниже приведено окно Поиска решения с заполненными полями: целевая функция, переменные и ограничения.

После запуска Поиска решения ответ будет вычислен за доли секунды: F=3.
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 – Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 – х; у = 2х + 3; у = (х + 3) 2 ; у = -(х – 4) 2 ;  .
.

Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).

Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).

Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):

Слайд 6 Найдите корни уравнения  , используя графический способ решения уравнений (Рис. 5).
, используя графический способ решения уравнений (Рис. 5).

2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение –х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):

- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).

При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул – сама формула (Рис. 8):

- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси – откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;

- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:

3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение  .
.
Для этого: в одной системе координат построить графики функций у1= и у2=1-х на промежутке [ -1; 4 ] с шагом 0,25; найти значение х точки пересечения графиков функций.
1 этап: Представление функций в табличной форме (рис. 1):

2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:

3 этап: Определение корней уравнения.
Графики функций у1= и у2=1-х пересекаются в одной точке (0;1) и, следовательно, уравнение имеет один корень – абсцисса этой точки: х=0.
III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения –х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=–х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения с точностью до 0,001.
- ввести функцию у=и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Линия тренда в Excel на разных графиках
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.
Рассмотрим, как добавить линию тренда на график в Excel.
Добавление линии тренда на график
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:
- Построим на основе таблицы график. Выделим диапазон – перейдем на вкладку «Вставка». Из предложенных типов диаграмм выберем простой график. По горизонтали – год, по вертикали – цена.
- Щелкаем правой кнопкой мыши по самому графику. Нажимаем «Добавить линию тренда».
- Открывается окно для настройки параметров линии. Выберем линейный тип и поместим на график величину достоверности аппроксимации.
- На графике появляется косая линия.
Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.
Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.
Внимание. Линию тренда нельзя добавить следующим типам графиков и диаграмм:
- лепестковый;
- круговой;
- поверхностный;
- кольцевой;
- объемный;
- с накоплением.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Полиномиальная линия тренда в Excel
Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).
Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.
Зато такой тренд позволяет составлять более-менее точные прогнозы.
Excel расчет линии тренда
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.
Рассмотрим, как добавить линию тренда на график в Excel.
Добавление линии тренда на график
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:
- Построим на основе таблицы график. Выделим диапазон – перейдем на вкладку «Вставка». Из предложенных типов диаграмм выберем простой график. По горизонтали – год, по вертикали – цена.
- Щелкаем правой кнопкой мыши по самому графику. Нажимаем «Добавить линию тренда».
- Открывается окно для настройки параметров линии. Выберем линейный тип и поместим на график величину достоверности аппроксимации.
- На графике появляется косая линия.
Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.
Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.
Внимание. Линию тренда нельзя добавить следующим типам графиков и диаграмм:
- лепестковый;
- круговой;
- поверхностный;
- кольцевой;
- объемный;
- с накоплением.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Полиномиальная линия тренда в Excel
Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).
Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.
Зато такой тренд позволяет составлять более-менее точные прогнозы.
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
-
Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».
Давайте для начала выберем линейную аппроксимацию.
В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».
Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.
Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
-
Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».
Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
После того, как вся информация внесена, жмем на кнопку «OK».
Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.
Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
-
Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».
Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
-
Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».
Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
-
Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».
Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.
Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
-
В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».
Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.
Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Это первая статья из серии “Как самостоятельно рассчитать прогноз продаж с учетом роста и сезонности”, из которой вы узнаете о 5 способах расчета значений линейного тренда в Excel.
Для того, чтобы легче было научиться прогнозировать продажи с учетом роста и сезонности, я разбил 1 большую статью о расчете прогноза на 3 части:
- Расчет значений тренда (рассмотрим на примере Линейного тренда в этой статье);
- Расчет сезонности;
- Расчет прогноза;
После изучения данного материала вы сможете выбрать оптимальный способ расчета значений линейного тренда, который будет удобен для решения вашей задачи, а в последствии, и для расчета прогноза наиболее удобным для вас способом.
Линейный тренд хорошо применять для временного ряда, данные которого увеличиваются или убывают с постоянной скоростью.
Рассмотрим линейный тренд на примере расчета прогноза продаж в Excel по месяцам.
Временной ряд продажи по месяцам (см. вложенный файл).
В этом временном ряду у нас есть 2 переменных:
Уравнение линейного тренда y(x)=a+bx, где
y — это объёмы продаж
x — номер периода (порядковый номер месяца)
a – точка пересечения с осью y на графике (минимальный уровень);
b – это значение, на которое увеличивается следующее значение временного ряда;
1-й способ расчета значений линейного тренда в Excel с помощью графика
Выделяем анализируемый объём продаж и строим график, где по оси Х — наш временной ряд (1, 2, 3… — январь, февраль, март …), по оси У — объёмы продаж. Добавляем линию тренда и уравнение тренда на график. Получаем уравнение тренда y=135134x+4594044
Для прогнозирования нам необходимо рассчитать значения линейного тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений линейного тренде нам будут известны:
- Время — значение по оси Х;
- Значение “a” и “b” уравнения линейного тренда y(x)=a+bx;
Рассчитываем значения тренда для каждого периода времени от 1 до 25, а также для будущих периодов с 26 месяца до 36.
Например, для 26 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=26 и получаем y=135134*26+4594044=8107551
27-го y=135134*27+4594044=8242686
2-й способ расчета значений линейного тренда в Excel — функция ЛИНЕЙН
1. Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel:
=ЛИНЕЙН(известные значения y, известные значения x, константа, статистика)
Для расчета коэффициентов в формулу вводим
известные значения y (объёмы продаж за периоды),
известные значения x (номера периодов),
вместо константы ставим 1,
вместо статистики 0,
Получаем 135135 — значение (b) линейного тренда y=a+bx;
Для того чтобы Excel рассчитал сразу 2 коэффициента (a) и (b) линейного тренда y=a+bx, необходимо
- установить курсор в ячейку с формулой и выделить соседнюю справа, как на рисунке;
- нажимаем клавишу F2, а затем одновременно — клавиши CTRL + SHIFT + ВВОД.
Получаем 135135, 4594044 — значение (b) и (a) линейного тренда y=a+bx;
2. Рассчитаем значения линейного тренда с помощью полученных коэффициентов . Подставляем в уравнение y=135134*x+4594044 номера периодов — x, для которых хотим рассчитать значения линейного тренда.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также быстрее.
3-й способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ТЕНДЕНЦИЯ(известные значения y; известные значения x; новые значения x; конста)
Подставляем в формулу
- известные значения y — это объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
- известные значения x — это номера периодов x для известных значений объёмов продаж y;
- новые значения x — это номера периодов, для которых мы хотим рассчитать значения линейного тренда;
- константа — ставим 1, необходимо для того, чтобы значения тренда рассчитывались с учетом коэффицента (a) для линейного тренда y=a+bx;
Для того чтобы рассчитать значения тренда для всего временного диапазона, в “новые значения x” вводим диапазон значений X, выделяем диапазон ячеек равный диапазону со значениями X с формулой в первой ячейке и нажимаем клавишу F2, а затем — клавиши CTRL + SHIFT + ВВОД.
4-й способ расчета значений линейного тренда в Excel — функция ПРЕДСКАЗ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ПРЕДСКАЗ(x; известные значения y; известные значения x)
Вместо X поставляем номер периода, для которого рассчитываем значение тренда.
Вместо “известные значения y” — объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
“известные значения x” — это номера периодов для каждого выделенного объёма продаж.
3-й и 4-й способ расчета значений линейного тренда быстрее, чем 1 и 2-й, однако с его помощью невозможно управлять коэффициентами тренда, как описано в статье “О линейном тренде”.
5-й способ расчета значений линейного тренда в Excel — Forecast4AC PRO
2. Заходим в меню программы и нажимаем “Start_Forecast”. Значения линейного тренда рассчитаны.
Для расчета прогноза осталось применить к значениям трендов будущих периодов коэффициенты сезонности, и прогноз продаж с учетом роста и сезонности готов.
В следующих статье “Как самостоятельно сделать прогноз продаж с учетом роста и сезонности” мы:
О том, что еще важно знать о линейном тренде, вы можете узнать в статье “Что важно знать о линейном тренде”.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
[spoiler title=”источники:”]
http://exceltable.com/grafiki/liniya-trenda-v-excel
http://web-shpargalka.ru/excel-raschet-linii-trenda.php
[/spoiler]
