Вектором является направленный отрезок. Длина этого отрезка является длиной вектора.
Длина вектора b⃗vec{b} обозначается ∣b⃗∣.left | vec{b} right |. Модуль числа имеет аналогичное обозначение и длина вектора часто называется модулем вектора.
Длина нулевого вектора равна нулю.
Нахождение длины вектора по его координатам
Длина вектора, который задан своими координатами, – это квадратный корень из суммы квадратов его координат.
Для того чтобы найти длину вектора, заданного своими координатами, нужно извлечь квадратный корень из суммы квадратов его координат.
- Для вектора b⃗=(bx;by),vec{b}=(b_{x};b_{y}), заданного на плоскости, длина вычисляется по формуле ∣b⃗∣left |vec{b} right|=bx2+by2sqrt {b_{x}^{2}+b_{y}^{2}}.
- Для вектора b⃗=(bx;by;bz),vec{b}=(b_{x};b_{y};b_{z}), заданного в пространстве, длина вычисляется по формуле ∣b⃗∣=bx2+by2+bz2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}.
Пример 1
Найти длину вектора b⃗=(6;−4).vec{b}=(6;-4).
Вектор задан на плоскости, поэтому воспользуемся первой формулой: ∣b⃗∣=bx2+by2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}}.
Подставим координаты вектора b⃗vec{b} в формулу, получим: ∣b⃗∣=62+(−4)2=36+16=52=213left | vec{b} right |=sqrt {6^{2}+(-4)^{2}}=sqrt {36+16}=sqrt {52}=2sqrt {13}.
Ответ: 2132sqrt {13}.
Пример 2
Найти длину вектора d⃗=(1;3;5).vec{d}=(1;3;5).
Вектор задан в пространстве, поэтому воспользуемся второй формулой:
∣d⃗∣=dx2+dy2+dz2left | vec{d} right |=sqrt {d_{x}^{2}+d_{y}^{2}+d_{z}^{2}}.
Подставим координаты вектора d⃗vec{d} в формулу, получим:
∣d⃗∣=12+32+52=1+9+25=35left | vec{d} right |=sqrt {1^{2}+3^{2}+5^{2}}=sqrt {1+9+25}=sqrt {35}.
Нахождение длины вектора по координатам точек его начала и конца
Для нахождения длины вектора CD⃗vec{CD}, где C(cx;cy)C(c_{x};c_{y}) и D(dx;dy)D(d_{x};d_{y}) существует определенная последовательность действий:
- Найти координаты вектора CD⃗vec{CD} по формуле: ∣CD⃗∣=(dx−cx;dy−cy)left | vec{CD} right |=(d_{x}-c_{x};d_{y}-c_{y}).
- Найти длину вектора по его координатам по формуле: ∣CD⃗∣=(dx−cx)2+(dy−cy)2left | vec{CD} right |=sqrt {(d_{x}-c_{x})^{2}+(d_{y}-c_{y})^{2}}.
Аналогично находится длина вектора CD⃗,vec{CD}, заданного в пространстве, где C(cx;cy;cz)C(c_{x};c_{y};c_{z}) и D(dx;dy;dz)D(d_{x};d_{y};d_{z}):
- Найти координаты вектора CD⃗vec{CD} по формуле: CD⃗=(dx−cx;dy−cy;dz−cz).vec{CD}=(d_{x}-c_{x};d_{y}-c_{y};d_{z}-c_{z}).
- Найти длину вектора по его координатам по формуле: ∣CD⃗∣=(dx−cx)2+(dy−cy)2+(dz−cz)2left | vec{CD} right |=sqrt {(d_{x}-c_{x})^{2}+(d_{y}-c_{y})^{2}+(d_{z}-c_{z})^{2}}.
Пример 1
На плоскости заданы точки E(−1;3)иK(3;−4)E(-1;3) и K(3;-4). Найти длину вектора EK⃗.vec{EK}.
Найдем координаты вектора EK⃗.vec{EK}. Для этого из координат конца вычтем координаты начала, получим:
EK⃗=(3−(−1);−4−3)=(3+1;−4−3)=(4;−7).vec{EK}=(3-(-1);-4-3)=(3+1;-4-3)=(4;-7).
Воспользуемся формулой ∣b⃗∣=bx2+by2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}} для нахождения длины вектора, получим:
∣EK⃗∣=42+(−7)2left | vec{EK} right |=sqrt {4^{2}+(-7)^{2}}=16+49sqrt {16+49}=65sqrt {65}.
Пример 2
В пространстве заданы точки C(1;2;3)C(1;2;3) и D(3;4;5).D(3;4;5). Найти длину вектора CD⃗.vec{CD}.
Найдем координаты вектора CD⃗.vec{CD}. Для этого из координат конца вычтем координаты начала, получим: CD⃗=(3−1;4−2;5−3)=(2;2;2).vec{CD}=(3-1;4-2;5-3)=(2;2;2).
Воспользуемся формулой ∣b⃗∣=bx2+by2+bz2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}+b_{z}^{2}} для нахождения длины вектора, получим: ∣b⃗∣=22+22+22=4+4+4=12=23left | vec{b} right |=sqrt {2^{2}+2^{2}+2^{2}}=sqrt {4+4+4}=sqrt {12}=2sqrt 3.
Нахождение длины вектора по теореме косинусов
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Для треугольника со сторонами a,b,ca, b, c и углами α,βalpha, beta и γ,gamma, противолежащими этим сторонам соответственно, справедливы равенства:
b=a2+c2−2a⋅c⋅cos(β),b=a^{2}+c^{2}-2acdot ccdot cos (beta), a=b2+c2−2b⋅c⋅cos(α),a=b^{2}+c^{2}-2bcdot ccdot cos (alpha), c=a2+b2−2a⋅b⋅cos(γ).c=a^{2}+b^{2}-2acdot bcdot cos (gamma).
Аналогично поступают и с векторами. Рассмотрим пример.
Пример 1
Длины векторов KL⃗vec{KL} и KM⃗vec{KM} равны соответственно 2 и 4, а угол между ними равен π4.frac{pi }{4}. Вычислите длину вектора LM⃗.vec{LM}.
Длина вектора LM⃗vec{LM} равна длине стороны LMLM в треугольнике LMKLMK. Также нам известны стороны KLKL и KMKM треугольника LMKLMK. Они равны длинам соответствующих векторов. Нам известен угол между векторами. Найдем сторону LMLM треугольника △KLM.triangle KLM.
LM2=KL2+KM2−2KL⋅KM⋅cos∠LKM.LM^2=KL^2+KM^2-2KLcdot KMcdot cos angle LKM.
LM2=22+42−2⋅2⋅4⋅cosπ4=4+16−82=20−82.LM^2=2^2+4^2-2cdot 2cdot4cdot cos frac{pi }{4}=4+16-8sqrt{2}=20-8sqrt{2}.
LM=20−82.LM=sqrt{20-8sqrt{2}}.
∣LM⃗∣=20−82.|vec{LM}|=sqrt{20-8sqrt{2}}.
Тест по теме «Как вычислить длину вектора»
Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Длина вектора
Как найти?
Длина вектора $ overline{a}$ обозначается как $ |overline{a}| $. Как найти длину вектора по его координатам? Для этого существует две формулы в зависимости от расположения вектора: на плоскости $ overline{a}=(a_x;a_y) $ или в пространстве $ overline{a} = (a_x; a_y; a_z) $.
Формула длины вектора на плоскости:
$$ |overline{a}| = sqrt{a_x ^2 + a_y ^2} $$
Формула длины вектора в пространстве:
$$ |overline{a}| = sqrt{a_x ^2 + a_y ^2 + a_z ^2 } $$
Если даны координаты точек начала и конца вектора $ A(a_x; a_y) $ и $ B(b_x; b_y) $, то найти длину можно по формулам:
$$ |overline{AB}| = sqrt{(a_x-b_x)^2 + (a_y-b_y) ^2} $$
$$ |overline{AB}| = sqrt{(a_x-b_x)^2 + (a_y-b_y)^2+ (a_z-b_z)^2} $$
Примеры решений
| Пример 1 |
| Найти длину вектора по его координатам $ overline{a} = (4;-3) $ |
| Решение |
|
Разберем вектор. Первая координата $ a_x = 4 $, а вторая координата $ a_y=-3 $. Так как даны две координаты, то делаем вывод, что задача плоская. Необходимо применить первую формулу. Подставляем в неё значения из условия задачи: $$|overline{a}| = sqrt{4^2+(-3)^2} = sqrt{16+9} = sqrt{25} = 5 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Длина вектора $|overline{a}| = 5 $ |
| Пример 2 |
| Найти длину вектора по координатам $ overline{a}=(4;2;4) $ |
| Решение |
|
Сразу замечаем, что дана пространственная задача. А именно $ a_x=4, a_y=2, a_z=4 $. Для нахождения длины вектора используем вторую формулу. Подставляем неизвестные в неё: $|overline{a}|=sqrt{4^2+2^2+4^2}=sqrt{36}=6 $ |
| Ответ |
| Длина вектора $|overline{a}|=6 $ |
| Пример 3 |
| Найти длину вектора, если известны координаты его начала и конца. $ A=(2;1), B=(-1;3) $ |
| Решение |
|
Задача дана плоская судя по наличию только двух координат у векторов. Но даны на этот раз начало и конец вектора. Поэтому сначала находим координаты вектора $ overline{AB} $, а только потом его длину по формуле координат: $ overline{AB}=(b_x-a_x;b_y-a_y)=(-1-2;3-1)=(-3;2) $ Теперь когда координаты вектора $ overline{AB} $ стали известны можно использовать привычную формулу: $|overline{AB}|=sqrt{(-3)^2+2^2}=sqrt{9+4}=sqrt{13} $ |
| Ответ |
| $|overline{AB}|=sqrt{13} $ |
В статье мы ответили на вопрос:”Как найти длину вектора?” с помощью формул. А также рассмотрели практические примеры решения задач на плоскости и в пространстве. Следует заметить, что существуют аналогичные формулы для пространств больше, чем трёхмерные.
Содержание:
- Формула
- Примеры вычисления длины вектора
Формула
Чтобы найти длину вектора, заданного своими координатами, нужно извлечь корень квадратный из суммы квадратов его координат.
Если вектор задан на плоскости и имеет координаты $bar{a}=left(a_{x} ; a_{y}right)$, его длина вычисляется по формуле:
$$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}$$
Если вектор задан в пространстве координатами $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$, то его длина вычисляется по формуле
$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}$
Примеры вычисления длины вектора
Пример
Задание. Найти длину вектора $bar{a}=(-3 ; 4)$
Решение. Для нахождения длины вектора, заданного на плоскости, воспользуемся формулой
$$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}$$
Подставляя в неё координаты заданного вектора, получим:
$$|bar{a}|=sqrt{(-3)^{2}+4^{2}}=sqrt{9+16}=sqrt{25}=5$$
Ответ. $|bar{a}|=5$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В пространстве заданы точки
$A(3 ;-2 ;-1)$ и $ B(1 ; 2 ;-5)$. Найти длину вектора
$overline{A B}$
Решение. Найдем сначала координаты вектора $overline{A B}$. Для этого из координат конца вычислим соответствующие координаты начала, получим:
$$overline{A B}=(1-3 ; 2-(-2) ;-5-(-1))=(-2 ; 4 ;-4)$$
нахождения длины вектора $overline{A B}$ воспользуемся формулой:
$$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}$$
Подставляя в эту формулу координаты вектора, получим
$$|overline{A B}|=sqrt{(-2)^{2}+4^{2}+(-4)^{2}}=sqrt{4+16+16}=sqrt{36}=6$$
Ответ. $|overline{A B}|=6$
Читать дальше: как найти модуль вектора.
Как найти длину вектора
ФОРМУЛА
Чтобы найти длину вектора, определяемого его координатами, вам нужно извлечь квадратный корень из суммы квадратов его координат. Если вектор определен на плоскости и имеет координаты (
overline{a}=left(a_{x} ; a_{y}right)
), его длина рассчитывается по формуле:
(
|overline{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}
)
Если вектор задан в пространстве координатами (
overline{a}=left(a_{x} ; a_{y} ; a_{z}right)
) , то его длина вычисляется по формуле
(
|overline{a}|=sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}
)
ПРИМЕРЫ РАСЧЕТА ВЕКТОРНОЙ ДЛИНЫ
ПРИМЕР
overline{a}=(-3 ; 4)
)
(
|overline{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}
)
Подставляя в него координаты заданного вектора, получаем:
(
|overline{a}|=sqrt{(-3)^{2}+4^{2}}=sqrt{9+16}=sqrt{25}=5
)
|overline{a}|=5
)
ПРИМЕР
A(3 ;-2 ;-1)quad{и}quad B(1 ; 2 ;-5)
). Найти длину вектора (
overline{A B}
)
overline{A B}
). Для этого из координат конца мы вычисляем соответствующие координаты начала, получаем:
(
overline{A B}=(1-3 ; 2-(-2) ;-5-(-1))=(-2 ; 4 ;-4)
)
Находя длину вектора (
overline{A B}
) мы используем формулу:
(
|overline{a}|=sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}
)
Подставляя в эту формулу координаты вектора, получим
(
|overline{A B}|=sqrt{(-2)^{2}+4^{2}+(-4)^{2}}=sqrt{4+16+16}=sqrt{36}=6
)
|overline{A B}|=6
)
Длина вектора – основные формулы
Длину вектора a→ будем обозначать a→. Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат Oxy. Пусть в ней задан некоторый вектор a→ с координатами ax;ay. Введем формулу для нахождения длины (модуля) вектора a→ через координаты ax и ay.
От начала координат отложим вектор OA→=a→. Определим соответственные проекции точки A на координатные оси как Ax и Ay . Теперь рассмотрим прямоугольник OAxAAy с диагональю OA.
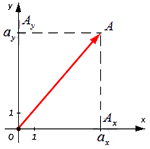
Из теоремы Пифагора следует равенство OA2=OAx2+OAy2, откуда OA=OAx2+OAy2. Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что OAx2=ax2 и OAy2=ay2, а по построению длина OA равна длине вектора OA→, значит, OA→=OAx2+OAy2.
Отсюда получается, что формула для нахождения длины вектора a→=ax;ay имеет соответствующий вид: a→=ax2+ay2.
Если вектор a→ дан в виде разложения по координатным векторам a→=ax·i→+ay·j→, то вычислить его длину можно по той же формуле a→=ax2+ay2, в данном случае коэффициенты ax и ay выступают в роли координат вектора a→ в заданной системе координат.
Вычислить длину вектора a→=7;e, заданного в прямоугольной системе координат.
Решение
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатамa→=ax2+ay2: a→=72+e2=49+e
Ответ: a→=49+e.
Формула для нахождения длины вектора a→=ax;ay;az по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
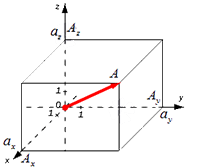
В данном случае OA2=OAx2+OAy2+OAz2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда OA=OAx2+OAy2+OAz2. Из определения координат вектора можем записать следующие равенства OAx=ax; OAy=ay; OAz=az; , а длина ОА равна длине вектора, которую мы ищем, следовательно, OA→=OAx2+OAy2+OAz2.
Отсюда следует, что длина вектора a→=ax;ay;az равна a→=ax2+ay2+az2.
Вычислить длину вектора a→=4·i→-3·j→+5·k→, где i→,j→,k→ – орты прямоугольной системы координат.
Решение
Дано разложение вектора a→=4·i→-3·j→+5·k→, его координаты равны a→=4,-3,5. Используя выше выведенную формулу получим a→=ax2+ay2+az2=42+(-3)2+52=52.
Ответ:a→=52.
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A(ax;ay) и B(bx;by), отсюда вектор AB→ имеет координаты (bx-ax; by-ay)значит, его длина может быть определена по формуле: AB→=(bx-ax)2+(by-ay)2
А если даны точки с заданными координатами A(ax;ay;az) и B(bx;by;bz) в трехмерном пространстве, то длину вектора AB→ можно вычислить по формуле
AB→=(bx-ax)2+(by-ay)2+(bz-az)2
Найти длину вектора AB→, если в прямоугольной системе координат A1, 3, B-3, 1.
Решение
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим AB→=(bx-ax)2+(by-ay)2: AB→=(-3-1)2+(1-3)2=20-23.
Второй вариант решения подразумевает под собой применение данных формул по очереди: AB→=(-3-1; 1-3)=(-4; 1-3); AB→=(-4)2+(1-3)2=20-23.-
Ответ: AB→=20-23.
Определить, при каких значениях длина вектора AB→ равна 30, еслиA(0, 1, 2); B(5, 2, λ2) .
Решение
Для начала распишем длину вектора AB→ по формуле: AB→=(bx-ax)2+(by-ay)2+(bz-az)2=(5-0)2+(2-1)2+(λ2-2)2=26+(λ2-2)2
Затем полученное выражение приравняем к 30, отсюда найдем искомые λ:
26+(λ2-2)2=3026+(λ2-2)2=30(λ2-2)2=4λ2-2=2 или λ2-2=-2 λ1=-2, λ2=2, λ3=0.
Ответ: λ1=-2, λ2=2, λ3=0.
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов AB→, AC→ и угол между ними (или косинус угла), а требуется найти длину вектора BC→ или CB→. В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ABC, вычислить длину стороны BC, которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Длины векторов AB→ и AC→ равны 3 и 7 соответственно, а угол между ними равен π3. Вычислить длину вектора BC→.
Решение
Длина вектора BC→ в данном случае равна длине стороны BC треугольника △ABC. Длины сторон AB и AC треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов:BC2=AB2+AC2-2·AB·AC·cos∠(AB,→AC→)=32+72-2·3·7·cosπ3=37 ⇒BC=37 Таким образом, BC→=37.
Ответ:BC→=37.
Итак, для нахождения длины вектора по координатам существуют следующие формулы a→=ax2+ay2 или a→=ax2+ay2+az2, по координатам точек начала и конца вектора AB→=(bx-ax)2+(by-ay)2 или AB→=(bx-ax)2+(by-ay)2+(bz-az)2, в некоторых случаях следует использовать теорему косинусов.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
