Гипербола: определение, свойства, построение
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и
есть величина постоянная
, меньшая расстояния
между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.
Фокальное свойство гиперболы
Точки и
называются фокусами гиперболы, расстояние
между ними — фокусным расстоянием, середина
отрезка
— центром гиперболы, число
— длиной действительной оси гиперболы (соответственно,
— действительной полуосью гиперболы). Отрезки
и
, соединяющие произвольную точку
гиперболы с ее фокусами, называются фокальными радиусами точки
. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение , где
, называется эксцентриситетом гиперболы. Из определения
следует, что
.
Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:
(3.50)
Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов и
. Для произвольной точки
, принадлежащей гиперболе, имеем:
Записывая это уравнение в координатной форме, получаем:
Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:
где , т.е. выбранная система координат является канонической.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.
Директориальное свойство гиперболы
Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее (рис.3.41,а). При
, когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.
Гиперболу с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки
(фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
(директориальное свойство гиперболы). Здесь
и
— один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
В самом деле, например, для фокуса и директрисы
(рис.3.41,а) условие
можно записать в координатной форме:
Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса
и директрисы
:
Уравнение гиперболы в полярной системе координат
Уравнение правой ветви гиперболы в полярной системе координат (рис.3.41,б) имеет вид
, где
— фокальный параметр гиперболы.
В самом деле, выберем в качестве полюса полярной системы координат правый фокус гиперболы, а в качестве полярной оси — луч с началом в точке
, принадлежащий прямой
, но не содержащий точки
(рис.3.41,б). Тогда для произвольной точки
, принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем
. Выражаем расстояние между точками
и
(см. пункт 2 замечаний 2.8):
Следовательно, в координатной форме уравнение гиперболы имеет вид
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус и делаем замены
:
что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для гиперболы,
для эллипса).
Геометрический смысл коэффициентов в уравнении гиперболы
Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение , находим абсциссы точек пересечения:
. Следовательно, вершины имеют координаты
. Длина отрезка, соединяющего вершины, равна
. Этот отрезок называется действительной осью гиперболы, а число
— действительной полуосью гиперболы. Подставляя
, получаем
. Длина отрезка оси ординат, соединяющего точки
, равна
. Этот отрезок называется мнимой осью гиперболы, а число
— мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.
Замечания 3.10.
1. Прямые ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).
2. Прямые , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).
Для равносторонней гиперболы, описываемой уравнением (т.е. при
), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат
(рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид
(гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).
В самом деле, повернем каноническую систему координат на угол (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами
Подставляя эти выражения в уравнение равносторонней гиперболы и приводя подобные члены, получаем
3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.
Действительно, если точка принадлежит гиперболе
. то и точки
и
, симметричные точке
относительно координатных осей, также принадлежат той же гиперболе.
Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.
4. Из уравнения гиперболы в полярных координатах (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси (
при
).
5. Эксцентриситет характеризует форму гиперболы. Чем больше
, тем шире ветви гиперболы, а чем ближе
к единице, тем ветви гиперболы уже (рис.3.43,а).
Действительно, величина угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника:
. Учитывая, что
и
, получаем
Чем больше , тем больше угол
. Для равносторонней гиперболы
имеем
и
. Для
угол
тупой, а для
угол
острый (рис.3.43,а).
6. Две гиперболы, определяемые в одной и той же системе координат уравнениями и
называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы
приводится к каноническому при помощи переименования координатных осей (3.38).
7. Уравнение определяет гиперболу с центром в точке
, оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение
определяет сопряженную гиперболу с центром в точке
.
Параметрическое уравнение гиперболы
Параметрическое уравнение гиперболы в канонической системе координат имеет вид
где — гиперболический косинус, a
гиперболический синус.
Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству .
Пример 3.21. Изобразить гиперболу в канонической системе координат
. Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.
Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — действительная полуось,
— мнимая полуось гиперболы. Строим основной прямоугольник со сторонами
с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя
в уравнение гиперболы, получаем
Следовательно, точки с координатами и
принадлежат гиперболе. Вычисляем фокусное расстояние
эксцентриситет ; фокальныи параметр
. Составляем уравнения асимптот
, то есть
, и уравнения директрис:
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру – значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде 
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения

- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение  называется уравнением фигуры, если
называется уравнением фигуры, если 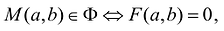 , то есть (а, b) – решение уравнения F(x,y) = 0.
, то есть (а, b) – решение уравнения F(x,y) = 0.
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения  , т.е. уравнение фигуры задает эту фигуру.
, т.е. уравнение фигуры задает эту фигуру.
Возможны два вида задач:
- дано уравнение
 и надо построить фигуру Ф, уравнением которой является
и надо построить фигуру Ф, уравнением которой является  ;
; - дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения  и решается, чаще всего, методами математического анализа.
и решается, чаще всего, методами математического анализа.
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
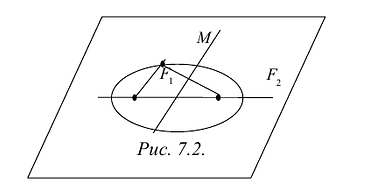
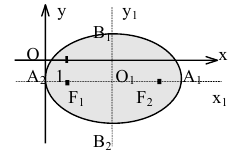
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 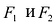 , есть величина постоянная (большая, чем расстояние между
, есть величина постоянная (большая, чем расстояние между 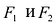 ).
).
Точки 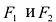 называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с<а. Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.
называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с<а. Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.
Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины 2а закрепить в точках  и натянуть нить острием карандаша, то при движении острия будет вычерчиваться эллипс с фокусами
и натянуть нить острием карандаша, то при движении острия будет вычерчиваться эллипс с фокусами  и с суммой расстояний от произвольной точки эллипса до фокусов, равной 2 а (Рис. 7.1).
и с суммой расстояний от произвольной точки эллипса до фокусов, равной 2 а (Рис. 7.1).
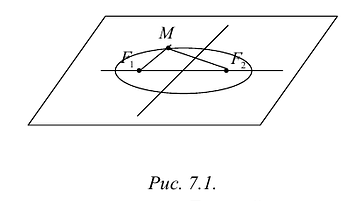
Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось Ох походила через фокусы  положительное направление оси – от
положительное направление оси – от  , начало координат выберем в середине отрезка
, начало координат выберем в середине отрезка  . Тогда координаты точек
. Тогда координаты точек  будут соответственно (-с,0) и (с,0).
будут соответственно (-с,0) и (с,0).
Пусть М(х,у) – произвольная точка эллипса, тогда: 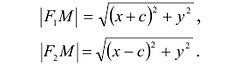
Подставляя сюда значения 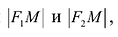 имеем:
имеем:
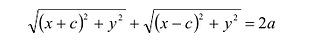 (7.1)
(7.1)
Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим
его:
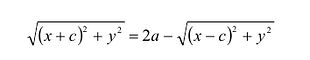
Возведя обе части уравнения в квадрат и приведя подобные члены, получим: 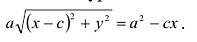
Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем 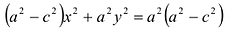 или
или
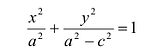 (7.2)
(7.2)
Положительную величину 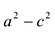 обозначим через
обозначим через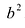 . Тогда уравнение (7.2) примет вид:
. Тогда уравнение (7.2) примет вид:
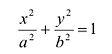 (7.3)
(7.3)
Оно называется каноническим уравнение эллипса.
Координаты точек эллипса ограничены неравенствами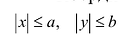 . Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами 2а и 2b •
. Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами 2а и 2b •
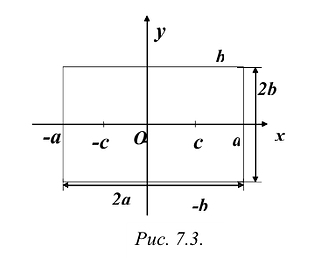
Заметим, что в уравнение (7.3) входят лишь четные степени х и у. Поэтому, если точка M(х,у) принадлежит эллипсу, то и точки  также ему принадлежат. А это означает, что эллипс – линия симметричная относительно координатных осей Ох и Оу.
также ему принадлежат. А это означает, что эллипс – линия симметричная относительно координатных осей Ох и Оу.
Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (7.3) имеем:
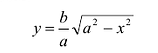 (7.4)
(7.4)
При возрастании x от 0 до а, у монотонно убывает от а до 0. График функции изображен на Рис. 7.4.
 Рис. 7.4
Рис. 7.4
Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис. 7.5). 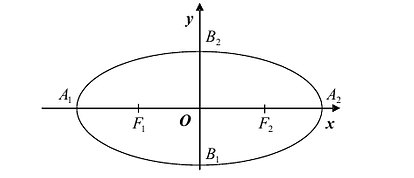
Рис. 7.5. Оси симметрии эллипса (оси Ох и Оу) называются просто его осями, а центр симметрии – точка О – центром эллипса. Точки 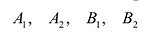 пересечения эллипса с осями координат называются вершинами эллипса. Отрезки
пересечения эллипса с осями координат называются вершинами эллипса. Отрезки 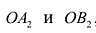 , а также их длины а и Ь называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси Ох (как в нашем случае), из равенства
, а также их длины а и Ь называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси Ох (как в нашем случае), из равенства 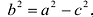 следует, что a>b. В этом случае а называется большой полуосью, a b – малой.
следует, что a>b. В этом случае а называется большой полуосью, a b – малой.
Если а =Ь, то уравнение (7.3) можно переписать в виде:
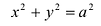 (7.5)
(7.5)
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 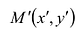 координаты которой задаются формулами
координаты которой задаются формулами 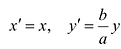 будет окружность (4) переводить в эллипс, заданный соотношением
будет окружность (4) переводить в эллипс, заданный соотношением 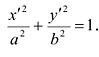
Число 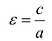 называется эксцентриситетом эллипса. Эксцентриситет
называется эксцентриситетом эллипса. Эксцентриситет 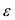 характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении
характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении 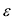 становится более вытянутым
становится более вытянутым
Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 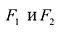 . Их длины
. Их длины 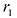 и
и 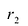 задаются формулами
задаются формулами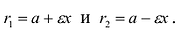 Прямые
Прямые 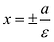 называются директрисами эллипса. Директриса
называются директрисами эллипса. Директриса 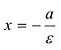 называется левой, а
называется левой, а 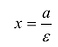 – правой. Так как для эллипса
– правой. Так как для эллипса 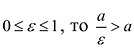 и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е. 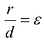
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 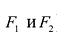 есть величина постоянная (не равная нулю и меньшая, чем расстояние между
есть величина постоянная (не равная нулю и меньшая, чем расстояние между 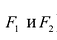 ).
).
Точки 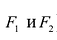 называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов
называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов 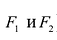 обозначим через а. По условию, а <с.
обозначим через а. По условию, а <с.
Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение: 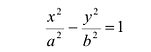 (7.6) где ху – координаты произвольной точки гиперболы,
(7.6) где ху – координаты произвольной точки гиперболы,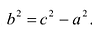
Уравнение (7.6) называется каноническим уравнением гиперболы.
Из уравнения (7.6) видно, что 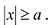 . Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми х = -а и х = а.
. Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми х = -а и х = а.
Так как в уравнение входят только четные степени x и у, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:
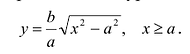
График этой функции от точки A(а,0) уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:
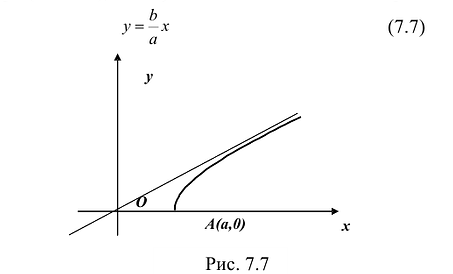
Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты
Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны 2а и 2Ь параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).
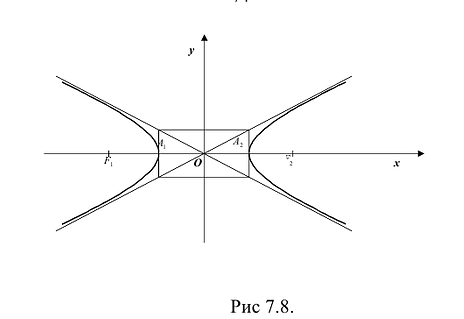
Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки  , пересечения гиперболы с осью Ох называются вершинами гиперболы. Величины а и Ь называются полуосями гиперболы. Если а=Ь, то гипербола называется равносторонней.
, пересечения гиперболы с осью Ох называются вершинами гиперболы. Величины а и Ь называются полуосями гиперболы. Если а=Ь, то гипербола называется равносторонней.
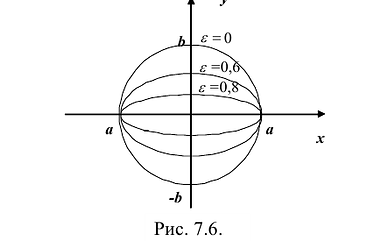
Эксцентриситетом гиперболы называется число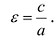 . Для любой гиперболы
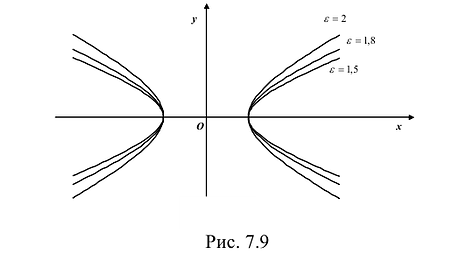
. Для любой гиперболы 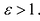 . Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси Ох. На рисунке 7.9 изображены гиперболы с различными значениями £.
. Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси Ох. На рисунке 7.9 изображены гиперболы с различными значениями £.
Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами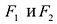 . Их длины
. Их длины 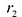 и
и 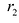 задаются формулами:
задаются формулами:
Для правой – ветви 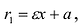 ,
,
Для левой – ветви 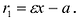
Прямые 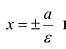 называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением
называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением 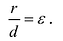
Парабола
Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой 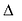 (директрисы).
(директрисы).
Для вывода канонического уравнения параболы ось Ох проводят через фокус F перпендикулярно директрисе 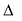 в направлении от директрисы к фокусу; начало координат берут в середине отрезка между фокусом F и точкой D пересечения оси Ох с директрисой
в направлении от директрисы к фокусу; начало координат берут в середине отрезка между фокусом F и точкой D пересечения оси Ох с директрисой 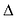 . Если обозначить через р расстояние фокуса от директрисы, то
. Если обозначить через р расстояние фокуса от директрисы, то 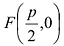 и уравнение директрисы будет иметь вид
и уравнение директрисы будет иметь вид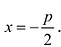
В выбранной системе координат уравнение параболы имеет вид:
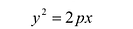 (7.8)
(7.8)
Это уравнение называется каноническим уравнением параболы. Из уравнения (7.8) видно, что л: может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси Оу. Так как уравнение (7.8) содержит у только в четной степени, то парабола симметрична относительно оси Ох и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти 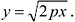 .
.
При неограниченном возрастании x неограниченно растет и у. Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии. Сделаем рисунок параболы (Рис. 7.10). 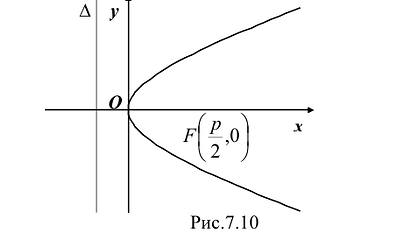
Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы.
Исследование на плоскости уравнения второй степени
Рассмотрим уравнение:
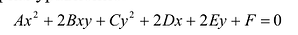 (7.9)
(7.9)
где среди коэффициентов А, В, С есть отличные от нуля, т.е. (7.9) – уравнение второй степени относительно х и у.
Возьмем на плоскости две прямоугольные системы координат: Оху, которую будем называть старой, и новую, полученную из Оху поворотом ее вокруг начала координат на угол 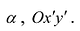
Старые координаты х, у выражаются через новые координаты 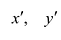 по формулам:
по формулам:
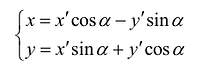 (7.10)
(7.10)
Подставив выражения для х и у в уравнение (8), получим: 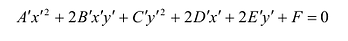 (7.11)
(7.11)
Это уравнение в системе координат 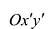 задает ту же линию, что и уравнение (7. 9) в системе Оху.
задает ту же линию, что и уравнение (7. 9) в системе Оху.
Если в уравнении (7.9) 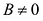 , то за счет выбора угла а в (7.10) можно добиться того, что В’ = 0. Для этого угол а надо взять таким, чтобы
, то за счет выбора угла а в (7.10) можно добиться того, что В’ = 0. Для этого угол а надо взять таким, чтобы 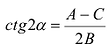 . Поэтому будем считать В’= 0, тогда уравнение (7.11) примет вид:
. Поэтому будем считать В’= 0, тогда уравнение (7.11) примет вид:
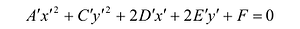 (7.12)
(7.12)
Преобразуя это уравнение и применяя параллельный перенос координатных осей, придем к уравнению:
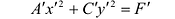 (7.13)
(7.13)
В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:
Рассматривая далее методично все случаи, придем к выводу: уравнение вида (7.9) задает одну из следующих фигур: эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, прямую, точку или пустое множество.
Кривые второго порядка в высшей математике
Выяснение взаимосвязей между различными показателями экономического характера часто приводит к форме этих связей в виде гиперболы и параболы. В этой лекции приведём краткие сведения обо всех кривых второго порядка.
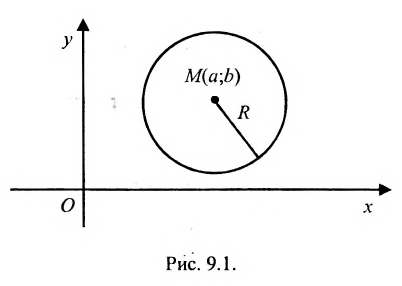
Окружность
Определение 9.1. Окружностью называется геометрическое место точек, равноудаленных от данной точки – центра окружности.
Если точка 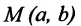 – центр (рис.9.1), N(x,y) – произвольная точка окружности и R – её радиус, то согласно определения можно записать
– центр (рис.9.1), N(x,y) – произвольная точка окружности и R – её радиус, то согласно определения можно записать
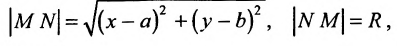
или

Найдём условия, при которых общее уравнение второй степени с двумя переменными
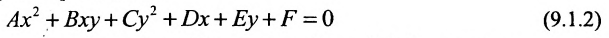
определяет окружность. Раскрыв скобки в (9.1.1), получим
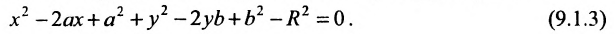
Сравнивая (9.1.2) и (9.1.3), находим условия А = С, В = О,
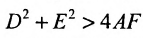 , при выполнении которых общее уравнение (9.1.2) определяет окружность.
, при выполнении которых общее уравнение (9.1.2) определяет окружность.
Эллипс
Определение 9.2. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами.
Пусть на плоскости хОу (рис. 9.2) дан эллипс с фокусами  и
и . Пусть начало координат лежит на середине отрезка
. Пусть начало координат лежит на середине отрезка 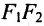 . Выведем уравнение эллипса.
. Выведем уравнение эллипса.
Если точка А – произвольная точка эллипса с координатами (х, у), то
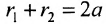 (9.2.1)
(9.2.1)
где 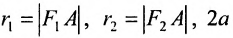 – постоянная сумма. Так как
– постоянная сумма. Так как 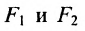
расположены симметрично относительно начала координат, то они имеют координаты (с,0) и (-с,0) соответственно. Воспользовавшись формулой для вычисления расстояния между двумя точками, находим 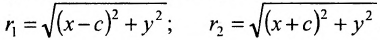 . Подставив значения
. Подставив значения 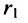
и 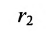 в (9.2.1), получаем уравнение
в (9.2.1), получаем уравнение 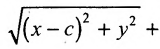
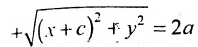
Обе части этого уравнения возведем в квад-Упростив и обозначив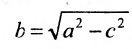
получим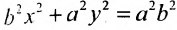 . Разделим обе части уравнения на правую часть
. Разделим обе части уравнения на правую часть
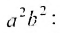

Уравнение (9.2.2) называется каноническим уравнением эллипса, где а – большая полуось, b – малая полуось.
Это уравнение второго порядка, следовательно, эллипс есть линия второго порядка. Для определения формы эллипса служит его эксцентриситет  , т.е. отношение расстояния между фокусами этого эллипса к длине его большей полуоси. Так как с
, т.е. отношение расстояния между фокусами этого эллипса к длине его большей полуоси. Так как с а, то эксцентриситет каждого эллипса меньше единицы. Поскольку
а, то эксцентриситет каждого эллипса меньше единицы. Поскольку
 , то подставив значение
, то подставив значение 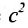 в равенство
в равенство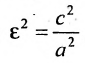 , получим
, получим 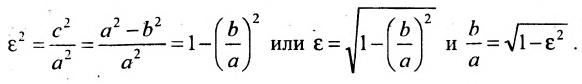
Следовательно, эксцентриситет определяется отношение осей эллипса; а отношение осей определяется эксцентриситетом. Чем ближе эксцентриситет к единице, тем меньше 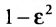 , тем меньше, следовательно, отношение
, тем меньше, следовательно, отношение 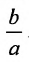 . Это значит, что эллипс вытянут вдоль оси Ох. В случае Ь=а и
. Это значит, что эллипс вытянут вдоль оси Ох. В случае Ь=а и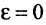 получаем окружность.
получаем окружность.
Две прямые, перпендикулярные к большей оси эллипса и расположенные симметрично относительно центра на расстоянии 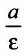 от него, называются директрисами эллипса. Уравнения директрис
от него, называются директрисами эллипса. Уравнения директрис
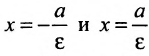
Пример:
Исследовать, какая линия определяется уравнением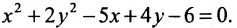
Решение:
Сгруппируем члены, содержащие одну и туже переменную, получим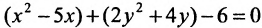
Из второй скобки вынесем коэффициент при 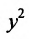 , после чего предыдущее уравнение примет вид
, после чего предыдущее уравнение примет вид
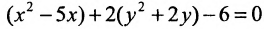
В каждой из скобок выделим полный квадрат
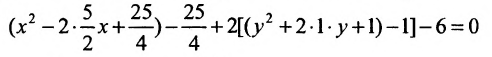
или 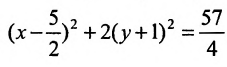
Произведём замену: 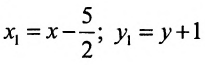 . Исследуемое уравнение принимает вид:
. Исследуемое уравнение принимает вид: 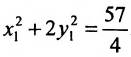 .
.
Разделив обе части этого уравнения на 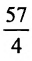 , получим канонический вид данного уравнения:
, получим канонический вид данного уравнения: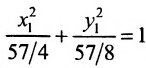
Заданное уравнение определяет эллипс с полуосями 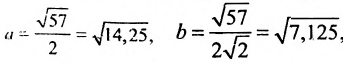 , центр которого находится в точке
, центр которого находится в точке 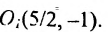
Выбираем на плоскости произвольным образом прямоугольную систему координат хОу. С помощью параллельного переноса переносим оси координат в новое начало в точку 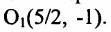 . В новой системе координат строим основной прямоугольник со сторонами
. В новой системе координат строим основной прямоугольник со сторонами 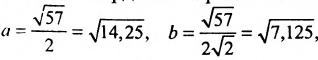 , стороны которого параллельны новым осям координат, а центр находится в точке
, стороны которого параллельны новым осям координат, а центр находится в точке 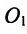 . Вписываем в него эллипс.
. Вписываем в него эллипс.
Гипербола
Определение 9.3.1. Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, меньшая, чем расстояние между фокусами и отличная от нуля (указанная разность берется по абсолютному значению). 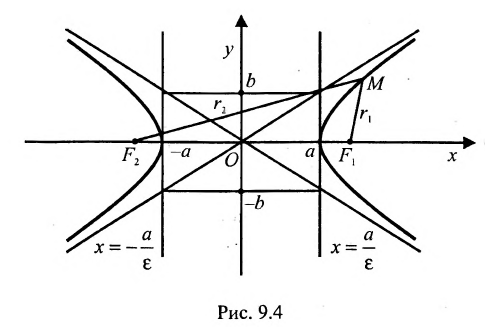
Пусть М- произвольная точка гиперболы с фокусами 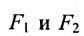 (рис. 9.4). Отрезки
(рис. 9.4). Отрезки 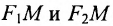 называются фокальными радиусами точки М и обозначаются
называются фокальными радиусами точки М и обозначаются 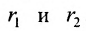 По определению гиперболы
По определению гиперболы 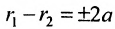 . Так как
. Так как 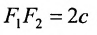 и т.к.
и т.к. 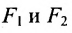 расположены симметрично относительно начала координат, то, применяя формулу для вычисления расстояния между двумя точками, находим
расположены симметрично относительно начала координат, то, применяя формулу для вычисления расстояния между двумя точками, находим 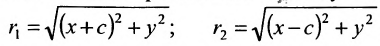 . Заменяя
. Заменяя 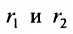 в равенстве
в равенстве 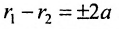 найденными выражениями, получаем:
найденными выражениями, получаем:
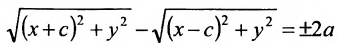 .
.
Возведя в квадрат обе части этого уравнения и обозначая 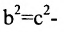
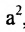 , получим:
, получим: 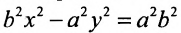 или, разделив все члены уравнения на правую часть, приводим его к виду:
или, разделив все члены уравнения на правую часть, приводим его к виду:

Уравнение (9.3.1)- это каноническое уравнение гиперболы, линии второго порядка.
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником. Его диагонали совпадают с асимптотами гиперболы 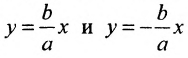 . Поэтому, если требуется построить гиперболу с полуосями а и b, то следует, прежде всего, построить ее основной прямоугольник, затем асимптоты.
. Поэтому, если требуется построить гиперболу с полуосями а и b, то следует, прежде всего, построить ее основной прямоугольник, затем асимптоты.
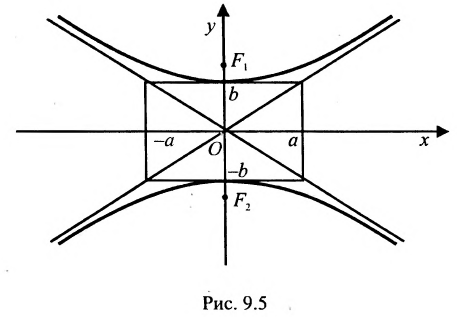
Уравнение вида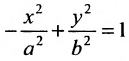 определяет гиперболу, вершины которой расположены на оси Оу (Рис. 9.5).
определяет гиперболу, вершины которой расположены на оси Оу (Рис. 9.5).
Форму гиперболы характеризует её эксцентриситет 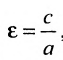 , т.е. отношение расстояния между фокусами этой гиперболы к расстоянию между её вершинами. Поскольку
, т.е. отношение расстояния между фокусами этой гиперболы к расстоянию между её вершинами. Поскольку 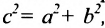 , то подставив в формулу
, то подставив в формулу 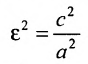 получим
получим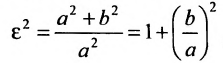 откуда
откуда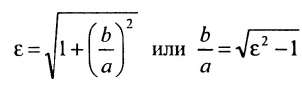 . Следовательно, эксцентриситет oредсляется отношением
. Следовательно, эксцентриситет oредсляется отношением 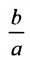 , а отношение
, а отношение 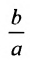 – эксцентриситетом. Следовательно, эксцентриситет характеризует форму гиперболы. Чем меньше эксцентриситет, тем меньше отношение
– эксцентриситетом. Следовательно, эксцентриситет характеризует форму гиперболы. Чем меньше эксцентриситет, тем меньше отношение 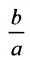 , а это значит, что основной прямоугольник вытянут в направлении оси, соединяющей вершины.
, а это значит, что основной прямоугольник вытянут в направлении оси, соединяющей вершины.
Прямые, заданные уравнениями 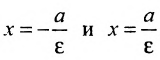 называются директрисами гиперболы.
называются директрисами гиперболы.
Пример:
Составить уравнение геометрического места точек, отношение расстояний которых от данной точки А(4, 0) и от данной прямой х=1 равно 2.
Решение:
В системе координат хОу построим точку А(4, 0) и прямую х = 1. Пусть М(х, у) – произвольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую х = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то её абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, B(1, у) (рис. 9.6).По условию задачи 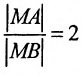 .Подставив значения расстояний
.Подставив значения расстояний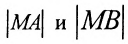 , которые находим по формуле расстояния между двумя точками, получим:
, которые находим по формуле расстояния между двумя точками, получим:
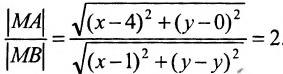
Возводя в квадрат левую и правую части равенства и последовательно преобразовывая, находим уравнение:
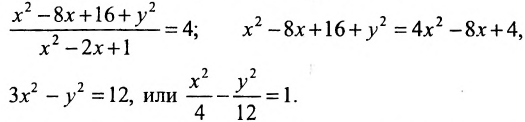
Полученное уравнение определяет гиперболу, у которой действительная полуось -а = 2, а мнимая 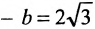 .
.
Определим фокусы гиперболы. Для гиперболы выполняется равенство 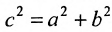 . Следовательно,
. Следовательно, 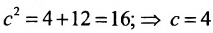 .А
.А 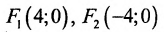 – фокусы гиперболы. Как видно, заданная точка
– фокусы гиперболы. Как видно, заданная точка
А(4, 0) является правым фокусом гиперболы.
Эксцентриситет полученной гиперболы равен 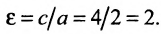
Подставив значения а и b в уравнения асимптот 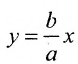 и
и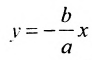
у =—получим уравнения асимптот гиперболы: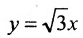 и
и 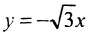 .
.
Для построения гиперболы строим основной прямоугольник с полуосями 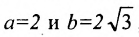 , затеем асимптоты
, затеем асимптоты 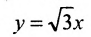 и
и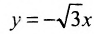 а далее строим и саму гиперболу (рис.9.6).
а далее строим и саму гиперболу (рис.9.6). 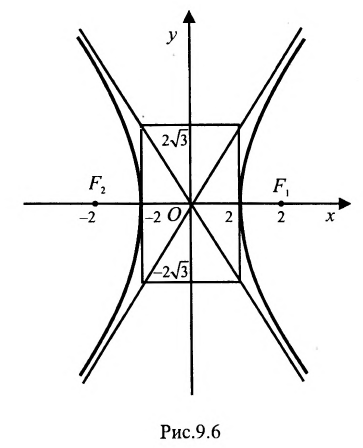
- Заказать решение задач по высшей математике
Парабола
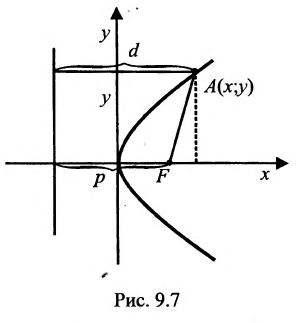
Определение 9.4.1. Параболой называется геометрическое место точек, для каждой из которых, расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой,(директриса не проходит через фокус).
Обозначим фокус параболы – F, расстояние от фокуса до директрисы – р(р > 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А – произвольная точка плоскости с координатами (х, у) и пусть 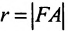 . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты
. Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты 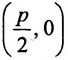 .
.
Тогда 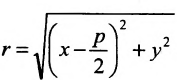 А расстояние
А расстояние 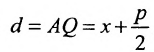 Подставив в формулу r=d, будем иметь
Подставив в формулу r=d, будем иметь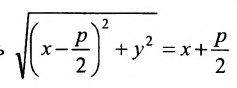 . Возведя обе части равенства в квадрат, получим
. Возведя обе части равенства в квадрат, получим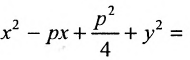
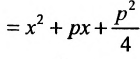 или
или
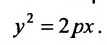 (9.4.1)
(9.4.1)
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 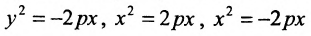 также определяют параболы.
также определяют параболы.
Легко показать, что уравнение 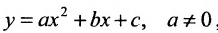 , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а
, определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а 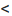 О. Для этого выделим полный квадрат:
О. Для этого выделим полный квадрат:
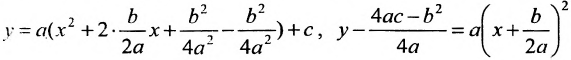
и сделаем параллельный перенос по формулам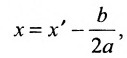
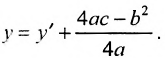
В новых координатах преобразуемое уравнение примет вид: 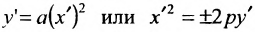 где р – положительное число, определяется равенством
где р – положительное число, определяется равенством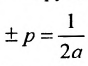 .
.
Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию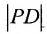 , называется параболой. Прямая у = -1 называется директрисой параболы, а точка F – фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию
, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F – фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию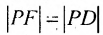 , запишем это равенство с помощью координат:
, запишем это равенство с помощью координат: 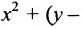
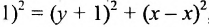 , или после упрощения
, или после упрощения 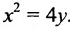 . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).
. Это уравнение геометрического места точек, образующих параболу (рис. 9.8).
Кривые второго порядка на плоскости
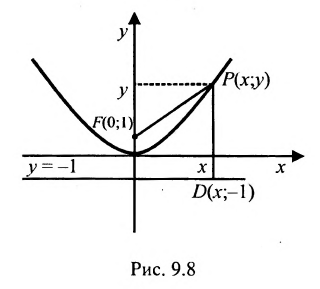
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
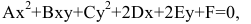
где коэффициенты А, В и С не равны одновременно нулю 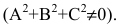
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС<0.
Кривая второго порядка принадлежит параболическому типу, если коэффициент В равен нулю: В=0 и только один из коэффициентов А и С не равен нулю: АС=0 и 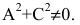
Рассмотрим канонические (простейшие) уравнения эллипса, гиперболы и параболы.
Эллипсом называется множество всех точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
Геометрическое свойство точек эллипса выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину, о которой идет речь в определении эллипса, обозначим через 2а: 2а>2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
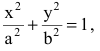 которое называют каноническим уравнением эллипса.
которое называют каноническим уравнением эллипса.
Число а называют большей полуосью эллипса, число 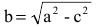 – мень-
– мень-
шей полуосью эллипса, 2а и 2b – соответственно большей и меньшей осями эллипса. Точки 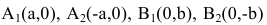 называют вершинами эллипса, а
называют вершинами эллипса, а 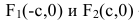 – его фокусами (рис. 12).
– его фокусами (рис. 12).
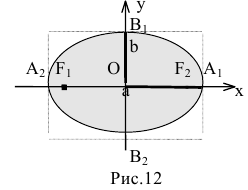
Координатные оси являются осями симметрии эллипса, а начало координат – его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 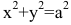 и определяет окружность радиуса а с центром в начале координат.
и определяет окружность радиуса а с центром в начале координат.
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
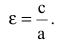
Эксцентриситет изменяется от нуля до единицы 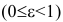 и характеризует форму эллипса. Для окружности
и характеризует форму эллипса. Для окружности 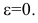 Чем больше эксцентриситет, тем более вытянут эллипс.
Чем больше эксцентриситет, тем более вытянут эллипс.
Пример:
Показать, что уравнение
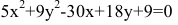
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
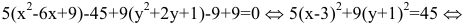
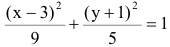 – каноническое уравнение эллипса с центром в точке
– каноническое уравнение эллипса с центром в точке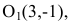 большей полуосью а=3 и меньшей полуосью
большей полуосью а=3 и меньшей полуосью 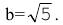
Найдем эксцентриситет эллипса:
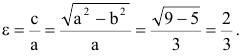
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 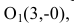 а оси
а оси 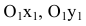 параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.
параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е. 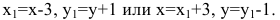
В новой системе координат координаты 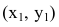 вершин и фокусов гиперболы будут следующими:
вершин и фокусов гиперболы будут следующими:
Переходя к старым координатам, получим:
Построим график эллипса.
 Задача решена.
Задача решена.
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а<2с. Точка М(х,у) принадлежит гиперболе тогда и только тогда, когда ее координаты удовлетворяют уравнению
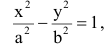 которое называют каноническим уравнением гиперболы.
которое называют каноническим уравнением гиперболы.
Число а называют действительной полуосью гиперболы, число
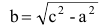 – мнимой полуосью гиперболы, 2а и 2b – соответственно действительной и мнимой осями гиперболы. Точки
– мнимой полуосью гиперболы, 2а и 2b – соответственно действительной и мнимой осями гиперболы. Точки 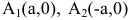 называют вершинами гиперболы,
называют вершинами гиперболы, 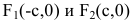 – ее фокусами (рис. 13).
– ее фокусами (рис. 13).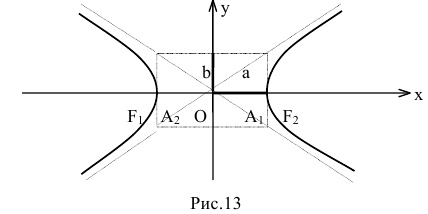
Координатные оси являются осями симметрии гиперболы, а начало координат – ее центром симметрии. Центр симметрии гиперболы называется центром гиперболы.
Точки гиперболы по мере удаления от начала координат неограниченно (асимптотически) приближаются к прямым у=±kх (где 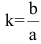 ), которые называются асимптотами гиперболы.
), которые называются асимптотами гиперболы.
Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси: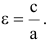
Эксцентриситет гиперболы изменяется от единицы до бесконечности 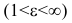 и характеризует форму гиперболы. Чем меньше эксцентриситет гиперболы, тем ее ветви более сжаты к оси Ох.
и характеризует форму гиперболы. Чем меньше эксцентриситет гиперболы, тем ее ветви более сжаты к оси Ох.
Замечание. Каноническое уравнение 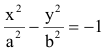 определяет сопряженную гиперболу с действительной полуосью b, вершинами в точках
определяет сопряженную гиперболу с действительной полуосью b, вершинами в точках 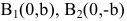 и фокусами на оси Оу.
и фокусами на оси Оу.
Пример:
Составить каноническое уравнение гиперболы с центром в начале координат, если ее действительная полуось равна трем, а эксцентриситет -четырем третьим.
Решение:
Каноническое уравнение гиперболы имеет вид
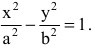 По условию задачи нам известно: а=3,
По условию задачи нам известно: а=3,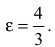 Найдем мнимую полуось.
Найдем мнимую полуось.
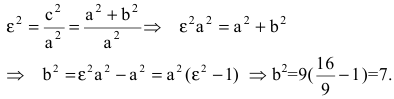
Следовательно, уравнение искомой гиперболы:
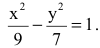 Задача решена.
Задача решена.
Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы, и от данной прямой, называемой директрисой и не проходящей через фокус.
Расстояние между фокусом и директрисой обозначим р. Для того чтобы точка М(х,у) принадлежала параболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 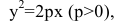 которое называется каноническим уравнением параболы.
которое называется каноническим уравнением параболы.
Точка O(0,0) называется вершиной параболы, число р – параметром параболы, 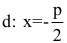 – директрисой пир,болы, а
– директрисой пир,болы, а 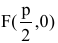 – ее фокусом. Прямая у=0 является осью симметрии параболы, ветви которой направлены вправо. Центра симметрии у параболы нет (рис. 14).
– ее фокусом. Прямая у=0 является осью симметрии параболы, ветви которой направлены вправо. Центра симметрии у параболы нет (рис. 14). 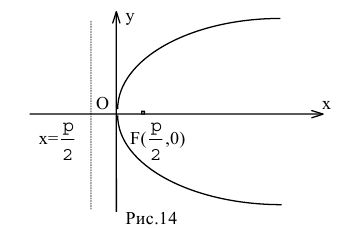
Если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид 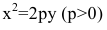 (уравнение параболы с вертикальной осью, уравнением директрисы
(уравнение параболы с вертикальной осью, уравнением директрисы 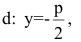 фокусом
фокусом 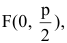 ветви направлены вверх).
ветви направлены вверх).
Замечание. Канонические уравнения параболы можно рассматривать и в случае, когда ветви направлены влево или вниз:
Пример:
Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе первого координатного угла отрезок длиной 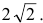
Решение:
Каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и ветвями, направленными вверх, имеет вид:
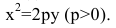
Уравнение биссектрисы первого координатного угла у=х. Найдем точки пересечения параболы с биссектрисой. Для этого решим систему уравнений
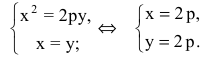
Следовательно, точка М(2р,2р) будет принадлежать параболе. С другой стороны, парабола отсекает на биссектрисе отрезок длиной 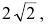 который является гипотенузой равнобедренного прямоугольного треугольника с катетами 2р.
который является гипотенузой равнобедренного прямоугольного треугольника с катетами 2р. 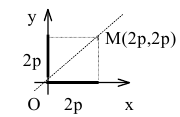
По теореме Пифагора
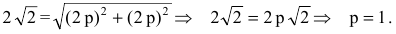
Тогда искомое уравнение параболы
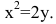
Уравнение директрисы параболы: у=-1, координаты ее фокуса F(0,1).
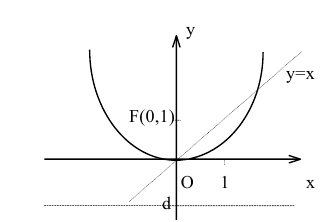
Задача решена.
- Евклидово пространство
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение
- Многочлен – виды, определение с примерами
- Числовые множества
- Вектор – определение и основные понятия
- Прямая – понятие, виды и её свойства
- Плоскость – определение, виды и правила
Эксцентриситетом
гиперболы называется отношение фокусного
расстояния к длине ее действительной
оси:
![]() или
или
![]()
Так как у гиперболы
с>a, то эксцентриситет гиперболы больше
единицы. Эксцентриситет характеризует
отношение сторон основного прямоугольника,
а следовательно, и форму самой гиперболы.
Фокальные радиусы
Из определения гиперболы
(для правой ветви) следует:
![]() .
.
Так как r1
– r2
= 2a, то
![]() .
.
Таким образом, получаем
формулы, выражающие фокальные радиусы
любой точки М(х;у) правой ветви через х:
 (1)
(1)
Для левой ветви эти
формулы примут вид:
 (2)
(2)
Выражая формулы (1) и
(2) через эксцентриситет, получим для
точек правой ветви гиперболы:
 (3)
(3)
для точек левой ветви
гиперболы:
 (4).
(4).
2.3. Парабола.
2.3.1. Определение параболы и ее уравнение.
Параболой
называется геометрическое место точек
на плоскости, каждая из которых
равноудалена от данной точки, называемой
фокусом, и данной прямой, называемой
директрисой (предполагается, что
эта прямая не проходит через фокус).
Для
вывода уравнения параболы за ось ОХ
возьмем прямую, проходящую через фокус
перпендикулярно директрисе. За
положительное направление оси абсцисс
возьмем направление от директрисы к
фокусу.

Рис. 7
За
начало координат возьмем точку 0, которая
делит пополам отрезок от директрисы до
фокуса. Длину этого отрезка, который
называется параметром параболы,
обозначим через Р. Фокус F будет иметь
координаты
![]() ,
,
а координаты точки оси ОХ, через которую
проходит директриса, будут
![]() .
.
Возьмем
произвольную точку М(х;у), лежащую на
параболе, соединим ее прямой с точкой
F, а затем опустим из точки М на директрису
перпендикуляр МК. Длина отрезка,
соединяющего точку М(х;у) параболы с
фокусом, называется фокальным радиусом
этой точки и обозначается через r (Рис.
1).
Согласно
определению параболы:
FM = KM (1)
Определяя
FM и КМ по формуле расстояния между двумя
точками, получим:

Следовательно,
 .
.
(2)
Уравнению
(2) будут удовлетворять координаты каждой
точки параболы.
Приведем
уравнение параболы к более удобному
виду, для чего возведем обе части
равенства (2) в квадрат:
![]() ,
,
Откуда,
у2 = 2рх. (3)
Уравнение
(3) называется каноническим уравнением
параболы. Сопоставляя равенства (1) и
(2), можно выразить фокальный радиус
точки М(х;у) параболы через абсциссу
этой точки:
![]() .
.
(4).
2.3.2. Исследование формы параболы.
Для
определения вида параболы найдем у из
канонического уравнения параболы:
![]() .
.
Из
уравнения (3) п.1 следует, что х не может
быть отрицательным. При х=0, y
= 0, следовательно, точка О(0;0) лежит на
параболе. Затем заключаем, что каждому
значению х>0 соответствуют два значения
у, равные по абсолютной величине, но
противоположные по знаку. Следовательно,
парабола представляет собой кривую,
расположенную вправо от начала координат
и симметричную относительно оси абсцисс.

Рис. 8
Из
формулы (3) п.1 следует, что по мере
возрастания х возрастает и |у|, и когда
х неограниченно растет, то и у по
абсолютной величине неограниченно
растет.
У
параболы, заданной каноническим
уравнением у2=2рх, осью симметрии
является ось абсцисс. Точка пересечения
параболы с осью симметрии называется
вершиной параболы. В данном случае
вершина параболы лежит в начале координат.
Заметим, что у параболы одна вершина, у
гиперболы – две, у эллипса – четыре.
Проведем
на Рис. 8 фокальный радиус перпендикулярно
оси симметрии и определим длину LF по
формуле (4) п.1. Так как абсцисса точки L
равна
![]() ,
,
то r=р. Следовательно, число Р равняется
длине фокального радиуса, перпендикулярного
к оси симметрии. В связи с этим число Р
называют фокальным параметром параболы.
Парабола,
уравнение которой у2=2рх, р>0,
является кривой, расположенной справа
от оси ординат.
Кривая,
уравнение которой у2=-2рх, р>0,
будет также параболой. Вершина этой
параболы лежит в начале координат, осью
симметрии является ось абсцисс. Все
точки этой параболы лежат слева от оси
ординат (Рис. 9, а)
|
|
|
|
|
а) |
б) |
в) |
Рис. 9
Рассуждая
аналогичным образом, заключаем, что
уравнение х2=2ру, р>0, является
уравнением параболы, вершина которой
лежит в начале координат, осью симметрии
является ось ординат (Рис. 9, б). Эта
парабола лежит выше оси абсцисс. Уравнение
же вида х2=-2ру, р>0, является
уравнением параболы, лежащей ниже оси
абсцисс, с вершиной в начале координат.
Осью симметрии этой параболы является
ось ординат (Рис. 9, в).
Примечание.
Условимся, наглядности ради, говорить,
что “ветви” параболы у2=2рх (р>0)
“направлены вправо”, “ветви” параболы
х2=2ру (р>0) “направлены вверх”
и т. д.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
фокусы которой расположены на оси абсцисс
симметрично относительно начала координат, зная,
кроме того, что:
515.1
515.2
фокусами 2c=10 и ось 2b=8;
515.3
фокусами 2c=6 и эксцентриситет e=3/2;
515.4
эксцентриситет e=5/4;
515.5
515.6
директрисами равно 228/13 и расстояние между
фокусами 2c=26;
515.7
директрисами равно 32/5 и ось 2b=6;
515.8
директрисами равно 8/3 и эксцентриситет e=3/2;
515.9
равно 64/5;
уравнение гиперболы, фокусы которого
расположены на оси ординат симметрично
относительно начала координат, зная, кроме того,
что:
(буквой а мы обозначаем полуось гиперболы,
расположенной на оси абсцисс);
фокусами 2с=10 и эксцентриситет e=5/3;
516.3
48;
директрисами равно 50/7 и эксценриситет e=7/5;
равно 32/5.
а и b каждой из следующих гипербол:
эксцентриситет, уравнения асимптот, уравнения
директрис.
эксцентриситет, уравнения асимптот, уравнения
директрис.
треугольника, образованного асимптотами
гиперболы
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
уравнения прямых, на которых лежат фокальные
радиусы точки М1.
точка М1(-5; 9/4) лежит
на гиперболе
М1.
гиперболы e=2, фокальный радиус ее точки М,
проведенный из некоторого фокуса, равен 16.
Вычислить расстояние от точки М до односторонней
с этим фокусом директрисы.
гиперболы e=3, расстояние от точки М гиперболы до
директрисы e=3, расстояние от точки М гиперболы до
директрисы равно 4. Вычислить расстояние от точки
М до фокуса, одностороннего с этой директрисой.
гиперболы e=2, центр ее лежит в начале координат,
один из фокусов F(12; 0). Вычислить расстояние от
точки М1 гиперболы
с абсциссой, равной 13, до директрисы,
соответствующей заданному фокусу.
гиперболы e=3/2, центр ее лежит в начале координат,
одна из директрис дана уравнением x=-8. Вычислить
расстояние от точки М1 гиперболы с абсциссой, равной 10, до
фокуса, соответствующего заданной директрисе.
гиперболы
правого фокуса равно 4,5.
гиперболы
левого фокуса равно 7.
гиперболы
ее оси, содержащей вершины. Определить
расстояние от фокусов до точек пересечения этого
перпендикуляра с гиперболой.
циркулем, построить фокусы гиперболы
что оси координат изображены и масштабная
единица задана).
уравнение гиперболы, фокусы которой лежат на оси
абсцисс симметрично относительно начала
координат, если даны:
-1), M2(-8;
3) гиперболы и эксцентриситет e=
-1) гиперболы с уравнения асимптот
5/2) гиперболы и уравнения
директрис
533
эксцентриситет равносторонней гиперболы.
эксцентриситет гиперболы, если отрезок между ее
вершинами виден из фокусов сопряженной
гиперболы под углом 600.
совпадают с фокусами эллипса
уравнение гиперболы, если ее эксцентриситет e=2.
уравнение гиперболы, фокусы которой лежат в
вершинах эллипса
проходят через фокусы этого эллипса.
расстояние от фокуса гиперболы
асимптоты равно b.
произведение расстояний от любой точки
гиперболы
величина постоянная, равная
площадь параллелограмма, ограниченного
асимптотами гиперболы
прямыми, проведенными через любую ее точку
параллельно асимптотами, есть величина
постоянная, равная ab/2.
уравнение гиперболы, если известны ее полуоси a и
b, центр C(x0; y0) и фокусы расположены на прямой:
каждое из следующих уравнений определяет
гиперболу, и найти координаты ее центра С,
полуоси, эксцентриситет, уравнения асимптот и
уравнения директрис:
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
542.1
542.2
уравнение гиперболы, зная, что:
вершинами равно 24 и фокусы суть F1(-10;
2), F2(16; 2);
расстояние между директрисами равно 3,6;
асимптотами равен 900 и фокусы суть F1(4; -4), F2(-2;
2).
уравнение гиперболы, если известны ее
эксцентриситет e=5/4, фокус F(5; 0) и уравнение
соответствующей директрисы
уравнение гиперболы, если известны ее
эксцентриситет e=13/12, фокус F(0; 13) и уравнение
соответствующей директирсы
на гиперболе, фокус которой F(-2; -3), а
соответствующая директриса дана уравнением
уравнение гиперболы, если известны ее
эксцентриситет e=
уравнение соответствующей директрисы
-2) лежит на гиперболе, фокус
которой F(-2; 2), а соответстующая директриса дана
уравнением
равносторонней гиперболы
ее уравнение в новой системе, приняв за оси
координат ее асимптоты.
каждое из следующих уравнений определяет
гиперболу, найти для каждой из них центр, полуоси,
уравнения асимптот и построить их на чертеже:
пересечения прямой
пересечения прямой
пересечения прямой
определить, как расположена прямая относительно
гиперболы: пересекает ли, касается или проходит
вне ее:
каких значениях m прямая
гиперболу
гиперболы.
при котором прямая
уравнение касательной к гиперболе
точке M1(x1; y1).
касательные к гипербле, проведенные в концах
одного и того же диаметра, параллельны.
уравнения касательных к гиперболе
к прямой
уравнения касательных к гиперболе
прямой
касательные к гиперболе
прямой
вычислить расстояние d от точки М1 до этой прямой.
уравнение касательной к гиперболе
из точки А(-1; -7).
проведены касательные к гиперболе
уравнение хорды, соединяющей точки касания.
проведены касательные к гиперболе
расстояние d от точки Р до хорды гиперболы,
соединяющей точки касания.
через точку А(
уравнение этой гиперболы при условии, что ее оси
совпадают с осями координат.
уравнение гиперболы, касающейся прямых
условии, что ее оси совпадают с осями координат.
точки пересечения эллипса
гиперболы
составить уравнения его сторон.
точка пересечения касательной с осью Ох, Q –
проекция точки касания на ту же ось. Доказать, что
фокусы гиперболы расположены по разные стороны
от любой ее касательной.
произведение расстояний от фокусов до любой
касательной к гиперболе
величина постоянная, равная b2.
гиперболы, фокусы которой находятся в точках F1(-3;
0), F2(3; 0). Составить
уравнение этой гиперболы.
уравнение гиперболы, фокусы которой расположены
на оси абсцисс симметрично относительно начала
координат, если известны уравнение касательной к
гиперболе
вершинами 2а=8.
прямая, касающаяся гиперболы в некоторой точке М,
составляет равные углы с фокальными радиусами F1M, F2M и проходит
внутри угла F1MF2.
гиперболы
оси Ох направлен луч света. Известно, что
до гиперболы, луч от нее отразился. Составить
уравнение прямой, на которой лежит отраженный
луч.
эллипс и гипербола, имеющие общие фокусы,
пересекаются под прямым углом.
равномерного сжатия плоскости к оси Ох равен 4/3.
Определить уравнение линии, в котороую при этом
сжатии преобразуется гипербола
равномерного сжатия плоскости к оси Оу равен 4/5.
Определить уравнение линии, в которую при этом
сжатии преобразуется гипербола
линии, в которую преобразуется гипербола
равноменых сжатиях плоскости к координатным
осям, если коэффициенты равномерного сжатия
плоскости к осям Ох и Оу соответствуют 2/3 и 5/3.
коэффициент q равномерного сжатия плоскости к
оси Ох, при котором гипербола
в гиперболу
коэффициент q равномерного сжатия плоскости к
оси Оу, при котором гипербола
в гиперболу
коэффициенты q1, q2 двух последовательных равномерных
сжатий плоскости к осям Ох и Оу, при которых
гипербола
Кривые второго порядка – определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру – значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде 
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения

- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение  называется уравнением фигуры, если
называется уравнением фигуры, если 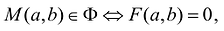 , то есть (а, b) – решение уравнения F(x,y) = 0.
, то есть (а, b) – решение уравнения F(x,y) = 0.
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения  , т.е. уравнение фигуры задает эту фигуру.
, т.е. уравнение фигуры задает эту фигуру.
Возможны два вида задач:
- дано уравнение
 и надо построить фигуру Ф, уравнением которой является
и надо построить фигуру Ф, уравнением которой является  ;
; - дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения  и решается, чаще всего, методами математического анализа.
и решается, чаще всего, методами математического анализа.
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек  , есть величина постоянная (большая, чем расстояние между
, есть величина постоянная (большая, чем расстояние между  ).
).
Точки  называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b – малой.
называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b – малой.
Если а =Ь, то уравнение (7.3) можно переписать в виде:
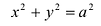 (7.5)
(7.5)
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку  координаты которой задаются формулами
координаты которой задаются формулами 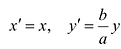 будет окружность (4) переводить в эллипс, заданный соотношением
будет окружность (4) переводить в эллипс, заданный соотношением 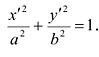
Число 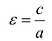 называется эксцентриситетом эллипса. Эксцентриситет
называется эксцентриситетом эллипса. Эксцентриситет 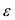 характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении
характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении 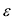 становится более вытянутым
становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами  . Их длины
. Их длины 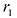 и
и 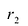 задаются формулами
задаются формулами 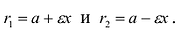 Прямые
Прямые 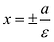 называются директрисами эллипса. Директриса
называются директрисами эллипса. Директриса 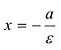 называется левой, а
называется левой, а 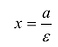 – правой. Так как для эллипса
– правой. Так как для эллипса 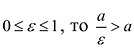 и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е. 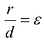
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 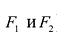 есть величина постоянная (не равная нулю и меньшая, чем расстояние между
есть величина постоянная (не равная нулю и меньшая, чем расстояние между 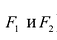 ).
).
Точки 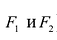 называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов
называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов 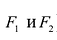 обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А – произвольная точка плоскости с координатами (х, у) и пусть
обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А – произвольная точка плоскости с координатами (х, у) и пусть 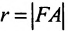 . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты
. Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты 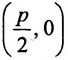 .
.

Тогда 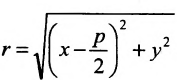 А расстояние
А расстояние 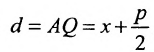 Подставив в формулу r=d, будем иметь
Подставив в формулу r=d, будем иметь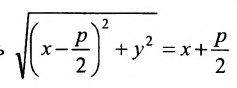 . Возведя обе части равенства в квадрат, получим
. Возведя обе части равенства в квадрат, получим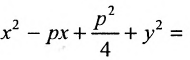
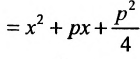 или
или
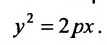 (9.4.1)
(9.4.1)
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 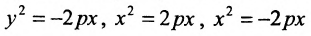 также определяют параболы.
также определяют параболы.
Легко показать, что уравнение 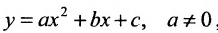 , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а
, определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а 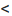 О. Для этого выделим полный квадрат:
О. Для этого выделим полный квадрат:
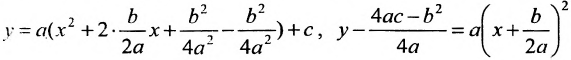
и сделаем параллельный перенос по формулам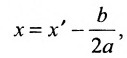
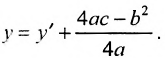
В новых координатах преобразуемое уравнение примет вид: 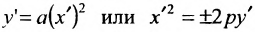 где р – положительное число, определяется равенством
где р – положительное число, определяется равенством 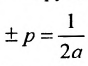 .
.
Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию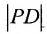 , называется параболой. Прямая у = -1 называется директрисой параболы, а точка F – фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию
, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F – фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию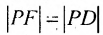 , запишем это равенство с помощью координат:
, запишем это равенство с помощью координат: 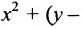
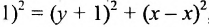 , или после упрощения
, или после упрощения 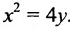 . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).
. Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
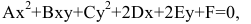
где коэффициенты А, В и С не равны одновременно нулю 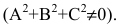
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
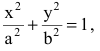 которое называют каноническим уравнением эллипса.
которое называют каноническим уравнением эллипса.
Число а называют большей полуосью эллипса, число 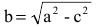 – мень-
– мень-
шей полуосью эллипса, 2а и 2b – соответственно большей и меньшей осями эллипса. Точки 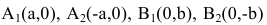 называют вершинами эллипса, а
называют вершинами эллипса, а 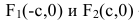 – его фокусами (рис. 12).
– его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат – его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид  и определяет окружность радиуса а с центром в начале координат.
и определяет окружность радиуса а с центром в начале координат.
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
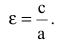
Эксцентриситет изменяется от нуля до единицы 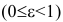 и характеризует форму эллипса. Для окружности
и характеризует форму эллипса. Для окружности 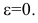 Чем больше эксцентриситет, тем более вытянут эллипс.
Чем больше эксцентриситет, тем более вытянут эллипс.
Пример:
Показать, что уравнение
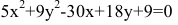
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
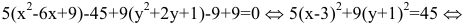
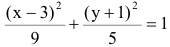 – каноническое уравнение эллипса с центром в точке
– каноническое уравнение эллипса с центром в точке 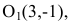 большей полуосью а=3 и меньшей полуосью
большей полуосью а=3 и меньшей полуосью 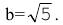
Найдем эксцентриситет эллипса:
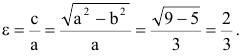
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 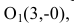 а оси
а оси 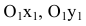 параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.
параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е. 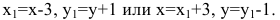
В новой системе координат координаты 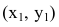 вершин и фокусов гиперболы будут следующими:
вершин и фокусов гиперболы будут следующими:
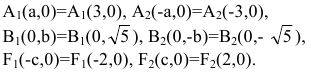
Переходя к старым координатам, получим:
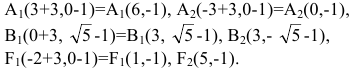
Построим график эллипса.
 Задача решена.
Задача решена.
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Фокальный радиус вектор параболы
Глава 20. Парабола
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы – буквой р. Число р называется параметром параболы.
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением
(1)
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение
.
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле
.
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат – с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид
(2)
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение
(3)
если она лежит в верхней полуплоскости (рис.), и
(4)
если в нижней полуплоскости (рис.)
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
- Аналитическая геометрия
- Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.
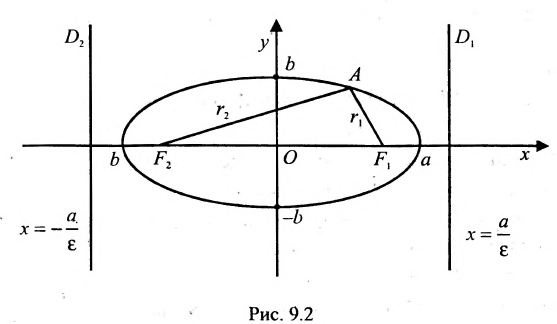
Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Эллипс.
Эллипс с каноническим уравнением $frac+frac=1, ageq b>0,$ и меет форму изображенную на рисунке.
Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ – главными осями а центр симметрии $O -$ центром эллипса.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами эллипса векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $frac+frac=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.
Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.
Теорема. ( Директориальное свойство эллипса)
Эллипс является множеством точек, отноше ние расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$
Примеры.
2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.
Приведем уравнение эллипса к каноническому виду:
а) Находим полуоси $a=5,$ $b=3.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$
$c=sqrt<5^2-3^2>=sqrt<16>=4Rightarrow F_1(-4, 0),qquad F_2(4, 0).$
г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),qquad F_2(4, 0);$ в) $e=frac<4><5>;$ г) $D_1: x=-frac<25><4>$ и $D_2: x=frac<25><4>.$
2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.
Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:
Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=sqrt 5.$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<3><2/3>=-frac<9> <2>$ и $D_2: x=frac<3><2/3>=frac<9><2>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=sqrt 5;$ $ e=frac<2><3>.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$
2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.
Решение.
Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$
Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, sqrt 3)$ в каноническое уравнение эллипса $frac+frac=1:$
Таким образом, уравнение эллипса $frac<16>+frac<4>=1.$
Далее найдем координаты фокусов:
$c=sqrt=sqrt<16-4>=2sqrt 3Rightarrow F_1(-2sqrt 3, 0),,,, F_2(2sqrt 3, 0).$
Отсюда находим $overline =(2+2sqrt 3, sqrt 3),$ $overline=(2-2sqrt 3, sqrt 3).$
Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$
Таким образом, расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_1: sqrt 3 x+8=0$
расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_2: sqrt 3 x-8=0$
Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) – $ ее вершинами. Оси симметрии $Ox$ и $Oy$ – действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами гиперболы, векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.
Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.
Теорема. (Директориальное свойство гиперболы).
Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей дирек трисы постоянно и равно $e.$
Примеры.
2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.
Приведем уравнение гиперболы к каноническому виду:
а) Находим полуоси $a=3,$ $b=4.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$
$c=sqrt<3^2+4^2>=sqrt<25>=5Rightarrow F_1(-5, 0),qquad F_2(5, 0).$
г) Асимптоты гиперболы находим по формулам $y=pmfracx:$
д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),qquad F_2(5, 0);$ в) $e=frac<5><3>;$ г) $y=pmfrac<4><3>x;$ д ) $D_1: x=-frac<9><5>$ и $D_2: x=frac<9><5>.$
2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.
Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:
Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$
Асимптоты гиперболы c центром в начале координат, находим по формулам $y=pmfracx,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=pmfrac(x-x_0),$
$$y+3=frac<4><3>(x-2)Rightarrow 3y+9=4x-8Rightarrow 4x-3y-17=0.$$
$$y+3=-frac<4><3>(x-2)Rightarrow 3y+9=-4x+8Rightarrow 4x+3y+1=0.$$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<3><5/3>=-frac<9> <5>$ и $D_2: x=frac<3><5/3>=frac<9><5>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=frac<5><3>,$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$
2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $frac<16>-frac<9>=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.
Решение.
Проверим, что заданная точка лежит на гиперболе:
Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $frac<16>-frac<9>=1.$
Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:
$c=sqrtRightarrow c=sqrt<16+9>=sqrt <25>=5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$
Фокальные радиусы точки, можно найти по формулам $r_1=|overline|$ и $r_2=|overline|.$
Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<4><5/4>Rightarrow x=-frac<16><5>Rightarrow 5x+16=0;$
$D_2: x=frac<4><5/4>Rightarrow x=frac<16><5>Rightarrow 5x-16=0;$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$
Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: sqrt 5x+16=0$
расстояние от точки $M(5, 9/4)$ до прямой $D_2: sqrt 5x-16=0$
Ответ: $r_1=9/4,$ $r_2=frac<41><4>;$ $d_1=frac<41><5>;$ $d_2=frac<9><5>.$
2.273. Найти точки гиперболы $frac<9>-frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$
Решение.
Из уравнения гиперболы находим полуоси: $a=3, , b=4.$ Следовательно, $c=sqrtRightarrow c=sqrt<9+16>=sqrt <25>=5.$
Отсюда находим $F_1=(-5, 0).$
Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$
Чтобы н айти точки гиперболы $frac<9>-frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений
Решим уравнение $5x^2+18x-72=0:$
Находим соответствующие координаты $y:$ $y_1=pmsqrt<24-2,4^2-10cdot 2,4>=sqrt<-5,76>$ – нет корней .
Ответ: $(-6, pm4sqrt 3).$
Парабола.
Парабола с каноническим уравнением $y^2=2px, p>0,$ и меет форму изображенную на рисунке.
Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ – осью параболы.
Точка $Fleft(frac
<2>, 0right)$ называется фокусом параболы, вектор $overline -$ фокальным радиус-векторам, а число $r=|overline| -$ фокальным радиусом точки $M,$ принадлежащей параболе.
Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.
Примеры.
2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.
Решение.
Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $
$$y^2=6xRightarrow y^2=2cdot 3xRightarrow p=2.$$
Ответ: $p=3.$
2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$
Решение.
Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:
Ответ: $y^2=-x.$
2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$
Решение.
Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$
Приведем заданное уравнние к такому виду:
Таким образом, $y^2=4(x^2-2)$ – парабола с центром в точке $(0, 2).$ Параметр $p=2.$
Ответ: $C(0, 2),$ $p=2.$
2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$
Решение.
Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12xRightarrow 36=12xRightarrow x=3.$$
Таким образом, точка $M$ имеет координаты $(3, 6).$
Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2cdot 6xRightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$
Далее находим фокальный параметр точки:
Ответ: $6.$
2.298. Из фокуса параболы $y^2=12x$ под острым углом $alpha$ к оси $Ox$ направлен луч света, причем $tgalpha=frac<3><4>.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.
Решение.
Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2cdot 6xRightarrow p=6.$
Координаты фокуса $F(p/2, 0)Rightarrow F(3,0).$
Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $alpha: tgalpha=frac<3><4>$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tgalpha=frac<3><4>.$
Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$
$0=frac<3><4>cdot 3+bRightarrow b=-frac<9><4>.$ Таким образом, уравнение луча, направленного из фокуса $y=frac<3><4>x-frac<9><4>.$
Далее, найдем точку пересечения найденной прямой с параболой:
Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=frac<18^2><12>=frac<324><12>=27.$
Таким образом, луч пересекает параболу в точке $(27, 18).$
Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$
Подставляем все найденные значения в уравнение касательной:
$y-18=frac<1><3>(x-27)Rightarrow 3y-54=x-27Rightarrow x-3y+27=0.$
Далее, найдем угол $beta$ между лучем $y=frac<3><4>x-frac<9><4>$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=frac<1+k_1cdot k_2>$
$$L_2: x-3y+27=0Rightarrow y=frac<1><3>x+9Rightarrow k_2=frac<1><3>.$$
Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $pi-2beta,$ а угол между отраженным лучем и осью $Ox$ $pi-(pi-2beta)-alpha=2beta-alpha.$
Зная $tgbeta=frac<1><3>$ и $tgalpha=k_1=frac<3><4>$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2beta-alpha):$
$$tg(2beta-alpha)=frac<1+tg2beta tgalpha>=frac<frac<3><4>-frac<3><4>><1+frac<3><4>frac<3><4>>=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$
[spoiler title=”источники:”]
http://a-geometry.narod.ru/problems/problems_20.htm
http://mathportal.net/index.php/analiticheskaya-geometriya/ellips-giperbola-parabola-direktorialnoe-svojstvo-ellipsa-i-giperboly
[/spoiler]



