Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
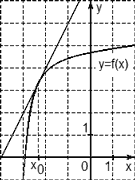
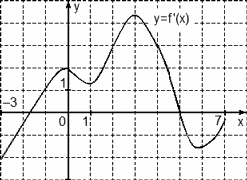
На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
2
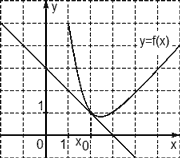
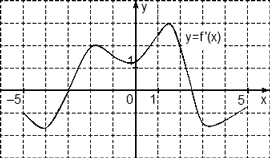
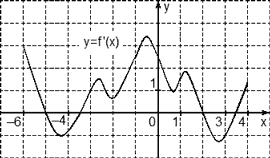
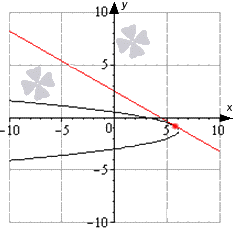
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней.
3
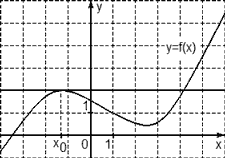
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
4
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
5
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Пройти тестирование по этим заданиям
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Угол наклона прямой y=kx+b называется угол α, который отсчитывается от положительного направления оси ох к прямой y=kx+b в положительном направлении.

На рисунке направление ох обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Угловой коэффициент прямой y=kx+b называют числовым коэффициентом k.
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.
- Угол наклона прямой равняется 0 только при параллельности ох и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0. Значит, вид уравнения будет y=b.
- Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<π2 или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
- Если α=π2, тогда расположение прямой перпендикулярно ох. Равенство задается при помощи равенства x=c со значением с, являющимся действительным числом.
- Если угол наклона прямой y=kx+b тупой, то соответствует условиям π2<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывает.
Секущей называют прямую, которая проходит через 2 точки функции f(x). Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что АВ является секущей, а f(x) – черная кривая, α – красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника АВС можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
k=tg α=BCAC=f(xB)-fxAxB-xA, где абсциссами точек А и В являются значения xA, xB, а f(xA), f(xB) – это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k=f(xB)-f(xA)xB-xA или k=f(xA)-f(xB)xA-xB, причем уравнение необходимо записать как y=f(xB)-f(xA)xB-xA·x-xA+f(xA) или
y=f(xA)-f(xB)xA-xB·x-xB+f(xB).
Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Касательная к графику функции f(x) в точке x0; f(x0) называется прямая, проходящая через заданную точку x0; f(x0), с наличием отрезка, который имеет множество значений х, близких к x0.
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y=x+1, считается касательной к y=2x в точке с координатами (1; 2). Для наглядности, необходимо рассмотреть графики с приближенными к (1; 2) значениями. Функция y=2x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y=2x сливается с прямой у=х+1.
Для определения касательной следует рассмотреть поведение касательной АВ при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.

Секущая АВ, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной αx.
Касательной к графику функции y=f(x) в точке А считается предельное положение секущей АВ при В стремящейся к А, то есть B→A.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей АВ для функции f(x), где А и В с координатами x0, f(x0) и x0+∆x, f(x0+∆x), а ∆x обозначаем как приращение аргумента. Теперь функция примет вид ∆y=∆f(x)=f(x0+∆x)-f(∆x). Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник АВС. Используем определение тангенса для решения, то есть получим отношение ∆y∆x=tg α. Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.
Отсюда следует, что f'(x0)=lim∆x→0∆y∆x=tg αx=kx, где kx обозначают в качестве углового коэффициента касательной.
То есть получаем, что f’(x) может существовать в точке x0 причем как и касательная к заданному графику функции в точке касания равной x0, f0(x0), где значение углового коэффициента касательной в точке равняется производной в точке x0. Тогда получаем, что kx=f'(x0).
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x0 при пересечении.
Уравнение касательной к графику функции y=f(x) в точке x0, f0(x0) принимает вид y=f'(x0)·x-x0+f(x0).
Имеется в виду, что конечным значением производной f'(x0) можно определить положение касательной, то есть вертикально при условии limx→x0+0f'(x)=∞ и limx→x0-0f'(x)=∞ или отсутствие вовсе при условии limx→x0+0f'(x)≠limx→x0-0f'(x).
Расположение касательной зависит от значения ее углового коэффициента kx=f'(x0). При параллельности к оси ох получаем, что kk=0, при параллельности к оу – kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.
Произвести составление уравнения касательной к графику функции y=ex+1+x33-6-33x-17-33 в точке с координатами (1; 3) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1; 3) является точкой касания, тогда x0=-1, f(x0)=-3.
Необходимо найти производную в точке со значением -1. Получаем, что
y’=ex+1+x33-6-33x-17-33’==ex+1’+x33′-6-33x’-17-33’=ex+1+x2-6-33y'(x0)=y'(-1)=e-1+1+-12-6-33=33
Значение f’(x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда kx=tg αx=y'(x0)=33
Отсюда следует, что αx=arctg33=π6
Ответ: уравнение касательной приобретает вид
y=f'(x0)·x-x0+f(x0)y=33(x+1)-3y=33x-9-33
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Выяснить наличие существования касательной к графику заданной функции
y=3·x-15+1 в точке с координатами (1;1). Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y’=3·x-15+1’=3·15·(x-1)15-1=35·1(x-1)45
Если x0=1, тогда f’(x) не определена, но пределы записываются как limx→1+035·1(x-1)45=35·1(+0)45=35·1+0=+∞ и limx→1-035·1(x-1)45=35·1(-0)45=35·1+0=+∞, что означает существование вертикальной касательной в точке (1;1).
Ответ: уравнение примет вид х=1, где угол наклона будет равен π2.
Для наглядности изобразим графически.

Найти точки графика функции y=115x+23-45×2-165x-265+3x+2, где
- Касательная не существует;
- Касательная располагается параллельно ох;
- Касательная параллельна прямой y=85x+4.
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x∈-∞; 2 и [-2; +∞). Получаем, что
y=-115×3+18×2+105x+176, x∈-∞; -2115×3-6×2+9x+12, x∈[-2; +∞)
Необходимо продифференцировать функцию. Имеем, что
y’=-115×3+18×2+105x+176′, x∈-∞; -2115×3-6×2+9x+12′, x∈[-2; +∞)⇔y’=-15(x2+12x+35), x∈-∞; -215×2-4x+3, x∈[-2; +∞)
Когда х=-2, тогда производная не существует, потому что односторонние пределы не равны в этой точке:
limx→-2-0y'(x)=limx→-2-0-15(x2+12x+35=-15(-2)2+12(-2)+35=-3limx→-2+0y'(x)=limx→-2+015(x2-4x+3)=15-22-4-2+3=3
Вычисляем значение функции в точке х=-2, где получаем, что
- y(-2)=115-2+23-45(-2)2-165(-2)-265+3-2+2=-2, то есть касательная в точке (-2;-2) не будет существовать.
- Касательная параллельна ох, когда угловой коэффициент равняется нулю. Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Когда x∈-∞; -2, тогда -15(x2+12x+35)=0, а при x∈(-2; +∞) получаем 15(x2-4x+3)=0.
Решим:
-15(x2+12x+35)=0D=122-4·35=144-140=4×1=-12+42=-5∈-∞; -2×2=-12-42=-7∈-∞; -2 15(x2-4x+3)=0D=42-4·3=4×3=4-42=1∈-2; +∞x4=4+42=3∈-2; +∞
Вычисляем соответствующие значения функции
y1=y-5=115-5+23-45-52-165-5-265+3-5+2=85y2=y(-7)=115-7+23-45(-7)2-165-7-265+3-7+2=43y3=y(1)=1151+23-45·12-165·1-265+31+2=85y4=y(3)=1153+23-45·32-165·3-265+33+2=43
Отсюда -5; 85, -4; 43, 1; 85, 3; 43 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 . Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
-15×2+12x+35=85×2+12x+43=0D=122-4·43=-28<0
Другое уравнение имеет два действительных корня, тогда
15(x2-4x+3)=85×2-4x-5=0D=42-4·(-5)=36×1=4-362=-1∈-2; +∞x2=4+362=5∈-2; +∞
Перейдем к нахождению значений функции. Получаем, что
y1=y(-1)=115-1+23-45(-1)2-165(-1)-265+3-1+2=415y2=y(5)=1155+23-45·52-165·5-265+35+2=83
Точки со значениями -1; 415, 5; 83 являются точками, в которых касательные параллельны прямой y=85x+4.
Ответ: черная линия – график функции, красная линия – график y=85x+4, синяя линия – касательные в точках -1; 415, 5; 83.

Возможно существование бесконечного количества касательных для заданных функций.
Написать уравнения всех имеющихся касательных функции y=3cos32x-π4-13, которые располагаются перпендикулярно прямой y=-2x+12.
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется -1, то есть записывается как kx·k⊥=-1. Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k⊥=-2, тогда kx=-1k⊥=-1-2=12.
Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x0 получаем, что kx=y'(x0). Из данного равенства найдем значения х для точек касания.
Получаем, что
y'(x0)=3cos32x0-π4-13’=3·-sin32x0-π4·32×0-π4’==-3·sin32x0-π4·32=-92·sin32x0-π4⇒kx=y'(x0)⇔-92·sin32x0-π4=12⇒sin32x0-π4=-19
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
32×0-π4=arcsin-19+2πk или 32×0-π4=π-arcsin-19+2πk
32×0-π4=-arcsin19+2πk или 32×0-π4=π+arcsin19+2πk
x0=23π4-arcsin19+2πk или x0=235π4+arcsin19+2πk, k∈Z
Z- множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у:
y0=3cos32x0-π4-13
y0=3·1-sin232x0-π4-13 или y0=3·-1-sin232x0-π4-13
y0=3·1–192-13 или y0=3·-1–192-13
y0=45-13 или y0=-45+13
Отсюда получаем, что 23π4-arcsin19+2πk; 45-13, 235π4+arcsin19+2πk; -45+13 являются точками касания.
Ответ: необходимы уравнения запишутся как
y=12x-23π4-arcsin19+2πk+45-13,y=12x-235π4+arcsin19+2πk-45+13, k∈Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [-10;10], где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y=-2x+12. Красные точки – это точки касания.

Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке xcenter; ycenter и радиусом R применяется формула x-xcenter2+y-ycenter2=R2.
Данное равенство может быть записано как объединение двух функций:
y=R2-x-xcenter2+ycentery=-R2-x-xcenter2+ycenter
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x0; y0, которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y=R2-x-xcenter2+ycenter или y=-R2-x-xcenter2+ycenter в указанной точке.
Когда в точках xcenter; ycenter+R и xcenter; ycenter-R касательные могут быть заданы уравнениями y=ycenter+R и y=ycenter-R, а в точках xcenter+R; ycenter и
xcenter-R; ycenter будут являться параллельными оу, тогда получим уравнения вида x=xcenter+R и x=xcenter-R.

Касательная к эллипсу
Когда эллипс имеет центр в точке xcenter; ycenter с полуосями a и b, тогда он может быть задан при помощи уравнения x-xcenter2a2+y-ycenter2b2=1.
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y=ba·a2-(x-xcenter)2+ycentery=-ba·a2-(x-xcenter)2+ycenter

Если касательные располагаются на вершинах эллипса, тогда они параллельны ох или оу. Ниже для наглядности рассмотрим рисунок.

Написать уравнение касательной к эллипсу x-324+y-5225=1 в точках со значениями x равного х=2.
Решение
Необходимо найти точки касания, которые соответствуют значению х=2. Производим подстановку в имеющееся уравнение эллипса и получаем, что
x-324x=2+y-5225=114+y-5225=1⇒y-52=34·25⇒y=±532+5
Тогда 2; 532+5 и 2; -532+5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y. Получим, что
x-324+y-5225=1y-5225=1-x-324(y-5)2=25·1-x-324y-5=±5·1-x-324y=5±524-x-32
Очевидно, что верхний полуэллипс задается с помощью функции вида y=5+524-x-32, а нижний y=5-524-x-32.
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2; 532+5 будет иметь вид
y’=5+524-x-32’=52·124-(x-3)2·4-(x-3)2’==-52·x-34-(x-3)2⇒y'(x0)=y'(2)=-52·2-34-(2-3)2=523⇒y=y'(x0)·x-x0+y0⇔y=523(x-2)+532+5
Получаем, что уравнение второй касательной со значением в точке
2; -532+5 принимает вид
y’=5-524-(x-3)2’=-52·124-(x-3)2·4-(x-3)2’==52·x-34-(x-3)2⇒y'(x0)=y'(2)=52·2-34-(2-3)2=-523⇒y=y'(x0)·x-x0+y0⇔y=-523(x-2)-532+5
Графически касательные обозначаются так:

Касательная к гиперболе
Когда гипербола имеет центр в точке xcenter; ycenter и вершины xcenter+α; ycenter и xcenter-α; ycenter, имеет место задание неравенства x-xcenter2α2-y-ycenter2b2=1, если с вершинами xcenter; ycenter+b и xcenter; ycenter-b, тогда задается при помощи неравенства x-xcenter2α2-y-ycenter2b2=-1.

Гипербола может быть представлена в виде двух объединенных функций вида
y=ba·(x-xcenter)2-a2+ycentery=-ba·(x-xcenter)2-a2+ycenter или y=ba·(x-xcenter)2+a2+ycentery=-ba·(x-xcenter)2+a2+ycenter

В первом случае имеем, что касательные параллельны оу, а во втором параллельны ох.
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Составить уравнение касательной к гиперболе x-324-y+329=1 в точке 7; -33-3.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x-324-y+329=1⇒y+329=x-324-1⇒y+32=9·x-324-1⇒y+3=32·x-32-4 или y+3=-32·x-32-4⇒y=32·x-32-4-3y=-32·x-32-4-3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7; -33-3.
Очевидно, что для проверки первой функции необходимо y(7)=32·(7-3)2-4-3=33-3≠-33-3, тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y(7)=-32·(7-3)2-4-3=-33-3≠-33-3, значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
Получаем, что
y’=-32·(x-3)2-4-3’=-32·x-3(x-3)2-4⇒kx=y'(x0)=-32·x0-3×0-32-4×0=7=-32·7-37-32-4=-3
Ответ: уравнение касательной можно представить как
y=-3·x-7-33-3=-3·x+43-3
Наглядно изображается так:

Касательная к параболе
Чтобы составить уравнение касательной к параболе y=ax2+bx+c в точке x0, y(x0), необходимо использовать стандартный алгоритм, тогда уравнение примет вид y=y'(x0)·x-x0+y(x0). Такая касательная в вершине параллельна ох.
Следует задать параболу x=ay2+by+c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что
x=ay2+by+c⇔ay2+by+c-x=0D=b2-4a(c-x)y=-b+b2-4a(c-x)2ay=-b-b2-4a(c-x)2a
Графически изобразим как:

Для выяснения принадлежности точки x0, y(x0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна оу относительно параболы.
Написать уравнение касательной к графику x-2y2-5y+3, когда имеем угол наклона касательной 150°.
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
-2y2-5y+3-x=0D=(-5)2-4·(-2)·(3-x)=49-8xy=5+49-8x-4y=5-49-8x-4
Значение углового коэффициента равняется значению производной в точке x0 этой функции и равняется тангенсу угла наклона.
Получаем:
kx=y'(x0)=tg αx=tg 150°=-13
Отсюда определим значение х для точек касания.
Первая функция запишется как
y’=5+49-8x-4’=149-8x⇒y'(x0)=149-8×0=-13⇔49-8×0=-3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150° для такой функции не существует.
Вторая функция запишется как
y’=5-49-8x-4’=-149-8x⇒y'(x0)=-149-8×0=-13⇔49-8×0=-3×0=234⇒y(x0)=5-49-8·234-4=-5+34
Имеем, что точки касания – 234; -5+34.
Ответ: уравнение касательной принимает вид
y=-13·x-234+-5+34
Графически изобразим это таким образом:
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Значение производной в точке касания как тангенс угла наклона
Если к кривой (f(x)) проведена касательная в точке с абсциссой (x_0), то
[{large{color{royalblue}{f'(x_0)=mathrm{tg}, alpha, }}},]
где (alpha) – угол наклона касательной.
Значит, верна формула: (f'(x_0)=mathrm{tg}, alpha=k).
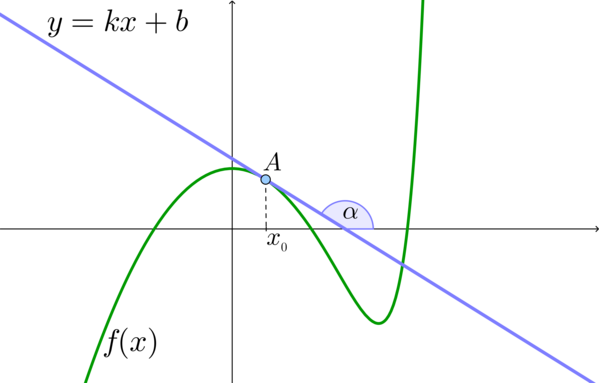
Заметим, что координаты точки (A) тогда можно записать как ( (x_0; f(x_0)) ) или ( (x_0; y_0) ),
где ( y_0=kx_0+b).
То есть ( y_0=f(x_0)).
Задание
1
#2090
Уровень задания: Равен ЕГЭ
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
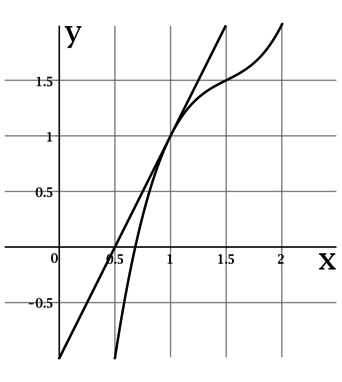
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))) (то есть угла между касательной к графику (f(x)) в точке ((x_0; f(x_0))) и положительным направлением оси (Ox)).
По рисунку видно, что касательная проходит через точки ((0,5; 0)) и ((1; 1)), тогда тангенс угла наклона касательной составляет (1 : 0,5
= 2), следовательно, (f'(x_0) = 2).
Ответ: 2
Задание
2
#2091
Уровень задания: Равен ЕГЭ
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
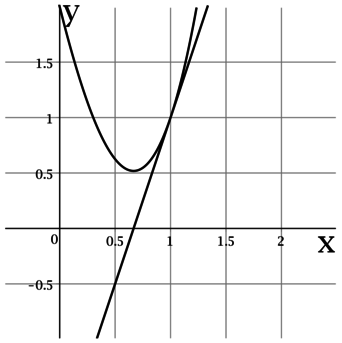
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((0,5; -0,5)) и ((1; 1)), тогда тангенс угла наклона касательной составляет (1,5 :
0,5 = 3), следовательно, (f'(x_0) = 3).
Ответ: 3
Задание
3
#2092
Уровень задания: Равен ЕГЭ
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
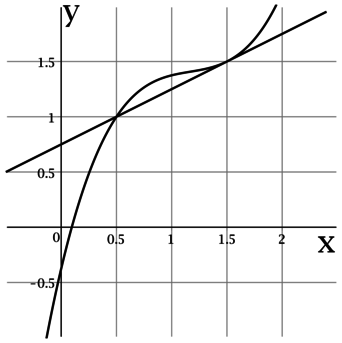
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((0,5; 1)) и ((1,5; 1,5)), тогда тангенс угла наклона касательной составляет (0,5
: 1 = 0,5), следовательно, (f'(x_0) = 0,5).
Ответ: 0,5
Задание
4
#2093
Уровень задания: Равен ЕГЭ
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
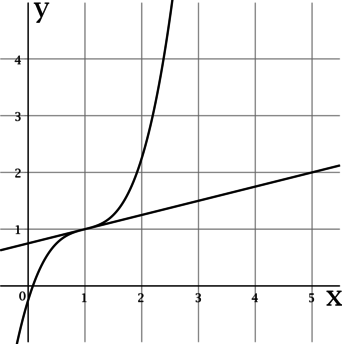
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((1; 1)) и ((5; 2)), тогда тангенс угла наклона касательной составляет ((2 – 1)
: (5 – 1) = 0,25), следовательно, (f'(x_0) = 0,25).
Ответ: 0,25
Задание
5
#3112
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y=f(x)) и отмечены точки (-2;
0; 2; 8). В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
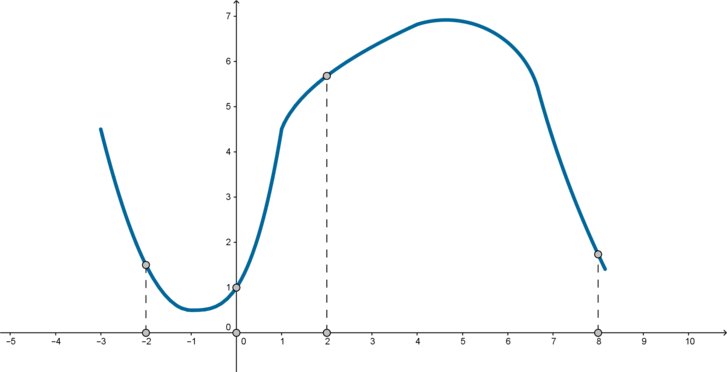
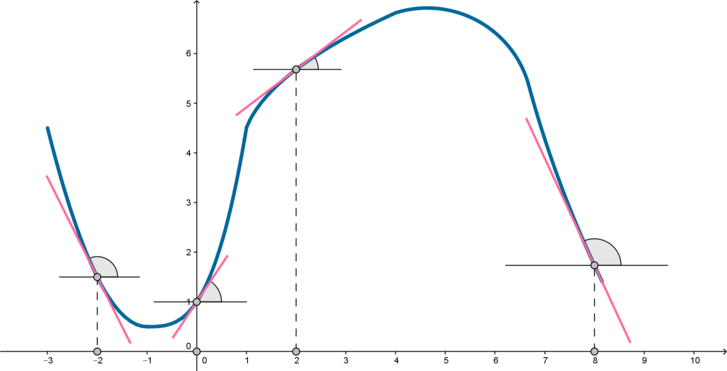
Проведем касательные к графику функции в этих точках. Так как тангенс угла (alpha) наклона касательной равен значению производной (f'(x)) в точке касания (x_0) ((f'(x_0)=mathrm{tg},alpha)), то нужно сравнить тангенсы углов, отмеченных на рисунке.
Вспомним, что если угол тупой, то его тангенс отрицательный, если острый – положительный. Следовательно, так как мы ищем наибольший тангенс, имеет смысл рассматривать только острые углы. Это углы, образованные касательными в точках (0) и (2). Заметим, что угол в точке (0) больше, следовательно, его тангенс также больше, чем тангенс угла в точке (2). Таким образом, ответ: (0).
Ответ: 0
Задание
6
#718
Уровень задания: Сложнее ЕГЭ
Производная (f'(x)) функции (f(x)) в точке (x_0) равна (10). Найдите котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
При всех (alpha), при которых (mathrm{tg}, alpha) и (mathrm{ctg}, alpha) имеют смысл, выполнено (mathrm{tg}, alphacdotmathrm{ctg}, alpha = 1), откуда котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равен (0,1).
Ответ: 0,1
Задание
7
#719
Уровень задания: Сложнее ЕГЭ
Производная (f'(x)) функции (f(x)) в точке (x_0) равна (5). Найдите сумму тангенса и котангенса угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
При всех (alpha), при которых (mathrm{tg}, alpha) и (mathrm{ctg}, alpha) имеют смысл, выполнено (mathrm{tg}, alphacdotmathrm{ctg}, alpha = 1), откуда котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равен (0,2), тогда сумма тангенса и котангенса угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равна (5,2).
Ответ: 5,2

УСТАЛ? Просто отдохни
15 марта 2011
В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).
- Точка x0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
![]()
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
![]()
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
![]()
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
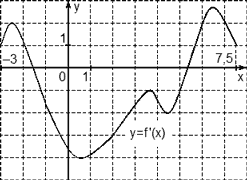
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
![]()
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
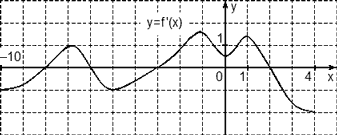
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
![]()
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
Смотрите также:
- ЕГЭ 2022, задание 6. Касательная к графику функции

- ЕГЭ 2022, задание 6. Касательная к графику функции

- Схема Бернулли. Примеры решения задач

- Решение задач B6: №362—377

- Четырехугольная пирамида: как найти координаты вершин

- Нестандартная задача B2: студенты, гонорары и налоги

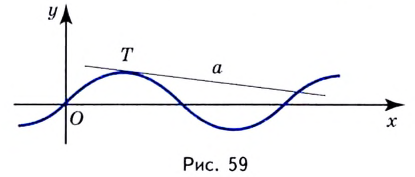
Вы уже знаете, какую прямую называют касательной к окружности. А что понимают, например, под касательной к синусоиде? Прямая 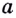
Пусть даны график функции 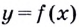 и на ней точка
и на ней точка 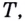 которая не является концом графика (рис. 60). Обозначим на данном графике по разные стороны от
которая не является концом графика (рис. 60). Обозначим на данном графике по разные стороны от 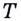 произвольные точки
произвольные точки 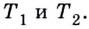 Прямые
Прямые 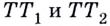 — секущие. Если же точки
— секущие. Если же точки 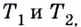 двигаясь по графику, приближать достаточно близко к
двигаясь по графику, приближать достаточно близко к 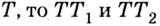 как угодно близко будут приближаться к некоторой прямой
как угодно близко будут приближаться к некоторой прямой 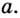 Такую прямую
Такую прямую 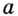 (если она существует) называют касательной к графику функции
(если она существует) называют касательной к графику функции 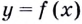 в точке
в точке 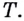
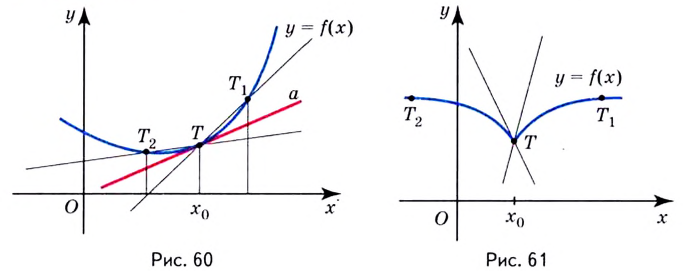
Если график функции такой, как показано на рисунке 61, то при неограниченном приближении точек 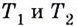 к точке
к точке 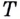 предельные положения секущих — прямые
предельные положения секущих — прямые 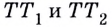 — не совпадут. Говорят, что в точке
— не совпадут. Говорят, что в точке 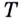 касательной к графику функции не существует.
касательной к графику функции не существует.
И если 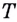 — крайняя точка графика, то касательной к нему в точке
— крайняя точка графика, то касательной к нему в точке 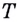 не существует.
не существует.
Понятие касательной к графику часто используют для исследования функций. Рассмотрим этот вопрос сначала в общем виде.
Касательная — это прямая. Её уравнение имеет вид 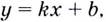 где
где 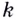 — угловой коэффициент — тангенс угла между лучом касательной, расположенным выше оси
— угловой коэффициент — тангенс угла между лучом касательной, расположенным выше оси 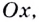 и положительным направлением этой оси. Обратите внимание на угловой коэффициент
и положительным направлением этой оси. Обратите внимание на угловой коэффициент 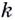 касательной, проведённой к графику какой-либо функции в его точке с абсциссой
касательной, проведённой к графику какой-либо функции в его точке с абсциссой 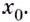 Если число
Если число 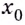 принадлежит промежутку возрастания функции, то соответствующее значение
принадлежит промежутку возрастания функции, то соответствующее значение 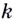 положительное (рис. 62). Если
положительное (рис. 62). Если 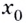 принадлежит промежутку убывания функции, то
принадлежит промежутку убывания функции, то 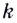 — отрицательное (рис. 63). И наоборот: если каждому значению
— отрицательное (рис. 63). И наоборот: если каждому значению 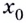 из некоторого промежутка
из некоторого промежутка 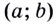 соответствует положительное значение
соответствует положительное значение 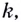 то на
то на 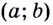 данная функция возрастает; если каждому значению
данная функция возрастает; если каждому значению 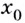 из некоторого промежутка
из некоторого промежутка 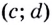 соответствует отрицательное значение
соответствует отрицательное значение 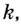 то на функция убывает. Заслуживают внимания и те точки графика функции, в которых касательная не существует, и в которых она параллельна оси
то на функция убывает. Заслуживают внимания и те точки графика функции, в которых касательная не существует, и в которых она параллельна оси 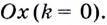
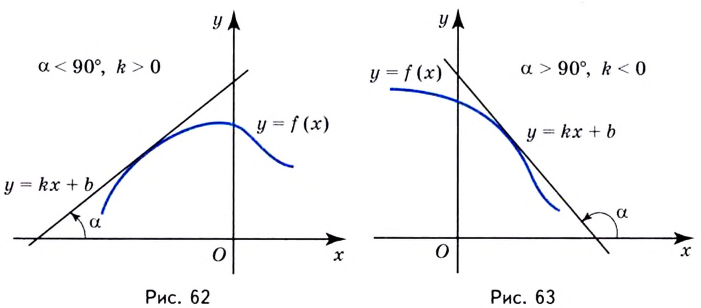
Итак, зная угловые коэффициенты касательных к графику функции в тех или иных точках, можно сделать вывод, возрастает данная функция в этих точках, или убывает.
Поскольку для исследования функций важно уметь определять угловой коэффициент касательной к её графику, то рассмотрим подробнее связь этого коэффициента с исследуемой функцией.
Пусть даны график функции 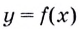 и на ней точку
и на ней точку 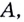 в которой существует касательная к графику (рис. 64). Если абсцисса точки
в которой существует касательная к графику (рис. 64). Если абсцисса точки 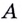 равна
равна 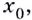 то её ордината —
то её ордината — 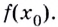 Дадим значению аргумента
Дадим значению аргумента 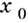 приращение
приращение 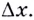 Тогда значению аргумента
Тогда значению аргумента 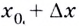 на графике функции соответствует точка
на графике функции соответствует точка 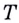 с абсциссой
с абсциссой 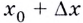 и ординатой
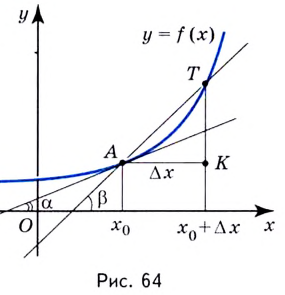
и ординатой 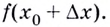
Через точки 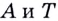 проведём прямые
проведём прямые 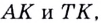 параллельные осям абсцисс и ординат. Они пересекутся в некоторой точке
параллельные осям абсцисс и ординат. Они пересекутся в некоторой точке 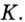 Тогда
Тогда 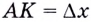 — приращение аргумента, а
— приращение аргумента, а 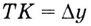 — приращение функции на
— приращение функции на 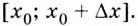
Угловой коэффициент секущей 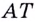 равен тангенсу угла
равен тангенсу угла 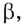 т. е. отношению
т. е. отношению 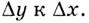
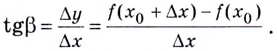
Если 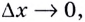 то секущая
то секущая 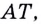 поворачиваясь вокруг точки
поворачиваясь вокруг точки 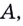 приближается к касательной, проведённой в точке
приближается к касательной, проведённой в точке 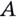 к графику данной функции. Итак, если
к графику данной функции. Итак, если 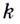 — угловой коэффициент этой касательной и
— угловой коэффициент этой касательной и 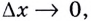 то
то
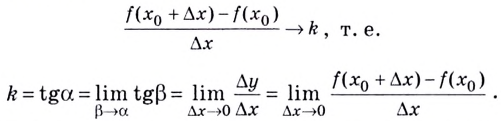
Так определяется угловой коэффициент касательной к графику функции 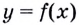 в некоторой точке
в некоторой точке 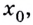 если касательная в ней не параллельна оси
если касательная в ней не параллельна оси 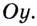 Если касательная к графику функции в некоторой точке параллельна оси
Если касательная к графику функции в некоторой точке параллельна оси 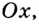 то угловой коэффициент этой касательной равен нулю.
то угловой коэффициент этой касательной равен нулю.
К вычислению значения выражения 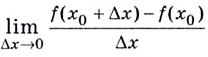 или
или 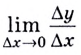 приводит решение многих задач по механике, электричеству, биологии, экономике, статистике и т. д. Именно поэтому это выражение получило специальное название — производная.
приводит решение многих задач по механике, электричеству, биологии, экономике, статистике и т. д. Именно поэтому это выражение получило специальное название — производная.
Производной функции 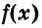 в точке
в точке 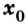 называют предел отношения приращения функции в точке
называют предел отношения приращения функции в точке 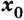 к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует.
к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует.
Производную функции 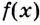 в точке
в точке 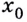 обозначают
обозначают 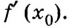 Её определение записывают также в виде равенства:
Её определение записывают также в виде равенства:
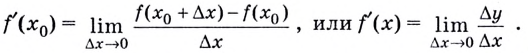
Пример:
Найдите производную функции 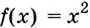 в точке
в точке 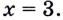
Решение:
Дадим аргументу 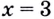 приращение
приращение 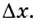 Соответствующее приращение функции
Соответствующее приращение функции 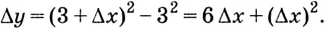
Тогда 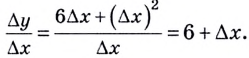 Если
Если 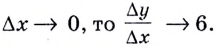
Следовательно, 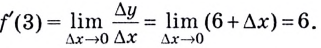
Ответ. 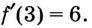
Так решают задачу, пользуясь определением производной функции в точке.
До сих пор речь шла о производной функции в точке. А можно рассматривать производную функции и как функцию. Пусть, например, дана функция 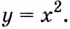 Найдём её производную в произвольной точке
Найдём её производную в произвольной точке 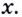 Для этого дадим значению
Для этого дадим значению 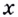 приращение
приращение 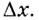 Соответствующее ему приращение функции
Соответствующее ему приращение функции
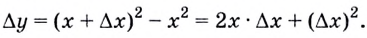
Поэтому 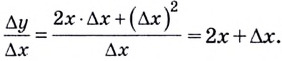 Если
Если 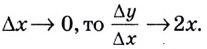
Имеем 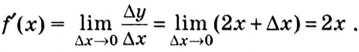
Следовательно, производная функции 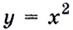 в каждой её точке
в каждой её точке 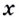 равна
равна 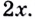 Пишут:
Пишут: 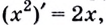 или, если
или, если 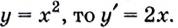
Обратите внимание! Производная функции в точке — это число. Когда же говорят о производной, не указывая «в точке», подразумевают производную как функцию: производной функции 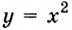 есть функция
есть функция 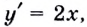 производной функции
производной функции 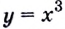 есть функция
есть функция 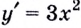 и т. д.
и т. д.
Зная это, производную функции в точке можно вычислять проще, чем по определению производной функции в точке. Пример 2. Дана функция 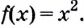 Найдите
Найдите 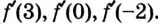 Решение. Производной функции
Решение. Производной функции 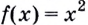 является функция
является функция 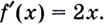 Поэтому
Поэтому 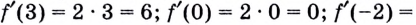
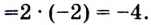
Нахождение производной называется дифференцированием. Функция, которая имеет производную в точке 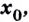 называется дифференцируемой в точке
называется дифференцируемой в точке 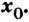 Функция, дифференцируемая в каждой точке некоторого промежутка, называется дифференцируемой на этом промежутке.
Функция, дифференцируемая в каждой точке некоторого промежутка, называется дифференцируемой на этом промежутке.
Докажем, например, что линейная функция 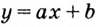 дифференцируема в каждой точке
дифференцируема в каждой точке 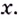 Действительно, приращению
Действительно, приращению 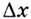 её аргумента
её аргумента 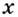 соответствует приращение функции
соответствует приращение функции 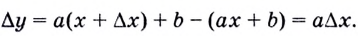 Поэтому
Поэтому 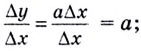 и если
и если 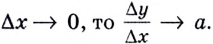 А это и значит, что в каждой точке
А это и значит, что в каждой точке 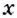 функция
функция 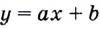 имеет производную
имеет производную 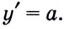
Пишут 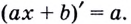
В частности: 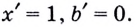
Производная постоянной равна нулю.
Из курса планиметрии известно, что уравнение прямой, проходящей через заданную точку 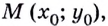 имеет вид
имеет вид 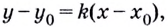 где
где 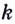 — угловой коэффициент прямой.
— угловой коэффициент прямой.
Поскольку для касательной к графику функции 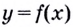 угловой коэффициент равен значению производной в точке касания
угловой коэффициент равен значению производной в точке касания 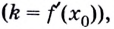 то можем записать общий вид уравнения касательной, проведённой к графику функции
то можем записать общий вид уравнения касательной, проведённой к графику функции 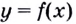 в точке касания
в точке касания 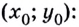
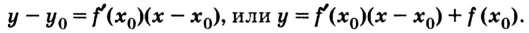
До сих пор речь шла о касательных к криволинейным графикам. Но графиком функции может быть и прямая или часть прямой. Поэтому для обобщения договариваются касательной к прямой в любой её точке считать эту самую прямую. Касательной к отрезку или лучу в любой его внутренней точке считают прямую, которой принадлежит этот отрезок или луч.
Выше было установлено, что производная линейной функции равна коэффициенту при переменной, т.е 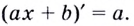
Полученный результат имеет очевидный геометрический смысл: касательная к прямой — графику функции 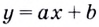 — есть эта самая прямая, её угловой коэффициент равен
— есть эта самая прямая, её угловой коэффициент равен 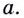
- Заказать решение задач по высшей математике
Пример:
Найдите угол, который образуете положительным направлением оси 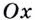 касательная к графику функции
касательная к графику функции 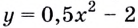 в точке
в точке 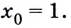
Решение:
Определим сначала угловой коэффициент этой касательной по формуле 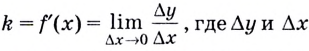 — приращения функции и приращения аргумента соответственно.
— приращения функции и приращения аргумента соответственно.
Найдем приращение функции 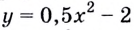 в точке
в точке 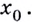
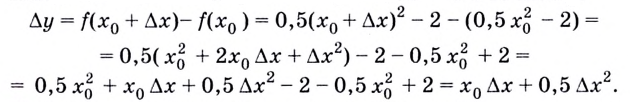
Найдём угловой коэффициент касательной:
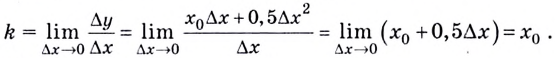
Поскольку 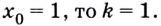
Известно также, что 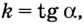 поэтому
поэтому 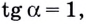 отсюда
отсюда 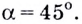
Пример:
Докажите, что для функции 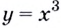 производной есть функция
производной есть функция 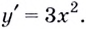
Решение:
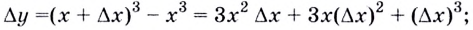
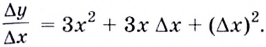 Если
Если 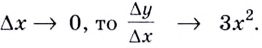 А это и означает, что производной функции
А это и означает, что производной функции 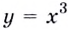 является функция
является функция 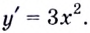
Пример:
Напишите уравнение касательной к графику функции 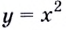 в его точке с абсциссой
в его точке с абсциссой 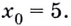
Решение:
Способ 1. Уравнение касательной имеет вид 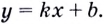 Угловой коэффициент
Угловой коэффициент 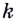 равен значению производной функции
равен значению производной функции 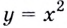 в точке
в точке 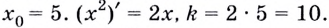 Значит, уравнение касательной
Значит, уравнение касательной 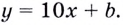 Координаты точки касания
Координаты точки касания 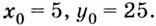 Точка с такими координатами принадлежит касательной, поэтому
Точка с такими координатами принадлежит касательной, поэтому 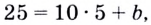 отсюда
отсюда 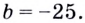 Следовательно, уравнение касательной имеет вид:
Следовательно, уравнение касательной имеет вид: 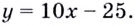
Способ 2. Запишем общий вид уравнения касательной:
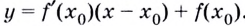
Найдём 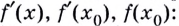
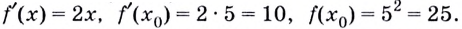
Подставим найденные значения в уравнение касательной:
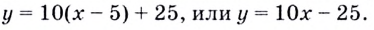
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
- Применение производной к исследованию функции
- Иррациональные неравенства
- Производная в математике
- Как найти производную функции
- Асимптоты графика функции