Содержание:
- Определение произведения чисел
- Свойства произведения чисел
Определение произведения чисел
Произведение $p$ чисел
$a_{1}, a_{2}, dots, a_{n}$ есть результат умножения этих чисел: $p=a_{1} cdot a_{2} cdot ldots cdot a_{n}$ .
В частности, если умножаются два числа $a$ и $b$, то
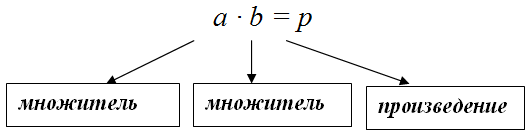
Пример
Задание. Найти произведение чисел:
1) 1.2$cdot 3$ ; 2) 4$cdot 5 cdot 13$
Ответ.
$1,2 cdot 3=3,6$
$4 cdot 5 cdot 13=260$
Свойства произведения чисел
- Коммутативность: $n cdot m=m cdot n$
-
Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
- Дистрибутивность: $(n+m) cdot k=n cdot k+m cdot k$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти произведение чисел удобным способом:
1) 5$cdot 17 cdot 2$ ; 2) 7$cdot 2 cdot 15 cdot 5$
Решение. По свойства умножения имеем:
$$5 cdot 17 cdot 2=(5 cdot 2) cdot 17=10 cdot 17=170$$
$$7 cdot 2 cdot 15 cdot 5=(7 cdot(2 cdot 15)) cdot 5=(7 cdot 30) cdot 5=210 cdot 5=1050$$
Ответ.
$5 cdot 17 cdot 2=170$
$7 cdot 2 cdot 15 cdot 5=1050$
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие
натуральные числа или
десятичные дроби.
Пример
Задание. Найти произведение чисел
1) 156$cdot 32$ ; 2) $4,71 cdot 3,1$
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое,
полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем
под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в
столбик
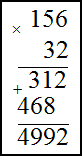
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби
перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после
запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором – один, значит, в ответе
нужно отделить справа три знака:
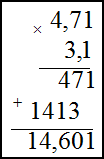
Ответ.
$156 cdot 32=4992$
$4,71 cdot 3,1=14,601$
Читать дальше: что такое простое число.
Определение
Произведением чисел в математике называется результат их умножения.
Пример: Найдите произведение чисел.
14×15=210
Здесь 14 и 15 называются — множители.
Свойства
1. Коммутативность.
Пример: Вычислить произведение чисел.
17×12=204 и 12×17=204
Переместительный закон: При перестановке множителей результат не меняется.
2. Ассоциативность.
Пример:
11×19×32=6688
(11×19)×32=6688
11×(19×32)=6688
Сочетательный закон: Если группу множителей заменить их произведением, результат не изменится.
3. Дистрибутивность.
Пример:
(15+12)×9=243 и 15×9+12×9=243
Распределительный закон: Умножая сумму на число, можно на это число каждое слагаемое умножить и результаты сложить.
Большие числа, а также десятичные дроби умножают в столбик.
Нет времени решать самому?
Наши эксперты помогут!
Произведение цифр числа
Пример: найти произведение цифр числа 428
4×2×8=64
Произведение суммы и разности чисел
(23+14)×(23-14)=37×9=333
Наименьшее произведение чисел
При умножении любого числа на 0, получится ноль. Наименьшее произведение чисел равно нулю.
Сумма двух произведений чисел
(7×8)+(9×3)=56+27=83
Ответ: 83
Пример: Найди сумму и произведение чисел 14 и 72
Решение:
14+72=86 — сумма
14×72=1008 — произведение
Математика
6 класс
Урок № 26
Произведение целых чисел. Часть 2
Перечень рассматриваемых вопросов:
- На уроке мы научимся формулировать и узнавать свойства умножения.
- Находить квадраты и кубы целых чисел.
- Вычислять значения числовых выражений, содержащих разные действия.
- Выполнять числовые подстановки в буквенные выражения и находить соответствующие им значения.
Тезаурус
Произведение любого целого числа a и нуля равно нулю.
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.
Степенью целого числа a с натуральным показателем n (n > 1) называется произведение n множителей, каждый из которых равен a.
Список литературы
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Мы уже изучали правила умножения целых чисел.
Сегодня рассмотрим свойства произведения целых чисел.
Умножение целых чисел на 0.
Произведение любого целого числа a и нуля равно нулю.
a ∙ 0 = 0
Рассмотрим примеры.
Найдите произведение целого положительного числа 209 и нуля.
Решение:
203 ∙ 0 = 0
Найдите произведение нуля и целого отрицательного числа (– 29).
Решение:
0 ∙ (– 29) = 0
Умножение целого числа на 1
Произведение целого числа и 1 равно cамому числу.
a ∙ 1 = a
Рассмотрим примеры.
Вычислите произведение положительного целого числа 64 и единицы.
Решение:
64 ∙ 1 = 64
Вычислите произведение единицы и отрицательного целого числа (– 475).
Решение:
1 ∙ (– 475) = – 475
Найдите произведение нуля и единицы.
Решение:
0 ∙ 1 = 0
Умножение на (– 1)
При умножении числа на (– 1) меняется только знак, то есть получается число, противоположное a.
a ∙ (– 1) = – a
Законы умножения
Переместительный и сочетательный законы умножения верны для любых целых чисел, и их можно применять для упрощения числовых выражений.
Переместительный закон умножения:
a ∙ b = b ∙ a
Сочетательный закон умножения:
a ∙ (b ∙ c) = (a ∙ b) ∙ c
Умножение или произведение нескольких целых чисел
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.
Вычислим произведение нескольких целых чисел:
9 ∙ (– 14) ∙ 5 ∙ (– 1)
Решение:
9 ∙ (– 14) ∙ 5 ∙ (– 1) = (9 ∙ (– 14)) ∙ 5 ∙ (– 1) = (– 126) ∙ 5 ∙ (– 1) = ((– 126) ∙ 5) ∙ (– 1) = (– 630) ∙ (– 1) = 630
Ответ: 630.
При перемножении целых чисел, результат всегда будет целым числом.
Выводы
1. Если в произведении нечётное количество отрицательных множителей, то произведение будет отрицательным.
2. Если в произведении чётное количество отрицательных множителей, то произведение будет положительным.
Степень целого числа a с натуральным показателем n
Определение: степенью целого числа a с натуральным показателем n (n > 1) называется произведение n множителей, каждый из которых равен a.
a ∙ a ∙ a ∙ a ·…∙ a = an
n множителей
Рассмотрим примеры.
1. Первая степень любого числа равна самому числу.
a1 = a
2. Вторая степень любого числа называется квадратом.
a2 = a ∙ a
3. Третья степень любого целого числа называется кубом.
a3 = a ∙ a ∙ a
Например,
24 = 2 ∙ 2 ∙ 2 ∙ 2 = 16
(– 5)3 = (– 5) ∙ (– 5) ∙ (– 5) = – 125
Итак, мы научились выполнять сложение, вычитание и умножение целых чисел. Рассмотрим, как найти значение выражения, которое содержит такие действия.
42 – 15 ∙ (– 6)
Решение
42 – 15 ∙ (– 6) = 42 – (15 ∙ (– 6)) = 42 – (– 90) = 42 + 90 = 132
Ответ: 132.
Дополнительный материал
Мы изучили правила и свойства умножения целых чисел.
Используя их, решим две задачи.
Задача №1
Чему равно произведение последовательных целых чисел, начинающихся числом (– 200) и оканчивающихся числом 200?
Решение
Между числами (– 200) и 200 находится 0, а любое число, умноженное на 0 равно 0. Поэтому произведение последовательных целых чисел от (– 200) до 200 равно 0.
Ответ: 0.
Задача №2
Чему равно произведение всех целых чисел?
Решение
Целые числа состоят из целых положительных, отрицательных чисел, а также нуля. При умножении любого числа на ноль будет 0. Поэтому произведение всех целых чисел равно 0.
Ответ: 0.
Разбор заданий тренировочного модуля
Тип 1. Разместите нужные подписи под изображениями.
Какие законы представлены в формулах?
Законы умножения
- a ∙ b = b ∙ а
- а ∙ (b ∙ с) = (а ∙ b) ∙ с
Варианты ответов:
Сочетательный закон умножения
Переместительный закон умножения
Свойство 0
Для ответа на вопрос задания обратимся к теоретическому материалу сегодняшнего урока.
Правильный ответ:
1. Переместительный закон умножения
2. Сочетательный закон умножения
Тип 2. Вставьте в текст нужные слова.
Чтобы найти … нескольких чисел, нужно найти произведение … чисел, … на третье число и так далее.
Варианты слов для вставки:
произведение
трёх
первого
двух первых
умножить
разделить
сложить
вычесть
Для ответа на вопрос задания обратимся к теоретическому материалу сегодняшнего урока.
Правильный ответ:
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.
Как найти произведение двух чисел
Существуют методики, позволяющие развивать математические возможности человеческого мозга вообще и методики вычисления произведений многоразрядных чисел в частности. Равно как и существуют люди с мозгами, которые от рождения имеют такие возможности. Однако в абсолютном большинстве случаев находить произведения чисел приходится людям без продвинутых математических способностей. Ниже описаны наиболее простые и эффективные возможности, которые им доступны.

Инструкция
Используйте знание таблицы умножения и свою краткосрочную память – зачастую этого достаточно для нахождения произведения двух двухзначных чисел в уме. При необходимости можно множитель разбить на несколько разрядов, умножить множимое на получившиеся числа и сложить результаты. Например, если надо умножить 325 на 115, то множитель можно разбить на числа 100, 10 и 5. Не старайтесь удерживать все в памяти, записывайте промежуточные результаты, ведь ваша цель – решить задачу, а не соблюсти принцип умножения в уме.
Воспользуйтесь школьными навыками умножения в столбик, если они еще не выветрились из головы и под рукой есть пишущий инструмент и бумага.
Если у вас есть доступ к компьютеру, то это означает, что вам доступен и стандартный калькулятор, встроенный в операционную систему. В ОС Windows для его запуска нажмите клавишу win, перейдите в раздел «Все программы», раскройте подраздел «Стандартные», войдите в секцию «Служебные» и выберите пункт «Калькулятор». Интерфейс этого приложения очень прост и операция нахождения произведения двух чисел с его помощью сложности не представляет – введите множимое, нажмите клавишу со звездочкой, введите множитель и нажмите enter.
Если у вас есть доступ в интернет, то можно обойтись не только без калькулятора, но и без компьютера – вполне достаточно мобильного телефона. Перейдите на главную страницу поисковой системы Google и введите вместо поискового запроса арифметическую операцию, результат которой вам требуется узнать. Например, если надо найти произведение чисел 325 и 115, то введите 325 * 115. Встроенный в поисковик калькулятор рассчитает и покажет вам результат операции. Такой же калькулятор встроен и в поисковую систему Nigma.
Не забывайте и о наличии встроенного в мобильный телефон калькулятора – сегодня редко какая модель этого устройства его не имеет. Нахождение произведения двух чисел в этом случае осуществляется нажатием тех же клавиш, что и в описанном выше программном калькуляторе.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Имея общее представление об умножении натуральных чисел и их свойств, легче понять принцип выполнений действий над ними. Мы разберем правила, по которым производится умножение натуральных чисел. Весь материал имеет конкретные примеры и подробные объяснения. Совершим проверки результатов для того, чтобы сверить полученные на выходе числа.
Таблица умножения
Умножая два натуральных числа, получаем результат, который производится при умножении однозначных натуральных чисел. Произведение чисел 6 и 3 приравнивается к сумме, состоящей из трех слагаемых, равных числу 6. Иначе это запишем: 6·3=6+6+6=18. Таким же образом получены все результаты умноженных однозначных натуральных чисел. Все занесены в таблицу, приведенную ниже.
| 1·1=1 | 2·1=2 | 3·1=3 |
| 1·2=2 | 2·2=4 | 3·2=6 |
| 1·3=3 | 2·3=6 | 3·3=9 |
| 1·4=4 | 2·4=8 | 3·4=12 |
| 1·5=5 | 2·5=10 | 3·5=15 |
| 1·6=6 | 2·6=12 | 3·6=18 |
| 1·7=7 | 2·7=14 | 3·7=21 |
| 1·8=8 | 2·8=16 | 3·8=24 |
| 1·9=9 | 2·9=18 | 3·9=27 |
| 4·1=4 | 5·1=5 | 6·1=6 |
| 4·2=8 | 5·2=10 | 6·2=12 |
| 4·3=12 | 5·3=15 | 6·3=18 |
| 4·4=16 | 5·4=20 | 6·4=24 |
| 4·5=20 | 5·5=25 | 6·5=30 |
| 4·6=24 | 5·6=30 | 6·6=36 |
| 4·7=28 | 5·7=35 | 6·7=42 |
| 4·8=32 | 5·8=40 | 6·8=48 |
| 4·9=36 | 5·9=45 | 6·9=54 |
| 7·1=7 | 8·1=8 | 9·1=9 |
| 7·2=14 | 8·2=16 | 9·2=18 |
| 7·3=21 | 8·3=24 | 9·3=27 |
| 7·4=28 | 8·4=32 | 9·4=36 |
| 7·5=35 | 8·5=40 | 9·5=45 |
| 7·6=42 | 8·6=48 | 9·6=54 |
| 7·7=49 | 8·7=56 | 9·7=63 |
| 7·8=56 | 8·8=64 | 9·8=72 |
| 7·9=63 | 8·9=72 | 9·9=81 |
Это и есть таблица умножения. Все результаты сгруппированы для удобного дальнейшего применения. Таблица сложения натуральных чисел выглядит подобным образом. Она предоставлена ниже.
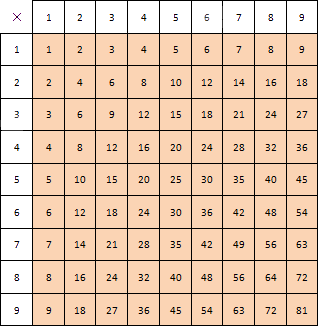
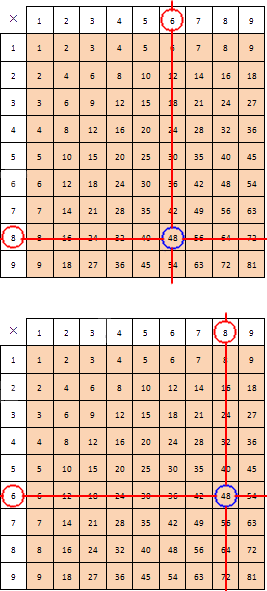
Чтобы выяснить, как пользоваться таблицей, приведем пример. Если необходимо найти произведение 6 и 8, необходимо отметить столбец верхней ячейки, где имеем 6 (8), и строку левой ячейки, где число 8 (6). Чтобы найти результат, следует найти их общую ячейку, то есть пересечение столбца и строки. На рисунке ниже изображен пример нахождения искомого умножения 6 и 8.
Умножение трех и более количества чисел
Мы дали определение понятию умножения двух чисел. Теперь поговорим об умножении трех и более имеющихся чисел. Таким образом, в такой ситуации применимо сочетательное свойство умножения натуральных чисел.
Сочетательное свойство умножения показывает равнозначность двух произведений a·(b·c) и (a·b)·c, где a, b и c могут быть любыми числами. Результат умножения данных чисел не будет зависеть от местоположения скобок. Поэтому чаще всего при произведении скобки отсутствуют, а запись имеет вид a·b·c. Данное выражение называют произведением трех чисел, причем все входящие в него числа – множители.
Сочетательное свойство умножения необходимо для того, чтобы легче было выявлять равные произведения. Это значит, что из приведенных (a·b)·(c·d), (a·(b·c))·d, ((a·b)·c)·d, a·(b·(c·d)) и a·((b·c)·d) можно сделать вывод, что они все равные. Положение скобок при умножении не играет роли. Это произведение может быть записано в виде a·b·c·d.
Обычно скобки опускаются при умножении. Произведение нескольких трех и более чисел без скобок приводит к последовательной замене двух соседних множителей до получения необходимого результата. Скобки могут быть расставлены произвольно, так как итог произведения не изменится.
Если взять пять натуральных чисел и записать их в виде произведения, то получим 2·1·3·1·8. Имеется два основных способы решения.
Первый способ заключается в том, что два множителя слева будут последовательно заменяться произведением. Тогда получим, что 2·1·3·1·8=2·3·1·8. Так как 2·3=6, то 2·3·1·8=6·1·8. Далее имеем, что 6·1=6, тогда в итоге получим результат 6·8=48. Умножение пяти заданных чисел будет равняться 48. Этот способ записывается, как (((2·1)·3)·1)·8.
Второй способ заключается в том, что скобки располагаются таким образом ((2·1)·3)·(1·8). Имеем, что 2·1=2 и 1·8=8, то ((2·1)·3)·(1·8)=(2·3)·8. При 2·3 равном 6 получим, что (2·3)·8=6·8. В итоге получим, что 6·8=48. Отсюда следует, что 2·1·3·1·8=48.
Порядок следования множителей не влияет на результат. Множители могут быть записаны в любом порядке. Это следует из свойств умножения натуральных чисел.
Даны четыре числа для умножения: 3, 9, 2, 1. Их произведение записывается в виде 3·9·2·1.
При замене произведения множителей 3 и 9 или 9 и 2 получим, что следующий этап необходимо будет произвести умножение двузначных чисел 27 и 18.
Чтобы избежать это, необходимо поменять слагаемые местами, иначе расставить скобки.
Тогда получим: 3·9·2·1=3·2·9·1=(3·2)·(9·1)=6·9=54.
При перемене мест множителей можно производить наиболее удобные комбинирования для вычисления. Рассмотрим задание, где решение приводит к умножению нескольких чисел.
Каждая коробка имеет по 3 предмета. В ящики положили 2 коробки. Какое количество предметов будет в 4 ящиках?
Решение
Нам дано, что в одном ящике 2 коробки, а в них соответственно по 3 предмета.
Тогда в одном ящике 3·2=6 предметов. Отсюда получим, что в 4 ящиках 6·4=24 предмета. Можно рассуждать иным образом. Один ящик вмещает в себя 2 коробки, отсюда в 4 ящиках 2·4=8 коробок. Каждая из коробок имеет 3 предмета, тогда имеем, что 8 коробок содержат 3·8=24 предмета.
Эти решения можно записать таким образом (3·2)·4=6·4=24 или 3·(2·4)=3·8=24.
Делаем вывод, что искомое количество предметов – это произведение 3,2,4, а значит, что 3·2·4=24.
Ответ: 24.
Подведем итоги.
При умножении трех и более чисел действия производятся последовательно. Используя переместительное и сочетательное свойства умножения, разрешается менять местами множителями и заменять их двумя другими умножаемыми числами.
Умножение суммы на натуральное число и наоборот
Благодаря распределительному свойству умножения сложение и умножение связаны. Это помогает в изучении сложения и умножения. Свойство способствует углубиться в изучение всех действий.
Если рассматривать распределительное свойство умножения относительно сложения, то получим такой вид записи с двумя слагаемыми: (a+b)·c=a·c+b·c, где a, b, c являются произвольными натуральными числами. Исходя из данного равенства при помощи метода математической индукции докажем справедливость предложенного (a+b+c)·d=a·d+b·d+c·d, (a+b+c+d)·h=a·h+b·h+c·h+d·h и т.д., где a, b, c, d, h являются натуральными числами.
Отсюда следует, что произведение суммы нескольких чисел и данного числа равна сумме произведений каждого из слагаемых с данным числом. Это правило применимо при умножении на заданное число.
Если взять сумму из пяти чисел 7, 2, 3, 8, 8 на 3, получим, что (7+2+3+8+8)·3=7·3+2·3+3·3+8·3+8·3. Отсюда имеем, что 7·3=21, 2·3=6, 3·3=9, 8·3=24, то 7·3+2·3+3·3+8·3+8·3=21+6+9+24+24, после чего находим сумму чисел 21+6+9+24+24=84.
Можно было сделать вычисления иначе, тогда следовало посчитать сумму, после чего умножение. Этот случай менее удобен, так как умножение двухзначного числа 7+2+3+8+8=28 на 3 мы пока не выполняли. Умножение двухзначных чисел – это тема, показанная в разделе умножения многозначного и однозначного натуральных чисел.
Используя переместительное свойство, мы можем переформулировать правило умножения суммы чисел на заданное число таким образом: произведение данного числа и суммы нескольких чисел равняется сумме произведений данного числа и каждого из слагаемых. Это правило умножения данного числа на заданную сумму.
Например, 2·(6+1+3)=2·6+2·1+2·3=12+2+6=20. Здесь применяем правила умножения числа на сумму.
Рассмотрим конкретный пример, где умножение решение сводится к умножению суммы чисел на данное число.
В коробке находятся по 3 красных, 7 зеленых и 2 синих предмета. Какой количество предметов имеется во всех четырех коробках?
Решение
Для определения количества предметов в одной коробке, вычислим 3+7+2. Отсюда следует, что четыре коробки содержат в 4 раза больше, значит, (3+7+2)·4 предметов.
Находим произведение суммы на число, применив полученное правило, тогда (3+7+2)·4=3·4+7·4+2·4=12+28+8=48.
Ответ: 48 предметов.
Умножение натурального числа на 10, 100, 1000 и так далее
Чтобы получить правило произвольного умножения натурального числа на 10, рассмотрим подробно.
Натуральные числа вида 20, 30, 40, …, 90 соответствуют 2, 3, 4, …, 9 десяткам. Это значит, что 20=10+10, 30=10+10+10, … отсюда следует, что умножением двух натуральных чисел их смысл суммы должен быть идентичным, тогда получим 2·10=20, 3·10=30, …, 9·10=90.
Таким же образом можно прийти к следующим неравенствам:
2·100=200, 3·100=300, …, 9·100=900; 2·1 000=2 000, 3·1 000=3 000, …, 9·1 000=9 000; 2·10 000=20 000, 3·10 000=30 000, …, 9·10 000=90 000; …
Выходит, что десяток десятков – это сотня, то 10·10=100;
что десяток сотен – это тысяча, тогда 100·10=1 000;
что десяток тысяч – это десять тысяч, то 1 000·10=10 000.
Исходя из рассуждений, получим 10 000·10=100 000, 100 000·10=1 000 000, …
рассмотрим пример для формулировки правила умножения произвольного натурального числа на 10.
Необходимо произвести умножение натурального числа 7032 на 10.
Решение
Чтобы быстрее подсчитать, необходимо представить число 7032 в виде суммы разрядных слагаемых.
Применим правило умножения суммы на число из предыдущего пункта, тогда получим 7 032·10=(7 000+30+2)·10=7 000·10+30·10+2·10. Число 7000 можно представить в виде произведения 7·1 000, число 30 произведением 3·10.
Отсюда получим, что сумма 7 000·10+30·10+2·10 будет равна сумме (7·1 000)·10+(3·10)·10+2·10. Тогда сочетательное свойство умножения можно зафиксировать, как (7·1 000)·10+(3·10)·10+2·10=7·(1 000·10)+3·(10·10)+2·10.
Отсюда получим, что 7·(1 000·10)+3·(10·10)+2·10=7·10 000+3·100+2·10=70 000+300+20. Сумма, полученная в результате, представляет собой разложение по рядам числа 70320: 70 000+300+20.
Ответ: 7 032·10=70 320.
Аналогичным способом мы можем умножить любое натуральное число на 10. В таких случаях запись всегда будет оканчиваться на 0.
Приведенные примеры и рассуждения дают возможность перейти к правилу умножения произвольного натурального число на 10. Если в конце записи дописать цифру 0, тогда заданное число будет служить результатом умножения на 10. Когда в записи натурального числа дописывают 0, то полученное число применяется как результат умножения на 10.
Приведем примеры: 4·10=40, 43·10=430, 501·10=5 010, 79 020·10=790 200 и так далее.
Основываясь на правиле умножения натурального числа на 10, можно получить умножение произвольного числа на 100, 1000 и выше.
Если 100=10·10,тогда умножение натурального числа на 100 приводит к умножению числа на 10 и еще одному умножению на 10.
Тогда получим:
17·100=17·10·10=170·10=1 700; 504·100=504·10·10=5 040·10=50 400; 100 497·100=100 497·10·10=1 004 970·10=10 049 700.
Если полученная запись имеет на 2 цифры 0 больше, тогда считается, что это результат умножения всего числа на 100. Это и называется правилом умножения числа на 100.
Произведение 1 000=100·10, тогда умножение любого натурального числа на 1000 приводит к умножению заданного числа на 100 и еще одному умножению на 10. Отсюда следует, что это правило умножения произвольного натурального числа на 1000. Когда в записи имеется 3 цифры 0, тогда считают, что это результат умножения числа на 1000.
Таким же образом производится умножение на 10000, 100000 и так далее. Идет дописывание нулей в конце числа.
В качестве примера запишем:
58·1 000=58 000; 6 032·1 000 000=6 032 000 000; 777·10 000=7 770 000.
Умножение многозначного и однозначного натуральных чисел
Имея навыки для выполнения умножения, разберем все правила на примере.
Найти произведение трехзначного числа 763 на 5.
Решение
Для начала представляем число в виде суммы разрядных слагаемых. Здесь получим, что 763=700+60+3. Отсюда получим, что 763·5=(700+60+3)·5.
Используя правило умножения суммы на число, получим, что:
(700+60+3)·5=700·5+60·5+3·5.
Произведения 700=7·100 и 60=6·10 и сумма 700·5+60·5+3·5 записывается, как (7·100)·5+(6·10)·5+3·5.
Применив переместительное и сочетательное свойство, получим (7·100)·5+(6·10)·5+3·5=(5·7)·100+(5·6)·10+3·5.
Так как 5·7=35, 5·6=30 и 3·5=15, то (5·7)·100+(5·6)·10+3·5=35·100+30·10+15.
Выполняем умножение на 100, на 10. После этого выполняем сложение 35·100+30·10+15=3 500+300+15=3 815
Ответ: произведение 763 и 5= 3815.
Чтобы закрепить материал, необходимо рассмотреть пример умножения.
Найти произведение 3 и 104558.
Решение
3·104 558=3·(100 000+4 000+500+50+8)==3·100 000+3·4 000+3·500+3·50+3·8==3·100 000+3·(4·1 000)+3·(5·100)+3·(5·10)+3·8==3·100 000+(3·4)·1 000+(3·5)·100+(3·5)·10+3·8==3·100 000+12·1 000+15·100+15·10+3·8==300 000+12 000+1 500+150+24=313 674.
Ответ: результат умножения 3 и 104558 = 313674.
Умножение двух многозначных натуральных чисел
Умножение двух многозначных натуральных чисел производится таким образом, что один из множителей раскладывается по разрядам, после этого применяют правило умножения на сумму. Изучение предыдущих статей позволит быстрее разобраться с имеющимся разделом.
Вычислить произведение 41 и 3806.
Решение
Необходимо произвести разложение числа 3806 по разрядам 3000+800+6, тогда 41·3 806=41·(3 000+800+6).
Правило умножения применимо для 41·(3 000+800+6)=41·3 000+41·800+41·6.
Так как 3 000=3·1 000 и 800=8·100, тогда справедливо равенство 41·3 000+41·800+41·6=41·(3·1 000)+41·(8·100)+41·6.
Сочетательное свойство способствует записи последней суммы (41·3)·1 000+(41·8)·100+41·6.
Вычисляя произведения 41·3, 41·8 и 41·6, представляем его в виде суммы
41·3=(40+1)·3=40·3+1·3=(4·10)·3+1·3=(3·4)·10+1·3=12·10+3=120+3=123; 41·8=(40+1)·8=40·8+1·8=(4·10)·8+1·8=(8·4)·10+1·8=32·10+8=320+8=328; 41·6=(40+1)·6=40·6+1·6=(4·10)·6+1·6=(6·4)·10+1·6=24·10+6=240+6=246
Получим, что
(41·3)·1 000+(41·8)·100+41·6=123·1 000+328·100+246=123 000+32 800+246
Вычислим сумму натуральных чисел:
123 000+32 800+246=156 046
Ответ: Произведение 41 и 3806 = 156046.
Теперь умеем умножать два любых натуральных числа.
Проверка результата умножения натуральных чисел
Умножение всегда требует проверки. Она производится при помощи деления по правилу: полученное произведение делят на один из множителей. Если полученное число равно одному из множителей, тогда вычисление произведено правильно. Если нет, то допущена ошибка.
Произвести умножение 11 на 13, равное 143. Необходимо выполнить проверку.
Решение
Проверка производится посредством деления 143 на 11. Тогда получим, что 143:11=(110+33):11=110:11+33:11=10+3=13.
Если получим число, равное одному из множителей, тогда задание решено верно.
Произведено умножение 37 на 14. Результат равен 528. Выполнить проверку.
Решение
Для выполнения проверки необходимо разделить 528 на 37. Должны получить число 14. Производится делением столбиком:
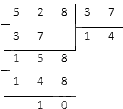
При делении мы выявили, что 528 делится на 37, но с остатком. Отсюда следует, что умножение 37 на 14 было выполнено неверно.
Ответ: проверка показала, что умножение было выполнено неверно.
Вычислить произведение чисел 53 и 7, после чего выполнить проверку.
Решение
Представляем число в виде суммы 50+3. Применим свойство умножения суммы двух чисел на натуральное число. Получим, что 53·7=(50+3)·7=50·7+3·7=350+21=371.
Для выполнения проверки, разделим 371 на 7: 371:7=(350+21):7=350:7+21:7=50+3=53. Значит, умножение произведено верно.
Ответ: 53·7=371.

