Схема замещения линии электропередачи — это представление линии электропередачи в виде математической модели для исследования различных режимов работы электрической сети.
Содержание
- 1 Общие положения
- 2 Воздушная линия электропередачи
- 3 Кабельная линия электропередачи
- 4 Схема замещения с сосредоточенными параметрами
- 5 Литература
- 6 Использованные источники
Общие положения
Активное сопротивление проводов и кабелей определяется материалом токоведущих жил, их сечением и частотой электрического тока. Для большинства расчётных задач зависимостью активного сопротивления провода от частоты переменного тока пренебрегают, вследствие низкой частоты тока в электрической сети (в России 50 Гц). Эта зависимость обусловлена наличием скин эффекта.
Активное сопротивление проводников электрического тока изменяется при их нагреве или охлаждении. При этом температура проводников изменяется при изменении величины протекающего электрического тока (более подробно можно ознакомиться здесь). Вследствие этого величины удельных активных сопротивлений являются переменными величинами, и определение их по справочным таблицам позволяет получить лишь приближённую оценку их величины. Зачастую этого приближения вполне достаточно, так как оно лежит в пределах точности задания других параметров электрической сети.
Магнитное поле, возникающее вокруг и внутри проводников, определяет их индуктивное сопротивление. Электродвижущая сила (э.д.с.), соответствующая индуктивному сопротивлению наводится в каждом проводнике линии электропередачи от проводов всех фаз. Поэтому её величина, а следовательно, и величина пропорционального её индуктивного сопротивления зависят от взаимного расположения проводов. Если это расположение обеспечивает одинаковое потокосцепление каждого провода, то наводимые в проводах э.д.с. становятся равными, а индуктивные сопротивления фазных проводов линии электропередачи одинаковыми. Такое равенство имеет место при расположении фазных проводов по вершинам равностороннего треугольника.
Индуктивные сопротивления фазных проводов линии электропередачи, у которой провода расположены горизонтально, по всей длине, отличаются друг от друга. Чтобы избежать появления нежелательной нессиметрии фазных значений сопротивлений, а следовательно токов и напряжений, применяют транспозицию проводов.
В большинстве случаев можно принять, что активное и реактивное сопротивление, активная и ёмкостная проводимости равномерно распределены по всей её длине. Для линий электропередач небольшой длины (при частоте 50 Гц границей можно считать длину 300 км) распределёность параметров можно не учитывать и можно использовать более простое представление в виде схемы замещения с сосредоточенными параметрами. Обычно в расчётах режимов работы энергосистем применяется П-образная схема замещения линии электропередач с сосредоточенными параметрами.
Воздушная линия электропередачи
Расчеты параметров приведены для одной цепи ЛЭП.
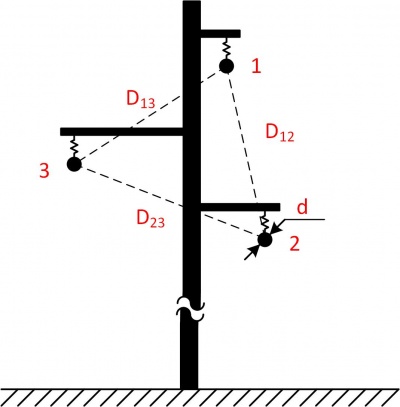
Рисунок — Пример треугольного расположения фазных проводов без расщепления на одноцепной опоре.
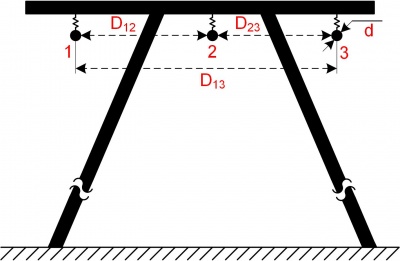
Рисунок — Пример горизонтального расположения фазных проводов без расщепления на одноцепной опоре.
Величина активного сопротивления воздушной линии электропередачи влияет на нагрев проводов, при протекании по ним электрического тока. Для сталеалюминиевых проводов, являющихся наиболее часто используемыми для воздушных ЛЭП, активное сопротивление определяется главным образом алюминиевой частью. Это обусловлено эффектом вытеснения переменного тока к поверхности проводника (скин-эфффект). Активное сопротивление в первую очередь зависит от материала, из которого изготовлен проводник, его длины и сечения. При расчётах режимов работы энергосистемы активное сопротивление принято измерять в [Ом]:
- [math]displaystyle
R = rho frac{L}{F},
[/math]
где [math]displaystyle rho[/math] — удельное активное сопротивление проводника [[math]displaystyle frac{text{Ом} cdot text{мм}^2}{text{км}} [/math]]; [math]L[/math] — длина проводника [км]; [math]F[/math] — площадь поперечного сечения проводника [[math]displaystyle text{мм}^2 [/math]].
Для сталеалюминиевых проводов (обозначение марки провода — АС), выполненных в виде стального многопроволочного сердечника и многопроволочной алюминиевой оболочки, из-за поверхностного эффекта и разницы в удельных сопротивлениях стали и алюминия практически весь ток протекает по алюминиевым проводникам. Если учесть также, что ток протекает по отдельным проводникам, навитым вокруг сердечника и имеющим длину на 3—4 % больше длины провода, то расчётное удельное сопротивление сталеалюминиевого провода, отнесенное к единице его длины, составит [math]displaystyle rho = 31,5 frac{text{Ом} cdot text{мм}^2}{text{км}}[/math].
Обычно в справочных материалах приводится удельное (погонное) сопротивление линии электропередачи [math]displaystyle R_0[/math] [Ом/км] для стандартных сечений, тогда результирующее сопротивление одного провода определяется как,
- [math]displaystyle
R = R_0 cdot L.
[/math]
Справочные значения приводятся для температуры окружающей среды 20°С. Активное сопротивление зависит от температуры, но при расчётах эта зависимость учитывается не всегда.
Индуктивное сопротивление воздушной ЛЭП определяется индуктивностью фаз ЛЭП по отношению к земле и взаимоиндукцией между фазами и, следовательно, зависит от взаимного расположения фаз, расстояния между фазами и диаметра провода.
Для устранения разницы в величине индуктивного сопротивления фаз (крайних и средней) производится транспозиция проводов.
Расположение проводов воздушной линии электропередачи на опоре может быть горизонтальным или треугольным.
Удельное индуктивное сопротивление фазы одноцепной транспонированной линии подсчитывается с учётом взаимоиндукции фаз по соотношению:
- [math]displaystyle
X_0 =0,1445 cdot lg frac{D_text{ср}}{r_{text{э}}} + frac{0,0157}{m}text{ }frac{text{Ом}}{text{км}}.
[/math]
где [math]displaystyle D_text{ср}[/math] — среднегеометрическое расстояние между фазами [м]; [math]displaystyle r_{text{э}}[/math] — эквивалентный радиус фазы, если нет расщепления то [math]displaystyle r_{text{э}}=r[/math] [м]; [math]r[/math] – радиус провода фазы [м]; [math]m[/math] — число проводов в фазе, если нет расщепления то [math]displaystyle m=1[/math] [шт.];
- [math]displaystyle
D_text{ср} =sqrt[3]{D_{1,2}D_{1,3}D_{2,3}};
[/math]
- [math]displaystyle
r_{text{э}} =sqrt[m]{r prod^m_{i=2}a_{1i} },
[/math]
где [math]displaystyle a_i[/math] — расстояние между первым и [math]displaystyle i[/math]-м проводом в фазе [м]; [math]displaystyle r = frac{d}{2}[/math] — радиус фазного проводника.
| Класс напряжения, кВ | 35 | 110 | 150 | 220 | 330 | 500 | 750 |
|---|---|---|---|---|---|---|---|
| Среднее геометрическое расстояние, м | 3,5 | 5,0 | 6,5 | 8,0 | 11,0 | 14,0 | 19,5 |
Удельная активная проводимость воздушной линии (характеризующая потери на корону крайне малый ток утечки через изоляторы) определяется по соотношению:
- [math]displaystyle
G_0 = frac{Delta P_{к.0}}{U^2_text{ном}},
[/math]
Эквивалентная активная проводимость определяется следующим образом:
- [math]displaystyle
G = G_0 cdot L.
[/math]
Для воздушных линий погонные потери активной мощности на корону существенно зависят от погодных условий и напряжения, поэтому активная погонная проводимость является переменным и нелинейным параметром. В большинстве случаев более целесообразно непосредственно учитывать для линии электропередачи в виде дополнительной нагрузки по концам линии (узлы 1 и 2) [math]displaystyle P_1=P_2=frac{Delta P_{к.0}}{2}[/math] или в виде активной проводимости на землю [math]displaystyle frac{G}{2} [/math].
Коронирование проводов приводит:
- к снижению КПД передачи электрической энергии;
- к усиленному окислению поверхности проводов;
- к появлению радиопомех.
Ёмкостная проводимость линии определяется токами смещения за счёт электростатического поля линии (между фазами и по отношению к земле). Эта проводимость создает так называемый зарядный, или ёмкостный, ток, вектор которого опережает на 90° вектор напряжения линии. Величина удельной ёмкостной проводимости
- [math]displaystyle
B_0 = frac{7,58}{lg frac{D_text{ср}}{r_{text{э}} }} cdot 10^{-6} [frac{text{См}}{text{км}}].
[/math]
Эквивалентная ёмкостная проводимость:
- [math]displaystyle
B = B_0 cdot L.
[/math]
Ёмкостная проводимость воздушных линий электропередачи слабо зависит от конструктивных особенностей ЛЭП и имеет значение от [math]2,55 cdot 10^{-6}[/math] до [math]2,80 cdot 10^{-6}[/math] [См/км] для ВЛ 110—220 кВ и от [math]displaystyle 3,4 cdot 10^{-6}[/math] до [math]displaystyle 4,2 cdot 10^{-6}[/math] [См/км] для ВЛ 330—750 кВ. Значения удельных проводимостей приводятся в справочной литературе[1].
Кабельная линия электропередачи
Кабельные линии электропередач в расчётах представляют такой же П-образной схемой замещения, что и воздушные линии. Удельные продольные активные и реактивные сопротивления определяются по справочным таблицам так же как и для воздушных линий.
Особенностью кабельных линий электропередач является близкое расположение фаз (по сравнению с воздушными линиями), что приводит к снижению удельного индуктивного сопротивления и увеличению удельной ёмкостной проводимости.
Для кабельных линий электропередачи напряжением 110 кВ и выше необходимо учитывать потери в изоляции кабеля. Они определяются по формуле:
- [math]
G = B cdot operatorname{tg} delta.
[/math]
Параметр [math]operatorname{tg} delta[/math] называется тангенс диэлектрчиеских потерь и определяется по данным завода изготовителя кабеля. Обычно находится в пределах от 0,003 до 0,006.
Схема замещения с сосредоточенными параметрами
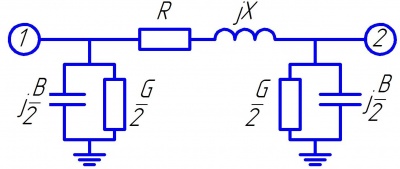
Рисунок — Полная П-образная схема замещения линии электропередачи. Цифрами 1 и 2 показаны узлы начала и конца линии электропередачи.
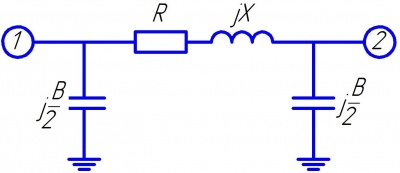
Рисунок — П-образная схема замещения линии электропередачи, только с ёмкостной проводимостью. Цифрами 1 и 2 показаны узлы начала и конца линии электропередачи.

Рисунок — П-образная схема замещения линии электропередачи, без учёта шунтов. Цифрами 1 и 2 показаны узлы начала и конца линии электропередачи.
При расчёте режима работы электрической сети воздушная трехфазная линия переменного тока напряжением до 500 кВ и длиной до 300 км может быть представлена схемой замещения с сосредоточенными параметрами П-образного вида. В случае превышения длины линии электропередачи 300 км необходимо изменить схему замещения одним из трёх способов:
- Разделить её на сегменты длиной менее 300 км.
- Представить линию волновыми параметрами.
- При длинах от 300 до 500 км можно использовать поправочные коэффициенты, значение которых при малых длинах близко к единице:
- [math]displaystyle K_R = 1 – frac{L^2}{3} X_0 B_0 [/math];
- [math]displaystyle K_X = 1 – frac{L^2}{6} X_0 B_0 (1 – frac{R^2_0}{X^2_0}) [/math];
- [math]displaystyle K_C = frac{3 + K_R}{2(1+K_R)}[/math].
В зависимости от класснапряжения воздушной ЛЭП можно использовать различные схемы замещения:
- 220 кВ и выше. Полная схема замещения с активным и ёмкостным шунтом.
- от 35 кВ до 220 кВ. Сокращённая схема замещения только с ёмкостным шунтом.
- до 35 кВ. Схема замещения без шунтов.
Для расчёта режимов электрической сети, как правило, используется П-образная схема замещения сети, параметры схемы замещения вычисляются для одной фазы. При расчётах режима удобно схемы замещения представлять в виде, представленном на рисунке.
Полное продольное сопротивление и проводимости (шунты узлов 1 и 2) схемы замещения имеют вид
- [math]displaystyle
Z = R +jX;
[/math]
- [math]displaystyle
Y_1 = Y_2 = frac{G}{2}+jfrac{B}{2}.
[/math]
Зачастую при расчётах установившихся режимов активная проводимость ЛЭП не учитывается, так как принятые меры борьбы с короной достаточно эффективны и, следовательно, потери на корону достаточно малы. Для воздушных линий классом напряжения менее 220 кВ потери на коронирование можно не учитывать, так как это существенно не скажется на полученной оценке параметров установившегося режима.
В случае исследования режимов воздушных линий напряжением менее 35 кВ можно не учитывать также ёмкостные шунты. В этом случае, схема замещения будет содержать только продольное сопротивление [math]Z[/math].
Литература
- Электрические системы. Электрические сети. / Под ред. д.т. н. В. А. Веникова. М.: Высшая школа — 1971.
Использованные источники
- ↑ 1,0 1,1 Справочник по проектированию электроэнергетических систем. Третье издание, переработанное и дополненное. Под редакцией С. С. Рокотяна, И. М. Шапиро. Авторы В. В. Ершевич, А. Н. Зейлигер, Г. А. Илларионов, Л. Я. Рудых, Д. Л. Файбисович, Р. М. Фришберг, Л. Д. Хабачев. И. М. Шапиро. М.: Энергоатомиздат, 1985
В данной статье будет рассматриваться пример определения индуктивного сопротивления воздушной линии 10 кВ.
Пример
Требуется определить индуктивное сопротивление воздушной линии 10 кВ со сталеалюминиевыми проводами марки АС-50/8,0, длина линии составляет 5 км, используется промежуточная опора П10-16.
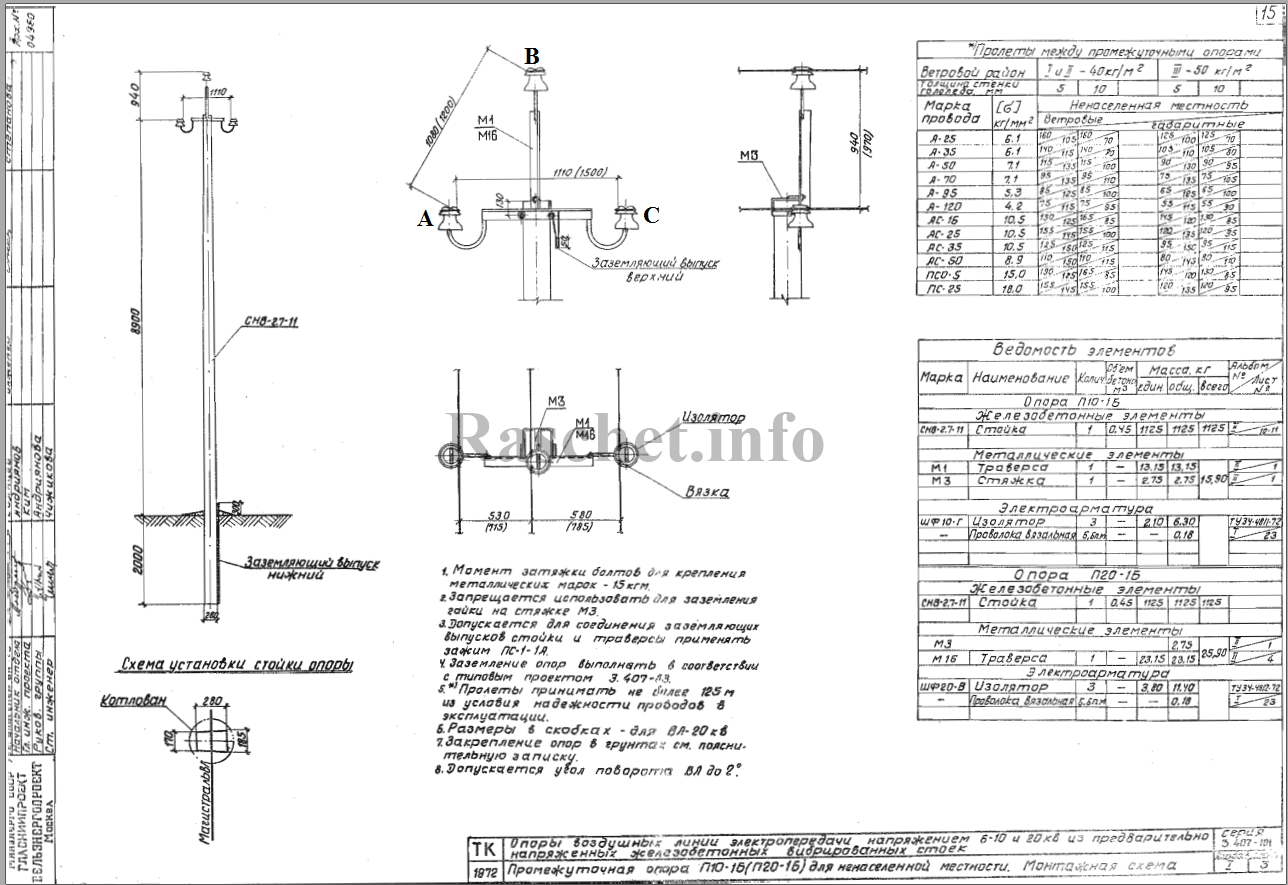
Рис.1 — Габаритный чертеж опоры П10-16
Решение
Определять индуктивное сопротивление проводов будем по формулам представленным в статье: «Определение активных и индуктивных сопротивлений проводов».
1. Определяем среднее геометрическое расстояние между проводами по формуле [Л1. с19], зная расстояния между фазами по габаритному чертежу на опору П10-16 (см. рис.1):
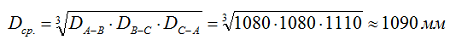
где:
- DА-В = 1080 мм — расстояние между проводами фаз А и В;
- DВ-С = 1080 мм — расстояние между проводами фаз В и С;
- DС-А = 1110 мм — расстояние между проводами фаз С и А.
2. Определяем индуктивное сопротивление для проводов марки АС-50/8,0 по формуле [Л1.с.19]:
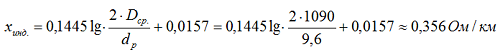
где:
- Dср. = 1090 мм – среднее геометрическое расстояние между проводами;
- dр = 9,6 мм – расчетный диаметр провода, определяется по ГОСТ 839-80, таблица 4;
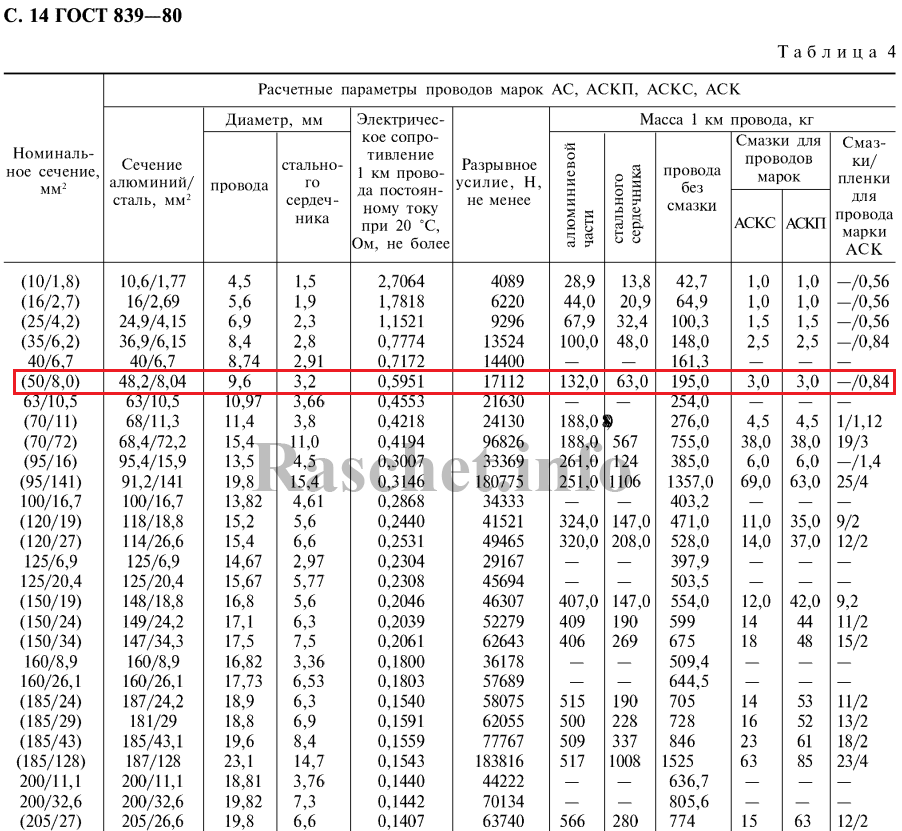
С не большой погрешностью, такой же результат можно получить по приложению П30 [Л1.с. 84], если кривую для провода сечением 50 мм2 продлить до Dср = 1,09 м, то индуктивное сопротивление будет равно 0,358 Ом/км. Принимаю хинд. = 0,356 Ом/км, так как считаю это более точное значение.
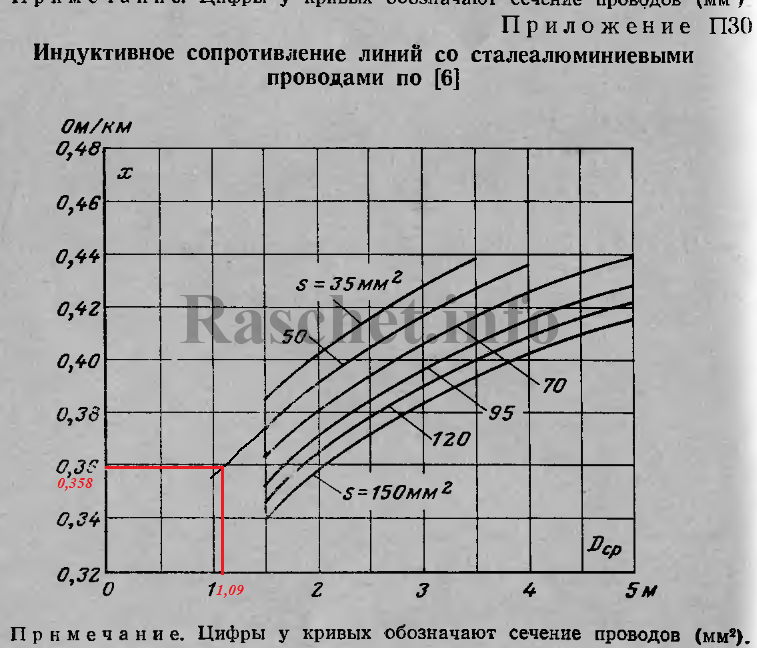
3. Определяем индуктивное сопротивление для всей линии:
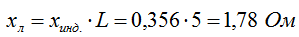
где: L = 5 км – длина воздушной линии 10 кВ.
Для упрощения расчетов индуктивного сопротивления проводов рекомендую использовать приложения П28-П31 [Л1.с.83-85], предварительно определив значение Dср.
Литература:
1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
индуктивное сопротивление, индуктивное сопротивление проводов, среднее геометрическое расстояние между проводами
Благодарность:
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding» и «PayPal».
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.
Содержание
- Пример определения индуктивного сопротивления ВЛ 10 кВ
- Характеристики и параметры элементов электрических систем. Сопротивления и проводимости линий электропередачи , страница 2
- Расчет основных параметров
Пример определения индуктивного сопротивления ВЛ 10 кВ
В данной статье будет рассматриваться пример определения индуктивного сопротивления воздушной линии 10 кВ.
Требуется определить индуктивное сопротивление воздушной линии 10 кВ со сталеалюминиевыми проводами марки АС-50/8,0, длина линии составляет 5 км, используется промежуточная опора П10-16.

Рис.1 — Габаритный чертеж опоры П10-16
Определять индуктивное сопротивление проводов будем по формулам представленным в статье: «Определение активных и индуктивных сопротивлений проводов».
1. Определяем среднее геометрическое расстояние между проводами по формуле [Л1. с19], зная расстояния между фазами по габаритному чертежу на опору П10-16 (см. рис.1):
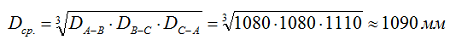
- DА-В = 1080 мм — расстояние между проводами фаз А и В;
- DВ-С = 1080 мм — расстояние между проводами фаз В и С;
- DС-А = 1110 мм — расстояние между проводами фаз С и А.
2. Определяем индуктивное сопротивление для проводов марки АС-50/8,0 по формуле [Л1.с.19]:
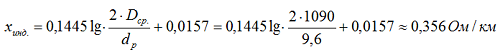
- Dср. = 1090 мм – среднее геометрическое расстояние между проводами;
- dр = 9,6 мм – расчетный диаметр провода, определяется по ГОСТ 839-80, таблица 4;

С не большой погрешностью, такой же результат можно получить по приложению П30 [Л1.с. 84], если кривую для провода сечением 50 мм2 продлить до Dср = 1,09 м, то индуктивное сопротивление будет равно 0,358 Ом/км. Принимаю хинд. = 0,356 Ом/км, так как считаю это более точное значение.

3. Определяем индуктивное сопротивление для всей линии:
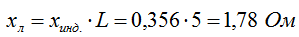
где: L = 5 км – длина воздушной линии 10 кВ.
Для упрощения расчетов индуктивного сопротивления проводов рекомендую использовать приложения П28-П31 [Л1.с.83-85], предварительно определив значение Dср.
1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
Источник
Характеристики и параметры элементов электрических систем. Сопротивления и проводимости линий электропередачи , страница 2
Индуктивное сопротивление любой линии определяется по формуле
где — удельное индуктивное сопротивление, Ом/км.
Величина одного провода (фазы) воздушной линии выражается следующей формулой
где среднегеометрическое расстояние между фазными проводами; R-радиус провода; m— магнитная проницаемость материала провода; f — частота переменного тока.
Для воздушных линий с проводами из цветных металлов при частоте 50 Гц формула (4.4) принимает вид
Среднегеометрическое расстояние зависит от вида расположения проводов на опоре, номинального напряжения линии и в общем случае определяется следующим выражением
где — расстояние между проводами соответственно фаз А, В и С.
При увеличении номинального напряжения воздушных линий расстояние между фазами значительно растет, что несколько повышает их индуктивные сопротивления.
В двухцепных линиях потокосцепление каждого фазного провода определяется магнитными потоками обеих цепей и поэтому индуктивное сопротивление зависит от взаимного расположения всех проводов.
Так, при переходе от варианта размещения фаз (рис.4.2,а) к варианту (рис.4.2,б) индуктивное сопротивление для линии снижается на 10%.
Линии электропередачи напряжением 330 кВ и выше выполняют с расщепленной фазой, когда каждая фаза состоит из нескольких проводов (рис.4.3). Это соответствует увеличению эквивалентного радиуса провода, определяемого по формуле
где — среднегеометрическое расстояние между проводами в расщепленной фазе; N — число проводов в расщепленной фазе.
Для таких линий формула (4.5) принимает следующий вид
При этом индуктивное сопротивление линии снижается. Индуктивное сопротивление уменьшается также в компактных линиях электропередачи, где из-за сближения фаз меньше по сравнению с обычными традиционными линиями.
Для определения удельного индуктивного сопротивления любых воздушных линий обычно пользуются справочными таблицами, в которых величина дается в зависимости от марки (сечения) провода и номинального напряжения линии или среднегеометрического расстояния между фазами.
Индуктивное сопротивление кабельных линий из-за малых расстояний между фазными токонесущими жилами значительно меньше, чем в воздушных линиях. Некоторое влияние на индуктивное сопротивление кабелей оказывают их конструктивные особенности. Поэтому величину кабелей указывают заводы-изготовители и ее значение приводят в справочных таблицах.
Активная проводимость линии электропередачи обусловлена потерями активной мощности от тока утечки через изоляцию и на корону.
Потери активной мощности от тока утечки через изоляцию и вызванная им активная проводимость незначительна в кабельных линиях и совсем мала в воздушных линиях. Практически ее рекомендуют учитывать в кабелях напряжением 110 кВ и выше.
Потери на корону более значительны. Они связаны с ионизацией воздуха вокруг проводов воздушных линий. Ионизационные процессы у поверхности проводов при рабочем напряжении возникают при напряженности электрического поля, соответствующей условию самостоятельного разряда. Эта форма разряда получила название коронного по внешнему признаку — слабому фиолетовому свечению в темноте и характерному потрескиванию вблизи проводов. В идеальном случае корона на чистых проводах воздушных линий с неповрежденной поверхностью отсутствует, когда максимальная напряженность электрического поля на поверхности провода при наибольшем рабочем напряжении не превосходит начальной напряженности коронного разряда. Однако неровности на поверхности провода, возникающие в связи с механическими повреждениями, загрязнениями и особенно осадками (дождь, роса, снег, изморозь, иней), приводят к значительному увеличению напряженности поля в этих местах, и в них возникает местная корона при меньшем напряжении, чем начальное напряжение самостоятельного разряда.
Действующее значение начальной напряженности короны можно определить по формуле
где m — коэффициент негладкости поверхности провода, mн=0,82; — относительная плотность воздуха; = 1,0 – 1,03; R — радиус провода.
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им. Даля 166
- ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им. Дегтярева 174
- КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им. Макарова 543
- НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им. Герцена 123
- РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им. Гагарина 114
- СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им. Каразина 305
- ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Полный список ВУЗов
- О проекте
- Реклама на сайте
- Правообладателям
- Правила
- Обратная связь
Чтобы распечатать файл, скачайте его (в формате Word).
Источник
Расчет основных параметров

Параметры связей
В качестве связей, то есть элементов схемы, которые соединяют два узла схемы, могут выступать линии электропередач, трансформаторы и выключатели. Рассмотрим, как определяют их параметры.
Линии электропередач
Как правило, при расчетах установившихся режимов на ПК линия электропередачи представляется П-образной схемой замещения (рисунок 1).

Линия электропередачи характеризуется продольным сопротивлением и поперечной проводимостью
и поперечной проводимостью 
Активная проводимость
Активная проводимость воздушных линий практически всецело определяется потерями на корону, в связи с чем, она в сильной степени зависит не только от конструкции линии, но также от рабочего напряжения и от погодных условий. В воздушных линиях (ВЛ) напряжением до 220 кВ потерями мощности на корону обычно пренебрегают, и величину принимают равной нулю. Для ВЛ напряжением 220 кВ и выше значения потерь на корону Pк для данного типа погоды, включают в нагрузки, либо можно рассчитать активные проводимости в схеме замещения:
где: Pok — удельные потери на корону, взятые из справочника для данного типа линии и для данного типа погоды, кВт/км;
l — длина линии, км;
Uном — номинальное напряжение, кВ.
Для кабельных линий активная проводимость определяет потери в изоляции кабеля. Они характеризуются тангенсом угла диэлектрических потерь, определяемым по данным завода изготовителя: 
В кабельных линиях напряжением до 110 кВ этими потерями обычно пренебрегают и принимают равной нулю.
Значения , , определяются длиной линии между соседними узлами расчетной схемы и значениями удельных параметров:  Величины r, x, b даются в справочной литературе, а также они могут быть рассчитаны по нижеследующим формулам, с учетом конструктивных особенностей линий электропередач.
Величины r, x, b даются в справочной литературе, а также они могут быть рассчитаны по нижеследующим формулам, с учетом конструктивных особенностей линий электропередач.
Активное сопротивление
Для алюминиевого и сталеалюминиевого проводов удельное сопротивление при температуре +20 0 С может быть приближенно определено из выражения:
где: F- расчетное сечение провода, мм 2 .
В случае, когда фаза состоит из n проводов (составляющих), полученную из вышеописанной формулы величину надо разделить на n.
При расчетах, связанных с определением потерь электроэнергии в ВЛ, необходимо учитывать зависимость активного сопротивления линии от температуры провода:  где:
где:
 – средняя температура за базовый период, 0 С;
– средняя температура за базовый период, 0 С;
 – удельное активное сопротивление при температуре +20 0 С.
– удельное активное сопротивление при температуре +20 0 С.
Индуктивное сопротивление
Удельное индуктивное сопротивление провода ВЛ зависит не только от размеров самого провода, но и от расстояния между фазами, а для линий сверхвысоких напряжений, фаза которых может состоять из нескольких проводов, также и от числа составляющих в фазе, и от расстояния между ними.

где: r – радиус единичного провода, м;
 — среднегеометрическое расстояние между фазами, м.
— среднегеометрическое расстояние между фазами, м.
Если фаза ВЛ состоит из n проводов, то в вышеуказанное выражение вместо величины r следует подставить величину:

где: r – радиус единичного провода, м,
a – среднегеометрическое расстояние между проводами одной фазы, м.
Для кабельных линий индуктивное сопротивление меньше, чем для воздушных, так как среднегеометрическое расстояние между фазами значительно меньше. Поэтому при расчетах режимов для кабельных сетей 10 кВ и ниже можно учитывать только активное сопротивление.
Емкостная проводимость
Удельная проводимость связана с удельной емкостью ВЛ соотношением:  где:
где:

В свою очередь, емкость ВЛ зависит от диаметра проводов, их взаимного расположения и расстояния между ними.
Если не учитывать влияние соседних цепей ВЛ и грозозащитных тросов (что вносит погрешность, не превышающую 5 %), то удельная емкостная проводимость ВЛ при одном проводе в фазе определяется как
При n составляющих в фазе в вышеприведенной формуле вместо r следует подставить величину rэ определенную по формуле:
Для воздушных линий напряжением ниже 110 кВ емкостную проводимость можно не учитывать.
Емкостная проводимость кабельных линий зависит от конструкции кабеля, и указывается заводом изготовителем, но для ориентировочных расчетов она может быть оценена по той же формуле. Емкостная проводимость в кабельных линиях больше, чем в воздушных, так как расстояния между проводами значительно меньше.
Источник
номинальными частотами. В последнем случае изменение частоты в одной системе не оказывает влияния на частоту в другой системе.
Контрольные вопросы к главе 1
1.Дайте определение энергетической системы, электроэнергетической системы и электрической сети.
2.Каково основное назначение электрической сети?
3.Из каких основных элементов состоит электрическая сеть?
4.Сформулируйте основные требования, предъявляемые к электрической
сети.
5.Как классифицируются электрические сети по напряжению?
6.Дайте классификацию электрических сетей по конструктивному выполнению.
7.Приведите классификацию электрических сетей по назначению и конфигурации.
8.Дайте классификацию электрических сетей по иерархическому признаку
иразмерам охватываемой территории.
9.Как классифицируются электрические сети по характеру питаемых потребителей и роду тока?
2.1. Схемы замещения и параметры линий электропередачи
Линии электропередачи характеризуются параметрами (сопротивлениями и проводимостями), равномерно распределенными по длине линии. Расчет линии электропередачи с учетом распределенности параметров очень сложен и применяется только для очень протяженных электропередач сверхвысокого напряжения, длина которых соизмерима с длиной электромагнитной волны.
Подавляющее большинство линий электропередачи в ЭЭС имеют длины, существенно меньшие длины волны. Учет распределенности параметров этих линий значительно усложняет расчеты электрических сетей, уничтожает наглядность результатов расчета при несущественном их уточнении. Поэтому расчет линий электропередачи длиной до 300 км выполняют при допущении о сосредоточенности ее параметров. Погрешности расчетов при таком допущении не превышают 1…2%, что вполне допустимо для инженерных расчетов.
Представление элемента электрической сети его параметрами называется схемой замещения. При расчетах симметричных режимов схемы замещения составляются для одной фазы.
Воздушные и кабельные линии электропередачи при расчетах электрических сетей представляются в общем случае П-образной схемой замещения (рис. 2.1). Такая схема является наиболее удобной расчетной моделью линии, отражающей главные характеристики происходящих в линии явлений.
7

Поскольку длины линий электропередачи различны, вводят понятия погонных параметров, т.е. параметров, приведенных к единице длины линии, например к одному километру. Погонные параметры линий электропередачи различной конструкции, различных напряжений, с различными сечениями проводников фаз приводятся в справочной литературе, например в [4] и [7].
Схема замещения линии электропередачи (рис. 2.1) состоит из продольной ветви и двух поперечных ветвей. В соответствии с этим различают продольные и поперечные параметры линии. Продольные параметры – это активное и индуктивное сопротивления R и X одной фазы линии, поперечные – это активная и емкостная проводимости G и В между фазой и землей (точкой нулевого потенциала).
Рис. 2.1. Схема замещения линии электропередачи
Активное сопротивление линии электропередачи. Проводниковые материалы (алюминий, медь, сплавы на их основе), используемые для проводов воздушных линий (ВЛ) и жил кабельных линий (КЛ) электропередачи, обладают электрическим сопротивлением. При протекании по линии тока в этом сопротивлении теряется активная мощность, идущая на нагревание материала проводника.
Различают два вида электрического сопротивления: омическое и активное. Омическое сопротивление – это сопротивление проводника постоянному току, активное – переменному току. Активное сопротивление больше омического вследствие эффекта вытеснения тока к поверхности проводника. Для промышленной частоты 50 Гц этот эффект проявляется незначительно, отличие активного и омического сопротивлений не превышает 0,5% и этим отличием обычно пренебрегают.
Электрическое сопротивление проводника зависит от его температуры
где α – температурный коэффициент изменения сопротивления; для алюминия и меди α = 0,004 1/оС;
R – сопротивление проводника при 20оС; θ – фактическая температура проводника.
8
В реальном диапазоне изменения температуры проводника его сопротивление меняется незначительно. Поэтому при выполнении инженерных расчетов температурным изменением сопротивлений проводников, как правило, пренебрегают.
Cтальные провода имеют существенно большее электрическое сопротивление, чем провода из цветных металлов. Кроме того, сталь является ферромагнитным материалом и проявляет свои магнитные свойства при протекании по ней переменного тока. Активное сопротивление стального провода
где Rом – омическое сопротивление провода;
Rдоб – добавочное сопротивление, обусловленное потерями активной мощности на перемагничивание стали (гистерезис) и вихревые токи; вследствие насыщения стали это сопротивление зависит от величины тока, протекающего по стальному проводнику.
Зависимость Rдоб от тока не выражается аналитически и может быть задана только в табличной форме. Поскольку стальные провода используются для ВЛ исключительно редко, далее внимания этим проводам уделяться не будет.
Для ВЛ применяются, главным образом, сталеалюминиевые и алюминиевые провода. У сталеалюминиевых проводов не принимают во внимание сопротивление стального сердечника. Считается, что ток протекает только по алюминиевой части провода. Следовательно, активное сопротивление алюминиевого и сталеалюминиевого проводов при одинаковых сечениях алюминиевой части равны.
Продольное активное сопротивление линии электропередачи составляет
где ro – погонное активное сопротивление, Ом/км; L – длина линии, км.
Величина погонного активного сопротивления ro для проводов ВЛ и жил КЛ из разных проводниковых материалов различного сечения приводится в справочных материалах.
Индуктивное сопротивление линии электропередачи. Из курса теоретической электротехники известно, что индуктивное сопротивление одиночного проводника определяется э.д.с. самоиндукции, наводимой в этом проводнике переменным магнитным полем, возникающим внутри и вне проводника при протекании по нему переменного тока. В трехфазной системе переменного тока в каждом фазном проводе дополнительно наводятся э.д.с. взаимоиндукции от проводов двух других фаз. Таким образом, индуктивное сопротивление провода одной фазы определяется результирующей э.д.с.
9

Если провода фаз ВЛ расположены симметрично, например, в вершинах равностороннего треугольника, то э.д.с. взаимоиндукции, наводимые в каждом проводе, будут одинаковыми и, следовательно, одинаковыми будут индуктивные сопротивления всех трех фаз.
При несимметричном расположении проводов, например, в горизонтальной плоскости э.д.с. взаимоиндукции проводов крайних фаз будут отличаться от э.д.с. взаимоиндукции среднего провода. Соответственно будут отличаться и индуктивные сопротивления проводов, что при достаточно большой длине линии приведет к несимметрии напряжений фаз.
Для ВЛ напряжением 110 кВ и выше длиной более 100 км при несимметричном расположении проводов выполняется транспозиция проводов, т.е. изменение взаимного расположения проводов с целью выравнивания индуктивных сопротивлений и, следовательно, напряжений разных фаз. Изменение расположения проводов выполняется через каждую треть длины линии.
Для двухцепных ВЛ отличие индуктивного сопротивления провода фазы при учете и без учета взаимного влияния одной цепи на другую составляет 5…6% и в практических инженерных расчетах не учитывается. Ниже будем считать, что индуктивные сопротивления проводов линии при любом их расположении как в одноцепной, так и двухцепной ВЛ одинаковые.
Погонное индуктивное сопротивление, Ом/км, для проводников из немагнитного материала (алюминий, медь) определяется по выражению
|
хо=0,144lg(Dср/Rпр)+0,016, |
(2.4) |
где Dср – среднегеометрическое расстояние между проводами, м; Rпр – радиус провода, м.
Первая составляющая выражения (2.4) определяется магнитным полем вне провода и называется внешним индуктивным сопротивлением; вторая составляющая определяется магнитным полем внутри провода и называется внутренним индуктивным сопротивлением.
Среднегеометрическое расстояние между проводами фаз a, b и с при их произвольном расположении определяется как
|
D |
= 3 D D D , |
(2.5) |
|
ср |
ab ac bc |
где Dаb, Dас, Dbc – расстояния между соответствующими фазами. При расположении фаз в вершинах равностороннего треугольника со
стороной D и горизонтальном расположении фаз при расстоянии D между соседними фазами величина среднегеометрического расстояния соответственно составляет
Dср=D;
10

Индуктивное сопротивление линии электропередачи составляет
Величина погонного индуктивного сопротивления хo для проводов ВЛ и жил КЛ различных напряжений и сечений рассчитывается по выражению (2.4) или определяется по справочным данным.
Активная проводимость линии электропередачи. Кроме потерь активной мощности, расходуемой на нагревание проводников, в линии электропередачи имеют место потери активной мощности, обусловленные:
•токами утечки через изоляцию вследствие ее несовершенства;
•ионизацией воздуха вокруг провода (явлением общей короны).
Эти два фактора обуславливают активную проводимость G линии электропередачи.
Токи утечки через изоляцию ВЛ очень незначительны и ими, как правило, пренебрегают. Токи утечки через изоляцию КЛ имеют заметную величину при напряжениях 220 кВ и выше.
Явление общей короны возникает при высокой напряженности электрического поля на поверхности проводника и сопровождается характерным потрескиванием и видимым свечением. Процессы ионизации воздуха вокруг коронирующего провода приводят к потерям активной мощности.
Потери активной мощности на корону зависят от погодных условий и напряжения линии. При дожде, мокром снеге, понижении атмосферного давления и увеличении напряжения потери на корону увеличиваются.
Значения потерь на корону для ВЛ различного напряжения, с различными сечениями проводов определяются, как правило, экспериментально. Существуют и эмпирические зависимости для приближенной оценки потерь на корону. Погонные значения потерь на корону ∆Ро, кВт/км, приводятся в справочных материалах, например в [4]. По этой величине через номинальное напряжение линии, кВ, определяется погонная активная проводимость, См/км
и полная активная проводимость линии
Емкостная проводимость линии электропередачи. Под действием электростатического поля между проводами фаз и между проводами и землей возникают токи смещения. Значения этих токов, называемых зарядными, определяются емкостями между фазами и между каждой
11

фазой и землей. Величины этих емкостей, зависящие от геометрических размеров и взаимного расположения проводников, а также от диэлектрических свойств изоляции, определяют емкостную проводимость линии электропередачи.
Погонная емкостная проводимость линии электропередачи bo, См/км, рассчитывается по формуле
|
bo=ωco=7,58.10-6/lg(Dср/Rпр), |
(2.10) |
а проводимость всей линии
Значения погонных емкостных проводимостей для линий электропередачи различного напряжения, сечения и конструкции приводятся в справочных материалах.
Наличие эквивалентной емкости между фазой и землей обуславливает зарядную мощность линии. Величина этой зарядной мощности, Мвар, определяется по выражению
|
Qc=Uном2В=Uном2boL, |
(2.12) |
где Uном – номинальное линейное напряжение линии электропередачи, кВ.
Параметры ВЛ с расщепленной фазой. Чем меньше индуктивное сопротивление линии, тем большую мощность можно по ней передать. Подробнее об этом изложено в п. 3.3. С целью увеличения передаваемой по линии мощности индуктивное сопротивление линии стремятся уменьшить. Из выражения (2.4) видно, что этого можно достичь, уменьшая расстояние между проводами или увеличивая сечение (радиус) провода.
Расстояние между проводами определяется классом напряжения ВЛ. Увеличение сечения провода до величин, заметно уменьшающих значение хо, приведет к неоправданному перерасходу цветного металла. Поэтому для уменьшения индуктивного сопротивления ВЛ каждую ее фазу расщепляют на несколько проводов. Обычно для ВЛ 330 кВ каждая фаза расщепляется на два провода, для ВЛ 500 кВ – на три, для ВЛ 750 кВ – на четыре. Иногда расщепление фазы на два провода применяется и для ВЛ напряжением 220 кВ.
В общем случае при расщеплении фазы на n проводов эквивалентный радиус расщепленной фазы составит
|
R = n R |
а |
а |
…а |
, |
(2.13) |
|
|
э |
пр |
12 |
13 |
1n |
где а1i (i=2, 3, … n) – расстояние от одного из проводов в фазе до всех остальных.
12

При расщеплении фазы на три провода последние располагаются в вершинах равностороннего треугольника, при расщеплении фазы на четыре провода – в вершинах квадрата. Величина Rэ для расщепления фазы на два, три и четыре провода определяется по выражениям, вытекающим из (2.13):
|
Rэ2= Rпра ; |
||||
|
Rэ3= 3 R |
а2 |
; |
(2.14) |
|
|
пр |
||||
|
Rэ4= 4 R |
пр |
а3 |
2 , |
|
где а – расстояние между соседними проводами фазы.
При расщеплении фазы на n проводов выражение (2.4) для вычисления погонного индуктивного сопротивления приобретает вид
хо=0,144lg(Dср/Rэ)+0,016/n. (2.15)
Эквивалентное активное сопротивление фазы при ее расщеплении на n проводов в n раз меньше активного сопротивления одного провода.
При определении погонной емкостной проводимости для ВЛ с расщепленной фазой в выражение (2.10) вместо радиуса провода Rпр подставляется эквивалентный радиус Rэ.
Потери активной мощности на корону для ВЛ с расщепленной фазой, как и для ВЛ без расщепления фазы, имеют величину, возрастающую с увеличением напряжения ВЛ.
Схемы замещения линий электропередачи. При расчетах электрических сетей воздушные и кабельные линии электропередачи представляются в общем случае П-образной схемой замещения (рис. 2.1). Продольные параметры R и Х представляются сосредоточенными в середине линии. Поперечные параметры B и G представляются сосредоточенными по концам линии. Поэтому проводимость каждой поперечной ветви будет в два раза меньше полной проводимости линии.
Для выбора целесообразного варианта схемы замещения конкретной линии электропередачи необходимо иметь представление о соотношениях величин погонных параметров линий различных напряжений и конструкций.
Величина погонного активного сопротивления проводов ВЛ и жил КЛ уменьшается с увеличением сечения провода. Так, для сечений сталеалюминиевого провода 10…500 мм2 активное сопротивление составляет 2,8…0,06 Ом/км.
Погонное индуктивное сопротивление ВЛ с проводами различных сечений без расщепления фазы изменяется в достаточно узком диапазоне
13
0,39…0,44 Ом/км. При расщеплении фазы это сопротивление уменьшается на 20…40% в зависимости от степени расщепления.
Для КЛ величина Dср значительно меньше, чем для ВЛ. Как следует из выражения (2.4), при одинаковых сечениях (радиусах) проводов ВЛ и жил КЛ величина погонного индуктивного сопротивления для КЛ меньше, чем для ВЛ. Поскольку величина Dср находится под знаком десятичного логарифма, индуктивные сопротивления КЛ в 3…7 раз меньше, чем индуктивные сопротивления ВЛ.
Из сказанного следует, что пренебрежение индуктивным сопротивлением допустимо для КЛ с малыми сечениями жил, так как для таких линий X<<R. Пренебрежение активными сопротивлениями допустимо для ВЛ с расщеплением проводов в фазе, так как для таких линий X>>R..
Для ВЛ напряжением 35 кВ и ниже потери на корону пренебрежительно малы. Для ВЛ напряжением 110…220 кВ потери на корону не представляют заметной величины в суммарных потерях активной мощности в линии, если сечение провода ВЛ 110 кВ не менее 70 мм2, ВЛ 150 кВ не менее 120 мм2, ВЛ 220 кВ не менее 240 мм2. Указанные сечения рекомендуются для ВЛ напряжением 110…220 кВ. При таких сечениях напряженность на поверхности провода не превышает критического значения, при котором наступает явление короны.
Для ВЛ напряжением 330…750 кВ с расщепленными фазами потери на корону могут достигать величины 3…15 кВт/км. По сравнению с передаваемыми по таким ВЛ мощностями потери на корону пренебрежительно малы и при расчетах установившихся режимов эти потери, как правило, не учитывают.
Токи утечки через изоляцию ВЛ всех напряжений пренебрежительно малы, а для КЛ имеют заметную величину при напряжениях 220 кВ и выше.
Погонная емкостная проводимость ВЛ с проводами различных сечений без расщепления фазы изменяется в достаточно узком диапазоне (2,5…3)10-6 См/км. При расщеплении фазы эта проводимость увеличивается на 25…60% в зависимости от степени расщепления. Согласно выражению (2.12) погонное значение зарядной мощности при незначительном изменении емкостной проводимости определяется, главным образом, напряжением линии. Для ВЛ напряжением 35 кВ и ниже величина зарядной мощности пренебрежимо мала. Для ВЛ напряжением 110…220 кВ эта мощность составляет уже заметную величину 30…130 квар/км, соизмеримую с потерями реактивной мощности в индуктивном сопротивлении ВЛ. Для ВЛ с расщепленной фазой напряжением 330…1150 кВ зарядная мощность достигает внушительных значений 0,4…6 Мвар/км.
Среднегеометрическое расстояние между жилами КЛ значительно меньше, чем между проводами ВЛ. Кроме того, диэлектрическая проницаемость изоляции кабеля выше, чем воздуха. Следовательно,
14
Соседние файлы в папке ES_EESiS_books
- #
13.03.201625.65 Mб67Герасимов – Электротехнический справочник. Том 3.djvu
- #
- #
Параметры связей
В качестве связей, то есть элементов схемы, которые соединяют два узла схемы, могут выступать линии электропередач, трансформаторы и выключатели. Рассмотрим, как определяют их параметры.
Линии электропередач
Как правило, при расчетах установившихся режимов на ПК линия электропередачи представляется П-образной схемой замещения (рисунок 1).

Линия электропередачи характеризуется продольным сопротивлением![]() и поперечной проводимостью
и поперечной проводимостью ![]()
Активная проводимость
Активная проводимость воздушных линий практически всецело определяется потерями на корону, в связи с чем, она в сильной степени зависит не только от конструкции линии, но также от рабочего напряжения и от погодных условий. В воздушных линиях (ВЛ) напряжением до 220 кВ потерями мощности на корону обычно пренебрегают, и величину принимают равной нулю. Для ВЛ напряжением 220 кВ и выше значения потерь на корону Pк для данного типа погоды, включают в нагрузки, либо можно рассчитать активные проводимости в схеме замещения:
где: Pok — удельные потери на корону, взятые из справочника для данного типа линии и для данного типа погоды, кВт/км;
l — длина линии, км;
Uном — номинальное напряжение, кВ.
Для кабельных линий активная проводимость определяет потери в изоляции кабеля. Они характеризуются тангенсом угла диэлектрических потерь, определяемым по данным завода изготовителя: ![]()
В кабельных линиях напряжением до 110 кВ этими потерями обычно пренебрегают и принимают равной нулю.
Значения , , определяются длиной линии между соседними узлами расчетной схемы и значениями удельных параметров: ![]() Величины r0, x0, b0 даются в справочной литературе, а также они могут быть рассчитаны по нижеследующим формулам, с учетом конструктивных особенностей линий электропередач.
Величины r0, x0, b0 даются в справочной литературе, а также они могут быть рассчитаны по нижеследующим формулам, с учетом конструктивных особенностей линий электропередач.
Активное сопротивление
Для алюминиевого и сталеалюминиевого проводов удельное сопротивление при температуре +20 0С может быть приближенно определено из выражения:
![]() , Ом/км,
, Ом/км,
где: F- расчетное сечение провода, мм2.
В случае, когда фаза состоит из n проводов (составляющих), полученную из вышеописанной формулы величину надо разделить на n.
При расчетах, связанных с определением потерь электроэнергии в ВЛ, необходимо учитывать зависимость активного сопротивления линии от температуры провода: ![]() где:
где:
![]() – средняя температура за базовый период, 0С;
– средняя температура за базовый период, 0С;
![]() – удельное активное сопротивление при температуре +20 0С.
– удельное активное сопротивление при температуре +20 0С.
Индуктивное сопротивление
Удельное индуктивное сопротивление провода ВЛ зависит не только от размеров самого провода, но и от расстояния между фазами, а для линий сверхвысоких напряжений, фаза которых может состоять из нескольких проводов, также и от числа составляющих в фазе, и от расстояния между ними.

где: r – радиус единичного провода, м;
![]() — среднегеометрическое расстояние между фазами, м.
— среднегеометрическое расстояние между фазами, м.
Если фаза ВЛ состоит из n проводов, то в вышеуказанное выражение вместо величины r следует подставить величину:
![]()
где: r – радиус единичного провода, м,
a – среднегеометрическое расстояние между проводами одной фазы, м.
Для кабельных линий индуктивное сопротивление меньше, чем для воздушных, так как среднегеометрическое расстояние между фазами значительно меньше. Поэтому при расчетах режимов для кабельных сетей 10 кВ и ниже можно учитывать только активное сопротивление.
Емкостная проводимость
Удельная проводимость связана с удельной емкостью ВЛ соотношением: ![]() где:
где:
![]()
– угловая частота.
В свою очередь, емкость ВЛ зависит от диаметра проводов, их взаимного расположения и расстояния между ними.
Если не учитывать влияние соседних цепей ВЛ и грозозащитных тросов (что вносит погрешность, не превышающую 5 %), то удельная емкостная проводимость ВЛ при одном проводе в фазе определяется как
При n составляющих в фазе в вышеприведенной формуле вместо r следует подставить величину rэ определенную по формуле:
Для воздушных линий напряжением ниже 110 кВ емкостную проводимость можно не учитывать.
Емкостная проводимость кабельных линий зависит от конструкции кабеля, и указывается заводом изготовителем, но для ориентировочных расчетов она может быть оценена по той же формуле. Емкостная проводимость в кабельных линиях больше, чем в воздушных, так как расстояния между проводами значительно меньше.


