Прямоугольник — это двухмерная продолговатая фигура, которая имеет 4 стороны и 4 прямых угла.
Находящиеся друг напротив друга стороны имеют одну длину, причем одна пара сторон длиннее другой.
Если все стороны прямоугольника одинакового размера, то он является квадратом. Другими словами,
квадрат — это особенный случай прямоугольника.
- Сторона прямоугольника через диагональ и угол между
диагональю и стороной - Сторона прямоугольника через диагональ и известную
сторону - Сторона прямоугольника через площадь и другую известную
сторону - Сторона прямоугольника через периметр и другую известную
сторону - Сторона прямоугольника через диагональ и угол между
диагоналями
Через диагональ и угол между диагональю и стороной
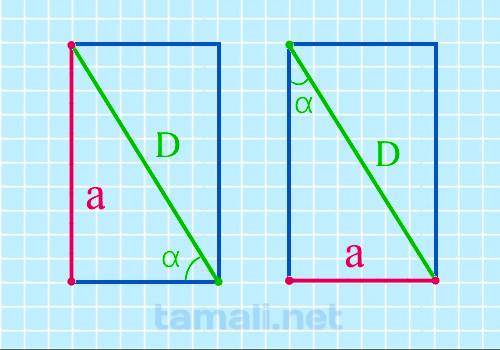
Определить неизвестную сторону прямоугольника можно в том случае, если знаешь длину диагонали и угол
средь ней и стороной. Такая конструкция образует пару прямоугольных треугольников, поэтому можно
воспользоваться следующей формулой:
a = d * sinα
где d — это диагональ, а, b — одна из сторон фигуры.
Цифр после
запятой:
Результат в:
Пример. Найти сторону прямоугольника, если диагональ равна 16 см, а угол между диагональю и этой
стороной — 60º.
Решение.
D = 16, β = 60º, b = ?
b = 16 cos 60º
b = 16 * 0.5 = 8 см.
Через его площадь и известную сторону
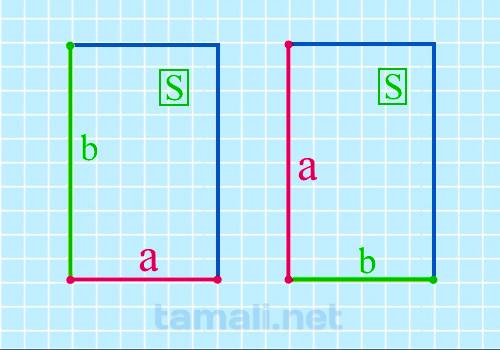
Площадь прямоугольника вычисляется по формуле: S = ab. Следовательно
a = S / b
где S — площадь прямоугольника, b — известная сторона.
Цифр после
запятой:
Результат в:
Пример. Площадь прямоугольника равна 60 единицам, а его длина равна 12 единицам. Подставляем
известные значения в формулу, Вычислив, получим ширину = 60/12, значит ширина равна 5.
Через диагональ и известную сторону
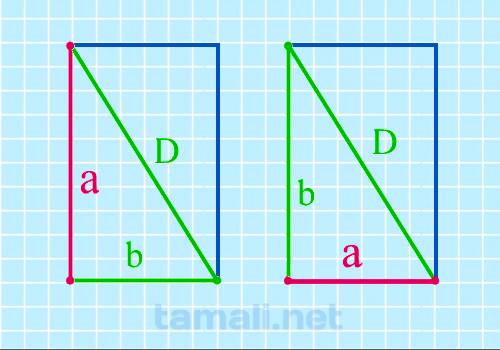
Сторону прямоугольника можно вычислить, если известны его диагональ и другая сторона.
Диагональ
— это отрезок прямой, соединяющий любые две несмежные вершины. Диагонали AC и BD равны. Одна из них
разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а
две соседние стороны — остальные стороны треугольника. Отсюда :
a = √(d² — b²)
где d — диагональ, а, b — стороны.
Цифр после
запятой:
Результат в:
Пример. Найти сторону прямоугольника, если диагональ равна 5 см, а другая сторона — 4 см.
Решение.
D=5, b=4, a=?
a = √(25 – 16) = √9 = 3 см.
Через диагональ и угол между диагоналями
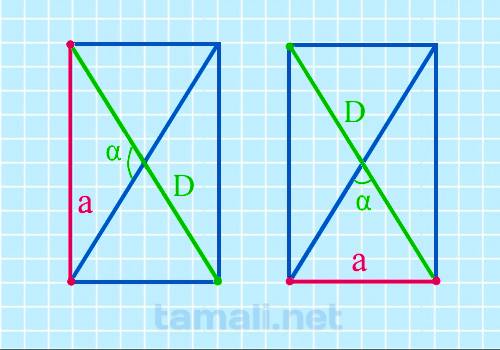
Зная значение угла между двумя диагоналями и длину по крайней мере одной из них, можем рассчитать
сторону прямоугольника, зная следующую формулу:
a = D • sin(α/2)
где D — диагональ, α — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Длина диагонали прямоугольника равна 20 см, а угол между диагоналями — 30º. Найти
сторону.
Решение.
a = 20 * (sin 30º / 2)
a = 20 * 0, 5 / 2 = 5 см.
Через периметр и другую известную сторону
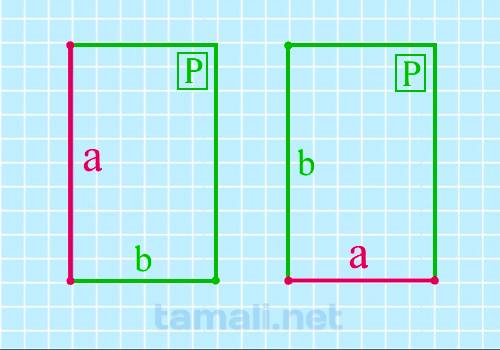
Длину же мы можем вычислить, если известны периметр и ширина. Мы можем использовать формулу периметра
для получения длины. P = 2 (a + b).
a = (P — 2b) / 2
где P — периметр прямоугольника, b — другая известная сторона.
Цифр после
запятой:
Результат в:
Так, если P — 32 см, а b — 4 см, Подставим известные нам значения, получим a = (32 — 2*4).Вычислив,
получим 12 см.
Другие примеры по решению задач на прямоугольник с использованием длины и ширины
- Длина и ширина прямоугольника равны 7 дюймам и 21 дюйму. Найдите его периметр.
Результат: P
прямоугольника = 2 (длина + ширина) = 2 (7 + 21) дюйма = 2 (28) дюймов = 56 дюймов - Длина и ширина прямоугольника равны 0,3 м и 15 см. Найдите его площадь. Результат: Длина = 0,3
м, ширина = 15 см. Длина и ширина прямоугольника находятся в различных значениях, поэтому мы
преобразуем одно из них. Переведем длину в сантиметры, умножив ее на 100, так как 1 м = 100 см.
Итак, длина = 0,3 100 см = 30 см. Площадь = длина ширина = 30 см 15 см = 450 см². - Одна сторона прямоугольника меньше другой на 7 см, а диагональ прямоугольника равна 17 см. Найти
периметр прямоугольника. Решение. Пусть АВ=х. Тогда AD=х+7. Зная, что диагональ BD=17,
используем теорему Пифагора и составим уравнение: AB² +AD² =BD².
Получаем: х² +(х+7)² =17² ⇒ х² +х² +14х+49=289; 2х² +14х-240=0; х² +7х-120=0,
отсюда по теореме Виета х1 =-15; х2 =8.Следовательно, АВ=8 см, AD=8+7=15 см. Периметр прямоугольника: P = 2∙ (AB+AD); P = 2∙ (8+15); P = 46 см.
Ответ: 46 см.
Прямоугольник обладает широким спектром свойств. Некоторые из важных свойств прямоугольника приведены
ниже.
- Прямоугольник — это четырехугольник.
- Противоположные стороны прямоугольника являются равными и параллельны друг другу.
- Внутренний угол прямоугольника при каждой вершине равен 90°.
- Сумма внутренних углов равна 360°.
- Диагонали пересекаются друг с другом.
- Длина диагоналей равна.
- Длина диагоналей может быть получена с помощью теоремы Пифагора. Длина диагонали со сторонами a
и b равна, диагональ = ( a2 + b2). - Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
- Все прямоугольники являются параллелограммами, но все параллелограммы не являются
прямоугольниками.
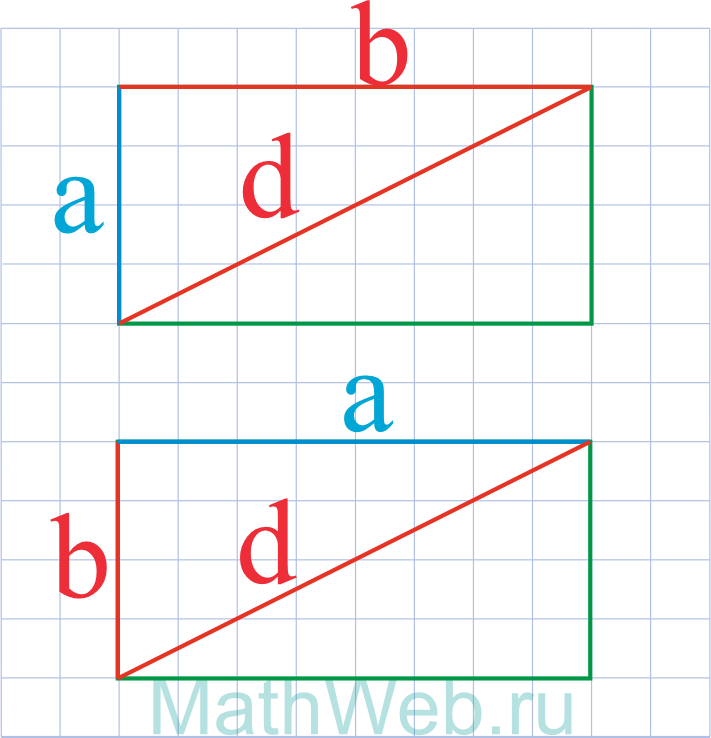
Где d – диагональ,b – сторона.
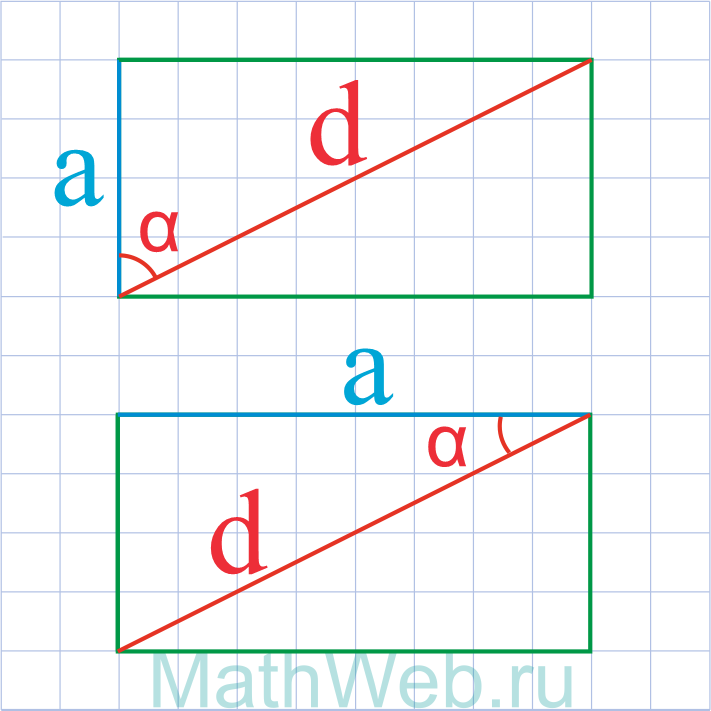
Где d – диагональ,α – угол между диагональю и искомой стороной.
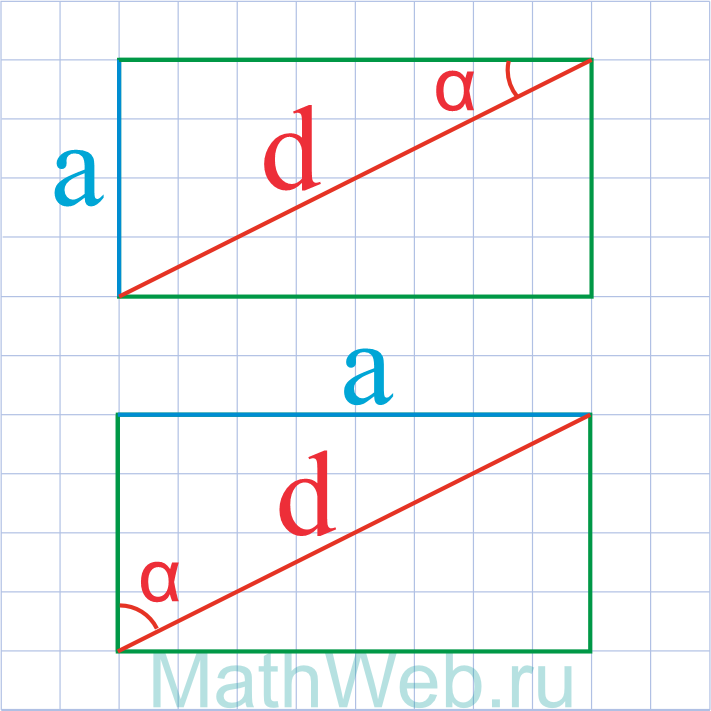
Где d – диагональ,α – угол между диагональю и другой стороной.
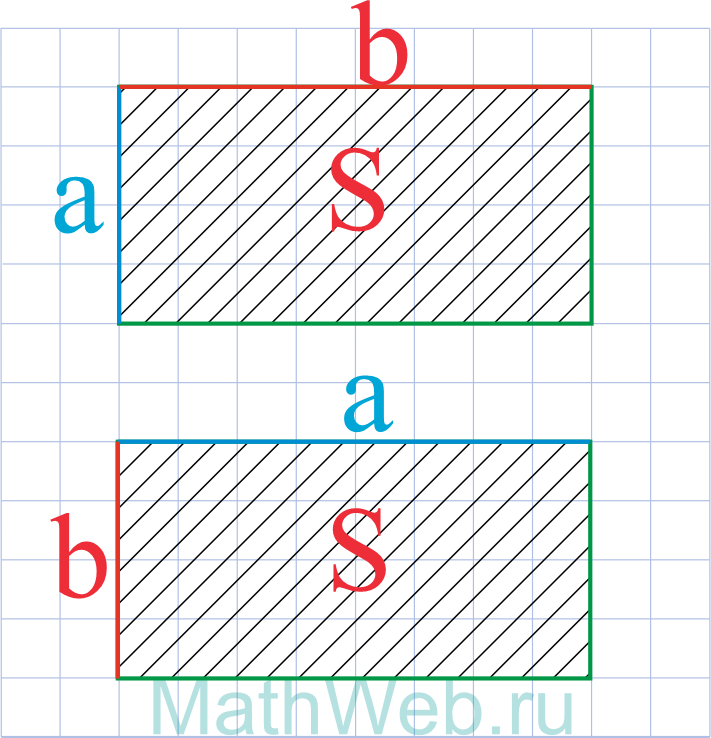
Где S – площадь, b– известная сторона.
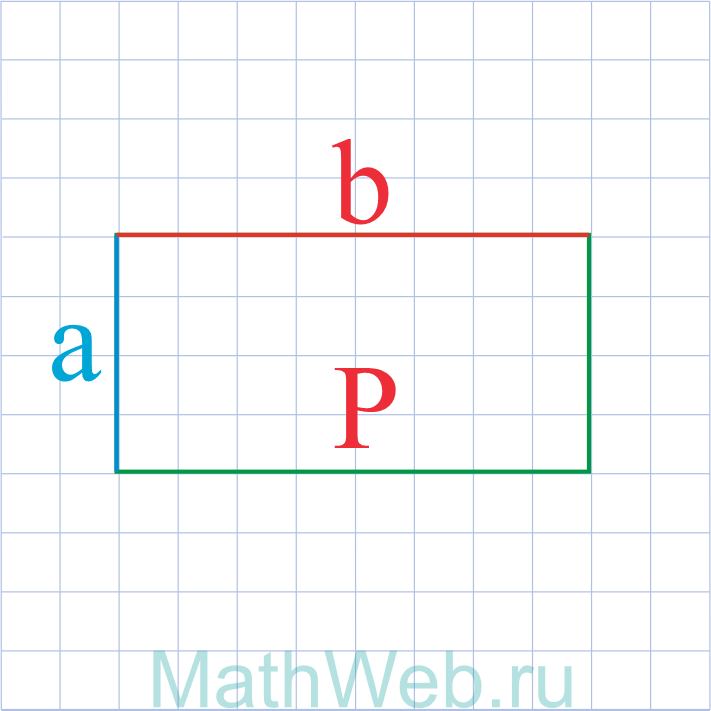
Где P – периметр, b – известная сторона.
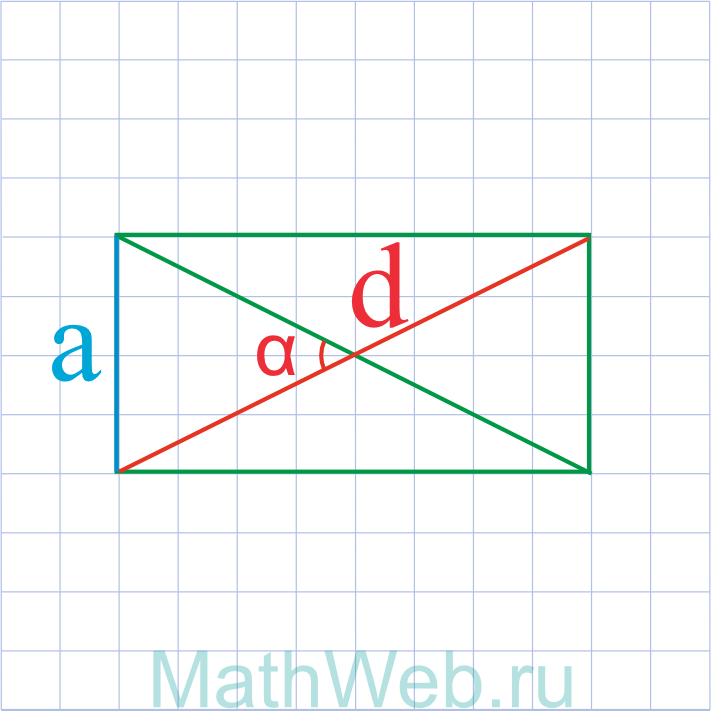
Где d – диагональ, α – угол между диагоналями.
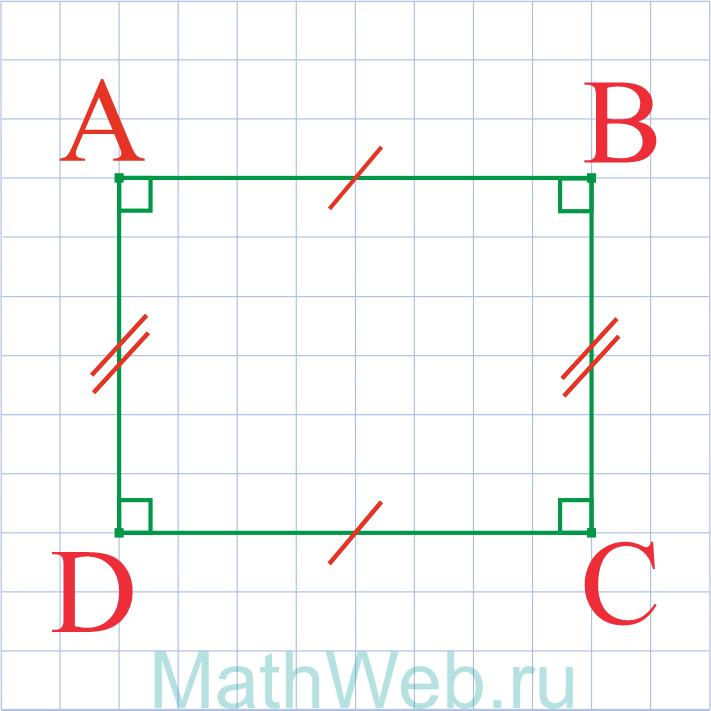
- Прямоугольник – это четырехугольник у которого противоположные стороны равны и параллельны AB = CD и BC = DA.
- Стороны прямоугольника являются его высотами.
- Между прилегающими сторонами угол всегда 90°.
Как найти длину стороны прямоугольника?
Сторона прямоугольника может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = √d2 ― b2 |
 |
a = d·cos(α) |
 |
a = d·sin(α) |
 |
a = S b |
 |
a = P – 2b 2 |
 |
a = d·sin(0.5·α) |
Как найти стороны прямоугольника, если известна диагональ
Прямоугольник – плоская фигура, у которой стороны попарно равны и параллельны. Диагонали прямоугольника тоже одинаковые. Одна диагональ делит исходную фигуру на два прямоугольных треугольника с острыми углами по сорок пять градусов. Исходя из этих данных можно легко найти стороны прямоугольника, зная только численное значение диагонали.

Инструкция
Для нахождения сторон прямоугольника нужно рассмотреть один из тех самых прямоугольных треугольников. В нем гипотенуза является диагональю прямоугольника, а катеты – его сторонами. Перед непосредственным вычислением с числовыми значениями нужно найти уравнения в общем виде. Для каждой стороны будет свое уравнение. Итак, для получения формул, в прямоугольном треугольнике обозначьте катеты латинскими буквами а и b, а гипотенузу – с.
Решение задачи заключается в определении синуса и теоремы Пифагора. Выберите любой из острых углов в треугольнике (они равны), с которым будете работать. Определите прилежащий к нему катет и, противолежащий от него, другой катет. Например, пусть, прилежащим к углу, будет катет b, а находящимся напротив – катет а.
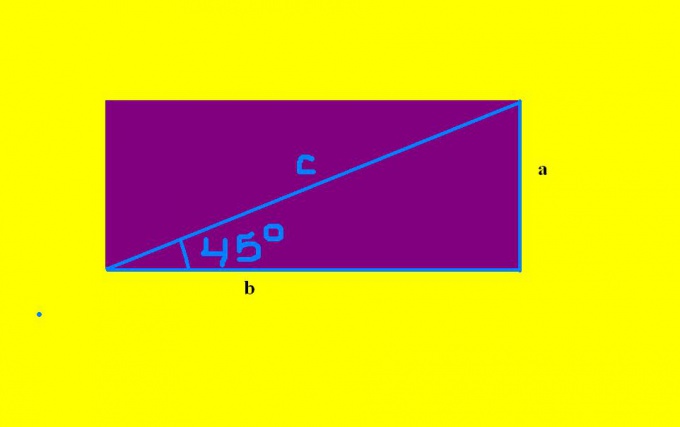
Далее, исходя из определения синуса, которое гласит, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе, составьте уравнение: sin 45 = а/с. В данном примере, по условию, известны: синус угла (sin 45 ~0,7) и гипотенуза с. Отсюда, получается уравнение 0,7=а/с, из которого а=0,7с. Осталось подставить численное значение с. Найденная сторона а будет равна параллельной стороне в прямоугольнике. Таким образом, известны две стороны фигуры.
Источники:
- Геометрия 7-9 классы. Погорелов. Просвещение 2010 год.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
как найти стороны прямоугольника если известна его диагональ
Елена
Знаток
(338),
закрыт
12 лет назад
Yustas
Искусственный Интеллект
(178477)
12 лет назад
диагональ делает два прямоугольных треугольника.
сумма квадратов катетов равна квадрату гипотенузы, то есть диагонали.
Однако, так можно найти сторону квадрата. У него стороны равны. То есть треугольник не только прямоугольный, но и равнобедренный.
А если это был прямоугольник ( то есть разные стороны) , то нужно знать еще углы на диагонали
Четырехугольник, у которого все углы прямые, противоположные стороны равны и параллельны друг другу, называется прямоугольником. Стороной прямоугольника является отрезок, соединяющий две вершины фигуры. Длинная сторона считается длиной, короткая сторона — шириной прямоугольника, прилегающие стороны перпендикулярны, они являются его высотами.
Расчет длины стороны прямоугольника через диагональ и сторону
Отрезок, соединяющий 2 противолежащие вершины прямоугольника, является его диагональю. В прямоугольнике две диагонали одинаковой длины. Каждая из них делит прямоугольник на два прямоугольных треугольника, гипотенузой которых является диагональ, а катетами — стороны прямоугольника. Соответственно, квадрат диагонали можно вычислить через теорему Пифагора: d2 = a2 + b2, а сумма квадратов диагоналей прямоугольника равна сумме квадратов его сторон:
2d2 = 2a2 + 2b2
где d — диагональ, а, b — стороны прямоугольника.
Если дана диагональ прямоугольника и одна из его сторон, находим длину другой стороны, как корень из разности: квадрат диагонали минус квадрат известной стороны:
a = √d2 — b2
b = √d2 — a2
где d — диагональ, а, b — стороны прямоугольника.
Расчет стороны прямоугольника через периметр и сорону
Периметр прямоугольника равняется сумме всех его сторон. Если известны длина (а) и ширина (b) прямоугольника, его периметр (Р) будет равен удвоенной сумме сторон, т.к. его противоположные стороны равны:
Р = 2a + 2b = 2 (а + b)
Если известны периметр и одна из сторон прямоугольника, другую находим по формуле:
a = (P — 2b) / 2
b = (P — 2a) / 2
Р — периметр, a — длина, b — ширина прямоугольника
Т.е. сторона прямоугольника равняется половине разности между периметром и удвоенной другой стороной.
Расчет стороны прямоугольника через площадь и сторону
Чтобы рассчитать площадь прямоугольника (S), необходимо его длину а умножить на ширину b:
S = аb
Если известна площадь прямоугольника и одна из его сторон, длину другой находим путем деления площади на длину известной стороны:
a = S / b
b = S / a
где S — площадь прямоугольника, a, b — его стороны.
