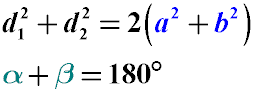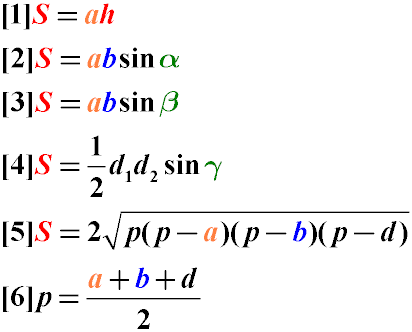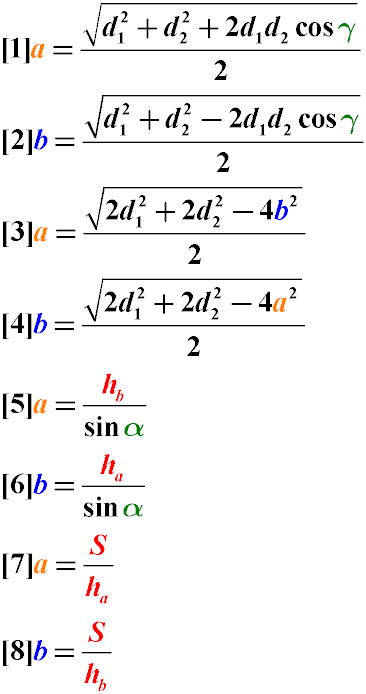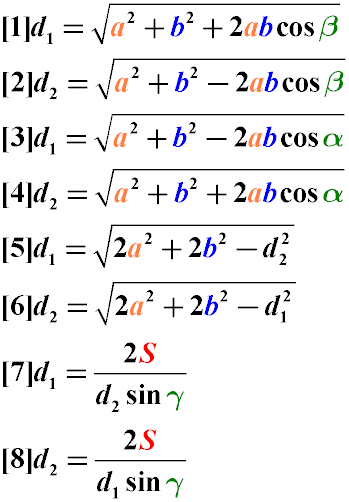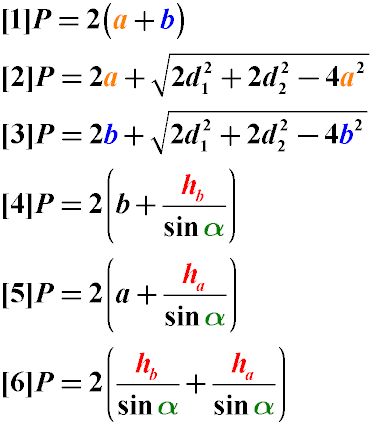Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
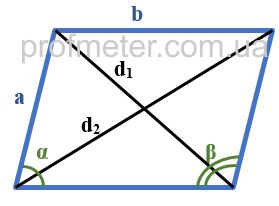
1. Формулы длины сторон через диагонали и угол между ними.
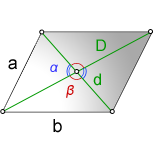
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α, β – углы между диагоналями
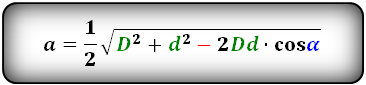
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):

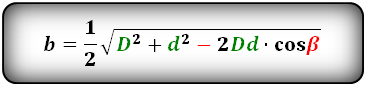
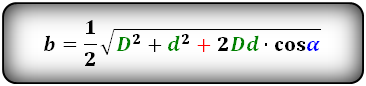
Формулы сторон параллелограмма через диагонали и сторону, (a, b):
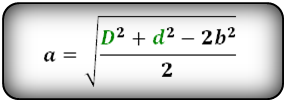
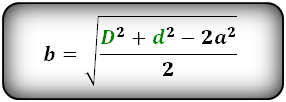
Формулы сторон параллелограмма , (a, b):

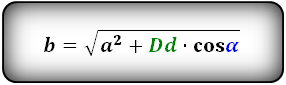
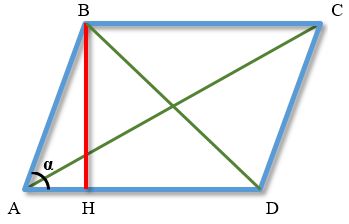
2. Формулы длины сторон параллелограмма через высоту.
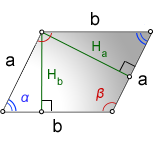
a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
α, β – углы параллелограмма
Формулы сторон параллелограмма через высоту, (a, b):
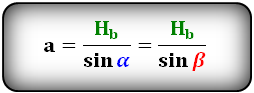
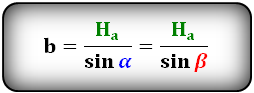
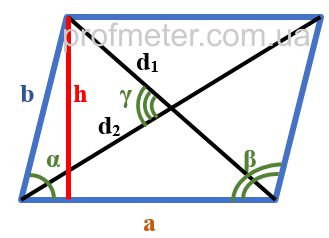
3. Дополнительные, интересные формулы параллелограмма:
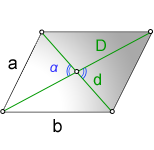
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол между диагоналями
Формула суммы квадратов диагоналей:
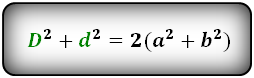
Формула разности квадратов сторон:
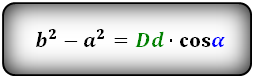
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 31 октября 2011
-
Обновлено: 13 августа 2021
Параллелограмм
- Высота
- Площадь
Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Если у параллелограмма все углы прямые, то такой параллелограмм называется прямоугольником, а прямоугольник, у которого все стороны равны, называется квадратом.
Все параллелограммы обладают следующими свойствами:

- противоположные стороны равны:
AB = CD и BC = DA;
- противолежащие углы равны:
∠ABC = ∠CDA и ∠DAB = ∠BCD;
- сумма углов, прилежащих к одной стороне, равна 180°:
∠ABC + ∠BCD = 180°,
∠BCD + ∠CDA = 180°,
∠CDA + ∠DAB = 180°,
∠DAB + ∠ABC = 180°;
- в точке пересечения диагонали делятся пополам:
AO = OC и BO = OD;
- каждая диагональ делит параллелограмм на два равных треугольника:
ΔABC = ΔCDA и ΔABD = ΔBCD;
- точка пересечения диагоналей — это центр симметрии параллелограмма:
Точка O — это центр симметрии.
Высота
Нижняя сторона параллелограмма называется его основанием, а перпендикуляр, опущенный на основание из любой точки противоположной стороны, — высотой.

AD — это основание параллелограмма, h — высота.
Высота выражает расстояние между противоположными сторонами, поэтому определение высоты можно сформулировать ещё так: высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны на противоположную ей сторону.
Площадь
Для измерения площади параллелограмма можно представить его в виде прямоугольника. Рассмотрим параллелограмм ABCD:

Построенные высоты BE и CF образуют прямоугольник EBCF и два треугольника: ΔABE и ΔDCF. Параллелограмм ABCD состоит из четырёхугольника EBCD и треугольника ABE, прямоугольник EBCF состоит из того же четырёхугольника и треугольника DCF. Треугольники ABE и DCF равны (по четвёртому признаку равенства прямоугольных треугольников), значит и площади прямоугольника с параллелограммом равны, так как они составлены из равных частей.
Итак, параллелограмм можно представить в виде прямоугольника, имеющего такое же основание и высоту. А так как для нахождения площади прямоугольника перемножаются длины основания и высоты, значит и для нахождения площади параллелограмма нужно поступить также:
площадь ABCD = AD · BE.
Из данного примера можно сделать вывод, что площадь параллелограмма равна произведению его основания на высоту.
Общая формула площади параллелограмма:
S = ah,
где S — это площадь параллелограмма, a — основание, h — высота.
Основание параллелограмма — это сторона, к которой можно
провести перпендикуляр из точки, лежащей на противоположной стороне.
У каждого параллелограмма только два основания. От любой
точки, лежащей на основании параллелограмма, можно провести
перпендикуляр только к одной точке на противоположной стороне.
Так, как у параллелограмма два основания, соответственно
перпендикуляры, которые проведены из любого основания,
оканчиваются на противоположном основании.
В параллелограмме все перпендикуляры,
имеют начало и конец на двух основаниях.
Площадь параллелограмма рассчитывается через
основание параллелограмма (a) и его высоту (h):
[ S = ah ]
Основания у параллелограмма параллельны
друг другу и не имеют общих точек.
Если отрезок можно провести из вершины параллелограмма
к его основанию, под углом 90 градусов, то этот отрезок разделит
параллелограмм на две геометрические фигуры — треугольник
и прямоугольную трапецию. Два отрезка уже разделят параллелограмм
на два треугольника и прямоугольник между ними.
Каждое основание параллелограмма имеет две общие точки с
двумя сторонами, которые не являются основаниями.
Как найти основание параллелограмма? Основание легко
найти, зная формулу площади параллелограмма. Исходя из
этой формулы, формула основания следующая:
[ a = frac{S}{h} ]
a — основание
S — площадь
h — высота
Углы, которые прилежат к любому из оснований,
составляют в сумме 180 градусов.
Опубликована отличная статья про признаки параллелограмма.
| Учебный курс | Решаем задачи по геометрии |
|
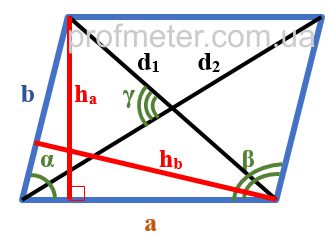
Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. Как выглядит параллелограмм На приведенном рисунке параллелограмм обозначен синими линиями. Элементы параллелограмма, указанные на рисунке: Свойства параллелограмма
Признаки параллелограммаЧетырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:
Как найти площадь параллелограмма
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Как найти периметр параллелограмма
Задачи с решениями про параллелограмм смотрите в уроках ниже:
Трапеция, описанная вокруг окружности | Описание курса | Параллелограмм. Задачи про площадь и стороны |
Обсудить на форуме
Записаться на курсы
Обратиться к консультанту
Пройти тест
Полный список курсов обучения
Бесплатные видеоуроки
Нужна информация!
Параллелограммом называют четырёхугольный многоугольник, две соседние стороны которого равны и
параллельны противоположным. Помимо этого, есть ещё несколько важных условий определения фигуры как
параллелограмма:
- В месте пересечения диагонали делятся пополам, а точка, в которой пересекаются диагонали,
является одновременно центром этих двух отрезков. При этом она всегда лежит внутри фигуры. - Любая диагональ данного четырёхугольника разделяет его на одинаковые треугольники, так как
проходит из одной вершины к противоположной, то есть по центру четырёхугольника. - Сумма квадратов сторон равна сумме квадратов диагоналей.
- Углы фигуры, расположенные друг напротив друга, попарно равны. Это условие вытекает из
утверждения, что параллельные стороны фигуры равны. - Сумма двух односторонних углов равна 180°. Это условие напрямую связано с теоремой о двух
параллельных прямых и секущей. И действительно, если рассматривать две противоположные и третью
между ними стороны параллелограмма как две параллельные прямые и секущую, то можно заметить, что
углы, принадлежащие одной стороне, будут соответствовать односторонним углам, сумма которых,
согласно теореме, равна 180°.
Только при выполнении всех условий четырёхугольный многоугольник будет считаться
параллелограммом.
- Длинная сторона параллелограмма через две диагонали и
острый угол между ними - Длинная сторона параллелограмма через две диагонали и тупой
угол между ними - Короткая сторона параллелограмма через две диагонали и
острый угол между ними - Короткая сторона параллелограмма через две диагонали и
тупой угол между ними - Сторона параллелограмма через две диагонали и другую
известную сторону - Сторона параллелограмма через высоту и синус угла
- Сторона параллелограмма через площадь и высоту
Нахождение длинной стороны через две диагонали и острый угол между ними
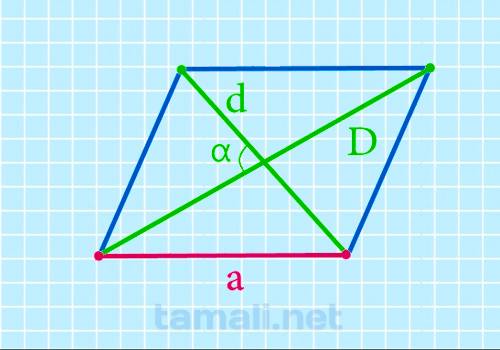
Длинную сторону параллелограмма можно найти, зная обе диагонали и острый угол между ними, по
формуле:
a = (√(D² + d² — 2 (D * d) * cosα)) / 2
где D – длинная диагональ, d – короткая диагональ, α — острый угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Допустим, дан параллелограмм, у которого диагонали 7 и 4 см, а угол между
ними 68º. Тогда, согласно формуле, сторона будет равна: a = (√(7² + 4² — 2 (7 * 4) * cos68º)) / 2 = 3,317 см. Ответ:
3,317 см.
Нахождение короткой стороны через две диагонали и острый угол между ними
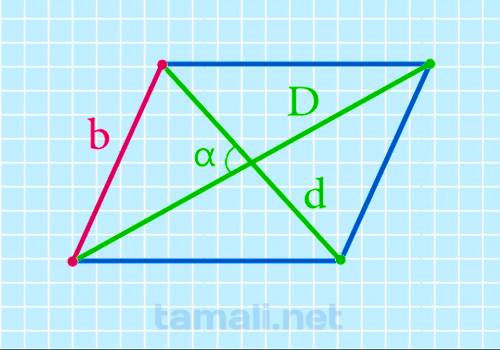
Можно вычислить и короткую сторону по формуле:
b = (√(D² + d² + 2 (D * d) * cosα)) / 2
где D – длинная диагональ, d – короткая диагональ, α — острый угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Теперь необходимо найти другую сторону параллелограмма. Данные останутся те
же, что и в прошлой задаче, но в уравнении поменяется знак, так как по отношению к углу поменялась
сторона, которую надо найти. Сторона b будет равна: b = (√(7² + 4² + 2 (7 * 4) * cos68º)) / 2 = 4.64.
Ответ: 4,64 см.
Нахождение длинной стороны через две диагонали и тупой угол между ними
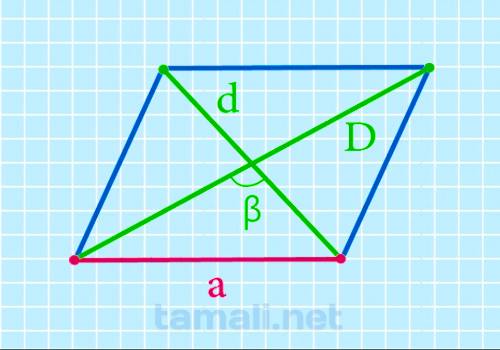
Стороны параллелограмма можно найти, зная диагонали и тупой угол между ними. Для этого нужно
использовать следующую формулу:
a = (√(D² + d² + 2 (D * d) * cosβ)) / 2
где D – длинная диагональ, d – короткая диагональ, β — тупой угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим нахождение сторон всё того же параллелограмма с диагоналями 7 и 4
см. Однако на этот раз возьмём между диагоналями другой угол: β=112º. В таком случае для стороны a
минус меняется на плюс, а сама сторона равна: a = (√(7² + 4² + 2 (7 * 4) * cos112º)) / 2 = 3.914
Нахождение короткой стороны через две диагонали и тупой угол между ними
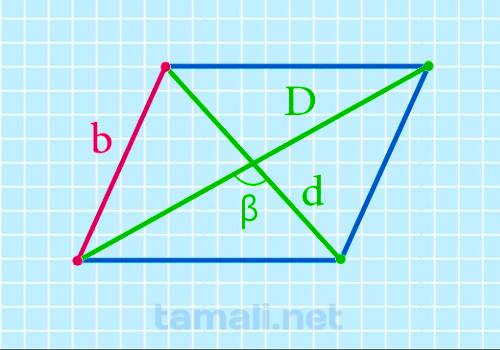
Аналогично можно найти и короткую сторону, зная диагонали и тупой угол между ними:
b = (√(D² + d² — 2 (D * d) * cosβ)) / 2
где D – длинная диагональ, d – короткая диагональ, β — тупой угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Для стороны b так же изменится знак в формуле, но наоборот: плюс на минус. Тогда
получается: b = (√(7² + 4² — 2 (7 * 4) * cos112)) / 2 = 4,64 см. Ответ совпал с ответом второй
задачи, все опять решено верно, а сторона в воображаемом параллелограмме действительно равна 4,64
см.
Нахождение стороны параллелограмма через диагонали и другую сторону
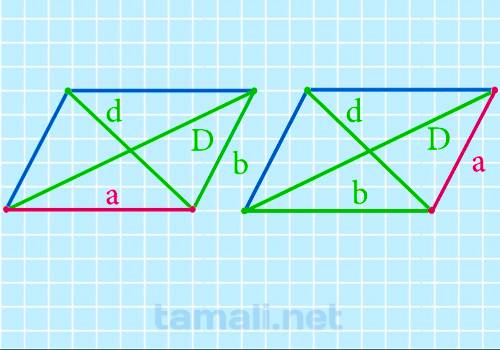
Как и в случае с прошлыми пунктами, существуют формула, которая позволяет найти сторону
параллелограмма с использованием диагоналей и известной стороны. Вот она:
a = √(D² + d² — 2b² / 2)
где D, d — диагонали, b — сторона.
Цифр после
запятой:
Результат в:
Выводится данная формулы из первого следствия теоремы косинусов.
Пример. Используем для следующих задач другой параллелограмм. Эта фигура будет с
диагоналями 9 и 5 см и стороной 6 см. Тогда другая сторона данного параллелограмма равна: a = √(9² + 5² — 2 * 6² / 2) = 4,1 см. Ответ: 4,1 см.
Для проверки ответа можем решить обратную задачу, при которой нам не известна сторона b, но известна
сторона a = 4,1 см. По обратной формуле получается b = √(9² + 5² — 2 * 4,1² / 2) = 6 см. Ответ
совпадает с изначальными данными первой задачи. А значит и этот воображаемый параллелограмм
действительно существует.
Нахождение стороны через синус угла и высоту
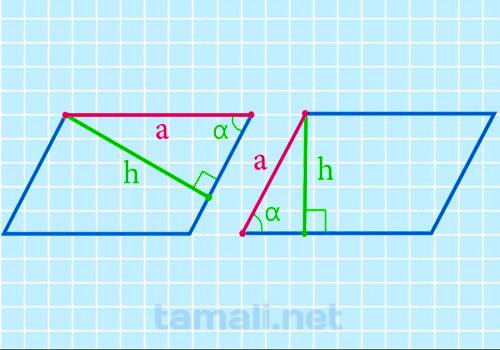
Высота – это отрезок, опущенный перпендикулярно из вершины фигуры на противоположную сторону. Есть
несколько интересных свойств у неё. Например, высоты, проведенные из острых углов, будут всегда
лежать вне фигуры, в то время как высоты из тупых углов всегда лежат внутри. Если из одного угла
опустить две высоты, то между ними образуется угол, равный смежному углу параллелограмма. Равными
будут те высоты, что заключены между параллельными сторонами четырёхугольника. Найти сторону
параллелограмма через эту величину достаточно просто, по формуле:
a = h / sinα
где: h — высота параллелограмма, sin α — угол.
Цифр после
запятой:
Результат в:
Стоит заметить, что высота должна быть опущена не к искомой стороне, а к соседней. При этом для
формулы сойдет синус любого известного угла параллелограмма.
Пример. Найти сторону параллелограмма, если высота, опущенная на соседнюю сторону
равна 10 см, а острый угол — 30º. Решение: a=10 / 0,5 = 20 см
Нахождение стороны через площадь и высоту
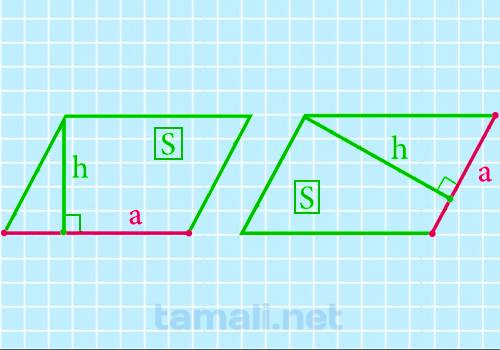
Более подробно о площади и высоте параллелограмма рассказано в пунктах выше. В этом достаточно легко
вывести единственную формулу, по которой можно найти сторону. Если площадь является произведением
стороны на высоту, то сторона будет равна отношению площади к высоте:
a = S / h
где S — площадь параллелограмма, h — высота.
Цифр после
запятой:
Результат в:
Причем не имеет значения, к какой стороне опущена высота: к искомой или соседней.
Пример. Найти сторону параллелограмма, если его площадь равна 20 см, а высота,
опущенная на одну из сторон — 5 см. Решение: a = 20 / 5 = 4 см.
Фигура кажется сложной для восприятия из-за того, что её нельзя постоянно наблюдать где-то в
повседневной жизни. Однако всё становится проще, если вспомнить, что есть более известные широкой
публике частные случаи параллелограмма. Их-то человек обычно наблюдает ежедневно. Это ромб,
прямоугольник и квадрат. Причем последний, хоть и наиболее известен, является и наиболее
интересным.
Ромб считается частным случаем, потому что представляет собой параллелограмм, диагонали которого в
точке пересечения образуют прямой угол. Прямоугольник является частным случаем, потому что это
параллелограмм, у которого все углы прямые. У квадрата же положение ещё интереснее, так как его
можно назвать не только частным случаем параллелограмма, но и прямоугольника, и ромба. Квадрат – это
комбо трёх предыдущих определений. Можно даже сказать, что квадрат одновременно является особенным
случаем и для параллелограмма, и для прямоугольника, и для ромба. Все его стороны равны,
противоположные стороны параллельны. Все углы являются прямыми, даже образующиеся при пересечении
диагоналей, которые к тому же делятся пополам в точке пересечения.