Виды экстремумов.
-
Локальный
экстремум
– это точка, в которой достигается
наибольшее (или наименьшее) значение
функции в НЕКОТОРОЙ (сколь угодно малой)
ОКРЕСТНОСТИ данной точки. -
Условный
экстремум
– это точка, в которой достигается
наибольшее (или наименьшее) значение
функции, при некотором УСЛОВИИ на
переменную.
(условный
экстремум, так же, как и обычный, может
быть локальным и глобальным).
-
Локальный
условный экстремум
– это точка, в которой достигается
наибольшее (или наименьшее) значение
функции в НЕКОТОРОЙ (сколь угодно малой)
ОКРЕСТНОСТИ данной точки, НА МНОЖЕСТВЕ,
удовлетворяющем условию связи. -
Глобальный
условный экстремум
– это точка, в которой достигается
наибольшее (или наименьшее) значение
функции НА ВСЁМ МНОЖЕСТВЕ, удовлетворяющем
условию связи.
Экстремум в Математическом анализе.
a)
Монотонность функции:
Функция

называется возрастающей на промежутке

,
если

для любых точек

и

из промежутка
,
удовлетворяющих неравенству
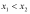
.
Функция называется убывающей на
,
если из условия
следует

.
Теорема.
Если функция

непрерывна на отрезке

,
дифференцируема на интервале

,
то для того, чтобы

была возрастающей (убывающей) необходимо
и достаточно, чтобы

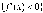
в каждой внутренней точке интервала
.
Дифференцируемая
функция является возрастающей на
промежутке
тогда и только тогда, когда

.
Пример.
Найти промежутки возрастания и убывания
функции

.
Вычислим:

:

.
Точки

делят числовую прямую

на три интервала:

.
Производная
положительна на интервалах
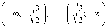
.
Следовательно, функция

возрастает на каждом из этих интервалов.
На интервале
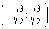
производная
неположительная, значит,
убывает на этом интервале.
б)
Локальный экстремум:
Точка

называется точкой локального максимума
функции
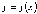
,
если существует интервал

,
содержащий точку
такой что

.
Точка
называется точкой локального минимума
функции
,
если существует интервал
,
содержащий точку
такой что
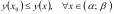
.
Точки
локального минимума и локального
максимума называются точками локального
экстремума.
Необходимым
условием локального экстремума
дифференцируемой функции является
выполнение равенства

.
Поэтому точки, в которых дифференцируемая
функция может иметь локальный экстремум,
находят, решая уравнение:
Решения
этого уравнения называют стационарными
точками.
в)
Исследование стационарных точек:
I
правило.
Если при возрастании

при переходе через стационарную точку
производная
меняет знак с + на , то
точка локального максимума. Если
меняет знак с на + , то

точка локального минимума функции

.
Если

не меняет знак в точке
,
то экстремума нет.
II
правило.
Если вторая производная

в стационарной точке
положительная, то
точка локального минимума функции
.
Если вторая производная
в стационарной точке
отрицательная, то
точка локального максимума функции
.
Точками
локального экстремума функции могут
быть такие точки, в которых производная
не существует или обращается в
бесконечность. Исследовать такие точки
можно по I правилу. Экстремум в такой
точке называется острым экстремумом.
Пример.
Найти экстремум функции

.

.
Функция
имеет стационарную точку

(в этой точке производная равна нулю).
В точке

производная обращается в бесконечность.
Поскольку

при

и

при

,
то функция имеет в точке
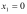
локальный минимум

.
Это будет острый минимум.
При
переходе через стационарную точку


производная меняет знак с на +, значит,
функция имеет локальный максимум.
г)
Глобальный экстремум
Непрерывная
на отрезке

функция

принимает свое наибольшее значение

и свое наименьшее значение

в точках этого отрезка. Эти значения
могут достигаться либо в стационарных
точках отрезка, либо в точках
недифференцируемости функции, либо в
граничных точках отрезка. Поэтому для
нахождения значений
и
поступают следующим образом.
-
Находят
стационарные точки
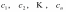
функции;
-
Находят
точки

,
в которых производная

не существует или обращается в
бесконечность; -
Вычисляют
значения:

и
выбирают среди этих чисел наибольшее
и наименьшее.
Это
и будут
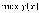
и

глобальные экстремальные значения.
Пример.
Найти наибольшее и наименьшее значения
функции
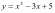
на отрезке

.

;

.
Вычисляем

.
Получаем числа

.
Следовательно,

,
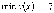
.
Исследование
функции и построение графика.
График
функции

,
заданной на множестве

,
т.е. множество точек плоскости с
координатами

,
обычно строят с некоторой степенью
приближения, так как точное построение
невозможно.
Для
построения графика функции

выясняют особенности поведения функции.
Существенную роль при этом играют
характерные точки: концевые точки
промежутков задания функции, точки
разрыва, стационарные точки и точки
недифференцируемости функции и ее
производной и т.д. По этим точкам
выделяются участки однообразного
поведения функции, а именно: промежутки
ее непрерывности; промежутки, на которых

и

сохраняют знак, что позволяет изучить
характер монотонности функции и
направление ее выпуклости.
Построение
графика функции может быть осуществлено
по следующему плану:
Если
функция задана аналитическими выражениями,
то выясняют естественную область
определения функции, т.е. множество
значений аргумента

,
при которых

имеет смысл.
Если
функция периодическая, то находят ее
период, т.е. число

такое, что

,

(обычно рассматривают наименьший
положительный период). Дальнейшее
изучение функции и построение графика
проводят для какого-либо отрезка длины
,
например, для

,
а затем периодически продолжают.
Для
четной функции:

,
или нечетной:

.
Исследование проводят на промежутке

.
Построенный график продолжают на все
множество

,
используя симметричное отражение
относительно оси
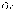
для четной функции и относительно точки

для нечетной функции.
Находят
точки разрыва и промежутки, на которых
она непрерывна. Выясняют характер точек
разрыва. Вычисляют предельные значения
функции в граничных точках множества
(если таковые имеются). Находят вертикальные
асимптоты (в точках бесконечного скачка).
Если
не ограничено, то вычисляют пределы
функции при

и

.
Если
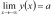
,
то график имеет горизонтальную
левостороннюю асимптоту

,
если

,
график имеет горизонтальную правостороннюю
асимптоту

.
Если пределы (или один из пределов)
бесконечны, то график может иметь
наклонные (левостороннюю и правостороннюю)
асимптоты

.
Коэффициенты левосторонней асимптоты
можно найти по формулам:

Аналогично
находят коэффициенты правосторонней
асимптоты (нужно вычислить пределы при

).
Вычисляют
производную

.
Находят критические точки функции
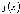
,
т.е. стационарные точки и точки, в которых

не существует. Выделяют промежутки, на
которых
сохраняет знак. Это позволяет исследовать
монотонность функции
.
Вычисляют
вторую производную

.
Находят критические точки производной
.
Выделяют промежутки, на которых
сохраняет знак, и, следовательно, график
функции
сохраняет направление выпуклости.
Находят точки перегиба, исследуя
критические точки производной
(т.е. точки, в которых
равны нулю или не существуют).
Исследуя
стационарные точки функции
,
находят точки локального экстремума и
локальные экстремальные значения
функции. Для этого можно изучить поведение
производной
в окрестности стационарной точки или
значение
в стационарной точке. Изучают точки
недифференцируемости функции, выясняя
наличие локальных экстремумов в таких
точках по поведению производной
в их окрестностях.
Опираясь
на характерные точки функции, строят
таблицу, в которую вносят все особенности
функции.
На
координатную плоскость в выбранном
масштабе наносят характерные точки
функции, асимптоты и строят график,
руководствуясь п. 16. Если нужно, строят
дополнительно несколько точек графика.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Исследование функций с помощью производных
Необходимое условие возрастания и убывания функции
Из определений возрастающей и убывающей функций следует необходимое условие возрастания и убывания функции.
Теорема: Если дифференцируемая функция 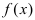
Доказательство: Пусть дифференцируемая функция 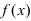 возрастает на сегменте
возрастает на сегменте 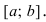 Возьмем произвольную точку
Возьмем произвольную точку 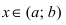 и дадим ей приращение
и дадим ей приращение 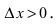 Тогда в силу возрастания функции ее приращение
Тогда в силу возрастания функции ее приращение 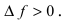 Отсюда следует,что величина
Отсюда следует,что величина 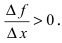 Совершая предельный переход в этом неравенстве при
Совершая предельный переход в этом неравенстве при 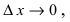 получим
получим 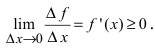 Аналогично теорема доказывается в случае, когда функция
Аналогично теорема доказывается в случае, когда функция 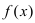 убывает на сегменте
убывает на сегменте 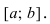
Замечание: С геометрической точки зрения возрастающая на сегменте 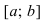 функция
функция 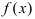 в каждой точке своего графика характеризуется касательной, которая образует с положительным направлением оси абсцисс острый угол. Если функция
в каждой точке своего графика характеризуется касательной, которая образует с положительным направлением оси абсцисс острый угол. Если функция 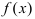 убывает на сегменте
убывает на сегменте 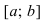 , то касательная образует с положительным направлением оси абсцисс тупой угол.
, то касательная образует с положительным направлением оси абсцисс тупой угол.
Пример:
Найти интервалы возрастания и убывания функции 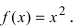
Решение:
Из графика этой функции видно, что 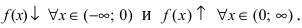 Согласно необходимому признаку возрастания и убывания функции
Согласно необходимому признаку возрастания и убывания функции 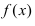 вычислим ее первую производную:
вычислим ее первую производную: 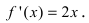 Эта производная будет отрицательной
Эта производная будет отрицательной 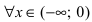 положительной
положительной 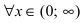 величиной. Следовательно, в полном соответствии с графиком функции
величиной. Следовательно, в полном соответствии с графиком функции 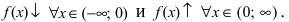
Достаточное условие возрастания и убывания функции
Теорема: Пусть функция 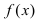 непрерывна на сегменте
непрерывна на сегменте 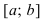 и дифференцируема на интервале
и дифференцируема на интервале 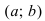 . Если ее первая производная
. Если ее первая производная 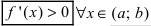 то функция возрастает на сегменте
то функция возрастает на сегменте 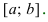 Если ее первая производная
Если ее первая производная 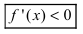
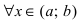 , то функция убывает на сегменте
, то функция убывает на сегменте 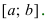
Доказательство: Пусть первая производная функции 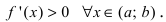 Возьмем из этого интервала две любые точки
Возьмем из этого интервала две любые точки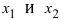 (для определенности примем, что
(для определенности примем, что 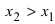 ). Тогда по теореме Лагранжа (см. Лекцию № 19) на интервале
). Тогда по теореме Лагранжа (см. Лекцию № 19) на интервале 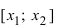 найдется хотя бы одна точка х такая, что
найдется хотя бы одна точка х такая, что 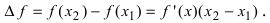 Так как на интервале
Так как на интервале 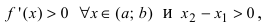 следовательно,
следовательно, 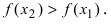
Таким образом, функция 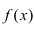 возрастает на сегменте
возрастает на сегменте 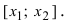 В силу произвольности выбранных точек
В силу произвольности выбранных точек 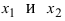 полученное утверждение справедливо для всего сегмента
полученное утверждение справедливо для всего сегмента 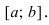 Достаточное условие убывания функции
Достаточное условие убывания функции 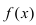 на сегменте
на сегменте 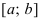 доказать самостоятельно.
доказать самостоятельно.
Условия постоянства функции на сегменте (a; b)
Условия постоянства функции на сегменте 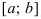 .
.
ТЗ. Пусть функция 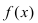 непрерывна на сегменте
непрерывна на сегменте 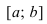 и дифференцируема на интервале
и дифференцируема на интервале 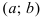 . Если ее первая производная
. Если ее первая производная 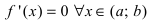 , то функция постоянна на сегменте
, то функция постоянна на сегменте 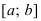 .
.
Доказательство: Пусть первая производная функции 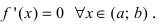 Возьмем произвольную точку
Возьмем произвольную точку 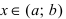 и рассмотрим сегмент
и рассмотрим сегмент 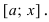 На этом сегменте выполняются все условия теоремы Лагранжа, следовательно,
На этом сегменте выполняются все условия теоремы Лагранжа, следовательно, 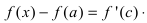
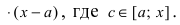 Так как по условию теоремы
Так как по условию теоремы 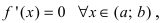 то и в точке с первая производная функции обращается в нуль. Отсюда получаем,что
то и в точке с первая производная функции обращается в нуль. Отсюда получаем,что 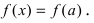 В силу произвольности точки х полученное равенство выполняется
В силу произвольности точки х полученное равенство выполняется 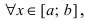 т.е. функция постоянна на сегменте
т.е. функция постоянна на сегменте 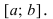
Минимум и максимум (экстремумы) функции
Пусть функция 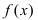 непрерывна в точке
непрерывна в точке 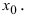
Определение: Функция 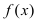 имеет в точке
имеет в точке 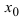 минимум (min), если существует такая
минимум (min), если существует такая 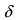 -окрестность точки
-окрестность точки 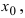 что
что 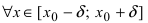 значение функции в любой другой точке
значение функции в любой другой точке 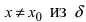 -окрестность точки
-окрестность точки  превышает значение функции в самой точке
превышает значение функции в самой точке 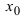 , т.е. выполняется неравенство
, т.е. выполняется неравенство 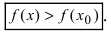
Обозначение 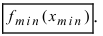
Определение: Функция 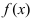 имеет в точке
имеет в точке 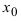 максимум (max), если существует такая
максимум (max), если существует такая 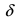 -окрестность точки
-окрестность точки 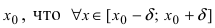 значение функции в любой другой точке
значение функции в любой другой точке 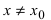 из
из 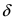 -окрестность точки х0
-окрестность точки х0 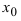 меньше значения функции в самой точке
меньше значения функции в самой точке 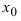 , т.е. выполняется неравенство
, т.е. выполняется неравенство 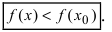
Обозначение 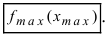
Пример:
Найти на заданном графике точки максимума и минимума (Рис. 77). 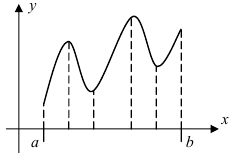
Рис. 77. Максимумы и минимумы заданной функции.
Решение:
Определение: Точки минимума и максимума объединяются под общим названием точки экстремума.
Замечание: Точки экстремума всегда являются внутренними точками области определения функции.
Замечание: Не следует путать минимальное значение функции 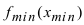 с наименьшим значением функции на сегменте
с наименьшим значением функции на сегменте 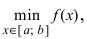 а максимальное значение функции
а максимальное значение функции 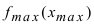 – с наибольшим значением функции на сегмен- те
– с наибольшим значением функции на сегмен- те 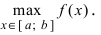
Замечание: Из определения экстремума следует, что в точке минимума выполняется неравенство 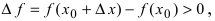 а в точке максимума –
а в точке максимума – 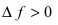 в некоторой малой
в некоторой малой 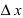 -окрестности точки
-окрестности точки 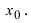
Необходимое условие существования экстремума функции
Теорема: Если дифференцируемая функция 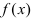 имеет в точке
имеет в точке 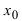 экстремум, то ее первая производная в этой точке равна нулю, т.е.
экстремум, то ее первая производная в этой точке равна нулю, т.е. 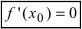
Доказательство: Пусть в точке 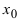 функция
функция 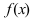 имеет максимум. Так как функция
имеет максимум. Так как функция 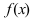 дифференцируема в точке
дифференцируема в точке 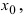 то в этой точке существует ее первая производная
то в этой точке существует ее первая производная 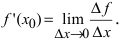 При стремлении
При стремлении 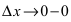 (слева) приращение аргумента
(слева) приращение аргумента 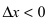 , а приращение функции
, а приращение функции 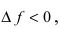 следовательно,
следовательно, 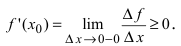 При стремлении
При стремлении 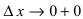 (справа) приращение аргумента
(справа) приращение аргумента 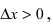 а приращение функции
а приращение функции 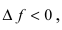 следовательно,
следовательно, 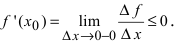 Так как производная в точке
Так как производная в точке 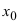 не может одновременно быть и отрицательной и положительной, то в этой точке она равна нулю, т.е.
не может одновременно быть и отрицательной и положительной, то в этой точке она равна нулю, т.е.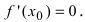 Случай, когда в точке х0
Случай, когда в точке х0 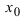 наблюдается минимум, доказать самостоятельно.
наблюдается минимум, доказать самостоятельно.
Замечание: Обращение в нуль первой производной функции в точке х0 я взлетел необходимым, но не достаточным условием существования экстремума в этой точке. Непрерывная функция может иметь экстремум в точке х0 даже в том случае, когда ее первая производная в этой точке не существует. В этом случае говорят об “острых” экстремумах.
Пример:
Доказать, что функция 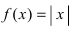 имеет “острый” экстремум в точке
имеет “острый” экстремум в точке 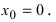
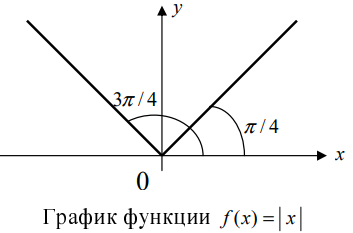
Решение:
Из Рис. 72 видно, что в точке 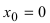 функция определена и непрерывна, одна- ко ее первая производная
функция определена и непрерывна, одна- ко ее первая производная 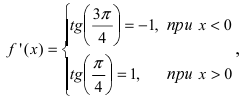 т.е. в точке
т.е. в точке 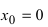 первая производная функции не существует. Однако по графику функции видно, что в точке
первая производная функции не существует. Однако по графику функции видно, что в точке 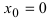 заданная функция имеет “острый” экстремум.
заданная функция имеет “острый” экстремум.
Определение: Точки, в которых первая производная функции обращается в нуль или не существует, называются критическими (стационарными или подозрительными на экстремум).
Замечание: Всякая точка экстремума является критической точкой, однако не любая критическая точка будет экстремумом.
Пример:
Доказать, что функция 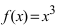 не имеет экстремума в точке
не имеет экстремума в точке 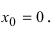
Решение:
В точке 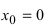 первая производная функции
первая производная функции 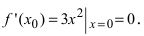 Однако из графика кубической параболы видно (график кубической параболы см. в Лекции № 22), что в точке
Однако из графика кубической параболы видно (график кубической параболы см. в Лекции № 22), что в точке 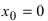 она экстремума не имеет. Следовательно, исследуемая точка является критической точкой, но не точкой экстремума.
она экстремума не имеет. Следовательно, исследуемая точка является критической точкой, но не точкой экстремума.
Исследование функций с помощью производных
Первый и второй достаточные признаки существования экстремума
Первый достаточный признак существования экстремума:
Теорема: Если функция 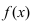 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки
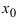 , кроме может быть самой точки
, кроме может быть самой точки 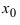 , и при переходе через эту точку слева направо ее первая произвол пая меняет свой знак с “+” на то в точке
, и при переходе через эту точку слева направо ее первая произвол пая меняет свой знак с “+” на то в точке 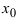 функция
функция 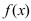 имеет максимум, а если ее первая производная меняет свой знак с на “+”, то в точке
имеет максимум, а если ее первая производная меняет свой знак с на “+”, то в точке 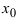 функция
функция 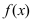 имеет минимум. Если при переходе через точку
имеет минимум. Если при переходе через точку 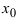 первая производная не меняет свой знак, то в этой точке экстремума нет.
первая производная не меняет свой знак, то в этой точке экстремума нет.
Второй достаточный признак существования экстремума:
Теорема: Если в точке 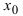 первая производная функции
первая производная функции 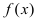 обращается в нуль(
обращается в нуль(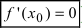 ), а вторая производная существует, непрерывна в некоторой окрестности этой точки и отлична от нуля в самой точке (
), а вторая производная существует, непрерывна в некоторой окрестности этой точки и отлична от нуля в самой точке (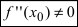 ), то в точке
), то в точке 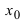 наблюдается экстремум. Если при этом
наблюдается экстремум. Если при этом 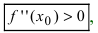 то точка
то точка 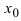 является точкой минимума, а при
является точкой минимума, а при 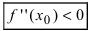 – точкой максимума.
– точкой максимума.
Пример:
Найти и определить тип экстремумов функции 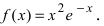
Решение:
Вычислим первую производную функции и приравняем ее к нулю с целью отыскания критических точек: 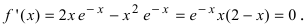 Так как показательная функция
Так как показательная функция 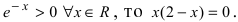 Отсюда находим критические точки
Отсюда находим критические точки 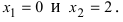 Отложим эти точки на числовой оси и на каждом интервале определим знак первой производной функции, т.е. применим первый достаточный признак существования экстремума:
Отложим эти точки на числовой оси и на каждом интервале определим знак первой производной функции, т.е. применим первый достаточный признак существования экстремума:

При переходе слева направо через точку 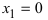 первая производная функция меняет свой знак с “-” на “+,” следовательно, в этой точке наблюдается минимум. При переходе слева направо через точку
первая производная функция меняет свой знак с “-” на “+,” следовательно, в этой точке наблюдается минимум. При переходе слева направо через точку 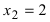 первая производная функция меняет свой знак с “+” на “-” следовательно, в этой точке наблюдается максимум. Применим второй достаточный признак существования экстремума, для чего вычислим вторую производную функции:
первая производная функция меняет свой знак с “+” на “-” следовательно, в этой точке наблюдается максимум. Применим второй достаточный признак существования экстремума, для чего вычислим вторую производную функции: 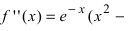
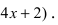 Вычислим значение второй производной функции в точке
Вычислим значение второй производной функции в точке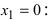
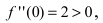 следовательно, в этой точке функция имеет минимум. Вычислим значение второй производной функции в точке
следовательно, в этой точке функция имеет минимум. Вычислим значение второй производной функции в точке 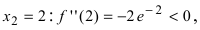 следовательно, в этой точке функция имеет максимум.
следовательно, в этой точке функция имеет максимум.
Наименьшее и наибольшее значения функции на сегменте (a; b)
Наименьшее и наибольшее значения функции на сегменте 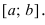
Пусть функция 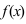 непрерывна на сегменте
непрерывна на сегменте 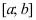 и имеет конечное число точек экстремума на этом интервале. Если наибольшее значение функция достигает внутри сегмента, то очевидно, что это будет один из максимумов (аналогично для наименьшего значения – один из минимумов). Однако возможны варианты, когда функция достигает своих наименьшего и наибольшего значений на концах заданного сегмента. Поэтому для отыскания этих значений применяют следующую схему:
и имеет конечное число точек экстремума на этом интервале. Если наибольшее значение функция достигает внутри сегмента, то очевидно, что это будет один из максимумов (аналогично для наименьшего значения – один из минимумов). Однако возможны варианты, когда функция достигает своих наименьшего и наибольшего значений на концах заданного сегмента. Поэтому для отыскания этих значений применяют следующую схему:
- Находят область определения функции и убеждаются в том, что заданный сегмент входит в эту область.
- Находят критические точки, для чего решают уравнение
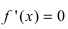 и точки, в которых первая производная функции не существует.
и точки, в которых первая производная функции не существует. - Вычисляют значения функции в критических точках, принадлежащих заданному сегменту, в точках, в которых первая производная функции не существует и на концах заданного сегмента.
- Из полученных чисел выбирают наименьшее
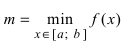 и наибольшее
и наибольшее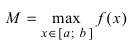 .
.
Пример:
Найти наименьшее и наибольшее значения функции 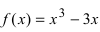 на сегменте
на сегменте 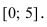
Решение:
Действуя согласно вышеприведенной схеме, находим:
1. 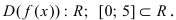 Следовательно, функция определена и непрерывна на заданном сегменте.
Следовательно, функция определена и непрерывна на заданном сегменте.
2. Вычислим первую производную 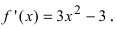 Производная существует на всей числовой оси, поэтому найдем критические точки
Производная существует на всей числовой оси, поэтому найдем критические точки 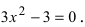 Отсюда на- ходим, что
Отсюда на- ходим, что 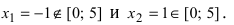
3. Вычислим значение функции в критических точках и на концах заданного сегмента: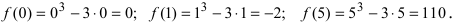
4. Из полученных чисел выбираем наименьшее 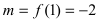 и наибольшее
и наибольшее 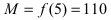 числа, которые определяют наименьшее и наибольшее значения функции
числа, которые определяют наименьшее и наибольшее значения функции 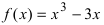 на сегменте
на сегменте 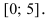
Выпуклость и вогнутость графика функции. Точки перегиба
Определение: График функции 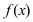 называется выпуклым на интервале
называется выпуклым на интервале 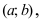 если он лежит ниже любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 78).
если он лежит ниже любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 78). 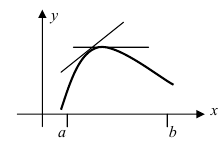
Рис. 78. Выпуклый график функции 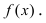
Определение: График функции 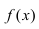 называется вогнутым на интервале
называется вогнутым на интервале 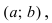 если он лежит выше любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 79).
если он лежит выше любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 79). 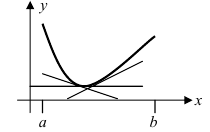
Рис. 79. Вогнутый график функции 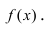
Достаточные условия выпуклости и вогнутости графика функции на том или ином интервале определяются теоремой:
ТЗ. Если вторая производная функции 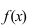 на интервале
на интервале 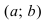 существует и положительна, то на этом интервале график функции
существует и положительна, то на этом интервале график функции 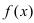 будет вогнутым. Если вторая производная функции
будет вогнутым. Если вторая производная функции 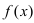 на интервале
на интервале 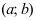 существует и отрицательна, то на этом интервале график функции
существует и отрицательна, то на этом интервале график функции 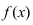 будет выпуклым.
будет выпуклым.
Пример:
Определить интервалы вогнутости и выпуклости графика функции 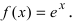
Решение:
Найдем вторую производную от заданной функции 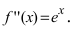 В силу того, что
В силу того, что 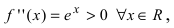 то график функции
то график функции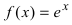 будет вогнутым на всей числовой оси.
будет вогнутым на всей числовой оси.
Пример:
Определить интервалы вогнутости и выпуклости графика функции 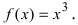
Решение:
Найдем вторую производную от заданной функции 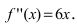 В силу того, что
В силу того, что
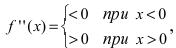 то график функции
то график функции 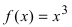 будет выпуклым при отрицательных значениях аргумента и вогнутым при положительных значениях аргумента.
будет выпуклым при отрицательных значениях аргумента и вогнутым при положительных значениях аргумента.
Определение: Точка, отделяющая вогнутую часть графика функции от выпуклой (или выпуклую часть графика функции от вогнутой), называется точкой перегиба.
Необходимое и достаточное условия существования точки перегиба
Рассмотрим необходимое условие существования точки перегиба.
Теорема: Если функция 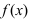 дважды непрерывно дифференцируема на некотором интервале, содержащем точку перегиба
дважды непрерывно дифференцируема на некотором интервале, содержащем точку перегиба 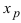 , то в точке перегиба вторая производная равна нулю, т.е.
, то в точке перегиба вторая производная равна нулю, т.е.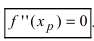
Замечание: Обращение в нуль второй производной функции в точке перегиба является необходимым, но не достаточным условием существования такой точки на графике функции.
Пример:
Доказать, что точка 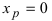 не является точкой перегиба графика функции
не является точкой перегиба графика функции 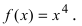
Решение:
Если вычислить вторую производную от заданной функции, то она будет равна 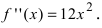 Если приравнять это выражение к нулю, то получим, что точка
Если приравнять это выражение к нулю, то получим, что точка 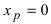 должна быть точкой перегиба графика функции
должна быть точкой перегиба графика функции 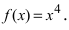 Однако график этой функции (см. Лекцию № 22) на всей числовой оси является вогнутым, т.е. точка
Однако график этой функции (см. Лекцию № 22) на всей числовой оси является вогнутым, т.е. точка 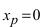 не является точкой перегиба графика функции
не является точкой перегиба графика функции 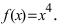
Теорема: Пусть функция 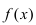 дважды непрерывно дифференцируема на некотором интервале, вторая производная которой в точке
дважды непрерывно дифференцируема на некотором интервале, вторая производная которой в точке 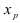 , принадлежащей этому интервалу, обращается в нуль (
, принадлежащей этому интервалу, обращается в нуль (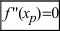 ) или не существует. Если при переходе через точку
) или не существует. Если при переходе через точку 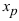 вторая производная функции меняет свой знак, то точка
вторая производная функции меняет свой знак, то точка 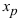 определяет точку перегиба графика функции
определяет точку перегиба графика функции 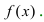
Пример:
Найти точки перегиба и интервалы выпуклости и вогнутости графика функции 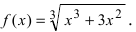
Решение:
Найдем вторую производную заданной функции 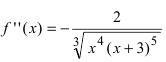 (найти самостоятельно). Найдем точки подозрительные на перегиб: а)
(найти самостоятельно). Найдем точки подозрительные на перегиб: а)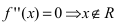 б)
б)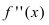 – не существует
– не существует  знаменатель дроби обращается в нуль при
знаменатель дроби обращается в нуль при 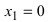 и
и 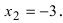 Отложим эти точки на числовой оси и определим знак второй производной на каждом интервале:
Отложим эти точки на числовой оси и определим знак второй производной на каждом интервале:

Из рисунка видно, что точка 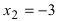 является точкой перегиба, так как при переходе через нее вторая производная изменяет свой знак. Точка
является точкой перегиба, так как при переходе через нее вторая производная изменяет свой знак. Точка 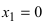 не является точкой перегиба, так как при переходе через нее вторая производная не изменяет своего знака.
не является точкой перегиба, так как при переходе через нее вторая производная не изменяет своего знака.
Асимптоты графика функции f (x)
Асимптоты графика функции 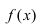
В большинстве практических случаев необходимо знать поведение функции при неограниченном росте (убыли) аргумента. Одним из наиболее интересных случаев, которые возникают при таком исследовании, является случай, когда график функции неограниченно приближается к некоторой прямой.
Определение: Прямая (l): 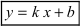 называется асимптотой графика функции
называется асимптотой графика функции 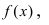 если расстояние от переменной точки графика до этой прямой стремится к нулю при стремлении аргумента
если расстояние от переменной точки графика до этой прямой стремится к нулю при стремлении аргумента 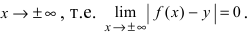
Замечание: График функции может приближаться к асимптоте сверху, снизу, слева, справа или колеблясь возле этой прямой (Рис. 80). 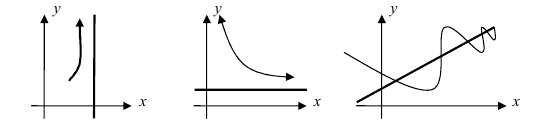
Рис. 80. Различные случаи приближения графика функции к асимптотам.
Различают вертикальные, горизонтальные и наклонные асимптоты.
Определение: Вертикальная прямая 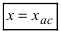 называется вертикальной асимптотой, если
называется вертикальной асимптотой, если 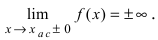 Горизонтальная прямая
Горизонтальная прямая 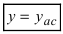 называется горизонтальной асимптотой, если
называется горизонтальной асимптотой, если 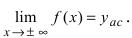 Прямая
Прямая 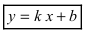 называется наклонной асимптотой (параметр
называется наклонной асимптотой (параметр 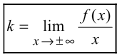 и параметр
и параметр 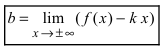 отличаются от
отличаются от 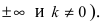
Горизонтальная асимптота является частным случаем наклонной асимптоты: если 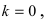 то наклонная асимптота вырождается в горизонтальную
то наклонная асимптота вырождается в горизонтальную 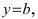 при условии, что
при условии, что 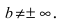 Если параметр
Если параметр 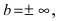 то горизонтальной асимптоты нет.
то горизонтальной асимптоты нет.
Полная схема исследования функции с помощью производных
Из изложенного в Лекциях № 20 и №21 материала следует следующая схема исследования функции с помощью производных:
- Находят область определения функции. При наличии точек разрыва II рода изучают поведение функции в их малой окрестности, т.е. вычисляют лево- и правосторонние пределы. При задании функции словесным образом также вычисляют лево- и правосторонние пределы для граничных точек интервалов, на которых функция описывается разными формулами.
- Находят точки пересечения с координатными осями.
- Определяют четная, нечетная или общего вида заданная функция.
- Определяют периодическая или непериодическая заданная функция.
- Находят критические точки, решая уравнение
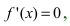 и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания (
и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания (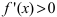 ) и убывания(
) и убывания( 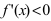 ) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках.
) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках. - Находят точки подозрительные на перегиб, решая уравнение
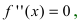 и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости (
и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости (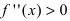 ) и выпуклости (
) и выпуклости (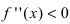 ) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках.
) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках. - Находят асимптоты графика функции.
- Результаты исследования заносят в сводную таблицу
- Поданным таблицы строят схематичный график функции.
Замечание: При нахождении области определения функции надо помнить о действиях, запрещенных в области действительного переменного:
- нельзя делить на нуль, поэтому выражение, стоящее в знаменателе дроби, не должно равняться нулю;
- нельзя извлекать корень четной степени из отрицательного числа, поэтому выражение, стоящее под корнем четной степени, должно быть неотрицательным (
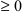 );
); - основание логарифмической функции должно быть строго положительным и не равным единице;
- выражение, стоящее под логарифмом, должно быть строго положительным;
- выражение, стоящее под знаком arcsin или arccos, по модулю не должно превышать единицу (
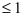 ).
).
Пример:
Исследовать и построить схематичный график функции 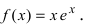
Решение:
Используя схему исследования графика функции с помощью производных, найдем:
1. 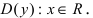
2. Найдем точки пересечения графика функции с координатными осями
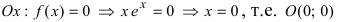 – точка пересечения с осью абсцисс;
– точка пересечения с осью абсцисс;
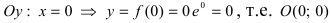 – точка пересечения с осью ординат.
– точка пересечения с осью ординат.
3. Вычислим 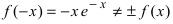 – функция общего вида.
– функция общего вида.
4. Функция непериодическая (периодическими среди элементарных функций являются функции: sinx, cosx, tgx и ctgx).
5. Найдем первую производную функции 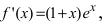 которая существует на всей числовой оси, следовательно, найдем критические точки, решая уравнение
которая существует на всей числовой оси, следовательно, найдем критические точки, решая уравнение 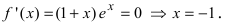 Отложим найденную точку на числовой оси и определим знак первой производной на каждом интервале
Отложим найденную точку на числовой оси и определим знак первой производной на каждом интервале
 Из рисунка видно, что
Из рисунка видно, что 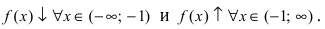 Так как при переходе слева направо через точку х = -1 первая производная меняет свой знак с “-” на “+”, то в точке наблюдается минимум. Вычислим значение функции в минимуме
Так как при переходе слева направо через точку х = -1 первая производная меняет свой знак с “-” на “+”, то в точке наблюдается минимум. Вычислим значение функции в минимуме 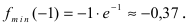
6. Найдем вторую производную функции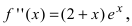 которая существует на всей числовой оси, следовательно, найдем точки, подозрительные на перегиб, решая уравнение
которая существует на всей числовой оси, следовательно, найдем точки, подозрительные на перегиб, решая уравнение 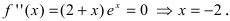 Отложим найденную точку на числовой оси и определим знак второй производной на каждом интервале
Отложим найденную точку на числовой оси и определим знак второй производной на каждом интервале  Из рисунка видно, что
Из рисунка видно, что 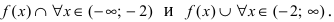 Так как при переходе слева направо через точку х = -2 вторая производная меняет свой знак, то в этой точке наблюдается точка перегиба. Вычислим значение функции в точке перегиба
Так как при переходе слева направо через точку х = -2 вторая производная меняет свой знак, то в этой точке наблюдается точка перегиба. Вычислим значение функции в точке перегиба 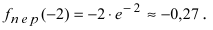
7. Найдем асимптоты графика функции, для чего вычислим угловой коэффициент прямой 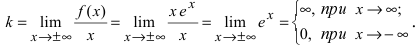 Таким образом, при
Таким образом, при 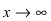 асимптот нет, а при
асимптот нет, а при 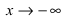 возможна горизонтальная асимптота. Вычислим параметр
возможна горизонтальная асимптота. Вычислим параметр 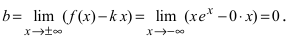 Следовательно, график заданной функции имеет горизонтальную асимптоту у = 0.
Следовательно, график заданной функции имеет горизонтальную асимптоту у = 0.
8. Построим сводную таблицу
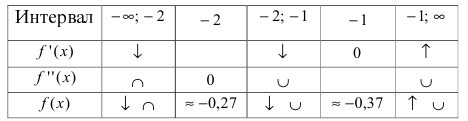
О(0; 0) – точка пересечения с координатными осями.
у = 0 – горизонтальная асимптота.
9. Построим схематичный график функции, выбрав по координатным осям разные масштабы измерения:
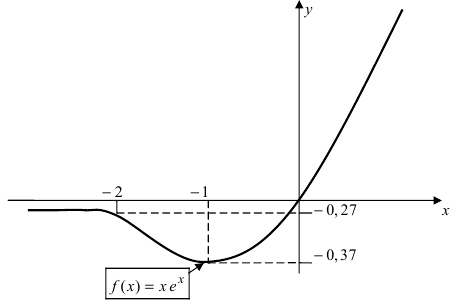
——–
Исследование функций с помощью производных
Определение 1. Функция y=f(x) называется возрастающей (убывающей) на интервале ( a,b ), если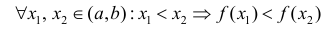
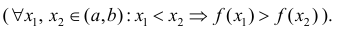
Функция y=f(x) называется неубывающей (невозрастающей) на
интервале ( a,b ), если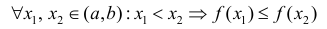
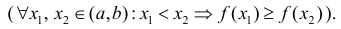
Возрастает:
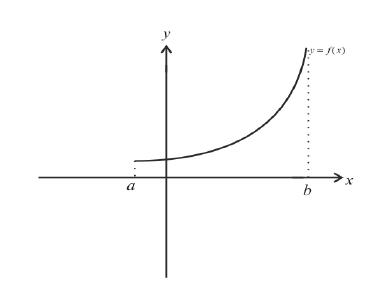
Убывает:
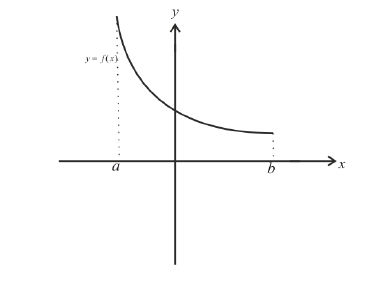
Неубывает:
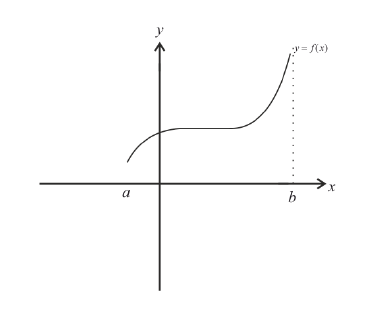
Невозрастает:
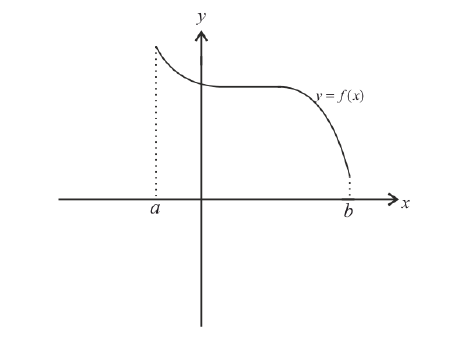
Функции из определения 1 называются монотонными.
Теорема 1. Для того, чтобы дифференцируемая на интервале ( a,b ) функция
y=f(x) не убывала (не возрастала) на этом интервале необходимо и достаточно,
чтобы 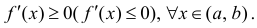
Доказательство. Необходимость. Рассмотрим случай, когда f(x) не
убывает и докажем, что производная 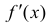 необходимо ≥ 0.
необходимо ≥ 0.
Пусть 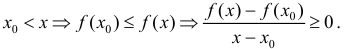
Пусть 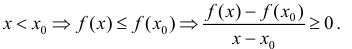
Таким образом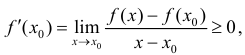 что и требовалось доказать.
что и требовалось доказать.
Достаточность. Рассмотрим случай, когда 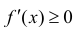 и докажем, что этого достаточно для того, чтобы функция не убывала. Пусть
и докажем, что этого достаточно для того, чтобы функция не убывала. Пусть 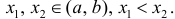
Тогда по теореме Лагранжа (теорема 4 § 12) ∃ точка 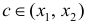 такая, что
такая, что
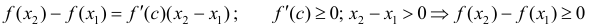 что и требовалось доказать.
что и требовалось доказать.
Теорема 2. Для того, чтобы дифференцируемая на интервале ( a,b ) функция
y=f(x) возрастала (убывала) на этом интервале достаточно, чтобы
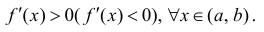 .
.
Доказательство теоремы аналогично доказательству достаточности в теореме 1. Нужно заметить, что условие 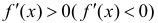 не является необходимым для возрастания (убывания) функции.
не является необходимым для возрастания (убывания) функции.
Пример 1.
Рассмотрим функцию 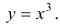 Она возрастает на промежутке ( -1;1). Но условие
Она возрастает на промежутке ( -1;1). Но условие 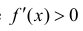 не выполнено в точке
не выполнено в точке 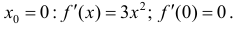
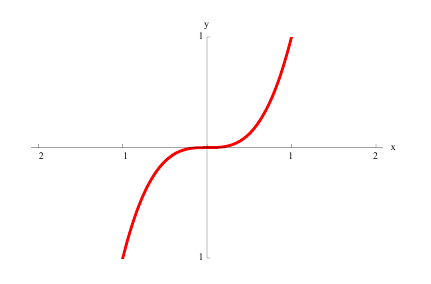
Теорема 3. (необходимое условие экстремума).
Пусть функция y=f(x) определена в некоторой окрестности точки  и имеет в этой точке локальный экстремум (см. определение 1 §12). Тогда ее производная в этой точке равна 0 или не существует.
и имеет в этой точке локальный экстремум (см. определение 1 §12). Тогда ее производная в этой точке равна 0 или не существует.
Доказательство.
Если производная 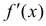 в точке
в точке  не существует, то все доказано. Предположим, что
не существует, то все доказано. Предположим, что 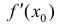 – существует. Тогда по теореме Фермa (теорема 1 §12)
– существует. Тогда по теореме Фермa (теорема 1 §12) 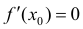 , что и требовалось доказать.
, что и требовалось доказать.
Определение 2. Пусть функция y=f(x) непрерывна в точке  и производная равна 0 или не существует. Тогда точка
и производная равна 0 или не существует. Тогда точка  называется критической точкой для функции y=f(x) или точкой возможного экстремума.
называется критической точкой для функции y=f(x) или точкой возможного экстремума.
Замечание. Для непрерывной функции любая точка локального экстремума
будет критической. Наоборот – не верно.
Пример 2.
Для функции 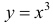 , точка
, точка 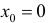 – критическая, но не является точкой локального экстремума.
– критическая, но не является точкой локального экстремума.
Для функции
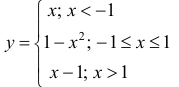
(см. пример 9 §5) 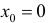 – критическая и локальный максимум;
– критическая и локальный максимум;  =1 критическая и локальный минимум.
=1 критическая и локальный минимум.
Для функции
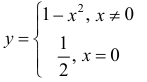
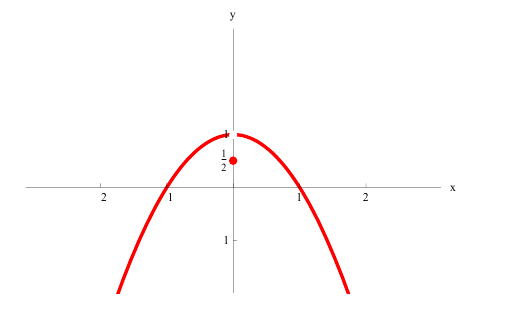
точка 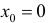 – локального минимума, производная y′ в точке
– локального минимума, производная y′ в точке  не существует. Точка
не существует. Точка  не является критической( в точке
не является критической( в точке  – разрыв 1-ого рода).
– разрыв 1-ого рода).
Для функции
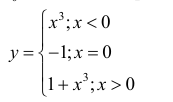
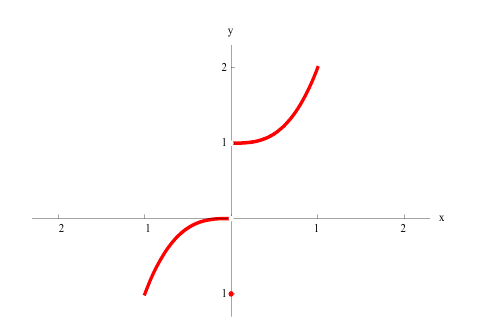
точка  = 0 – точка локального минимума. Точка
= 0 – точка локального минимума. Точка  не является критической( в точке
не является критической( в точке  – разрыв 1-ого рода).
– разрыв 1-ого рода).
Теорема 4. (достаточное условие экстремума функции). Пусть функция y=f(x)
дифференцируема в некоторой окрестности 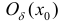 своей критической точки
своей критической точки
 за исключением может быть самой точки
за исключением может быть самой точки  .
.
а) Пусть при переходе через точку  производная
производная 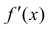 меняет знак с « − »
меняет знак с « − »
на «+» :
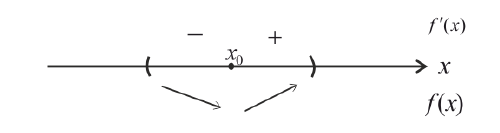
Тогда  – точка локального минимума.
– точка локального минимума.
Пусть при переходе через точку  производная
производная 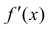 меняет знак с «+» на « − »:
меняет знак с «+» на « − »:
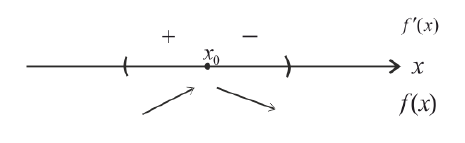
Тогда  – точка локального максимума.
– точка локального максимума.
б) Пусть при переходе через точку  производная
производная 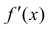 не меняет знака.
не меняет знака.
Тогда  не является точкой локального экстремума.
не является точкой локального экстремума.
Доказательство следует из теоремы 2. При этом важно, чтобы функция y=f(x) была непрерывна в точке  (см. пример 2), а также то, что
(см. пример 2), а также то, что  изолированная критическая точка.
изолированная критическая точка.
Теорема 5. (второе достаточное условие экстремума функции).
Пусть  – стационарная точка для функции y=f(x), то есть
– стационарная точка для функции y=f(x), то есть 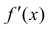 =0.
=0.
Пусть 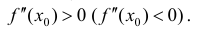 Тогда
Тогда  – точка локального минимума (локального
– точка локального минимума (локального
максимума).
Доказательство. Запишем формулу Тейлора 2-ого порядка для функции y=f(x) в окрестности точки  :
:
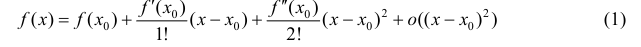
(см. теорему 1 §14).
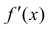 =0, поэтому из (1) следует:
=0, поэтому из (1) следует:
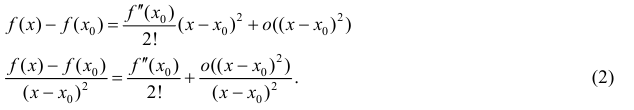
Из (2) следует, что ∃ окрестность точки  , такая что знак
, такая что знак 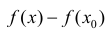 совпадает со знаком
совпадает со знаком 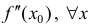 из этой окрестности, что и требовалось доказать.
из этой окрестности, что и требовалось доказать.
Теорема 6. Пусть функция y=f(x) имеет в точке  n производных, причем
n производных, причем
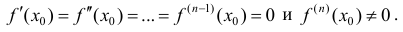 Тогда:
Тогда:
1) если n – четное и 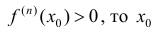 – точка локального минимума;
– точка локального минимума;
2) если n – четное и 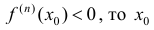 – точка локального максимума;
– точка локального максимума;
3) если n – нечетное, то в точке  локального экстремума нет.
локального экстремума нет.
Доказательство аналогично доказательству теоремы 5.
Пример 3.
Исследовать на экстремум функцию 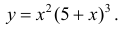
Решение. Функция непрерывна ∀x∈R .
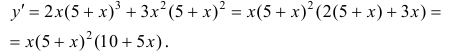
Найдем критические точки: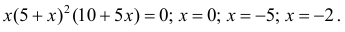
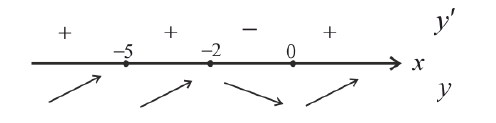
x=-2 – точка локального максимума: y(-2) = 108 y;
x = 0 – точка локального минимума; y(0) = 0.
x = −5 – не является точкой экстремума.
При исследовании функции на экстремум точки разрыва(если они есть)
также наносят на числовую прямую. При переходе через эти точки может
изменятся направление возрастания (убывания) функции.
Замечание. При решении ряда технических и экономических задач приходится находить не локальные, а глобальные экстремумы (наибольшие и наименьшие значения функций на некотором множестве). Из теоремы Вейерштрасса (см. теорему 1 §11) следует, что для непрерывной функции y=f(x) заданной на отрезке [ a,b] глобальные min и max существуют. При этом точки с 1 и с 2 – глобального min и max лежат либо на концах отрезка [ a,b], либо являются критическими для функции f(x).
Пример 4.
Найти наибольшее и наименьшее значение функции 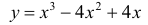 на отрезке [ 0, 3 ].
на отрезке [ 0, 3 ].
Решение. Функция непрерывна ∀x∈R. Найдем критические точки:

Пример 5.
Боковые стороны и меньшее основание трапеции = а . Найти
длину большего основания, при котором площадь трапеции – наибольшая.
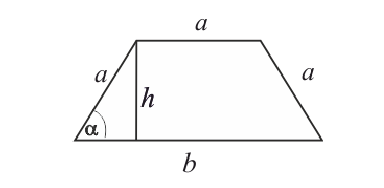
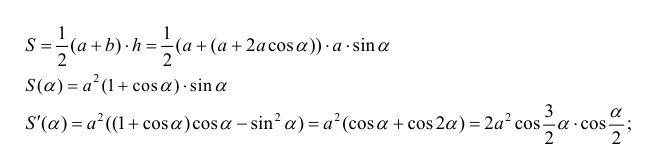
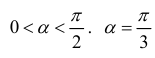 критическая точка для функции S(α).
критическая точка для функции S(α).
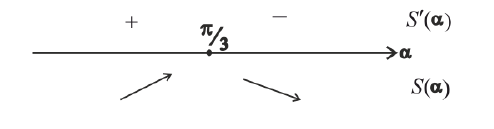
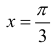 – точка локального максимума.
– точка локального максимума.
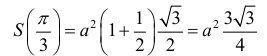 – наибольшее значение площади, при этом
– наибольшее значение площади, при этом
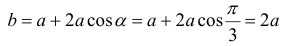 -длина большего основания.
-длина большего основания.
——-
Исследование функций с помощью производных(часть вторая)
Определение 1. Пусть функция y=f(x) дифференцируема на интервале ( a,b) . И пусть 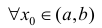 график функции y=f(x) расположен ниже (не выше), чем касательная y=y(x) к нему в точке
график функции y=f(x) расположен ниже (не выше), чем касательная y=y(x) к нему в точке 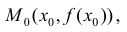 то есть
то есть
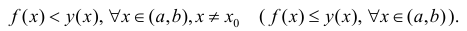 Тогда f( x ) называется выпуклой(нестрого выпуклой вверх).
Тогда f( x ) называется выпуклой(нестрого выпуклой вверх).
Пусть 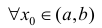 график функции y=f(x) расположен выше (не ниже), чем касательная y=y(x) к нему в точке
график функции y=f(x) расположен выше (не ниже), чем касательная y=y(x) к нему в точке 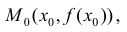 то есть
то есть
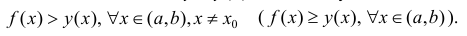 Тогда f(x) называется вогнутой (нестрого вогнутой).
Тогда f(x) называется вогнутой (нестрого вогнутой).
Пример 1.
а) 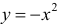 − выпукла на всей оси ( −∞; +∞):
− выпукла на всей оси ( −∞; +∞):
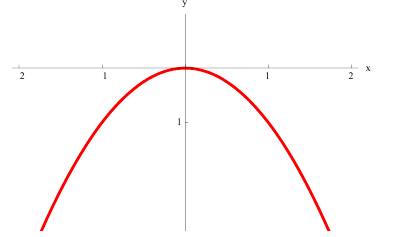
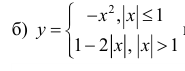 нестрого выпукла вверх на всей оси (−∞; +∞)
нестрого выпукла вверх на всей оси (−∞; +∞)
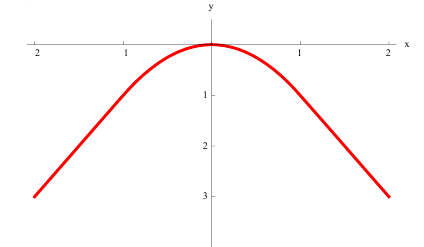
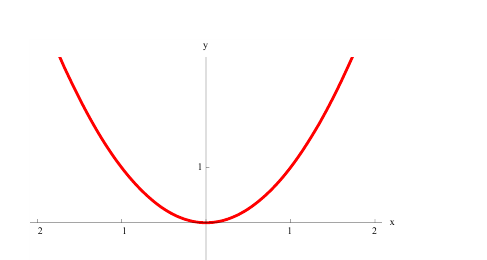
в) 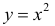 вогнута на всей оси (−∞; +∞):
вогнута на всей оси (−∞; +∞):
г) 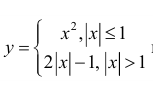 нестрого вогнута на всей оси (−∞; +∞):
нестрого вогнута на всей оси (−∞; +∞):
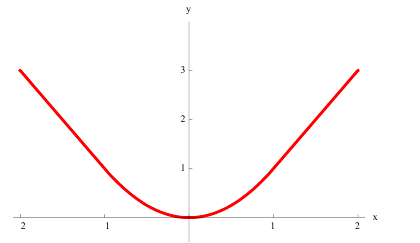
Теорема 1. Для того, чтобы дифференцируемая функция y=f(x) была вогнутой (выпуклой) на интервале ( a,b ) необходимо и достаточно, чтобы ее производная 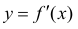 возрастала(убывала) на этом интервале.
возрастала(убывала) на этом интервале.
Докажем для случая, когда y=f(x) – вогнута.
Необходимость. Пусть 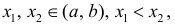
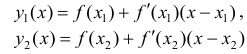 – касательные к графику y=f(x) в точках
– касательные к графику y=f(x) в точках 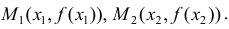 Так как y=f(x) – вогнута, то
Так как y=f(x) – вогнута, то
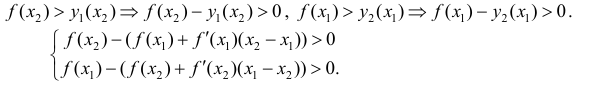
Сложим эти неравенства:
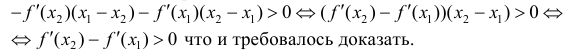
Достаточность. Пусть 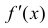 – возрастает. Докажем, что y=f(x) – вогнута.
– возрастает. Докажем, что y=f(x) – вогнута.
Пусть 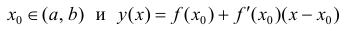 – уравнение касательной в точке
– уравнение касательной в точке 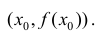
Пусть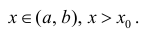 Найдем разность
Найдем разность 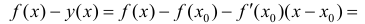 по теореме Лагранжа (терема 4 параграфа 12) =
по теореме Лагранжа (терема 4 параграфа 12) =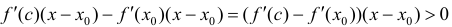 что и требовалось доказать.
что и требовалось доказать.
Теорема 2. Для того, чтобы дифференцируемая функция y=f(x) была нестрого вогнутой (нестрого выпуклой) на интервале ( a,b ) необходимо и достаточно, чтобы производная 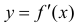 неубывала (невозрастала) на этом интервале.
неубывала (невозрастала) на этом интервале.
Доказательство аналогично доказательству теоремы 1.
Теорема 3. Для того, чтобы дважды дифференцируемая на интервале (a,b) функция y=f(x) была не строго вогнутой (не строго выпуклой) необходимо и
достаточно, чтобы 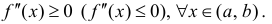
Доказательство следует из теоремы 2 и теоремы 1 §15.
Теорема 4. Для того, чтобы дважды дифференцируемая на интервале (a,b)
функция y=f(x) была вогнутой (выпуклой) на этом интервале достаточно, чтобы 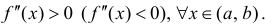
Доказательство следует из теоремы 1 и теоремы 2 §15. Нужно заметить, что
условие 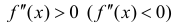 не является необходимым для вогнутости (выпуклости) функции.
не является необходимым для вогнутости (выпуклости) функции.
Пример 2.
Рассмотрим функцию 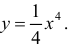 Она вогнута на интервале ( -1;1). Но условие
Она вогнута на интервале ( -1;1). Но условие 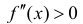 не выполнено в точке
не выполнено в точке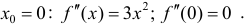
Теорема 6 (достаточное условие перегиба функции). Рассмотрим функцию
y=f(x) дважды дифференцируемую в некоторой окрестности 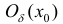 точки
точки
возможного перегиба 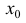 за исключением может быть самой точки
за исключением может быть самой точки 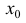
Предположим также, что вторая производная 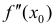 меняет знак при переходе
меняет знак при переходе
через точку 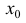 . Тогда
. Тогда 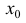 будет точкой перегиба для функции y=f(x).
будет точкой перегиба для функции y=f(x).
Доказательство следует из теоремы 4.
Пример 3.
Найдем точки перегиба и интервалы выпуклости-вогнутости функции
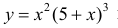 из примера 3 §15.
из примера 3 §15.
Решение.
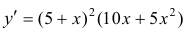 (см. пример 3 §15).
(см. пример 3 §15).
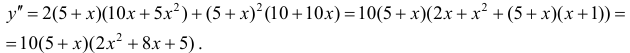
Найдем точки возможного перегиба(точки, где y′′ равна 0 или не существует).
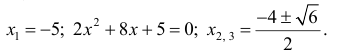
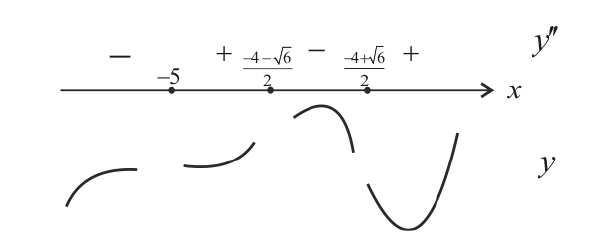
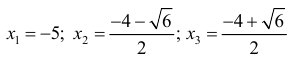 точки перегиба функции.
точки перегиба функции.
При нахождении интервалов выпуклости-вогнутости точки, где функции
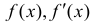 имеют разрывы также наносят на числовую прямую. При переходе
имеют разрывы также наносят на числовую прямую. При переходе
через эти точки может меняться направление выпуклости-вогнутости.
Определение 4. Прямая y= kx +b называется наклонной асимптотой функции y=f(x) при x →+∞ (x→−∞), если 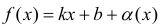 , где a(x) бесконечно-малая функция при x →+∞ (x→−∞) , то есть
, где a(x) бесконечно-малая функция при x →+∞ (x→−∞) , то есть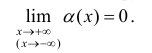
Теорема 7. Для того, чтобы прямая y =kx +b была наклонной асимптотой для функции y=f(x) при x →+∞ (x→−∞) необходимо и достаточно, чтобы существовали пределы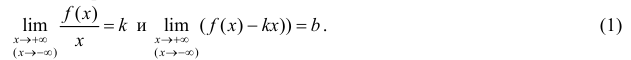
Доказательство. Рассмотрим, например, случай x → +∞ .
Необходимость. Пусть 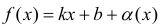 , где a(x) бесконечно-малая функция. Докажем, что выполняются пределы (1).
, где a(x) бесконечно-малая функция. Докажем, что выполняются пределы (1).
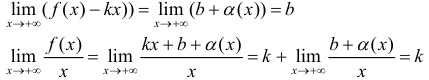 что и требовалось доказать.
что и требовалось доказать.
Достаточность. Пусть выполняется (1). Докажем, что y =kx +b – асимптота для y=f(x).
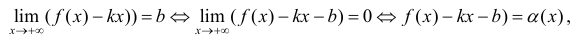 , где a(x) бесконечно-малая функция при x → +∞ , что и требовалось доказать. Таким образом теорема доказана.
, где a(x) бесконечно-малая функция при x → +∞ , что и требовалось доказать. Таким образом теорема доказана.
Замечание. Наличие наклонной асимптоты значит, что при x →+∞ (x→−∞) график функции очень близок к прямой линии y =kx +b.
Пример 4.
Для функции 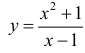 (см. пример 1 §5) y = x+1 – наклонная асимптота при x →±∞ .
(см. пример 1 §5) y = x+1 – наклонная асимптота при x →±∞ .
Для функции 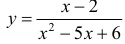 (пример 8 §5) y = 0 – горизонтальная асимптота при x →±∞ (k=0).
(пример 8 §5) y = 0 – горизонтальная асимптота при x →±∞ (k=0).
Для функции 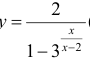 (пример 10 §5) y = −1 – горизонтальная асимптота при x →±∞ .
(пример 10 §5) y = −1 – горизонтальная асимптота при x →±∞ .
Для функции , 1(0 1) 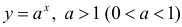 (пример 2 §5) y = 0 – горизонтальная
(пример 2 §5) y = 0 – горизонтальная
асимптота при x →+∞ (x→−∞).
Определение 5. Прямая 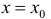 называется вертикальной асимптотой функции y=f(x), если хотя бы один из пределов
называется вертикальной асимптотой функции y=f(x), если хотя бы один из пределов 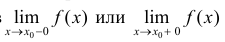 равен ∞.
равен ∞.
Пример 5.
Для функции 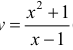 (см. пример 1 §5) прямая x = 1 – вертикальная асимптота, для функции
(см. пример 1 §5) прямая x = 1 – вертикальная асимптота, для функции 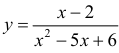 (пример 8 §5) прямая x = 3 – вертикальная асимптота, для функции
(пример 8 §5) прямая x = 3 – вертикальная асимптота, для функции 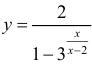 (пример 10 §5) прямая x = 0 – вертикальная асимптота, для функции
(пример 10 §5) прямая x = 0 – вертикальная асимптота, для функции 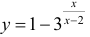 − из упражнения 1 §5 прямая x = 2 – вертикальная асимптота
− из упражнения 1 §5 прямая x = 2 – вертикальная асимптота
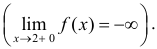
При построении графиков функции используют результаты §15, 16. Это можно проводить по следующей схеме:
1. Найти область определения D(f) функции и исследовать поведение функции в граничных точках D(f) . Определить точки разрыва, вертикальные асимптоты, нули функции, исследовать функцию на периодичность, четность, нечетность.
2. Найти наклонные асимптоты.
3. Найти интервалы монотонности, точки локального экстремума.
4. Найти интервалы выпуклости, вогнутости, точки перегиба.
5. Построить график.
Пример 6.
Провести полное исследование и построить график функции 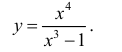
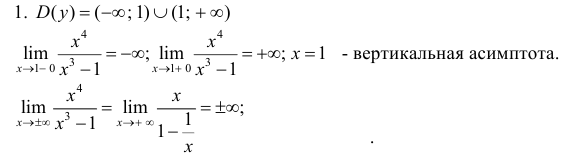
Нули функции 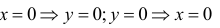
Таким образом график пересекает оси координат в точке О(0; 0). Функция
ни четная, ни нечетная, не периодическая.
2. Наклонные асимптоты. По формулам (1);

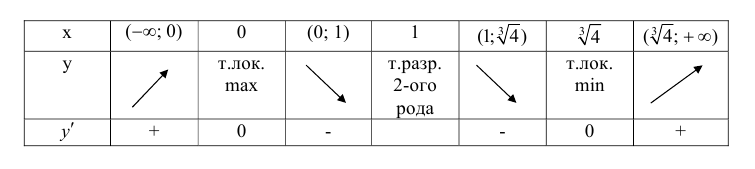
x = 0 – точка локального максимума; 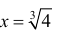 – точка локального минимума;
– точка локального минимума;
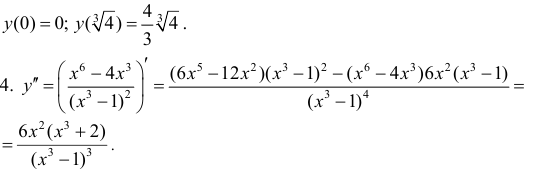
Точки где y′′ равна 0 или не существует: 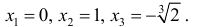
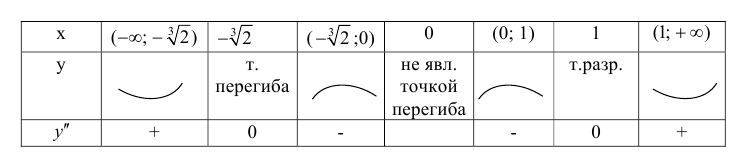
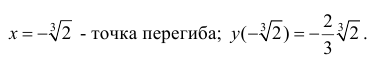
5. График функции.
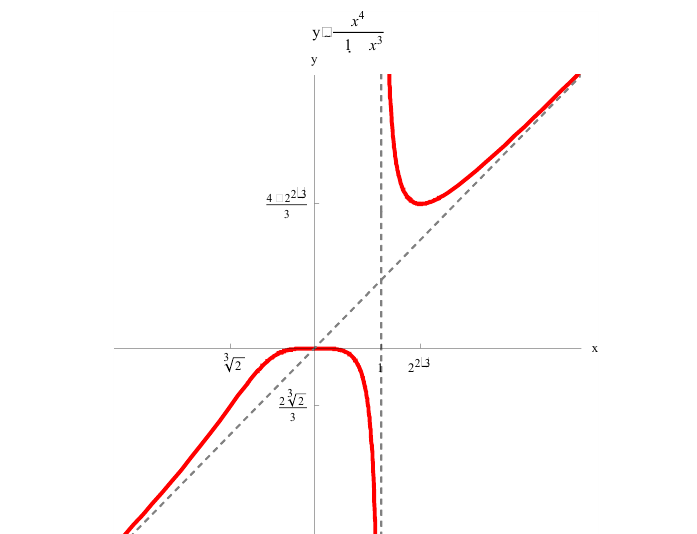
——–
Исследование функции с помощью производных
Монотонность функции
Теорема 9.1. Пусть функция 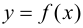 определена на отрезке
определена на отрезке 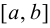 и внутри отрезка имеет конечную производную
и внутри отрезка имеет конечную производную 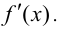 Для того, чтобы функция
Для того, чтобы функция 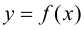 была монотонно возрастающей (убывающей), достаточно, чтобы
была монотонно возрастающей (убывающей), достаточно, чтобы 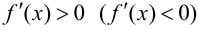 для
для 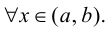
Доказательство.
Возьмем отрезок 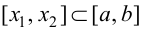 таким образом, чтобы
таким образом, чтобы 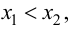 и применим к функции
и применим к функции 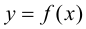 на этом промежутке формулу Лагранжа:
на этом промежутке формулу Лагранжа:
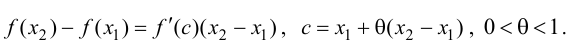
Тогда, если 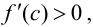 то
то 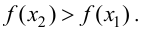 Следовательно, функция
Следовательно, функция 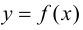 возрастает. Если
возрастает. Если 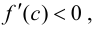 то
то 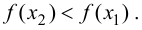 Следовательно, функция
Следовательно, функция 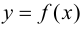 убывает.
убывает.
Замечание 9.1. Утверждение теоремы сохраняет силу и в том случае, если 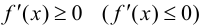 при условии, что производная
при условии, что производная 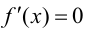 в конечном числе точек внутри отрезка
в конечном числе точек внутри отрезка 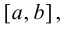 т. е. вышесказанное условие не является необходимым.
т. е. вышесказанное условие не является необходимым.
Пример 9.1. Рассмотрим функцию 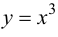 на отрезке
на отрезке 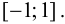 Хотя
Хотя 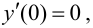 функция возрастает на отрезке
функция возрастает на отрезке 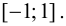
- Заказать решение задач по высшей математике
Достаточные условия экстремума
Теорема 9.2 (первое достаточное условие экстремума). Пусть функция 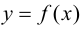 дифференцируема в некоторой проколотой окрестности точки
дифференцируема в некоторой проколотой окрестности точки 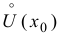 и непрерывна в точке
и непрерывна в точке 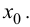 Тогда, если
Тогда, если 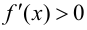 при
при 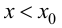 и
и 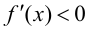 при
при 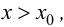 то в точке
то в точке 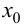 функция имеет локальный максимум; если
функция имеет локальный максимум; если 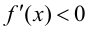 при
при 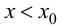 и
и 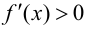 при
при 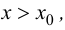 то в точке
то в точке 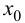 функция имеет локальный минимум.
функция имеет локальный минимум.
Доказательство следует из теоремы 9.1.
Теорема 9.3 (второе достаточное условие экстремума). Если в критической точке 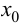 функции
функции 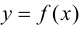 существует
существует 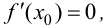 а
а 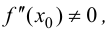 то при
то при 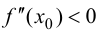 функция имеет локальный максимум, при
функция имеет локальный максимум, при 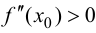 — локальный минимум.
— локальный минимум.
Доказательство.
Если в точке 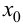 существует вторая производная
существует вторая производная 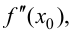 то первая производная
то первая производная 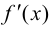 существует в некоторой окрестности этой точки
существует в некоторой окрестности этой точки 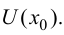 Тогда
Тогда 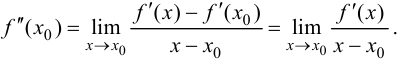
Пусть 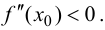 Тогда
Тогда 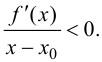
При 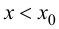 производная
производная 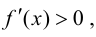 т. е., согласно теореме 9.1, функция
т. е., согласно теореме 9.1, функция 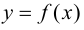 возрастает; при
возрастает; при 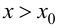 производная
производная 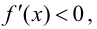 т. е. функция
т. е. функция 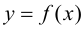 убывает. На основании теоремы 9.2: в точке
убывает. На основании теоремы 9.2: в точке 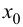 функция имеет локальный максимум.
функция имеет локальный максимум.
Случай 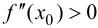 рассматривается аналогично.
рассматривается аналогично.
Замечание 9.2. Так как теорема формулирует только достаточное условие, то при 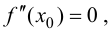 функция может как иметь, так и не иметь экстремум.
функция может как иметь, так и не иметь экстремум.
Пример 9.2. Функция 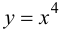 имеет в точке
имеет в точке 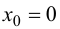 минимум, при этом
минимум, при этом 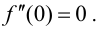 Функция
Функция 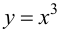 не имеет в точке
не имеет в точке 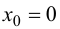 экстремума, при этом также
экстремума, при этом также 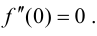
Наибольшее и наименьшее значения функции на отрезке
Пусть функция 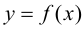 непрерывна на отрезке
непрерывна на отрезке 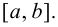 Тогда на этом отрезке функция достигает наибольшего и наименьшего значений, теорема 4.3 Вейерштрасса (раздел 1). Будем предполагать, что на данном отрезке функция
Тогда на этом отрезке функция достигает наибольшего и наименьшего значений, теорема 4.3 Вейерштрасса (раздел 1). Будем предполагать, что на данном отрезке функция 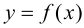 имеет конечное число критических точек. Если наибольшее и наименьшее значения достигаются внутри отрезка
имеет конечное число критических точек. Если наибольшее и наименьшее значения достигаются внутри отрезка 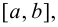 то очевидно, что эти значения будут наибольшим максимумом и наименьшим минимумом функции (если имеется несколько экстремумов). Однако может наблюдаться такая ситуация, что наибольшее или наименьшее значения будут достигаться на одном из концов отрезка (рис. 9.1).
то очевидно, что эти значения будут наибольшим максимумом и наименьшим минимумом функции (если имеется несколько экстремумов). Однако может наблюдаться такая ситуация, что наибольшее или наименьшее значения будут достигаться на одном из концов отрезка (рис. 9.1).
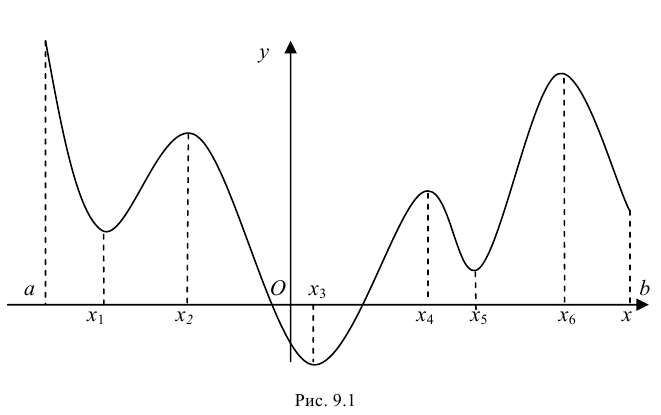
Таким образом, непрерывная функция 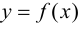 на отрезке достигает своего наибольшего и наименьшего значений либо на концах этого отрезка, либо в таких точках этого отрезка, которые являются точками экстремума.
на отрезке достигает своего наибольшего и наименьшего значений либо на концах этого отрезка, либо в таких точках этого отрезка, которые являются точками экстремума.
Исходя из вышесказанного, можно предложить следующий алгоритм поиска наибольшего и наименьшего значений непрерывной функции 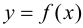 на отрезке
на отрезке 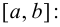
1. Найти все критические точки. Если критическая точка 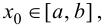 то нужно вычислить в ней значение функции
то нужно вычислить в ней значение функции 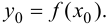 Если критическая точка
Если критическая точка 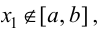 то в дальнейшем решении эта точка во внимание не принимается.
то в дальнейшем решении эта точка во внимание не принимается.
2. Вычислить значения функции на концах отрезка, т. е. найти 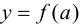 и
и
3. Из всех полученных выше значений функции выбрать наибольшее и наименьшее, они и будут представлять собой наибольшее и наименьшее значения функции 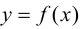 на отрезке
на отрезке 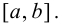
Пример 9.3. Найти наибольшее и наименьшее значения функции 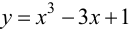 на отрезке [—3; 3].
на отрезке [—3; 3].
Решение.
Так как функция 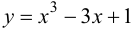 непрерывна на отрезке [-3; 3], то задача имеет решение.
непрерывна на отрезке [-3; 3], то задача имеет решение.
1. Найдем критические точки функции.
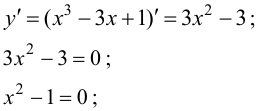
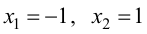 – критические точки.
– критические точки.
Так как 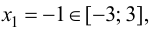 то вычислим
то вычислим 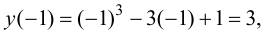
так как 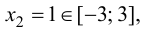 то вычислим
то вычислим 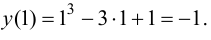
2. Определим значения функции на концах отрезка:
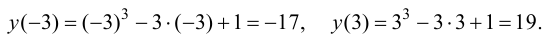
3. Сравним вычисленные значения функции и выберем наибольшее и наименьшее:
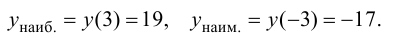
Ответ: 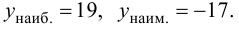
Выпуклость и вогнутость графика функции, точки перегиба
Пусть функция 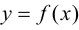 задана на интервале
задана на интервале 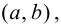 непрерывна на этом интервале и в каждой точке графика этой функции существует единственная касательная.
непрерывна на этом интервале и в каждой точке графика этой функции существует единственная касательная.
Определение 9.1. График функции 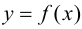 называется выпуклым или выпуклым вверх на интервале
называется выпуклым или выпуклым вверх на интервале 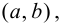 если он расположен ниже любой своей касательной, т. е.
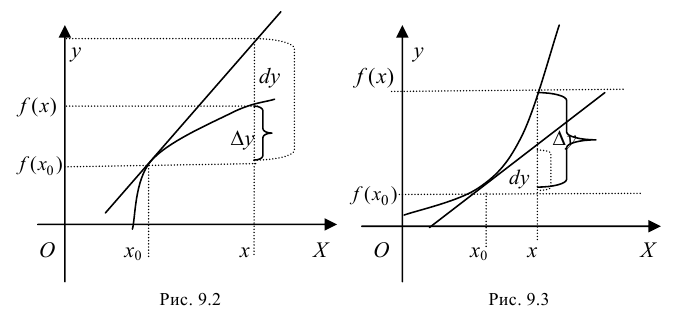
если он расположен ниже любой своей касательной, т. е. 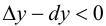 (рис. 9.2); график функции
(рис. 9.2); график функции 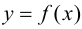 называется вогнутым или выпуклым вниз на интервале
называется вогнутым или выпуклым вниз на интервале 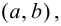 если он расположен выше любой своей касательной, т. е.
если он расположен выше любой своей касательной, т. е. 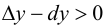 (рис. 9.3).
(рис. 9.3).
Определение 9.2. Точки графика функции, в которых выпуклость сменяется вогнутостью или наоборот, называются точками перегиба графика.
Теорема 9.4. Пусть функция 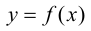 определена и дважды дифференцируема на интервале
определена и дважды дифференцируема на интервале 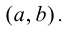 Тогда если
Тогда если 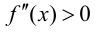 для
для 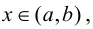 то на этом интервале график функции вогнутый; если
то на этом интервале график функции вогнутый; если 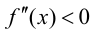 для
для 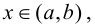 то на этом интервале график функции выпуклый.
то на этом интервале график функции выпуклый.
Доказательство.
Рассмотрим разность 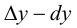 на отрезке
на отрезке 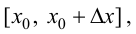 если
если 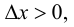 и на отрезке
и на отрезке 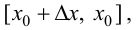 если
если 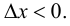 Согласно теореме 7.4 (Лагранжа):
Согласно теореме 7.4 (Лагранжа):
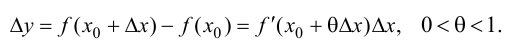
Поэтому 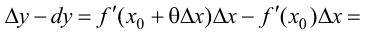
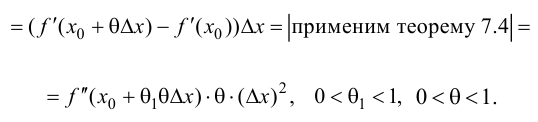
Тогда, при 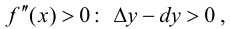 следовательно на этом отрезке график функции будет вогнутый; при
следовательно на этом отрезке график функции будет вогнутый; при 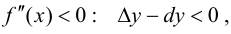 следовательно на этом отрезке график функции будет выпуклый.
следовательно на этом отрезке график функции будет выпуклый.
Теорема 9.5 (необходимое условие точки перегиба). Пусть график функции 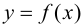 имеет перегиб в точке
имеет перегиб в точке 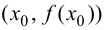 и пусть функция
и пусть функция 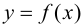 имеет в точке Xq непрерывную вторую производную. Тогда
имеет в точке Xq непрерывную вторую производную. Тогда 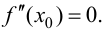
Доказательство.
Пусть 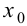 – абсцисса точки перегиба графика функции
– абсцисса точки перегиба графика функции 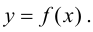 Для определенности будем считать, что выпуклость сменяется вогнутостью, т. е. при
Для определенности будем считать, что выпуклость сменяется вогнутостью, т. е. при 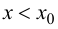 справедливо неравенство
справедливо неравенство 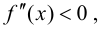 при
при 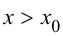 справедливо неравенство
справедливо неравенство 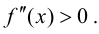 Тогда
Тогда 
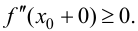 Так как, по условию теоремы, вторая производная в точке
Так как, по условию теоремы, вторая производная в точке 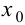 существует, то
существует, то 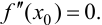
Определение 9.3. Точка 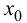 из области определения функции
из области определения функции 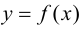 называется критической (стационарной) точкой второго рода, если вторая производная функции в этой точке обращается в нуль
называется критической (стационарной) точкой второго рода, если вторая производная функции в этой точке обращается в нуль 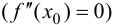 или не существует.
или не существует.
Замечание 9.3. Не всякая точка 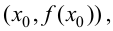 для которой
для которой 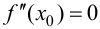 является точкой перегиба.
является точкой перегиба.
Пример 9.4. График функции 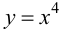 не имеет перегиба в точке (0; 0), хотя
не имеет перегиба в точке (0; 0), хотя 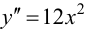 обращается в 0 при
обращается в 0 при 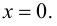
Теорема 9.6 (достаточное условие точки перегиба). Пусть функция 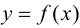 определена и дважды дифференцируема в некоторой окрестности точки
определена и дважды дифференцируема в некоторой окрестности точки 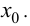 Тогда если в пределах указанной окрестности
Тогда если в пределах указанной окрестности 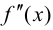 имеет разные знаки слева и справа от точки
имеет разные знаки слева и справа от точки 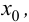 то график функции
то график функции 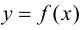 имеет перегиб в точке
имеет перегиб в точке
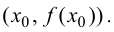
Доказательство.
Из того, что 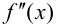 слева и справа от точки
слева и справа от точки 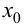 имеет разные знаки, на основании теоремы 9.4 можно сделать заключение, что направление выпуклости графика функции слева и справа от точки
имеет разные знаки, на основании теоремы 9.4 можно сделать заключение, что направление выпуклости графика функции слева и справа от точки 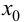 является различным. Это и означает наличие перегиба в точке
является различным. Это и означает наличие перегиба в точке 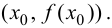
Замечание 9.4. Теорема остается верной, если функция 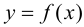 имеет вторую производную в некоторой окрестности точки
имеет вторую производную в некоторой окрестности точки 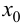 и существует касательная к графику функции в точке
и существует касательная к графику функции в точке 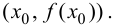 Тогда если в пределах указанной окрестности
Тогда если в пределах указанной окрестности 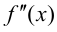 имеет разные знаки справа и слева от точки
имеет разные знаки справа и слева от точки 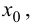 то график функции
то график функции 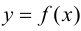 имеет перегиб в точке
имеет перегиб в точке 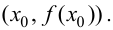
Пример 9.5. Точка (0; 0) является точкой перегиба графика функции 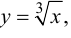 хотя вторая производная функции при
хотя вторая производная функции при 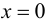 не существует. Касательная к графику функции
не существует. Касательная к графику функции 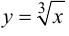 в точке (0; 0) совпадает с осью
в точке (0; 0) совпадает с осью 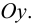
Асимптоты графика функции
При исследовании поведения функции на бесконечности, т. е. при 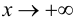 и при
и при 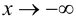 или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к некоторой прямой.
или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к некоторой прямой.
Определение 9.4. Прямая 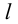 называется асимптотой графика функции
называется асимптотой графика функции 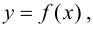 если расстояние
если расстояние 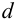 от переменной точки графика функции
от переменной точки графика функции 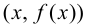 до прямой
до прямой 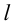 стремится к нулю при удалении точки
стремится к нулю при удалении точки 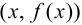 от начала системы координат.
от начала системы координат.
Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение 9.5. Прямая 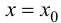 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 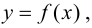 если хотя бы одно из предельных значений
если хотя бы одно из предельных значений 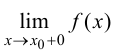 или
или 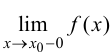 равно
равно 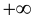 или
или 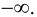
В этом случае расстояние от точки графика функции 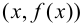 до прямой
до прямой 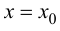 равно
равно 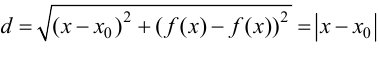 и, следовательно,
и, следовательно, 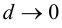 при
при 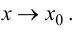
Пример 9.6. График функции 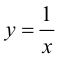 имеет вертикальную асимптоту
имеет вертикальную асимптоту 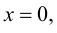 так как
так как 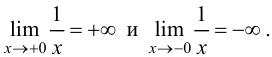
Определение 9.6. Прямая 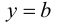 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 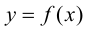 при
при 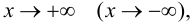 если
если 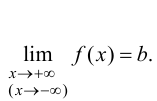
В этом случае расстояние от точки графика функции 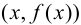 до прямой
до прямой 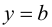 равно
равно 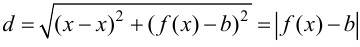 и, следовательно,
и, следовательно, 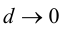 при
при 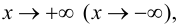 так как
так как 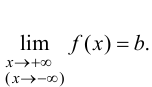
Пример 9.6 (продолжение). График функции 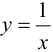 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 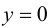 и при
и при 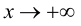 и при
и при 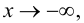 так как
так как 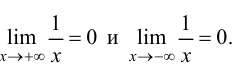
Определение 9.7. Прямая 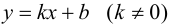 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 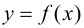 при
при 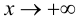
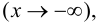 если функцию
если функцию 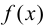 можно представить в виде
можно представить в виде
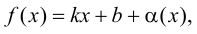 (9.1)
(9.1)
где 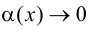 при
при 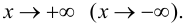
Теорема 9.7. Для того чтобы прямая 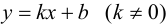 являлась наклонной асимптотой графика функции
являлась наклонной асимптотой графика функции 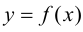 при
при 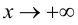
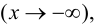 необходимо и достаточно, чтобы существовали конечные пределы:
необходимо и достаточно, чтобы существовали конечные пределы:
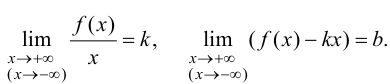 (9.2)
(9.2)
Доказательство. Рассмотрим случай 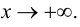
Необходимость.
Если 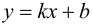 – наклонная асимптота графика функции
– наклонная асимптота графика функции 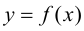 при
при 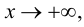 то, используя представление функции по формуле (9.1), получим:
то, используя представление функции по формуле (9.1), получим:
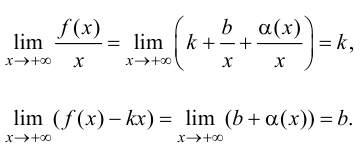
Достаточность.
Пусть существуют пределы (9.2). Тогда из второго равенства следует, что
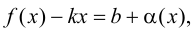 где
где 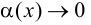 при
при 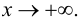
Полученное равенство легко преобразовать к виду (9.1), т. е. прямая 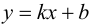 – наклонная асимптота графика функции
– наклонная асимптота графика функции  при
при 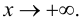
Схема исследования функции и построения ее графика
Рассмотрим примерный план, по которому целесообразно исследовать поведение функции и строить ее график:
1. Найти область определения функции.
2. Проверить выполнение свойств четности или нечетности, периодичности.
3. Указать промежутки непрерывности, точки разрыва и их тип, проверить наличие асимптот.
4. Найти промежутки монотонности и точки экстремума.
5. Найти промежутки выпуклости и вогнутости, точки перегиба.
6. Найти точки пересечения графика функции с осями координат.
7. Построить график функции.
Замечание 9.5. Если исследуемая функция 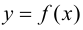 четная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график четной функции симметричен относительно оси ординат.
четная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график четной функции симметричен относительно оси ординат.
Замечание 9.6. Если исследуемая функция 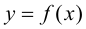 нечетная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график нечетной функции симметричен относительно начала координат.
нечетная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график нечетной функции симметричен относительно начала координат.
Пример 9.7. Исследовать функцию 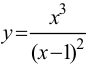 и построить ее график.
и построить ее график.
Решение.
1. 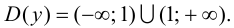
2. Так как область определения функции несимметрична относительно начала координат, то эта функция общего вида, т. е. функция ни четная, ни нечетная, непериодическая.
3. Функция непрерывна на области определения как элементарная. Точкой разрыва является 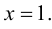 Так как
Так как
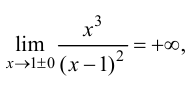
то 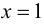 – точка разрыва второго рода. Можно также сделать заключение, что прямая
– точка разрыва второго рода. Можно также сделать заключение, что прямая 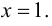 будет являться вертикальной асимптотой графика функции.
будет являться вертикальной асимптотой графика функции.
Проверим наличие горизонтальных асимптот. Так как
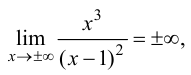
то данная функция не имеет горизонтальных асимптот. Проверим наличие наклонных асимптот. Так как
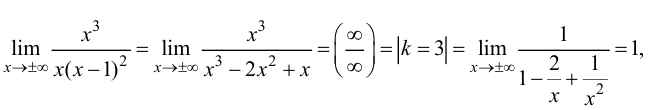
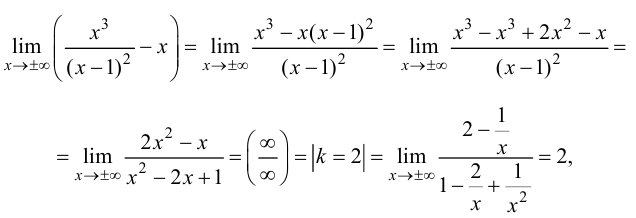
то график функции имеет наклонную асимптоту с угловым коэффициентом 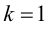 и свободным членом
и свободным членом 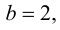 т. е.
т. е. 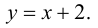
4. Определим промежутки возрастания и убывания функции, точки экстремума. Для этого найдем критические точки первого рода:
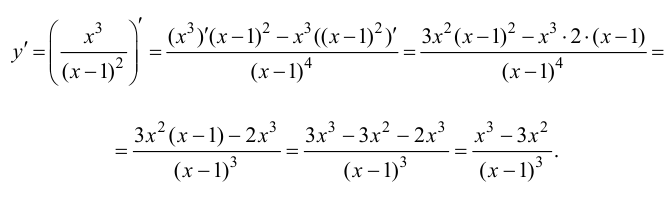
Решим уравнение 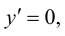 т.е.
т.е. 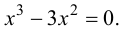 Получаем
Получаем 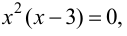
откуда 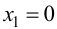 и
и 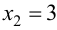 – критические точки первого рода. Изменение знака первой производной покажем на числовой оси (рис. 9.4).
– критические точки первого рода. Изменение знака первой производной покажем на числовой оси (рис. 9.4).
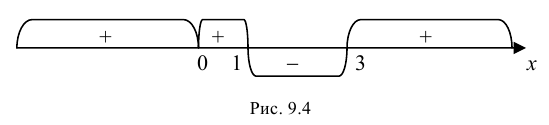
Так как 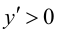 при
при 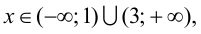 то функция возрастает на указанных промежутках; так как
то функция возрастает на указанных промежутках; так как 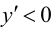 при
при 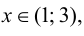 то функция убывает на указанном промежутке. При переходе через точку
то функция убывает на указанном промежутке. При переходе через точку 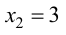 производная
производная 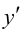 изменяет знак с «-» на «+», следовательно, в этой точке функция имеет минимум, причем
изменяет знак с «-» на «+», следовательно, в этой точке функция имеет минимум, причем 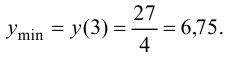
5. Определим промежутки выпуклости и вогнутости графика функции, точки перегиба. Для этого найдем критические точки второго рода:
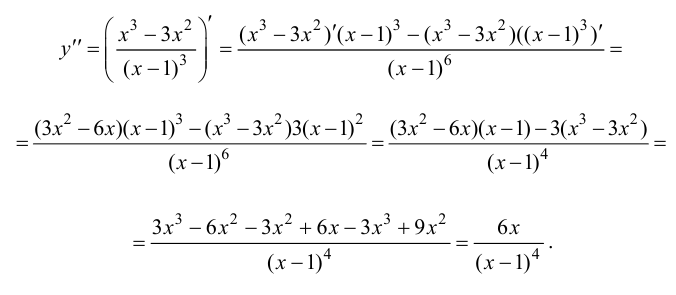
Решим уравнение 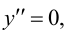 т. е.
т. е. 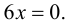 Получаем единственное решение
Получаем единственное решение 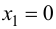 – критическая точка второго рода. Изменение знака второй производной покажем на числовой оси (рис. 9.5).
– критическая точка второго рода. Изменение знака второй производной покажем на числовой оси (рис. 9.5).
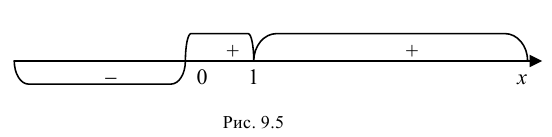
Так как 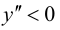 при
при 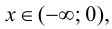 то график функции будет выпуклым на данном промежутке; так как
то график функции будет выпуклым на данном промежутке; так как 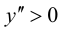 при
при 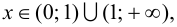 то график функции будет вогнутым на указанных промежутках. При переходе через точку
то график функции будет вогнутым на указанных промежутках. При переходе через точку 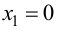 выпуклость графика функции сменяется вогнутостью, следовательно, это абсцисса точки перегиба, тогда ордината
выпуклость графика функции сменяется вогнутостью, следовательно, это абсцисса точки перегиба, тогда ордината 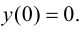 Таким образом, (0; 0) – точка перегиба графика функции.
Таким образом, (0; 0) – точка перегиба графика функции.
6. Найдем точки пересечения графика функции с осями координат.
Для точек оси 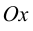 всегда
всегда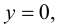 т. е.
т. е. 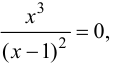 откуда
откуда 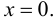
Для точек оси 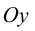 всегда
всегда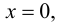 т. е.
т. е. 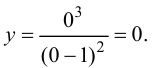
Таким образом, единственной точкой пересечения графика функции с осями координат является начало системы координат 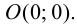
7. Построим график функции на рис. 9.6.
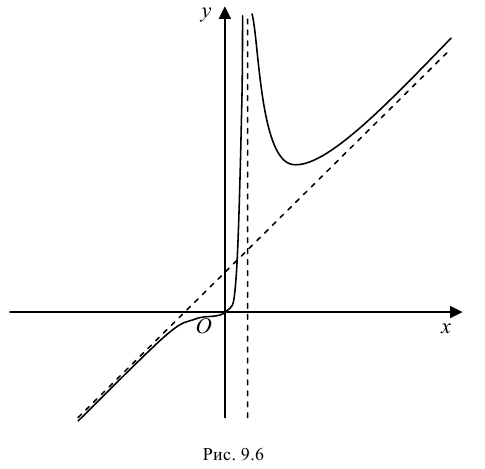
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Возрастание и убывание функции на интервале
Функция y=f(x) будет возрастать на интервале x, когда при любых x1∈X и x2∈X , x2>x1неравенство f(x2)>f(x1) будет выполнимо. Иначе говоря, большему значению аргумента соответствует большее значение функции.
Функция y=f(x) считается убывающей на интервале x, когда при любых x1∈X, x2∈X, x2>x1 равенство f(x2)>f(x1) считается выполнимым. Иначе говоря, большему значению функции соответствует меньшее значение аргумента. Рассмотрим рисунок, приведенный ниже.

Замечание: Когда функция определенная и непрерывная в концах интервала возрастания и убывания, то есть (a;b), где х=а, х=b, точки включены в промежуток возрастания и убывания. Определению это не противоречит, значит, имеет место быть на промежутке x.
Основные свойства элементарных функций типа y=sinx – определенность и непрерывность при действительных значениях аргументах. Отсюда получаем, что возрастание синуса происходит на интервале -π2; π2, тогда возрастание на отрезке имеет вид -π2; π2.
Точки экстремума, экстремумы функции
Точка х0 называется точкой максимума для функции y=f(x), когда для всех значений x неравенство f(x0)≥f(x) является справедливым. Максимум функции – это значение функции в точке, причем обозначается ymax.
Точка х0 называется точкой минимума для функции y=f(x), когда для всех значений x неравенство f(x0)≤f(x) является справедливым. Минимум функции – это значение функции в точке, причем имеет обозначение вида ymin.
Окрестностями точки х0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.

Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.

Первый рисунок говорит о том, что необходимо найти наибольшее значение функции из отрезка [a;b]. Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х=b.
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Пусть задана функция y=f(x), которая дифференцируема в ε окрестности точки x0, причем имеет непрерывность в заданной точке x0. Отсюда получаем, что
- когда f'(x)>0 с x∈(x0-ε; x0) и f'(x)<0 при x∈(x0; x0+ε), тогда x0 является точкой максимума;
- когда f'(x)<0 с x∈(x0-ε; x0) и f'(x)>0 при x∈(x0; x0+ε), тогда x0 является точкой минимума.
Иначе говоря, получим их условия постановки знака:
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком, то есть с + на -, значит, точка называется максимумом;
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком с – на +, значит, точка называется минимумом.
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
- найти область определения;
- найти производную функции на этой области;
- определить нули и точки, где функция не существует;
- определение знака производной на интервалах;
- выбрать точки, где функция меняет знак.
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Найти точки максимума и минимума заданной функции y=2(x+1)2x-2.
Решение
Область определения данной функции – это все действительные числа кроме х=2. Для начала найдем производную функции и получим:
y’=2x+12x-2’=2·x+12’·(x-2)-(x+1)2·(x-2)'(x-2)2==2·2·(x+1)·(x+1)’·(x-2)-(x+1)2·1(x-2)2=2·2·(x+1)·(x-2)-(x+2)2(x-2)2==2·(x+1)·(x-5)(x-2)2
Отсюда видим, что нули функции – это х=-1, х=5, х=2, то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:

Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х=-2, х=0, х=3, х=6.
Получаем, что
y'(-2)=2·(x+1)·(x-5)(x-2)2x=-2=2·(-2+1)·(-2-5)(-2-2)2=2·716=78>0, значит, интервал -∞; -1 имеет положительную производную. Аналогичным образом получаем, что
y'(0)=2·(0+1)·0-50-22=2·-54=-52<0y'(3)=2·(3+1)·(3-5)(3-2)2=2·-81=-16<0y'(6)=2·(6+1)·(6-5)(6-2)2=2·716=78>0
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Получим, что в точке х=-1 функция будет непрерывна, значит, производная изменит знак с + на -. По первому признаку имеем, что х=-1 является точкой максимума, значит получаем
ymax=y(-1)=2·(x+1)2x-2x=-1=2·(-1+1)2-1-2=0
Точка х=5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
ymin=y(5)=2·(x+1)2x-2x=5=2·(5+1)25-2=24
Графическое изображение

Ответ: ymax=y(-1)=0, ymin=y(5)=24.
Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x0, этим и упрощает вычисление.
Найти точки максимума и минимума функции y=16×3=2×2+223x-8.
Решение.
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
-16×3-2×2-223x-8, x<016×3-2×2+223x-8, x≥0
После чего необходимо найти производную:
y’=16×3-2×2-223x-8′, x<016×3-2×2+223x-8′, x>0y’=-12×2-4x-223, x<012×2-4x+223, x>0
Точка х=0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
lim y’x→0-0=lim yx→0-0-12×2-4x-223=-12·(0-0)2-4·(0-0)-223=-223lim y’x→0+0=lim yx→0-012×2-4x+223=12·(0+0)2-4·(0+0)+223=+223
Отсюда следует, что функция непрерывна в точке х=0, тогда вычисляем
lim yx→0-0=limx→0-0-16×3-2×2-223x-8==-16·(0-0)3-2·(0-0)2-223·(0-0)-8=-8lim yx→0+0=limx→0-016×3-2×2+223x-8==16·(0+0)3-2·(0+0)2+223·(0+0)-8=-8y(0)=16×3-2×2+223x-8x=0=16·03-2·02+223·0-8=-8
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
-12×2-4x-223, x<0D=(-4)2-4·-12·-223=43×1=4+432·-12=-4-233<0x2=4-432·-12=-4+233<0
12×2-4x+223, x>0D=(-4)2-4·12·223=43×3=4+432·12=4+233>0x4=4-432·12=4-233>0
Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x=-6, x=-4, x=-1, x=1, x=4, x=6. Получим, что
y'(-6)=-12×2-4x-223x=-6=-12·-62-4·(-6)-223=-43<0y'(-4)=-12×2-4x-223x=-4=-12·(-4)2-4·(-4)-223=23>0y'(-1)=-12×2-4x-223x=-1=-12·(-1)2-4·(-1)-223=236<0y'(1)=12×2-4x+223x=1=12·12-4·1+223=236>0y'(4)=12×2-4x+223x=4=12·42-4·4+223=-23<0y'(6)=12×2-4x+223x=6=12·62-4·6+223=43>0
Изображение на прямой имеет вид

Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
x=-4-233, x=0, x=4+233, тогда отсюда точки максимума имеют значениx=-4+233, x=4-233
Перейдем к вычислению минимумов:
ymin=y-4-233=16×3-22+223x-8x=-4-233=-8273ymin=y(0)=16×3-22+223x-8x=0=-8ymin=y4+233=16×3-22+223x-8x=4+233=-8273
Произведем вычисления максимумов функции. Получим, что
ymax=y-4+233=16×3-22+223x-8x=-4+233=8273ymax=y4-233=16×3-22+223x-8x=4-233=8273
Графическое изображение

Ответ:
ymin=y-4-233=-8273ymin=y(0)=-8ymin=y4+233=-8273ymax=y-4+233=8273ymax=y4-233=8273
Второй признак экстремума функции
Если задана функция f'(x0)=0, тогда при ее f”(x0)>0 получаем, что x0 является точкой минимума, если f”(x0)<0, то точкой максимума. Признак связан с нахождением производной в точке x0.
Найти максимумы и минимумы функции y=8xx+1.
Решение
Для начала находим область определения. Получаем, что
D(y): x≥0x≠-1⇔x≥0
Необходимо продифференцировать функцию, после чего получим
y’=8xx+1’=8·x’·(x+1)-x·(x+1)'(x+1)2==8·12x·(x+1)-x·1(x+1)2=4·x+1-2x(x+1)2·x=4·-x+1(x+1)2·x
При х=1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х=1. Получаем:
y”=4·-x+1(x+1)2·x’==4·(-x+1)’·(x+1)2·x-(-x+1)·x+12·x'(x+1)4·x==4·(-1)·(x+1)2·x-(-x+1)·x+12’·x+(x+1)2·x'(x+1)4·x==4·-(x+1)2x-(-x+1)·2x+1(x+1)’x+(x+1)22x(x+1)4·x==-(x+1)2x-(-x+1)·x+1·2x+x+12x(x+1)4·x==2·3×2-6x-1x+13·x3⇒y”(1)=2·3·12-6·1-1(1+1)3·(1)3=2·-48=-1<0
Значит, использовав 2 достаточное условие экстремума, получаем, что х=1 является точкой максимума. Иначе запись имеет вид ymax=y(1)=811+1=4.
Графическое изображение

Ответ: ymax=y(1)=4..
Третье достаточное условие экстремума
Функция y=f(x) имеет ее производную до n-го порядка в ε окрестности заданной точки x0 и производную до n+1-го порядка в точке x0. Тогда f'(x0)=f”(x0)=f”'(x0)=…=fn(x0)=0.
Отсюда следует, что когда n является четным числом, то x0 считается точкой перегиба, когда n является нечетным числом, то x0 точка экстремума, причем f(n+1)(x0)>0, тогда x0 является точкой минимума, f(n+1)(x0)<0, тогда x0 является точкой максимума.
Найти точки максимума и минимума функции yy=116(x+1)3(x-3)4.
Решение
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
y’=116x+13′(x-3)4+(x+1)3x-34’==116(3(x+1)2(x-3)4+(x+1)34(x-3)3)==116(x+1)2(x-3)3(3x-9+4x+4)=116(x+1)2(x-3)3(7x-5)
Данная производная обратится в ноль при x1=-1, x2=57, x3=3. То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что
y”=116x+12(x-3)3(7x-5)’=18(x+1)(x-3)2(21×2-30x-3)y”(-1)=0y”57=-368642401<0y”(3)=0
Значит, что x2=57 является точкой максимума. Применив 3 достаточный признак, получаем, что при n=1 и f(n+1)57<0.
Необходимо определить характер точек x1=-1, x3=3. Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что
y”’=18(x+1)(x-3)2(21×2-30x-3)’==18(x-3)(105×3-225×2-45x+93)y”'(-1)=96≠0y”'(3)=0
Значит, x1=-1 является точкой перегиба функции, так как при n=2 и f(n+1)(-1)≠0. Необходимо исследовать точку x3=3. Для этого находим 4 производную и производим вычисления в этой точке:
y(4)=18(x-3)(105×3-225×2-45x+93)’==12(105×3-405×2+315x+57)y(4)(3)=96>0
Из выше решенного делаем вывод, что x3=3 является точкой минимума функции.
Графическое изображение

Ответ: x2=57 является точкой максимума, x3=3 – точкой минимума заданной функции.
Содержание:
- Необходимое условие экстремума
- Первое достаточное условие экстремума
- Второе достаточное условие экстремума
Определение
Точка $x_{0}$ называется точкой локального максимума
функции $f(x)$, если существует такая окрестность
этой точки, что для всех $x$ из этой окрестности
выполняется неравенство: $f(x) leq fleft(x_{0}right)$.
Точка $x_{0}$ называется точкой локального минимума
функции $f(x)$, если существует такая окрестность этой
точки, что для всех $x$ из этой окрестности
$f(x) geq fleft(x_{0}right)$.
Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума –
локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
Точка $x_{0}$ называется точкой строгого локального
максимума функции $y=f(x)$, если для всех
$x$ из окрестности этой точки будет справедливо
строгое неравенство $f(x) lt fleft(x_{0}right)$.
Точка $x_{0}$ называется точкой строгого локального
минимума функции $y=f(x)$, если для всех
$x$ из окрестности этой точки будет
справедливо строгое неравенство $f(x)>fleft(x_{0}right)$.
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.
Замечание
Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
Необходимое условие экстремума
Теорема
(Необходимое условие экстремума)
Если функция $y=f(x)$ имеет экстремум в точке
$x_{0}$, то ее производная
$f^{prime}left(x_{0}right)$ либо равна нулю, либо не существует.
Точки, в которых производная равна нулю: $f^{prime}(x)=0$,
называются стационарными точками функции.
Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются
критическими точками этой функции. То есть критические точки – это либо стационарные точки (решения
уравнения $f^{prime}(x)=0$), либо это точки, в которых производная
$f^{prime}(x)$ не существует.
Замечание
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
Первое достаточное условие экстремума
Теорема
(Первое достаточное условие экстремума)
Пусть для функции $y=f(x)$ выполнены следующие условия:
- функция непрерывна в окрестности точки $x_{0}$;
- $f^{prime}left(x_{0}right)=0$ или $f^{prime}left(x_{0}right)$ не существует;
- производная $f^{prime}(x)$ при переходе через точку $x_{0}$ меняет свой знак.
Тогда в точке $x=x_{0}$ функция
$y=f(x)$ имеет экстремум, причем это минимум, если
при переходе через точку $x_{0}$ производная меняет свой
знак с минуса на плюс; максимум, если при переходе через точку $x_{0}$
производная меняет свой знак с плюса на минус.
Если производная $f^{prime}(x)$ при переходе через точку
$x_{0}$ не меняет знак, то экстремума в точке
$x=x_{0}$ нет.
Таким образом, для того чтобы исследовать функцию $y=f(x)$
на экстремум, необходимо:
- найти производную $f^{prime}(x)$;
- найти критические точки, то есть такие значения $x$,
в которых $f^{prime}(x)=0$ или
$f^{prime}(x)$ не существует; - исследовать знак производной слева и справа от каждой критической точки;
- найти значение функции в экстремальных точках.
Пример
Задание. Исследовать функцию $y(x)=x^{4}-1$ на экстремум.
Решение. Находим производную заданной функции:
$y^{prime}=left(x^{4}-1right)^{prime}=4 x^{3}$
Далее ищем критические точки функции, для этого решаем уравнение $y^{prime}(x)=0$:
$y^{prime}=4 x^{3}=0 Rightarrow x=0$
Первая производная определена во всех точках. Таким образом, имеем одну критическую точку
$x=0$. Наносим эту точку на координатную прямую и
исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное
значение и находим значение производной в выбранной точке, определяем знак полученной величины):

Так как при переходе через точку $x=0$ производная
сменила свой знак с “-” на “+”, то в этой точке функция достигает минимума (или минимального значения), причем
$y_{min }=y(0)=0^{4}-1=-1$.
Замечание. Также можно определить интервалы
монотонности функции: так как на интервале
$(-infty ; 0)$ производная
$y^{prime}(x) lt 0$, то на этом интервале функция
$y(x)=x^{4}-1$ является убывающей; на интервале
$(0 ;+infty)$ производная
$y^{prime}(x)>0$, значит заданная функция возрастает на нем.
Ответ. $y_{min }=y(0)=-1$
Второе достаточное условие экстремума
Теорема
(Второе достаточное условие экстремума)
Пусть для функции $y=f(x)$ выполнены следующие условия:
- она непрерывна в окрестности точки $x_{0}$;
- первая производная $f^{prime}(x)=0$ в точке $x_{0}$;
- $f^{prime prime}(x) neq 0$ в точке $x_{0}$ .
Тогда в точке $x_{0}$ достигается экстремум,
причем, если $f^{prime prime}left(x_{0}right)>0$, то в точке
$x=x_{0}$ функция
$y=f(x)$ имеет минимум; если
$f^{prime prime}left(x_{0}right) lt 0$, то в точке
$x=x_{0}$ функция
$y=f(x)$ достигает максимум.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Исследовать функцию $y(x)=frac{x^{2}-1}{x^{2}+1}$ на экстремум с помощью второй производной.
Решение. Находим первую производную заданной функции:
$y^{prime}(x)=left(frac{x^{2}-1}{x^{2}+1}right)^{prime}=frac{2 xleft(x^{2}+1right)-left(x^{2}-1right) cdot 2 x}{left(x^{2}+1right)^{2}}=frac{4 x}{left(x^{2}+1right)^{2}}$
Находим точки, в которых первая производная равна нулю:
$y^{prime}(x)=0 Rightarrow frac{4 x}{left(x^{2}+1right)^{2}}=0 Rightarrow x=0$
Вторая производная заданной функции:
$y^{prime prime}(x)=left(frac{4 x}{left(x^{2}+1right)^{2}}right)^{prime}=frac{4left(x^{2}+1right)^{2}-4 x cdot 2left(x^{2}+1right) cdot 2 x}{left(x^{2}+1right)^{4}}=$
$=-frac{4left(3 x^{2}-1right)}{left(x^{2}+1right)^{3}}$
В стационарной точке $x=0$ вторая производная
$y^{prime prime}(0)=-frac{4 cdot(-1)}{1^{3}}=4>0$, а значит, в этой точке функция достигает
минимум, причем $y_{min }=y(0)=frac{0^{2}-1}{0^{2}+1}=-1$.
Ответ. $y_{min }=y(0)=-1$
Остались вопросы?
Здесь вы найдете ответы.
Что подразумевается под понятием «экстремум»?
Экстремум представляет собой значение функции на определенном интервале в
момент достижения им минимального или максимального показания. Под
понятием «экстремумы» или по-другому минимумы/максимумы подразумевается
значение функции (у).
Точка экстремума – что это такое?
Если в определенной точке достигается экстремум или, иными словами,
максимальное/минимальное значение функции на заданном интервале, то эта
точка носит название точки экстремума. Из этого следует, что при
достижении минимума, точка экстремума будет названа точкой минимума, и,
наоборот, при достижении максимума эта точка будет называться точкой
максимума. В случае, когда указываются точки экстремумов (или
минимумов/максимумов) подразумеваются иксы, в которых достигаются
минимальные или максимальные значения.
Что имеется в виду под понятием «точка минимума функции»?
Любая точка x₀ будет определена в качестве точки минимума функции y = f(x)
при соблюдении условия о том, что имеется такая V, представляющая собой
окрестность (x₀ – V; x₀+V) упомянутой ранее точки, из которой для каждого
значения x <> x₀ действительно следующее неравенство:
f(x)>f(x₀).
Как описать точку минимума функции?
Под понятием «минимум функции» имеется в виду та точка на ней, в которой
функция имеет значение, являющееся наименьшим среди всех значений,
приобретаемых ею в любой из других соседних точек. Другими словами, это
означает, что в случае, когда функция, достигнув определенной точки,
прекращает падать, а, наоборот, наблюдается ее рост, то данная точка и
представляет собой точку ее минимума.
Каким образом можно вычислить значение функции y=x⁴-4x³+6x²-4x, которого она
достигает в точке своего минимума?
Для ответа на поставленный вопрос нужно отыскать точку минимума указанной
функции, в которой ее значение перестает падать. Это можно сделать
следующим образом:
y’ = 4x³ – 12x² + 12x – 4
Предположив, что минимальное значение данной функции равно 0, можно
переписать равенство в следующем виде:
4x³ – 12x² + 12x – 4 = 0
Сократим данное уравнение на 4:
x³ – 3x² + 3x – 1 = 0
Получившееся равенство также может быть записано в следующем виде после
перемены местами слагаемых:
(x³ – 1) + (-3x² + 3x) = 0
Распишем слагаемые в ином виде, чтобы избавиться от третьей степени:
(x – 1)(x² + x + 1) -3x(x – 1) = 0
Это же уравнение может выглядеть так:
(x -1)(x² + x + 1- 3x) = 0
Произведем сложение слагаемых х и -3х:
(x – 1) (x² -2x + 1) = 0
Теперь для упрощения можно переписать уравнение в таком виде:
(x – 1)(x-1)² = 0
Получившееся равенство:
(x – 1)³ = 0
В этом случае х = 1
-∞ 1 +∞
Знаками «+» и «-» обозначены значения производной.
После проведенных вычислений было установлено, что х = 1, что является
точкой минимума функции:
у = 1⁴- 4*1³ + 6*1² – 4*1 = 1 – 4 +6 – 4 = -1
Какие расчеты нужно произвести, для того чтобы вычислить точку максимума для
функции y = -x/x²+484?
Точкой максимума называется то значение х, достигнув которого, производная
начинает менять свой знак с плюса на минус. Зная это, можно перейти к
поиску точки максимума для функции, указанной в задании.
Для этого нужно начать с поиска производной, используя следующую формулу:
(U/V)’ = (U’V – UV’)/V²
Подставляем приведенные в задании значения и получаем:
y’ = (-(x² + 484) – 2x)/(x² + 484)² = (-x²-484 -2x)/(x² +484)²
Теперь следует приравнять производную к 0 и начать решать получившееся
уравнение:
(-x²-484 -2x)/(x² +484)² = 0
Упростим уравнение и получим:
(-x²-484 -2x) = 0
(x² +484)² ≠ 0
-x²-484 -2x = 0
Избавимся от минусов в уравнении:
x² + 2x +484 = 0
D < 0
В результате вычислений стало ясно, что корней нет. Это значит, что
невозможно поставить их на числовой прямой, для того чтобы проверить знаки
производной по соседству с этими точками. На основании этого можно сделать
вывод о том, что указанная в задании функция не имеет точек экстремума.
Что представляет собой точка максимума функции?
Под точкой максимума функции понимается та точка, в которой она достигает
значения, являющегося наибольшим среди тех значений, что достигаются ею в
соседних точках. Это означает, что в точке, при пересечении которой
функция прекращает расти, и наблюдается ее падение, и достигается ее
максимум.
Имеется график производной функции. Каким образом можно вычислить точки ее
максимума и минимума?
В случае, если имеется график производной функции, и при этом требуется
определить ее экстремумы, то необходимо вычислить точки пересечения этого
графика производной с осью Ох. По-другому они называются «нулями»
производной. В случае, когда, пересекая конкретную точку, график
производной восходит из области со знаком «-» в область со знаком «+», и в
это время производная меняет свой знак на противоположный, функция также
изменяется с убывания на рост. В этом случае данная точка, которая
пересекается графиком производной, представляет собой точку минимума. Если
же при пересечении графиком производной какой-либо точки он идет из
положительной в отрицательную область, а функция из возрастания меняется
на убывание, то речь идет о точке ее максимума.
Как можно вычислить экстремумы и точки экстремума функции y=4x⁴+2x²+1?
Для того чтобы найти ответ на поставленный вопрос, сначала нужно
приравнять функцию к 0:
у = 0
Это же означает, что:
4X⁴ + 2X² + 1 = 0
Введем обозначения:
Х2 = А, при этом А больше 0.
С учетом введенных обозначений равенство будет иметь следующий вид:
4A² + 2A + 1 = 0
D = 4 – 4 = 0 ; √ D = 0
A = (- 2) : 4 = (- 0,5) (< 0) 1
Очевидно, что корней нет.
Ответ: х = 0, у = 1.
Дана функция y = x² -3x+2. Как можно вычислить экстремум этой функции?
Имеется функция y = x² -3x+2, которую также можно переписать в следующем
виде:
у = -0,25+ (x-1,5)²
Отсюда следует, что:
miny = – 0,25 при условии, что х-1,5 = 0
Можно сделать вывод о том, что х = 1,5.
Запишем производную данной функции:
y ‘= (x² -3x+2)’ =2x -3
А затем приравняем ее к 0:
y ‘ = 0, значит:
2x -3 = 0.
Это позволяет сделать вывод о том, что:
x = 3/2.
Получается, что, если x < 3/2, то производная y’ < 0, и при этом функция убывает.
Если же x >3/2, то производная y’ > 0, и в этом случае функция возрастает.
x =3/2=1,5 – это единственная точка экстремума, которая является точкой
минимума.
miny =(1,5)² -3*1,5+2 = -0,25.
Как раскрыть понятие «критическая точка функции»?
Критическая точка функции представляет собой ту точку, при пересечении с
которой производная данной функции становится равной 0, либо она вовсе не
существует.
Возможно ли привести доказательства того, что функция f(x) =2x – 3/x не
может иметь критической точки?
Для начала нужно определить, что под критической точкой функции
подразумевается та точка, при пересечении с которой производная
приобретает нулевое значение, либо же эта производная просто не существует
в этой точке, что означает, что функцию в данной точке невозможно
дифференцировать.
Проверим, применимо ли это утверждение к упомянутой в задании функции:
f ‘(x) =(sin2x – 3x)’ = 2sin2x-3
Приравняем производную функции к 0:
f ‘(x) = 0, это значит, что 2sin2x-3 = 0.
Следовательно:
sin2x= 3 2 не имеет решения
Ответ: заданная функция не имеет критических точек и существует при любых
х.
Каким способом можно определить критические точки функции y=|x|/1+x²?
Под критическими точками функции понимаются те точки, в которых ее
производная равна 0 или вовсе не существует.
В задании дана функция:
y=|x|/(1+x²)
Предположим, что x<0, тогда:
y=-x/(1+x²)
Запишем производную функции и приравняем ее к 0:
y`=(-1-x²+2x²)/(1+x²)²=(x²-1)/(1+x²)²=(x-1)(x+1)/(1+x²)²=0
х = 1 не соответствует условию, значит х = -1.
Теперь предположим, что x≥0.
Снова записываем производную имеющейся функции и приравниваем ее к 0:
y`=(1+x²-2x²)/(1+x²)²=(1-x²)/(1+x²)²=(1-x)(x+1)/(1+x²)²=0
х = – 1 не отвечает условию, значит х = 1.
Ответ: х = 1, х = -1.
Читать дальше: наибольшее и наименьшее значение функции.
