Как найти расстояние от прямой до сферы

Нужно добиться следующего результат, как показано на рисунке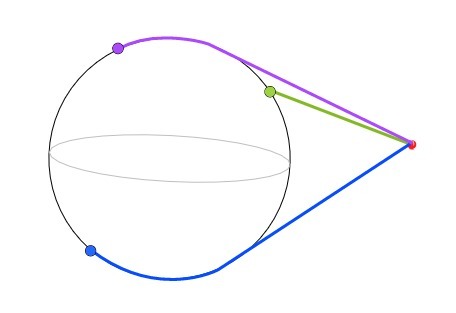

Известны координаты красной точки и координаты (широта/долгота) на сфере (из можно конвертировать в мировые (3D)

Если провести прямую до нужной точки, то в случае ее нахождения по ту сторону сферы прямая будет пересекать сферу. Конечно, можно было бы перевести первую точку пересечения в координаты сферы и уже по широте/долготе найти расстояние и прибавить его к расстоянию к первой точке, но так расстояние будет преувеличеным, если точка находится ровно с обратной стороны.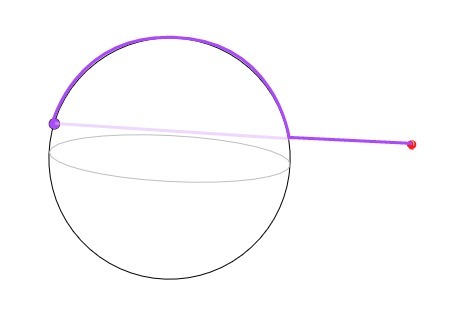

UPD: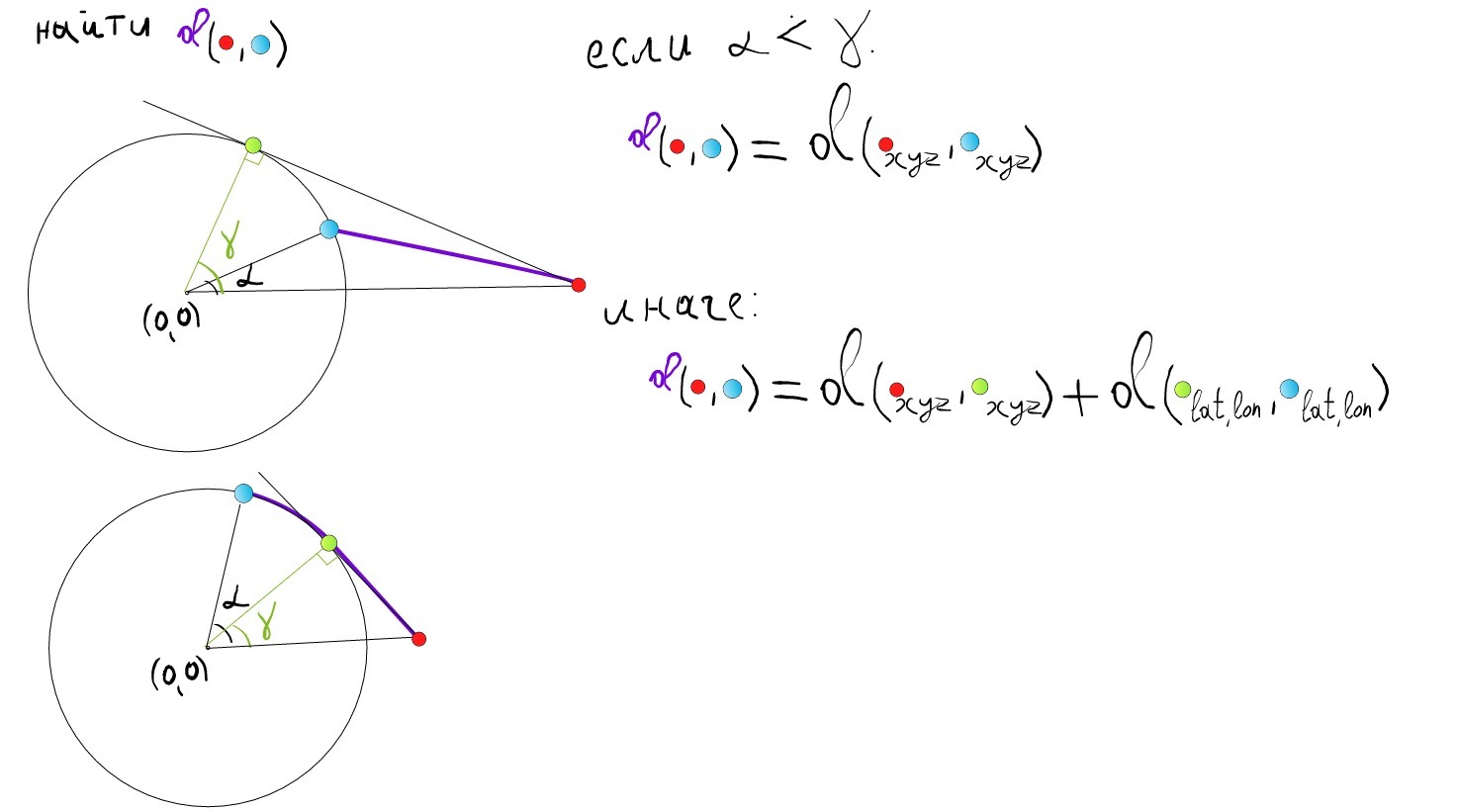

осталось разобраться как найти точку касательной к сфере

Вот мое собственное решение, основанное на идее в спроси доктора Матема. Буду рад услышать ваш отзыв.

Отказ от ответственности в первую очередь. Это решение подходит для сфер. Земля не является сферой, и система координат (WGS 84) не предполагает, что это сфера. Так что это всего лишь приближение, и я не могу точно оценить ошибку. Кроме того, для очень малых расстояний, вероятно, также можно получить хорошее приближение, если предположить, что все является просто компланарностью. Опять же, я не знаю, насколько «маленькими» должны быть расстояния.

Теперь к делу. Я назову концы линий A, B и третью точку C. По сути, алгоритм заключается в следующем:

1. сначала преобразовать координаты в декартовы координаты (с началом в центре Земли) – например здесь.

2. Вычислите T, точку на прямой AB, ближайшую к C, используя следующие 3 векторных произведения:

   G = А х В

   Ф = С х Г

   Т = G x F

3. Нормализовать T и умножить на радиус Земли.

4. Преобразуйте T обратно в долготу широту.
5. Рассчитайте расстояние между T и C – например здесь.

Этих шагов достаточно, если вы ищете расстояние между C и большим кругом, определяемым A и B.Если, как и меня, вас интересует расстояние между C и более коротким отрезком линии, вам нужно сделать дополнительный шаг, чтобы проверить, что T действительно находится на этом участке. Если это не так, то ближайшей точкой обязательно будет один из концов A или B – проще всего проверить, какой из них.

В общем, идея трех векторных произведений заключается в следующем. Первый (G) дает нам плоскость большого круга A и B (то есть плоскость, содержащую A, B и начало координат). Вторая (F) дает нам большую окружность, проходящую через C и перпендикулярную G. Тогда T – это пересечение больших окружностей, определяемых F и G, полученное до правильной длины путем нормализации и умножения на R.

Вот часть кода Java для этого.

Нахождение ближайшей точки на большом круге. Входы и выходы представляют собой массивы длиной 2. Промежуточные массивы имеют длину 3.

double[] nearestPointGreatCircle(double[] a, double[] b, double c[])
{
    double[] a_ = toCartsian(a);
    double[] b_ = toCartsian(b);
    double[] c_ = toCartsian(c);

    double[] G = vectorProduct(a_, b_);
    double[] F = vectorProduct(c_, G);
    double[] t = vectorProduct(G, F);
    normalize(t);
    multiplyByScalar(t, R_EARTH);
    return fromCartsian(t);
}

Поиск ближайшей точки на отрезке:

double[] nearestPointSegment (double[] a, double[] b, double[] c)
{
   double[] t= nearestPointGreatCircle(a,b,c);
   if (onSegment(a,b,t))
     return t;
   return (distance(a,c) < distance(b,c)) ? a : c;
} 

Это простой метод проверки, находится ли точка T, которая, как мы знаем, находится на том же большом круге, что и A и B, на более коротком сегменте этого большого круга. Однако есть более эффективные методы для этого:

   boolean onSegment (double[] a, double[] b, double[] t)
   {
     // should be   return distance(a,t)+distance(b,t)==distance(a,b), 
     // but due to rounding errors, we use: 
     return Math.abs(distance(a,b)-distance(a,t)-distance(b,t)) < PRECISION;
   }    

8.3. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ

СПОВЕРХНОСТЬЮ ВРАЩЕНИЯ

Точками пересечения прямой с поверхностью вращения являются точки пересечения этой прямой с контуром сечения поверхности вспомогательной плоскостью, проведенной через эту прямую (рис. 8.14).

а)

б)

Рис. 8.14. Пересечение прямой линии с поверхностью: а) модель; б) эпюр

В общем случае, алгоритм решения задачи построения точек пересечения прямой с поверхностью вращения состоит в следующем:

1. Провести плоскость частного положения α через прямую l. Вспомогательная секущая плоскость должна пересекать поверхность по линии, проекции которой можно легко построить – по окружности или прямой.

159

2.Построить линию сечения поверхности плоскостью α.

3.Определить точки пересечения прямой l с линией сечения – точки А и В.

4.Обвести чертеж прямой с учетом видимости точек пересечения. Видимую линию обводят толстой основной линией, невидимую – тонкой штриховой, а внутри между точками входа и выхода – сплошной тонкой линией (считается, что линия отсутствует).

Построение значительно упрощается, если:

– прямая является проецирующей (рис. 8.15, а). Вырожденная проекция прямой (точка) обладает собирательным свойством. Поэтому вырожденная проекция прямой совпадает с проекциями точек пересечения прямой с поверхностью вращения. Другие проекции точек пересечения определяются при помощи построения параллелей. На примере, вырож-

денная проекция прямой l3 совпадает с А3 и В3. На плоскости П1 проекции А1 и В1 строятся при помощи параллели (окружности), на П2 – по линии связи;

– поверхностью вращения является цилиндр (рис. 8.15, б). Вырожденная проекция цилиндра (окружность) обладает собирательным свойством. Поэтому проекции точек пересечения прямой с поверхностью лежат на вырожденной проекции цилиндра. Другие проекции точек пересечения определяются по линии связи. На примере, вырожденная про-

екция цилиндра находится на П3. Пересечение прямой и вырожденной проекции определяют проекции А3 и В3. На плоскости П2 и П1 проекции точек А и В строятся по линии связи.

а) б)

Рис. 8.15. Пересечение: а) проецирующей прямой с тором; б) прямой с цилиндром

160

Задача 1.

Построить пересечение прямой l с поверхностью сферы: Дано: Решение:

161

Задача 2.

Построить пересечение прямой l с поверхностью конуса: Дано: Решение:

162

Дано:

Дано:

Задача 3.

Построить пересечение прямой l с поверхностью тора:

Решение:

Решение:

164

Дано:

Дано:

Задача 4.

Построить пересечение прямой l с поверхностью цилиндра:

Решение:

Решение:

165

8.4. ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ ОТ ТОЧКИ ДО ПОВЕРХНОСТИ

Расстоянием от точки A до поверхности вращения является расстояние от точки A до образующей поверхности вращения, которая лежит в плоскости , заданной данной точкой A и осью i поверхности вращения.

Для определения натуральной величины расстояния от точки A до поверхности вращения необходимо выполнить следующие преобразова-

ния (рис.8.16):

1.Вращением точки A вокруг оси i вывести точку A в плоскость ‘, параллельную плоскости проекций (на одной плоскости проекций проекция точки A движется по окружности, а на другой плоскости проекций проекция точки A перемещается по линии, параллельной смежной плоскости проекций).

2.После такого преобразования, из точки A’ опустить перпендикуляр к контурной образующей поверхности вращения до пересечения в точке В’. Отрезок перпендикуляра A’В’ – натуральная величина расстояния от точки до поверхности вращения.

3.Чтобы найти точку В, необходимо выполнить обратное преобра-

зование – вращение плоскости ‘ со всеми точками в исходное положение.

Рис. 8.16. Определение расстояния от точка до поверхности вращения

Рассмотрим решение задач по изучаемой теме.

166

Задача 1.

Определить расстояние от точки А до поверхности сферы: Дано: Решение:

Задача 2.

Определить расстояние от точки А до поверхности цилиндра: Дано: Решение:

167

Задача 3.

Определить расстояние от точки А до поверхности конуса: Дано: Решение:

Задача 4.

Определить расстояние от точки А до поверхности тора: Дано: Решение:

168