Цель этой
работы: с помощью экспериментальной установки определить ускорение
скольжения бруска по наклонной плоскости.
Для выполнения этой работы мы будем использовать оборудование
из комплекта № 5 в составе: штатив с креплением для наклонной плоскости,
направляющая со шкалой, деревянный брусок с пусковым магнитом, электронный
секундомер с датчиками, линейка и транспортир.
Прежде чем приступить к работе давайте с вами вспомним, что неравномерное
движение — это такое движение, при котором тело, за любые равные промежутки
времени совершает разные перемещения.
Из всех видов неравномерного движения в школе изучают самое
простое — прямолинейное равноускоренное движение. Так называют движение,
при котором за любые равные промежутки времени скорость тела изменяется на одну
и туже величину, а траекторией движения тела является прямая линия.
Для того,
чтобы описать насколько быстро меняется скорость тела, в физике ввели величину,
которую назвали ускорением тела. Ускорение — это физическая векторная
величина, равная отношению изменения скорости к промежутку времени, в течение
которого это изменение произошло:
Именно ускорение тела нам и предстоит определить в данной
работе. Однако очевидно, что данная формула нам не подходит, так как в ней
фигурирует скорость тела, измерить которую прямыми измерения в классе мы не
можем. А анализ оборудования нам говорит о том, что для определения ускорения
мы с вами должны воспользоваться формулой, для определения перемещения тела при
его равноускоренном движении:
Так как мы будем изучать прямолинейное равноускоренное
движение без начальной скорости при котором направление векторов перемещения и
ускорения совпадают, то мы с вами можем записать, что модуль вектора
перемещения прямо пропорционален квадрату промежутка времени, в течение
которого это перемещение было совершено:
Отсюда, зная пройденный телом путь и время его движения, мы с
вами легко можем определить модуль ускорения, с которым двигалось тело:
Теперь
приступим к выполнению работы. Итак, для начала давайте соберём экспериментальную
установку. Для этого на штативе закрепим наклонную плоскость. После этого,
используя транспортир, установим направляющую под углом 45° к поверхности
стола.
Далее
установим на направляющей датчики секундомера: первый расположим в точке 0, а
второй — в точке 40 см. При пуске бруска пусковой магнит мы установим на пол
сантиметра выше первого датчика.
Далее мы
сделаем рисунок нашей установки. Для этого схематически изобразим штатив с
прикреплённой к нему направляющей. На направляющей расположим брусок так, как
это показано на экране. Также на рисунке мы должны будем указать перемещение
тела и направление вектора ускорения. Не лишним будет показать и угол, под
которым установлена направляющая.
Запишем формулы, которыми будем пользоваться при выполнении
данной работы. Как мы уже вспоминали, при прямолинейном равноускоренном
движении без начальной скорости при котором направление векторов перемещения и
ускорения совпадают, модуль вектора перемещения (путь) прямо пропорционален
квадрату промежутка времени, в течение которого это перемещение было совершено:
С формулами разобрались, теперь запишем результат измерения
пути, пройденного бруском, с учётом абсолютной погрешности измерения (путь нам
дан в условии задания):
Теперь приступим непосредственно к выполнению работы. Итак,
подключаем электронные датчики к секундомеру, а брусок устанавливаем так, чтобы
пусковой магнит находился на пол сантиметра выше первого датчика. Отпускаем
брусок.
Значение промежутка времени, за которое брусок преодолел
заданный отрезок пути, записываем в бланке ответов с учётом погрешности
измерения:
Опыт повторяем ещё два раза, каждый раз записывая результаты
измерений.
Прямы измерения мы с вами завершили. Теперь давайте определим
среднее значение промежутка времени, как среднее арифметическое значение всех
трёх опытов:
Найденное среднее значение времени мы должны записать также с
учётом погрешности измерения:
И, наконец, мы определяем ускорение бруска. Для чего в
расчётную формулу подставляем значения пути и среднего времени движения бруска
на этом отрезке пути:
В выводе напишем: ускорение бруска при его движении по
наклонной плоскости равно 4,76 м/с2.
Содержание
- Чему равен модуль ускорения бруска при скольжении по столу
- Что такое модуль ускорения?
- Как вычислить модуль ускорения бруска при скольжении по столу?
- Почему необходимо знать модуль ускорения бруска при скольжении по столу?
- Итог
- Чему равен модуль ускорения бруска при скольжении по столу
- Что такое модуль ускорения
- Чему равен модуль ускорения бруска при скольжении по столу
- Вывод
Чему равен модуль ускорения бруска при скольжении по столу
Скольжение на твердой поверхности является одним из основных механизмов перемещения как для механизмов, так и для людей. Когда мы помещаем брусок на стол и начинаем толкать его с некоторой начальной скоростью, у него появляется ускорение, которое зависит от множества параметров, таких как масса бруска, сила трения и прочность поверхности.
Что такое модуль ускорения?
Модуль ускорения — это величина, которая определяет скорость изменения скорости тела во времени. Он измеряется в метрах в секунду в квадрате (м/с^2).
Как вычислить модуль ускорения бруска при скольжении по столу?

Модуль ускорения бруска зависит от многих факторов. Одним из самых важных является сила трения между бруском и поверхностью стола. Если эта сила мала, то ускорение бруска будет большим. Если же сила трения большая, ускорение будет меньшим. Ускорение бруска также зависит от его массы и силы, с которой мы его толкаем.
Точную формулу для вычисления модуля ускорения можно представить следующим образом:
Fтр / m = a
Где Fтр — это сила трения, m — масса бруска, а a — модуль ускорения.
Почему необходимо знать модуль ускорения бруска при скольжении по столу?

Знание модуля ускорения бруска при скольжении по столу полезно при производстве различных технических устройств, таких как конвейеры, подъемники и т.д. Оно также необходимо при проведении экспериментов и в исследовательских работах.
Итог
Модуль ускорения бруска при скольжении по столу — это важная физическая величина, которая определяет скорость изменения скорости тела во времени. Он зависит от многих факторов, таких как сила трения, масса бруска и сила, с которой мы его толкаем. Знание этой величины полезно в различных областях промышленности и науки.
Чему равен модуль ускорения бруска при скольжении по столу

В физике очень важно понимать, что все тела находятся в движении, и при переходе из движения на покой и наоборот тело испытывает ускорение. При этом ускорение может быть равномерным или переменным. В случае с бруском, который скользит по столу, модуль ускорения играет ключевую роль в понимании его движения.
Что такое модуль ускорения
Модуль ускорения является векторной физической величиной, которая обозначается через символ а (от лат. acceleratio). Модуль того самого ускорения равен отношению разности скоростей (v) к разности временных промежутков (t), за которые это изменение скорости происходит.
а = (v1 — v2) / (t1 — t2)
Именно это значение может помочь определить движение бруска при его скольжении по столу.
Чему равен модуль ускорения бруска при скольжении по столу
Если брусок находится в покое, то его ускорение равно нулю. Но если брусок начнет движение, то сразу же он испытает ускорение. В случае со скольжением по столу, ускорение бруска будет зависеть от нескольких факторов.
- Первый фактор — это сила трения, которая возникает между поверхностью стола и бруском.
- Второй фактор — это масса бруска, которая также влияет на ускорение.

Причем, чем меньше масса бруска, тем меньше будет сила трения и тем выше будет его ускорение. В свою очередь, при большой массе бруска, и сила трения будет больше, а ускорение — меньше.
Также стоит учитывать, что ускорение бруска будет направлено в противоположную сторону к силе трения между бруском и столом.
Вывод
Таким образом, модуль ускорения бруска при скольжении по столу зависит от нескольких факторов, таких как масса бруска и сила трения. Более легкие бруски скользят по столу быстрее, а более тяжелые — медленнее. Также стоит учитывать, что ускорение бруска будет направлено в противоположную сторону к усилию, приводящему к скольжению.
Задание № 24585
В эксперименте была поставлена задача определить ускорение бруска при скольжении вниз по наклонной плоскости длиной I (1).
Сначала была получена формула для расчёта ускорения:
[math]a=frac{mgsinalpha-mu mgcosalpha}m=g(sinalpha-mu cosalpha)[/math]
Затем был исполнен подробный рисунок с размерами наклонной плоскости а (2), с (3) и положением векторов сил и их проекций.
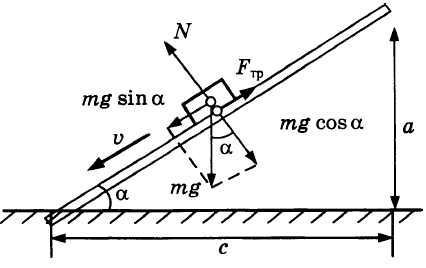
Значение коэффициента трения [math]mu[/math] (4) дерева по дереву экспериментатор взял из справочных данных. Сила трения Fтр (5) и сила тяжести mg (6) были измерены динамометром.
Какими из помеченных цифрами величин достаточно воспользоваться, чтобы определить ускорение бруска?
Показать ответ
Комментарий:
Величины 1,2,3 нужны для вычисления синуса и косинуса нужно угла, а коэффициент [math]mu[/math] поможет посчитать силу трения. Всё остальное уже известно, значит для вычисления ускорения нужны величины 1,2,3,4.
Ответ: 1234
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.
Брусок массой 2 кг скользит по горизонтальной плоскости под действием груза массой 0,5 кг, прикрепленного к концу нерастяжимой нити, перекинутой через неподвижный блок. Коэффициент трения бруска о поверхность равен 0,1. Найти ускорение движения бруска и силу натяжения нити.
Оцените сложность задачи:
0 голосов, средняя сложность: 0.0000
Решения задачи
Данные задачи: брусок скользит по горизонтальной плоскости
| Масса бруска | $m_{1}$ | $2$ | $кг$ |
|---|---|---|---|
| Масса груза | $m_{2}$ | $0,5$ | $кг$ |
| Коэффициент трения бруска о поверхность | $μ$ | $0,1$ | |
| Ускорение движения бруска | $a$ | $?$ | |
| Сила натяжения нити | $T$ | $?$ |
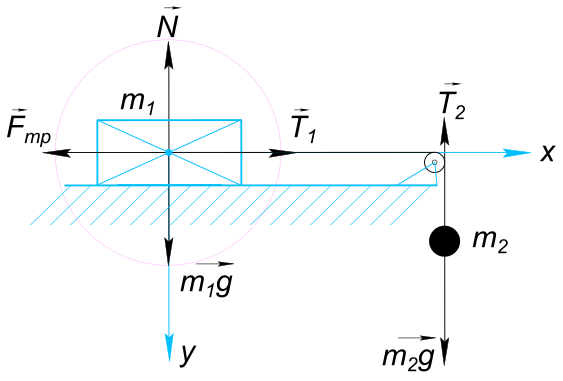
Изобразим на рисунке условия задачи
На брусок действуют силы:
Сила тяжести
$ m_{1}g $
Сила нормальной реакции опоры
$ N $
Сила натяжения нити
$ T_{1} $
Сила трения
$ F_{тр} $
На груз действуют силы:
Сила тяжести
$ m_{2}g $
Сила натяжения нити
$ T_{1} $
Запишем для бруска и для груза уравнения в векторной форме
$ vect{m_{1}g}+vect{N_{}}+vect{T_{1}}+vect{F_{тр}} = vect{m_{1}a_{1}} $
$ vect{m_{2}g}+vect{T_{2}} = vect{m_{2}a_{2}} $
Спроецируем силы действующие на брусок на выбранные направления осей x и y, получим:
ось x:
$ T_{1}-F_{тр} = m_{1}a_{1} $
ось y:
$ m_{1}g – N = 0 $
Из уравнения для оси y
$ m_{1}g = N $
Поэтому
$ F_{тр} = μN = μm_{1}g $
Тогда уравнение для оси x принимает вид
$ T_{1}-μm_{1}g = m_{1}a_{1} $
Спроецируем силы действующие на груз на направление оси y, получим:
ось y:
$ m_{2}g – T_{2} = m_{2}a_{2} $
Так как нить невесомая и нерастяжимая, а масса блока пренебрежимо мала, поэтому
$ T_{1} = T_{2} = T $
и
$ |a_{1}| = |a_{2}| = a $
Тогда уравнения для бруска и для груза принимаю вид
$ T – μm_{1}g = m_{1}a $
$ m_{2}g – T = m_{2}a $
Решаем их как систему уравнений:
$ m_{2}g – m_{2}a = T $
тогда
$ m_{2}g – m_{2}a – μm_{1}g = m_{1}a $
и
$ (m_{2} – μm_{1})g = (m_{2}+m_{1})a $
откуда
$ a = frac{(m_{2} – μm_{1})g}{m_{2}+m_{1}}=frac{(0,5 – 0,1×2)×10}{0,5+2}=1,2 frac{м}{с^{2}} $
и
$ T = m_{2}(g – a) = 0,5×(10 – 1,2) = 4,4 Н $
Ответ:
$ Ускорение движения бруска 1,2 frac{м}{с^{2}} $
и
$ Сила натяжения нити 4,4 Н $
Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь
1. Тела в начальном состоянии движутся друг относительно друга
Пусть на гладком столе лежит доска длиной L и массой mд. На краю доски находится небольшой брусок массой mб (рис. 24.1). Коэффициент трения между бруском и доской μ. В начальный момент доска покоится, а бруску толчком сообщают начальную скорость  0, направленную вдоль доски.
0, направленную вдоль доски.
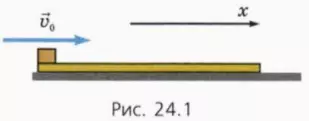
Как будут двигаться тела?
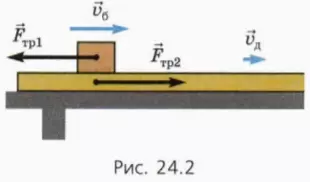
При скольжении бруска по доске на него и на доску действуют противоположно направленные равные по модулю силы трения скольжения  тр1 и
тр1 и  тр2 (рис. 24.2). В результате скорость бруска будет уменьшаться, а скорость доски – увеличиваться.
тр2 (рис. 24.2). В результате скорость бруска будет уменьшаться, а скорость доски – увеличиваться.
Возможны два варианта дальнейшего развития событий:
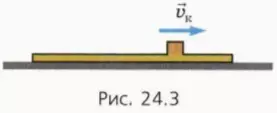
1) брусок будет скользить по доске, пока их скорости не станут равными, то есть пока брусок не остановится относительно доски. Начиная с этого момента силы трения перестанут действовать на доску и брусок, и они будут скользить по гладкому столу вместе как единое целое с постоянной конечной скоростью  к (рис. 24.3);
к (рис. 24.3);
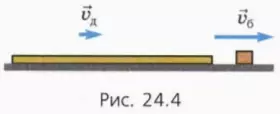
2) скорости бруска и доски не успеют сравняться до того момента, когда брусок дойдёт до противоположного конца доски. В таком случае брусок соскользнёт с доски, после чего они будут двигаться по столу с различными скоростями  б и
б и  д, причём vб > vд (рис. 24.4).
д, причём vб > vд (рис. 24.4).
Рассмотрим сначала случай, когда доска с бруском будут двигаться как единое целое (см. рис. 24.3), и выведем условие, при котором этот случай реализуется.
? 1. Как зависят от времени проекции скорости бруска и доски на ось x, показанную на рисунке 24.1?
? 2. Через какой промежуток времени доска и брусок будут двигаться как единое целое?
? 3. Чему будет равна скорость доски с бруском, когда они будут двигаться как единое целое?
Найдём теперь условие того, что брусок будет скользить по доске до тех пор, пока их скорости не сравняются.
Так произойдёт, если путь l, пройденный бруском относительно доски, не превышает длины доски L. Путь l мы найдём, определив ускорение бруска относительно доски.
? 4. Чему равно ускорение бруска относительно доски?
? 5. Чему равен путь l, пройденный бруском относительно доски до того момента. когда их скорости сравнялись?
? 6. При выполнении какого условия доска и брусок будут двигаться как единое целое?
Рассмотрим конкретный пример.
? 7. Небольшой брусок массой 200 г находится на краю доски массой 1 кг, лежащей на гладком столе. Коэффициент трения между доской и бруском 0,5. В начальный момент скорость бруска 2,4 м/с, а доска покоится. Через некоторое время брусок и доска стали двигаться как единое целое.
а) С каким ускорением относительно доски двигался брусок?
б) Сколько времени брусок двигался по доске?
в) Какова минимально возможная длина доски?
г) Чему равна скорость доски с бруском, когда они движутся как единое целое?
Пусть теперь условие того, что доска и брусок станут двигаться как единое целое, не выполнено. Тогда брусок соскользнёт с доски, и скорость каждого тела при дальнейшем скольжении по столу останется такой, какой она была в момент соскальзывания бруска.
Чтобы найти конечные скорости бруска и доски, можно поступить, например, так.
1) Зная длину доски L, начальную скорость бруска v0 и ускорение бруска относительна доски, найдём время tск, в течение которого брусок будет скользить по доске.
2) Зная время tск, найдём скорости бруска и доски в момент соскальзывания бруска с доски. С этими скоростями они и будут скользить далее по столу.
Воспользуйтесь этими советами при выполнении следующего задания.
? 8. Небольшой брусок массой 400 г находится на краю доски длиной 1 м и массой 800 г, лежащей на гладком столе (рис. 24.1). Коэффициент трения между доской и бруском 0,2. В начальный момент скорость бруска 3 м/с, а доска покоится.
а) С каким по модулю ускорением движется брусок относительно доски?
б) Какой должна была бы быть длина доски, чтобы скорость бруска относительно доски стала равной нулю?
в) Сколько времени брусок движется по доске согласно условию задания?
г) Чему равна скорость бруска относительно стола в тот момент, когда брусок соскользнёт с доски?
д) Какой путь пройдёт доска относительно стола до того момента, когда брусок соскользнёт с доски?
2. Тела в начальном состоянии покоятся друг относительно друга
На гладком столе лежат один на другом два бруска (рис. 24.5). Массу нижнего бруска обозначим mн‚ в массу верхнего — mв. Коэффициент трения между брусками μ.
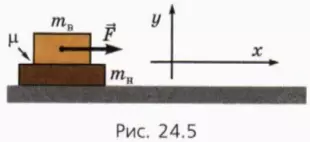
К верхнему бруску прикладывают горизонтально направленную вправо силу  .
.
Самое главное в таких задачах — увидеть две возможности:
1) бруски могут начать двигаться друг относительно друга — тогда между ними будут действовать силы трения скольжения;
2) бруски могут начать двигаться как единое целое — тогда между ними будут действовать силы трения покоя.
Начнём с первой возможности: в таком случае модуль силы трения скольжения, действующей на каждое тело, равен μmвg. Модуль же силы трения покоя заранее неизвестен.
? 9. Объясните, почему в случае, когда верхний брусок скользит по нижнему, их ускорения относительно стола выражаются формулами
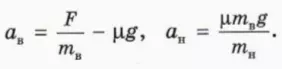
Учтём теперь, что сила  приложена к верхнему бруску и что бруски вначале покоились. Если верхний брусок скользит по нижнему, то ускорение верхнего бруска больше, чем ускорение нижнего. Это позволяет получить условие того, что бруски движутся друг относительно друга.
приложена к верхнему бруску и что бруски вначале покоились. Если верхний брусок скользит по нижнему, то ускорение верхнего бруска больше, чем ускорение нижнего. Это позволяет получить условие того, что бруски движутся друг относительно друга.
? 10. Объясните, почему бруски будут двигаться друг относительно друга, если
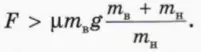
? 11.На столе стоит тележка массой 500 г, а на ней лежит кирпич массой 2,5 кг. Коэффициент трения между кирпичом и тележкой 0,5, трением между тележкой и столом можно пренебречь. С какой горизонтальной силой надо тянуть кирпич, чтобы стащить его с тележки?
Итак, чтобы стащить тяжёлый кирпич со сравнительно лёгкой тележки, надо приложить к нему горизонтальную силу, которая в несколько раз превышает вес кирпича!
? 12. Объясните, почему тела движутся как единое целое, если
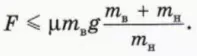
? 13. Объясните, почему, когда бруски движутся как единое целое, их (общее) ускорение а и модуль действующей на каждый брусок силы трения покоя Fтр.пок выражаются формулами
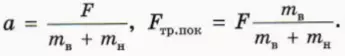
Рассмотрим теперь пример, когда горизонтальная сила приложена к нижнему бруску.
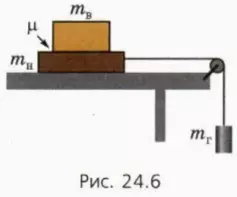
Пусть на гладком горизонтальном столе лежит брусок массой mн, а на нём — брусок массой mв (рис. 24.6). Коэффициент трения между брусками μ. К нижнему бруску привязана лёгкая нерастяжимая нить, переброшеивая через блок, а к нити подвешен груз массой mг. Как будут двигаться тела?
В этой ситуации тоже есть две возможности:
1) бруски могут начать двигаться друг относительно друга;
2) бруски могут начать двигаться как единое целое.
На этот раз проще начать со второй возможности, потому что, когда бруски движутся как единое целое, мы можем рассматривать систему, состоящую только из двух тел — объединённого бруска массой M = mв + mн и груза массой mг.
? 14. С каким ускорением движутся бруски как единое целое?
? 15. С каким максимально возможным ускорением могут двигаться бруски как единое целое?
Подсказка. Ускорение верхнему бруску сообщает сила трения покоя, которая не превышает силу трения скольжения.
? 16. Объясните, почему бруски движутся как единое целое, если выполнено соотношение
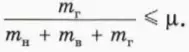
Если это соотношение не выполнено. то бруски будут двигаться порознь. Ускорение верхнему бруску сообщает в таком случае сила трения скольжения, равная по модулю μmвg. Такая же по модулю, но противоположно направленная сила трения скольжения действует на нижний брусок.
? 17. Каковы ускорения брусков, если они движутся друг относительно друга?
? 18. На гладком горизонтальном столе лежит брусок массой mн = 0,5 кг, а на нём — другой брусок массой mв = 0,3 кг (см. рис. 24.6). К нижнему бруску привязана лёгкая нерастяжимая нить, переброшенная через блок, и к нити подвешен груз массой mг = 0,2 кг. В начальный момент бруски покоятся.
а) При каком наименьшем коэффициенте трения μmin между брусками они будут двигаться как единое целое?
б) С каким ускорением (ускорениями) движутся бруски при коэффициенте трения между ними 0,5?
в) С каким ускорением (ускорениями) движутся бруски, если коэффициент трения между ними равен 0,1?
Дополнительные вопросы и задания
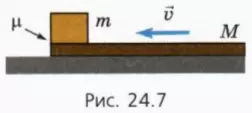
19. На гладком столе лежит доска длиной l и массой M. На одном конце доски находится небольшой брусок массой m (рис. 24.7). Коэффициент трения между бруском и доской μ. В начальный момент тела покоятся. Какую наименьшую скорость надо толчком сообщить доске, чтобы она выскользнула из-под бруска?
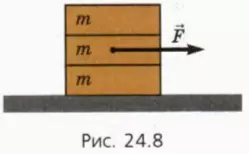
20. На гладком столе лежат один на другом три одинаковых бруска массой m = 100 г каждый (рис. 24.8). Коэффициент трения между брусками μ = 0,2. К среднему бруску приложена горизонтально направленная сила  .
.
а) С каким максимально возможным ускорением может двигаться верхний брусок?
б) С каким максимально возможным ускорением может двигаться нижний брусок?
в) При каких значениях силы F все бруски будут двигаться как единое целое?