Данный калькулятор предназначен для построения графиков функций онлайн.
Графики функций – это множество всех точек, представляющих геометрический вид функции; при этом x – любая точка из области определения функции, а все y – точки, равные соответствующим значениям функции. Другими словами, график функции y=f(x) является множеством всех точек, абсциссы и ординаты которых соответствуют уравнению y=f(x).
Изобразить график функции абсолютно точно в большинстве случаев невозможно, так как точек бесконечно много, трудно найти все точки графика функции. В таких случаях можно построить приблизительный график функции. Чем больше точек берется в расчет, тем график более точный.
Данный сервис дает возможность провести исследование графика функции наиболее точно, так как программа строит график функции онлайн в прямоугольной системе координат на определенном интервале значений с учетом максимального количества точек. Также можно построить несколько графиков функций в одной координатной плоскости. Подробная инструкция с примерами по вводу исходных данных представлена ниже.

 : x^a
: x^a
модуль x: abs(x)
Сервис поддерживает возможность построения графиков функций как вида  , так и вида
, так и вида  . Для того, чтобы построить график функции
. Для того, чтобы построить график функции  на отрезке
на отрезке ![x in left[ {a,b} right]](https://upload.wikimedia.org/math/7/4/2/742cbcce0d00d20060f55c3603104e64.png) нужно написать в строке: f[x],{x, a, b}. Если Вы хотите, чтобы диапазон изменения ординаты
нужно написать в строке: f[x],{x, a, b}. Если Вы хотите, чтобы диапазон изменения ординаты  был конкретным, например
был конкретным, например ![y in left[ {c,d} right]](https://upload.wikimedia.org/math/5/3/0/530e43b31b783941629e7b4a8d2c8866.png) , нужно ввести: f[x],{x, a, b},{y, c, d}.
, нужно ввести: f[x],{x, a, b},{y, c, d}.
- Примеры
- x^2+x+2, {x,-1,1};
- x^2+x+2, {x,-1,1},{y,-1,5};
- Sin[x]^x, {x,-Pi,E};
- Sin[x]^x, {x,-Pi,E},{y,0,1}.
Если Вам требуется построить сразу несколько графиков на одном
рисунке, то перечислите их, используя союз
«И»:f[x]&&g[x]&&h[x]&&…&&t[x],{x,
a, b}.
- Примеры
- x&&x^2&&x^3, {x,-1,1},{y,-1,1};
- Sin[x]&&Sin[5x]&&Sin[10x]&&Sin[15x], {x,-5,5}.
Для того, чтобы построить график функции  на прямоугольнике
на прямоугольнике ![x in left[ {a,b} right],y in left[ {c,d} right]](https://upload.wikimedia.org/math/8/2/b/82b905749a5dce2a347335bbfa1eb8f1.png) , нужно написать в строке: f[x, y],{x, a, b},{y, c, d}. К сожалению, диапазон изменения аппликаты
, нужно написать в строке: f[x, y],{x, a, b},{y, c, d}. К сожалению, диапазон изменения аппликаты  пока что нельзя сделать конкретным. Тем не менее, интересно отметить, что при построении графика функции
пока что нельзя сделать конкретным. Тем не менее, интересно отметить, что при построении графика функции  Вы получите не только поверхность, которую она определяет, но и «контурную карту» поверхности (линии уровня).
Вы получите не только поверхность, которую она определяет, но и «контурную карту» поверхности (линии уровня).
- Примеры
- Sin[x^2+y^2],{x,-1,-0.5},{y,-2,2};
- xy,{x,-4,4},{y,-4,4}.
|
|||||||||
|
|||||||||
|
|||||||||
|
Для задания области (например, 1≤x≤7) используйте пределы <= или >=.
Примеры ограничений для функции:
Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3).
Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3).
Также можно начертить график по точкам. Необходимо вставить данные для X (первый столбец) и Y (второй и последующие столбцы).
Построение графика функции в Excel осуществляется в два этапа:
- На первом этапе при заданном интервале [a;b] и шаге h рассчитываются значения функции
y=f(x). - На втором этапе с помощью инструмента Excel Мастер диаграмм строится визуализация рассчитанных значений.
Чтобы построить трехмерный график в Excel, необходимо указать функцию f(x,y), пределы по x и y и шаг сетки h.
Точки пересечения функций

Примеры кривых
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- – умножение
- 3/x
- – деление
- x^2
- – возведение в квадрат
- x^3
- – возведение в куб
- x^5
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- – число Пи
- e
- – основание натурального логарифма
- i
- – комплексное число
- oo
- – символ бесконечности
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


на главную
Построить график функции онлайн
Поддержать сайт![]()
←Вернуться в «Калькуляторы онлайн»
| y = | |||
| y = | |||
Здесь будет анализ функции… |
Инструкции
- Чтобы построить график функции онлайн:
- укажите функцию в поле выше в виде «y = x2 – 3»;
- нажмите кнопку «Построить график функции»;
- ожидайте результат анализа функции (точки пересечения с осями координат) и график функции под полем задания функции.
При необходимости вы можете построить одновременно графики двух функций онлайн. Для этого нажмите кнопку
«Добавить функцию».
В случае построения двух графиков функции будут показаны их точки пересечения.
Таблица обозначений для задания функций
| Математическая операция | Символ | Пример использования | ||||
|---|---|---|---|---|---|---|
| Десятичная дробь | Можно и через точку, и через запятую. | «2,789» или «2.879» | ||||
| Сложение | «+» | x + 1 | ||||
| Вычитание | «-» | x – 2.5 | ||||
| Умножение | «*»(shift + 8) |
2 * x
Коэффициент при «x» можно записывать без знака умножения. Но при умножении скобок обязательно использовать символ «*». Правильно: «(2x – 1) * (6.7 – x)». |
||||
| Деление | «/» (знак вопроса на английской раскладке) | (x – 1) / 2 | ||||
| Дробь |
Кнопка 
|
|
||||
| Модуль |
Кнопка 
|
|x – 2.3| | ||||
| Возведение в степень |
Кнопка 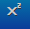 или «^»(shift + 6) |
При нажатой кнопке Другой способ задания степени через знак «^». Например: |
||||
| Корень |
Кнопка
|
2 √(x – 2) — квадратный корень 3 √(2x – 1) — кубический корень |
||||
| Синус |
Кнопка 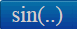
|
sin(x + 1) | ||||
| Косинус |
Кнопка 
|
cos(x) | ||||
| Тангенс |
Кнопка 
|
tg(2.5 – x)
|
||||
| Число π (пи) |
Кнопка 
|
sin(x + π) + 2 | ||||
| Логарифм |
Кнопка 
|
log2(2x – 1,4) | ||||
| Натуральный логарифм |
Кнопка 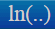
|
ln(x) – 2 | ||||
| Десятичный логарифм |
Кнопка 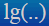
|
lg(2.3 – x) | ||||
| Основание натурального логарифма (число Эйлера) |
Кнопка 
|
ex |
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
20 апреля 2023 в 6:08
Илья Костромин

Профиль
Благодарили: 0
Сообщений: 1

Илья Костромин
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
