Онлайн калькулятор для нахождения медианы ряда чисел. Медианой (серединой) набора чисел называется число стоящее посередине упорядоченного по возрастанию ряда чисел. Если количество чисел в ряду чётное, то медианой ряда является полусумма двух стоящих посередине чисел.
Применяется в математической статистике — число, характеризующее выборку (например, набор чисел), также используется для вычисления медианной зарплаты.
Формула медианы числового набора, пример вычисления медианы числового ряда: 3, 7, 1, 6, 9
Решение: упорядочиваем список чисел в порядке возрастания: 1, 3, 6, 7, 9. Поскольку количество чисел в ряду нечётное, то число 6 стоящее по середине и будет являться медианой данного ряда.
Пример нахождения медианы ряда чисел: 1, 5, 8, 4, 3, 9
Решение: записываем все числа ряда в порядке возрастания: 1, 3, 4 ,5, 8, 9. Поскольку чисел в ряду чётное, то медиана этого ряда будет равна полусумме двух средних чисел: (4+5)/2 = 4.5
Понятие медианы чисел широко используется в математической статистике. И хотя вычисление медианы не составляет большой сложности, мы сделали калькулятор, который поможет рассчитать медианное значение ряда чисел онлайн с подробным решением. Причем количество чисел не важно, он рассчитает медиану 3, 4, 5 чисел так же быстро, как и для 1000 чисел.
Калькулятор медиана чисел
Как найти медиану чисел
Лучше рассмотреть процесс вычисления медианы на примере. Пусть у нас есть ряд чисел: 13 19 24 17 15 11. Для удобства числа будет записывать через пробел. Найдем его медиану. Для начала необходимо расположить числа в порядке возрастания. Эта процедура называется сортировкой. Получим новый ряд: 11 13 15 17 19 24. Так как количество чисел в ряду равно 6, а число 6 четное, то середина ряда будет между числами 15 и 17. Найдем среднее этих двух чисел: (15 + 17) / 2 = 16. Это и будет медианой ряда. Не стоит путать медиану, среднее гармоническое и среднее арифметическое — это принципиально разные понятия.
Рассмотрим другой пример, когда количество чисел в ряду нечетное. Есть такой ряд: 18 46 10 5 38. Найдем медиану набора этих чисел. Отсортируем ряд по возрастанию и получим ряд: 5 10 18 38 48. Так как количество чисел в этом ряду 5, то у него есть середина — это элемент с номером 2. Значит медиана этого ряда равна элементу с номером 2. Получаем ответ 18.
И еще пример — найдем медиану чисел 158 166 134 130 132. Отсортируем и получим ряд 130 132 134 158 166. Количество чисел нечетное и равно 5, значит средний элемент имеет номер 3. Третий элемент нашего отсортированного ряда — число 134. Это и есть медиана.
Ваша оценка
[Оценок: 259 Средняя: 3]
Медиана ряда чисел Автор admin средний рейтинг 3/5 – 259 рейтинги пользователей
Если в числовом ряде есть дробные числа, используйте точку для их записи. Например, 0.42, 0.55.
Медианой ряда
чисел (или медианой числового ряда) называется число, стоящее посередине
упорядоченного по возрастанию ряда чисел — в случае, если
количество чисел нечётное. Если же количество чисел в ряду чётно, то медианой ряда является полусумма двух стоящих
посередине чисел упорядоченного по возрастанию ряда.
Как найти медиану ряда чисел
Чтобы разобраться, как находить медиану ряда чисел, мы рассмотрим несколько примеров.
Пример 1. Найти медиану числового ряда
Решение. Записываем все числа ряда в порядке возрастания: . Количество чисел в ряду
чётно, поэтому медиана этого ряда будет равна полусумме двух средних чисел: .
Пример 2. Найти медиану числового ряда
Решение. записываем все числа ряда в порядке возрастания: . Количество чисел в ряду
нечётно, поэтому медиана этого ряда будет равна стоящему посередине числу, то есть равна .
Загрузить PDF
Загрузить PDF
Среднее значение, медиана и мода — значения, которые часто используются в статистике и математике. Эти значения найти довольно легко, но их легко и перепутать. Мы расскажем, что они из себя представляют и как их найти.
-

1
Сложите все числа, которые вам даны. Допустим, вам даны числа 2, 3 и 4. Сложим их: 2 + 3 + 4 = 9.
-

2
Сосчитайте количество чисел. У нас есть три цифры.
-

3
Разделите сумму чисел на их количество. Берем 9, делим на 3. 9/3 = 3. Среднее значение в данном случае равно 3. Помните, что не всегда получается целое число.
Реклама
-

1
Запишите все числа, которые вам даны, в порядке возрастания. Например, нам даны числа: 4, 2, 8, 1, 15. Запишите их от меньшего к большему, вот так: 1, 2, 4, 8, 15.
-

2
Найдите два средних числа. Мы расскажем, как это сделать, если у вас имеется четное количество чисел, и как это сделать, если количество чисел нечетное:
- Если у вас нечетное количество чисел, вычеркните левое крайнее число, затем правое крайнее число и так далее. Один оставшийся номер и будет искомой медианой. Если вам дан ряд чисел 4, 7, 8, 11, 21, тогда 8 — медиана, так как 8 стоит посередине.
- Если у вас четное количество чисел, вычеркните по одному числу с каждой стороны, пока у вас не останется два числа посередине. Сложите их и разделите на два. Это и есть значение медианы. Если вам дан ряд чисел 1, 2, 5, 3, 7, 10, то два средних числа — это 5 и 3. Сложим 5 и 3, получим 8, разделим на два, получим 4. Это и есть медиана.
Реклама
-

1
Запишите все числа в ряд. Например, вам даны числа 2, 4, 5, 5, 4 и 5. Запишите их в порядке возрастания.
-

2
Найдите число, которое чаще всего встречается. В данном случае это 5. Если два числа встречаются одинаково часто, то этот ряд двухвершинный или бимодальный, а если больше — то мультимодальный.
Реклама
Советы
- Вам будет легче найти моду и медиану, если вы запишете числа в порядке возрастания.
Реклама
Об этой статье
Эту страницу просматривали 353 377 раз.
Была ли эта статья полезной?
Как найти медиану ряда
Для обобщенной оценки длинного ряда значений применяются различные вспомогательные методы и величины. Одной из таких величин является медиана. Хотя ее можно назвать средним значением ряда, но ее смысл и метод ее вычисления отличаются от других вариаций на тему среднего значения.
Инструкция
Самым распространенным способом оценить среднюю величину в ряду значений является среднее арифметическое. Чтобы его вычислить, нужно сумму всех значений ряда разделить на число этих значений. Например, если дан ряд 3, 4, 8, 12, 17, то его среднее арифметическое равно (3 + 4 + 8 + 12 + 17)/5 = 44/5 = 8,6.
Еще одно среднее, часто встречающееся в математических и статистических задачах, называется средним гармоническим. Среднее гармоническое от чисел a0, a1, a2… an равно n/(1/a0 + 1/a1 + 1/a2… +1/an). Например, для того же ряда, что и в предыдущем примере, среднее гармоническое будет равно 5/(1/3 + 1/4 + 1/8 + 1/12 + 1/17) = 5/(347/408) = 5,87. Среднее гармоническое всегда меньше среднего арифметического.
Различные средние используются в разных видах задач. Например, если известно, что автомобиль первый час ехал со скоростью A, а второй — со скоростью B, то его средняя скорость за время пути будет равна среднему арифметическому между A и B. Но если известно, что автомобиль проехал один километр со скоростью A, а следующий — со скоростью B, то, чтобы вычислить его среднюю скорость за время пути, нужно будет взять среднее гармоническое между A и B.
Для статистических целей среднее арифметическое представляет удобную и объективную оценку, но только в тех случаях, когда среди значений ряда нет резко выделяющихся. Например, для ряда 1, 2, 3, 4, 5, 6, 7, 8, 9, 200 среднее арифметическое будет равно 24, 5 — заметно больше всех членов ряда, кроме последнего. Очевидно, что такую оценку нельзя считать полностью адекватной.
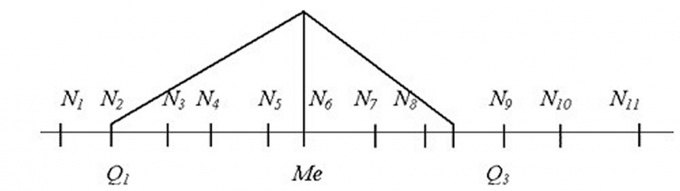
В таких случаях следует вычислить медиану ряда. Это средняя величина, значение которой находится ровно посередине ряда так, что все члены ряда, расположенные до медианы — не больше нее, а все, расположенные после — не меньше. Конечно, для этого нужно вначале упорядочить члены ряда по возрастанию.
Если в ряду a0… an нечетное количество значений, то есть n = 2k + 1, то за медиану принимается член ряда с порядковым номером k + 1. Если же количество значений четное, то есть n = 2k, то медианой считается среднее арифметическое членов ряда с номерами k и k + 1.
Например, в уже рассмотренном ряду 1, 2, 3, 4, 5, 6, 7, 8, 9, 200 десять членов. Следовательно, его медиана — среднее арифметическое между пятым и шестым членами, то есть (5 + 6)/2 = 5,5. Эта оценка гораздо лучше отражает усредненное значение типичного члена ряда.
Источники:
- Задачи по статистике с решениями: Мода и медиана
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
