12. Исследование функций с помощью производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Поиск точек экстремума локального минимума и максимума функций
(blacktriangleright) Если функция задана как частное двух других функций, то [{Large{left(dfrac fgright)’=dfrac{f’cdot
g-fcdot g’}{g^2}}}]
(blacktriangleright) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]
Задание
1
#881
Уровень задания: Равен ЕГЭ
Найдите точку локального минимума функции
(y = -dfrac{x^2 + 2016^2}{x}).
ОДЗ: (x neq 0). Решим на ОДЗ:
1) [y’ = -dfrac{2x^2 – (x^2 + 2016^2)}{x^2} = dfrac{2016^2 – x^2}{x^2}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует):
[dfrac{2016^2 – x^2}{x^2} = 0qquadLeftrightarrowqquad x^2 = 2016^2] – на ОДЗ, откуда находим корни (x_1 = -2016, x_2 = 2016). Производная функции (y) не существует при (x = 0), но (x = 0) не входит в ОДЗ. Таким образом, [y’ = dfrac{(2016-x)(2016+x)}{x^2}.] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
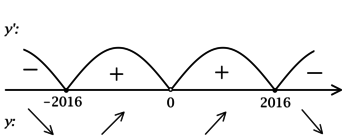
3) Эскиз графика (y):
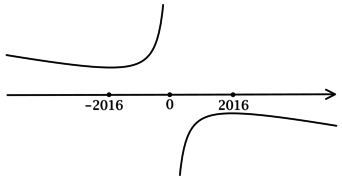
Таким образом, (x = -2016) – точка локального минимума функции (y).
Ответ: -2016
Задание
2
#882
Уровень задания: Равен ЕГЭ
Найдите точку локального максимума функции
(y = dfrac{3,2}{x} + 5x + 1024).
ОДЗ: (x neq 0). Решим на ОДЗ:
1) [y’ = -dfrac{3,2}{x^2} + 5 = dfrac{5x^2-3,2}{x^2} = 5dfrac{x^2 – 0,64}{x^2}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [5dfrac{x^2 – 0,64}{x^2} = 0qquadLeftrightarrowqquad x^2 – 0,64] – на ОДЗ, откуда находим корни (x_1 = -0,8, x_2 = 0,8). Производная функции (y) не существует при (x = 0), но (x = 0) не входит в ОДЗ. Таким образом, [y’ = 5dfrac{(x – 0,8)(x + 0,8)}{x^2}.] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
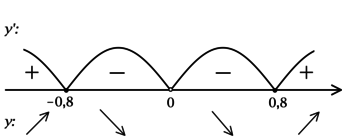
3) Эскиз графика (y):
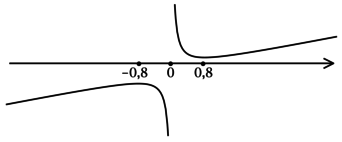
Таким образом, (x = -0,8) – точка локального максимума функции (y).
Ответ: -0,8
Задание
3
#6920
Уровень задания: Равен ЕГЭ
Найдите точку локального максимума функции
(y = dfrac{3x^2 + 1875}{x}).
ОДЗ: (x neq 0). Решим на ОДЗ:
1) [y’ = dfrac{6x^2 – (3x^2 + 1875)}{x^2} = dfrac{3x^2 –
1875}{x^2} = 3cdot dfrac{x^2 – 625}{x^2}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [3cdot dfrac{x^2 – 625}{x^2} = 0qquadLeftrightarrowqquad x^2-625=0, xne 0] – на ОДЗ, откуда находим корни (x_1 = 25, x_2 = -25). Производная функции (y) не существует при (x = 0), но (x = 0) не входит в ОДЗ. Таким образом, [y’ = 3cdot dfrac{(x – 25)(x + 25)}{x^2}.] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
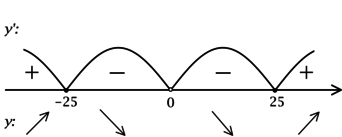
3) Эскиз графика (y):
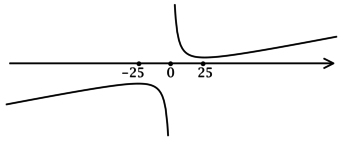
Таким образом, (x = -25) – точка локального максимума функции (y).
Ответ:
-25
Задание
4
#884
Уровень задания: Равен ЕГЭ
Найдите точку локального минимума функции
(y = dfrac{e^x}{x + 1}).
ОДЗ: (x neq -1). Решим на ОДЗ:
1) [y’ = e^xleft(dfrac{1}{x + 1} – dfrac{1}{(x + 1)^2}right) = dfrac{e^x}{(x + 1)^2}x.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{e^x}{(x + 1)^2}x = 0qquadLeftrightarrowqquad x = 0] – на ОДЗ (так как (e^{x} > 0) при любом (x)). Производная функции (y) не существует при (x = -1), но (x = -1) не входит в ОДЗ. Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
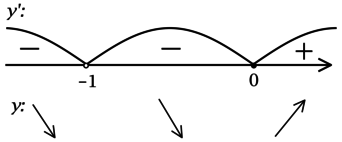
3) Эскиз графика (y):
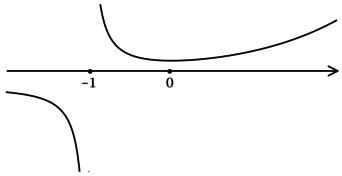
Таким образом, (x = 0) – точка локального минимума функции (y).
Ответ: 0
Задание
5
#2359
Уровень задания: Равен ЕГЭ
Найдите точку максимума функции (y = dfrac{x}{e^x}).
ОДЗ: (x) – произвольный.
1) [y’ = dfrac{1cdot e^x – e^xcdot x}{e^{2x}} = dfrac{1 – x}{e^x}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1 – x}{e^x} = 0qquadLeftrightarrowqquad x = 1,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:
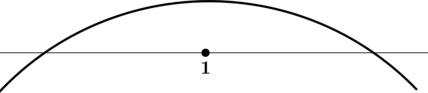
Таким образом, (x = 1) – точка максимума функции (y).
Ответ: 1
Задание
6
#2360
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции (y = dfrac{x^2 – 1}{x^2 + 1}) на отрезке ([-15; 15]).
ОДЗ: (x) – произвольный.
1) [y’ = dfrac{2xcdot (x^2 + 1) – 2xcdot(x^2 – 1)}{(x^2 + 1)^2} = dfrac{4x}{(x^2 + 1)^2}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{4x}{(x^2 + 1)^2} = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-15; 15]):

4) Эскиз графика на отрезке ([-15; 15]):
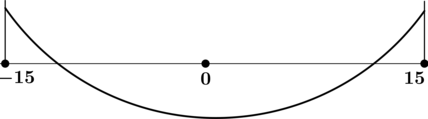
Таким образом, (x = 0) – точка минимума функции (y) на отрезке ([-15; 15]).
Ответ: 0
Задание
7
#2361
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции (y = dfrac{x^2}{x^3 + 1}) на промежутке ((-1; 1]).
ОДЗ: (xneq -1).
1) [y’ = dfrac{2x(x^3 + 1) – 3x^2cdot x^2}{(x^3 + 1)^2} = dfrac{-x^4 + 2x}{(x^3 + 1)^2}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{-x^4 + 2x}{(x^3 + 1)^2} = 0qquadLeftrightarrowqquad
left[
begin{gathered}
x = 0\
x = sqrt[3]{2}
end{gathered}
right.] Производная не существует при (x = – 1).
2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом промежутке ((-1; 1]):

4) Эскиз графика на промежутке ((-1; 1]):
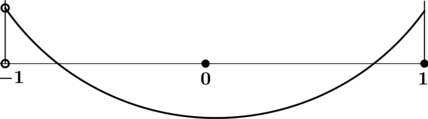
Таким образом, (x = 0) – точка минимума функции (y) на промежутке ((-1; 1]).
Ответ: 0

УСТАЛ? Просто отдохни
Содержание:
Экстремум функции
Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при 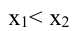
Если дифференцируемая функция у = f(x) на отрезке 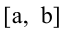 возрастает (убывает), то ее производная на этом отрезке
возрастает (убывает), то ее производная на этом отрезке 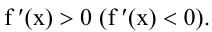
Точка 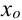 называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции 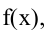 если существует окрестность точки
если существует окрестность точки 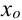 для всех точек которой верно неравенство
для всех точек которой верно неравенство 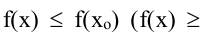
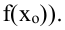
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках – ее экстремумами.
Необходимые условия экстремума. Если точка хо является точкой экстремума функции 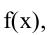 то либо
то либо 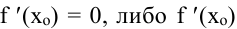 не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек. Первое достаточное условие. Пусть
не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек. Первое достаточное условие. Пусть 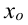 – критическая точка. Если f'(х) при переходе через точку
– критическая точка. Если f'(х) при переходе через точку  меняет знак плюс на минус, то в точке
меняет знак плюс на минус, то в точке  функция имеет максимум, в противном случае – минимум. Если при переходе через критическую точку производная не меняет знак, то в точке хо экстремума нет.
функция имеет максимум, в противном случае – минимум. Если при переходе через критическую точку производная не меняет знак, то в точке хо экстремума нет.
Второе достаточное условие. Пусть функция 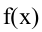 имеет производную f'(х) в окрестности точки
имеет производную f'(х) в окрестности точки  и вторую производную
и вторую производную 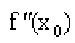 в самой точке
в самой точке  . Если
. Если 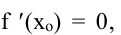
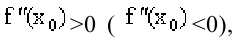 то точка
то точка  является точкой локального минимума (максимума) функции f(x). Если же
является точкой локального минимума (максимума) функции f(x). Если же 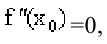 то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
На отрезке 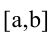 функция у = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка
функция у = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка 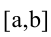 .
.
Пример:
Найти экстремумы функции 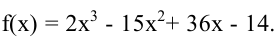
Решение:
Так как 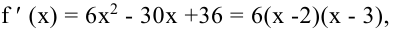 то критические точки функции
то критические точки функции 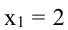 и
и 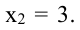 Экстремумы могут быть только в этих точках. Так как при переходе через точку
Экстремумы могут быть только в этих точках. Так как при переходе через точку 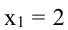 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку
производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку 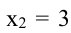 производная меняет знак минус на плюс, поэтому в точке
производная меняет знак минус на плюс, поэтому в точке 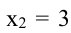 у функции минимум. Вычислив значения функции в точках
у функции минимум. Вычислив значения функции в точках 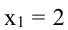 и
и 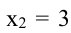 найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) =13.
найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) =13.
Пример:
Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется а погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Решение:
Обозначим стороны площадки через 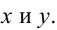 Площадь площадки равна
Площадь площадки равна 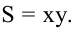 Пусть у – это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2х + у = а. Поэтому
Пусть у – это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2х + у = а. Поэтому 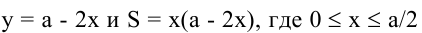 (длина и ширина площадки не могут быть отрицательными).
(длина и ширина площадки не могут быть отрицательными). 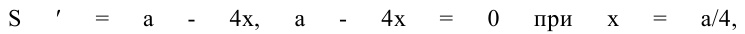 откуда
откуда 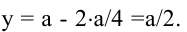 Поскольку
Поскольку 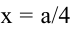 – единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При
– единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При 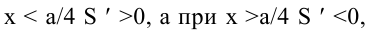 значит, в точке
значит, в точке 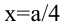 функция S имеет максимум. Значение функции
функция S имеет максимум. Значение функции 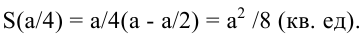
Поскольку S непрерывна на 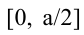 и ее значения на концах
и ее значения на концах 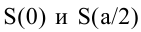 равны нулю, то найденное значение будет наибольшим значением функции.
равны нулю, то найденное значение будет наибольшим значением функции.
Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является у = 2х.
Пример:
Требуется изготовить закрытый цилиндрический бак вместимостью 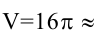
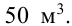 Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?
Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?
Решение:
Площадь полной поверхности цилиндра равна 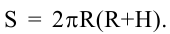 Мы знаем объем цилиндра
Мы знаем объем цилиндра 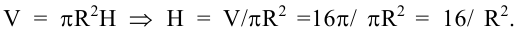 Значит,
Значит, 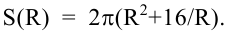 Находим производную этой функции:
Находим производную этой функции: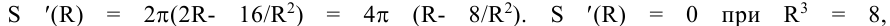 следовательно,
следовательно, 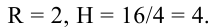
Экстремумы функции
Введём несколько новых понятий. Окрестностью точки 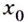 называется любой промежуток, для которого
называется любой промежуток, для которого 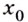 является внутренней точкой.
является внутренней точкой.
Точка 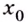 называется точкой минимума (максимума) функции
называется точкой минимума (максимума) функции 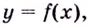 если для всех
если для всех 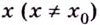 из некоторой окрестности точки
из некоторой окрестности точки 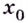 выполняется неравенство
выполняется неравенство 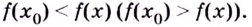
Точки минимума и максимума обозначают 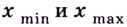 соответственно.
соответственно.
Значение функции в точке минимума называется минимумом функции, а в точке максимума — максимумом функции. Обозначают их: 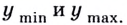
Точки минимума и максимума функции называют точками экстремума (лат. extremum — край, конец). Значения функции в точках её экстремума — её экстремальные значения, или экстремумы.
Например, для функции 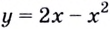 точка
точка  является точкой максимума (рис. 77). Её максимум:
является точкой максимума (рис. 77). Её максимум: 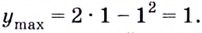
Для функции 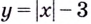 точка
точка 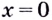 является точкой минимума (рис. 78). Её минимум:
является точкой минимума (рис. 78). Её минимум: 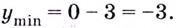
Функция, график которой изображён на рисунке 75, имеет четыре экстремальные точки: 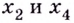 — точки максимума;
— точки максимума; 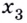 и
и 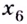 — точки минимума.
— точки минимума.
Точка экстремума функции не может принадлежать промежутку, на котором эта функция возрастает или убывает (почему?). Следовательно, те точки, в которых производная функции положительная или отрицательная, не могут быть точками её экстремума. Все остальные точки области определения функции являются её критическими точками. Поэтому точками экстремума функции могут быть только её критические точки. Это — необходимое условие существования экстремума.
Выбрать из критических точек функции точки экстремума позволяет достаточное условие существования экстремума.
Пусть функция  непрерывна на промежутке
непрерывна на промежутке 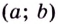 и
и 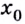 — её критическая точка,
— её критическая точка, 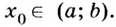 Тогда: точка
Тогда: точка 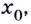 при переходе через которую в направлении роста аргумента производная меняет знак с «плюса» на «минус», является точкой максимума, а точка, при переходе через которую производная меняет знак с «минуса» на «плюс» — точкой минимума.
при переходе через которую в направлении роста аргумента производная меняет знак с «плюса» на «минус», является точкой максимума, а точка, при переходе через которую производная меняет знак с «минуса» на «плюс» — точкой минимума.
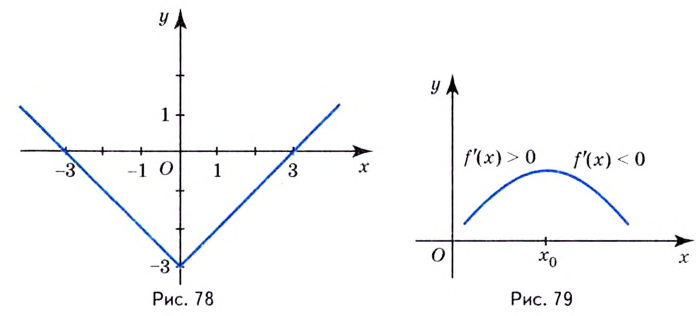
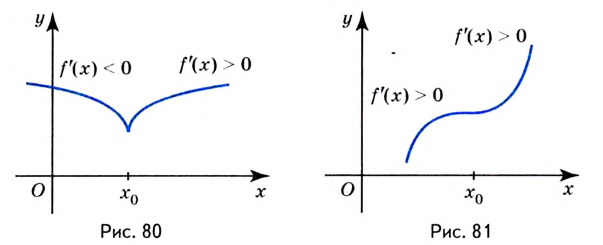
Действительно, если производная функции 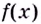 отрицательная, то при переходе через точку
отрицательная, то при переходе через точку 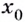 возрастание функции изменяется на убывание (рис. 79). В этом случае
возрастание функции изменяется на убывание (рис. 79). В этом случае 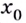 — точка максимума. Если же при переходе через точку
— точка максимума. Если же при переходе через точку 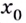 убывание функции изменяется на возрастание, то
убывание функции изменяется на возрастание, то 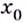 — точка минимума (рис. 80).
— точка минимума (рис. 80).
Если же производная функции в точке 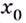 равна нулю, а слева и справа от
равна нулю, а слева и справа от 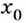 производная функции положительная (рис.81) или слева и справа отрицательная, то
производная функции положительная (рис.81) или слева и справа отрицательная, то 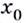 не является точкой экстремума.
не является точкой экстремума.
- Заказать решение задач по высшей математике
Пример №552
Найдите точки экстремума и экстремальные значения функции 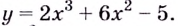
Решение:
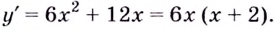
Критические точки функции: 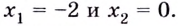 При переходе через точку
При переходе через точку 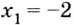 производная меняет знаке
производная меняет знаке 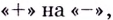 поэтому
поэтому 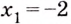 —точка максимума. При переходе через точку
—точка максимума. При переходе через точку 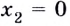 производная меняет знак с
производная меняет знак с 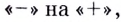 поэтому
поэтому 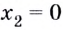 — точка минимума (рис. 82).
— точка минимума (рис. 82).
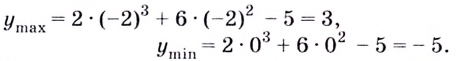
Ответ. 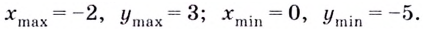
Нахождение экстремумов функции можно оформлять в виде таблицы, как на с. 176. Особенно это удобно при общем исследовании функции, когда находят не только её экстремумы, но и другие свойства, строят её график.
Чтобы исследовать функцию, можно пользоваться следующей схемой:
- найти область определения функции;
- исследовать функцию на чётность, нечётность, периодичность;
- найти точки пересечения графика функции с осями координат;
- исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;
- найти точки экстремума и экстремальные значения функции;
- найти асимптоты графика функции;
- построить график функции.
Пример №553
Исследуйте функцию 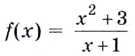 и постройте её график.
и постройте её график.
Решение:
Область определения функции — все действительные числа, кроме 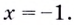 Поскольку она не симметрична относительно нуля, то функция не может быть чётной или нечётной. Функция непериодическая.
Поскольку она не симметрична относительно нуля, то функция не может быть чётной или нечётной. Функция непериодическая.
Уравнение 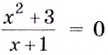 не имеет решений, поэтому график функции не пересекает ось
не имеет решений, поэтому график функции не пересекает ось 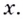 Ось
Ось 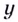 он пересекает в точке с ординатой
он пересекает в точке с ординатой 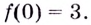
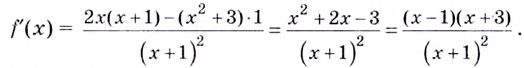
Критические точки: 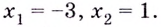
Составим и заполним таблицу.

На промежутках 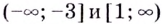 функция возрастает, на промежутках
функция возрастает, на промежутках 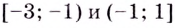 функция убывает.
функция убывает.  — точка максимума,
— точка максимума, 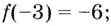
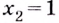 —точка минимума,
—точка минимума, 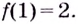
Область значений функции: 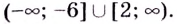
График функции имеет вертикальную асимптоту  так как
так как 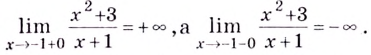
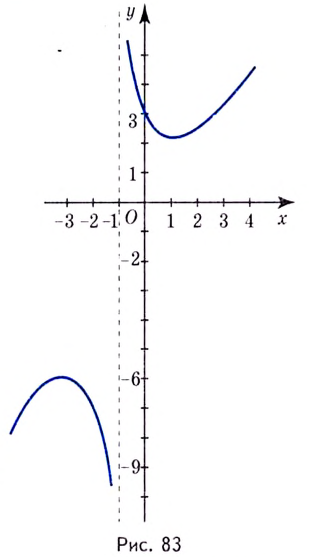
График этой функции изображён на рисунке 83.
Пример №554
Может ли нечётная функция иметь экстремум в точке 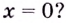 А чётная функция?
А чётная функция?
Решение:
Нечётная функция не может. Если в окрестности точки 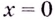 функция имеет экстремум, то с одной стороны от нуля она возрастает, а с другой — убывает, или наоборот. А нечётная функция — или только возрастает, или только убывает в окрестности точки
функция имеет экстремум, то с одной стороны от нуля она возрастает, а с другой — убывает, или наоборот. А нечётная функция — или только возрастает, или только убывает в окрестности точки  Чётная функция может. Например, функция
Чётная функция может. Например, функция 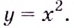
Пример №555
Существуют ли такие числа 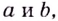 при которых имеет экстремум функция
при которых имеет экстремум функция 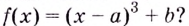
Решение:
При любых действительных значениях 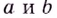
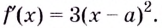 В каждой точке
В каждой точке 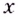 производная данной функции неотрицательная. Функция
производная данной функции неотрицательная. Функция 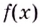 возрастает на
возрастает на 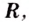 поэтому не может иметь экстремумов.
поэтому не может иметь экстремумов.
Ответ. Не существуют.
Пример №556
Исследуйте функцию 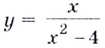 и постройте её график.
и постройте её график.
Решение. 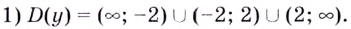
2) Функция — нечётная, поскольку 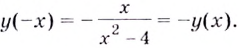
Следовательно, её график симметричен относительно начала координат и достаточно исследовать функцию на промежутке 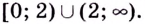
3) если 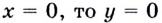 — график пересекает оси координат только в точке
— график пересекает оси координат только в точке 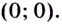
4) Найдём производную функции:
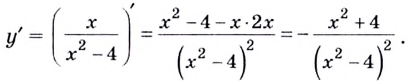
Очевидно, что 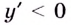 для всех х из области определения. Следовательно, функция убывает на каждом из промежутков
для всех х из области определения. Следовательно, функция убывает на каждом из промежутков 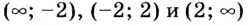 и не имеет максимумов и минимумов.
и не имеет максимумов и минимумов.
Для более точного построения вычислим значение функции в нескольких точках:
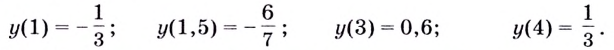
График функции имеет вертикальные асимптоты 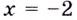 и
и 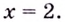 (Убедитесь самостоятельно.)
(Убедитесь самостоятельно.)
График функции изображён на рисунке 84.
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод

Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
16
Добавлен:
25.03.2015
Размер:
253.17 Кб
Скачать

Лекция 8. ЛОКАЛЬНЫЕ ЭКСТРЕМУМЫ
1. Признаки монотонности функции.
2. Точки локального и глобального экстремума функции.
3. Необходимое и достаточное условия существования локального экстремума функции.
4. Наибольшее и наименьшее значение функции на отрезке.
1. Признаки монотонности функции.
С помощью производной функции можно произвести полное ее исследование (найти промежутки возрастания и убывания, экстремумы, точки перегиба, промежутки выпуклости и вогнутости, асимптоты графика) и построить график этой функции.
Теорема 1. Для того чтобы дифференцируемая на (a;b) функция не убывала (не возрастала) на этом интервале, необ-
|
ходимо и достаточно, чтобы |
′ |
′ |
|
|
f (x)≥ 0 |
( f (x)≤ 0 ) для всех |
||
|
x (a;b). Если же для любого x (a;b) f |
′ |
′ |
|
|
(x)> 0 |
( f (x)< 0 ), то |
функция f возрастает (убывает) на этом интервале.
► 1. Рассмотрим случай неубывающей функции. Необходимость: Пусть f (x) не убывает на (a;b). Тогда
|
x (a;b) |
при ∆x >0 приращение ∆y = f (x +∆x)− f (x)≥0 . |
|||||
|
Значит, |
∆y ≥ 0 . |
|||||
|
∆x |
∆y |
|||||
|
Тогда x (a;b) |
имеем lim |
= |
f |
′ |
||
|
∆x |
(x)≥ 0 . |
|||||
|
∆x→0 |
||||||
|
Достаточность. Пусть x (a;b) |
′ |
|||||
|
выполняется f (x)≥0 . То- |
||||||
|
гда по формуле Лагранжа имеем |
(ξ)(x2 − x1 ). |
|||||
|
f (x2 )− f (x1 )= f |
||||||
|
′ |
||||||
|
Так как |
′ |
(x1 <ξ < x2 ), то |
x1, x2 (a;b): x1 < x2 |
|||
|
f (ξ)≥0 |
||||||
|
f (x2 )− f (x1 )≥0 , |
||||||
|
т.е. f не убывает на (a;b). |
||||||
|
2. Докажем теорему для случая возрастающей функции. |
||||||
|
′ |
||||||
|
Пусть f (x)>0 на (a;b). |
||||||
|
Тогда ξ (a;b) |
′ |
|||||
|
f (ξ)>0 и поэтому x1, x2 : x1 < x2 |
||||||
|
67 |
f (x2 )− f (x1 )= f ′(ξ)(x2 − x1 )> 0 .
Значит f (x) возрастает на (a;b). ◄
Замечание. Условия теоремы для возрастающей и убывающей функций являются достаточными, но не необходимыми.
|
Пример. Функция |
y = x3 |
возрастает на (−1;1), однако произ- |
||||
|
водная в точке x = 0 обращается в нуль. |
||||||
|
Геометрический смысл теоремы: |
касательная |
к графику |
||||
|
возрастающей на |
′ |
|||||
|
(a;b) функции ( f (x)>0 ) составляет острый |
||||||
|
угол с осью Ox , касательная к графику убывающей на |
(a;b) |
|||||
|
′ |
Ox . |
Если |
||||
|
функции, ( f (x)< 0 ) образует тупой угол с осью |
||||||
|
функция f (x) |
на |
(a;b) |
является |
постоянной: |
f (x)=С, |
С =const , то f ′(x)= 0 и касательная к графику функции параллельна оси Ox .
2.Точки локального и глобального экстремума функции.
Особую роль в исследовании поведения функции на множе-
стве играют точки, разделяющие интервалы возрастания и убывания функции. Для функции y = f (x) на интервале (a;b) такой
|
точкой является точка x0 , отделяющая |
интервал возрастания |
|
f (x) (a; x0 ) от интервала убывания (x0 ;b) |
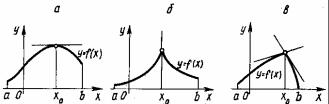
функции. Из рисунка |
1 видно, что существует U (δ; x0 ), δ >0 , такая, что f (x0 )> f (x) x U (δ; x0 ).
Рис.1.
Определение 1. Точка x0 называется точкой локального максимума (минимума) функции f (x) если существует δ –
68
o
окрестность точки x0 , такая, что для всех x U (δ; x0 ) выполня-
ется неравенство
∆f (x0 )= f (x)− f (x0 )<0 ( ∆f (x0 )= f (x)− f (x0 )>0 ).
Значение f (x0 ) называется локальным максимумом (мини-
мумом) функции.
Обозначается:
max( ) f (x)= f (x0 )
x U δ; x0
( min( ) f (x)= f (x0 )).
x U δ; x0
Точки максимума или минимума функции называются точками экстремума функции, а максимумы и минимумы функции называются экстремумами функции.
Экстремумы функции носят локальный характер – это наибольшее или наименьшее значения функции по сравнению с близлежащими ее значениями. Если функция f (x) на [a;b] име-
ет несколько максимумов и минимумов, то возможен случай, когда максимум функции меньше ее минимума.
Наименьшее и наибольшее значения функции на [a;b] назы-
ваются абсолютными минимумом и максимумом или глобальными экстремумами функции f (x)
Обозначается: min f (x), max f (x).
x [a;b] x [a;b]
3. Необходимое и достаточное условия существования локального экстремума функции.
Теорема 2. Если в точке x0 функция f (x) достигает экс-
тремума, то ее производная в этой точке равна нулю или не существует.
► Пусть f (x) в точке x0 достигает максимума. Тогда суще-
|
o |
o |
|
ствует U (δ; x0 ) такая, что для любого x U (δ; x0 ) |
|
|
f (x0 )> f (x) или |
f (x0 )> f (x0 +∆x) при ∆x ≠ 0 . |
|
69 |
|
При ∆x <0 имеем |
f (x0 + ∆x)− f (x0 ) |
> 0 , |
||
|
∆x |
||||
|
при ∆x >0 имеем |
f (x0 + ∆x)− f (x0 ) |
< 0 . |
||
|
∆x |
||||
Если пределы левых частей этих неравенств при ∆x →0 су-
|
ществуют, то: |
f (x0 |
+ ∆x)− f (x0 ) |
|||
|
lim |
= f−′(x0 )≥ 0 , |
||||
|
∆x |
|||||
|
∆x→0 |
|||||
|
(∆x<0) |
f (x0 |
+ ∆x)− f (x0 ) |
|||
|
lim |
= f+′(x0 )≤0 . |
||||
|
∆x |
|||||
|
∆x→0 |
|||||
|
(∆x>0) |
|||||
|
Когда производные функции f−′(x0 ) |
и f+′(x0 ) в точке x0 рав- |
ны нулю, то существует производная f ′(x0 ) и f ′(x0 )= f−′(x0 )= f+′(x0 )= 0 .
В случае, если f−′(x0 ) и f+′(x0 ), отличны от нуля, то производная f ′(x0 ) не существует.
Аналогично доказывается случай, когда x0 точка минимума.◄
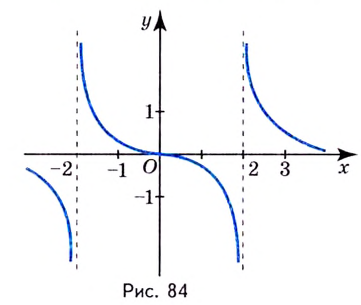
Геометрический смысл теоремы: в точках экстремума функции f (x) касательная к ее графику
1) параллельна оси абсцисс, если существует f ′(x0 )= 0 (рис.2.а);
2)параллельна оси ординат, если f ′(x0 ) бесконечна (рис.2.б);
3)существуют не совпадающие левая и правая касательные, если f−′(x0 )≠ f+′(x0 ) (рис.2.в).
Рис.2
Определение 2 . Точки, в которых производная функ-
70

ции y = f (x) обращается в нуль или не существует, называют
критическими или точками возможного экстремума. Точки,
в которых производная функции y = f (x) обращается в нуль,
|
называют стационарными. |
||||
|
Критическая точка x0 |
называется угловой точкой функции |
|||
|
f (x) если f−′(x0 )≠ f+′(x0 ) |
(см. рис.в). Критическая точка x0 на- |
|||
|
зывается точкой возврата функции, если ее левая f−′(x0 ) и пра- |
||||
|
вая f+′(x0 ) производные бесконечны (см. рис.2.б). |
||||
|
Не всякая критическая точка функции |
f (x) является точкой |
|||
|
ее локального экстремума. |
||||
|
Пример. Для функции |
f (x)= x5 точка |
x =0 – критическая |
||
|
′ |
4 |
|||
|
точка, так как f (x)=5x |
и при x =0 обращается в нуль. Одна- |
|||
ко, x = 0 не является точкой локального экстремума функции. В этой точке функция возрастает.
Выяснить, какая из критических точек функции будет точкой ее локального экстремума, можно с помощью трех достаточных признаков существования экстремума функции.
Теорема 3 (первый достаточный признак существования
|
экстремума функции). Пусть |
x0 |
– критическая точка непре- |
||
|
рывной функции f (x). Если f |
′ |
при переходе через точку x0 |
||
|
(x) |
||||
|
меняет знак с «+» на «–», то |
x0 |
– точка локального максиму- |
||
|
′ |
при переходе через точку x0 меняет знак с «–» |
|||
|
ма; если f (x) |
||||
|
на «+», то x0 |
′ |
|||
|
– точка локального минимума; если f (x) при пе- |
реходе через точку x0 не меняет знак, то x0 не является точкой локального экстремума.
|
► Пусть x0 – точка возможного экстремума. |
||
|
При x U (δ; x0 −0) имеем |
′ |
f (x0 )> f (x). |
|
f (x)> 0 . Значит |
||
|
При x U (δ; x0 +0) имеем |
′ |
f (x0 )< f (x). |
|
f (x)< 0 . Значит |
||
|
Поэтому существует окрестность U (δ; x0 ) такая, что для всех |
||
|
x из этой окрестности f (x0 )> f (x), т. е. точка |
x0 является точ- |
кой локального максимума.
71
Рис.3.
Аналогично доказывается и существование точки локального
минимума.
Если f ′(x) сохраняет знак в окрестности точки x0 , то в этой окрестности функция монотонна, т.е. точка x0 не является точкой локального экстремума. ◄
|
Теорема 4 (второй достаточный признак существования |
|||||
|
экстремума функции). Стационарная точка x0 функции f (x), |
|||||
|
дважды дифференцируемой в U (δ; x0 ), является точкой ло- |
|||||
|
кального минимума f (x), если f ′′(x0 )> 0 , |
и точкой локального |
||||
|
максимума, если f ′′(x0 )< 0 . |
f ′′(x0 )> 0 . Тогда |
||||
|
► Пусть выполнены условия теоремы и |
|||||
|
f ′(x) в U (δ; x0 ) возрастает. По условию |
f ′(x0 )= 0 . Следова- |
||||
|
′ |
меняет знак с «–» |
||||
|
тельно, в окрестности U (δ; x0 ) функция f (x) |
|||||
|
на «+» (рис.3). Согласно теореме 3, точка |
x0 |
является точкой |
|||
|
локального минимума функции f (x). |
|||||
Рис.3.
Если f ′′(x0 )< 0 , то f ′(x) в U (δ; x0 ) убывает. Однако
72

f ′(x0 )= 0 . Значит, в окрестности U (δ; x0 ) производная функции f ′(x) меняет знак с «+» на «–». Согласно теореме 3, точка x0 является точкой локального максимума функции f (x).◄
|
Теорема 5 (третий достаточный признак существования |
|
|
экстремума функции). Пусть функция f (x) |
– n раз непрерыв- |
|
но дифференцируема в точке x0 и |
|
|
f ′(x0 )= f ′′(x0 )=… = f (n−1)(x0 )= 0 , |
f (n)(x0 )≠ 0 . |
|
Тогда: 1) если n – четное и f (n)(x0 )< 0 , то x0 – точка ло- |
|
|
кального максимума. |
2) если n – четное и f (n)(x0 )>0 , то x0 – точка локального минимума;
3) если n – нечетное, то x0 не является точкой локального
экстремума.
Без доказательства.
4.Наибольшее и наименьшее значения функции на отрезке.
Одной из основных характеристик функции f (x) на отрезке
[a;b] являются ее глобальные экстремумы, т.е. наибольшее и наименьшее значения f (x) на [a;b].
Если функция f (x) непрерывна на [a;b], то наибольшее и наименьшее значения она принимает на концах этого отрезка
|
или в точках ее локального экстремума. Следовательно, для |
|
|
отыскания абсолютных экстремумов min |
f (x), max f (x) надо |
|
x [a;b] |
x [a;b] |
|
найти ее значения на концах отрезка [a;b] |
в точках локального |
экстремума и выбрать соответственно наименьшее и наибольшее из них.
Если x1 , x2 , …, xn – точки локальных экстремумов, то
min[ ] f (x)= min{f (a); f (b); f (x1 );…;(xn )},
x a;b
max[ ] f (x)= max{f (a); f (b); f (x1 );…; f (xn )}
x a;b
Пример. Найти абсолютные экстремумы функции f (x)= x3 −6x2 +9x на [−1;4] (рис.4).
73
Решение. 1) Определяем стационарные точки f (x): f ′(x)=3x2 −12x +9 , 3x2 −12x +9 = 0 .
Рис.4.
Значит, x1 =1 и x2 =3 .
2) Вычисляем значения f (x) на концах отрезка и в стационарных точках: f (−1)= −16 , f (4)= 4 , f (1)= 4 , f (3)=0 . Тогда
min f (x)= min{−16,4,4,0}= −16 ,
x [−1;4]
max f (x)= max{−16,4,4,0}= 4
x [−1;4]
Наименьшее значение данная функция принимает на левом конце отрезка в точке x = −1 , наибольшее – в стационарной точке x =1 и на правом конце отрезка в точке x = 4 .
Вопросы для самоконтроля
1.Какие условия должны выполнятся, чтобы функция возрастала, убывала, была неубывающей и невозрастающей?
2.Какая точка называется точкой локального экстремума?
3.Какая точка называется точкой абсолютного экстремума?
4.Сформулируйте необходимое условие локального экстре-
мума.
5.Сформулируйте достаточные условия экстремума.
6.Как находится глобальный экстремум функции на отрезке?
74
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Отыскание локальных максимумов и минимумов не обходится без дифференцирования и является необходимым при исследовании функции и построении ее графика.
Точка 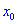 называется точкой локального максимума (или минимума) функции
называется точкой локального максимума (или минимума) функции 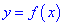 , сли существует такой окрестность
, сли существует такой окрестность 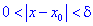 этой точки, принадлежащий области определения функции, и для всех
этой точки, принадлежащий области определения функции, и для всех 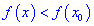 из этого окрестности выполняется неравенство
из этого окрестности выполняется неравенство 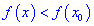 (или
(или 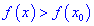 ).
).
Точки максимума и минимума называются точками экстремума функции, а значения функции в экстремальных точках – ее экстремальными значениями.
НЕОБХОДИМОЕ УСЛОВИЕ ЛОКАЛЬНОГО ЭКСТРЕМУМА:
Если функция имеет в точке 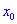 локальный экстремум, то либо производная равна нулю
локальный экстремум, то либо производная равна нулю 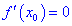 , либо не существует.
, либо не существует.
Точки которые удовлетворяют выписанным выше требованиям называют критическими точками.
Однако в каждой критической точке функция имеет экстремум. Ответ на вопрос: будет критическая точка точкой экстремума дает следующая теорема.
ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА ФУНКЦИИ
Теорема І. Пусть функция  непрерывна в некотором интервале, содержащем критическую точку
непрерывна в некотором интервале, содержащем критическую точку 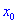 и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки
и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки 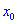 ).
).
Тогда для точки 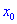 функция имеет максимум, если для аргументов
функция имеет максимум, если для аргументов 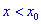 выполняется условие, что производная больше нуля
выполняется условие, что производная больше нуля 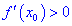 , а для
, а для 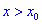 условие – производная меньше нуля
условие – производная меньше нуля 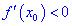 .
.
Если же для 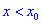 производная меньше нуля
производная меньше нуля 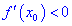 , а для
, а для 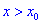 больше нуля
больше нуля 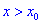 , то для точки
, то для точки 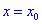 функция имеет минимум.
функция имеет минимум.
Теорема ІІ. Пусть функция дважды дифференцируема в окрестности точки 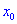 и производная равна нулю
и производная равна нулю 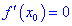 . Тогда в точке
. Тогда в точке 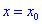 функция имеет локальный максимум, если вторая производная меньше нуля
функция имеет локальный максимум, если вторая производная меньше нуля 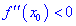 и локальный минимум, если наоборот
и локальный минимум, если наоборот 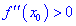 .
.
Если же вторая производная равна нулю 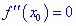 , то точка
, то точка 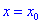 может и не быть точкой экстремума.
может и не быть точкой экстремума.
При исследовании функций на экстремумы используют обе теоремы. Первая на практике проще, поскольку не требует нахождения второй производной.
ПРАВИЛА НАХОЖДЕНИЯ ЕКСТРЕМУМОВ (МАКСИМУМОВ И МИНИМУМОВ) С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ
1) найти область определения 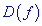 ;
;
2) найти первую производную 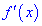 ;
;
3) найти критические точки;
4) исследовать знак производной 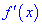 на интервалах, которые получили от разбиения критическими точками области определения
на интервалах, которые получили от разбиения критическими точками области определения 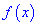 .
.
При этом критическая точка 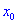 является точкой минимума, если при переходе через нее слева направо производная
является точкой минимума, если при переходе через нее слева направо производная 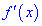 меняет знак с отрицательного
меняет знак с отрицательного 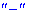 на положительный
на положительный  , в противном случаэ
, в противном случаэ 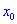 является точкой максимума.
является точкой максимума.
Вместо данного правила можно определять вторую производную 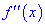 и исследовать согласно второй теоремы.
и исследовать согласно второй теоремы.
5) вычислить значения функции в точках экстремума.
Рассмотрим теперь исследование функции на экстремумы на конкретных примерах.
———————————–
Примеры.
Сборник В.Ю. Клепко, В.Л. Голец “Высшая математика в примерах и задачах”
1. (4.53.7)
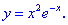
1) Областью определения будет множество действительных чисел
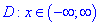 ;
;
2) Находим производную
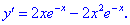
3) Вычисляем критические точки
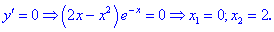
Они разбивают область определения на следующие интервалы
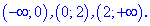
4) Исследуем знак производной на найденных интервалах методом подстановки значений
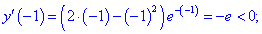
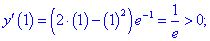
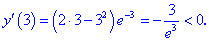
Таким образом первая точка 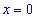 является точкой минимума, а вторая
является точкой минимума, а вторая 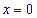 – точкой максимума.
– точкой максимума.
5) Вычисляем значение функции
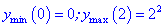
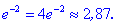
——————————
2. (4.53.9)
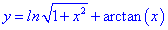
1) Областью определения будет множество действительных чисел  , так корень всегда больше единицы
, так корень всегда больше единицы
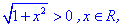
и функция арктангенс определена на всей действительной оси.
2) Находим производную
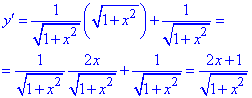
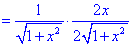
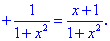
3) С условия равенства производной нулю находим критическую точку

Она разбивает область определения на два интервала
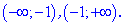
4) Определим знак производной в каждой из областей
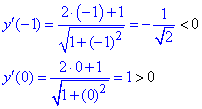
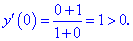
Таким образом находим, что в критической точке 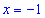 функция принимает минимальное значение.
функция принимает минимальное значение.
5) Вычислим экстремум функции

——————————
3. (4.53.13)
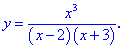
1) Функция определена когда знаменатель не превращается в ноль
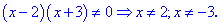
Из этого следует, что область определения состоит из трех интервалов
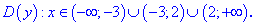
2) Вычисляем производную
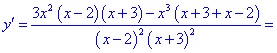
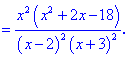
3) Приравниваем производную к нулю и находим критические точки.
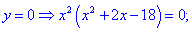
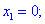
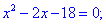
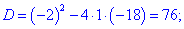
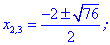
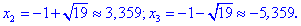
4) Устанавливаем знак производной в каждой из областей, подстановкой соответствующих значений.
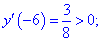
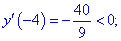
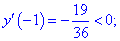
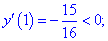
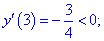
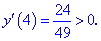
Таким образом точка 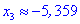 является точкой локального максимума, а
является точкой локального максимума, а 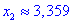 локального минимума. В
локального минимума. В 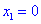 имеем перегиб функции, но о нем будет больше материала в следующих статьях.
имеем перегиб функции, но о нем будет больше материала в следующих статьях.
5) Находим значение в критических точках
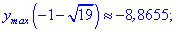
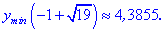
Несмотря на то, что значение функции 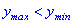 , первая точка является точкой локального максимума, а дуга – минимума. Не бойтесь, если у Вас выйдут подобные результаты, при определении локальных экстремумов такие ситуации допустимы.
, первая точка является точкой локального максимума, а дуга – минимума. Не бойтесь, если у Вас выйдут подобные результаты, при определении локальных экстремумов такие ситуации допустимы.
———————————————-
Посмотреть материалы:
- Исследования функции и построения графика
- Интервалы монотонности функции
- Наибольшее и наименьшее значение функции на отрезке
- Выпуклость и вогнутисть графика функции
- Асимптоты функции
- Область определения функции
Содержание:
- Необходимое условие экстремума
- Первое достаточное условие экстремума
- Второе достаточное условие экстремума
Определение
Точка $x_{0}$ называется точкой локального максимума
функции $f(x)$, если существует такая окрестность
этой точки, что для всех $x$ из этой окрестности
выполняется неравенство: $f(x) leq fleft(x_{0}right)$.
Точка $x_{0}$ называется точкой локального минимума
функции $f(x)$, если существует такая окрестность этой
точки, что для всех $x$ из этой окрестности
$f(x) geq fleft(x_{0}right)$.
Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума –
локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
Точка $x_{0}$ называется точкой строгого локального
максимума функции $y=f(x)$, если для всех
$x$ из окрестности этой точки будет справедливо
строгое неравенство $f(x) lt fleft(x_{0}right)$.
Точка $x_{0}$ называется точкой строгого локального
минимума функции $y=f(x)$, если для всех
$x$ из окрестности этой точки будет
справедливо строгое неравенство $f(x)>fleft(x_{0}right)$.
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.
Замечание
Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
Необходимое условие экстремума
Теорема
(Необходимое условие экстремума)
Если функция $y=f(x)$ имеет экстремум в точке
$x_{0}$, то ее производная
$f^{prime}left(x_{0}right)$ либо равна нулю, либо не существует.
Точки, в которых производная равна нулю: $f^{prime}(x)=0$,
называются стационарными точками функции.
Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются
критическими точками этой функции. То есть критические точки – это либо стационарные точки (решения
уравнения $f^{prime}(x)=0$), либо это точки, в которых производная
$f^{prime}(x)$ не существует.
Замечание
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
Первое достаточное условие экстремума
Теорема
(Первое достаточное условие экстремума)
Пусть для функции $y=f(x)$ выполнены следующие условия:
- функция непрерывна в окрестности точки $x_{0}$;
- $f^{prime}left(x_{0}right)=0$ или $f^{prime}left(x_{0}right)$ не существует;
- производная $f^{prime}(x)$ при переходе через точку $x_{0}$ меняет свой знак.
Тогда в точке $x=x_{0}$ функция
$y=f(x)$ имеет экстремум, причем это минимум, если
при переходе через точку $x_{0}$ производная меняет свой
знак с минуса на плюс; максимум, если при переходе через точку $x_{0}$
производная меняет свой знак с плюса на минус.
Если производная $f^{prime}(x)$ при переходе через точку
$x_{0}$ не меняет знак, то экстремума в точке
$x=x_{0}$ нет.
Таким образом, для того чтобы исследовать функцию $y=f(x)$
на экстремум, необходимо:
- найти производную $f^{prime}(x)$;
- найти критические точки, то есть такие значения $x$,
в которых $f^{prime}(x)=0$ или
$f^{prime}(x)$ не существует; - исследовать знак производной слева и справа от каждой критической точки;
- найти значение функции в экстремальных точках.
Пример
Задание. Исследовать функцию $y(x)=x^{4}-1$ на экстремум.
Решение. Находим производную заданной функции:
$y^{prime}=left(x^{4}-1right)^{prime}=4 x^{3}$
Далее ищем критические точки функции, для этого решаем уравнение $y^{prime}(x)=0$:
$y^{prime}=4 x^{3}=0 Rightarrow x=0$
Первая производная определена во всех точках. Таким образом, имеем одну критическую точку
$x=0$. Наносим эту точку на координатную прямую и
исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное
значение и находим значение производной в выбранной точке, определяем знак полученной величины):

Так как при переходе через точку $x=0$ производная
сменила свой знак с “-” на “+”, то в этой точке функция достигает минимума (или минимального значения), причем
$y_{min }=y(0)=0^{4}-1=-1$.
Замечание. Также можно определить интервалы
монотонности функции: так как на интервале
$(-infty ; 0)$ производная
$y^{prime}(x) lt 0$, то на этом интервале функция
$y(x)=x^{4}-1$ является убывающей; на интервале
$(0 ;+infty)$ производная
$y^{prime}(x)>0$, значит заданная функция возрастает на нем.
Ответ. $y_{min }=y(0)=-1$
Второе достаточное условие экстремума
Теорема
(Второе достаточное условие экстремума)
Пусть для функции $y=f(x)$ выполнены следующие условия:
- она непрерывна в окрестности точки $x_{0}$;
- первая производная $f^{prime}(x)=0$ в точке $x_{0}$;
- $f^{prime prime}(x) neq 0$ в точке $x_{0}$ .
Тогда в точке $x_{0}$ достигается экстремум,
причем, если $f^{prime prime}left(x_{0}right)>0$, то в точке
$x=x_{0}$ функция
$y=f(x)$ имеет минимум; если
$f^{prime prime}left(x_{0}right) lt 0$, то в точке
$x=x_{0}$ функция
$y=f(x)$ достигает максимум.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Исследовать функцию $y(x)=frac{x^{2}-1}{x^{2}+1}$ на экстремум с помощью второй производной.
Решение. Находим первую производную заданной функции:
$y^{prime}(x)=left(frac{x^{2}-1}{x^{2}+1}right)^{prime}=frac{2 xleft(x^{2}+1right)-left(x^{2}-1right) cdot 2 x}{left(x^{2}+1right)^{2}}=frac{4 x}{left(x^{2}+1right)^{2}}$
Находим точки, в которых первая производная равна нулю:
$y^{prime}(x)=0 Rightarrow frac{4 x}{left(x^{2}+1right)^{2}}=0 Rightarrow x=0$
Вторая производная заданной функции:
$y^{prime prime}(x)=left(frac{4 x}{left(x^{2}+1right)^{2}}right)^{prime}=frac{4left(x^{2}+1right)^{2}-4 x cdot 2left(x^{2}+1right) cdot 2 x}{left(x^{2}+1right)^{4}}=$
$=-frac{4left(3 x^{2}-1right)}{left(x^{2}+1right)^{3}}$
В стационарной точке $x=0$ вторая производная
$y^{prime prime}(0)=-frac{4 cdot(-1)}{1^{3}}=4>0$, а значит, в этой точке функция достигает
минимум, причем $y_{min }=y(0)=frac{0^{2}-1}{0^{2}+1}=-1$.
Ответ. $y_{min }=y(0)=-1$
Остались вопросы?
Здесь вы найдете ответы.
Что подразумевается под понятием «экстремум»?
Экстремум представляет собой значение функции на определенном интервале в
момент достижения им минимального или максимального показания. Под
понятием «экстремумы» или по-другому минимумы/максимумы подразумевается
значение функции (у).
Точка экстремума – что это такое?
Если в определенной точке достигается экстремум или, иными словами,
максимальное/минимальное значение функции на заданном интервале, то эта
точка носит название точки экстремума. Из этого следует, что при
достижении минимума, точка экстремума будет названа точкой минимума, и,
наоборот, при достижении максимума эта точка будет называться точкой
максимума. В случае, когда указываются точки экстремумов (или
минимумов/максимумов) подразумеваются иксы, в которых достигаются
минимальные или максимальные значения.
Что имеется в виду под понятием «точка минимума функции»?
Любая точка x₀ будет определена в качестве точки минимума функции y = f(x)
при соблюдении условия о том, что имеется такая V, представляющая собой
окрестность (x₀ – V; x₀+V) упомянутой ранее точки, из которой для каждого
значения x <> x₀ действительно следующее неравенство:
f(x)>f(x₀).
Как описать точку минимума функции?
Под понятием «минимум функции» имеется в виду та точка на ней, в которой
функция имеет значение, являющееся наименьшим среди всех значений,
приобретаемых ею в любой из других соседних точек. Другими словами, это
означает, что в случае, когда функция, достигнув определенной точки,
прекращает падать, а, наоборот, наблюдается ее рост, то данная точка и
представляет собой точку ее минимума.
Каким образом можно вычислить значение функции y=x⁴-4x³+6x²-4x, которого она
достигает в точке своего минимума?
Для ответа на поставленный вопрос нужно отыскать точку минимума указанной
функции, в которой ее значение перестает падать. Это можно сделать
следующим образом:
y’ = 4x³ – 12x² + 12x – 4
Предположив, что минимальное значение данной функции равно 0, можно
переписать равенство в следующем виде:
4x³ – 12x² + 12x – 4 = 0
Сократим данное уравнение на 4:
x³ – 3x² + 3x – 1 = 0
Получившееся равенство также может быть записано в следующем виде после
перемены местами слагаемых:
(x³ – 1) + (-3x² + 3x) = 0
Распишем слагаемые в ином виде, чтобы избавиться от третьей степени:
(x – 1)(x² + x + 1) -3x(x – 1) = 0
Это же уравнение может выглядеть так:
(x -1)(x² + x + 1- 3x) = 0
Произведем сложение слагаемых х и -3х:
(x – 1) (x² -2x + 1) = 0
Теперь для упрощения можно переписать уравнение в таком виде:
(x – 1)(x-1)² = 0
Получившееся равенство:
(x – 1)³ = 0
В этом случае х = 1
-∞ 1 +∞
Знаками «+» и «-» обозначены значения производной.
После проведенных вычислений было установлено, что х = 1, что является
точкой минимума функции:
у = 1⁴- 4*1³ + 6*1² – 4*1 = 1 – 4 +6 – 4 = -1
Какие расчеты нужно произвести, для того чтобы вычислить точку максимума для
функции y = -x/x²+484?
Точкой максимума называется то значение х, достигнув которого, производная
начинает менять свой знак с плюса на минус. Зная это, можно перейти к
поиску точки максимума для функции, указанной в задании.
Для этого нужно начать с поиска производной, используя следующую формулу:
(U/V)’ = (U’V – UV’)/V²
Подставляем приведенные в задании значения и получаем:
y’ = (-(x² + 484) – 2x)/(x² + 484)² = (-x²-484 -2x)/(x² +484)²
Теперь следует приравнять производную к 0 и начать решать получившееся
уравнение:
(-x²-484 -2x)/(x² +484)² = 0
Упростим уравнение и получим:
(-x²-484 -2x) = 0
(x² +484)² ≠ 0
-x²-484 -2x = 0
Избавимся от минусов в уравнении:
x² + 2x +484 = 0
D < 0
В результате вычислений стало ясно, что корней нет. Это значит, что
невозможно поставить их на числовой прямой, для того чтобы проверить знаки
производной по соседству с этими точками. На основании этого можно сделать
вывод о том, что указанная в задании функция не имеет точек экстремума.
Что представляет собой точка максимума функции?
Под точкой максимума функции понимается та точка, в которой она достигает
значения, являющегося наибольшим среди тех значений, что достигаются ею в
соседних точках. Это означает, что в точке, при пересечении которой
функция прекращает расти, и наблюдается ее падение, и достигается ее
максимум.
Имеется график производной функции. Каким образом можно вычислить точки ее
максимума и минимума?
В случае, если имеется график производной функции, и при этом требуется
определить ее экстремумы, то необходимо вычислить точки пересечения этого
графика производной с осью Ох. По-другому они называются «нулями»
производной. В случае, когда, пересекая конкретную точку, график
производной восходит из области со знаком «-» в область со знаком «+», и в
это время производная меняет свой знак на противоположный, функция также
изменяется с убывания на рост. В этом случае данная точка, которая
пересекается графиком производной, представляет собой точку минимума. Если
же при пересечении графиком производной какой-либо точки он идет из
положительной в отрицательную область, а функция из возрастания меняется
на убывание, то речь идет о точке ее максимума.
Как можно вычислить экстремумы и точки экстремума функции y=4x⁴+2x²+1?
Для того чтобы найти ответ на поставленный вопрос, сначала нужно
приравнять функцию к 0:
у = 0
Это же означает, что:
4X⁴ + 2X² + 1 = 0
Введем обозначения:
Х2 = А, при этом А больше 0.
С учетом введенных обозначений равенство будет иметь следующий вид:
4A² + 2A + 1 = 0
D = 4 – 4 = 0 ; √ D = 0
A = (- 2) : 4 = (- 0,5) (< 0) 1
Очевидно, что корней нет.
Ответ: х = 0, у = 1.
Дана функция y = x² -3x+2. Как можно вычислить экстремум этой функции?
Имеется функция y = x² -3x+2, которую также можно переписать в следующем
виде:
у = -0,25+ (x-1,5)²
Отсюда следует, что:
miny = – 0,25 при условии, что х-1,5 = 0
Можно сделать вывод о том, что х = 1,5.
Запишем производную данной функции:
y ‘= (x² -3x+2)’ =2x -3
А затем приравняем ее к 0:
y ‘ = 0, значит:
2x -3 = 0.
Это позволяет сделать вывод о том, что:
x = 3/2.
Получается, что, если x < 3/2, то производная y’ < 0, и при этом функция убывает.
Если же x >3/2, то производная y’ > 0, и в этом случае функция возрастает.
x =3/2=1,5 – это единственная точка экстремума, которая является точкой
минимума.
miny =(1,5)² -3*1,5+2 = -0,25.
Как раскрыть понятие «критическая точка функции»?
Критическая точка функции представляет собой ту точку, при пересечении с
которой производная данной функции становится равной 0, либо она вовсе не
существует.
Возможно ли привести доказательства того, что функция f(x) =2x – 3/x не
может иметь критической точки?
Для начала нужно определить, что под критической точкой функции
подразумевается та точка, при пересечении с которой производная
приобретает нулевое значение, либо же эта производная просто не существует
в этой точке, что означает, что функцию в данной точке невозможно
дифференцировать.
Проверим, применимо ли это утверждение к упомянутой в задании функции:
f ‘(x) =(sin2x – 3x)’ = 2sin2x-3
Приравняем производную функции к 0:
f ‘(x) = 0, это значит, что 2sin2x-3 = 0.
Следовательно:
sin2x= 3 2 не имеет решения
Ответ: заданная функция не имеет критических точек и существует при любых
х.
Каким способом можно определить критические точки функции y=|x|/1+x²?
Под критическими точками функции понимаются те точки, в которых ее
производная равна 0 или вовсе не существует.
В задании дана функция:
y=|x|/(1+x²)
Предположим, что x<0, тогда:
y=-x/(1+x²)
Запишем производную функции и приравняем ее к 0:
y`=(-1-x²+2x²)/(1+x²)²=(x²-1)/(1+x²)²=(x-1)(x+1)/(1+x²)²=0
х = 1 не соответствует условию, значит х = -1.
Теперь предположим, что x≥0.
Снова записываем производную имеющейся функции и приравниваем ее к 0:
y`=(1+x²-2x²)/(1+x²)²=(1-x²)/(1+x²)²=(1-x)(x+1)/(1+x²)²=0
х = – 1 не отвечает условию, значит х = 1.
Ответ: х = 1, х = -1.
Читать дальше: наибольшее и наименьшее значение функции.
