Как найти уравнение высоты проходящей через точку

Как найти уравнение высоты проходящей через точку

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

  1. Найти уравнение стороны треугольника.
  2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Пример.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

Решение:

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

    [left{ begin{array}{l} - 3 = k cdot 5 + b; \ 8 = k cdot 1 + b; \ end{array} right. Rightarrow k = - frac{{11}}{4};b = frac{{43}}{4}.]

Таким образом, уравнение прямой BC —

    [y = - frac{{11}}{4}x + frac{{43}}{4}.]

Угловой коэффициент прямой, перпендикулярной BC,

    [k_2 = - frac{1}{{k_1 }} = - frac{1}{{ - frac{{11}}{4}}} = frac{4}{{11}}.]

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

    [y = frac{4}{{11}}x + b.]

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

    [2 = frac{4}{{11}} cdot ( - 7) + b, Rightarrow b = frac{{50}}{{11}}.]

Итак, уравнение высоты, проведённой к стороне BC:

    [y = frac{4}{{11}}x + frac{{50}}{{11}}.]

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

    [left{ begin{array}{l} 2 = k cdot ( - 7) + b; \ - 3 = k cdot 5 + b; \ end{array} right. Rightarrow k = - frac{5}{{12}};b = - frac{{11}}{{12}}.]

Уравнение прямой AB:

    [y = - frac{5}{{12}}x - frac{{11}}{{12}}.]

Угловой коэффициент перпендикулярной ей прямой

    [k_2 = - frac{1}{{k_1 }} = - frac{1}{{ - frac{5}{{12}}}} = frac{{12}}{5} = 2,5.]

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

    [left{ begin{array}{l} 2 = k cdot ( - 7) + b; \ 8 = k cdot 1 + b; \ end{array} right. Rightarrow k = frac{3}{4};b = frac{{29}}{4}.]

Угловой коэффициент прямой, перпендикулярной AC,

    [k_2 = - frac{1}{{k_1 }} = - frac{1}{{frac{3}{4}}} = - frac{4}{3}.]

Таким образом, уравнение перпендикулярной AC прямой имеет вид

    [y = - frac{4}{3}x + b.]

Подставив в него координаты точки B(5;-3), найдём b:

    [- 3 = - frac{4}{3} cdot 5 + b, Rightarrow b = frac{{11}}{3}.]

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

    [y = - frac{4}{3}x + frac{{11}}{3}.]

uravnenie-vysoty-treugolnika

Источник

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Уравнение высоты треугольника по координатам формула

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

  1. Найти уравнение стороны треугольника.
  2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Даны координаты вершин треугольника .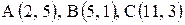

1) Вычислить длину стороны .

2) Составить уравнение линии .

3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.

4) Найти точку пересечения медиан.

5) Найти косинус внутреннего угла при вершине В.

6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.

А

1. Длина стороны ВС равна модулю вектора .

; .

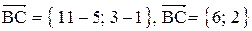2. Уравнение прямой ВС: ; ; .

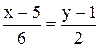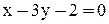3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку перпендикулярно вектору :

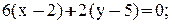
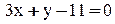. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: .

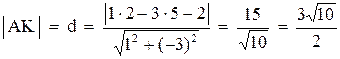4. Найдем координаты точки N – середины стороны ВС:

; ; .

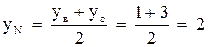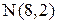Точка пересечения медиан О делит каждую медиану на отрезки в отношении .

Используем формулы деления отрезка в данном отношении :

.

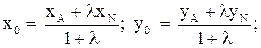
5. Косинус угла при вершине В найдем как косинус угла между векторам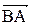и и ;

.

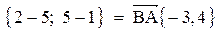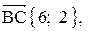
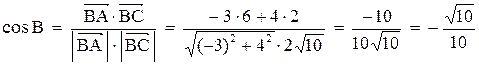6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы 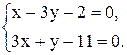Систему решим по формулам Крамера: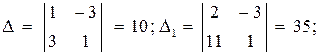

.

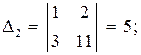
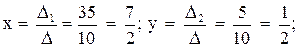
Точка К является серединой отрезка АМ.

.

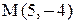Контрольные варианты к задаче 2

Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение линии ВС;

3) составить уравнение высоты, проведенной из вершины А;

4) вычислить длину высоты, проведенной из вершины А;

5) найти точку пересечения медиан;

6) вычислить внутренний угол при вершине В;

7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.

1. 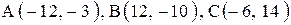. 2. .
3. . 4. .
5. . 6. .
7. . 8. .
9. 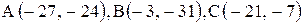. 10. .
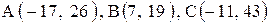11. 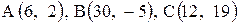. 12. .
13. . 14. .
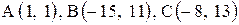15. 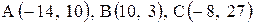. 16. .
17. 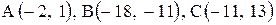. 18. .
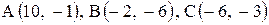19. 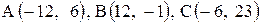. 20. .
21. 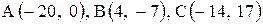. 22. .
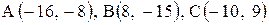23. 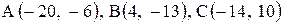. 24. .
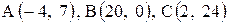25. . 26. .
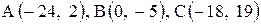27. 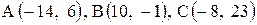. 28. .
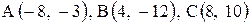29. 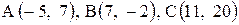. 30. .

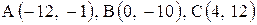Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10637 – | 8008 – или читать все.

Вы можете заказать решение работы
по адресу , вместо бульдога ставьте @

Нужны сторона AB, высота CD, медиана AE и площадь. Координаты вершин А(-8;-3) В(4;-12) С(8;10)

Уравнение прямой, проходящей через две точки (x1,y1) и (x2,y2), описывается уравнением:

Для прямой AB:
(x+8)·(-9)-(y+3)·12 = 0
-9x-72-12y-36 = 0
9x+12y+108 = 0
3x + 4y + 36 = 0

Для отыскания уравнения высоты CD найдем сначала уравнение прямой, которая ей перпендикулярна. Это прямая AB (уравнение у нас есть). Выразим y через x явно:
y = -(3/4)x-9

Если прямая задана уравнением y = kx+b, то перпендикулярная ей прямая будет иметь вид y = (-1/k)x + d. Поэтому искомая высота имеет уравнение:

y = (4/3)x + d. Постоянную d найдем из условия, что высота проходит через точку С.

10 = (32/3) + d,
d = -2/3

Таким образом, уравнение высоты CD: y = (4/3)x – 2/3, или, что то же, 4x-3y-2 = 0

Медиана AE проходит через две точки – точку А и середину отрезка BC. Найдем координаты середины BC по формуле:
X = (x1+x2)/2, Y = (y1+y2)/2. Искомые координаты: XE = 6, YE = -1

Теперь ищем уравнение прямой, идущей через две точки: A(-8;-3) и E(6;-1) по указанному выше уравнению.

(x+8)·2-(y+3)·14 = 0
x+8-7y-21 = 0
x-7y-13 = 0

Это уравнение медианы AE.

Площадь треугольника, заданного на плоскости координатами вершин (x1,y1) (x2,y2) (x3,y3) определяется выражением:

S = (1/2)·|(x3-x1)·(y2-y1) – (y3-y1)·(x2-x1)|
S = (1/2)·|16·(-9)-13·12| = 300/2 = 150 (кв. ед.)

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik

http://4apple.org/uravnenie-vysoty-treugolnika-po-koordinatam/

[/spoiler]

Источник

1. Уравнение сторон АВ и ВС и их угловые коэффициенты.
В задании даны координаты точек, через которые проходят эти прямые, поэтому воспользуемся уравнением прямой, проходящей через две заданные точки $$frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}$$ подставляем и получаем уравнения
уравнение прямой AB $$frac{x+6}{6+6}=frac{y-8}{-1-8} => y = -frac{3}{4}x + frac{7}{2}$$ угловой коэффициент прямой AB равен (k_{AB} = -frac{3}{4})
уравнение прямой BC $$frac{x-4}{6-4}=frac{y-13}{-1-13} => y = -7x + 41$$ угловой коэффициент прямой BC равен (k_{BC} = -7)

2. Угол В в радианах с точностью до двух знаков
Угол B – угол между прямыми AB и BC, который рассчитывается по формуле $$tgphi=|frac{k_2-k_1}{1+k_2*k_1}|$$подставляем значения угловых коэффициентов этих прямых и получаем $$tgphi=|frac{-7+frac{3}{4}}{1+7*frac{3}{4}}| = 1 => phi = frac{pi}{4} approx 0.79$$
3.Длину стороны АВ
Длина стороны AB рассчитывается как расстояние между точками и равна (d = sqrt{(x_2-x_1)^2+(y_2-y_1)^2}) => $$d_{AB} = sqrt{(6+6)^2+(-1-8)^2} = 15$$
4.Уравнение высоты CD и ее длину.
Уравнение высоты будем находить по формуле прямой проходящей через заданную точку С(4;13) в заданном направлении – перпендикулярно прямой AB по формуле (y-y_0=k(x-x_0)). Найдем угловой коэффициент высоты (k_{CD}) воспользовавшись свойством перпендикулярных прямых (k_1=-frac{1}{k_2}) получим $$k_{CD}= -frac{1}{k_{AB}} = -frac{1}{-frac{3}{4}} = frac{4}{3}$$ Подставляем в уравнение прямой, получаем $$y – 13 = frac{4}{3}(x-4) => y = frac{4}{3}x+frac{23}{3}$$ Длину высоты будем искать как расстояние от точки С(4;13) до прямой AB по формуле $$d = frac{Ax_0+By_0+C}{sqrt{A^2+B^2}}$$ в числителе уравнение прямой AB, приведем его к этому виду (y = -frac{3}{4}x + frac{7}{2} => 4y+3x-14 = 0) , подставляем полученное уравнение и координаты точки в формулу $$d = frac{4*13+3*4-14 }{sqrt{4^2+3^2}} = frac{50}{5} =10$$

5. Уравнение медианы АЕ и координаты точки К пересечение этой медианы с высотой CD.
Уравнение медианы будем искать как уравнение прямой, проходящей через две заданные точки А(-6;8) и E , где точка E – середина между точками B и C и ее координаты находятся по формуле (E(frac{x_2+x_1}{2};frac{y_2+y_1}{2})) подставляем координаты точек (E(frac{6+4}{2};frac{-1+13}{2})) => (E(5; 6)), тогда уравнение медианы AE буде следующее $$frac{x+6}{5+6}=frac{y-8}{6-8} => y = -frac{2}{11}x + frac{76}{11}$$Найдем координаты точки пересечения высот и медианы, т.е. найдем их общую точку Для этого составим систему уравнение $$begin{cases}y = -frac{2}{11}x + frac{76}{11}\y = frac{4}{3}x+frac{23}{3}end{cases}=>begin{cases}11y = -2x +76\3y = 4x+23end{cases}=>$$$$begin{cases}22y = -4x +152\3y = 4x+23end{cases}=> begin{cases}25y =175\3y = 4x+23end{cases}=> $$$$begin{cases}y =7\ x=-frac{1}{2}end{cases}$$ Координаты точки пересечения (K(-frac{1}{2};7))

6.Уравнение прямой что проходит через точку К параллельно к стороне АВ.
Если прямая параллельны, то их угловые коэффициенты равны, т.е. (k_{AB}=k_{K} = -frac{3}{4}) , также известны координаты точки (K(-frac{1}{2};7)), т.е. для нахождения уравнения прямой применим формулу уравнения прямой, проходящей через заданную точку в заданном направлении (y – y_0=k(x-x_0)), подставляем данные и получаем $$y – 7= -frac{3}{4}(x-frac{1}{2}) => y = -frac{3}{4}x + frac{53}{8}$$

8. Координаты точки М которая симметрична точке А относительно прямой CD.
Точка M лежит на прямой AB, т.к. CD – высота к этой стороне. Найдем точку пересечения CD и AB для этого решим систему уравнений $$begin{cases}y = frac{4}{3}x+frac{23}{3}\y = -frac{3}{4}x + frac{7}{2}end{cases} =>begin{cases}3y = 4x+23\4y =-3x + 14end{cases} => $$$$begin{cases}12y = 16x+92\12y =-9x + 42end{cases} =>
begin{cases}0= 25x+50\12y =-9x + 42end{cases} => $$$$begin{cases}x=-2\y=5 end{cases}$$ Координаты точки D(-2;5). По условию AD=DK, это расстояние между точками находится по формуле Пифагора (d = sqrt{(x_2-x_1)^2+(y_2-y_1)^2}), где AD и DK – гипотенузы равных прямоугольных треугольников, а (Δx =x_2-x_1) и (Δy=y_2-y_1) – катеты этих треугольников, т.е. найдем катеты найдем и координаты точки M. (Δx=x_D-x_A = -2+6=4), а (Δy=y_D-y_A = 5-8=-3), тогда координаты точки M будут равны (x_M-x_D = Δx => x_D +Δx =-2+4=2 ), а (y_M-y_D = Δy => y_D +Δy =5-3=2 ), получили, что координаты точки (M(2;2))

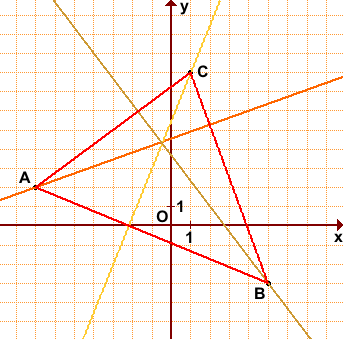
9. Нанесем точки и прямые на декартовую систему координат

Источник

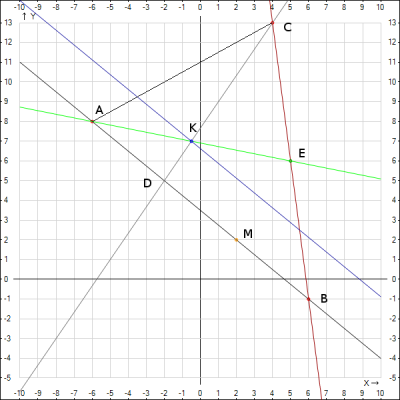
Пример 1:

Построить треугольник, вершины которого находятся в точках А (2; 4), В (-3; 2), С (-3; -4). Найти:

1) уравнения сторон треугольника АВС;

2) координаты точки пересечения медиан;

3) длину и уравнение высоты, опущенной из вершины А;

4) площадь треугольника.

Решение от преподавателя:

Уравнение, прямой проходящей через две точки
1) Уравнения сторон треугольника АВС

2) Координаты точки пересечения медиан

Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Координаты т. E как середины отрезка ВС.

Уравнение АЕ

Координаты т. К как середины отрезка АВ.

Уравнение СК

3) Длина и уравнение высоты, опущенной из вершины А

Расстояние от точки до прямой

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

Уравнение AN

4) Площадь треугольника

Длина ВС

Пример 2:

Решение от преподавателя:


Пример 3:

По координатам вершин треугольника ABC найти:

  • периметр треугольника;
  • уравнения сторон AB и BC;
  • уравнение высоты AD; угол ABC;
  • площадь треугольника.

Сделать чертеж.

А(1; 2); В (–1; 2); С(3; 0).

Решение от преподавателя:



Пример 4:

Даны координаты вершин треугольникаА, В, С.

Требуется найти:

1) уравнение и длину стороны ВС;

2) уравнение и длину высоты, проведённой из вершиныА;

3) уравнение медианы, проведённой из вершиныА;

4) площадь треугольника.

Сделать чертёж.

А(4;-3), B(-2;-1), C(3;-2).

Решение от преподавателя:

Пример 5:

Решение от преподавателя:

1)

2)

3) Находим координаты точки М – середины стороны ВС:

       

Определяем длину медианы АМ:

4) Составляем уравнение медианы – прямой АМ:

5) Если ВН – высота, проведенная из вершины В к стороне АС, то, поскольку ВН проходит через точку В перпендикулярно вектору , то составляем уравнение высоты по формуле , где (a,b) – координаты вектора перпендикулярного искомой прямой,  – координаты точки, принадлежащей этой прямой. Находим координаты вектора АС:

и подставляем в формулу, ,

6) Длину высоты ВН находим как расстояние от точки В до прямой АС:

7) Площадь треугольника АВС:

8) Находим угол ВАС треугольника:

9) Составляем уравнение прямой, проходящей через т.А параллельно ВС:

Ответ:

Пример 6:

Решение от преподавателя:

  1. Уравнение прямой 
    Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями: 
    https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%20x_%7b1%7d%7d%7bx_%7b2%7d%20-%20x_%7b1%7d%7d%20=%20frac%7by%20-%20y_%7b1%7d%7d%7by_%7b2%7d%20-%20y_%7b1%7d%7d
    Уравнение прямой AB 
    Каноническое уравнение прямой: 
    https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%2010%7d%7b-4%20-%2010%7d%20=%20frac%7by%20%2B%202%7d%7b4%20-%20(-2)%7d
    или 
    https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%2010%7d%7b-14%7d%20=%20frac%7by%20%2B%202%7d%7b6%7d
    или 
    y = -3/7x + 16/7 или 7y + 3x – 16 = 0 
  2. Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 
    https://chart.googleapis.com/chart?cht=tx&chl=x_%7bm%7d%20=%20frac%7bx_%7bA%7d%20%2B%20x_%7bB%7d%7d%7b2%7d%20=%20frac%7b10%20%2B%20(-4)%7d%7b2%7d%20=%203
    https://chart.googleapis.com/chart?cht=tx&chl=y_%7bm%7d%20=%20frac%7by_%7bA%7d%20%2B%20y_%7bB%7d%7d%7b2%7d%20=%20frac%7b-2%20%2B%204%7d%7b2%7d%20=%201
    M(3;1) 
    Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-8;2) и М(3;1), поэтому: 
    Каноническое уравнение прямой: 
    https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20%2B%208%7d%7b3%20-%20(-8)%7d%20=%20frac%7by%20-%202%7d%7b1%20-%202%7d
    или 
    https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20%2B%208%7d%7b11%7d%20=%20frac%7by%20-%202%7d%7b-1%7d
    или 
    y = -1/11x + 14/11 или 11y + x – 14 = 0 
  3. Уравнение высоты через вершину C 
    Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 
    https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%20x_%7b0%7d%7d%7bA%7d%20=%20frac%7by%20-%20y_%7b0%7d%7d%7bB%7d
    Найдем уравнение высоты через вершину C 
    https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%20(-8)%7d%7b3%7d%20=%20frac%7by%20-%202%7d%7b7%7d
    y = 7/3x + 62/3 или 3y -7x – 62 = 0
  4. уравнение параллельной прямой AB, проходящей через точку (-8,2)
    Уравнение прямой AB: y = -3/7x + 16/7
    Уравнение KN параллельно AB находится по формуле:
    y – y0 = k(x – x0)
    Подставляя x0 = -8, k = -3/7, y0 = 2 получим:
    y-2 = -3/7(x-(-8))
    или
    y = -3/7x – 10/7 или 7y + 3x +10 = 0

Пример 7:

Даны координаты вершин треугольника: A(1,1), B(4,13), C(10,5). 

Решение от преподавателя:

4) Уравнение высоты через вершину C 
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = -1/4x + 15/2 или 4y +x -30 = 0 
Данное уравнение можно найти и другим способом. Для этого найдем угловой коэффициент k1 прямой AB. 
Уравнение AB: y = 4x -3, т.е. k1 = 4 
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k1*k = -1. 
Подставляя вместо k1 угловой коэффициент данной прямой, получим: 
4k = -1, откуда k = -1/4 
Так как перпендикуляр проходит через точку C(10,5) и имеет k = -1/4,то будем искать его уравнение в виде: y-y0 = k(x-x0). 
Подставляя x0 = 10, k = -1/4, y0 = 5 получим: 
y-5 = -1/4(x-10) 
или 
y = -1/4x + 15/2 или 4y + x – 30 = 0 
Найдем точку пересечения с прямой AB: 
Имеем систему из двух уравнений: 
y -4x +3 = 0 
4y + x – 30 = 0 
Из первого уравнения выражаем y и подставим во второе уравнение. 
Получаем: 
x = 42/17 
y = 117/17 
D(42/17;117/17) 
Длина высоты треугольника, проведенной из вершины C 
Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины: 

Найдем расстояние между точкой C(10;5) и прямой AB (y -4x +3 = 0) 

5,7) Уравнение медианы треугольника 
Обозначим середину стороны BC буквой Е. Тогда координаты точки Е найдем по формулам деления отрезка пополам. 


Е(7;9) 
Уравнение медианы AЕ найдем, используя формулу для уравнения прямой, проходящей через две заданные точки A(1;1) иЕ(7;9), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = 4/3x -1/3 или 3y -4x +1 = 0 
Найдем длину медианы. 
Расстояние между двумя точками выражается через координаты формулой: 

6) CD–диаметр окружности. Центр окружности точка О лежит в середине отрезка CD

Уравнение окружности  (x-x0)2+(y-y0)2=r2

(x-106/17)2+(y-101/17)2=256/17 

8) Уравнение прямой, параллельной CD, проходящей через точку A 

Так как прямая  проходит через точку А(1,1) и имеет k = -1/4, ( так как уравнение CD:y = -1/4x + 15/2 или 4y + x – 30 = 0 ),
то будем искать уравнение в виде: y-y0 = k(x-x0). 
Подставляя x0 = 1, k = -1/4, y0 = 1получим: 
y-1 = -1/4(x-1) 
или 
y = -1/4x + ¼+1 или 4y + x – 5 = 0 

Пример 8:

Решение от преподавателя:

Точка D – середина стороны АВ , ее координаты равны полусумме координат А и В. Получим D(1, -1)

Пример 9:

Даны координаты вершин треугольника АВС: А (3,-2), В (-5,-4),  С (-1,6).

Найдите: 1) уравнения сторон треугольника АВ, ВС и АС;

2) периметр (сумму длин) треугольника;

3) уравнение высоты СН;

4) расстояние d от точки С до прямой АВ;

5) сделайте чертеж.

Решение от преподавателя:

Решение.

1) уравнения сторон треугольника АВ, ВС и АС

Уравнение, прямой проходящей через две точки

2) периметр (сумму длин) треугольника

Расстояние между двумя точками

3) уравнение высоты СН

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

4) расстояние d от точки С до прямой АВ

Расстояние от точки до прямой

Пример 10:

Даны вершины A (x1; y1), B (x2; y2), C (x3; y3)    треугольника.

Найти: 1) уравнение стороны AB;

2) уравнение медианы, проведенной из вершины C;

3) уравнение высоты, проведенной из вершины C ;

4) уравнение прямой, проходящей через вершину C параллельно стороне AB .

A (6; 0), B (2; − 6), C (−3; −9).

Решение от преподавателя:

Пример 11:

Решение от преподавателя:

Пример 12:

Дан треугольник  с координатами вершин найти:

а) длину стороны AB;

б) косинус угла ABC;

в) площадь треугольника ABC (через векторное произведение);

Решение от преподавателя:

Пример 13:

Решение от преподавателя:

Даны координаты вершин треугольника: A(6,0), B(2,-6), C(-3,-9). 
1) Уравнение прямой 
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями: 

Уравнение прямой AB 
Каноническое уравнение прямой: 

или 

или 
y = 3/2x -9 или 2y -3x +18 = 0 

2) Уравнение медианы треугольника 
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(4;-3) 
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-3;-9) и М(4;-3), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = 6/7x -45/7 или 7y -6x +45 = 0 
3) Уравнение высоты через вершину C 
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = -2/3x -11 или 3y +2x + 33 = 0 
4) Уравнение прямой, параллельной AB, проходящей через С(-3,-9) 
Уравнение прямой AB: 2y -3x +18 = 0 
Уравнение СN параллельно AB находится по формуле: 

Или     2y -3x +9 = 0 

Пример 14:

Даны вершины треугольника А(8,1), В(0,3), С(-2,-3). Напишите уравнения стороны AB, медианы AD, высоты BE.

Решение от преподавателя:

Даны координаты вершин треугольника: A(8,1), B(0,3), C(-2,-3). 
1) Уравнение прямой (АВ)
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями: 

Уравнение прямой AB 


или 

или 
 4y + x – 12 = 0 

2)Уравнение медианы (АD)

Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(-1;0) 
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(8;1) и М(-1;0), поэтому: 

или 

или 
y = 1/9x + 1/9 или 9y -x – 1 = 0 
3) Уравнение высоты через вершину B

Найдем уравнение высоты через вершину B 

Для этого найдем угловой коэффициент k1 прямой AC. 

Уравнение прямой AC 
уравнение прямой, проходящей через 2 точки: 

или 

или 
y = 2/5x -11/5  т.е. k1 = 2/5 
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k1*k = -1. 
Подставляя вместо k1 угловой коэффициент данной прямой, получим: 
2/5k = -1, откуда k = -5/2 
Так как перпендикуляр проходит через точку B(0,3) и имеет k = -5/2,то будем искать его уравнение в виде: y-y0 = k(x-x0). 
Подставляя x0 = 0, k = -5/2, y0 = 3 получим: 
y-3 = -5/2(x-0) 
или 
y = -5/2x + 3 или 2y + 5x – 6 = 0    – уравнение (ВЕ)

Пример 15:

Дан треугольник АВС. Найти:

а) величину угла А;

б) уравнение стороны АС;

в) уравнение высоты и медианы, опущенных из вершины В.

Сделать чертеж.

А(-1,2); В(1,3); С(3,-4).

Решение от преподавателя:

Пример 16:

Треугольник задан вершинами А(-6; -2);  В(4; 8); С(2; -8). Найти:

а) уравнение прямой BN, параллельной  стороне АС;

б) уравнение медианы CD;

в) уравнение высоты АЕ;

Решение от преподавателя:

а) уравнение прямой BN, параллельной  стороне АС;

Уравнение прямой AC:

Каноническое уравнение прямой:
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20%2B%206%7d%7b2%20-%20(-6)%7d%20=%20frac%7by%20%2B%202%7d%7b-8%20-%20(-2)%7d
или
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20%2B%206%7d%7b8%7d%20=%20frac%7by%20%2B%202%7d%7b-6%7d
или
y = -3/4x -13/2 или 4y + 3x +26 = 0

Уравнение BN параллельно AC находится по формуле:
y – y0 = k(x – x0)
Подставляя x0 = 4, k = -3/4, y0 = 8 получим:
y-8 = -3/4(x-4)
или
y = -3/4x + 11 или 4y + 3x – 44 = 0

б) уравнение медианы CD;

Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.
https://chart.googleapis.com/chart?cht=tx&chl=x_%7bm%7d%20=%20frac%7bx_%7bA%7d%20%2B%20x_%7bB%7d%7d%7b2%7d%20=%20frac%7b-6%20%2B%204%7d%7b2%7d%20=%20-1
https://chart.googleapis.com/chart?cht=tx&chl=y_%7bm%7d%20=%20frac%7by_%7bA%7d%20%2B%20y_%7bB%7d%7d%7b2%7d%20=%20frac%7b-2%20%2B%208%7d%7b2%7d%20=%203
M(-1;3)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(2;-8) и М(-1;3), поэтому:
Каноническое уравнение прямой:
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%202%7d%7b-1%20-%202%7d%20=%20frac%7by%20%2B%208%7d%7b3%20-%20(-8)%7d
или
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%202%7d%7b-3%7d%20=%20frac%7by%20%2B%208%7d%7b11%7d
или
y = -11/3x -2/3 или 3y + 11x +2 = 0

в) уравнение высоты АЕ;

Прямая, проходящая через точку Е0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%20x_%7b0%7d%7d%7bA%7d%20=%20frac%7by%20-%20y_%7b0%7d%7d%7bB%7d
Найдем уравнение высоты через вершину A
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%20(-6)%7d%7b-8%7d%20=%20frac%7by%20-%20(-2)%7d%7b1%7d
y = -1/8x – 11/4 или 8y +x + 22 = 0

Пример 17:

A(1, 2), В(5, 8), С(11, 3).

Решение от преподавателя:


Пример 18:

В ∆ABC вершины имеют координаты точки А (-3;4), точки В (-4;-3), точки С (8;1).

Составить уравнения стороны (AB), высоты (ВК)  и медианы (CМ).

Решение от преподавателя:

Уравнение прямой AB
Каноническое уравнение прямой:
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20%2B%204%7d%7b-4%20-%20(-4)%7d%20=%20frac%7by%20-%204%7d%7b-3%20-%204%7d
или
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20%2B%204%7d%7b0%7d%20=%20frac%7by%20-%204%7d%7b-7%7d
или
x +4 = 0 или x = -4
Уравнение прямой AC
Каноническое уравнение прямой:
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20%2B%204%7d%7b8%20-%20(-4)%7d%20=%20frac%7by%20-%204%7d%7b1%20-%204%7d
или
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20%2B%204%7d%7b12%7d%20=%20frac%7by%20-%204%7d%7b-3%7d
или
y = -1/4x + 3 или 4y + x – 12 = 0

Найдем уравнение высоты через вершину B
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%20(-4)%7d%7b1%7d%20=%20frac%7by%20-%20(-3)%7d%7b4%7d
y = 4x + 13 или y -4x – 13 = 0

Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(8;1) и М(-4;1/2), поэтому:
Каноническое уравнение прямой:
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%208%7d%7b-4%20-%208%7d%20=%20frac%7by%20-%201%7d%7b%7b1%20over%202%7d%20-%201%7d
или
https://chart.googleapis.com/chart?cht=tx&chl=frac%7bx%20-%208%7d%7b-12%7d%20=%20frac%7by%20-%201%7d%7b%7b-1%20over%202%7d%7d
или
y = 1/24x + 2/3 или 24y -x – 16 = 0

Пример 19:

Дан треугольник ABC с координатами вершин A(-5;-3; 2), B(-2;-6;-3) и C(-2; 2;-1).
Найти:
а) длину стороны АВ;
б) косинус угла ABC;
в) площадь треугольника АВС (через векторное произведение).

Решение от преподавателя:

Источник

4) вычислим cos β для a . Направление вектора определяется углами α, β, γ, образованными с осями координат Ox, Oy, Oz. Косинус угла β определяются по формуле: cos β = ya1 .

Тогда cos β =

y

−6

.

2

=

a

286

5) вычислим

a +b

.

a +b = (35;−3; 9).

Сумма векторов равна вектору с координатами:

Тогда длина

этого

вектора равна

a +b

= 352 +(−3)2 +92 =

1225 +9 +81

=

1315

.

6) вычислим прb a .

Проекцией

вектора a на

вектор b называется

число, равное

пр a

=

a

b

.

Тогда

b

b

пр a

=

a

b

= 15 20 −6 3 −5 16 =

202

.

b

b

20

2 +32 +162

665

Опр. Всякий ненулевой вектор, коллинеарный данной прямой, называется ее направляющим вектором.

Опр. Если вектор n перпендикулярен направляющему вектору апрямой l, то он называется

нормальным вектором прямой l.

1)каноническое уравнениями прямой, проходящей через точку М0(x0, y0) и имеющей направляющий вектор а = (а1, а2 ):

x − x0

=

y − y0

(1)

a

a

2

1

2) уравнение прямой, проходящей через две точки М0(x0, y0) и М1(x1, y1):

x − x0

=

y − y0

(2)

x

− x

0

y

− y

0

1

1

3)общее уравнение прямой на плоскости. Вектор a = (−B, A)является направляющим вектором прямой, а вектор n = (А, В) является нормальным вектором прямой, заданной

общим уравнением:

4) уравнением прямой, проходящей через точку М0(x0, y0) перпендикулярно вектору

n = (А, В):

А(x − x0 ) + В(y − y0 )= 0

(4)

5)расстояние d от точки М0(x0, y0) до прямой, заданной общим уравнением вычисляется формулой:

d =

Ax0 + By0 +C

(5)

A2 + B2

6) расстояние d между двумя точками М0(x0, y0)

и М1(x1, y1) вычисляется по формуле:

d =

(x

− x

0

)2 + (y

1

−y

0

)2

(6)

1

7) координаты точки М(x, y), делящей отрезок М1М2 пополам вычисляется по формуле:

x

1

+ x

2

x =

2

(7)

y

1

+ y

2

y =

2

8) условие перпендикулярности прямых: прямые l1

и l2 перпендикулярны, если нормальные

векторыn1 = (A1, B1 ) иn2 = (A2 , B2 ) ортогональны, т.е. A1 A2 + B1 B2 = 0 .

9)условие параллельности прямых: прямые l1 и l2 параллельны, если их направляющие векторыa = (−B1, A1 ) иb = (−B2 , A2 ) коллинеарны, т.е. координаты этих векторов

пропорциональны: А1 = В1 .

А2 В2

Задача 4. Известны координаты вершин треугольника ABC: A(4; 3); B(-3; –3); C(2; 7). Найти:

1)общее уравнение всех сторон;

2)уравнение всех высот в общем виде (AN1, BN2, CN3);

3)уравнение всех медиан в общем виде (AM1, BM2, CM3);

4)расстояние от точки C до прямой AB;

5)уравнение прямой CC1, проходящей параллельно AB;

6)длину стороны AB;

7)длину медианы AM1;

8)длину высоты AN1;

9)площадь треугольника ABC.

Решение.

1) Найдем общее уравнение всех сторон.

Найдем уравнение стороны AB как уравнение прямой, проходящей через две точки A(4; 3) и B(-3; –3) согласно формуле (2):

y −3

=

x − 4

y −3

=

x − 4

– 7(y – 3)= (−6)(x − 4) 6x – 7y – 3 = 0.

−3 −3

−3 − 4

−6

−7

Найдем уравнение стороны BС как уравнение прямой, проходящей через две точки B(-3; –3)

и C(2; 7):

y +3

=

x +3

y +3

=

x +3

5(y +3)=10(x +3) 2x – y +3 = 0 .

7 +3

2 +3

10

5

Найдем уравнение стороны AС как уравнение прямой, проходящей через две точки A(4; 3) и

C(2; 7):

y −3

=

x − 4

y −3

=

x − 4

– 2(y – 3)= 4(x − 4) 2x + y -11 = 0 .

7 −3

2 − 4

4

− 2

2) Найдем общее уравнение всех высот (AN1, BN2, CN3).

Найдем общее уравнение высоты AN1

как уравнением прямой, проходящей через точку

М0(x0, y0) перпендикулярно нормальному векторуn = (А, В). Так как прямая проходящая через точку А(4, 3) перпендикулярно нормальному вектору BC = (5,10), то уравнение данной прямой будет иметь вид:

5(x − 4) +10(y −3)= 0 5x − 20 +10y −30 = 0 5x +10y −50 = 0 x + 2y −10 = 0 .

Найдем общее уравнение высоты BN2 как уравнением прямой, проходящей через точку через точку B(-3, -3) перпендикулярно нормальному вектору AC = (−2,4), то уравнение данной прямой будет иметь вид:

− 2(x +3) + 4(y +3)= 0 − 2x −6 + 4y +12 = 0 − 2x + 4y + 6 = 0 x − 2y −3 = 0 .

Найдем общее уравнение высоты CN3 как уравнением прямой, проходящей через точку через точку C(2, 7) перпендикулярно нормальному вектору AB = (−7,−6), то уравнение данной прямой будет иметь вид:

−7(x − 2) −6(y −7)= 0 −7x +14 −6y + 42 = 0 −7x −6y +56 = 0 7x + 6y −56 = 0..

3)Найдем уравнение всех медиан в общем виде (AM1, BM2, CM3).

Чтобы найти уравнение медианы AM1, нужно найти координаты точки M1 – середины

отрезка ВС, по формуле (7) имеем: х =

х1 + х2

;

у =

у1 + у2

.

2

2

Тогда х = 2 −2 3 = − 12 ; у = 7 −2 3 = 2 М1 (−0,5;2) .

Пусть a = AМ1 = (−4,5;−1)– направляющий вектор прямой.

х− x

у− y

1

Тогда из канонического уравнения прямой на плоскости (1) имеем:

1

=

.

a

a

2

1

Следовательно,

х−4

=

у−3

AМ1 : 2x −9y +19 =0.

−1

−4,5

Аналогично уравнение

медианы BM2 в общем виде:

4x −3y +3 =0,

медианы

СM2: 14x −3y −7 =0.

4) Найдем расстояние от точки C до прямой AB.

Расстояние от точки C(2; 7) до прямой AB, заданной общим уравнением 6x – 7y – 3 = 0

вычисляется формулой (5): d =

Ax3

+ By3

+C

.

A2 + B2

Следовательно, d =

6 2 −7 7 −3

=

− 40

=

40

.

62 + (−7)2

85

85

5) Найдем уравнение прямой CC1, проходящей параллельно AB.

Прямая СС1 проходит через точку C(2; 7) и параллельна AB, заданной общим уравнением 6x – 7y – 3 = 0. Таким образом, прямая CC1, заданная общим Ax + By + C = 0 и параллельна прямой AB, если ее коэффициенты при x и y пропорциональны (согласно условию

параллельности прямых), т.е. A6 = −B7 . Взяв A = 6, B = -7 (при коэффициенте

пропорциональности,

равном 1),

получим уравнение

прямой CC1: 6x – 7y + С = 0 .

Коэффициент

С найдем с учетом того, что координаты точки С(2;7), лежащей на прямой,

должны удовлетворять ее уравнению, т.е.

6 2 – 7 7 + С = 0 , откуда С = 37 и уравнение

прямой СС1 примет вид: 6x – 7y +37 = 0.

6) Найдем длину стороны AB.

Длина стороны AB – это расстояние от точки А до точки

B и находится по формуле (6):

=

AB

=

(x

− x )2 +(y

− y )2

, тогда

AB

=

(−3 − 4)2 + (−3 −3)2

2

2

85.

1

1

7) Найдем длину медианы AM1.

Длина медианы AM1 – это расстояние от точки А до точки М1 (−0,5;4) и находится по формуле (6): AМ1 = (−0,5 − 4)2 + (3 − 4)2 = 21,25.

8) Найдем длину высоты AN1.

Длина высоты AN1 – это расстояние от точки А(4;3) до прямой BC и вычисляется по

формуле (5): d =

Ax1 + By1 +C

.

Так

как общее уравнение прямой BC имеет вид

A2 + B2

2x – y +3 = 0, то d =

2 4 −1 3 +3

=

8

=

8

.

22 + (−1)2

5

5

9)Найдем площадь треугольника ABC.

Площадь треугольника вычисляется по формуле: S∆ = 12 AB× AC

Имеем AB = (−7;−6;0), AC = (−2;4;0).

Тогда q = AB × AC =

i

j

k

= k (−1)1+3

−7

−6

= (−28 −12)k

= −40k.

−7

−6

0

− 2

4

0

− 2

4

Следовательно, вектор q = (0,0,−40).

1

1

1

0

2

+ 0

2

+ (−40)

2

=

40 =

20 (кв. ед.)

Тогда S∆ = 2

q

= 2

2

Соседние файлы в папке Subj

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Добавить комментарий