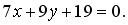Электронная библиотека
Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: и и уравнение одной из его диагоналей: . Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой определяется по формуле:
Стороны параллельны, так как имеют одинаковый угловой коэффициент:
Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:
Наметим план решения: 1) находим вершины ромба P и Q ; 2) находим точку пересечения диагоналей ромба N ; 3) через точку N проводим диагональ D 2 ; 4) находим оставшиеся вершины ромба R и S .1) Так как точка P является точкой пересечения прямых L 2 и D 1 , то ее координаты находим из системы уравнений:
Из рис. 4.1 сразу находим координаты точки Q (- 2, 0) . 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка является серединой отрезка PQ , поэтому ее координаты — полусумма соответствующих координат точек P и Q :
3) Так как диагонали ромба взаимно перпендикулярны, то прямая D 2 перпендикулярна вектору . Найдем его координаты:
По формуле (3.1) находим уравнение диагонали D 2 как уравнение прямой, проходящей через точку N (- 3, 1) перпендикулярно вектору = <2; — 2>:
2( x — (- 3)) + (- 2)( y — 1) = 0, x — y + 4 = 0.
4) Вершины ромба R и S — точки пересечения прямых L 2 и D 2 , L 1 и D 2 , соответственно, находим из уравнений:
Ответ: P (- 4, 2) R (- 6, — 2), Q (- 2, 0), S (0, 4).

Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, — 7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин. Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:
h : 3 x + y + 11 = 0, m : x + 2 y + 7 = 0 ,
План решения:1) находим уравнение прямой PQ ;2) находим координаты точки R ;3) находим уравнения прямых RP и RQ .1) Находим нормальный вектор прямой h : . Уравнение стороны PQ , проходящей через точку P (2, — 7) параллельно вектору , запишем в виде:
Находим координаты точки Q — точки пересечения прямых PQ и m :
2) По свойству медианы треугольника PQR точка S ( x S , y S ) является серединой отрезка RP . Следовательно:
Точка S лежит на медиане m , значит,
Точка R лежит на высоте h , значит,
Из последних двух уравнений определяем координаты точки R , решая систему: 3) Используя формулу (3.4), составим уравнение прямой RP , проходящей через две заданные точки R и P : Аналогично, составим уравнение прямой RQ : Ответ: x — 3 y — 23 = 0, ,
даны уравнения двух сторон ромба 2x+y-2=0 и 2x+y-8=0 и ур-е его диагонали x+y-4=0. найти координаты вершин
даны уравнения двух сторон ромба 2x+y-2=0 и 2x+y-8=0 и ур-е его диагонали x+y-4=0. найти координаты вершин
ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ. ))
нужно само решение)
я получила 2 точки с координатами, вершины из которых идет диагональ, как найти остальные точки? так то их видно и найти можно, но как это записать правильно? нужно точное решение (
Избыточное количество уравнений
х=4-у
Первые вершины:
8-2у+у-2=0 6-у=0 у=6
и. т. д
Далее рисуешь по координатам и находишь остальные точки
Решение математических задач
Дана система линейных уравнений:
Доказать её совместность и решить двумя способами:
- 1) Методом Гаусса;
- 2) средствами матричного исчисления.
Докажем совместность системы. Составим расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
rang(A)= rang()=3по теореме Кронекера-Капелли система совместна.
1) Решим систему по формулам Крамера:
2) Решим систему средствами матричного исчисления.
Решение системы АХ=В находится по формуле:
где А -1 – матрица, обратная к матрице А.
А -1 находится по формуле:
Даны векторы а(4; 7; 8),b (9; 1; 3),c(2; -4; 1) и d(1; -13; -13) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора d в этом базисе.
Векторы образуют базис, если они линейно независимы. Условием линейной независимости векторов служит следующее условие: смешанное произведение векторов отлично от нуля.
Вычислим смешанное произведение векторов .
векторы линейно независимы, а значит образуют базис.
Пусть координаты вектора в базисе следующие: . Разложение вектора по базису имеет вид: . Подставим координаты векторов:
Решим систему методом Крамера:
Ответ: координаты вектора в базисе следующие: (-2;1;0).
Даны координаты вершины пирамиды А1А2А3А4:
- 1)длину ребра А1А2;
- 2)угол между ребрами А1А2 ИА1А4;
- 3)угол между ребром А1А4 и гранью А1А2А3;
- 4)площадь грани А1А2А3;
- 5)объем пирамиды;
- 6)уравнение прямой А1А2;
- 7)уравнение плоскости А1А2А3;
- 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
1) Длина ребра А1А2 совпадает с длиной вектора
2) Угол между ребрами А1А2 И А1А4 найдем используя формулу скалярного произведения:
3) Угол между прямой (L) и плоскостью () Ax+By+Cz+D=0 находится по формуле:
(m;n;p)-это координаты направляющего вектора прямой А1А4.
Вектор является направляющим вектором прямой А1А4.
Для нахождения уравнения плоскости, содержащей грань А1А2А3 используем уравнение плоскости, проходящей через три точки:
4) Площадь треугольника, построенного на векторах и находится по формуле:
– векторное произведение векторов
5) Площадь пирамиды, построенной на векторах , и находится по формуле:
где – смешанное произведение векторов.
6)Для нахождения уравнение прямой А1А2 воспользуемся каноническим уравнением прямой:
где (m;n;p) – координаты направляющего вектора прямой А1А2.
Вектор является направляющим вектором прямой А1А2.
- 7) Уравнение плоскости А1А2А3:
- 8) Высота (Н), опущенная из вершины А4 на грань А1А2А3 перпендикулярна плоскости А1А2А3, а значит направляющий вектор прямой Н параллелен вектору-нормали плоскости А1А2А3, поэтому в качестве направляющего вектора прямой Н можно взять вектор-нормаль плоскости . Высота Н проходит через вершину А4, поэтому можно записать каноническое уравнение высоты:
- 1)
- 2)
- 3)
- 4)
- 5)
- 6)
- 7)
- 8)
Даны уравнения одной из сторон ромба x – 3y + 10 = 0 и одной его диагоналей x + 4y – 4 = 0; диагонали ромба пересекаются в точке P(0;1). Найти уравнения остальных сторон ромба. Сделать чертеж.
Найдем точку М – точку пересечения стороны и диагонали:
Диагонали ромба точкой пересечения делятся пополам, поэтому Р(0;1) – середина отрезка MN, где M и N противоположные вершины ромба.
Запишем уравнение стороны NK, проходящей параллельно стороне (МТ):
Если прямые параллельны, то их угловые коэффициенты равны.
– уравнение прямой NK
Найдем уравнение второй диагонали ромба (ТК). Диагонали ромба перпендикулярны, поэтому их угловые коэффициенты связаны соотношением: .
- (ТК)
- (ТК)
Найдем точку Т – точку пересечения диагонали ТК и прямой МТ:
Запишем уравнение прямой ТN, используя формулу прямой, проходящей через две точки:
– уравнение стороны ТN
Сторона КМ параллельна стороне TN, поэтому угловые коэффициенты этих прямых равны.
– уравнение стороны МК
Составить уравнение и построить линию, расстояние каждой точки которой от точки А (-1; 0) вдвое меньше расстояния ее от прямой x = -4.
Пусть М(x;y) – точка, лежащая на искомой прямой.
Расстояние от точки (х0;у0) до прямой Ах+Ву+С=0 определяется формулой:
Расстояние от М до прямой равно:
По условию задачи , т.е.
Возведем обе части равенства в квадрат:
– уравнение искомой линии.
График полученной линии – парабола, ветви направлены вправо, вершина параболы в точке (-2,5;0), пересечение с осью ординат в точках (0;) и (0;).
Линия задана уравнением в полярной системе координат
- 1) построить линию по точкам, начиная от до и придавая значения через промежуток ;
- 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
- 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
1) Построим линию по точкам, начиная от до и придавая значения через промежуток
[spoiler title=”источники:”]
http://sprashivalka.com/tqa/q/26537739
http://vuzlit.com/887071/reshenie_matematicheskih_zadach
[/spoiler]
Очевидно, вершинами будут точки пересечения стороны и диагонали, другой стороны и диагонали.
Чтобы понять прямо по клеточкам нарисуй прямые сторон и диагнональки.
1. Реши 2 системы из 2 линейных уравнений. Первая x+2y=4 и y=x+2 даст одну вершинку ромба. (отметь на рисунке) .
Вторая x+2y=10 и y=x+2. (http://www.bymath.net/studyguide/alg/sec/alg15.html – пример нижний)
2. Отметь точки и проведи через них две параллельные прямые – найди координаты по графику 2 других вершин.
Я применила 2 метода и графический и алгебраический, т. к. не в курсе того какой раздел матики ты проходишь.
Еше можно: вторая диагональ ромба – это серединный перпендикуляр первой диагональки. Применить условие перпендикулярности прямых. найдешь угловой коэффициент = -1.
Найти координаты точки, делящей пополам первую диагональ.
Теперь по точке и угловому к-ту составишь уравнение второй диагонали.
И найди недостающие 2 вершины
2x-5y-1=0
y = 2/5x-1/5 (1)
2x-5y-34=0
y = 2/5x-34/5 (2)
x+3y-6=0
y = -1/3x+2 (3)
Прямые (1) и (2) параллельны, т.к. угловые коэффициенты равны. Значит (1) и (2) — противоположные стороны ромба.
Найдём координаты точек пересечения диагонали со сторонами ромба:
1) 2/5x-1/5 = -1/3x+2
×15
6x-3 = -5x+30
6x+5x = 30+3
11x = 33
x = 3
y(3) = 2/5*3-1/5 = 6/5-1/5 = 5/5 = 1
A(3; 1)
2) 2/5x-34/5 = -1/3x+2
×15
6x-102 = -5x+30
6x+5x = 102+30
11x = 132
x = 12
y(12) = 2/5*12-34/5 = 24/5-34/5 = -10/5 = -2
C(12; -2)
AC — диагональ ромба. Вторая диагональ BD проходит перпендикулярно AC через её середину. Найдём точку O пересечения диагоналей. Это — середина отрезка AC.
O((3+12)/2; (1-2)/2) = (15/2; -1/2) = (7,5; -0,5)
Найдём уравнение диагонали BD. Это прямая, проходящая через точку O перпендикулярно AC. Угловой коэффициент этой прямой k = 1/3.
y-(-0,5) = -1/(-1/3)
·(x-7,5)
y+0,5 = 3*(x-7,5)
y+0,5 = 3x-22,5
y = 3x-23
Найдём точки пересечения диагонали BD с прямыми (1) и (2). Это и будут координаты вершин B и D.
1) 2/5x-1/5 = 3x-23 ×5
2x-1 = 15x-115
15x-2x = 115-1
13x = 114
x = 114/13 = 8 10/13
y(114/13) = 2/5*114/13-1/5 = 228/65-13/65 = 215/65 = 43/13 = 3 4/13
B(8 10/13; 3 4/13)
2) 2/5x-34/5 = 3x-23 ×5
2x-34 = 15x-115
15x-2x = 115-34
13x = 81
x = 81/13 = 6 3/13
y(81/13) = 2/5*81/13-34/5 = 162/65-442/65 = -310/65 = -62/13 = -4 10/13
D(6 3/13; -4 10/13) Ответ: A(3; 1), B(8 10/13; 3 4/13), C(12; -2), D(6 3/13; -4 10/13)
Электронная библиотека
Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: и и уравнение одной из его диагоналей: . Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой определяется по формуле:
Стороны параллельны, так как имеют одинаковый угловой коэффициент:
Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:
Наметим план решения: 1) находим вершины ромба P и Q ; 2) находим точку пересечения диагоналей ромба N ; 3) через точку N проводим диагональ D 2 ; 4) находим оставшиеся вершины ромба R и S .1) Так как точка P является точкой пересечения прямых L 2 и D 1 , то ее координаты находим из системы уравнений:
Из рис. 4.1 сразу находим координаты точки Q (- 2, 0) . 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка является серединой отрезка PQ , поэтому ее координаты — полусумма соответствующих координат точек P и Q :
3) Так как диагонали ромба взаимно перпендикулярны, то прямая D 2 перпендикулярна вектору . Найдем его координаты:
По формуле (3.1) находим уравнение диагонали D 2 как уравнение прямой, проходящей через точку N (- 3, 1) перпендикулярно вектору = <2; — 2>:
2( x — (- 3)) + (- 2)( y — 1) = 0, x — y + 4 = 0.
4) Вершины ромба R и S — точки пересечения прямых L 2 и D 2 , L 1 и D 2 , соответственно, находим из уравнений:
Ответ: P (- 4, 2) R (- 6, — 2), Q (- 2, 0), S (0, 4).

Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, — 7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин. Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:
h : 3 x + y + 11 = 0, m : x + 2 y + 7 = 0 ,
План решения:1) находим уравнение прямой PQ ;2) находим координаты точки R ;3) находим уравнения прямых RP и RQ .1) Находим нормальный вектор прямой h : . Уравнение стороны PQ , проходящей через точку P (2, — 7) параллельно вектору , запишем в виде:
Находим координаты точки Q — точки пересечения прямых PQ и m :
2) По свойству медианы треугольника PQR точка S ( x S , y S ) является серединой отрезка RP . Следовательно:
Точка S лежит на медиане m , значит,
Точка R лежит на высоте h , значит,
Из последних двух уравнений определяем координаты точки R , решая систему: 3) Используя формулу (3.4), составим уравнение прямой RP , проходящей через две заданные точки R и P : Аналогично, составим уравнение прямой RQ : Ответ: x — 3 y — 23 = 0, ,
Уравнение ромба в декартовой системе координат

Составление и решение уравнений многоугольников
Скачать:
| Вложение | Размер |
|---|---|
| составление и решение уравнений многоугольников | 124.82 КБ |
Предварительный просмотр:
Автор работы: Шпакова Маргарита Андреевна, г.о. Тольятти, МБУ СОШ
Научный руководитель: Владимирова Ольга Ивановна, учитель математики первой категории МБУ СОШ № 58.
В школьном курсе математики учащиеся часто встречаются с алгебраическими уравнениями, уравнениями прямых, уравнениями окружностей, квадратными уравнениями и т.д. Что собой представляют уравнения многоугольников, учащиеся не знают.
Как, например, выглядит уравнение треугольника? Можно ли по фигуре на плоскости составить уравнение? Можно ли рассчитать площадь фигуры по заданному уравнению? Можно ли по заданному уравнению определить, что за многоугольник? Решение этих вопросов меня и заинтересовало. В них есть проблема моей исследовательской работы.
Цель работы: изучить и исследовать на примерах методы, которые дают возможность получить уравнение с модулем любого выпуклого многоугольника на плоскости, координаты вершин которого известны. Найти взаимосвязь площади фигуры от ее уравнения.
Основные ЗАДАЧИ исследования:
- Познакомиться с некоторыми видами уравнений прямых на плоскости (уравнение прямой в отрезках, уравнение прямой, проходящей через две различные точки на плоскости);
- Научиться составлять уравнение прямой через заданную точку и параллельную другой прямой;
- Научиться составлять уравнение прямой, проходящей через две заданные точки;
- Научиться по уравнению строить многоугольник на плоскости и наоборот, по чертежу составлять уравнение многоугольника;
- Изучить метод областей при решении уравнений, содержащих знак модуля.
Как известно из курса геометрии, любая прямая на координатной плоскости может быть задана уравнением вида
Подобное уравнение называют линейным. Уравнение такого вида называют также общим уравнением прямой на плоскости.
Если ax+by+c = 0 – уравнение некоторой прямой m, то уравнение ax+by+c = p, где р ≠ 0, задает прямую m`, параллельную m. Это следует из того, что данные два уравнения не имеют общих решений, а значит, прямые не имеют общих точек.
У параллельных прямых
Пример1 . Составим уравнение прямой, проходящей через точку М (1;-2) и параллельной прямой 3x-4y+5=0
Подставляя координаты точки М в левую часть уравнения, получаем значение 16. Значит, искомым уравнением прямой будет 3x+4y+5=16 или окончательно 3x+4y-11=0.
Пусть известны координаты двух точек М 1 (x 1 ;y 2 ), М 2 (x 2 ;y 2 ), лежащих на данной прямой. Составим уравнение прямой, проходящей через две заданные точки:
(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0
Пример 2 . Составим уравнение прямой, проходящей через точку М 1 (3;1) и М 2 (2;2).
Получаем такое уравнение (x-3)(2-1)-(y-1)(2-3)=0
после преобразований выходит х+у-4=0.
Если известны координаты (а;0) и (0;b) точек пересечения прямой с осями Ох и Оу, то для этой прямой проще всего записать уравнение в отрезках + = 1.
Рассмотрим на координатной плоскости ху треугольник с вершинами в точках А (х 1 ;у 1 ), В (х 2 ;у 2 ), С (х 3 ;у 3 ). Уравнение прямой, на которой лежит сторона АВ этого треугольника, можно записать в виде
(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0.
Подставим координаты третьей вершины С (х 3 ;у 3 ) в левую часть этого уравнения,
получим некоторое значение
q=(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )
Чтобы понять геометрический смысл числа q, заметим, что уравнение
(х-х 1 )(у 2 -у 1 )-(у-у 1 )(х 2 -х 1 )=q задает прямую, параллельную стороне АВ данного треугольника. Поэтому для каждой точки этой прямой результат подстановки ее координат в левую часть уравнения тот же, что и для точки C (х 3 ;у 3 ), и дает число q. Значит, то же значение получится и для точки С 1 (х 4 ;у 1 ) пересечения упомянутой прямой с прямой у=у 1 , параллельной оси абсцисс и проходящей через вершину A треугольника. Но в этой точке
(х-х 1 )(у 2 -у 1 )-(у-у 2 )(х 2 -х 1 ) = (х 4 -х 1 )(у 2 -у 1 ). Геометрический смысл последнего выражения понять уже несложно: |(х 4 -х 1 )(у 2 -у 1 )| площадь параллелограмма со сторонами АВ и АС 1 . Длина стороны АС 1 равна |х 4 -х 1 |, а длина высоты параллелограмма, опущенной из вершины B на эту сторону, есть |у 2 -у 1 |. Поэтому |q| есть площадь ΔАВС 1 , но она такая же, что и у ΔАВС. В результате приходим к следующей формуле для площади треугольника
S = |(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )|. (3, стр. 169).
Если треугольник задан в декартовой системе координат и имеет своими вершинами точки А (х 1 ;у 1 ), В (х 2 ;у 2 ), С (х 3 ;у 3 ), то можно составить уравнение треугольника:
|(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )| + |(x-x 2 )(y 3 -y 2 )-(y-y 2 )(x 3 -x 2 )| +
+ |(x-x 3 )(y 1 -y 3 )–(y-y 3 )(x 1 -x 3 )| = 2S, где
S = |(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )|.
Пример 3 . Составим уравнение треугольника, изображенного на рисунке. Для этого составим уравнения прямых, которые являются его сторонами, по формуле
(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0, задающей уравнение прямой по двум ее точкам. При этом допустимым считаем раскрытие скобок и приведение подобных слагаемых и недопустимым – умножение обеих частей уравнения на некоторое число (за исключением -1) .
Уравнения сторон имеют вид: х-у+1=0, х+у-1=0, 2у=0. Сложив модули левых частей этих уравнений, и приравняв полученное выражение к удвоенной площади ΔАВС, равной в данном случае 1, приходим к искомому уравнению |x-y+1|+|x+y-1|+2|y|=2.
Описанный метод дает возможность получить уравнение любого выпуклого многоугольника на плоскости, координаты вершин которого известны.
Уравнение квадрата, ромба
Пример 4 . Составить уравнение квадрата:
|x-1| + |y-1| + |x| + |y| = 1. Площадь равна 1.
Пример 5 . Составить уравнение ромба:
Через точки с координатами (1;0), (0;1) уравнение прямой: x +y -1 = 0.
Через точки с координатами (-1;0), (0;1) уравнение прямой: x – y + 1 = 0.
Через точки с координатами (-1;0), (0;-1) уравнение прямой: x + y + 1 = 0.
Через точки с координатами (0;-1), (1;0) уравнение прямой: -x + y + 1 = 0.
Получили: | x + y – 1| + | x – y + 1| + | x + y + 1| + | -x + y + 1 | = 4.
Этот же ромб имеет другое уравнение: |х| + |у| = 1, которое лучше решать «методом областей». Площадь ромба равна 2.
Пример 6 . Докажите, что уравнения: |x + y| + |x – y| = 2 и |x + 1| + |y + 1| + |x -1| +|y – 1| =4 относятся к одному квадрату.
Первое уравнение лучше решать «методом областей», где вся плоскость разбивается прямыми у =-х и у=х на четыре области, значит, искомая фигура четырехугольник, стороны которого параллельны осям координат. Из уравнений каждой области у=1, х=1и т.д. понимаем, что это квадрат, площадь которого равна 4.
Второе уравнение наглядно изображено, подтверждая первое.
Пример 7. Определить вид многоугольника по уравнениям:
|х| + 3|у| = 6; |х-3| + |у+3| = 3; |х-1| + 7|у| = 1.
Во всех случаях даны уравнения ромба .
Пример 8 . Изобразить на плоскости многоугольник по данному уравнению: |x|+|y|+|x+y|=4.
Из данного уравнения следует, что х=0, у=0, х= -у –прямые, которые разбивают плоскость на несколько областей.
Найдем уравнение прямой, стороны многоугольника, в каждой из областей:
Проанализируем расположение квадрата на координатной плоскости.
В общем случае уравнение квадрата в декартовой (прямоугольной) системе координат принимает вид:
где точка О`(a;b) – точка пересечения диагоналей квадрата;
d – длина диагонали квадрата.
В частном случае, когда точка О(0;0) – начала координат, является одновременно и точкой пересечения диагоналей квадрата, уравнение квадрата принимает вид:
где d– длина диагонали квадрата.
Одно из уравнений квадрата можно записать так
|x| + |y| = a
обычно так рисуют ромб, но это квадрат
Вопрос:
Как выглядит уравнение квадрата, если его положить на сторону? Иными словами, стороны квадрата должны быть параллельны осям координат.
Указания к решению заданий по алгебре 1 часть
Алгебра и аналитическая геометрия. Математический анализ
Индивидуальные задания и методические указания
для студентов ФДПО ИНО специальности 220100
Вычислительные машины, комплексы, системы и сети
УДК 519.24.001.5
Кандидат техн. наук, доцент кафедры высшей математики
Контрольные задания по алгебре и аналитической геометрии и математическому анализу для студентов ФДПО ИНО специальности 220100 Вычислительные машины, комплексы, системы и сети/ Курск. гос. техн. ун-т; Сост. Л.В.Карачевцева. Курск, 2004. 77 с.
В данной работе содержатся индивидуальные задания и методические указания, необходимые для выполнения работы.
Работа предназначена для студентов технических специальностей.
Табл. 2. Библиогр.: 11 назв.
Текст печатается в авторской редакции
ИД №06430 от 10. 12. 2001. ПЛД № 50-25 от 01. 04.97.
Подписано в печать ________ . Формат 60х84 1/16. Печать офсетная.
Усл. печ. л. 0,56. Уч.-изд. л. 0,52. Тираж 50 экз. Заказ ……….
Курский государственный технический университет.
Издательско-полиграфический центр Курского государственного технического университета. 305040 Курск, ул. 50 лет Октября, 94.
Содержание
1. Индивидуальные задания по алгебре и аналитической геометрии.……..5
2. Указания к решению заданий по алгебре и аналитической
2.1. Пример выполнения задания 1……………………………………….15
2.2. Пример выполнения задания 2……………………………………….20
2.3. Пример выполнения задания 4……………………………………….22
2.4. Пример выполнения задания 5……………………………………….27
3. Индивидуальные задания по математическому анализу……….……..33
4. Указания к выполнению заданий по математическому анализу………55
4.1. Указания к заданию 1…………..……………………………………55
4.1.1. Основные теоретические положения…………………………55
4.1.2. Пример выполнения задания 1………………………………..57
4.2. Указания к заданию 2……..…………………………………………61
4.2.1. Основные теоретические положения…………………………61
4.2.2. Пример выполнения задания 2………………………………..62
4.3. Указания к заданиям 3 и 4……..…………………………………….64
4.3.1. Основные теоретические положения…………………………64
4.3.2. Пример выполнения задания 3………………………………..66
4.3.3. Пример выполнения задания 4………………………………..67
4.4. Указания к заданию 5……..……………………………………….. 68
4.4.1. Основные теоретические положения…………………………68
4.4.2. Пример выполнения задания 5………………………………. 69
4.5. Указания к заданию 6…………..……………………………………71
4.5.1. Основные теоретические положения…………………………71
4.5.2. Пример выполнения задания 6………………………………. 73
Список рекомендуемой литературы ………………………………………77
Введение
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по конспектам лекций и учебникам, решение задач, самопроверка усвоения материала, выполнение контрольных работ. В помощь заочникам университет организует установочные лекции, практические занятия и консультации. Однако студент должен помнить, что только при систематической и упорной самостоятельной работе помощь вуза окажется достаточно эффективной.
В процессе изучения курсов алгебры и аналитической геометрии и математического анализа студент должен выполнить контрольную работу по каждому разделу, главная цель которых — оказать студенту помощь в его работе и подготовке к экзамену. Рецензия на эти работы позволяет студенту судить о степени усвоения им материала, указывает на имеющиеся у него проблемы.
Каждая работа должна быть выполнена в отдельной тетради в клетку чернилами синего или черного цветов. Необходимо оставлять поля шириной 4-5 см для замечаний рецензента.
В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины. В конце работы следует поставить дату ее выполнения и подпись студента.
В контрольную работу студента должны быть включены все задания. Работа, содержащая не все задания, а также задания не своего варианта, не рассматривается.
Перед решением каждой задачи надо полностью выписать ее условие. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. Все исправления и дополнения, на которые указал рецензент, должны быть выполнены на чистых листах в той же тетради, что и прорецензированная работа. Вносить исправления в сам текст работы после ее рецензирования запрещается.
Контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. Без предъявления прорецензированной контрольной работы студент не допускается к сдаче экзамена.

Индивидуальные задания по алгебре
И аналитической геометрии
Задание 1
Решить систему линейных уравнений тремя способами:
а) методом Гаусса;
б) по формулам Крамера;
в) с помощью обратной матрицы.

 1.
1.  ; 2.
; 2.  ;
;

 3.
3.  ; 4.
; 4.  ;
;

 5.
5.  ; 6.
; 6.  ;
;

 7.
7.  ; 8.
; 8.  ;
;

 9.
9.  ; 10.
; 10.  ;
;

 11.
11.  ; 12.
; 12. 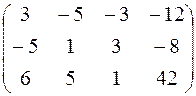 ;
;

 13.
13.  ; 14.
; 14. 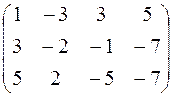 ;
;

 15.
15.  ; 16.
; 16.  ;
;

 17.
17.  ; 18.
; 18.  ;
;

 19.
19.  ; 20.
; 20. 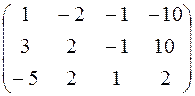 ;
;

 21.
21.  ; 22.
; 22.  ;
;

 23.
23.  ; 24.
; 24.  ;
;

 25.
25.  ; 26.
; 26.  .
.
Задание 2
Решить матричное уравнение  .
.
Ответ проверить подстановкой в уравнение.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8. 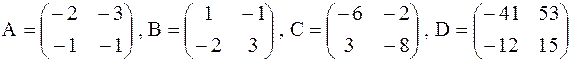 .
.
9.  .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
14.  .
.
15.  .
.
16.  .
.
17. 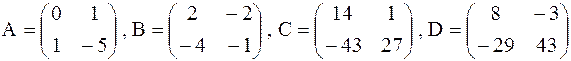 .
.
18.  .
.
19.  .
.
20.  .
.
21.  .
.
22.  .
.
23.  .
.
24.  .
.
25.  .
.
26.  .
.
Задание 3
1. На прямой  найти точку равноудаленную от двух данных точек А(1; 1), В(3; 0).
найти точку равноудаленную от двух данных точек А(1; 1), В(3; 0).
2. Найти координаты точки, симметричной точке (2; -4) относительно прямой  .
.
3. Найти уравнение диагонали параллелограмма, проходящей через точку пересечения его сторон  и
и  , если известно, что диагонали параллелограмма пересекаются в точке F(-1; 0).
, если известно, что диагонали параллелограмма пересекаются в точке F(-1; 0).
4. Составить уравнение прямой, проходящей через точку А(2; 6) и образующей с осями координат треугольник, который находится во второй четверти и имеет площадь 3 кв.ед.
5. Вычислить координаты вершин ромба, если известны уравнения двух его сторон  и
и  и уравнение одной из его диагоналей
и уравнение одной из его диагоналей  .
.
6. Даны уравнения одной из сторон ромба 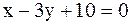 и одной из его диагоналей
и одной из его диагоналей  . Диагонали ромба пересекаются в точке Р(0; 1). Найти уравнение трех остальных сторон ромба.
. Диагонали ромба пересекаются в точке Р(0; 1). Найти уравнение трех остальных сторон ромба.
7. Уравнения двух сторон параллелограмма 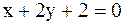 и
и  , а уравнение одной из диагоналей
, а уравнение одной из диагоналей  . Найти координаты вершин.
. Найти координаты вершин.
8. Даны уравнения сторон треугольника: (АВ) 7x-2y+32=0; (АС) x+ +y +2=0; (ВС) 4x+y-1=0. Найти точку пересечения его высот.
9. Даны стороны треугольника: (АС)2x-15y-55=0; (АВ)4x-3y+25=0; (ВС) 14x+3y-61=0. Составить уравнение прямой, проходящей через вершину С и через точку на стороне АВ, делящую ее (считая от вершины А) в отношении 1:4.
10.Окружность проходит через точки М(1; 0) и N(2; 1). Найти центр этой окружности, если известно, что он лежит на прямой  .
.
11.Точки В(1; 2) и С(3;-6) симметричны относительно некоторой прямой. Составить уравнение этой прямой.
12.Площадь прямоугольного треугольника, катетами которого являются оси координат, равна 8. Составить уравнение гипотенузы, если известно, что она проходит через точку А(-4; 8).
13.Даны две стороны  и
и  и диагональ
и диагональ 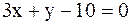 ромба. Найти вершины ромба.
ромба. Найти вершины ромба.
14.Найти координаты вершин параллелограмма, в котором известны две стороны  и
и 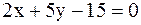 и диагональ
и диагональ  .
.
15.Две стороны треугольника заданы уравнениями  и
и  , а середина третьей стороны — точка (2;3). Составить уравнение третьей стороны.
, а середина третьей стороны — точка (2;3). Составить уравнение третьей стороны.
16.Даны стороны треугольника: (АВ) 4x+3y-10=0; (ВС) 3x+2y-8=0; (АС) 8x+5y-18=0. Составить уравнение прямой, проходящей через точку С и делящей сторону АВ в отношении 2:3 (считая от вершины А).
17.Даны стороны треугольника: (АВ) 4x-3y+26=0; (АС) х+2y+1=0; (ВС) 7x+3y-37=0. Найти точку пересечения медианы, проведенной из вершины В и высоты, проходящей через вершину С.
18.Точка К отстоит на одинаковых расстояниях от точек Р(7;8) и Q(1;2). Найти координаты точки К, если известно, что она лежит на прямой  .
.
19.Известны уравнения двух сторон ромба 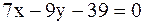 и
и  и одной из его диагоналей
и одной из его диагоналей  . Вычислить координаты вершин ромба.
. Вычислить координаты вершин ромба.
20.Написать уравнение сторон ромба, если известны диагональ  , точка ее пересечения с другой диагональю (0; 2) и одна из сторон
, точка ее пересечения с другой диагональю (0; 2) и одна из сторон  .
.
21.Стороны треугольника заданы уравнениями: (АВ)  (ВС) 3х-4y=0; (АС) 5х+12y-10=0. Найдите радиус описанной окружности.
(ВС) 3х-4y=0; (АС) 5х+12y-10=0. Найдите радиус описанной окружности.
22.Найти точку пересечения высот треугольника, стороны которого лежат на прямых  ,
, 
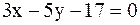 .
.
23.Даны стороны треугольника: (АС) 9x-2y-51=0; (АВ) 4x+3y+24=0; (ВС) x+2y+1=0. Составить уравнение прямой, проходящей через вершину С и точку К на стороне АВ, делящую ее в отношении 3:7 (считая от вершины В).
24.Даны уравнения сторон треугольника  ;
;  ,
, 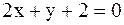 . Найти точку пересечения высот.
. Найти точку пересечения высот.
25.Даны вершины А(2;-2) и В(3;-1) и точка Р(1; 0) пересечения медиан треугольника. Составить уравнение высоты треугольника, проведенной через третью вершину С.
26.Диагонали ромба пересекаются в точке К(-2; 4). Составить уравнение диагонали, не проходящей через точку пересечения сторон  и
и  .
.
Задание 4
На плоскости даны точки  ,
,  ,
,  . Сделать чертеж треугольника и найти:
. Сделать чертеж треугольника и найти:
а) длину и уравнение ребра ВС (записать общее, каноническое, параметрические уравнения, а также уравнения в отрезках и с угловым коэффициентом, если это возможно);
б) косинус угла А;
в) уравнение прямой, проходящей через точку А параллельно стороне ВС;
г) высоту, проведенную к стороне ВС, и ее уравнение;
д) уравнение медианы, проведенной к стороне ВС;
е) координаты центра и радиус описанной окружности;
ж) площадь треугольника;
з) центр тяжести треугольника.
Координаты точек А, В, С
| n | x1 | y1 | х2 | y2 | x3 | y3 |
| -2 | -2 | |||||
| -3 | -11 | -3 | ||||
| -7 | -7 | |||||
| -4 | -3 | -3 | ||||
| -1 | -7 | -1 | ||||
| -1 | -3 | |||||
| -9 | -11 | |||||
| -5 | -14 | |||||
| -3 | -1 | -9 | ||||
| -5 | -3 | |||||
| -9 | -9 | -5 | -5 | |||
| -7 | -3 | -7 | ||||
| -6 | -2 | -2 | ||||
| -2 | -4 | |||||
| -1 | -1 | -8 | -1 | |||
| -7 | -7 | -4 | ||||
| -6 | -14 | -6 | -8 | |||
| -7 | -2 | -2 | ||||
| -5 | -1 | -1 | -1 | |||
| -5 | -4 | |||||
| -3 | -1 | -3 | ||||
| -1 | -6 | |||||
| -9 | ||||||
| -3 | -7 | |||||
| -9 | -3 | -1 |
Задание 5
В пространстве даны точки  ,
, 
 . Сделать схематично чертеж пирамиды SABC и найти:
. Сделать схематично чертеж пирамиды SABC и найти:
а) длину и уравнения ребра АВ;
б) площадь и уравнение грани АВС;
в) высоту, проведенную из вершины S к грани АВС, и ее уравнения;
г) проекцию вершины S на плоскость АВС;
д) уравнения проекции ребра АS на грань АВС;
е) уравнения прямой, проходящей через вершину S параллельно ребру АВ;
ж) уравнение плоскости, проходящей через вершину S парал-
лельно грани АВС;
з) угол между ребрами АВ и AS;
и) угол между ребром AS и гранью АВС;
к) угол между гранями АВС и АВS;
л) координаты центра тяжести пирамиды АВСS;
м) объем пирамиды АВСS.
Значения 
| n | a1 | a2 | a3 |
| -2 | |||
| -3 | |||
| -4 | |||
| -5 | |||
| -6 | |||
| -7 | |||
| -1 | |||
| -2 | |||
| -3 | |||
| -4 | |||
| -5 | |||
| -6 | |||
| -7 | |||
| -1 | |||
| -2 | |||
| -3 | |||
| -4 | |||
| -5 | |||
| -6 | |||
| -7 | |||
| -1 | |||
| -2 | |||
| -3 | |||
| -4 | |||
| -5 | |||
| -6 |
Указания к решению заданий по алгебре
И аналитической геометрии
Пример выполнения задания 1
Решить систему линейных уравнений

 .
.
а) методом Гаусса:




— к элементам первой и третьей строк прибавим соответствующие элементы второй строки:

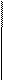


— к элементам второй строки прибавим соответствующие элементы первой строки, умноженные на -4;
— к элементам третьей строки прибавим соответствующие элементы первой строки:
источники:
http://4apple.org/uravnenie-romba-v-dekartovoj-sisteme-koordinat/
http://allrefrs.ru/5-46679.html
Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: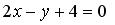 и
и  и уравнение одной из его диагоналей:
и уравнение одной из его диагоналей: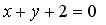 . Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой
. Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой 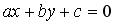 определяется по формуле:
определяется по формуле:
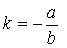
.
Стороны параллельны, так как имеют одинаковый угловой коэффициент:

.
Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:
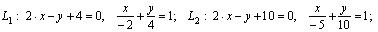
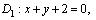
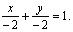
Наметим план решения: 1) находим вершины ромба P и Q ; 2) находим точку пересечения диагоналей ромба N ; 3) через точку N проводим диагональ D 2 ; 4) находим оставшиеся вершины ромба R и S .1) Так как точка P является точкой пересечения прямых L 2 и D 1 , то ее координаты находим из системы уравнений:
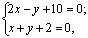
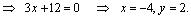

Из рис. 4.1 сразу находим координаты точки Q (- 2, 0) . 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка 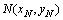 является серединой отрезка PQ , поэтому ее координаты — полусумма соответствующих координат точек P и Q :
является серединой отрезка PQ , поэтому ее координаты — полусумма соответствующих координат точек P и Q :
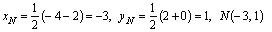
.
3) Так как диагонали ромба взаимно перпендикулярны, то прямая D 2 перпендикулярна вектору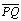 . Найдем его координаты:
. Найдем его координаты:
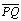 = — 2 — (- 4); 0 — 2 = {2; — 2}.
= — 2 — (- 4); 0 — 2 = {2; — 2}.
По формуле (3.1) находим уравнение диагонали D 2 как уравнение прямой, проходящей через точку N (- 3, 1) перпендикулярно вектору 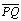 = {2; — 2}:
= {2; — 2}:
2( x — (- 3)) + (- 2)( y — 1) = 0, x — y + 4 = 0.
4) Вершины ромба R и S — точки пересечения прямых L 2 и D 2 , L 1 и D 2 , соответственно, находим из уравнений:
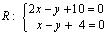 ,
, 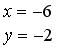 ,
, 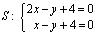 ,
,  .
.
Ответ: P (- 4, 2) R (- 6, — 2), Q (- 2, 0), S (0, 4).
Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, — 7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин. Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:
h : 3 x + y + 11 = 0, m : x + 2 y + 7 = 0 ,
m : x + 2 y + 7 = 0 , 
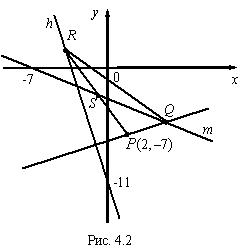
План решения:1) находим уравнение прямой PQ ;2) находим координаты точки R ;3) находим уравнения прямых RP и RQ .1) Находим нормальный вектор прямой h :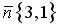 . Уравнение стороны PQ , проходящей через точку P (2, — 7) параллельно вектору
. Уравнение стороны PQ , проходящей через точку P (2, — 7) параллельно вектору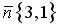 , запишем в виде:
, запишем в виде:
 , x — 3 y — 23 = 0 .
, x — 3 y — 23 = 0 .
Находим координаты точки Q — точки пересечения прямых PQ и m :
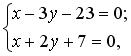 x = 5 , y = — 6.
x = 5 , y = — 6.
2) По свойству медианы треугольника PQR точка S ( x S , y S ) является серединой отрезка RP . Следовательно:
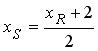 ,
, 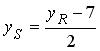 .
.
Точка S лежит на медиане m , значит,
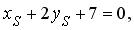
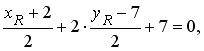
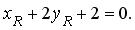
Точка R лежит на высоте h , значит,
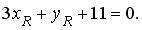
Из последних двух уравнений определяем координаты точки R , решая систему:
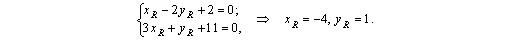
3) Используя формулу (3.4), составим уравнение прямой RP , проходящей через две заданные точки R и P :
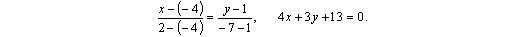
Аналогично, составим уравнение прямой RQ :
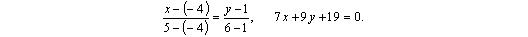
Ответ: x — 3 y — 23 = 0, 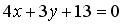 ,
,