Содержание:
- Определение произведения чисел
- Свойства произведения чисел
Определение произведения чисел
Произведение $p$ чисел
$a_{1}, a_{2}, dots, a_{n}$ есть результат умножения этих чисел: $p=a_{1} cdot a_{2} cdot ldots cdot a_{n}$ .
В частности, если умножаются два числа $a$ и $b$, то
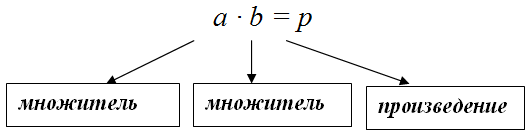
Пример
Задание. Найти произведение чисел:
1) 1.2$cdot 3$ ; 2) 4$cdot 5 cdot 13$
Ответ.
$1,2 cdot 3=3,6$
$4 cdot 5 cdot 13=260$
Свойства произведения чисел
- Коммутативность: $n cdot m=m cdot n$
-
Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
- Дистрибутивность: $(n+m) cdot k=n cdot k+m cdot k$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти произведение чисел удобным способом:
1) 5$cdot 17 cdot 2$ ; 2) 7$cdot 2 cdot 15 cdot 5$
Решение. По свойства умножения имеем:
$$5 cdot 17 cdot 2=(5 cdot 2) cdot 17=10 cdot 17=170$$
$$7 cdot 2 cdot 15 cdot 5=(7 cdot(2 cdot 15)) cdot 5=(7 cdot 30) cdot 5=210 cdot 5=1050$$
Ответ.
$5 cdot 17 cdot 2=170$
$7 cdot 2 cdot 15 cdot 5=1050$
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие
натуральные числа или
десятичные дроби.
Пример
Задание. Найти произведение чисел
1) 156$cdot 32$ ; 2) $4,71 cdot 3,1$
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое,
полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем
под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в
столбик
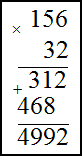
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби
перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после
запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором – один, значит, в ответе
нужно отделить справа три знака:
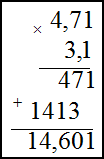
Ответ.
$156 cdot 32=4992$
$4,71 cdot 3,1=14,601$
Читать дальше: что такое простое число.

Прочтите, чтобы получить простое объяснение этих концепций вместе с полезными примерами.
Canva
Если вас просят вычислить произведение двух или более чисел, вам нужно перемножить эти числа. Если вас просят найти сумму двух или более чисел, вам нужно сложить числа.
Ниже мы вместе рассмотрим несколько примеров.
В двух словах
«Продукт» означает умножение.
«Сумма» означает добавить.
Каковы произведение и сумма 6 и 8?
- Продукт 6 и 8 составляет 6 × 8 = 48
- Сумма 6 и 8 составляет 6 + 8 = 14
Каковы произведение и сумма 9 и 3?
Определите произведение и сумму 9 и 3.
- Произведение 9 и 3 равно 9 × 3 = 27.
- Сумма 9 и 3 равна 9 + 3 = 12.
Каковы произведение и сумма -7 и 9?
- Произведение -7 и 9 равно –7 × 9 = -63.
- Сумма -7 и 9 равна –7 + 9 = 2.
Запишите два числа, в которых произведение равно 42.
Все, что вам нужно сделать, это найти два числа, которые умножаются и дают 42. Есть несколько возможных ответов:
- 1 и 42
- 2 и 21
- 3 и 14
- 6 и 7
- -1 и -42
- -2 и -21
- -3 и -14
- -6 и -7
Каковы произведение и сумма 2, 4 и 9?
Составьте произведение 2, 4 и 9.
Произведение означает, что вам нужно умножить три числа.
Сумма означает, что вам нужно сложить три числа.
Вопросы и Ответы
Вопрос: Сможете ли вы найти два числа, в которых произведение 12 и сумма 7?
Ответ: 4 и 3 – это ответы.
4 умножить на 3 равно 12. 4 добавить 3 равно 7.
Вопрос: Как умножить сумму 12 и 8 на их разницу?
Ответ: Сумма 12 и 8 равна 12 плюс 8, что равно 20.
Разница между 12 и 8 составляет 12 минус 8, что составляет 4.
Теперь 20 умножить на 4 будет 80.
Вопрос: какова сумма и произведение -5 и -12?
Ответ: Сумма означает, что вам нужно сложить числа (-5 + -12 = -5 – 12 = -17).
Произведение означает, что вам нужно умножить числа (-5 умножить на -12 = 60).
Вопрос: Произведение двух чисел равно 45. Их сумма равна 18. Какие числа?
Ответ: два числа – 15 и 3, так как 15 умноженное на 3 равно 45, а 15, добавленное к 3, будет 18.
Вопрос: Какие два числа имеют произведение десяти?
Ответ: Есть несколько ответов, 1 и 10 или 2 и 5 – самые очевидные.
Вопрос: Каков ответ этого целого числа: 53 – (- 4) + (- 6) -5?
Ответ: это то же самое, что 53 + 4-6-5 = 46.
Вопрос: Что такое произведение (17/9) (-3/5)?
Ответ: Умножьте числители, чтобы получить -51, и умножьте знаменатели, чтобы получить 45.
Итак, ответ -51/45, что упрощается до -17/15.
Вопрос: Если к сумме 17 и 42 прибавить 10. Какая сумма?
Ответ: Сумма 17 и 42 составляет 59.
Теперь 59 прибавляем 10 равно 69.
Вопрос: Как вам произведение 8 и 6?
Ответ: Чтобы найти произведение 8 и 6, вычислите 8, умноженное на 6, что составляет 48.
Вопрос: Какова сумма и произведение для 7 и 18?
Ответ: Сумма 7 плюс 18, что равно 25.
Произведение 7 умножается на 18, что составляет 126.
Вопрос: Какова сумма 19 и 25, умноженная на их разницу?
Ответ: Сначала вычислите сумму 19 и 25, сложив два числа вместе, чтобы получить 44.
Затем найдите разницу 25 и 19, вычтя числа, чтобы получить 6.
Теперь умножьте 44 на 6, чтобы получить 264.
Вопрос: Что вы получите, если удвоите 15?
Ответ: просто умножьте число на 2, чтобы получить 30.
Вопрос: Произведение двух чисел равно 48. Если одно из чисел равно 6, какое другое число?
Ответ: просто разделите 48 на 6, чтобы получить 8.
Вопрос: Какое число умножается на 12, полученное произведение прибавляется к 6, а сумма равна произведению 6 и 5?
Ответ: произведение 6 и 5 составляет 6 умножить на 5, что равно 30.
30 минус 6 равно 24.
Итак, число равно 2, поскольку 2 умножить на 12 равно 24.
Вопрос: Что представляет собой произведение 0,009 и 2,84?
Ответ: Чтобы найти произведение любых двух чисел, просто умножьте их.
0,009, умноженное на 2,84, дает 0,02556.
Вопрос: Сможете ли вы найти два числа, у которых есть произведение 60 и сумма 100?
Ответ: Эти два числа не являются целыми числами, поэтому однозначного ответа нет.
Вам нужно будет решить одновременные уравнения xy = 60 и x + y = 100, чтобы получить x
Два ответа: 99,3963 и 0,6036 с округлением до 4 знаков после запятой.
Вопрос: Как я могу рассчитать произведение 18 и 4?
Ответ: Все, что вам нужно сделать, это 18 умножить на 4, что равно 72.
Вопрос: К сумме 17 и 42 прибавляется десять. Какая сумма?
Ответ: просто сложите три числа, чтобы получить 69.
Вопрос: Каково произведение 3 (3 + x)?
Ответ: Вам просто нужно умножить скобку, чтобы получить 9 + 3x.
Вопрос: Можете ли вы найти два числа, у которых есть произведение -18 и сумма -7?
Ответ: два числа -9 и 2.
Это потому, что -9, умноженное на 2, равно -18, а -9 плюс 2 равно -7.
Вопрос: Как знание того, что 2 и 9 = 18, помогает найти произведение 4 и 9 без умножения?
Ответ: 4 – это удвоение 2, поэтому вам просто нужно удвоить 18, чтобы получить 36.
Вопрос: Как найти произведение двух чисел?
Ответ: Просто умножьте два числа.
Вопрос: Что такое произведение (3 + 20) (4-30)?
Ответ: Сначала прорабатываем скобки:
3 к 20 дает 23, а 4 минус 30 – 26.
Теперь умножьте 23 на -26, чтобы получить окончательный ответ -598.
Вопрос: Сумма чисел 17, а произведение 70, какие числа?
Ответ: Два ответа – 7 и 10 (так как 7, добавленное к 10, будет 17, а 7, умноженное на 10, будет 70).
Вопрос: Найдите произведение (-3) * (- 6) * (- 2) * (- 1)?
Ответ: -3 умножить на -6 равно 18.
18 умножить на -2 равно -36.
-36 умножить на -1 равно 36.
Вопрос: Что такое 4 (10 + 9)?
Ответ: сначала сложите 10 к 9, чтобы получить 19, а затем умножьте 19 на 4, чтобы получить 76.
Вопрос: Какая пара чисел представляет собой сумму 5 и произведение 4?
Ответ: Двумя числами, которые решают эту задачу, являются 1 и 4.
Это потому, что 1 + 4 дает 5 (сумма означает сложение), а 1, умноженное на 4, дает 4 (prouct означает умножение).
Вопрос: Что получается из трех, четырех и пяти?
Ответ: Чтобы найти произведение, умножьте три числа вместе в любом порядке.
3, умноженное на 4, равно 12, а 12, умноженное на 5, дает 60.
Вопрос: Найдите сумму 5/6 и {-8/6}?
Ответ: Ответ: -3/6 или -1/2 в упрощенном виде.
Вопрос: Сможете ли вы найти два числа, у которых есть произведение 8 и сумма 7?
Ответ: Да, можно, но ответы не целые (целые числа).
Вам нужно будет решить одновременные уравнения xy = 8 и x + y = 7.
Вопрос: Произведение 5 целых чисел равно 3. Какова сумма этих чисел?
Ответ: Произведение означает умножение, поэтому 5 целых чисел, которые умножаются вместе и дают 3, равны 1, 1, 1, 1 и 3 (то есть четыре единицы и одна 3).
Поскольку «сумма» означает «сложить», то 1 + 1 + 1 + 1 + 3 дает окончательный ответ 7.
Вопрос: Можете ли вы найти два числа, в которых произведение 741 и сумма 70?
Ответ: Вам нужны два числа: 57 и 13.
Это потому, что 57 умноженное на 13 дает 741, а 57, добавленное к 13, дает 70.
Вопрос: Произведение 4/3 и число равно 84. Что такое число?
Ответ: разделите 84 на 4/3, чтобы получить 63.
Вопрос: Какие два числа дают сумму 12 и произведение 36?
Ответ: Помните, сумма означает сложение, а произведение – умножение.
На этот вопрос отвечают два числа: 6 и 6.
Это потому, что 6 сложить 6 равно 12, а 6, умноженное на 6, равно 36.
Вопрос: Что такое 1/3 от суммы шести и трех?
Ответ: Прежде всего, вычислите сумму 6 и 3, сложив их вместе, чтобы получить 9.
Теперь, чтобы найти треть чего-либо, нужно разделить на 3, так что 9, разделенное на 3, будет 3.
Вопрос: Какая пара чисел имеет сумму 5 произведений на 4?
Ответ: Сумма означает сложение, а произведение означает умножение.
Следовательно, необходимы два числа: 1 и 4, потому что 1, добавленное к 4, равно 5, а 1, умноженное на 4, равно 4.
Вопрос: Какова сумма 2 и 7?
Ответ: Два числа необходимо сложить вместе, если вы рассчитываете сумму.
Итак, 2 + 7 = 9.
Вопрос: Произведение двух чисел равно 72, а сумма равна 18, что это за два числа?
Ответ: два числа – 6 и 12, потому что 6 умноженное на 12 равно 72, а 6, добавленное к 12, будет 18.
Вопрос: Сможете ли вы найти число, в котором произведение -14 и сумма 5?
Ответ: Два числа – это -2 и 7, так как -2, умноженное на 7, равно -14, а -2 + 7 равно 5.
Вопрос: Какие два числа имеют сумму и произведение 1 и 9?
Ответ: Сумму можно найти, сложив 1 и 9, чтобы получить 10.
Произведение 1 и 9 можно найти, умножив 1 и 9, чтобы получить 9.
Вопрос: Произведение двух целых чисел равно 648, а их сумма равна 51. Что это за два числа?
Ответ: Два числа – 24 и 27.
Это потому, что 24, умноженное на 27, дает 648.
Кроме того, добавление 24 к 27 дает 51.
Помните, продукт означает умножение, а сумма означает сложение.
Вопрос: Как я могу вычислить сумму 2/12 и 6/12?
Ответ: Чтобы найти сумму, просто сложите две дроби вместе, чтобы получить 8/12, что упрощается до 2/3.
Вопрос: Каков ответ, чтобы разделить произведение 5 и 12 вдвое?
Ответ: Прежде всего выработайте произведение 5 и 12.
Следовательно, умножьте 5 на 12, чтобы получить 60 (поскольку произведение означает умножение).
Теперь половина 60, чтобы дать окончательный ответ 30.
Вопрос: Каково произведение 1 и 5?
Ответ: просто умножьте 1 на 5, чтобы получить ответ 5.
Вопрос: Что представляют собой произведения 7/12 и 14?
Ответ: Преобразуйте 7/12 в десятичное число, разделив 7 на 12, чтобы получить 0,583…, теперь умножьте это на 14, чтобы получить 8,17 с округлением до 2 десятичных знаков или 49/6, если вы предпочитаете дробь.
Вопрос: Какие два числа имеют сумму 15 и произведение 36?
Ответ: Ответы 3 и 12, так как 3 + 12 = 15, а 3, умноженное на 12, равно 36.
Вопрос: Сможете ли вы найти два числа, в которых сумма 13 и произведение 12?
Ответ: Сумма означает сложение, а произведение означает умножение.
Два числа – 1 и 12, так как 1 + 12 = 13 и 1, умноженная на 12, дает 12.
Вопрос: Число в квадрате равно 81. Найти число?
Ответ: На этот вопрос есть два ответа.
Первый – 9, потому что 9, умноженное на 9, дает 81.
Второй ответ – -9, потому что -9, умноженное на -9, также равно 81 (два отрицательных числа, умноженные вместе, дают положительный ответ).
Вопрос: Сможете ли вы найти пару чисел с суммой 9 и произведением 20?
Ответ: Продукт означает умножение, а сумма означает сложение.
Итак, два числа, которые решают эту проблему, – это 4 и 5 (поскольку 4, добавленное к 5, дает 9, а 4, умноженное на 5, получается 20).
Вопрос: Из коробки, содержащей 24 кг помидоров, продавец продал 17 1/2 кг. Сколько у него осталось?
Ответ: Чтобы определить, сколько осталось, вам нужно определить разницу между 24 кг и 17,5 кг.
24 – 17,5 = 6,5 кг.
Итак, осталось 6,5 кг помидоров.
© 2011 Марк
Определение
Произведением чисел в математике называется результат их умножения.
Пример: Найдите произведение чисел.
14×15=210
Здесь 14 и 15 называются — множители.
Свойства
1. Коммутативность.
Пример: Вычислить произведение чисел.
17×12=204 и 12×17=204
Переместительный закон: При перестановке множителей результат не меняется.
2. Ассоциативность.
Пример:
11×19×32=6688
(11×19)×32=6688
11×(19×32)=6688
Сочетательный закон: Если группу множителей заменить их произведением, результат не изменится.
3. Дистрибутивность.
Пример:
(15+12)×9=243 и 15×9+12×9=243
Распределительный закон: Умножая сумму на число, можно на это число каждое слагаемое умножить и результаты сложить.
Большие числа, а также десятичные дроби умножают в столбик.
Нет времени решать самому?
Наши эксперты помогут!
Произведение цифр числа
Пример: найти произведение цифр числа 428
4×2×8=64
Произведение суммы и разности чисел
(23+14)×(23-14)=37×9=333
Наименьшее произведение чисел
При умножении любого числа на 0, получится ноль. Наименьшее произведение чисел равно нулю.
Сумма двух произведений чисел
(7×8)+(9×3)=56+27=83
Ответ: 83
Пример: Найди сумму и произведение чисел 14 и 72
Решение:
14+72=86 — сумма
14×72=1008 — произведение
Содержание материала
- Определение произведения чисел
- Видео
- Что такое множитель по математике?
- Основное свойство произведения
- Как называются числа при умножении?
- Переместительный закон умножения
- Умножение многозначного числа на однозначное
- Изменение произведения чисел при изменении его сомножителей
- Умножение любого натурального числа на нуль
Определение произведения чисел
Произведение двух чисел это есть не что иное, как взятое одно из чисел в количестве другого числа.
Еще раз! Если произведение будет С, то номинальное значение одного из чисел пусть а, взятое в количестве b раз и будет этим произведением. Можно записать скажем так
С=а1+а2+а3+а4…+аb где 1,2,3,4…b будут индексом указывающим на то, какое это число а по порядку и не более того!

Пример Найти произведение чисел:
1) 1.2⋅3 ;
Ответ.1,2⋅3=3,6
2) 4⋅5⋅13
Ответ: 4⋅5⋅13=260
Видео
Что такое множитель по математике?
Компоненты умножения называются множители. Первый множитель показывает, какое число прибавляют, второй множитель показывает – сколько раз прибавляют это число. Результат умножения называется произведение.
Основное свойство произведения
Произведение не изменяется от перемены порядка производителей.
Доказательство. Умножить 7 на 3 значит 7 повторить три раза. Заменив 7 суммою 7 единиц и вложив их в вертикальном порядке, имеем:

Таким образом, при умножении двух чисел мы можем считать множителем любой из двух производителей. На этом основании производители называются сомножителями или просто множителями.
Самый общий прием умножения состоит в сложении равных слагаемых; но, если производители велики, этот прием приводит к длинным вычислениям, поэтому самое вычисление располагают иначе.
Как называются числа при умножении?
Так же, как и при сложении и вычитании, числа при умножении тоже имеют свое название. Первое число при умножении называется первый множитель. Второе число при умножении называется второй множитель. Результат умножения называют произведение.
Переместительный закон умножения
Рассмотрим задачу:
Мы отдали по два яблока 5 своим друзьям. Математически запись будет выглядеть так: 2⋅5. Или мы отдали по 5 яблок двум своим друзьям. Математически запись будет выглядеть так: 5⋅2. В первом и втором случаем мы раздадим одинаковое количество яблок равное 10 штукам.
Если мы умножим 2⋅5=10 и 5⋅2=10, то результат не поменяется.
2⋅5=5⋅2
Свойство переместительного закона умножения: От перемены мест множителей произведение не меняется. m⋅n=n⋅m
Умножение многозначного числа на однозначное
Умножение числа 8094 на 3 обозначают тем, что подписывают множитель под множимым, ставят слева знак умножения и проводят черту с тем, чтобы отделить произведение.

Умножить многозначное число 8094 на 3 значит найти сумму трех равных слагаемых

следовательно, для умножения нужно все порядки многозначного числа повторить три раза, то есть умножить на 3 единицы, десятки, сотни, и т. п. Сложение начинают с единицы, следовательно, и умножение нужно начинать с единицы, а затем переходят от правой руки к левой к единицам высшего порядка.
При этом ход вычислений выражают словесно:
-
Начинаем умножение с единиц: 3 × 4 составляют 12, подписываем под единицами 2, а единицу (1 десяток) прикладываем к произведению следующего порядка на множитель (или запоминаем ее в уме).
-
Умножаем десятки: 3 × 9 составляет 27, да 1 в уме составят 28; подписываем под десятками 8 и 2 в уме.
-
Умножаем сотни: Нуль, умноженный на 3, дает нуль, да 2 в уме составит 2, подписываем под сотнями 2.
-
Умножаем тысячи: 3 × 8 = 24, подписываем вполне 24, ибо не имеем следующих порядков.
Это действие выразится письменно:

Из предыдущего примера выводим следующее правило. Чтобы умножить многозначное число на однозначное, нужно:
-
Подписать множитель под единицами множимого, поставить слева знак умножения и провести черту.
-
Умножение начинать с простых единиц, затем, переходя от правой руки к левой, последовательно умножают десятки, сотни, тысячи и т. д.
-
Если при умножении произведение выражается однозначным числом, то его подписывают под умножаемой цифрой множимого.
-
Если же произведение выражается двухзначным числом, то цифру единиц подписывают под тем же столбцом, а цифру десятков прибавляют к произведению следующего порядка на множитель.
-
Умножение продолжается до тех пор, пока не получат полного произведения.
Изменение произведения чисел при изменении его сомножителей
Чтобы понять, что происходит с произведением чисел при изменении одного или нескольких сомножителей, нужно вспомнить, что действие умножения – это частный случай действия сложения, а также переместительный и сочетательный законы сложения.
Если увеличить один из сомножителей в несколько раз, произведение также увеличится в это же число раз.
Рассмотрим пример 18 ∙2. Увеличив второй сомножитель, к примеру, в 3 раза, мы получим другое выражение: 18 ∙6.
Умножение любого натурального числа на нуль
6⋅0=0 или 0⋅6=0 a⋅0=0 или 0⋅a=0 При умножении любого натурального числа на нуль произведение будет равно нулю.
Вопросы к теме “Умножение”:
Что такое произведение чисел? Ответ: произведением чисел или умножение чисел называется выражение m⋅n, где m – слагаемое, а n – число повторений этого слагаемого.
Для чего нужно умножение? Ответ: чтобы не писать длинное сложение чисел, а писать сокращенно. Например, 3+3+3+3+3+3=3⋅6=18
Что является результатом умножения? Ответ: значение произведения.
Что означает запись умножения 3⋅5? Ответ: 3⋅5=5+5+5=3+3+3+3+3=15
Если умножить миллион на нуль, чему будет равно произведение? Ответ: 0
Пример №1: Замените сумму произведением: а) 12+12+12+12+12 б)3+3+3+3+3+3+3+3+3 Ответ: а)12⋅5=60 б) 3⋅9=27
Пример №2: Запишите в виде произведения: а) а+а+а+а б) с+с+с+с+с+с+с Решение: а)а+а+а+а=4⋅а б) с+с+с+с+с+с+с=7⋅с
Задача №1: Мама купила 3 коробки конфет. В каждой коробке по 8 конфет. Сколько конфет купила мама? Решение: В одной коробке 8 конфет, а у нас таких коробок 3 штуки. 8+8+8=8⋅3=24 конфеты Ответ: 24 конфеты.
Задача №2: Учительница рисования сказала приготовить своим восемью ученикам по семь карандашей на урок. Сколько всего карандашей вместе было у детей? Решение: Можно посчитать суммой задачу. У первого ученика было 7 карандашей, у второго ученика было 7 карандашей и т.д. 7+7+7+7+7+7+7+7=56 Запись получилась неудобная и длинная, заменим сумму на произведение. 7⋅8=56 Ответ 56 карандашей.
Теги
Математика
6 класс
Урок № 26
Произведение целых чисел. Часть 2
Перечень рассматриваемых вопросов:
- На уроке мы научимся формулировать и узнавать свойства умножения.
- Находить квадраты и кубы целых чисел.
- Вычислять значения числовых выражений, содержащих разные действия.
- Выполнять числовые подстановки в буквенные выражения и находить соответствующие им значения.
Тезаурус
Произведение любого целого числа a и нуля равно нулю.
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.
Степенью целого числа a с натуральным показателем n (n > 1) называется произведение n множителей, каждый из которых равен a.
Список литературы
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Мы уже изучали правила умножения целых чисел.
Сегодня рассмотрим свойства произведения целых чисел.
Умножение целых чисел на 0.
Произведение любого целого числа a и нуля равно нулю.
a ∙ 0 = 0
Рассмотрим примеры.
Найдите произведение целого положительного числа 209 и нуля.
Решение:
203 ∙ 0 = 0
Найдите произведение нуля и целого отрицательного числа (– 29).
Решение:
0 ∙ (– 29) = 0
Умножение целого числа на 1
Произведение целого числа и 1 равно cамому числу.
a ∙ 1 = a
Рассмотрим примеры.
Вычислите произведение положительного целого числа 64 и единицы.
Решение:
64 ∙ 1 = 64
Вычислите произведение единицы и отрицательного целого числа (– 475).
Решение:
1 ∙ (– 475) = – 475
Найдите произведение нуля и единицы.
Решение:
0 ∙ 1 = 0
Умножение на (– 1)
При умножении числа на (– 1) меняется только знак, то есть получается число, противоположное a.
a ∙ (– 1) = – a
Законы умножения
Переместительный и сочетательный законы умножения верны для любых целых чисел, и их можно применять для упрощения числовых выражений.
Переместительный закон умножения:
a ∙ b = b ∙ a
Сочетательный закон умножения:
a ∙ (b ∙ c) = (a ∙ b) ∙ c
Умножение или произведение нескольких целых чисел
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.
Вычислим произведение нескольких целых чисел:
9 ∙ (– 14) ∙ 5 ∙ (– 1)
Решение:
9 ∙ (– 14) ∙ 5 ∙ (– 1) = (9 ∙ (– 14)) ∙ 5 ∙ (– 1) = (– 126) ∙ 5 ∙ (– 1) = ((– 126) ∙ 5) ∙ (– 1) = (– 630) ∙ (– 1) = 630
Ответ: 630.
При перемножении целых чисел, результат всегда будет целым числом.
Выводы
1. Если в произведении нечётное количество отрицательных множителей, то произведение будет отрицательным.
2. Если в произведении чётное количество отрицательных множителей, то произведение будет положительным.
Степень целого числа a с натуральным показателем n
Определение: степенью целого числа a с натуральным показателем n (n > 1) называется произведение n множителей, каждый из которых равен a.
a ∙ a ∙ a ∙ a ·…∙ a = an
n множителей
Рассмотрим примеры.
1. Первая степень любого числа равна самому числу.
a1 = a
2. Вторая степень любого числа называется квадратом.
a2 = a ∙ a
3. Третья степень любого целого числа называется кубом.
a3 = a ∙ a ∙ a
Например,
24 = 2 ∙ 2 ∙ 2 ∙ 2 = 16
(– 5)3 = (– 5) ∙ (– 5) ∙ (– 5) = – 125
Итак, мы научились выполнять сложение, вычитание и умножение целых чисел. Рассмотрим, как найти значение выражения, которое содержит такие действия.
42 – 15 ∙ (– 6)
Решение
42 – 15 ∙ (– 6) = 42 – (15 ∙ (– 6)) = 42 – (– 90) = 42 + 90 = 132
Ответ: 132.
Дополнительный материал
Мы изучили правила и свойства умножения целых чисел.
Используя их, решим две задачи.
Задача №1
Чему равно произведение последовательных целых чисел, начинающихся числом (– 200) и оканчивающихся числом 200?
Решение
Между числами (– 200) и 200 находится 0, а любое число, умноженное на 0 равно 0. Поэтому произведение последовательных целых чисел от (– 200) до 200 равно 0.
Ответ: 0.
Задача №2
Чему равно произведение всех целых чисел?
Решение
Целые числа состоят из целых положительных, отрицательных чисел, а также нуля. При умножении любого числа на ноль будет 0. Поэтому произведение всех целых чисел равно 0.
Ответ: 0.
Разбор заданий тренировочного модуля
Тип 1. Разместите нужные подписи под изображениями.
Какие законы представлены в формулах?
Законы умножения
- a ∙ b = b ∙ а
- а ∙ (b ∙ с) = (а ∙ b) ∙ с
Варианты ответов:
Сочетательный закон умножения
Переместительный закон умножения
Свойство 0
Для ответа на вопрос задания обратимся к теоретическому материалу сегодняшнего урока.
Правильный ответ:
1. Переместительный закон умножения
2. Сочетательный закон умножения
Тип 2. Вставьте в текст нужные слова.
Чтобы найти … нескольких чисел, нужно найти произведение … чисел, … на третье число и так далее.
Варианты слов для вставки:
произведение
трёх
первого
двух первых
умножить
разделить
сложить
вычесть
Для ответа на вопрос задания обратимся к теоретическому материалу сегодняшнего урока.
Правильный ответ:
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.

