1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Четные и нечетные функции
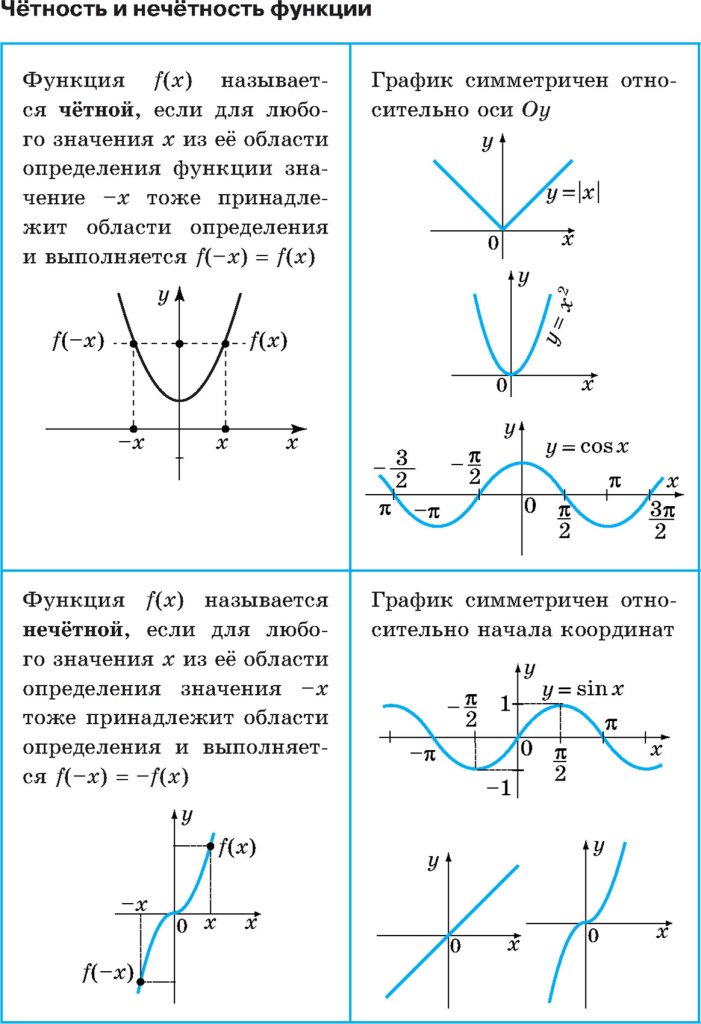
(blacktriangleright) Функция (f(x)) называется четной, если при всех (x) из ее области определения верно: (f(-x)=f(x)).
График четной функции симметричен относительно оси (y):
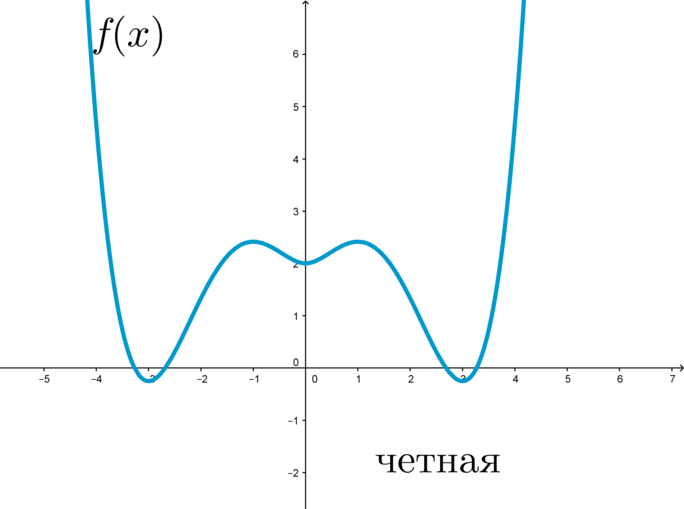
Пример: функция (f(x)=x^2+cos x) является четной, т.к. (f(-x)=(-x)^2+cos{(-x)}=x^2+cos x=f(x)).
(blacktriangleright) Функция (f(x)) называется нечетной, если при всех (x) из ее области определения верно: (f(-x)=-f(x)).
График нечетной функции симметричен относительно начала координат:
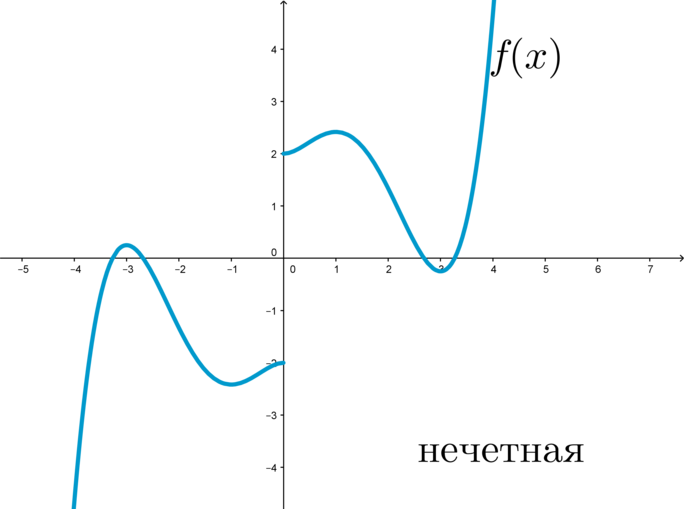
Пример: функция (f(x)=x^3+x) является нечетной, т.к. (f(-x)=(-x)^3+(-x)=-x^3-x=-(x^3+x)=-f(x)).
(blacktriangleright) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
Например, функция (f(x)=x^2-x) является суммой четной функции (f_1=x^2) и нечетной (f_2=-x).
(blacktriangleright) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
5) Если (f(x)) — четная функция, то уравнение (f(x)=c (cin
mathbb{R})) имеет единственный корень тогда и только когда, когда (x=0).
6) Если (f(x)) — четная или нечетная функция, и уравнение (f(x)=0) имеет корень (x=b), то это уравнение обязательно будет иметь второй корень (x=-b).
(blacktriangleright) Функция (f(x)) называется периодической на (X), если для некоторого числа (Tne 0) выполнено (f(x)=f(x+T)), где (x,
x+Tin X). Наименьшее (T), для которого выполнено данное равенство, называется главным (основным) периодом функции.
У периодической функции любое число вида (nT), где (nin mathbb{Z}) также будет являться периодом.
Пример: любая тригонометрическая функция является периодической;
у функций (f(x)=sin x) и (f(x)=cos x) главный период равен (2pi), у функций (f(x)=mathrm{tg},x) и (f(x)=mathrm{ctg},x) главный период равен (pi).
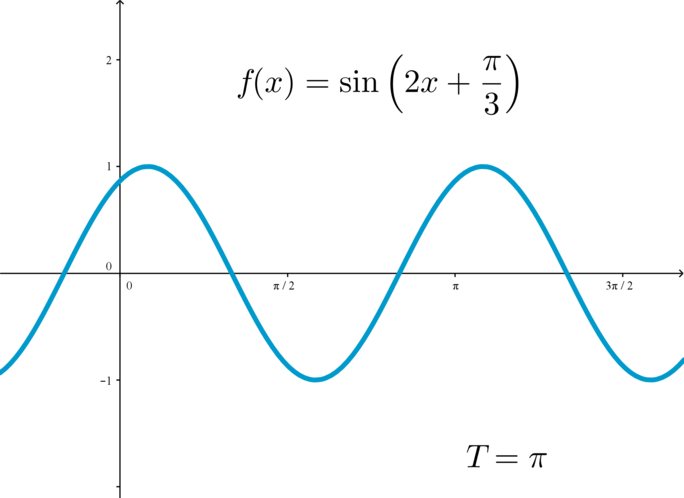
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной (T) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
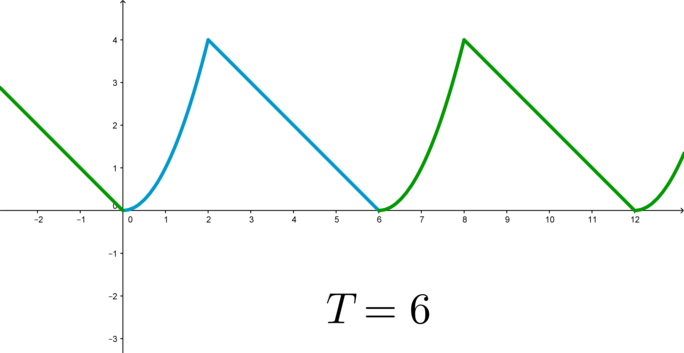
(blacktriangleright) Область определения (D(f)) функции (f(x)) — это множество, состоящее из всех значений аргумента (x), при которых функция имеет смысл (определена).
Пример: у функции (f(x)=sqrt x+1) область определения: (xin
[0;+infty)).
(blacktriangleright) Область значений (E(f)) функции (f(x)) — это множество, состоящее из всех значений функции (f(a)), где (ain
D(f)).
Пример: у функции (f(x)=sqrt x +1) область значений: (f(x)in
[1;+infty)).
(blacktriangleright) Уравнение (f(x)=a) имеет решение тогда и только тогда, когда (a) принадлежит области значений функции (f(x)), т.е. (ain E(f)).
(blacktriangleright) Если область значений функции (f(x)) не превышает некоторого числа (A), т.е. (f(x)leq A) при всех (xin
D(f)), а функция (g(x)geq A) при всех (xin D(g)), то уравнение [{large{f(x)=g(x)}} Leftrightarrow begin{cases} f(x)=A\g(x)=Aend{cases}]
Задание
1
#6364
Уровень задания: Равен ЕГЭ
При каких значениях параметра (a) уравнение
[2x^2+amathrm{tg},(cos x)+a^2=0]
имеет единственное решение?
Заметим, что так как (x^2) и (cos x) — четные функции, то если уравнение будет иметь корень (x_0), оно также будет иметь и корень (-x_0).
Действительно, пусть (x_0) – корень, то есть равенство (2x_0^2+amathrm{tg},(cos x_0)+a^2=0) верно. Подставим (-x_0): (2
(-x_0)^2+amathrm{tg},(cos(-x_0))+a^2=2x_0^2+amathrm{tg},(cos
x_0)+a^2=0).
Таким образом, если (x_0ne 0), то уравнение уже будет иметь как минимум два корня. Следовательно, (x_0=0). Тогда:
[2cdot 0+amathrm{tg},(cos 0)+a^2=0 quad Rightarrow quad
a^2+amathrm{tg},1=0 quad Rightarrow quad left[
begin{gathered}begin{aligned}
&a=0\
&a=-mathrm{tg},1 end{aligned} end{gathered}right.]
Мы получили два значения параметра (a). Заметим, что мы использовали то, что (x=0) точно является корнем исходного уравнения. Но мы нигде не использовали то, что он единственный. Следовательно, нужно подставить получившиеся значения параметра (a) в исходное уравнение и проверить, при каких именно (a) корень (x=0) действительно будет единственным.
1) Если (a=0), то уравнение примет вид (2x^2=0). Очевидно, что это уравнение имеет лишь один корень (x=0). Следовательно, значение (a=0) нам подходит.
2) Если (a=-mathrm{tg},1), то уравнение примет вид [2x^2-mathrm{tg},1cdot mathrm{tg},(cos x)+mathrm{tg}^2,1=0] Перепишем уравнение в виде [2x^2+mathrm{tg}^2,1=mathrm{tg},1cdot mathrm{tg},(cos x)qquad (*)] Так как (-1leqslant cos xleqslant 1), то (-mathrm{tg},1leqslant mathrm{tg},(cos x)leqslant
mathrm{tg},1). Следовательно, значения правой части уравнения (*) принадлежат отрезку ([-mathrm{tg}^2,1; mathrm{tg}^2,1]).
Так как (x^2geqslant 0), то левая часть уравнения (*) больше или равна (0+
mathrm{tg}^2,1).
Таким образом, равенство (*) может выполняться только тогда, когда обе части уравнения равны (mathrm{tg}^2,1). А это значит, что [begin{cases} 2x^2+mathrm{tg}^2,1=mathrm{tg}^2,1 \
mathrm{tg},1cdot mathrm{tg},(cos x)=mathrm{tg}^2,1
end{cases}
quadLeftrightarrowquad begin{cases} x=0\
mathrm{tg},(cos x)=mathrm{tg},1
end{cases}quadLeftrightarrowquad x=0] Следовательно, значение (a=-mathrm{tg},1) нам подходит.
Ответ:
(ain {-mathrm{tg},1;0})
Задание
2
#3923
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых график функции [f(x)=3mathrm{tg},dfrac{ax}5 +2sin dfrac{8pi a-3x}4]
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено (f(-x)=-f(x)) для любого (x) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено (f(-x)=-f(x).)
[begin{aligned}
&3mathrm{tg},left(-dfrac{ax}5right)+2sin dfrac{8pi a+3x}4=
-left(3mathrm{tg},left(dfrac{ax}5right)+2sin dfrac{8pi
a-3x}4right)quad Rightarrowquad -3mathrm{tg},dfrac{ax}5+2sin
dfrac{8pi a+3x}4=
-left(3mathrm{tg},left(dfrac{ax}5right)+2sin dfrac{8pi
a-3x}4right) quad Rightarrow\[3ex]
Rightarrowquad &sin dfrac{8pi a+3x}4+sin dfrac{8pi a-3x}4=0
quad Rightarrow quad2sin dfrac12left(dfrac{8pi
a+3x}4+dfrac{8pi a-3x}4right)cdot cos dfrac12
left(dfrac{8pi a+3x}4-dfrac{8pi a-3x}4right)=0 quad
Rightarrowquad sin (2pi a)cdot cos frac34 x=0
end{aligned}]
Последнее уравнение должно быть выполнено для всех (x) из области определения (f(x)), следовательно, (sin(2pi a)=0 Rightarrow
a=dfrac n2, ninmathbb{Z}).
Ответ:
(dfrac n2, ninmathbb{Z})
Задание
3
#3069
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [f(x)=|a+2|sqrt[3]x] имеет 4 решения, где (f) – четная периодическая с периодом (T=dfrac{16}3) функция, определенная на всей числовой прямой, причем (f(x)=ax^2) при (0leqslant xleqslant dfrac83.)
(Задача от подписчиков)
Так как (f(x)) – четная функция, то ее график симметричен относительно оси ординат, следовательно, при (-dfrac83leqslant
xleqslant 0) (f(x)=ax^2). Таким образом, при (-dfrac83leqslant
xleqslant dfrac83), а это отрезок длиной (dfrac{16}3), функция (f(x)=ax^2).
1) Пусть (a>0). Тогда график функции (f(x)) будет выглядеть следующим образом: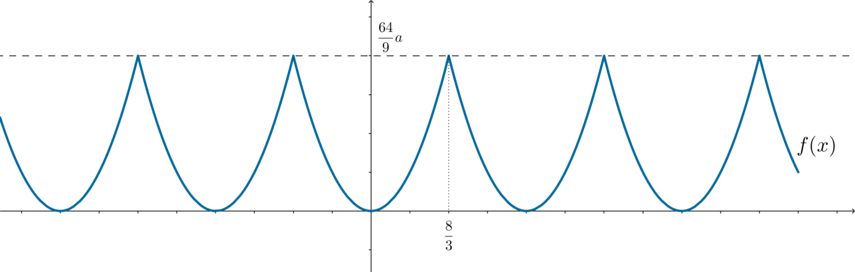
Тогда для того, чтобы уравнение имело 4 решения, нужно, чтобы график (g(x)=|a+2|cdot sqrt[3]x) проходил через точку (A):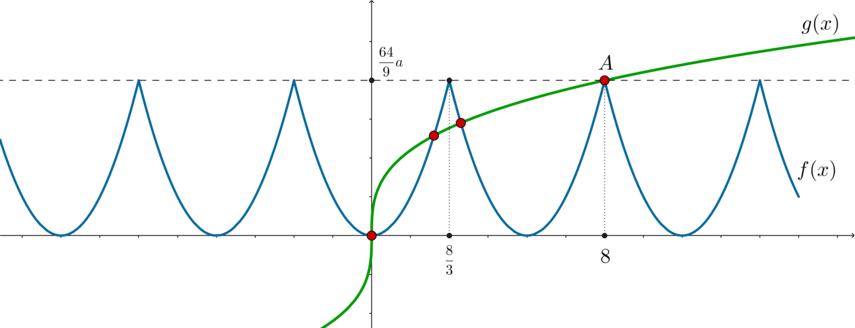
Следовательно, [dfrac{64}9a=|a+2|cdot sqrt[3]8 quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &9(a+2)=32a\
&9(a+2)=-32a end{aligned} end{gathered}right.
quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &a=dfrac{18}{23}\[2ex]
&a=-dfrac{18}{41} end{aligned} end{gathered}right.] Так как (a>0), то подходит (a=dfrac{18}{23}).
2) Пусть (a<0). Тогда картинка окажется симметричной относительно начала координат: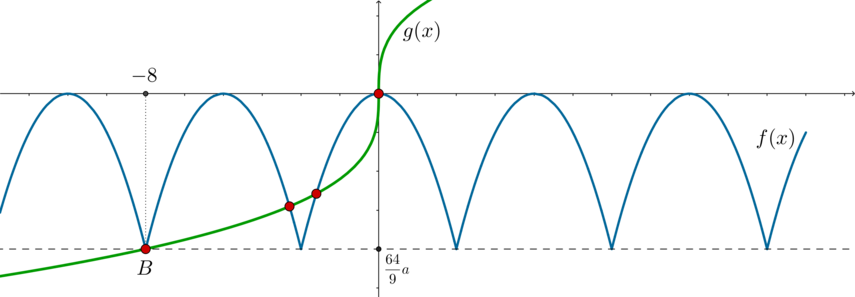
Нужно, чтобы график (g(x)) прошел через точку (B): [dfrac{64}9a=|a+2|cdot sqrt[3]{-8} quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &a=dfrac{18}{23}\[2ex]
&a=-dfrac{18}{41} end{aligned} end{gathered}right.] Так как (a<0), то подходит (a=-dfrac{18}{41}).
3) Случай, когда (a=0), не подходит, так как тогда (f(x)=0) при всех (x), (g(x)=2sqrt[3]x) и уравнение будет иметь только 1 корень.
Ответ:
(ain left{-dfrac{18}{41};dfrac{18}{23}right})
Задание
4
#3072
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых уравнение [a^2-7a+7sqrt{2x^2+49}=3|x-7a|-6|x|]
имеет хотя бы один корень.
(Задача от подписчиков)
Перепишем уравнение в виде [7sqrt{2x^2+49}=3|x-7a|-6|x|-a^2+7a] и рассмотрим две функции: (g(x)=7sqrt{2x^2+49}) и (f(x)=3|x-7a|-6|x|-a^2+7a).
Функция (g(x)) является четной, имеет точку минимума (x=0) (причем (g(0)=49)).
Функция (f(x)) при (x>0) является убывающей, а при (x<0) – возрастающей, следовательно, (x=0) – точка максимума.
Действительно, при (x>0) второй модуль раскроется положительно ((|x|=x)), следовательно, вне зависимости от того, как раскроется первый модуль, (f(x)) будет равно (kx+A), где (A) – выражение от (a), а (k) равно либо (-9), либо (-3). При (x<0) наоборот: второй модуль раскроется отрицательно и (f(x)=kx+A), где (k) равно либо (3), либо (9).
Найдем значение (f) в точке максимума: [f(0)=-a^2+7a+21|a|]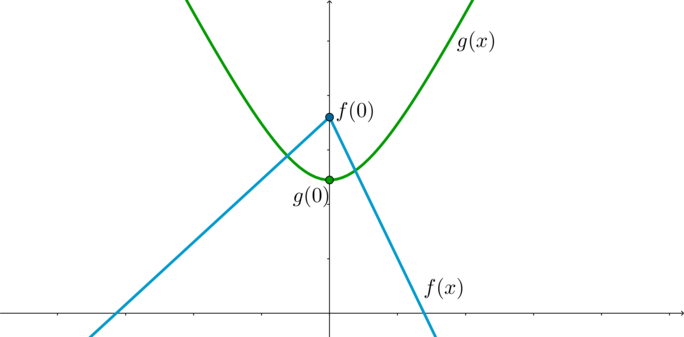
Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций (f) и (g) имели хотя бы одну точку пересечения. Следовательно, нужно: [f(0)geqslant g(0) quadRightarrowquad -a^2+7a+21|a|geqslant 49
quadLeftrightarrowquad left[ begin{gathered} begin{aligned}
&begin{cases} a>0\
a^2-28a+49leqslant 0 end{cases}\
&begin{cases} a<0\
a^2+14a+49leqslant 0 end{cases}\
&begin{cases} a=0\
0geqslant 49end{cases} end{aligned} end{gathered}right.] Решая данную совокупность систем, получим ответ: [ain {-7}cup [14-7sqrt3;14+7sqrt3]]
Ответ:
(ain {-7}cup[14-7sqrt3;14+7sqrt3])
Задание
5
#3912
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [2^{x^3-3x^2+4}+(a-10)cdot (sqrt2)^{x^3-3x^2+4}+12-a=0]
имеет шесть различных решений.
Сделаем замену ((sqrt2)^{x^3-3x^2+4}=t), (t>0). Тогда уравнение примет вид [t^2+(a-10)t+12-a=0quad (*)] Будем постепенно выписывать условия, при которых исходное уравнение будет иметь шесть решений.
Заметим, что квадратное уравнение ((*)) может максимум иметь два решения. Любое кубическое уравнение (Ax^3+Bx^2+Cx+D=0) может иметь не более трех решений. Следовательно, если уравнение ((*)) имеет два различных решения (положительных!, так как (t) должно быть больше нуля) (t_1) и (t_2), то, сделав обратную замену, мы получим: [left[begin{gathered}begin{aligned}
&(sqrt2)^{x^3-3x^2+4}=t_1\[2ex]
&(sqrt2)^{x^3-3x^2+4}=t_2end{aligned}end{gathered}right.] Так как любое положительное число можно представить как (sqrt2) в какой-то степени, например, (t_1=(sqrt2)^{log_{sqrt2} t_1}), то первое уравнение совокупности перепишется в виде [x^3-3x^2+4=log_{sqrt2} t_1] Как мы уже говорили, любое кубическое уравнение имеет не более трех решений, следовательно, каждое уравнение из совокупности будет иметь не более трех решений. А значит и вся совокупность будет иметь не более шести решений.
Значит, чтобы исходное уравнение имело шесть решений, квадратное уравнение ((*)) должно иметь два различных решения, а каждое полученное кубическое уравнение (из совокупности) должно иметь три различных решения (причем ни одно решение одного уравнения не должно совпадать с каким-либо решением второго!)
Очевидно, что если квадратное уравнение ((*)) будет иметь одно решение, то мы никак не получим шесть решений у исходного уравнения.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение ((*)) имело два различных решения, его дискриминант должен быть положительным: [D=a^2-16a+52>0quadLeftrightarrowquad
ain (-infty;8-2sqrt3)cup(8+2sqrt3;+infty)]
2) Также нужно, чтобы оба корня были положительными (так как (t>0)). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: [begin{cases} 12-a>0\-(a-10)>0end{cases}quadLeftrightarrowquad a<10]
Таким образом, мы уже обеспечили себе два различных положительных корня (t_1) и (t_2).
3) Давайте посмотрим на такое уравнение [x^3-3x^2+4=log_{sqrt2} t] При каких (t) оно будет иметь три различных решения?
Рассмотрим функцию (f(x)=x^3-3x^2+4).
Можно разложить на множители: [x^3-3x^2+4=x^3+x^2-4x^2+4=x^2(x+1)-4(x+1)(x-1)=(x+1)(x-2)^2] Следовательно, ее нули: (x=-1;2).
Если найти производную (f'(x)=3x^2-6x), то мы получим две точки экстремума (x_{max}=0, x_{min}=2).
Следовательно, график выглядит так:
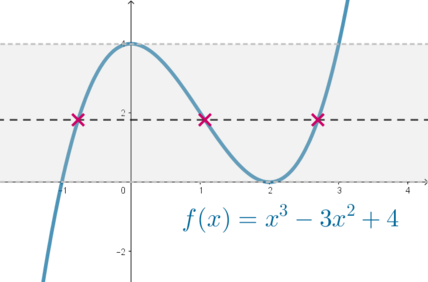
Мы видим, что любая горизонтальная прямая (y=k), где (0<k<4), пересекает график в трех точках. При всех остальных значениях (k) будет меньше трех точек пересечения. Следовательно, для того, чтобы уравнение (x^3-3x^2+4=log_{sqrt2} t) имело три различных решения, нужно, чтобы (0<log_ {sqrt2}t<4).
Таким образом, нужно: [begin{cases} 0<log_{sqrt2}t_1<4\ 0<log_{sqrt2}t_2<4end{cases}qquad (**)] Давайте также сразу заметим, что если числа (t_1) и (t_2) различны, то и числа (log_{sqrt2}t_1) и (log_{sqrt2}t_2) будут различны, значит, и уравнения (x^3-3x^2+4=log_{sqrt2} t_1) и (x^3-3x^2+4=log_{sqrt2} t_2) будут иметь несовпадающие между собой корни.
Систему ((**)) можно переписать так: [begin{cases} 1<t_1<4\
1<t_2<4end{cases}]
Таким образом, мы определили, что оба корня уравнения ((*)) должны лежать в интервале ((1;4)). Как записать это условие?
В явном виде выписывать корни мы не будем.
Рассмотрим функцию (g(t)=t^2+(a-10)t+12-a). Ее график – парабола с ветвями вверх, которая имеет две точки пересечения с осью абсцисс (это условие мы записали в пункте 1)). Как должен выглядеть ее график, чтобы точки пересечения с осью абсцисс были в интервале ((1;4))? Так:
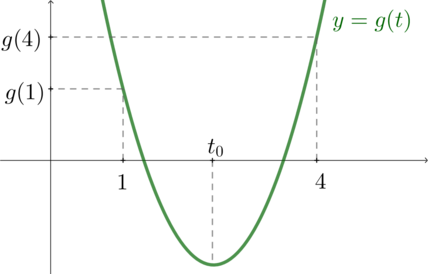
Во-первых, значения (g(1)) и (g(4)) функции в точках (1) и (4) должны быть положительными, во-вторых, вершина параболы (t_0) должна также находиться в интервале ((1;4)). Следовательно, можно записать систему: [begin{cases}
1+a-10+12-a>0\[1ex]
4^2+(a-10)cdot 4+12-a>0\[2ex]
1<dfrac{-(a-10)}2<4end{cases}quadLeftrightarrowquad 4<a<8]
Таким образом, нам нужно пересечь значения параметра (a), найденные в 1-ом, 2-ом и 3-ем пунктах, и мы получим ответ: [begin{cases} ain (-infty;8-2sqrt3)cup(8+2sqrt3;+infty)\ a<10\
4<a<8end{cases}quadLeftrightarrowquad 4<a<8-2sqrt3]
Ответ:
((4;8-2sqrt3))
Задание
6
#1828
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение
[25x^5+25(a-1)x^3-4(a-7)x=0]
имеет ровно пять различных решений, а сами решения, упорядоченные по возрастанию, образуют арифметическую прогрессию.
Заметим, что данное уравнение при любых значениях (a) всегда имеет как минимум один корень (x=0). Значит, для выполнения условия задачи нужно, чтобы уравнение [25x^4+25(a-1)x^2-4(a-7)=0 qquad (*)]
имело четыре различных корня, отличных от нуля, представляющих вместе с (x=0) арифметическую прогрессию.
Заметим, что функция (y=25x^4+25(a-1)x^2-4(a-7)) является четной, значит, если (x_0) является корнем уравнения ((*)), то и (-x_0) будет являться его корнем. Тогда необходимо, чтобы корнями этого уравнения были упорядоченные по возрастанию числа: (-2d, -d, d, 2d) (тогда (d>0)). Именно тогда данные пять чисел будут образовывать арифметическую прогрессию (с разностью (d)).
Чтобы этими корнями являлись числа (-2d, -d, d, 2d), нужно, чтобы числа (d^{,2}, 4d^{,2}) являлись корнями уравнения (25t^2+25(a-1)t-4(a-7)=0). Тогда по теореме Виета:
[begin{cases}
-dfrac{4(a-7)}{25}=d^{,2}cdot 4d^{,2}\[4pt]
-dfrac{25(a-1)}{25}=d^{,2}+4d^{,2}
end{cases} quad Rightarrow quad begin{cases}
d^{,4}=dfrac{7-a}{25}\
dfrac{7-a}{25}=left(dfrac{1-a}{5}right)^2
end{cases} quad Rightarrow quad
left[begin{gathered}begin{aligned} &a=-2\&a=3
end{aligned} end{gathered} right.]
Причем при (a=-2) (d=pm sqrt{frac35}), а при (a=3) (din
varnothing). Значит, подходит значение (a=-2) и (d=sqrt{frac35}) (т.к. должно быть (d>0)).
Ответ:
(ain {-2})
Задание
7
#3198
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых уравнение [a^2+13|x|+2^{x^2+2}=20a+2|5x+12a|]
имеет хотя бы один корень.
Перепишем уравнение в виде [13|x|-2|5x+12a|=20a-a^2-2^{x^2+2}] и рассмотрим две функции: (g(x)=20a-a^2-2^{x^2+2}) и (f(x)=13|x|-2|5x+12a|).
Функция (g(x)) имеет точку максимума (x=0) (причем (g_{text{верш}}=g(0)=-a^2+20a-4)):
(g'(x)=-2^{x^2+2}cdot ln 2cdot 2x). Ноль производной: (x=0). При (x<0) имеем: (g’>0), при (x>0): (g'<0).
Функция (f(x)) при (x>0) является возрастающей, а при (x<0) – убывающей, следовательно, (x=0) – точка минимума.
Действительно, при (x>0) первый модуль раскроется положительно ((|x|=x)), следовательно, вне зависимости от того, как раскроется второй модуль, (f(x)) будет равно (kx+A), где (A) – выражение от (a), а (k) равно либо (13-10=3), либо (13+10=23). При (x<0) наоборот: первый модуль раскроется отрицательно и (f(x)=kx+A), где (k) равно либо (-3), либо (-23).
Найдем значение (f) в точке минимума: [f_{text{верш}}=f(0)=-24|a|]
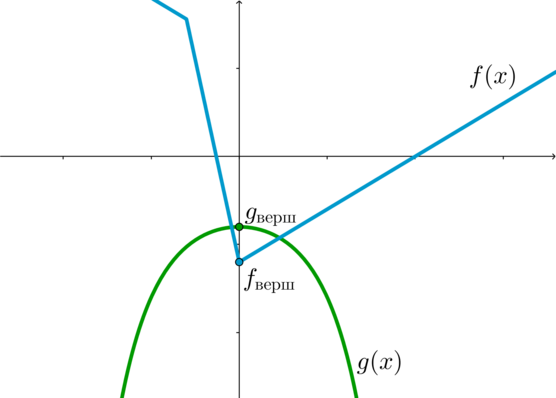
Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций (f) и (g) имели хотя бы одну точку пересечения. Следовательно, нужно: [f(0)leqslant g(0) quadRightarrowquad a^2-20a+4leqslant 24|a|
quadLeftrightarrowquad left[ begin{gathered} begin{aligned}
&begin{cases} ageqslant 0\
a^2-44a+4leqslant 0 end{cases}\
&begin{cases} a<0\
a^2+4a+4leqslant 0 end{cases} end{aligned}
end{gathered}right.] Решая данную совокупность систем, получим ответ: [ain {-2}cup[22-4sqrt{30};22+4sqrt{30}]]
Ответ:
(ain {-2}cup[22-4sqrt{30};22+4sqrt{30}])

УСТАЛ? Просто отдохни
Знаток
(307),
на голосовании
8 лет назад
Голосование за лучший ответ
Александр Анатольевич
Гуру
(3934)
8 лет назад
если y(-x)=y(x) то функция четная. На графике – функция симметрична относительно оси Y
если y(-x)=-y(x) то функция нечетная. На графике – функция симметрична относительно точки пересечения осей (0,0).
Если ни то, ни другое, то и функция не является ни четной, ни нечетной, как и в данном случае
ольга ориняк
Профи
(582)
8 лет назад
Функция не может быть четной ибо при четности должна выполнятся симметрия относительно оси Оу. А здесь ООФ x>=0 если только х под корнем или х-3>=0
Построим график функции
y=x3
и на его примере рассмотрим свойства функции корня (n)-й степени, где (n) — нечётное число ((3,5,7)…).
Для построения графика при
x≥0
заполним таблицу:
|
(x) |
(0) |
18 |
(1) |
8 |
|
(y) |
(0) |
12 |
(1) |
2 |
Отметим полученные точки на координатной плоскости и соединим их плавной кривой, затем к построенной ветви добавим ветвь,
симметричную ей относительно начала координат.

Если (n) — нечётное число, то график функции
y=xn
имеет вид,
представленный на рисунке:

Свойства функции
y=xn
, где (n) — нечётное число
1) Область определения функции
D(f)=−∞;+∞
;
2) область значений функции
E(f)=−∞;+∞
;
3) функция возрастает при
x∈−∞;+∞
;
4) не имеет наибольшего и наименьшего значений;
5) не ограничена сверху и снизу;
6) непрерывна;
7) функция выпуклая вниз на луче
−∞;0
, выпуклая вверх на луче
0;+∞)
;
8) нечётная функция.
Четность и нечетность функции как определить, примеры решения задач на исследование функции на определение четности и нечетности, условие » Kupuk.net
Анализ функции на четность и нечетность — распространенный тип задач. Однако операция требует определенных знаний, поскольку очень часто возникают ситуации, в которых трудно принять верное решение. Специалисты рекомендуют использовать специальный алгоритм, позволяющий без ошибок произвести исследование. Для его реализации следует приобрести соответствующие базовые знания.
Общие сведения
Исследование функции на четность и нечетность — базовый элемент, показывающий ее поведение, которое зависит от значения аргумента. Последний является независимой переменной, соответствующей определенным допустимым значениям. Множество чисел, которое может принимать неизвестная независимого типа, называется областью определения. Областью значений функции вида y = f (x) являются все значения зависимой переменной «y».
Теперь следует сформулировать список базовых знаний, которые необходимы для анализа выражений на четность. Если нужно выполнить другие процедуры исследования, то его следует расширить. Например, для нахождения максимума следует ознакомиться с производной. Необходимый минимум знаний о функциях следующий:
Первый элемент необходим для выявления аргумента, при котором можно узнать его недопустимые значения, а также определить симметричность. От свойств и вида также зависит четность. Первое рекомендуется применять в частных случаях, например, произведение двух нечетных тождеств. Результат следует проверять при помощи соответствующего программного обеспечения. Например, онлайн-калькулятор четности и нечетности функций позволяет следить за правильностью решения.
Область определения
Первый элемент, который нужен для анализа, следует рассмотреть подробнее. Область определения функции z = g (y) специалисты рекомендуют обозначать литерой «D». Полная запись выглядит таким образом: D (z). Кроме того, следует выяснить симметричность множества. Под последним понимается некоторый интервал, который нужно найти.
Область определения функции z = g (y) специалисты рекомендуют обозначать литерой «D». Полная запись выглядит таким образом: D (z). Кроме того, следует выяснить симметричность множества. Под последним понимается некоторый интервал, который нужно найти.
D (z) записывается в виде множества. Например, D (z) = [1;8]. Запись значит ограниченность аргумента, принимающего значения от 1 включительно до 8 включительно, то есть следующие цифры: 1, 2, 3, 4, 5, 6, 7 и 8. Если указана запись в виде (1;4), то ее нужно трактовать таким образом: от 1 не включительно до 4 не включительно, то есть в интервал входят только числа 2 и 3.
Для определения величины D (z) необходимо решить неравенство, корнем которого являются все значения аргумента. Для этих целей можно использовать и специализированное программное обеспечение. Математики рекомендуют свести пользование решебниками и программами к минимуму, поскольку не всегда предоставится возможность воспользоваться ими на экзаменах или контрольных.
Основные виды
Исследование функции зависит от ее вида, который нужно правильно определять. Для начала следует обозначить сложность, поскольку от этого параметра зависят дальнейшие действия и свойства, которыми придется руководствоваться. Математики производят разделение таким образом:
- Простые: алгебраические, трансцендентные и тригонометрические.
- Составные или сложные.
Алгебраические делятся на рациональные (без корня) и иррациональные (наличие радикала). Первые состоят из целых и дробных. D (z) для этих типов — все множество действительных чисел. Если функция представлена в виде обыкновенной дроби, то значение аргумента, приводящее к пустому множеству (знаменатель равен нулю), нужно исключить. Когда аргумент находится под знаком радикала (корня), тогда она считается иррациональной. Однако следует проверить, чтобы под корнем четной степени не было отрицательного значения, которое приводит к неопределенности.
Все функции, содержащие sin, cos, tg и ctg, являются тригонометрическими. Кроме того, arcsin, arccos, arctg и arcctg — обратные тригонометрические. Трансцендентные можно разделить на такие три группы: показательные, степенные и логарифмические.
Второе отличается от первого формулой. Другой тип классификации основан на периодичности. В зависимость от этого параметра все функции делятся на периодические и непериодические. Параметр периодичности означает повторение ее поведения через определенный период Т.
Существует еще один критерий. Он называется монотонностью. В зависимости от него, функции бывают монотонными и немонотонными. Первая группа характеризуется постоянностью, то есть она либо убывает, либо возрастает. Все остальные могут убывать и возрастать на определенных промежутках. Примером является y = cos (x), поскольку она является убывающей и возрастающей через определенный период.
Следствия из утверждений
Свойства или следствия из утверждений расчетов позволяют оптимизировать процесс решения, поскольку нет необходимости выполнять какие-либо действия. Очень часто приходится тратить много времени на задание, которое можно решить за несколько минут. Математики выделяют следующие свойства для таких функций:
Очень часто приходится тратить много времени на задание, которое можно решить за несколько минут. Математики выделяют следующие свойства для таких функций:
- Симметричность графика: четная — относительно ОУ, а нечетная — относительно начала координат.
- Функция эквивалентна сумме четной и нечетной.
- Результат комбинации четных эквивалентен четной, а нечетных — нечетной.
- Результирующее произведение: 2 четных — четное, 2 нечетных — четная, а 2 разной четности — нечетной.
- Композиция: 2 нечетных — нечетна, четная и нечетная — четна, любая с четной — четна (не наоборот).
- При взятии производной от четной результирующая является нечетной, а от нечетной — четной.
- Определенный интеграл вида ∫(g (x))dx с границами от -А до А равен двойным интегралам ∫(g (x))dx с границей от -А до 0 и от 0 до А: ∫(g (x))dx |(-A;A) = 2∫(g (x))dx |(-A;0) = 2∫(g (x))dx |(0;A).
- Определенный интеграл нечетной функции с границами -А и А равен 0.
- Ряд Маклорена: четные степени соответствуют четной и наоборот.
- Ряд Фурье: четная содержит только выражения с cos, а нечетная — sin.
Второе свойство можно записать математически таким образом: z (x) = y (x) + w (x). Выражение y (x) можно выразить следующим образом: y (x) = [z (x) — z (-x)] /2. Тождество w (x) выражается через z (x) формулой: w (x) = [z (x) + z (-x)] /2.
Классификация по четности
Специалисты давно уже исследовали некоторые функции. Примеры четных и нечетных можно классифицировать по признаку четности. Эти данные значительно ускоряют процесс анализа любого выражения. К нечетным функциям относятся следующие (следует учитывать, что аргумент «x» принадлежит множеству действительных чисел Z):
- Возведение в степень, показатель которой является целым и нечетным.
- Сигнум (sgn) — кусочно-постоянный тип, который задан несколькими формулами, объединенными в систему.
- Радикал положительной нечетной степени.
 2) / 2c 2 ].
2) / 2c 2 ]. - Кардинальный синус: sinc (x).
Остальные составляют класс общего вида, который не принадлежит к четным и нечетным. При решении задач необходимо иметь таблицу всех функций, которая должна быть составлена перед обучением. Следует учитывать, что на экзаменах и контрольных функции, используемые для описания каких-либо процессов, практически не исследуются. Зная алгоритм, не составит особого труда проверить выражение на четность. Следующим этапом, который поможет закрепить теоретические знания, считается практика.
Пример решения
Задачи исследования функции на четность встречаются редко, поскольку этот элемент входит в полный анализ ее поведения. Пусть дано тождество z (y) = (y 2 — y — 2) / (y 2 — 1). В этом случае следует действовать по алгоритму:
- Состоит из двух элементов: g (y) = y 2 — y — 2 и h (y) = y 2 — 1.
- Область значений: D (y 2 — y — 2) = (-бесконечность; +бесконечность) и D (y 2 — 1) = (-бесконечность; -1) U (-1;1) U (1; +бесконечность).
 2 — 1 = y 2 — 1.
2 — 1 = y 2 — 1. - В двух случаях функции являются нечетными: в первом — изменение знака, а во втором — от четной отнимается 1. Следовательно, искомое выражение является нечетной функцией.
Задачу можно решить вторым способом — проанализировать составляющие элементы. Например, знаменатель всегда будет нечетным, поскольку от четного y 2 отнимается нечетное число (6 — 1 = 5). Этот способ используется в некоторых языках программирования, для написания подпрограмм и процедур, позволяющих проверить или отобрать все нечетные значения. Числитель также является нечетным, поскольку он содержит нечетный элемент «y». Если построить график, используя любой из веб-ресурсов, то он окажется симметричным относительно начала координат.
Первое свойство свидетельствует о том, что функция является нечетной. Некоторые новички делают распространенную ошибку, считая, что отношение нечетных есть величина четная. Однако такое утверждение не применимо в этом случае. Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.
Однако такое утверждение не применимо в этом случае. Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.
Таким образом, для исследования функции на предмет ее четности или нечетности нужно воспользоваться специальным алгоритмом, который рекомендуют математики. Он позволит выполнить операцию без ошибок и за короткий промежуток времени.
Четность и нечетность функции с корнем. Четность функции
Функция
называется четной (нечетной), если для
любогои выполняется равенство
.
График четной
функции симметричен относительно оси
.
График нечетной
функции симметричен относительно начала
координат.
Пример 6.2.
Исследовать на четность или нечетность
функции
1)
;
2)
;
3)
.
Решение
.
1) Функция определена
при
.
Найдем
.
Т.е.
.
Значит, данная функция является четной.
2) Функция определена
при
Т.е.
.
Таким образом, данная функция нечетная.
3) функция определена
для
,
т.е. для
,
.
Поэтому функция не является ни четной,
ни нечетной. Назовем ее функцией общего
вида.
3. Исследование функции на монотонность.
Функция
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
Функции возрастающие
(убывающие) на некотором интервале
называются монотонными.
Если функция
дифференцируема на интервале
и имеет положительную (отрицательную)
производную
,
то функция
возрастает (убывает) на этом интервале.
Пример 6.3
.
Найти интервалы монотонности функций
1)
;
3)
.
Решение
.
1) Данная функция
определена на всей числовой оси. Найдем
Найдем
производную
.
Производная равна
нулю, если
и
.
Область определения – числовая ось,
разбивается точками
,
на интервалы. Определим знак производной
в каждом интервале.
В интервале
производная отрицательна, функция на
этом интервале убывает.
В интервале
производная положительна, следовательно,
функция на этом интервале возрастает.
2) Данная функция
определена, если
или
.
Определяем знак
квадратного трехчлена в каждом интервале.
Таким образом,
область определения функции
Найдем производную
,
,
если
,
т.е.
,
но
.
Определим знак производной в интервалах
.
В интервале
производная отрицательна, следовательно,
функция убывает на интервале
.
В интервале
производная положительна, функция
возрастает на интервале
.
4. Исследование функции на экстремум.
Точка
называется точкой максимума (минимума)
функции
,
если существует такая окрестность точки,
что для всех
из этой окрестности выполняется
неравенство
.
Точки максимума
и минимума функции называются точками
экстремума.
Если функция
в точкеимеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
Точки, в которых
производная равна нулю или не существует
называются критическими.
5. Достаточные условия существования экстремума.
Правило 1
.
Если при переходе (слева направо) через
критическую точку
производная
меняет знак с «+» на «–», то в точкефункция
имеет максимум; если с «–» на «+», то
минимум; если
не меняет знак, то экстремума нет.
Правило 2
.
Пусть в точке
первая производная функции
равна нулю
,
а вторая производная существует и
отлична от нуля. Если
,
то– точка максимума, если
,
то– точка минимума функции.
Пример
6.4
.
Исследовать на максимум и минимум
функции:
1)
;
2)
;
3)
;
4)
.
Решение.
1) Функция определена
и непрерывна на интервале
.
Найдем производную
и решим уравнение
,
т.е.
.Отсюда
– критические точки.
Определим знак
производной в интервалах
,
.
При переходе через
точки
и
производная меняет знак с «–» на «+»,
поэтому по правилу 1
– точки минимума.
При переходе через
точку
производная меняет знак с «+» на «–»,
поэтому
– точка максимума.
,
.
2) Функция определена
и непрерывна в интервале
.
Найдем производную
.
Решив уравнение
,
найдем
и
– критические точки. Если знаменатель
,
т.е.
,
то производная не существует. Итак,
– третья критическая точка. Определим
знак производной в интервалах.
Следовательно,
функция имеет минимум в точке
,
максимум в точках
и
.
3) Функция определена
и непрерывна, если
,
т.е. при
.
Найдем производную
.
Найдем критические
точки:
Окрестности точек
не принадлежат области определения,
поэтому они не являются т. {2}-3
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1
будет соответствовать значение функции −3
; а значению x=2
будет соответствовать y=0
и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x
. Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией
, когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
.
{2}} neq 1
для любого x in [-1;1]
.
Ограниченной
принято называть функцию y=f(x), x in X
тогда, когда существует такое число K > 0
, для которого выполняется неравенство left | f(x) right | neq K
для любого x in X
.
Пример ограниченной функции: y=sin x
ограничена на всей числовой оси, так как left | sin x right | neq 1
.
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции
тогда, когда большему значению x
будет соответствовать большее значение функции y=f(x)
. Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1}
и x_{2}
, причем x_{1} > x_{2}
, будет y(x_{1}) > y(x_{2})
.
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией
тогда, когда большему значению x
будет соответствовать меньшее значение функции y(x)
. Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1}
и x_{2}
, причем x_{1} > x_{2}
, будет y(x_{1})
Корнями функции
принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а)
Если при x > 0
четная функция возрастает, то убывает она при x
б)
Когда при x > 0
четная функция убывает, то возрастает она при x
в)
Когда при x > 0
нечетная функция возрастает, то возрастает она и при x
г)
Когда нечетная функция будет убывать при x > 0
, то она будет убывать и при x
Экстремумы функции
Точкой минимума функции
y=f(x)
принято называть такую точку x=x_{0}
, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}
), и для них тогда будет выполняться неравенство f(x) > f(x_{0})
. y_{min}
— обозначение функции в точке min.
Точкой максимума функции
y=f(x)
принято называть такую точку x=x_{0}
, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}
), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0}
будет точкой минимума; - x_{0}
— будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0}
.
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x)
; - Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку
; - Находятся значения функции f(x)
в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться
наименьшим значением функции
, а большее — наибольшим
.
Для этого воспользуйтесь миллиметровкой или графическим калькулятором. Выберите несколько любых числовых значений независимой переменной x {displaystyle x}
и подставьте их в функцию, чтобы вычислить значения зависимой переменной y {displaystyle y}
. Найденные координаты точек нанесите на координатную плоскость, а затем соедините эти точки, чтобы построить график функции. {2}+1}
{2}+1}
мы получили следующие координаты точек:
- (1,3) и (-1,3)
- (2,9) и (-2,9)
Проверьте, симметричен ли график функции относительно начала координат.
Начало координат – это точка с координатами (0,0). Симметрия относительно начала координат означает, что положительному значению y {displaystyle y}
(при положительном значении x {displaystyle x}
) соответствует отрицательное значение y {displaystyle y}
(при отрицательном значении x {displaystyle x}
), и наоборот. Нечетные функции обладают симметрией относительно начала координат.
- Если в функцию подставить несколько положительных и соответствующих отрицательных значений x {displaystyle x}
, значения y {displaystyle y}
будут различаться по знаку. {2}}
{2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
Четная функция.
Четной
называется функция, знак которой не меняется при изменении знака x
.
x
выполняется равенство f
(–x
) = f
(x
). Знак x
не влияет на знак y
.
График четной функции симметричен относительно оси координат (рис.1).
Примеры четной функции:
y
= cos x
y
= x
2
y
= –x
2
y
= x
4
y
= x
6
y
= x
2 + x
Пояснение:
Возьмем функцию y
= x
2 или y
= –x
2 .
При любом значении x
функция положительная. Знак x
Знак x
не влияет на знак y
. График симметричен относительно оси координат. Это четная функция.
Нечетная функция.
Нечетной
называется функция, знак которой меняется при изменении знака x
.
Говоря иначе, для любого значения x
выполняется равенство f
(–x
) = –f
(x
).
График нечетной функции симметричен относительно начала координат (рис.2).
Примеры нечетной функции:
y
= sin x
y
= x
3
y
= –x
3
Пояснение:
Возьмем функцию y = –x
3 .
Все значения у
в ней будут со знаком минус. То есть знак x
влияет на знак y
. Если независимая переменная – положительное число, то и функция положительная, если независимая переменная – отрицательное число, то и функция отрицательная: f
(–x
) = –f
(x
).
График функции симметричен относительно начала координат. Это нечетная функция.
Это нечетная функция.
Свойства четной и нечетной функций:
ПРИМЕЧАНИЕ:
Не все функции являются четными или нечетными. Есть функции, которые не подчиняются такой градации. К примеру, функция корня у
= √х
не относится ни к четным, ни к нечетным функциям (рис.3). При перечислении свойств подобных функций следует давать соответствующее описание: ни четна, ни нечетна.
Периодические функции.
Как вы знаете, периодичность – это повторяемость определенных процессов с определенным интервалом. Функции, описывающие эти процессы, называют периодическими функциями
. То есть это функции, в чьих графиках есть элементы, повторяющиеся с определенными числовыми интервалами.
Исследование
функции.
1) D(y)
– Область опрделения: множество всех
тех значений переменной х. при которых
алгебраические выражения f(x)
и g(x)
имеют смысл.
Если функция задана формулой,
то область определения состоит из всех
значений независимой переменной, при
которых формула имеет смысл.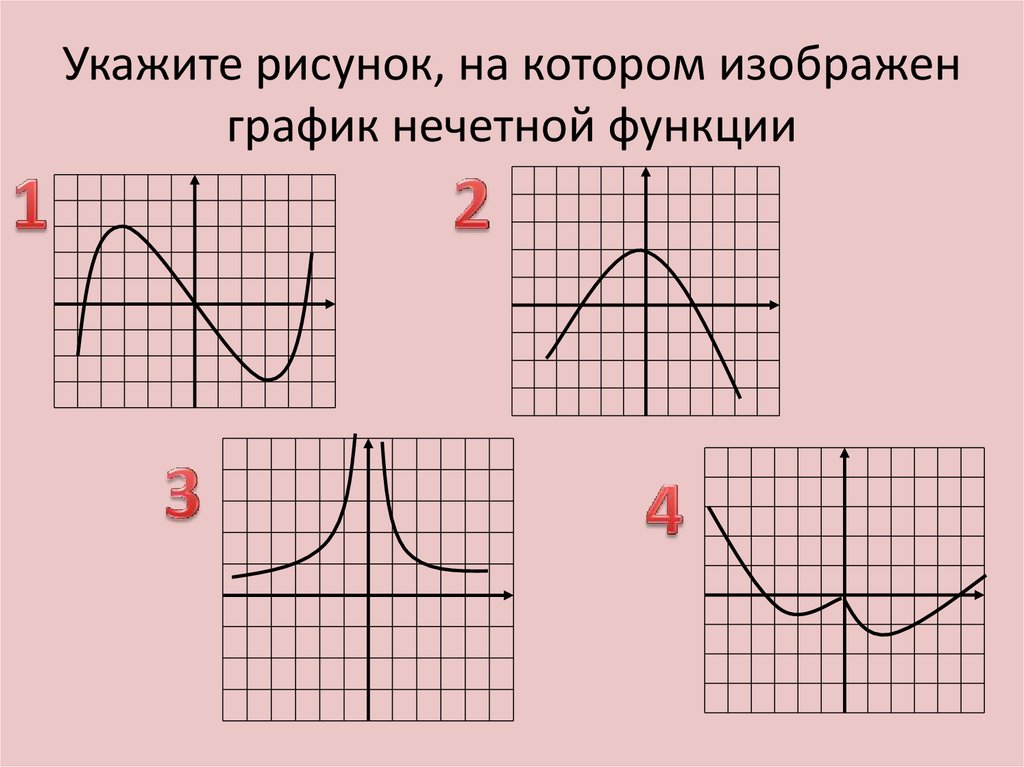
2) Свойства функции:
четность/нечетность, периодичность:
Нечётными
и
чётными
называются
функции,
графики которых обладают
симметрией
относительно
изменения знака аргумента.
Нечётная
функция
—
функция, меняющая значение на
противоположное при изменении знака
независимой переменной
(симметричная относительно
центра координат).
Чётная
функция
—
функция, не изменяющая своего значения
при изменении знака независимой
переменной (симметричная относительно
оси ординат).
Ни
чётная ни нечётная функция
(функция
общего вида)
—
функция, не обладающая симметрией. В
эту категорию относят функции, не
подпадающие под предыдущие 2 категории.
Функции,
не принадлежащие ни одной из категорий
выше, называются ни
чётными ни нечётными
(или
функциями общего вида).
Нечётные
функции
Нечётная степень где —
произвольное целое
число.
Чётные
функции
Чётная
степень где —
произвольное целое
число.
Периоди́ческая
фу́нкция
― функция,
повторяющая свои значения через некоторый
регулярный интервал аргумента, то есть
не меняющая своего значения при добавлении
к аргументу некоторого фиксированного
ненулевого числа (пери́ода
функции)
на всей области определения.
3)
Нули
(корни) функции — точки, где она
обращается в ноль.
Нахождение
точки пересечения графика с осью Oy
. Для
этого нужно вычислить значение f
(0).
Найти также точки пересечения графика
с осью Ox
,
для чего найти корни уравнения f
(x
)
= 0 (или
убедиться в отсутствии корней).
Точки, в
которых график пересекает
ось ,
называют нулями
функции
.
Чтобы найти нули функции нужно решить
уравнение ,
то есть найти те
значения «икс»
,
при которых функция обращается в ноль.
4)
Промежутки
постоянства знаков, знаки в них.
Промежутки,
где функция f(x) сохраняет знак.
Интервал
знакопостоянства – это интервал, в
каждой точке которого
функция
положительна либо отрицательна.
ВЫШЕ
оси абсцисс.
НИЖЕ
оси .
5)
Непрерывность (точки разрыва, характер
разрыва, ассимптоты).
Непрерывная
функция
—
функция без «скачков», то есть такая, у
которой малые изменения аргумента приводят
к малым изменениям значения функции.
Устранимые
точки разрыва
Если
предел функции существует
,
но функция не определена в этой точке,
либо предел не совпадает со значением
функции в данной точке:
,
то
точка называется точкой
устранимого разрыва
функции (в комплексном
анализе -устранимая
особая точка).
Если
«поправить» функцию в
точке устранимого разрыва и положить ,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением
функции до непрерывной
или доопределением
функции по непрерывности
,
что и обосновывает название точки, как
точки устранимого
разрыва.
Точки
разрыва первого и второго рода
Если
функция имеет разрыв в данной точке (то
есть предел функции в данной точке
отсутствует или не совпадает со значением
функции в данной точке), то для числовых
функций возникает два возможных варианта,
связанных с существованием у числовых
функций односторонних
пределов
:
если
оба односторонних предела существуют
и конечны, то такую точку называют точкой
разрыва первого рода
.
Точки устранимого разрыва являются
точками разрыва первого рода;
если
хотя бы один из односторонних пределов
не существует или не является конечной
величиной, то такую точку называют точкой
разрыва второго рода
.
Аси́мпто́та
— прямая
,
обладающая тем свойством, что расстояние
от точки кривой до этой прямой
стремится
к нулю при удалении точки вдоль ветви
вбесконечность.
Вертикальная
Вертикальная
асимптота — прямая предела .
Как
правило, при определении вертикальной
асимптоты ищут не один предел, а два
односторонних (левый и правый). Это
делается с целью определить, как функция
ведёт себя по мере приближения к
вертикальной асимптоте с разных сторон.
Например:
Горизонтальная
Горизонтальная
асимптота — прямая
вида при
условии существования предела
.
Наклонная
Наклонная
асимптота — прямая
вида при
условии существования пределов
Замечание:
функция может иметь не более двух
наклонных (горизонтальных) асимптот.
Замечание:
если хотя бы один из двух упомянутых
выше пределов не существует (или равен ),
то наклонной асимптоты при (или )
не существует.
если в
п. 2.), то ,
и предел находится
по формуле горизонтальной асимптоты, .
6)
Нахождение
промежутков монотонности.
Найти
интервалы монотонности функции f
(x
)(то
есть интервалы возрастания и убывания).
Это делается с помощью исследования
знака производной f
(x
).
Для этого находят производную f
(x
) и
решают неравенство f
(x
)0.
На промежутках, где это неравенство
выполнено, функция f
(x
)возрастает.
Там, где выполнено обратное неравенство
f
(x
)0,
функция f
(x
)убывает.
Нахождение
локального экстремума.
Найдя
интервалы монотонности, мы можем сразу
определить точки локального экстремума
там, где возрастание сменяется убыванием,
располагаются локальные максимумы, а
там, где убывание сменяется возрастанием
— локальные минимумы. Вычислить значение
Вычислить значение
функции в этих точках. Если функция
имеет критические точки, не являющиеся
точками локального экстремума, то
полезно вычислить значение функции и
в этих точках.
Нахождение
наибольшего и наименьшего значений
функции y = f(x) на отрезке
(продолжение)
1.
Найти
производную функции: f
(x
).
2.
Найти
точки, в которых производная равна
нулю: f
(x
)=0x
1, x
2 ,…
3.
Определить
принадлежность точек х
1 , х
2 , …
отрезку
[a
; b
]:
пусть x
1a
;b
,
а x
2a
;b
.
Как определить четность и нечетность функции примеры
Привет всем посетителям! Сегодня рассматриваем вопрос четности и нечетности функций.
Если , то функция четная.
Если , то функция нечетная.
При этом важно, чтобы область определения функции была бы симметричной относительно оси ординат, а при наличии в ней выколотых точек или интервалов они также должны располагаться симметрично.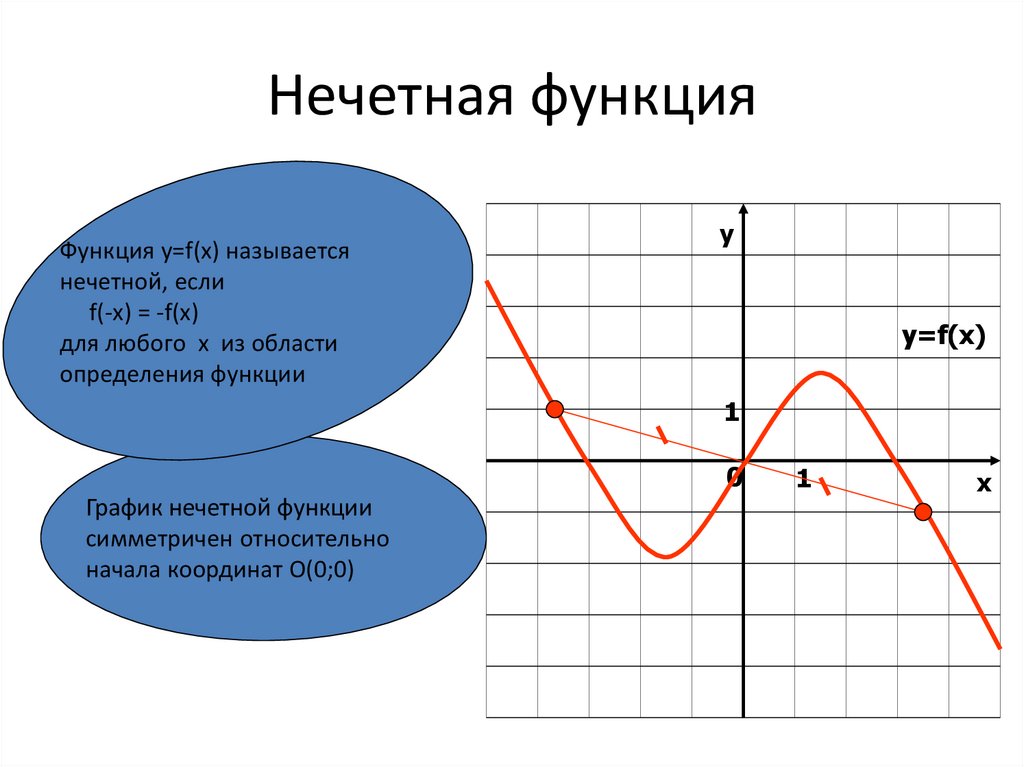
Установить, симметрична ли область определения функции. Если это так, то найти и сравнить с
Если то функция — четная.
Если , то функция нечетная.
Функция совсем не обязана быть четной или нечетной, она может быть «никакой», несмотря на то, что область определения симметрична.
1. Определить, является ли четной функция: .
Область определения этой функции – все действительные числа, то есть она симметрична. Теперь подставим вместо x – (-x) и посмотрим, что получится:
– функция четна.
Надо отметить, что график четной функции симметричен относительно оси ординат, она для него словно зеркало. Поэтому графики таких функций можно строить в правой полуплоскости, а в левую просто отражать.
Верно и следующее: если функция задана графиком, который симметричен относительно оси ординат, то она четная.
2. Определить, является ли четной функция: .
Область определения этой функции может быть найдена из системы неравенств:
=0><<1-x+x^2>>=0>>><>” title=”delim<1><<< x^2+x+1>>=0><<1-x+x^2>>=0>>><>”/>2>
Оба неравенства всегда соблюдаются, так как дискриминант обоих трехчленов всегда меньше 0, и ветви парабол направлены вверх – таким образом, мы установили, что область определения симметрична – это вся числовая ось.
Теперь подставим вместо x – (-x): – данная функция нечетна.
График нечетной функции симметричен относительно начала координат, то есть каждой его точке соответствует точка, получить которую можно поворотом на 180 градусов относительно начала координат. Поэтому графики таких функций можно строить в правой полуплоскости, а изображение в левой полуплоскости получить, повернув картинку на 180 градусов.
Верно и следующее: если функция задана графиком, который симметричен относительно начала координат, то она нечетная.
3. Определить, является ли четной функция: .
Область определения может быть найдена из системы неравенств:
0><<1-x><>0>>><>” title=”delim<1><<</<1-x>>>0><<1-x><>0>>><>”/>2>
Таким образом, область определения симметрична, и не содержит выколотые точки (1) и (-1).
Подставляем (-х) вместо х:
– исходную функцию не получили, а получили совсем другую – значит, исходная функция не является ни четной, ни нечетной (что и подтверждает график). Мы убедились, что симметрия области определения еще не означает, что функция четная или же нечетная.
Мы убедились, что симметрия области определения еще не означает, что функция четная или же нечетная.
4. Определить, является ли четной функция: .
Область определения – вся числовая ось, кроме 0 – симметричная.
Подставляем (-х) вместо х:
– функция нечетна.
5. Определить, является ли четной функция: .
Область определения – вся числовая ось, кроме точек 3 и (-3) – симметричная.
Подставляем (-х) вместо х:
– функция четная.
6. Определить, является ли четной функция: .
Область определения – вся числовая ось – симметричная.
Подставляем (-х) вместо х:
– функция четная.
7. Определить, является ли четной функция: .
Область определения – вся числовая ось, кроме 0 – симметричная.
Подставляем (-х) вместо х:
– функция нечетная.
Кроме того, здесь мы имеем дело с суммой двух функций.
Сумма двух нечётных функций – нечётна.
Сумма двух чётных функций – чётна.
А вот сумма двух функций разной четности – как правило, ни четна, ни нечетна.
Определим четность этих функций по отдельности.
– функция нечетная.
– функция нечетная.
8. Исследуем теперь такую функцию:
Одна из них нечётна – это мы только что показали, а вторая?
Область определения функции симметрична, функция нечётна, так как . Тогда по правилу сложение двух нечетных функций даст функцию нечетную.
9. Наконец, последняя:
– имеем произведение двух функций.
Произведение или частное двух нечётных функций чётно.
Произведение или частное двух чётных функций чётно.
Произведение или частное нечётной и чётной функций нечётно.
Так как обе функции являются чётными, то и их произведение чётно.
Область определения – вся числовая ось. Производим подстановку:
– функция четная.
Общие сведения
Исследование функции на четность и нечетность — базовый элемент, показывающий ее поведение, которое зависит от значения аргумента. Последний является независимой переменной, соответствующей определенным допустимым значениям. Множество чисел, которое может принимать неизвестная независимого типа, называется областью определения. Областью значений функции вида y = f (x) являются все значения зависимой переменной «y».
Последний является независимой переменной, соответствующей определенным допустимым значениям. Множество чисел, которое может принимать неизвестная независимого типа, называется областью определения. Областью значений функции вида y = f (x) являются все значения зависимой переменной «y».
Теперь следует сформулировать список базовых знаний, которые необходимы для анализа выражений на четность. Если нужно выполнить другие процедуры исследования, то его следует расширить. Например, для нахождения максимума следует ознакомиться с производной. Необходимый минимум знаний о функциях следующий:
- Область определения — D (f).
- Виды.
- Правила.
- Свойства для четных и нечетных.
- Классификация.
Первый элемент необходим для выявления аргумента, при котором можно узнать его недопустимые значения, а также определить симметричность. От свойств и вида также зависит четность. Первое рекомендуется применять в частных случаях, например, произведение двух нечетных тождеств. Результат следует проверять при помощи соответствующего программного обеспечения. Например, онлайн-калькулятор четности и нечетности функций позволяет следить за правильностью решения.
Результат следует проверять при помощи соответствующего программного обеспечения. Например, онлайн-калькулятор четности и нечетности функций позволяет следить за правильностью решения.
Область определения
Первый элемент, который нужен для анализа, следует рассмотреть подробнее. Область определения функции z = g (y) специалисты рекомендуют обозначать литерой «D». Полная запись выглядит таким образом: D (z). Кроме того, следует выяснить симметричность множества. Под последним понимается некоторый интервал, который нужно найти.
D (z) записывается в виде множества. Например, D (z) = [1;8]. Запись значит ограниченность аргумента, принимающего значения от 1 включительно до 8 включительно, то есть следующие цифры: 1, 2, 3, 4, 5, 6, 7 и 8. Если указана запись в виде (1;4), то ее нужно трактовать таким образом: от 1 не включительно до 4 не включительно, то есть в интервал входят только числа 2 и 3.
Для определения величины D (z) необходимо решить неравенство, корнем которого являются все значения аргумента. Для этих целей можно использовать и специализированное программное обеспечение. Математики рекомендуют свести пользование решебниками и программами к минимуму, поскольку не всегда предоставится возможность воспользоваться ими на экзаменах или контрольных.
Для этих целей можно использовать и специализированное программное обеспечение. Математики рекомендуют свести пользование решебниками и программами к минимуму, поскольку не всегда предоставится возможность воспользоваться ими на экзаменах или контрольных.
Основные виды
Исследование функции зависит от ее вида, который нужно правильно определять. Для начала следует обозначить сложность, поскольку от этого параметра зависят дальнейшие действия и свойства, которыми придется руководствоваться. Математики производят разделение таким образом:
- Простые: алгебраические, трансцендентные и тригонометрические.
- Составные или сложные.
Алгебраические делятся на рациональные (без корня) и иррациональные (наличие радикала). Первые состоят из целых и дробных. D (z) для этих типов — все множество действительных чисел. Если функция представлена в виде обыкновенной дроби, то значение аргумента, приводящее к пустому множеству (знаменатель равен нулю), нужно исключить. Когда аргумент находится под знаком радикала (корня), тогда она считается иррациональной. Однако следует проверить, чтобы под корнем четной степени не было отрицательного значения, которое приводит к неопределенности.
Когда аргумент находится под знаком радикала (корня), тогда она считается иррациональной. Однако следует проверить, чтобы под корнем четной степени не было отрицательного значения, которое приводит к неопределенности.
Все функции, содержащие sin, cos, tg и ctg, являются тригонометрическими. Кроме того, arcsin, arccos, arctg и arcctg — обратные тригонометрические. Трансцендентные можно разделить на такие три группы: показательные, степенные и логарифмические.
Второе отличается от первого формулой. Другой тип классификации основан на периодичности. В зависимость от этого параметра все функции делятся на периодические и непериодические. Параметр периодичности означает повторение ее поведения через определенный период Т.
Существует еще один критерий. Он называется монотонностью. В зависимости от него, функции бывают монотонными и немонотонными. Первая группа характеризуется постоянностью, то есть она либо убывает, либо возрастает. Все остальные могут убывать и возрастать на определенных промежутках. Примером является y = cos (x), поскольку она является убывающей и возрастающей через определенный период.
Примером является y = cos (x), поскольку она является убывающей и возрастающей через определенный период.
Правила для выявления
Для того чтобы исследовать на четность, существует два правила или теоремы, которые записываются в виде двух формул. Четная — функция вида w (x), для которой справедливо такое равенство: w (-x) = w (x). Для нечетной соотношение немного другое: w (-x) = w (x). Однако бывают выражения, к которым не применимы эти тождества. Они принадлежат общему виду.
Для оптимизации решения специалисты рекомендуют использовать некоторую последовательность действий или специальный алгоритм. Он позволяет определить четность за минимальный промежуток времени и без ошибок. Необходимо обратить внимание на пункты или шаги, по которым выполняется подробная оценка:
- Разложить при необходимости на простые элементы.
- Определить D (z). Если ее график симметричный, то нужно переходить к следующему шагу.
 В противном случае результатом является функция общего вида.
В противном случае результатом является функция общего вида. - Проверить, подставив в выражение отрицательное значение аргумента w (-x).
- Выполнить сравнение: w (-x) = w (x).
- Сделать соответствующий вывод.
Если w (-x) = w (x), то это свидетельствует о четности. При выполнении тождества w (-x) = -w (x) функция является нечетной. Важно обратить внимание на D, поскольку в некоторых точках равенства и условия могут не выполняться. Это свидетельствует о том, что искомая функция принадлежит к общему виду, то есть не является четной и нечетной.
Одним интересным способом является графический метод (принцип). Для его реализации нужно выполнить построение графика. Если он будет симметричным относительно оси ординат ОУ, то равенство w (-x) = w (x) будет выполняться. В случае симметричности относительно начала системы координат (точка пересечения осей абсцисс и ординат), будет справедливым равенство w (-x) = -w (x).
Следствия из утверждений
Свойства или следствия из утверждений расчетов позволяют оптимизировать процесс решения, поскольку нет необходимости выполнять какие-либо действия. Очень часто приходится тратить много времени на задание, которое можно решить за несколько минут. Математики выделяют следующие свойства для таких функций:
Очень часто приходится тратить много времени на задание, которое можно решить за несколько минут. Математики выделяют следующие свойства для таких функций:
- Симметричность графика: четная — относительно ОУ, а нечетная — относительно начала координат.
- Функция эквивалентна сумме четной и нечетной.
- Результат комбинации четных эквивалентен четной, а нечетных — нечетной.
- Результирующее произведение: 2 четных — четное, 2 нечетных — четная, а 2 разной четности — нечетной.
- Композиция: 2 нечетных — нечетна, четная и нечетная — четна, любая с четной — четна (не наоборот).
- При взятии производной от четной результирующая является нечетной, а от нечетной — четной.
- Определенный интеграл вида ∫(g (x))dx с границами от -А до А равен двойным интегралам ∫(g (x))dx с границей от -А до 0 и от 0 до А: ∫(g (x))dx |(-A;A) = 2∫(g (x))dx |(-A;0) = 2∫(g (x))dx |(0;A).
- Определенный интеграл нечетной функции с границами -А и А равен 0.
- Ряд Маклорена: четные степени соответствуют четной и наоборот.
- Ряд Фурье: четная содержит только выражения с cos, а нечетная — sin.
Второе свойство можно записать математически таким образом: z (x) = y (x) + w (x). Выражение y (x) можно выразить следующим образом: y (x) = [z (x) — z (-x)] /2. Тождество w (x) выражается через z (x) формулой: w (x) = [z (x) + z (-x)] /2.
Классификация по четности
Специалисты давно уже исследовали некоторые функции. Примеры четных и нечетных можно классифицировать по признаку четности. Эти данные значительно ускоряют процесс анализа любого выражения. К нечетным функциям относятся следующие (следует учитывать, что аргумент «x» принадлежит множеству действительных чисел Z):
- Возведение в степень, показатель которой является целым и нечетным.
- Сигнум (sgn) — кусочно-постоянный тип, который задан несколькими формулами, объединенными в систему.
- Радикал положительной нечетной степени.
 2) / 2c 2 ].
2) / 2c 2 ]. - Кардинальный синус: sinc (x).
Остальные составляют класс общего вида, который не принадлежит к четным и нечетным. При решении задач необходимо иметь таблицу всех функций, которая должна быть составлена перед обучением. Следует учитывать, что на экзаменах и контрольных функции, используемые для описания каких-либо процессов, практически не исследуются. Зная алгоритм, не составит особого труда проверить выражение на четность. Следующим этапом, который поможет закрепить теоретические знания, считается практика.
Пример решения
Задачи исследования функции на четность встречаются редко, поскольку этот элемент входит в полный анализ ее поведения. Пусть дано тождество z (y) = (y 2 — y — 2) / (y 2 — 1). В этом случае следует действовать по алгоритму:
- Состоит из двух элементов: g (y) = y 2 — y — 2 и h (y) = y 2 — 1.
- Область значений: D (y 2 — y — 2) = (-бесконечность; +бесконечность) и D (y 2 — 1) = (-бесконечность; -1) U (-1;1) U (1; +бесконечность).
 2 — 1 = y 2 — 1.
2 — 1 = y 2 — 1. - В двух случаях функции являются нечетными: в первом — изменение знака, а во втором — от четной отнимается 1. Следовательно, искомое выражение является нечетной функцией.
Задачу можно решить вторым способом — проанализировать составляющие элементы. Например, знаменатель всегда будет нечетным, поскольку от четного y 2 отнимается нечетное число (6 — 1 = 5). Этот способ используется в некоторых языках программирования, для написания подпрограмм и процедур, позволяющих проверить или отобрать все нечетные значения. Числитель также является нечетным, поскольку он содержит нечетный элемент «y». Если построить график, используя любой из веб-ресурсов, то он окажется симметричным относительно начала координат.
Первое свойство свидетельствует о том, что функция является нечетной. Некоторые новички делают распространенную ошибку, считая, что отношение нечетных есть величина четная. Однако такое утверждение не применимо в этом случае.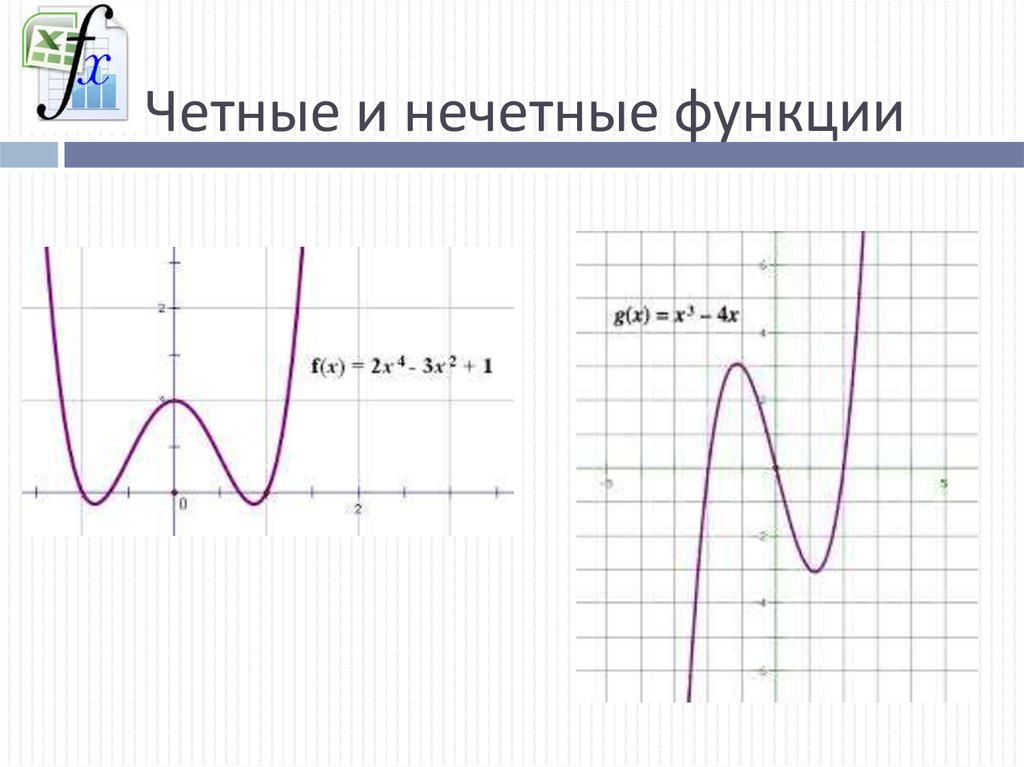 Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.
Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.
Таким образом, для исследования функции на предмет ее четности или нечетности нужно воспользоваться специальным алгоритмом, который рекомендуют математики. Он позволит выполнить операцию без ошибок и за короткий промежуток времени.
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Тема урока, введение
В этом уроке будут даны строгие определения четных и нечетных функций, рассмотрены их свойства, решены некоторые задачи.
Основные определения
Определение 1: Функция Определение 2: Функция 1. 2. 3. 4. Определение 3: Функцию
2.
Из определения вытекает важное свойство четной функции:
График четной функции симметричен относительно оси y (Рис. 1).
Дадим развернутое определение нечетной функции.
Определение 4: Функцию 1. Область определения симметрична относительно нуля, т.е.
2.
Из определения нечетной функции вытекает свойство: График нечетной функции симметричен относительно т. (0; 0) (Рис. 2).
Если функция не является ни четной, ни нечетной, то ее называют функцией общего вида.
Примеры
Пример 1. Определите вид функции
четная функция, ее график симметричен относительно оси y.
Пример 2. Определите вид функции
В точке Пример 3.Определите вид функции
Обе точки выколотые, график и область определения симметричны относительно начала координат, функция четная.
Пример 4. Определите вид функции
рафик и область определения симметричны относительно начала координат, функция нечетная.
Пример 5. Определите вид функции
В точке с абсциссой 2 функция не существует, в точке с абсциссой -2 существует. Область определения несимметрична относительно нуля, это функция общего вида.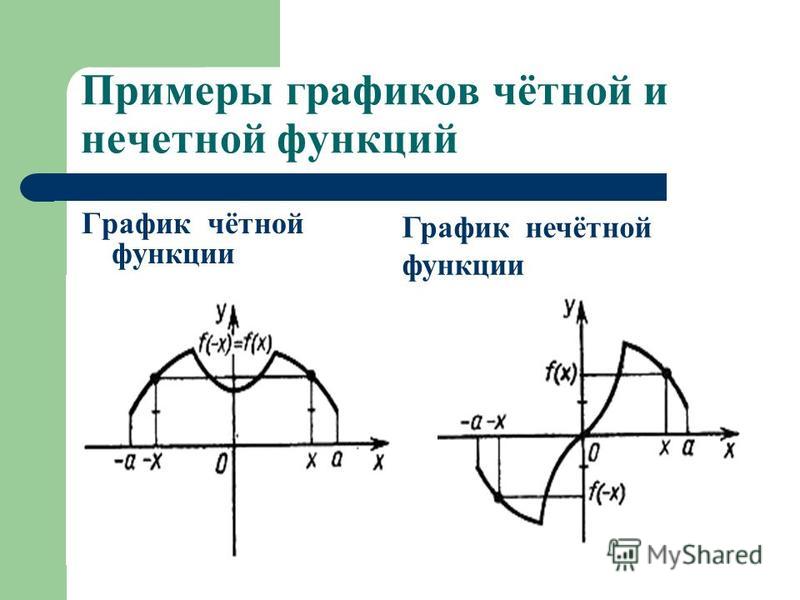
Пример 6. Определите вид функции
Область определения симметрична относительно нуля, функция нечетная.
Примеры на исследование функции
Рассмотрим примеры на свойства четных и нечетных функций.
Пример 7: Исследовать на четность функцию
,функция четная.
Возведем в квадрат обе части равенства. Тогда вместо уравнения получим систему:
Второе уравнение полученной системы – уравнение окружности с центром в т.(0; 0) радиусом 4. Но т.к.
График симметричен относительно оси y, поэтому функция четная.
Ответ: Функция четная.
Пример 8. Известно, что функция Нам известно, что функция убывает на луче График четной функции симметричен относительно оси y, т.е. функция возрастает на луче
В качестве примера изобразим график функции (Рис. 10).
Ответ: Функция возрастает при
Пример 9. Дана функция Задайте Если функция четная, ее график симметричен относительно оси y, т.е. (Рис. 11).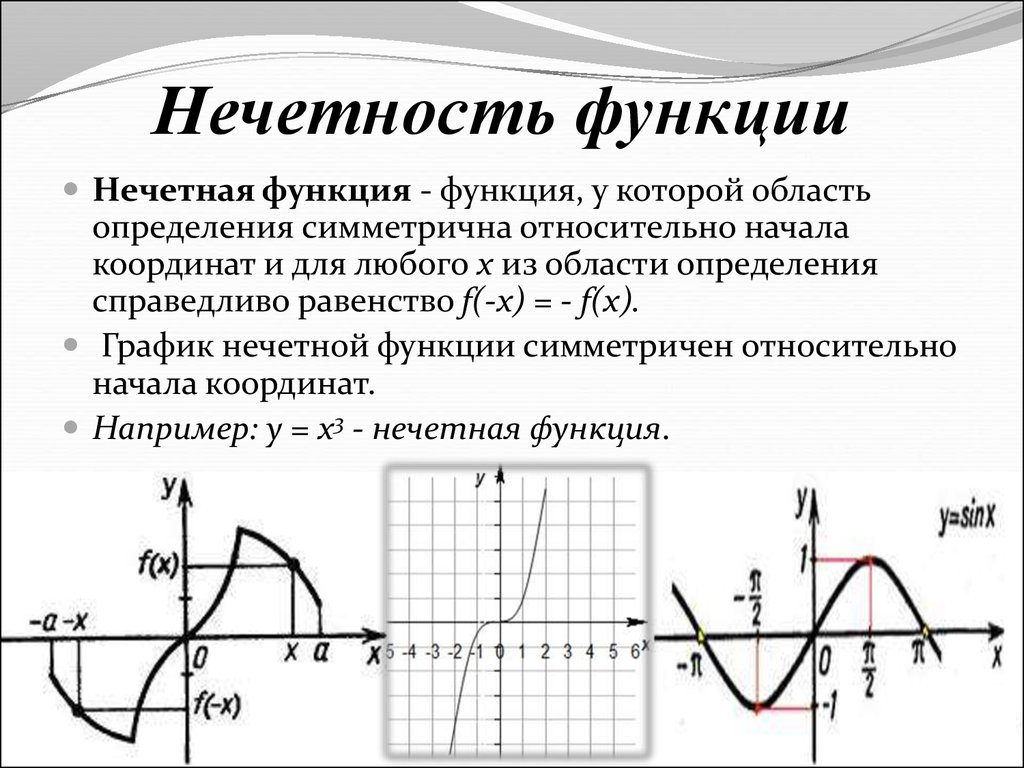
Если функция нечетная, ее график симметричен относительно т. (0; 0), т.е. (Рис. 12).
Заключение, вывод
Мы рассмотрели определения и свойства четных и нечетных функций, решили некоторые типовые задачи На следующем уроке мы продолжим изучение свойств четных и нечетных функций.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 275 – 278.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
«>
Четность и нечетность функции — онлайн справочник для студентов
Определения и свойства четных и нечетных функций
ОПРЕДЕЛЕНИЕ
Функция
(
f(x)
) называется четной функцией, если для любого x из области определения выполняется равенство (
f(-x)=f(x)
)
Функция (
f(x)
) называется нечетной функцией, если для любого x из области определения выполняется равенство (
f(-x)=-f(x)
)
Если ни одно из условий (
f(-x)=f(x)
) или (
f(-x)=-f(x)
) не выполняется, то говорят, что функция (
f(x)
) не является ни четной, ни нечетной (или функцией общего вида)
График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.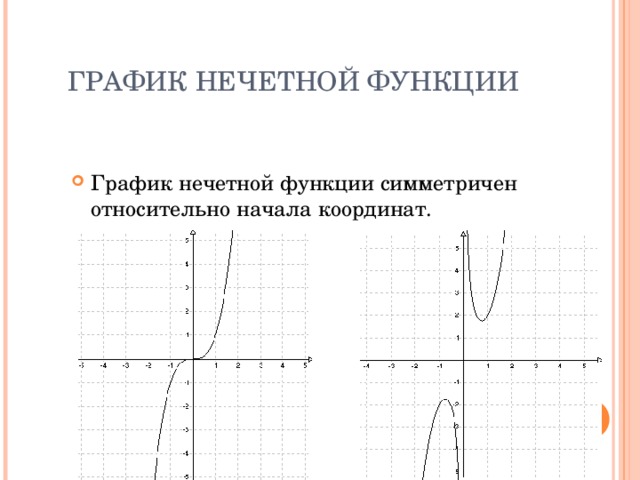 {4}+7}
{4}+7}
) .Тогда исходную функцию (
f(x)
) можно представить в виде произведения четных функций (
f(x)=g(x) cdot frac{1}{h(x)}
) , следовательно, по свойству 2, (
f(x)
) — четная.
Исследованная функция четная.
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Область значений функции Область определения функции Квадратная матрица Диагональная матрица
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое
Принимаю Политику
конфиденциальности
Подпишись на рассылку,
чтобы не пропустить информацию об акциях
3.
 Четность и нечетность
Четность и нечетность
Определение
5. Функция
,
заданная на множестве
,
называется четной,
если
.
Определение
6. Функция
,
заданная на множестве
,
называется нечетной,
если
.
Например,
функция
четна, а функция
нечетна. Вообще, если число
четно, то и функция
четна, а если число
нечетно, то и функция
нечетна.
Замечание.
Для четных и нечетных
функций область определения
должна обладать следующим свойством
симметричности: вместе
с каждым числом
ей должно принадлежать противоположное
ему число
.
Пример
14. Докажем, что функция
,
,
не является ни четной, ни нечетной.
Решение.
Область определения
этой функции не обладает указанным выше
свойством симметрии: ей принадлежит
число 7, но не принадлежит число –7.
Поэтому функция не является ни четной,
ни нечетной.
При
исследовании на четность или нечетность
функции
,
заданной своим выражением, заменяют в
этом выражении
на
и проверяют: а) тождественно ли получившееся
выражение выражению, задающему
;
б) отличается ли оно от него лишь знаком.
Пример
15. Докажем, что функция
четная.
Решение.
При замене
на
в выражении
получаем
.
Значит, данная функция четная.
Пример
16. Докажем, что функция
нечетная.
Решение.
Имеем
.
Значит, данная функция нечетная.
При
доказательстве четности или нечетности
функций бывают полезны следующие
утверждения:
а) Сумма двух
четных (нечетных) функций является
четной (нечетной) функцией.
б) Произведение
двух четных или нечетных функций является
четной функцией.
в) Произведение
четной функции на нечетную является
нечетной функцией.
г) Если
функция
четная, а функция
определена на
,
то функция
тоже четная.
д) Если
функция
нечетная, а функция
определена на
и является четной (нечетной), то функция
четная (нечетная).
Пример
17. Докажем, что любая
Докажем, что любая
функция вида
является нечетной.
Решение.
Функция
четная, следовательно, и
тоже четная в силу утверждения г). Поэтому
данная функция является произведением
нечетной функции
на четную
,
а значит, нечетна в силу утверждения
в).
Теорема.
Любую функцию, заданную
на симметричном множестве, можно
представить в виде суммы четной и
нечетной функций.
Для графиков
четных и нечетных функций справедливы
следующие утверждения.
1. График
четной функции симметричен относительно
оси ординат (рис. 5).
2.График
нечетной функции симметричен относительно
начала координат (рис.6).
Рис. 5
Рис. 6
Справедливы
и обратные утверждения:
1. Если график
функции симметричен относительно оси
ординат, то эта функция четна.
2. Если график
Если график
функции симметричен относительно начала
координат, то эта функция нечетна.
Определение
7. Функция
,
заданная на множестве
,
называется периодической
с периодом
,
если
выполняется равенство
.
Число
является периодом любой функции, а
вместе с
и
является периодом. Поэтому достаточно
рассматривать лишь положительные
периоды.
Замечание.
Из определения следует,
что область определения функции
,
имеющей период
,
сама должна обладать следующим свойством
периодичности: вместе с каждым числом
множества
содержит числа
и
.
Поэтому,
например, функция, заданная лишь на луче
,
не может быть периодической.
Пусть
и
– периоды функции
.
Тогда их сумма
также является периодом
.
В частности, если
кратно периоду
для функции
,
т.е.
,
,
то
также является периодом для
.
Значит, периодическая
функция имеет бесконечное множество
периодов. Если среди
Если среди
положительных периодов функции есть
наименьший, то его называют основным
периодом этой функции.
В этом случае все периоды
кратны основному периоду.
Пусть
функция
имеет основной период
.
Тогда, зная значения
на
или
,
легко найти остальные значения, пользуясь
периодичностью функции. Поэтому при
построении графика периодической
функции достаточно построить этот
график на
или на
,
а потом сдвинуть полученный график на
,
,
и т.д. вдоль оси абсцисс.
Пример
18. Найдем основной
период функции
.
Решение.
Так как основной период
функции
равен
,
то имеем
.
Таким образом данная функция представляется
в виде суммы трех функций, имеющих
основные периоды
,
и
.
Период всей функции должен быть кратен
этим трем числам, поэтому основной
период данной функции
— общее наименьшее кратное периодов
,
и
.
Пример
19. Найдем основной
период функции
,
где
– дробная часть числа
.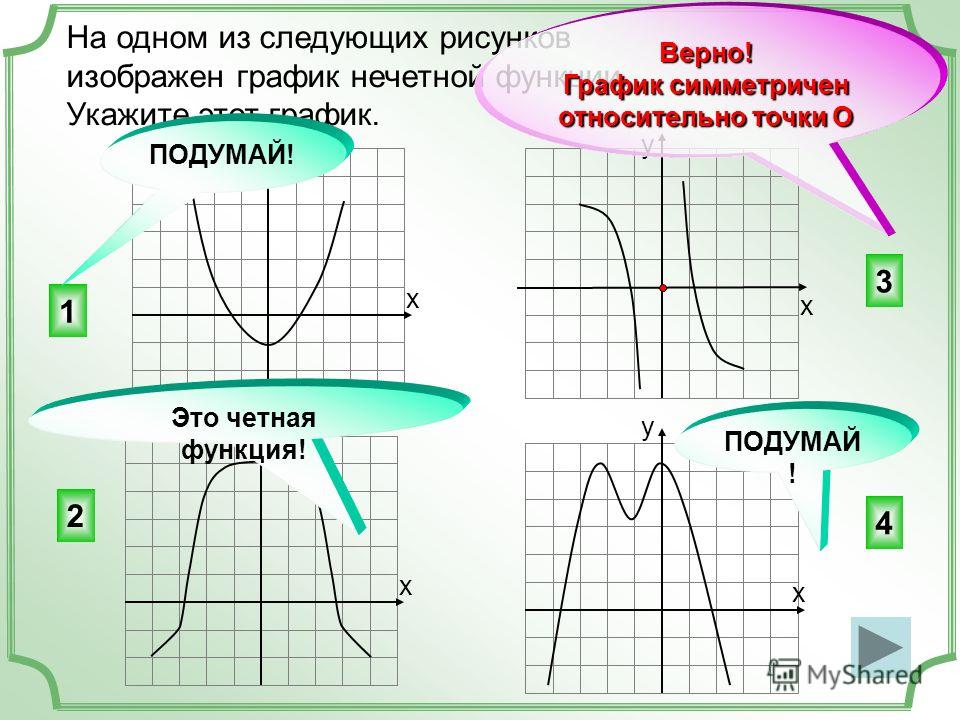
Решение.
Для любого
имеем
,
так как дробные части чисел
,
,
совпадают. Значит, число 1 – период
функции
.
Этот период основной, поскольку при
равенство
не выполняется для
.
График функции
изображен на рис. 7.
Рис. 7
Пример
20. Пусть
– функция Дирихле (см. п. 3.1). Покажем,
что любое рациональное число
является периодом этой функции.
Решение.
Пусть
– иррациональное число. Тогда
и
тоже иррациональные числа, а потому
.
Аналогично, если
– рациональное число, то и
,
– рациональные числа, а потому
.
Значит, при любом
имеем
,
т.е.
– период функции
.
Поскольку среди рациональных чисел нет
наименьшего положительного, функция
не имеет основного периода.
Пример
21. Докажем, что функция
не является периодической.
Решение.
Решим уравнение
.
Имеем
()
и
.
Выпишем найденный корни:
.
Замечаем,
что разности двух соседних чисел не
одинаковы для различных пар чисел. Это
значит, что точки пересечения графика
функции
с осью
не повторяются периодически, а потому
функция
не является периодической.
В заключение
отметим, что если функция
задана на
и имеет период
,
а функция
задана на
,
то функция
имеет тот же период.
Например,
функция
имеет период
.
Тогда тот же период имеют функции
,
и т.д.
Четная и нечетная функция примеры по рисункам. Четность и нечетность функции. Период функции. Экстремумы функции
Главная > Двери > Четная и нечетная функция примеры по рисункам. Четность и нечетность функции. Период функции. Экстремумы функции
Функция
— это одно из важнейших математических понятий. Функция — зависимость переменной у
от переменной x
, если каждому значению х
соответствует единственное значение у
. Переменную х
Переменную х
называют независимой переменной или аргументом. Переменную у
называют зависимой переменной. Все значения независимой переменной (переменной x
) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y
), образуют область значений функции.
Графиком функции
называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x
, а по оси ординат откладываются значения переменной y
. Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!
Для построения графика функции советуем использовать нашу программу — Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!
Основные свойства функций.
1) Область определения функции и область значений функции
.
Область определения функции — это множество всех допустимых действительных значений аргумента x
(переменной x
), при которых функция y = f(x)
определена.
Область значений функции — это множество всех действительных значений y
, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции
.
Значения х
, при которых y=0
, называется нулями функции
. Это абсциссы точек пересечения графика функции с осью Ох.
3) Промежутки знакопостоянства функции
.
Промежутки знакопостоянства функции – такие промежутки значений x
, на которых значения функции y
либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.
4) Монотонность функции
.
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции
.
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х
f(-x) = f(x)
. График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любогох
из области определения справедливо равенство f(-x) = — f(x
). График нечетной функции симметричен относительно начала координат.
Четная функция
1) Область определения симметрична относительно точки (0; 0), то есть если точка a
принадлежит области определения, то точка -a
также принадлежит области определения.
2) Для любого значения x
f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Нечетная функция
обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x
, принадлежащего области определения, выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).
Не всякая функция является четной или нечетной. Функции общего вида
не являются ни четными, ни нечетными.
6) Ограниченная и неограниченная функции
.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.
7) Периодическость функции
.
Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
(Тригонометрические формулы).
Функция f
называется периодической, если существует такое число, что при любом x
из области определения выполняется равенство f(x)=f(x-T)=f(x+T)
. T
— это период функции.
Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.
Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.
Графики четной и нечетной функции обладают следующими особенностями:
Если функция является четной, то ее график симметричен относительно оси ординат. Если функция является нечетной, то ее график симметричен относительно начала координат.
Пример.
Построить график функции (y=left|x right|).
Решение.
Рассмотрим функцию: (fleft(x right)=left|x right|) и подставим вместо (x ) противоположное (-x ).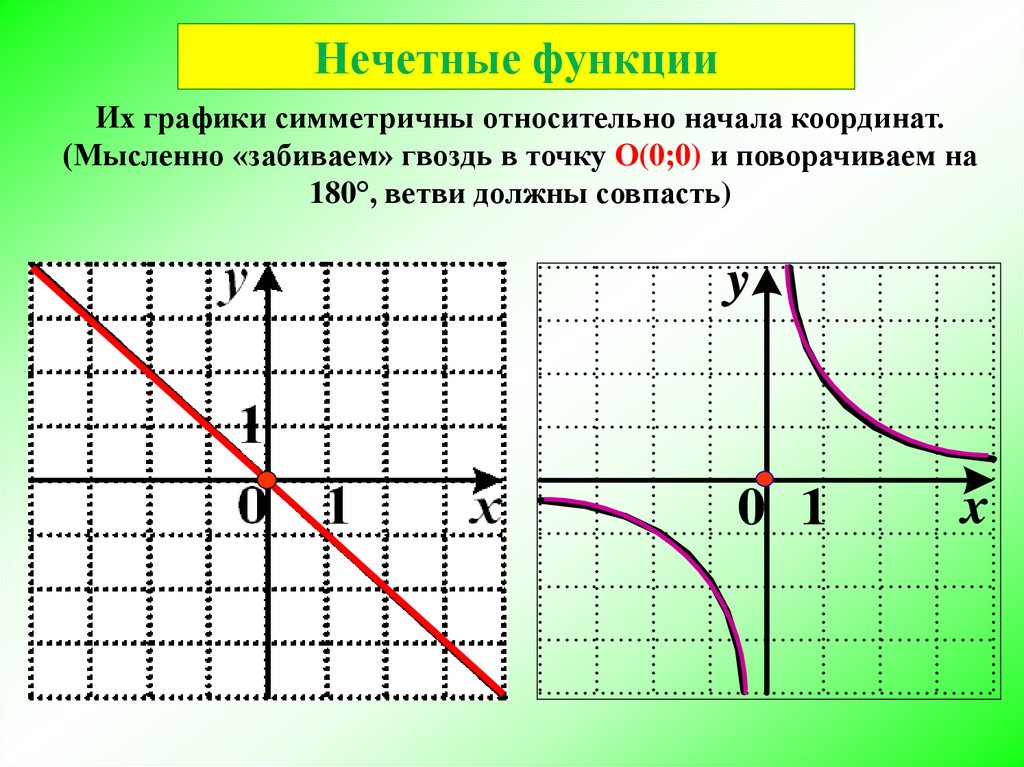 В результате не сложных преобразований получим:
В результате не сложных преобразований получим:
$$fleft(-x right)=left|-x right|=left|x right|=fleft(x right)$$
Другими словами, если аргумент заменить на противоположный по знаку, функция не изменится.
Значит эта функция — четная, а ее график будет симметричен относительно оси ординат (вертикальной оси). График этой функции приведен на рисунке слева. Это означает что при построении графика, можно строить только половину, а вторую часть (левее вертикальной оси рисовать уже симметрично правой части). Определив симметричность функции перед началом построения ее графика, можно намного упростить процесс построения или исследования функции. Если сложно выполнять проверку в общем виде, можно поступить проще: подставить в уравнение одинаковые значения разных знаков. Например -5 и 5. Если значения функции получатся одинаковыми, то можно надеяться что функция будет четной. С математической точки зрения такой подход не совсем правильный, но с практической — удобный. Чтобы увеличить достоверность результата можно подставить несколько пар таких противоположных значений. 2$$
2$$
В результате получим, что:
$$fleft(-x right)not=fleft(x right),fleft(-x right)not=-fleft(x right)$$
А это означает, что функция не является ни четной, ни нечетной.
Вывод: функция не симметрична ни относительно начала координат ни относительно центра системы координат. Это произошло потому, что она представляет собой сумму двух функций: четной и не четной. Такая же ситуация будет если вычитать две разные функции. А вот умножение или деление приведет к другому результату. Например, произведение четной и нечетной функций дает нечетную. Или частное двух нечетных приводит к четной функции.
Исследование
функции.
1) D(y)
– Область опрделения: множество всех
тех значений переменной х. при которых
алгебраические выражения f(x)
и g(x)
имеют смысл.
Если функция задана формулой,
то область определения состоит из всех
значений независимой переменной, при
которых формула имеет смысл.
2) Свойства функции:
четность/нечетность, периодичность:
Нечётными
и
чётными
называются
функции,
графики которых обладают
симметрией
относительно
изменения знака аргумента.
Нечётная
функция
—
функция, меняющая значение на
противоположное при изменении знака
независимой переменной
(симметричная относительно
центра координат).
Чётная
функция
—
функция, не изменяющая своего значения
при изменении знака независимой
переменной (симметричная относительно
оси ординат).
Ни
чётная ни нечётная функция
(функция
общего вида)
—
функция, не обладающая симметрией. В
эту категорию относят функции, не
подпадающие под предыдущие 2 категории.
Функции,
не принадлежащие ни одной из категорий
выше, называются ни
чётными ни нечётными
(или
функциями общего вида).
Нечётные
функции
Нечётная степень где —
произвольное целое
число.
Чётные
функции
Чётная
степень где —
произвольное целое
число.
Периоди́ческая
фу́нкция
― функция,
повторяющая свои значения через некоторый
регулярный интервал аргумента, то есть
не меняющая своего значения при добавлении
к аргументу некоторого фиксированного
ненулевого числа (пери́ода
функции)
на всей области определения.
3)
Нули
(корни) функции — точки, где она
обращается в ноль.
Нахождение
точки пересечения графика с осью Oy
. Для
этого нужно вычислить значение f
(0).
Найти также точки пересечения графика
с осью Ox
,
для чего найти корни уравнения f
(x
)
= 0 (или
убедиться в отсутствии корней).
Точки, в
которых график пересекает
ось ,
называют нулями
функции
.
Чтобы найти нули функции нужно решить
уравнение ,
то есть найти те
значения «икс»
,
при которых функция обращается в ноль.
4)
Промежутки
постоянства знаков, знаки в них.
Промежутки,
где функция f(x) сохраняет знак.
Интервал
знакопостоянства – это интервал, в
каждой точке которого
функция
положительна либо отрицательна.
ВЫШЕ
оси абсцисс.
НИЖЕ
оси .
5)
Непрерывность (точки разрыва, характер
разрыва, ассимптоты).
Непрерывная
функция
—
функция без «скачков», то есть такая, у
которой малые изменения аргумента приводят
к малым изменениям значения функции.
Устранимые
точки разрыва
Если
предел функции существует
,
но функция не определена в этой точке,
либо предел не совпадает со значением
функции в данной точке:
,
то
точка называется точкой
устранимого разрыва
функции (в комплексном
анализе -устранимая
особая точка).
Если
«поправить» функцию в
точке устранимого разрыва и положить ,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением
функции до непрерывной
или доопределением
функции по непрерывности
,
что и обосновывает название точки, как
точки устранимого
разрыва.
Точки
разрыва первого и второго рода
Если
функция имеет разрыв в данной точке (то
есть предел функции в данной точке
отсутствует или не совпадает со значением
функции в данной точке), то для числовых
функций возникает два возможных варианта,
связанных с существованием у числовых
функций односторонних
пределов
:
если
оба односторонних предела существуют
и конечны, то такую точку называют точкой
разрыва первого рода
.
Точки устранимого разрыва являются
точками разрыва первого рода;
если
хотя бы один из односторонних пределов
не существует или не является конечной
величиной, то такую точку называют точкой
разрыва второго рода
.
Аси́мпто́та
— прямая
,
обладающая тем свойством, что расстояние
от точки кривой до этой прямой
стремится
к нулю при удалении точки вдоль ветви
вбесконечность.
Вертикальная
Вертикальная
асимптота — прямая предела .
Как
правило, при определении вертикальной
асимптоты ищут не один предел, а два
односторонних (левый и правый). Это
делается с целью определить, как функция
ведёт себя по мере приближения к
вертикальной асимптоте с разных сторон.
Например:
Горизонтальная
Горизонтальная
асимптота — прямая
вида при
условии существования предела
.
Наклонная
Наклонная
асимптота — прямая
вида при
условии существования пределов
Замечание:
функция может иметь не более двух
наклонных (горизонтальных) асимптот.
Замечание:
если хотя бы один из двух упомянутых
выше пределов не существует (или равен ),
то наклонной асимптоты при (или )
не существует.
если в
п. 2.), то ,
и предел находится
по формуле горизонтальной асимптоты, .
6)
Нахождение
промежутков монотонности.
Найти
интервалы монотонности функции f
(x
)(то
есть интервалы возрастания и убывания).
Это делается с помощью исследования
знака производной f
(x
).
Для этого находят производную f
(x
) и
решают неравенство f
(x
)0.
На промежутках, где это неравенство
выполнено, функция f
(x
)возрастает.
Там, где выполнено обратное неравенство
f
(x
)0,
функция f
(x
)убывает.
Нахождение
локального экстремума.
Найдя
интервалы монотонности, мы можем сразу
определить точки локального экстремума
там, где возрастание сменяется убыванием,
располагаются локальные максимумы, а
там, где убывание сменяется возрастанием
— локальные минимумы. Вычислить значение
Вычислить значение
функции в этих точках. Если функция
имеет критические точки, не являющиеся
точками локального экстремума, то
полезно вычислить значение функции и
в этих точках.
Нахождение
наибольшего и наименьшего значений
функции y = f(x) на отрезке
(продолжение)
1.
Найти
производную функции: f
(x
).
2.
Найти
точки, в которых производная равна
нулю: f
(x
)=0x
1, x
2 ,…
3.
Определить
принадлежность точек х
1 , х
2 , …
отрезку
[a
; b
]:
пусть x
1a
;b
,
а x
2a
;b
.
Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.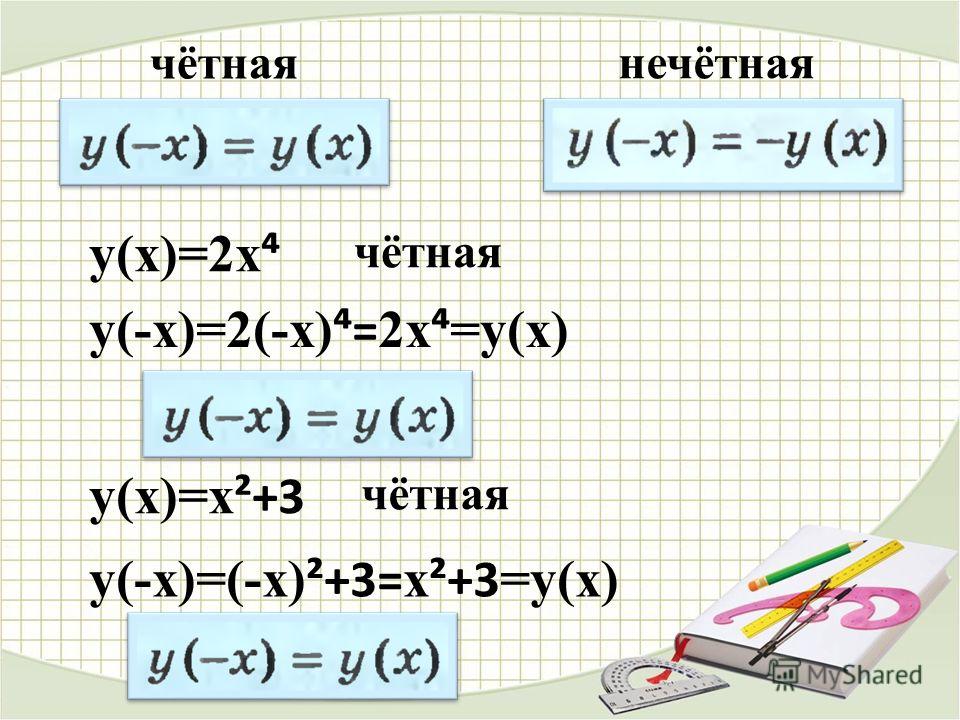
Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.
Дадим более строгое определение. Рассмотрим некоторую функцию f (x), которая задана в области D. Она будет четной, если для любой точки x, находящейся в области определения:
- -x (противоположная точка) также лежит в данной области определения,
- f (-x) = f (x).
Из приведенного определения следует условие, необходимое для области определения подобной функции, а именно, симметричность относительно точки О, являющейся началом координат, поскольку если некоторая точка b содержится в области определения четной функции, то соответствующая точка — b тоже лежит в этой области. Из вышесказанного, таким образом, вытекает вывод: четная функция имеет симметричный по отношению к оси ординат (Oy) вид.
Как на практике определить четность функции?
Пусть задается с помощью формулы h(x)=11^x+11^(-x). (-x))=- h(x). Следовательно, h(x) — нечетная.
(-x))=- h(x). Следовательно, h(x) — нечетная.
Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.
Четные функции обладают рядом интересных свойств:
- в результате сложения подобных функций получают четную;
- в результате вычитания таких функций получают четную;
- четной, также четная;
- в результате умножения двух таких функций получают четную;
- в результате умножения нечетной и четной функций получают нечетную;
- в результате деления нечетной и четной функций получают нечетную;
- производная такой функции — нечетная;
- если возвести нечетную функцию в квадрат, получим четную.
Четность функции можно использовать при решении уравнений.
Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами. {2}-3
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1
будет соответствовать значение функции −3
; а значению x=2
будет соответствовать y=0
и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x
. Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией
, когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
.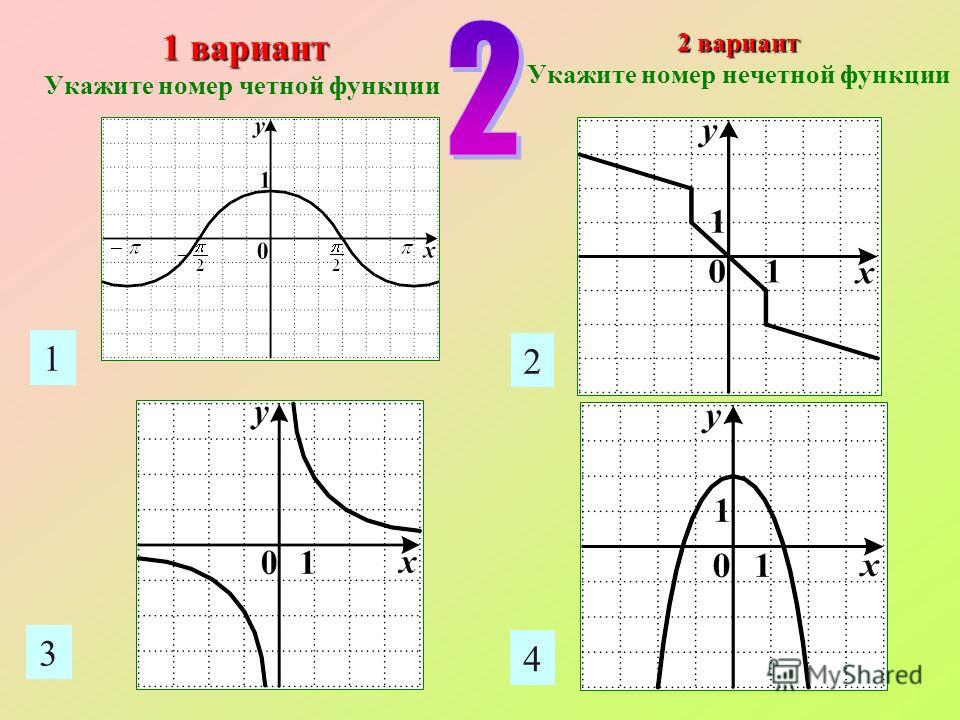 {2}} neq 1
{2}} neq 1
для любого x in [-1;1]
.
Ограниченной
принято называть функцию y=f(x), x in X
тогда, когда существует такое число K > 0
, для которого выполняется неравенство left | f(x) right | neq K
для любого x in X
.
Пример ограниченной функции: y=sin x
ограничена на всей числовой оси, так как left | sin x right | neq 1
.
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции
тогда, когда большему значению x
будет соответствовать большее значение функции y=f(x)
. Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1}
и x_{2}
, причем x_{1} > x_{2}
, будет y(x_{1}) > y(x_{2})
.
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией
тогда, когда большему значению x
будет соответствовать меньшее значение функции y(x)
. Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1}
и x_{2}
, причем x_{1} > x_{2}
, будет y(x_{1})
Корнями функции
принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а)
Если при x > 0
четная функция возрастает, то убывает она при x
б)
Когда при x > 0
четная функция убывает, то возрастает она при x
в)
Когда при x > 0
нечетная функция возрастает, то возрастает она и при x
г)
Когда нечетная функция будет убывать при x > 0
, то она будет убывать и при x
Экстремумы функции
Точкой минимума функции
y=f(x)
принято называть такую точку x=x_{0}
, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}
), и для них тогда будет выполняться неравенство f(x) > f(x_{0})
. y_{min}
— обозначение функции в точке min.
Точкой максимума функции
y=f(x)
принято называть такую точку x=x_{0}
, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}
), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0}
будет точкой минимума; - x_{0}
— будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0}
.
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x)
; - Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку
; - Находятся значения функции f(x)
в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции
, а большее — наибольшим
.
Суммы и произведения четных и нечетных функций (3 ключевые идеи) – JDM Educational
Графики четных и нечетных функций имеют симметрию (относительно оси Y или начала координат). Однако мы также можем сказать, какой тип функции мы получим, сложив или умножив два или более из них вместе.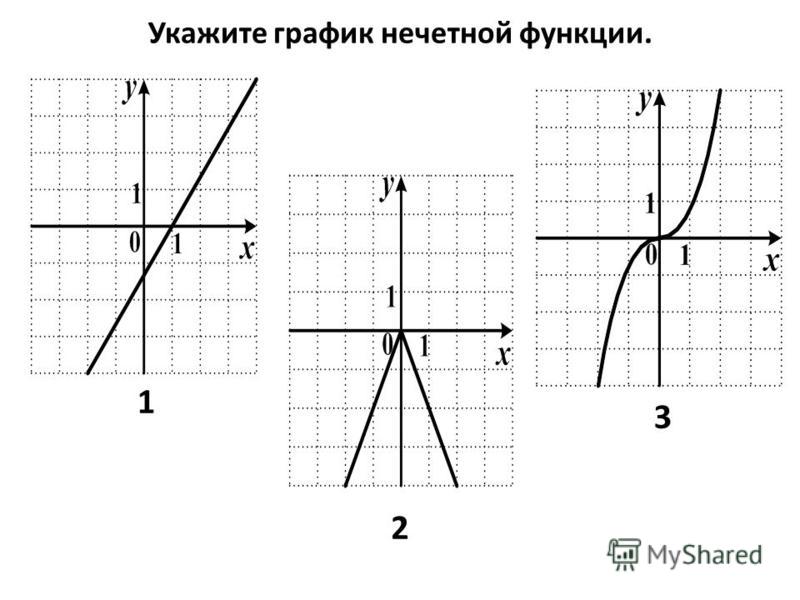
Итак, что вам нужно знать о суммах и произведениях четных и нечетных функций? Сумма или произведение двух четных функций четно. Произведение двух нечетных функций также четно. Сумма двух нечетных функций нечетна. Произведение четной и нечетной функции также нечетно. Сумма четной функции и нечетной функции не является ни четной, ни нечетной, если только одна или обе не равны нулю.
Конечно, мы можем добавить столько четных функций, сколько захотим, и все равно получить четную функцию. Точно так же мы можем добавить столько нечетных функций, сколько захотим, и все равно получить нечетную функцию.
В этой статье мы более подробно рассмотрим суммы и произведения как четных, так и нечетных функций. Мы также рассмотрим несколько примеров, чтобы прояснить концепцию.
Начнем.
Суммы и произведения четных и нечетных функций
Помните, что четные и нечетные функции имеют следующие ключевые характеристики:
- Для четной функции f(x): f(-x) = f(x) для всех x в области.

- Для нечетной функции f(x): f(-x) = -f(x) для всех x в области.
В таблице ниже показано, чего следует ожидать при сложении или умножении четных и нечетных функций.
| f(x) | g(x) | Sum (f+g) |
Product (f*g) |
|---|---|---|---|
| Even | Even | Even | Even |
| Even | Odd | Neither | Odd |
| Odd | Odd | Odd | Even |
This table summarizes what to expect
when adding or multiplying
even and odd функции.
Начнем с суммы двух четных функций.
Сумма двух четных функций
Сумма двух четных функций всегда будет четной. Чтобы доказать это, предположим, что f(x) и g(x) — четные функции.
Тогда f(-x) = f(x) и g(-x) = g(x). Глядя на их сумму:
- (f + g)(-x)
- =f(-x) + g(-x) [по определению суммы функций]
- =f( x) + g(x) [поскольку f(x) и g(x) являются четными функциями]
- = (f + g)(x) [по определению суммы функций]
Итак (f + g)(-x) = (f + g)(x), что означает, что сумма f(x) и g(x) четна.
Обратите внимание, что разность двух четных функций также является четной, поскольку на самом деле это сумма двух четных функций (изменение знака четной функции означает, что она все еще четная).
Обратите внимание, что мы можем добавить любое количество четных функций, и сумма будет четной (мы можем доказать это, взглянув на группу из 2 функций одновременно).
Пример: сумма двух четных функций
Пусть f(x) = x 2 + 1 и g(x) = x 4 + 3.
Обе функции f(x) и g(x) четны функции, так как они являются полиномами, члены которых имеют четные степени x.
График четной функции f(x) = x 2 + 1. График четной функции g(x) = x 4 + 3.
Их сумма равна:
- f(x) + g(x)
- =(x 2 + 1) + (x 4 90 90 + 0 6) f(x) и g(x)]
- =x 4 + x 2 + 4 [переставить и объединить одинаковые члены]
Это также четная функция, поскольку это многочлен, члены которого имеют четные степени x.
Четная функция
Сумма двух нечетных функций
Сумма двух нечетных функций всегда будет нечетной. Чтобы доказать это, предположим, что f(x) и g(x) — нечетные функции.
Тогда f(-x) = -f(x) и g(-x) = -g(x). Глядя на их сумму:
Глядя на их сумму:
- (f + g)(-x)
- =f(-x) + g(-x) [по определению суммы функций]
- =-f (x) + -g(x) [поскольку f(x) и g(x) являются нечетными функциями]
- =-(f + g)(x) [по определению суммы функций]
Итак, (f + g)(-x) = -(f + g)(x), что означает, что сумма f(x) и g(x) нечетна.
Обратите внимание, что разность двух нечетных функций также является нечетной, поскольку на самом деле она является суммой двух нечетных функций (изменение знака нечетной функции означает, что она все еще нечетная).
Обратите внимание, что мы можем добавить любое количество нечетных функций, и сумма будет нечетной (мы можем доказать это, взглянув на группу из 2 функций одновременно).
Пример: сумма двух нечетных функций
Пусть f(x) = x 3 + 2x и g(x) = x 7 + 4x 5 .
И f(x), и g(x) являются нечетными функциями, поскольку они являются полиномами, члены которых имеют нечетные степени x.
График нечетной функции f(x) = x 3 + 2x. График нечетной функции g(x) = x 7 + 4x 5 .
Их сумма равна:
- f(x) + g(x)
- =(x 3 + 2x) + (x 7 + 4x 5 f(
) [определение
) ) и g(x)]
- =x 7 + 4x 5 + x 3 + 2x [переставить члены]
нечетные степени х.
График нечетной функции
Сумма четной и нечетной функций
Сумма ни четной, ни нечетной функции ни нечетным, если только одна или обе функции не равны нулю (ноль бывает и четным, и нечетным).
Чтобы доказать это, предположим, что f(x) — четная функция, а g(x) — нечетная функция.
Тогда f(-x) = f(x) и g(-x) = -g(x). Глядя на их сумму:
- (f + g)(-x)
- =f(-x) + g(-x) [по определению суммы функций]
- =f(x) + -g(x) [поскольку f(x) — четная функция, а g(x) — нечетная функция]
- =f(x) – g(x)
Теперь рассмотрим (f + g)(x) :
- (f + g)(x)
- =f(x) + g(x) [по определению суммы функций]
Это не то же самое, что (f + g )(-x), если только g(x) = 0.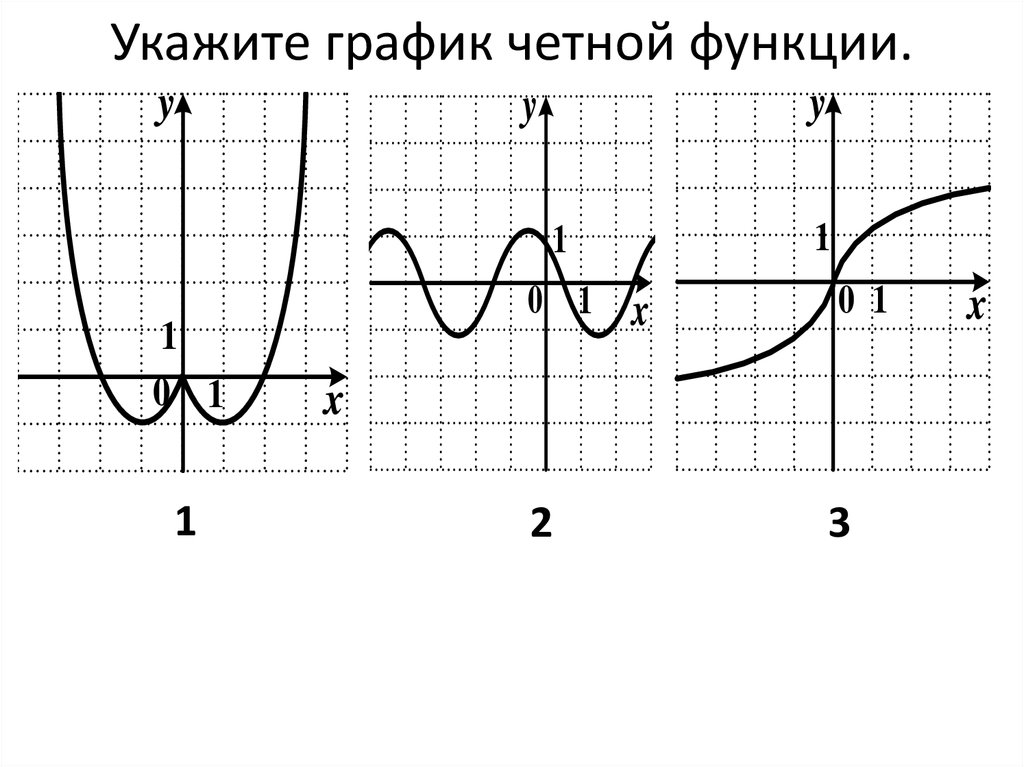 Итак, (f + g)(x) нечетно.
Итак, (f + g)(x) нечетно.
Глядя на –(f + g)(x):
- -(f + g)(x)
- =-f(x) – g(x) [по определению суммы функции]
Это не то же самое, что (f + g)(-x), если только f(x) = 0. Итак, (f + g)(x) не нечетно.
Таким образом, (f + g)(x) не является ни четным, ни нечетным, если только:
- Если f(x) = 0, то (f + g)(x) нечетно.
- Если g(x) = 0, то (f + g)(x) четно.
- Если f(x) = 0 и g(x) = 0, то (f + g)(x) одновременно четно и нечетно (поскольку сумма равна нулю).
Пример: сумма четной и нечетной функций
Пусть f(x) = x 2 + 3 и g(x) = x 3 – 4x.
Тогда f(x) — четная функция (многочлен с четными показателями), а g(x) — нечетная функция (многочлен с нечетными показателями).
График четной функции f(x) = x 2 + 3. График нечетной функции g(x) = x 3 – 4x.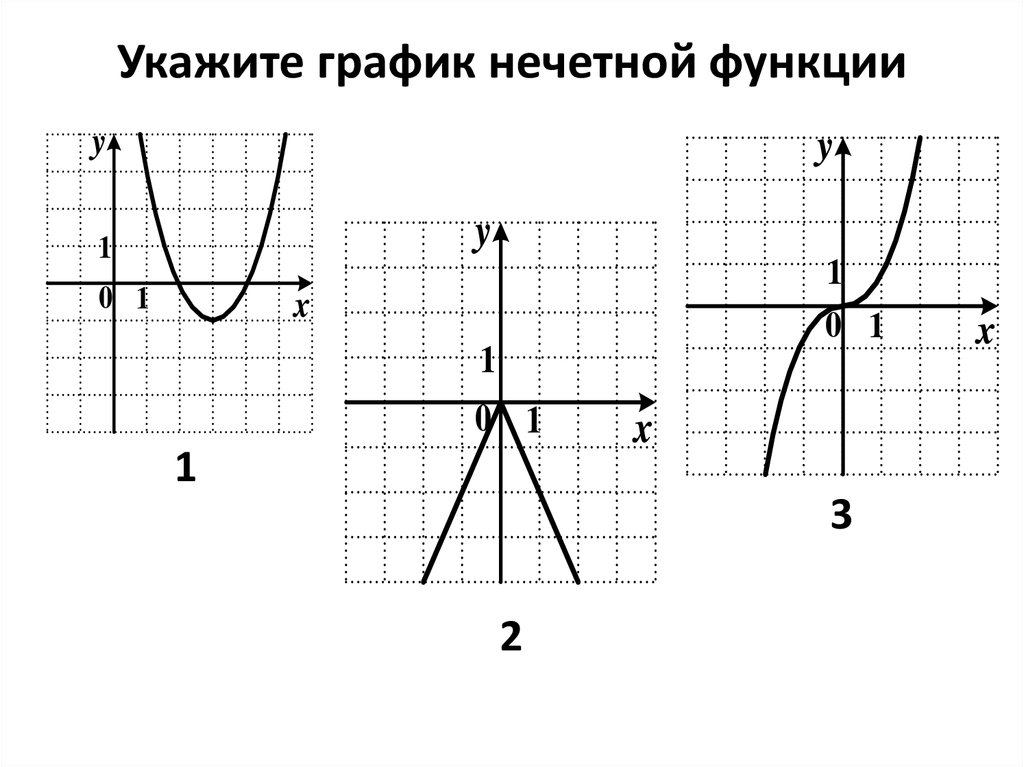
Их сумма:
- f(x) + g(x)
- =(x 2 + 3) + (x 3 – 4x) [определение f(x) и g(x)]
- =x 3 + x 9 9 4x + 3 [переставить члены]
Эта функция не является ни четной, ни нечетной, так как это полином с четными и нечетными показателями.
График функции
Произведение двух четных функций
Произведение двух четных функций всегда будет четным. Чтобы доказать это, предположим, что f(x) и g(x) — четные функции.
Тогда f(-x) = f(x) и g(-x) = g(x). Глядя на их произведение:
- (f*g)(-x)
- =f(-x)*g(-x) [по определению произведения функций]
- =f( x)*g(x) [поскольку f(x) и g(x) являются четными функциями]
- =(f*g)(x) [по определению суммы функций]
Итак (f*g)(-x) = (f*g)(x), что означает, что произведение f(x) и g(x) четно.
Обратите внимание, что частное двух четных функций также является четным, поскольку на самом деле оно является произведением двух четных функций (взятие обратной величины четной функции все равно дает нам четную функцию). Единственное, на что нужно обратить внимание, это нулевые знаменатели!
Обратите внимание, что мы можем умножать любое количество четных функций, и произведение будет четным (мы можем доказать это, взглянув на группу из 2 функций одновременно).
Пример: Произведение двух четных функций
Пусть f(x) = 3x 2 + 5 и g(x) = x 4 – 2.
И f(x), и g(x) четные функции, так как они являются полиномами, члены которых имеют четные степени x.
График четной функции f(x) = 3x 2 + 5. График четной функции g(x) = x 4 – 2.
Их продукт:
- f(x)*g(x)
- =(3x 2 + 5)*(x 4 90 119 – 06 определение [определение [определение] f (x) и g (x)]
- = 3x 6 — 6x 2 + 5x 4 — 10 [Фольга]
- = 3x 6 + 5x 4 — 6x 6 + 5x 4
— 6x + 5x 4
— 6x + 5x 4
— 6x 6 + 5x 4
— 6x .
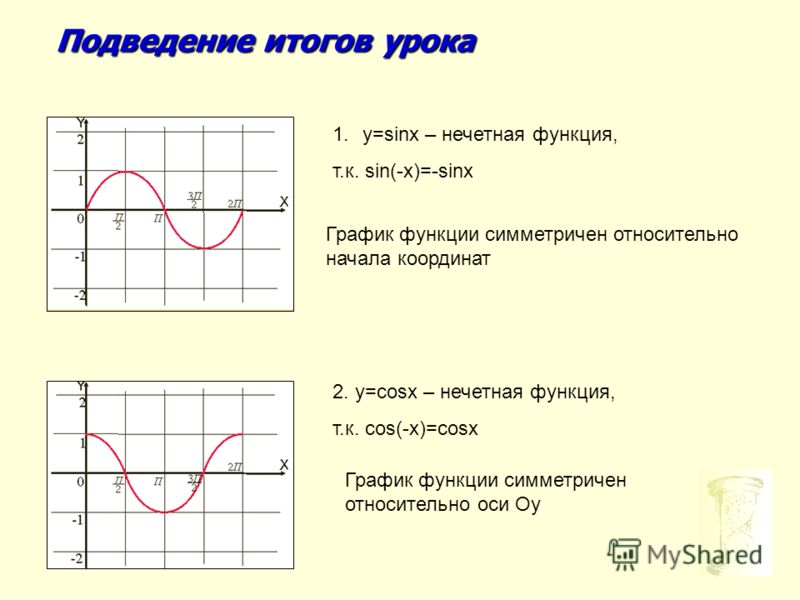 2 – 10 [переставить члены]
2 – 10 [переставить члены]
Это также четная функция, поскольку это полином, члены которого имеют четные степени x.
График четной функции
Произведение двух нечетных функций
Произведение двух четных нечетных функций всегда будет. Чтобы доказать это, предположим, что f(x) и g(x) — нечетные функции.
Тогда f(-x) = -f(x) и g(-x) = -g(x). Глядя на их произведение:
- (f*g)(-x)
- =f(-x)*g(-x) [по определению произведения функций]
- =-f(x)*-g(x) [поскольку f(x) и g(x) являются нечетными функциями]
- =f(x)*g(x) [произведение двух отрицательных значений равно положительный]
- = (f*g)(x) [по определению суммы функций]
Итак, (f*g)(-x) = (f*g)(x), что означает, что произведение f(x) и g(x) четно.
Обратите внимание, что частное двух нечетных функций также является нечетным, поскольку на самом деле оно является произведением двух нечетных функций (взятие обратной величины нечетной функции означает, что оно все еще нечетное).
Обратите внимание, что если мы умножаем более 2 нечетных функций, необходимо рассмотреть 2 случая:
- Произведение четного числа нечетных функций четно.
- Произведение нечетного числа нечетных функций нечетно.
Пример: Произведение двух нечетных функций
Пусть f(x) = 4x 5 – 8x и g(x) = 5x 3 + x.
И f(x), и g(x) являются нечетными функциями, поскольку они являются полиномами, члены которых имеют нечетные степени x.
График нечетной функции f(x) = 4x 5 – 8x. График нечетной функции g(x) = 5x 3 + x.
Их произведение равно:
- f(x)*g(x)
- =(4x 5 – 8x) + (5x 3 + x) ) и g(x) (x)]
- = 20x 8 + 4x 6 – 40x 4 – 8x 2 [FOIL]
х.
График четной функции
Произведение четной и нечетной функций 90 является нечетной функцией, если ни одна из функций не равна нулю, и в этом случае произведение равно нулю (что является одновременно четным и нечетным).
Чтобы доказать это, предположим, что f(x) — четная функция, а g(x) — нечетная функция.
Тогда f(-x) = f(x) и g(-x) = -g(x). Глядя на их продукт:
- (f*g)(-x)
- =f(-x)*g(-x) [по определению произведения функций]
- =f(x)*-g (x) [поскольку f(x) — четная функция, а g(x) — нечетная функция]
- =-f(x)*g(x)
- =-(f*g)( x)
Поскольку (f*g)(-x) = -(f*g)(x), мы знаем, что (f*g)(x) — нечетная функция.
Пример: Произведение четной и нечетной функций
Пусть f(x) = x 4 – 5 и g(x) = x 5 + 2 шт.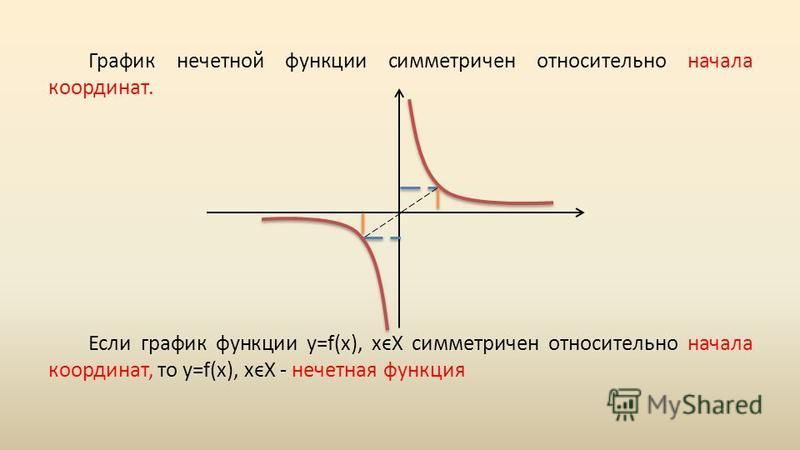
Тогда f(x) — четная функция (многочлен с четными показателями), а g(x) — нечетная функция (многочлен с нечетными показателями).
График четной функции f(x) = x 4 – 5. График нечетной функции g(x) = x 5 + 2x.
Их произведение:
- f(x)*g(x)
- =(x 4 – 5)*(x 5 + 2x) и g (х)]
- =х 9 + 2x 5 — 5x 5 — 10x [Фольга]
- = x — 3x 5 — 10x [Комбинированные термины]
многочлен с нечетными показателями.
График нечетной функции
Заключение
Теперь вы знаете случаи сумм и произведений четных и нечетных функций, а также частные случаи (когда одна или обе функции равны нулю).
Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!
~Джонатон
1.2: нечетные и четные функции
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 106799
- Марсия Левитус
- Университет штата Аризона
Многие из вас наверняка слышали о нечетных и четных функциях в предыдущих курсах, а для тех, кто не слышал, вот краткое введение.
- Нечетная функция подчиняется соотношению (f(x) = −f(−x)). Например, (sin x) нечетно, потому что (sin x = — sin(-x)).
- Четная функция подчиняется соотношению (f(x) = f(−x)).
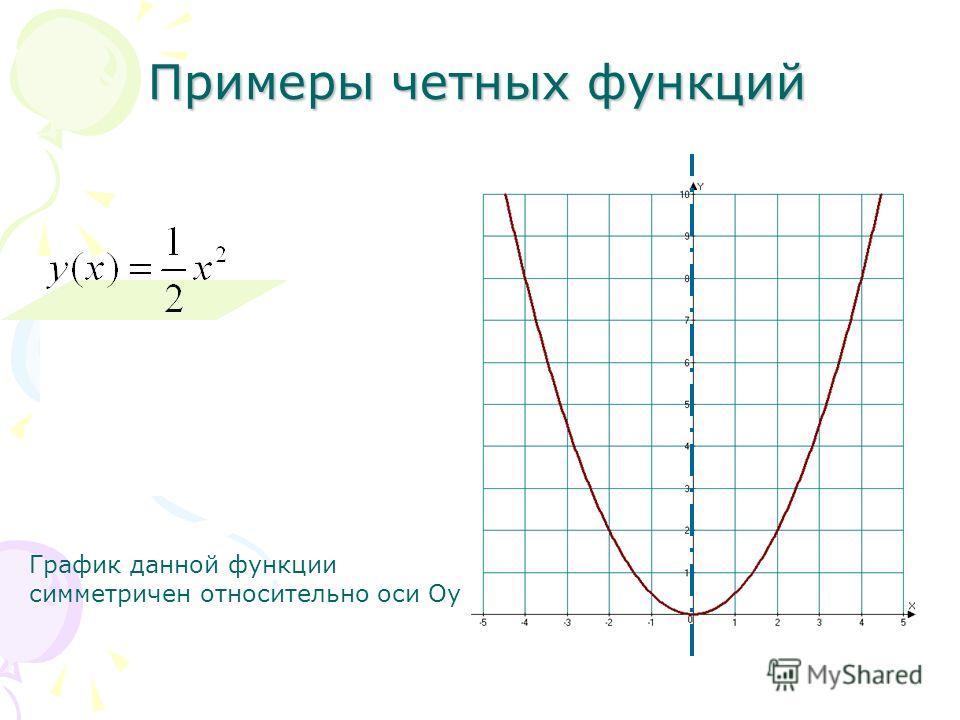 Например, (cos x) четно, потому что (cos x = cos(-x)).
Например, (cos x) четно, потому что (cos x = cos(-x)).
Четные функции симметричны относительно оси Y. Другими словами, если бы вы поместили зеркало перпендикулярно экрану в точке (x = 0), правая сторона графика дала бы отражение, перекрывающееся с левой стороной графика. Посмотрите на рисунок (PageIndex{1}), чтобы убедиться, что вы понимаете, что это значит.
Рисунок (PageIndex{1}): Нечетные и четные функции. (CC BY-NC-SA; Марсия Левитус) 9{а} f(x)dx = 0]
Это должно быть очевидно, если посмотреть на график (sin x). Площадь под кривой между 0 и (a) сокращается с площадью под кривой между (−a) и 0. Это отличная новость, потому что это означает, что нам не нужно беспокоиться об интегрировании нечетных функций до тех пор, пока поскольку пределы интегрирования простираются от (-a) до (a), где a может быть любым числом, включая бесконечность. Как оказалось, это часто происходит в квантовой механике, так что об этом стоит помнить! 92 х) есть произведение двух четных функций и, следовательно, четно.
Рисунок (PageIndex{2}): Произведения нечетных и четных функций. (CC BY-NC-SA; Marcia Levitus)
Нужна помощь в понимании того, как определить нечетные и четные функции? Внешние ссылки:
Нечетное, четное или ни то, ни другое?
Проверьте, сможете ли вы классифицировать функции, показанные в этом коротком тесте.
http://tinyurl.com/l4pehb8
Эта страница под названием 1.2: Нечетные и четные функции распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Марсией Левитус с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или страница
- Автор
- Марсия Левитус
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу Содержание
- нет на странице
-
- Теги
-
- четные функции
- нечетная функция
- источник@https://www.
 public.asu.edu/~mlevitus/chm240/book.pdf
public.asu.edu/~mlevitus/chm240/book.pdf
Калькулятор четных, нечетных или ни одной функции
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:
Просмотрите полный список инструментов dCode
Четная или нечетная функция
Инструмент для проверки четности функции (четные или нечетные функции): он определяет способность функции (ее кривую ) для проверки симметричных отношений.
Результаты
Четная или нечетная функция — dCode
Теги: Функции
Поделиться
dCode и многое другое решать каждый день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор четных и нечетных функций
Выражение функции f(x)= or y=
Переменная
| Я хочу | Проверить, является ли функция четной или нечетной Проверить, является ли функция четной Проверить, является ли функция нечетной Вычислить f(-x ) Вычислить -f(-x) |
См. также: Решатель уравнений
также: Решатель уравнений
Ответы на вопросы (FAQ)
Что такое четность функции? (Определение)
Четность функции – это свойство, придающее кривой характеристики функции симметрию (осевую или центральную).
— Функция чётная, если равенство $$ f(x) = f(-x) $$ верно для всех $ x $ из области определения. Четная функция предоставит идентичное изображение для противоположных значений. Графически это означает, что противоположные абсциссы имеют одинаковые ординаты, это означает, что ось ординат y является осью симметрии кривой, представляющей $f$.
— Функция называется нечетной, если равенство $$ f(x) = -f(-x) $$ верно для всех $ x $ из области определения. Нечетная функция предоставит противоположное изображение для противоположных значений. Графически это означает, что противоположные абсциссы имеют противоположные ординаты, это означает, что начало координат (центральная точка) (0,0) является центром симметрии кривой, представляющей $f$.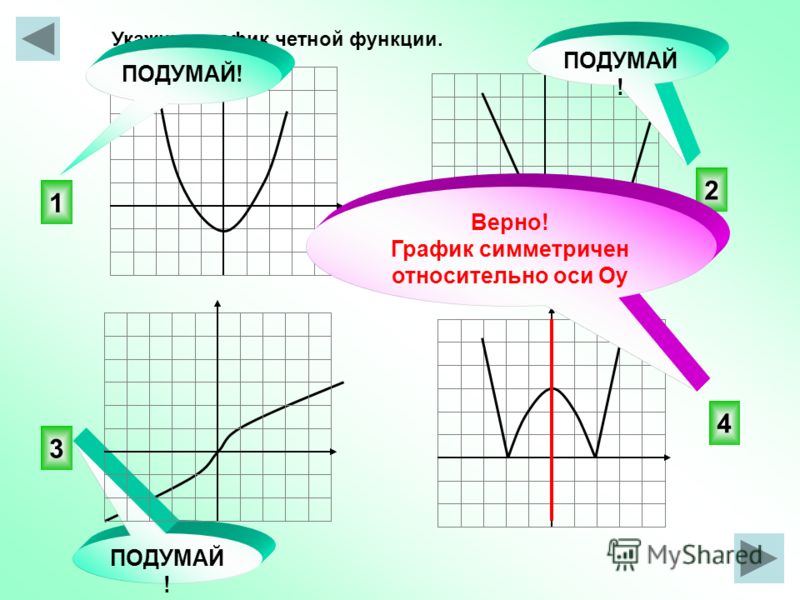 3 = f(x)$, поэтому функция куба $f(x)$ нечетна.
3 = f(x)$, поэтому функция куба $f(x)$ нечетна.
Доказав равенство для единственного значения типа $f(2) = -f(-2)$, мы не можем сделать вывод о наличии нечетности, а лишь можем сказать, что 2 и -2 имеют противоположные образы функцией $f $.
Как проверить, является ли функция ни четной, ни нечетной?
Функция не является ни нечетной, ни четной, если не выполняется ни одно из двух вышеприведенных равенств, то есть: $$ f(x) neq f(-x) $$ и $$ f(x) neq -f (-x) $$
Пример: Определить четность $ f(x) = x/(x+1) $, первое вычисление: $ f(-x) = -x/(-x+1) = x/(x-1) neq f(x) $ и второе вычисление: $ -f(-x) = -(-x/(-x+1)) = -x/(x-1) = x /(-x+1) neq f(x) $, поэтому функция $f $ не является ни четной, ни нечетной.
Какова четность тригонометрических функций (cos, sin, tan)?
В тригонометрии функции часто бывают симметричными:
Функция косинуса $ cos(x) $ четна.
Функция синуса $ sin(x) $ нечетная.
Касательная функция $ tan(x) $ нечетна.
Почему функции называются четными или нечетными?
Развертки в сходящихся степенных рядах или многочленах четных (соответственно нечетных) функций имеют четные степени (соответственно нечетные).
Есть ли функция, которая одновременно является четной и нечетной?
Да, функция $ f(x) = 0 $ (функция с постоянным нулем) является одновременно четной и нечетной, поскольку она соблюдает 2 равенства $ f(x) = f(-x) = 0 $ и $ f(x) = -f(-x) = 0 $
Исходный код
dCode сохраняет право собственности на исходный код «Четная или нечетная функция». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Четная или нечетная функция», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Четного или Odd Function» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т.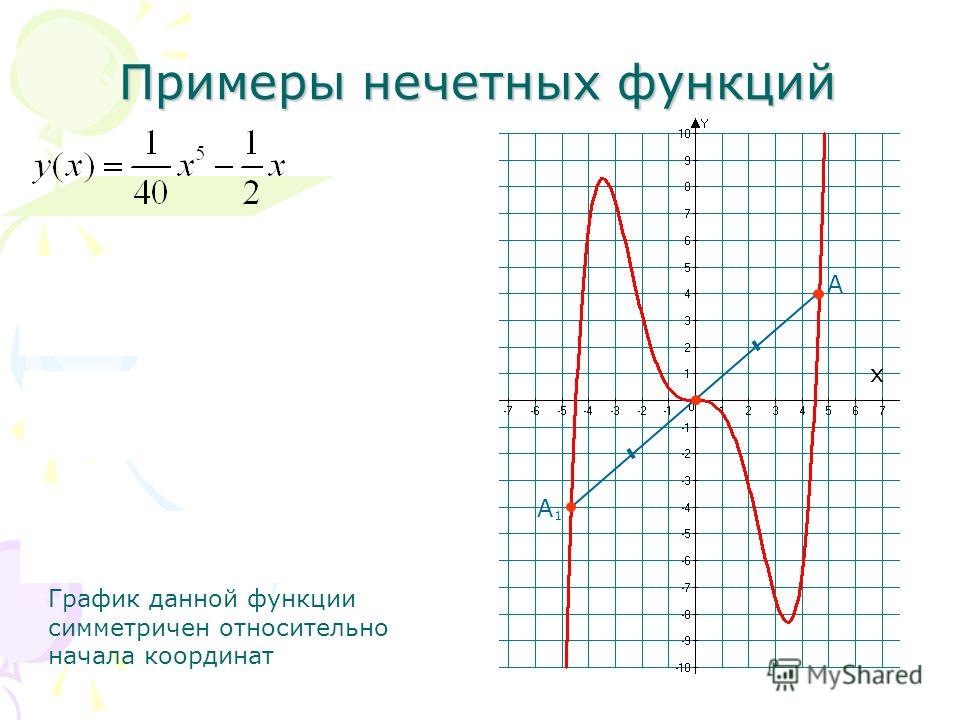 д.) и все данные загрузка, сценарий или доступ к API для «Четной или нечетной функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильном телефоне, планшете, iPhone или в приложении для Android!
д.) и все данные загрузка, сценарий или доступ к API для «Четной или нечетной функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильном телефоне, планшете, iPhone или в приложении для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Четная или нечетная функция» или любых ее результатов разрешена, если вы цитируете dCode!
Цитировать как источник (библиографию):
Четная или нечетная функция на dCode.fr [онлайн-сайт], получено 03 октября 2022 г., https://www.dcode.fr/even-odd-function
Сводка
- Калькулятор четных и нечетных функций
- Что такое четность функции? (Определение)
- Как проверить четность функции?
- Как проверить, является ли функция нечетной?
- Как проверить, является ли функция ни четной, ни нечетной?
- Какова четность тригонометрических функций (cos, sin, tan)?
- Почему функции называются четными или нечетными?
- Есть ли функция, которая одновременно является четной и нечетной?
Похожие страницы
- Решатель уравнений
- Период функции
- N-я производная
- Предел функции
- Polynomial Root
- Reciprocal Function
- Newton Interpolating Polynomial
- DCODE’S TOOLS LIST
Support
- Paypal
- Patreon
- More
Forum/Help
Keywords
even,odd,function ,четность,симметрия,тригонометрический,косинус,синус
Ссылки
▲
Четные и нечетные функции — свойства и примеры
При работе с функциями и графиками вы столкнетесь со случаями, когда функции описываются как четные или нечетные. Если вам интересно четные и нечетные функции, вы только что нашли нужную статью. Начнем с их определения:
Если вам интересно четные и нечетные функции, вы только что нашли нужную статью. Начнем с их определения:
Четные и нечетные функции — это специальные функции, обладающие особой симметрией относительно оси Y и начала координат соответственно.
Зачем нам знать, является ли функция четной или нечетной? Знание этого важного свойства функции может помочь нам:
- Знать поведение графика функции.
- Сэкономьте время на графических функциях и вместо этого применяйте свойства нечетных и четных функций.
- Предсказать природу произведения и суммы двух функций.
Видя, что это может помочь нам работать над следующими темами намного быстрее, мы должны убедиться, что охватываем все аспекты нечетных и четных функций. Начнем с последнего!
Что такое четная функция?
В этом разделе будет подробно изучена даже функция, включая ее определение, свойства и график. Ниже приведены некоторые функции, широко известные как четные функции:
- Функции абсолютного значения
- Косинусоидальные функции
- Большинство функций с четной степенью
Мы сможем понять, почему приведенные выше функции являются четными, после следующих двух разделов.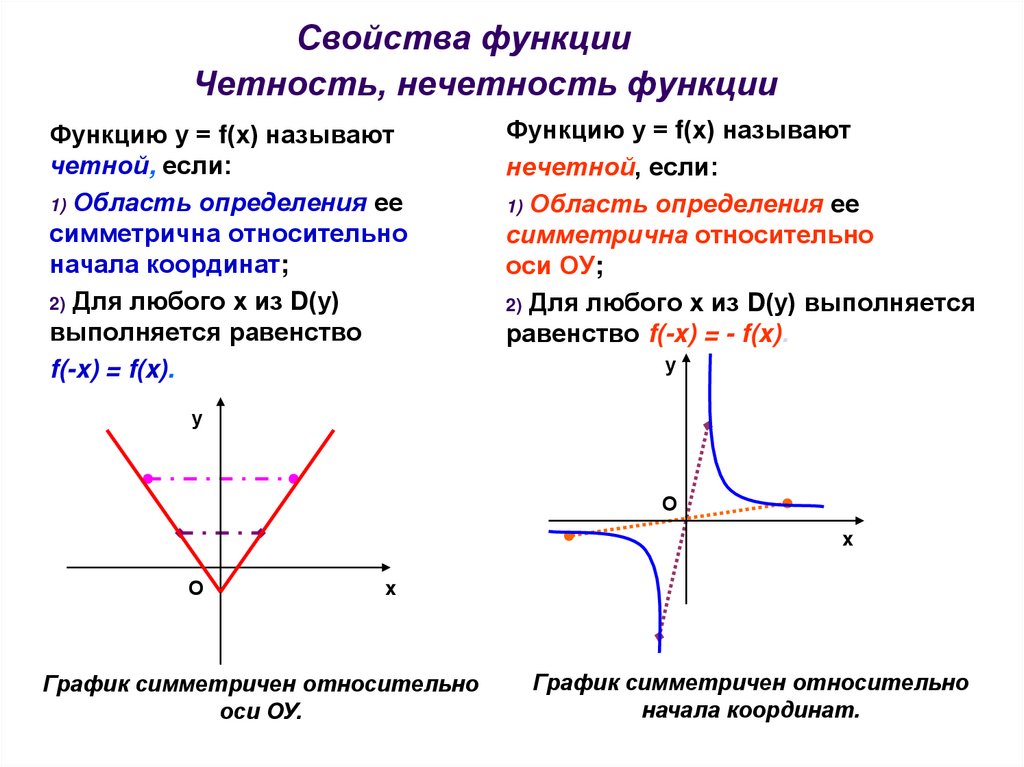 Итак, как мы узнаем, является ли данная функция четной?
Итак, как мы узнаем, является ли данная функция четной?
Определение функции четности
Функции четности — это функции, которые возвращают одно и то же выражение как для x , так и для -x . Это означает, что если f(x) является четной функцией , когда f(-x) = f(x) . Таблица значений четной функции также будет иметь симметричные значения. Квадратичная функция, f(x) = x 2 , — четная функция. Обратите внимание, как это соответствует определению четных функций:
f(-x) = (-x) 2
= x 2
Мы можем видеть, что [x, f(x)] → [-x, f(x)], показывающий, как f(x) удовлетворяет определению четной функции. Теперь взгляните на его таблицу значений.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
As can be seen, x and its значение отрицательного аналога будет иметь те же значения, что сделает каждую половину таблицы идентичной.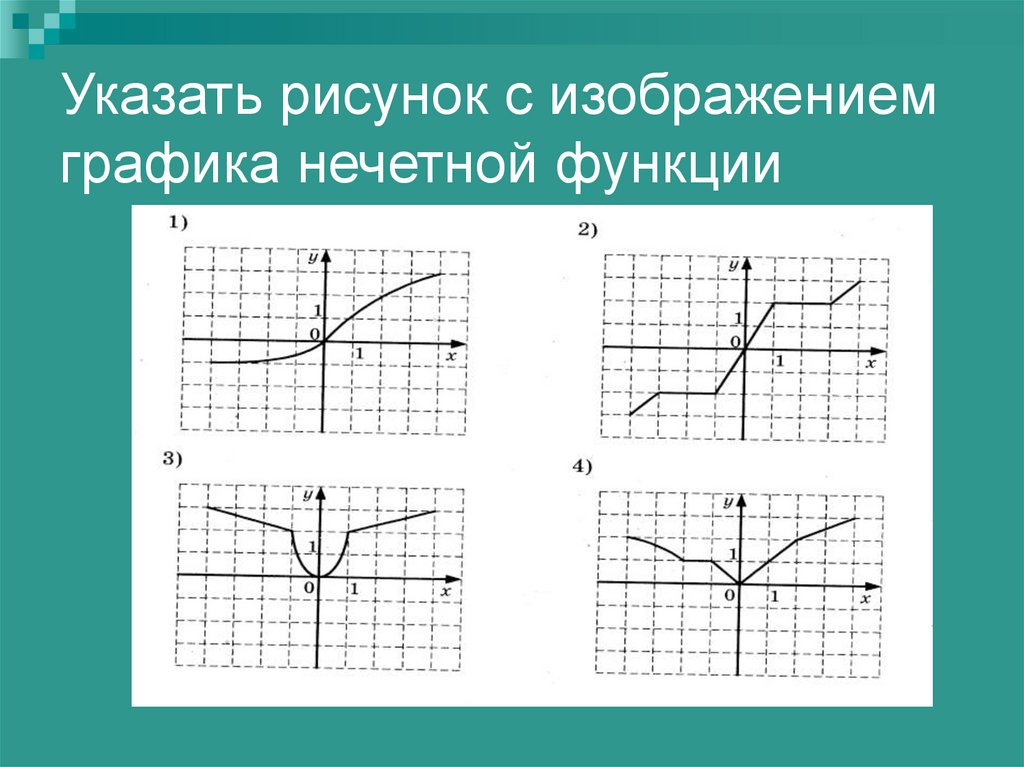
График четной функции и понимание ее симметрии
Поскольку у нас уже есть таблица значений для f(x) = x 2 , , почему бы нам не использовать их для построения графика функции?
На приведенном выше графике показано, что квадратичная функция также симметрична относительно оси Y. Что это значит для нашего движения вперед?
Вы можете построить график половины любых четных функций, а затем отразить его по оси Y. Это экономит нам много времени, поскольку нам нужны только упорядоченные пары для построения графика левой или правой части четной функции.
Почему бы нам не попробовать, построив половину функции абсолютного значения, f(x) = |x| , первый?
| x | 0 | 1 | 2 | 3 | 4 |
| f(x) | 0 | 1 | 4 | 9 | 16 |
Once we’ ve построил правую часть f(x) = |x| , давайте отразим его относительно оси, чтобы показать завершенный график функции.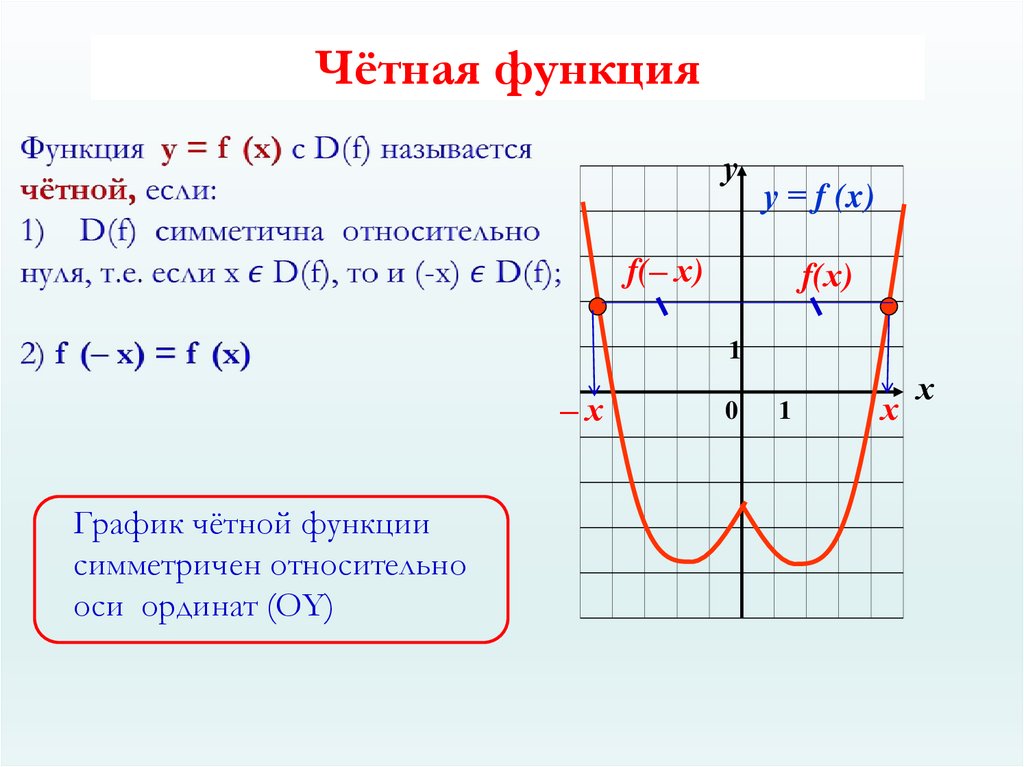
Этот метод построения графиков сэкономит ваше время, особенно при работе с более сложными выражениями. Не забудьте, однако, перепроверить и убедиться, что функция даже.
Что такое нечетная функция?
Теперь, когда мы узнали о четных функциях, пришло время освежить наши знания о нечетных функциях. Вот некоторые из хорошо известных нечетных функций, с которыми вы, возможно, уже сталкивались:
- Обратные функции
- Синусоидальные и тангенсные функции
- Большинство функций с нечетной степенью
Мы поймем, почему упомянутые выше функции являются нечетные функции после следующих двух разделов. Итак, что делает нечетные функции особенными?
Определение нечетной функции
Нечетные функции — это функции, которые возвращают свою отрицательную инверсию при замене x на –x . Это означает, что f(x) является нечетной функцией, когда f(-x) = -f(x) .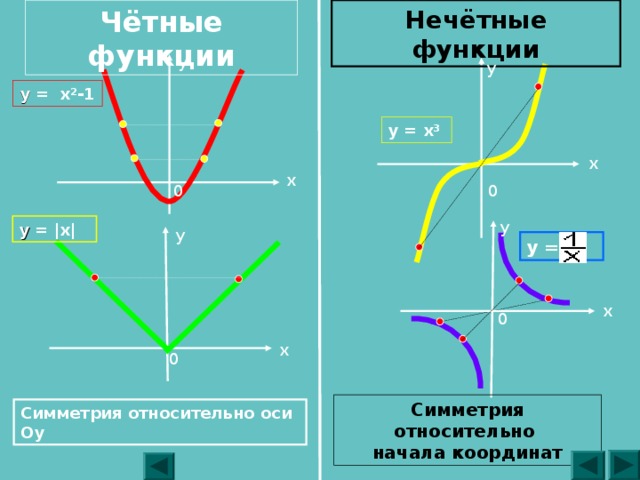 Давайте попробуем наблюдать f(x) = x 3 , нечетную функцию и посмотрим, как это повлияет на ее таблицу значений.
Давайте попробуем наблюдать f(x) = x 3 , нечетную функцию и посмотрим, как это повлияет на ее таблицу значений.
f(-x) = (-x) 3
= – x 3
Это подтверждает, что [x, f(x)] → [-x, -f ]. Таблица значений для f(x) = x 3 , как показано ниже. Заметили некоторые закономерности?
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | -27 | -8 | -1 | 0 | 1 | 8 | 27 |
Видите, как f(1) = -f(1)? Эта закономерность согласуется с остальными значениями. В левой части таблицы показаны отрицательные значения его аналога с правой стороны.
График нечетной функции и понимание ее симметрии
Мы также можем наблюдать, как нечетные функции ведут себя на координате xy , построив график f(x) = x 3 . Используйте таблицу значений, показанную в предыдущем разделе, для построения точек, которые соединят кривую f(x) = x 3 .
Используйте таблицу значений, показанную в предыдущем разделе, для построения точек, которые соединят кривую f(x) = x 3 .
Этот график ясно показывает нам, насколько нечетные функции симметричны относительно начала координат. Мы также можем использовать это свойство, чтобы сократить время, необходимое для построения графика нечетных функций. Хотите увидеть пример? Давайте попробуем построить график f(x) = 1/x .
| x | 1/4 | 1/2 | 1 | 2 | 4 |
| f(x) | 4 | 2 | 1 | 1/2 | 1 /4 |
После построения верхней части обратной функции мы можем отразить ее в начале координат, чтобы завершить график. Посмотрите на пунктирную линию как на руководство того, как мы отражаем графики о происхождении.
Попрактиковавшись на примерах, вы определенно сможете легко строить графики четных и нечетных функций. Давайте всегда не забывать проверять, является ли график нечетным или четным, прежде чем применять соответствующую технику.
Давайте всегда не забывать проверять, является ли график нечетным или четным, прежде чем применять соответствующую технику.
Какими свойствами обладают четные и нечетные функции?
Теперь, когда мы узнали о нечетных и четных функциях, какие еще свойства мы можем наблюдать у этих типов функций?
- Сумма, разность, частное или произведение двух четных функций будут четными. То же самое касается нечетных функций.
- Пример: f(x) = sin x и g(x) = tan x нечетны, поэтому h(x) = sin x + tan x также будет нечетным.
- Состав двух четных функций будет четным. То же правило применимо и к нечетным функциям.
- Пример: f(x) = x 2 и g(x) = cos x четны, поэтому f(g(x)) = (cos x)2 также будет нечетным.
Как определить четная функция или нечетная?
Что, если нам дана функция, и мы не знаем, четная она или нечетная? Это не будет проблемой! Давайте воспользуемся тем, что мы уже узнали, чтобы определить, является ли функция четной или нечетной.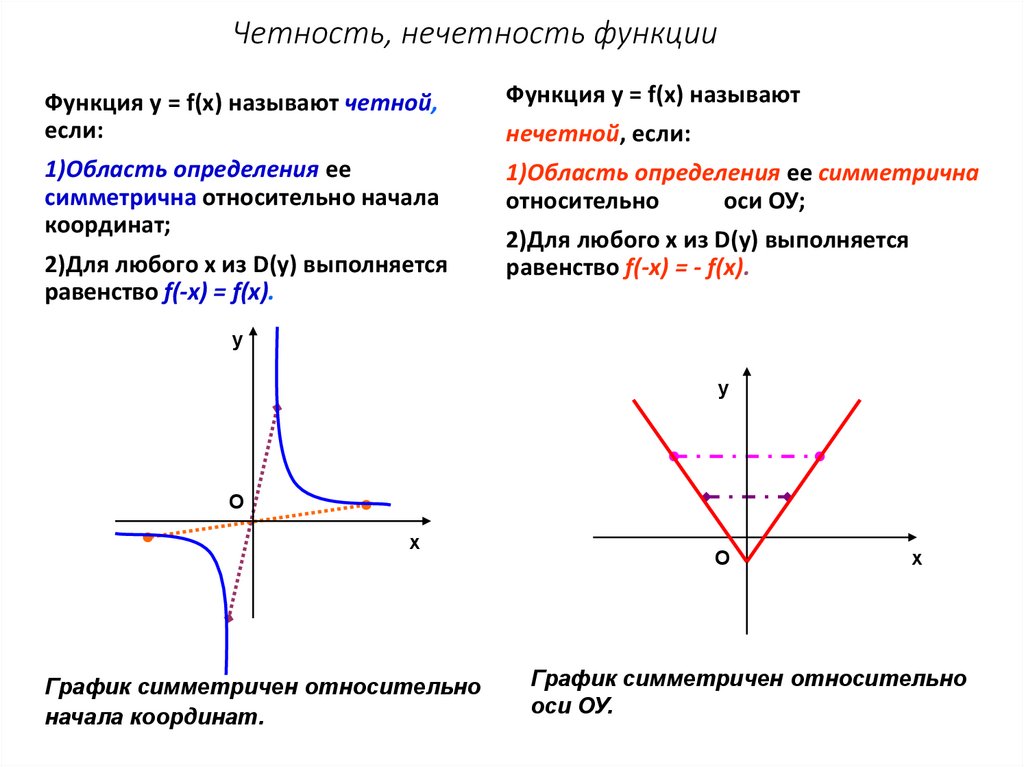
При задании функции : посмотрите, что произойдет, если мы заменим x с –x .
- Когда вы подставили –x в f(x), функция осталась прежней? Если да, то f(x) четно.
- Когда вы подставили –x в f(x), изменился ли знак коэффициента функции? Если да, то f(x) нечетно.
При наличии графика : определить, является ли график симметричным относительно начала координат или оси Y.
- Если график симметричен относительно оси y , функция равна даже . как нам это сделать?
- Представьте, что вы складываете график по вертикали и смотрите, будут ли два графика лежать рядом друг с другом.
- Вы также можете определить несколько точек и посмотреть, имеют ли x и –x одну и ту же координату.
- Если график симметричен относительно начала координат , функция нечетная .
 как нам это сделать?
как нам это сделать?
- Представьте, что сложите график по диагонали (проверьте оба направления) и посмотрите, будут ли два графика лежать рядом друг с другом.
- Вы также можете найти несколько точек и посмотреть, разделяют ли x и –x y-
Существуют ли функции, которые не являются ни нечетными, ни четными?
Должны ли все функции быть четными или нечетными? Нет. Бывают случаи, когда функция не соответствует ни четным, ни нечетным функциям. Функция f(x) = (x + 1) 2 является примером функции, которая не является ни нечетной, ни четной.
Давайте продолжим и посмотрим на выражение для f(-x) :
f(x) = (x + 1) 2
f(-x) = (-x + 1) 2
= (1 – x) 2
= 1 – 2x + x 2
Сравните это выражение с расширенной формой f(x) и –f(x).
| Проверка нечетной функции: f(-x) = -f(x) | Проверка четной функции: f(-x) = f(x) |
|
-f(x) = — (х + 1) 2 =-(х 2 + 2х + 1) =-x 2 – 2x – 1 f(-x) ≠ -f(x) |
f(x) = (x + 1) 2 =x 2 + 2 + 1 f(-x) ≠ f(x)
|
Это показывает, что такая функция, как f(x) = (x + 1) 2 , не может быть ни нечетной, ни четной.
Если вы посмотрите на график f(x) , вы увидите, что он не симметричен относительно начала координат или оси Y. Это еще раз подтверждает, что функция не является ни нечетной, ни четной.
Вот так мы рассмотрели все основные темы по четным и нечетным функциям. Со всеми свойствами, правилами и определениями, которые мы только что изучили, мы теперь готовы работать над дополнительными примерами, чтобы понять еще больше и странные функции.
Пример 1
Заполните пропуск либо нечетным , либо четным , чтобы следующие утверждения были верными.
- Функции f(x) и g(x) являются четными функциями, поэтому их сумма также будет _________ функцией.
- Композиция f(x) и g(x) возвращает нечетную функцию, поэтому и f(x), и g(x) являются _________ функциями.
- Абсолютное значение нечетной функции является _____________ функцией.
Решение
- Сумма двух четных функций также будет четным .

- Состав двух нечетных функций также будет нечетным .
- Предположим, что f(x) нечетно, поэтому f(-x) равно -f(x). Взятие абсолютного значения этой функции возвращает f(x) обратно. Это означает, что функция даже .
Пример 2
Определите, F (x) , G (x) и H (x) — даже или нечетные функции, использующие их Tables of Tables of T. значения, показанные ниже.
а.
17
17
17
| x | -4 | -2 | 0 | 2 | 4 |
| F (x) | |||||
| F (x) | |||||
| F (x) | |||||
| F (x) | |||||
| F (x) | |||||
| F (x) | |||||
| F (X)0852 5 | 17 |
17 17
б.
| x | -3 | -1 | 0 | 1 | 3 |
| f(x) | 18 | 4 | 1 | 4 | 18 |
в.
| x | -4 | -2 | -1/2 | 0 | 1/2 | 2 | 4 |
| h(x) | -64 | -8 | -1/8 | 0 | 1/8 | 8 | 64 |
. Равны ли соответствующие значения? Являются ли значения слева отрицательными значениями справа?
- Мы видим, что таблица значений для f(x) показывает одинаковые значения для f(-x) и f(x), функция четная.
- То же самое можно сказать и о значениях, показанных для g(x), так что функция четная.
- В левой части таблицы отрицательные значения той, что сбоку, поэтому функция нечетная.
Пример 3
Определите, являются ли следующие функции четными, нечетными или ни теми, ни другими.
- f(x) = x 2 – 1
- g(x) = |x -1|
- h(x) = -3x 5
Решение
Замените x на -x и проверьте выражение функции. Если f(-x) возвращает ту же функцию, мы можем сделать вывод, что функция четная. Если он возвращает ту же функцию, но с коэффициентами, имеющими разные знаки, он нечетный.
Если f(-x) возвращает ту же функцию, мы можем сделать вывод, что функция четная. Если он возвращает ту же функцию, но с коэффициентами, имеющими разные знаки, он нечетный.
- Проверим первую функцию, f(x) = x 2 – 1.
f(-x) = (-x) 2 – 1
– 6 x 5
Так как f(-x) возвращает то же самое выражение для f(x), функция четна .
Используя тот же процесс для b и c, мы получаем следующие результаты.
2.
g(-x) = |x – 1|
= |-х – 1|
= |-(х + 1)|
=|х + 1|
Поскольку g(-x) не равно ни g(x), ни -g(x), g(x) равно ни нечетному, ни четному .
3.
H (-x) = -3 (-x) 5
= -3 (-x 5 )
= 3x 5
=-(-3x 5 )
Мы видим, что h(-x) = -h(x), поэтому h(x) является нечетной функцией .
Пример 4
Определите, являются ли следующие функции четными, нечетными или ни тем, ни другим, изучив графики следующих функций.
а.
б.
в.
Решение
Имея график, мы можем идентифицировать нечетные и четные функции на основе симметрии графика.
- Первый график показывает, что он симметричен относительно оси Y , поэтому это четная функция .
- Второй график показывает, что он симметричен относительно начала координат , поэтому это нечетная функция .
- Поскольку третий график не симметричен относительно начала координат или оси Y , это ни нечетное , ни четное .
Пример 5
Дополните приведенную ниже таблицу, используя свойства функций.
- Функция f(x) нечетная.
| x | -1 | -1/2 | -1/4 | 1/2 | 1/4 | 1 |
| f(x) | -2 | -4 | -8 |
2.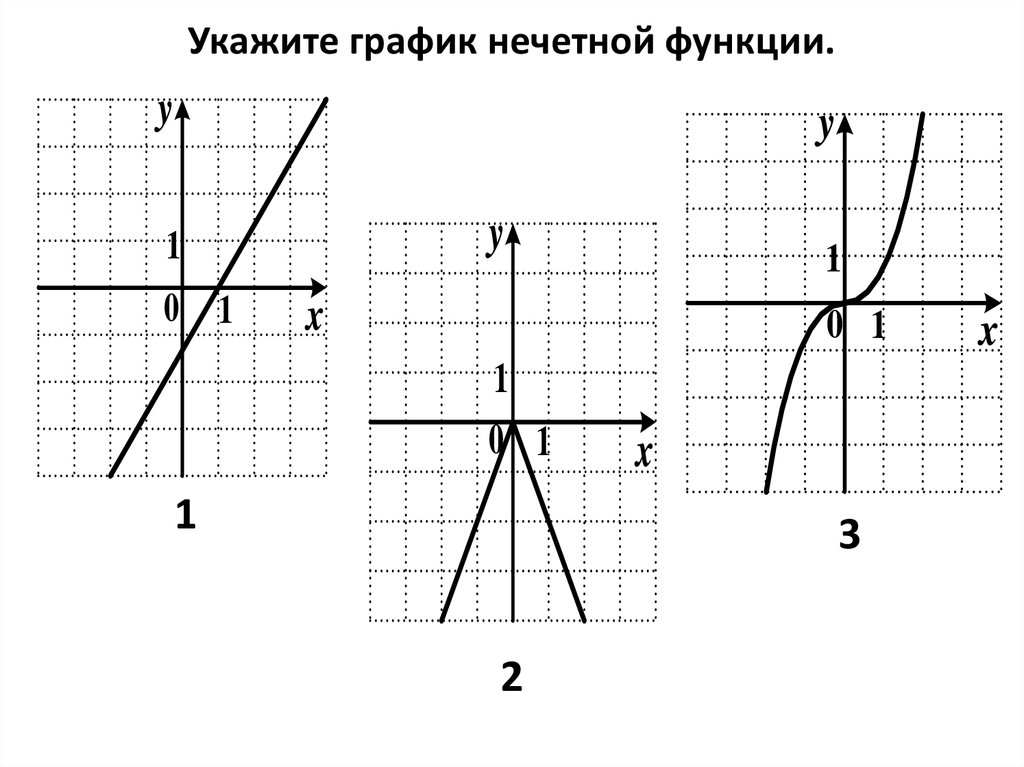 Функция f(x) четна.
Функция f(x) четна.
| x | -3 | -1 | 0 | 1 | 3 |
| f(x) | -6 | -5 | -3 |
Решение
- Поскольку функция нечетная, мы заполняем незаполненные значения отрицательными обратными значениями -2, -4 и -8. Следовательно, у нас есть 2, 4 и 8.
- Поскольку функция четная, мы заполняем незаполненные значения, которые будут такими же, как f(1) и f(3). Следовательно, у нас есть 3 и 1.
Пример 6
Используйте приведенную ниже таблицу значений и тот факт, что f(x) четно графику f(x).
| x | -3 | -2 | -1 | 0 |
| f(x) | 0 | -2 | -4 | -6 |
Решение
Давайте продолжим и сначала нанесем точки. Соедините их, чтобы построить график части f(x).
Соедините их, чтобы построить график части f(x).
Помните, что f(x) — четная функция. Его график будет симметричен относительно оси Y. Это означает, что для завершения графика f(x) мы отражаем график относительно оси y.
График выше показывает полный график функции f(x). Вы также можете убедиться в этом, визуализировав оставшуюся половину графика функции, «свернув» график по оси Y.
Это показывает, что понимание свойств нечетных и четных функций может сэкономить нам время при решении задач и построении графиков функций.
Интегралы четных/нечетных функций — Photomath
Исследовать интегралы
Мы уже знаем, что представляют собой интегралы и как решать неопределенные и определенные интегралы, но задумывались ли вы когда-нибудь, что произойдет, если нам нужно найти интеграл четной или нечетной функции? Упростят ли эти свойства вычисление интегралов?
Давайте выясним.
Что такое интеграл четной/нечетной функции?
Прежде чем объяснять интегралы от четных и нечетных функций, напомним себе, что вообще такое четные и нечетные функции.
Функция $$f$$ четна, если для каждого $$x$$ в ее области определения верно следующее:
$$f(-x)=f(x)$$
График четного функция симметрична относительно оси $$y$$.
Функция $$f$$ нечетна, если для каждого $$x$$ в ее области определения верно следующее: 9{a}{f(x),dx}=0$$
Важно помнить, что это работает, только если интеграл вычисляется на замкнутом интервале, симметричном относительно нуля. Имейте это в виду на потом!
Дальнейшая оценка этих интегралов осуществляется с помощью наших обычных подозреваемых: специальные методы или свойства интегралов.
Вот наша любимая таблица, которую следует держать рядом при работе с интегралами:
| Постоянное кратное свойство интегралов | $$int{(ctimes f(x))}dx=ctimes int{f(x)}dx$$ |
| Правило сумм для интегралов | $$int{(f(x) + g(x))}dx=int{f(x)}dx + int{g(x)}dx$$ |
| Правило разности интегралов | $$int{(f(x) — g(x))}dx=int{f(x)}dx — int{g(x)}dx$$ |
| Сборка по частям | $$int{u}dv=uv-int{v}du$$ |
9{ простое число} (t) dt = int {f (x)} dx $ $
Почему интегралы от четных/нечетных функций так полезны?
Когда у нас есть симметричный интервал, знание того, является ли функция четной или нечетной, может значительно упростить вычисление интеграла! Например, предположим, что мы хотим вычислить $$int_{-1}^{1}x$$.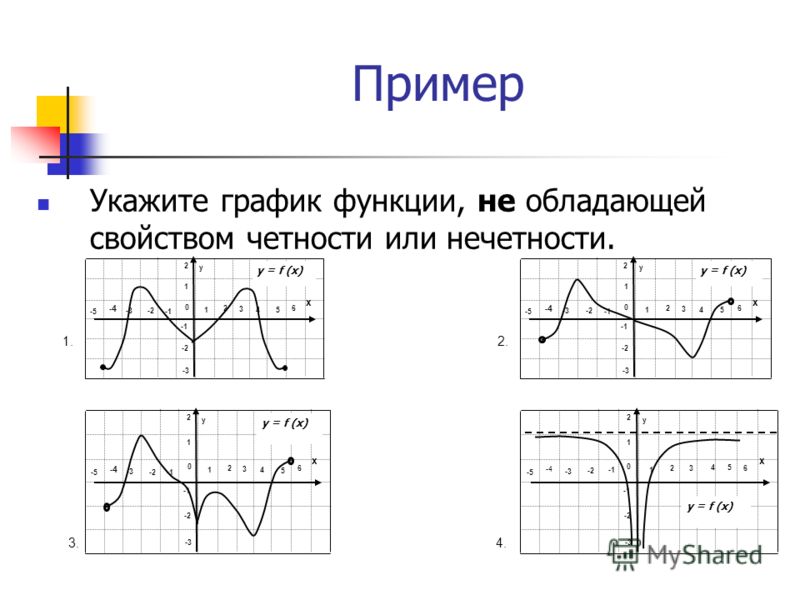 Вместо того, чтобы проводить весь расчет, проще просто сделать вывод, что функция $$f(x)=x$$ нечетна, а значит, результатом будет $$0$$. 9{pi}sin({x})dx$$
Вместо того, чтобы проводить весь расчет, проще просто сделать вывод, что функция $$f(x)=x$$ нечетна, а значит, результатом будет $$0$$. 9{pi}sin({x})dx$$
Определить, является ли функция четной, нечетной или ни одной:
$$f(x)=sin(x)$$
Подставить $$- x$$ for $$x$$:
$$f(-x)=sin(-x)$$
Упростите выражение, используя тождество для функции синуса, $$sin(-x) =-sin(x)$$:
$$f(-x)=-sin(x)$$
Используйте исходное уравнение $$f(x)=sin(x)$$ для замены $$f(x)$$ для $$sin(x)$$:
$$f(-x)=-f(x)$$
Поскольку $$f(-x)=-f( x)$$, мы знаем, что функция нечетная: 93}{3}$$
Упростите выражение:
$$frac{2}{3}$$
Мы сделали это!
Нужен краткий обзор наших шагов по решению? Вот он:
Резюме исследования
- Определить, является ли функция четной, нечетной или ни той, ни другой.
-
Если функция нечетная и верхний и нижний пределы противоположны, интеграл равен нулю.

91 |х| дх$$
Решения:
- $$frac{64}{5}$$
- $$0$$
- $$0$$
- $$1$$
Если вы все еще боретесь с процессом решения, ничего страшного! Несколько раз спотыкаться полезно для обучения. Если вы слишком застряли или заблудились, отсканируйте проблему с помощью приложения Photomath, и мы проведем вас на другую сторону!
Вот краткий обзор того, что вы увидите:
00:00
/
00:00
Есть домашнее задание по математике?
Зайдите в приложение Photomath, чтобы быстро найти пошаговые решения всех ваших математических задач.
Четные и нечетные функции ‹ OpenCurriculum
Цели статьи
Введение
Четные и нечетные функции имеют значение в графическом анализе, особенно тригонометрических функций.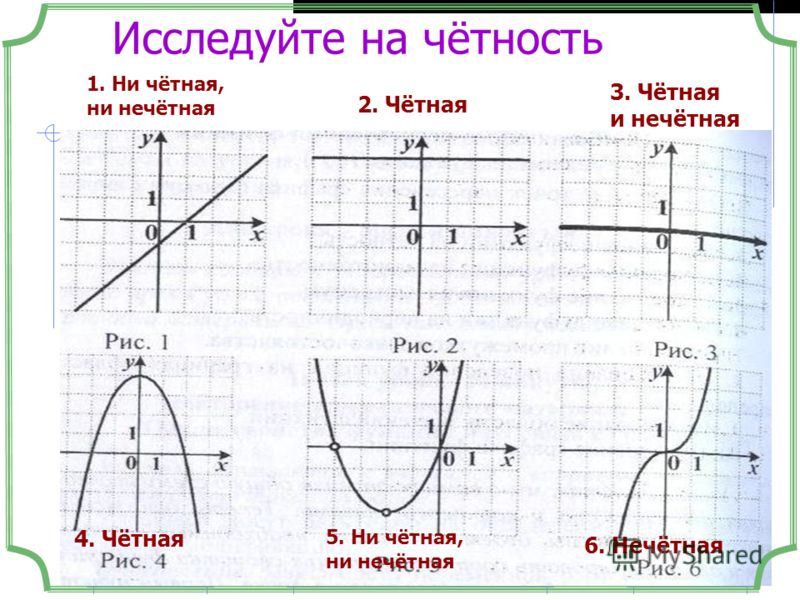 Концепция относительно проста и основана на определенных симметриях графов. 97$$
Концепция относительно проста и основана на определенных симметриях графов. 97$$
Косинус — четная функция. Достаточно интересно:
Функция синуса является нечетной функцией, потому что она симметрична относительно начала координат.
Объединение двух классов
Во многих задачах придется работать как с четными, так и с нечетными функциями. Вот несколько примеров.
Пример 3: Какая функция (в декартовой системе координат) является одновременно четной и нечетной?
Решение: Так как четные функции определены как
$$f(-x) = f(x)$$
и нечетные функции определяются как
$$f(-x) = -f(x),$$
переходным свойством равенства , мы можем заменить, чтобы получить
$$f(x) = -f(x)$$
Единственная функция, которая удовлетворяет этому уравнению, $$f(x) = 0.$$ Графическое изображение функции подтверждает, что она бывает и четным, и нечетным.
Пример 4: Основываясь на графике (f(x) = sqrt{x}), почему оно не может быть четным или нечетным?
Решение: (f(x)) определено только для неотрицательных чисел, что означает, что на графике (f(x)) на декартовой плоскости все пространство слева от y- ось полностью пуста.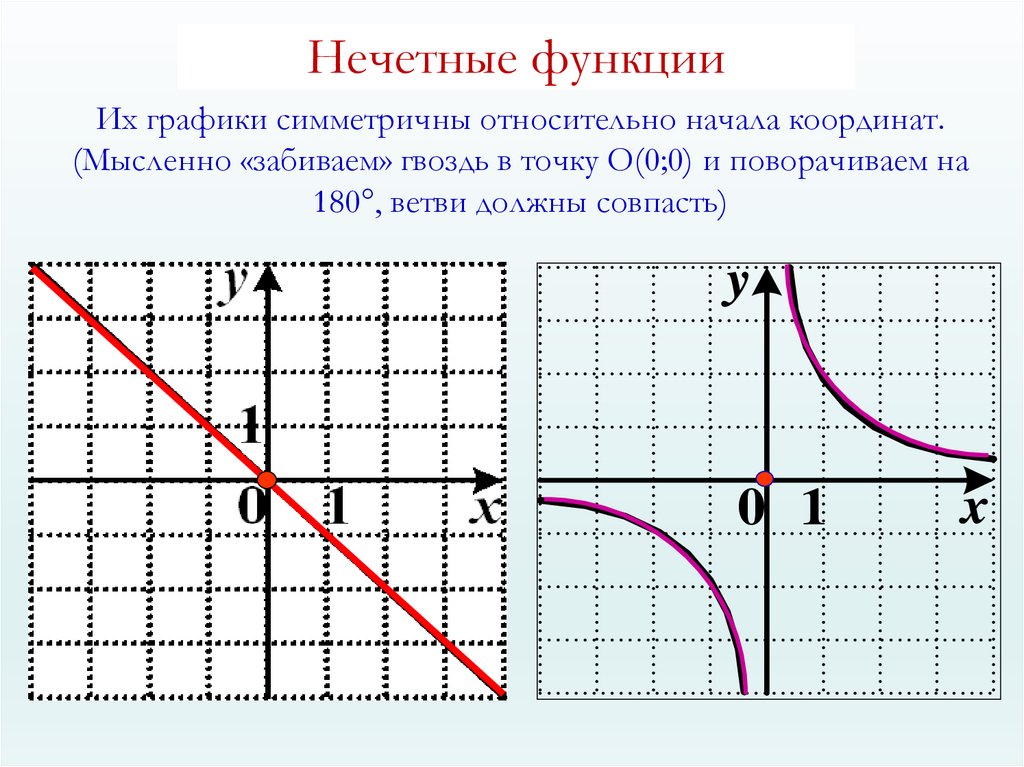 Следовательно, график не может быть симметричным относительно оси Y или начала координат, а также не является четным или нечетным.
Следовательно, график не может быть симметричным относительно оси Y или начала координат, а также не является четным или нечетным.
Следующая пара примеров показывает пару интересных свойств четных и нечетных функций.
Пример 5: Покажите, что произведение двух нечетных функций является четной функцией.
Решение: Пусть (h(x)) определено так, что
$h(x) = f(x) cdot g(x)$$
Тогда из постановки задачи следует следующие три утверждения, основанные на определениях четных и нечетных функций:
$$h(-x) = h(x)$$
$$f(-x) = -f(x)$$
$$g(-x) = -g(x)$$
Мы хотим доказать, что произведение двух нечетных функций равно четной функции, поэтому составим уравнение, представляющее это:
$$h(-x) = f(-x) cdot g(-x) )$$
(h(x)) является четной функцией, поэтому это уравнение принимает вид
$$h(x) = f(-x) cdot g(-x)$$
Так как ( f(x)) и (g(x)) — нечетные функции, аналогичную замену можно сделать в правой части уравнения:
$$h(x) = -f(x) cdot -g(x) Rightarrow$$
$$h(x) = f(x) cdot g(x)$$
Это исходный оператор, который мы использовали для определения трех функций в терминах друг друга; поэтому наша теорема верна.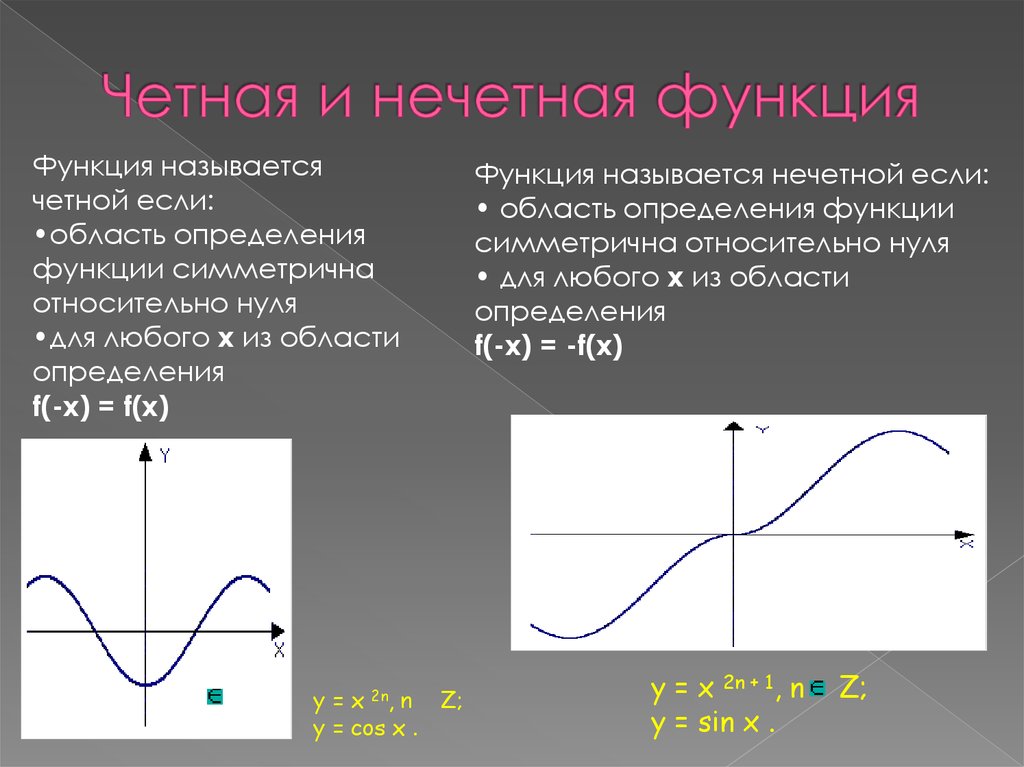
������� ������
�������� �����: ���������� ������ �� �����, ������� ������ ����������.
���������� ������ �� ����� a — ��� ����� �����, ������� �������� (��������� ��������� �� ����) ����� a, �� ���� ������� ��������� x2 = a ������������ ���������� x
���������� ������ ��� ������������ �������
������ ������� $$y = sqrt{x}$$
���������� ������ �������� ����� ������� $$ sqrt{x}$$ ������������ ���������� x, ������� ������� $$xge 0$$ ������ � ������������ �������������� �������� �����.
�������� ������� $$y = sqrt{x}$$
- ������� ����������� – ��� $$[�;+infty)$$.
��� ������� ��, ���� ��� ��������� $$ sqrt{x}$$ ���������� ���� ��� $$x ge 0$$. - ������� $$y = sqrt{x}$$ �� �����, �� �������.
- ������� $$y = sqrt{x}$$ ���������� �� ���� $$[�;+infty)$$.
�������� ������� $$y = root 3 of {x}$$
- ������� ����������� ������� $$y = root 3 of {x}$$ – ��� �������� ������
- ������� $$y = root 3 of {x}$$ �������, ��� ��� $$root 3 of {-x}= – root 3 of {x}$$.
- ������� $$y = root 3 of {x}$$ ���������� �� ���� �������� ������.
������� $$y = root n of {x}$$.
- ��� ������ n ������� $$y = root n of {x}$$ �������� ���� �� ����������, ��� � ������� $$y = sqrt{x}$$ � ������ �� ���������� ������ ������� $$y = sqrt{x}$$.
- ��� �������� n ������� $$y = root n of {x}$$ �������� ���� �� ����������. ��� � ������� $$y = root 3 of {x}$$, � ������ �� ���������� ������ ������� $$y = root 3 of {x}$$.
��������� ������� � ������������� ������� �����������.
��������� ������� � ������������� ������� ����������� ��� �������, �������� �������� y = xr, ��� r – ������������� ������������ �����.
�������� ������� y = xr:
- ������� ����������� – ��� $$[�;+infty)$$.
- ������� ������ ����, �.�. �� ������, �� ��������.
- ������� y = xr ���������� �� $$[�;+infty)$$.
�� ������ ������ ������� y = x5/2, �������� ����� ��������� ������� y = x2 � y = x3, �������� �� ����������
$$[�;+infty)$$.
�������� ��� ����� ����� ������ ������� ���� y = xr, ��� r > 1, � ������ ����� ��������� ������� y = xr, ��� 0< r <1 ����� ��� ������� �� ������ y = x2/3.
��������� ������� � ������������� ������� �����������.
��������� ������� � ������������� ������� ����������� ��� �������, �������� �������� y = x – r,
��� r – ������������� ������������ �����.
�������� ������� y = x – r:
- ������ ����������� – ���������� $$(�;+infty)$$.
- ������� ������ ����, �.�. �� ������, �� ��������.
- ������� y = x – r ������� �� $$(�;+infty)$$.
- ������ ������� y = x – r ������� ����� ���������, ����������� �� ������������� ��������� ��������� �������.


